-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2024; 14(3): 67-69
doi:10.5923/j.ijtmp.20241403.01
Received: Jun. 10, 2024; Accepted: Jun. 22, 2024; Published: Jun. 24, 2024

Does Linearity of the Lorentz Transformation Follow from the two Postulates of Special Relativity
Edward P. Krisner
Department of Mathematics, University of Pittsburgh at Greensburg, Greensburg, USA
Correspondence to: Edward P. Krisner, Department of Mathematics, University of Pittsburgh at Greensburg, Greensburg, USA.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

One would be hard pressed to find a derivation of the Lorentz transformation (LT) that uses only the two postulates of special relativity, and that is entirely mathematically rigorous. Most, if not all, derivations presume that, in addition to the two postulates, the LT has a particular form such as linearity.We will give several examples of such derivations from several esteemed textbooks. We will also discuss how Einstein derived the LT in his revolutionary 1905 paper, “On the Electrodynamics of Moving Bodies.” Then, we will provide a rigorous derivation of the LT using only the two postulates.
Keywords: Lorentz Transform, Mathematically Rigorous Derivation, Special Relativity, Postulates of Relativity
Cite this paper: Edward P. Krisner, Does Linearity of the Lorentz Transformation Follow from the two Postulates of Special Relativity, International Journal of Theoretical and Mathematical Physics, Vol. 14 No. 3, 2024, pp. 67-69. doi: 10.5923/j.ijtmp.20241403.01.
Article Outline
1. Introduction
- It is well known that two inertial frames in special relativity are related via the LT. What appears to be unknown is how to derive the LT without making any additional assumptions about the form of the transformation. In most cases, authors presume that the transformation is linear, i.e., that it has the form
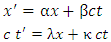 | (1) |
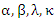 are constants to be determined. As will be elaborated upon in the following section, some authors will, at best, give a “hand-waving” argument as to why the transformation is linear. Failure to provide a rigorous proof of why the two postulates imply linearity leaves open the possibility that there may be a nonlinear transformation that is consistent with the two postulates. Our ultimate goal is to eliminate nonlinearity as a possibility. In the following section we will discuss several example derivations of the LT that appear in the literature. Subsequently, we will provide a rigorous proof that the LT is a consequence of the two postulates without making any additional assumptions.
are constants to be determined. As will be elaborated upon in the following section, some authors will, at best, give a “hand-waving” argument as to why the transformation is linear. Failure to provide a rigorous proof of why the two postulates imply linearity leaves open the possibility that there may be a nonlinear transformation that is consistent with the two postulates. Our ultimate goal is to eliminate nonlinearity as a possibility. In the following section we will discuss several example derivations of the LT that appear in the literature. Subsequently, we will provide a rigorous proof that the LT is a consequence of the two postulates without making any additional assumptions. 2. Example Derivations
- Let us first describe the familiar setting that is common to all of the examples that we intend to discuss. Consider two inertial frames,
 and
and  . We’ll assume that the
. We’ll assume that the 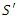 frame is moving at a speed
frame is moving at a speed 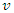 in the direction of increasing values of
in the direction of increasing values of 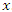 . Moreover, our derivation will be based on the conventional that
. Moreover, our derivation will be based on the conventional that 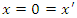 whenever
whenever 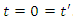 .Since there is no motion in either the
.Since there is no motion in either the 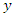 or
or 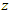 direction it is taken that
direction it is taken that 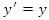 and
and 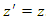 . So all that remains to determine the interrelatedness between
. So all that remains to determine the interrelatedness between 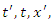 and
and 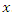 .
.2.1. Spacetime Physics
- Arguably, Spacetime Physics by Taylor and Wheeler, [1], is among one of the most popular texts on special relativity. On page 100, it is asserted that the LT has the form (1). Let us now discuss the argument given in [1] of why the two reference frames are related via a linear transformation. An observer at rest in frame S observes three events that occur in the same spatial location at three equally spaced times, say t=1, t=2, and t=3. The time dilation formula,
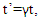 was previously established with rigor. Hence, an observer at rest in S’ will also see these same three events occur at equally spaced times,
was previously established with rigor. Hence, an observer at rest in S’ will also see these same three events occur at equally spaced times, 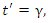
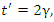 and
and 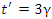 .Subsequently, the transformation given by
.Subsequently, the transformation given by 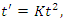 where
where 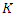 is a constant, is considered. Under this particular transformation, the authors demonstrate that an observer in
is a constant, is considered. Under this particular transformation, the authors demonstrate that an observer in 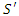 does not see the three events occurring at three equally spaced times. The fact that equally spaced times in one frame yields equally spaced times in the other may indeed only be possible if the frames are related via a linear transformation. But to provide a rigorous proof, the task of ruling out an arbitrary nonlinear transformation must be completed.
does not see the three events occurring at three equally spaced times. The fact that equally spaced times in one frame yields equally spaced times in the other may indeed only be possible if the frames are related via a linear transformation. But to provide a rigorous proof, the task of ruling out an arbitrary nonlinear transformation must be completed. 2.2. Hyperbolic Trigonometric Functions
- The invariance of the speed of light leads to the equation
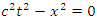 | (2) |
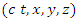 are the coordinates of an arbitrary inertial reference frame. This motivates the likes of [2] and [3] to consider a transformation of the form
are the coordinates of an arbitrary inertial reference frame. This motivates the likes of [2] and [3] to consider a transformation of the form 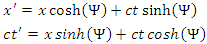 | (3) |
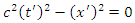 follows from both (2) and (3). However, once again, we have a situation whereby
follows from both (2) and (3). However, once again, we have a situation whereby 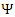 is tacitly assumed to be independent of both
is tacitly assumed to be independent of both 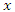 and
and 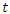 . So not only is (3) a linear transformation, it’s a linear transformation of a particular form. It’s worth re-emphasizing that we are not arguing that the (3) is incorrect. We will ultimately prove that it is correct. But if
. So not only is (3) a linear transformation, it’s a linear transformation of a particular form. It’s worth re-emphasizing that we are not arguing that the (3) is incorrect. We will ultimately prove that it is correct. But if 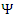 is simply assumed to be independent of
is simply assumed to be independent of 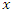 and
and 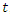 , then a transformation of the form (3) in which
, then a transformation of the form (3) in which 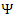 depends on
depends on 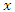 and/or
and/or 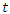 remains possible. It is worth pursuing the argument presented in [2] a bit further. In letting
remains possible. It is worth pursuing the argument presented in [2] a bit further. In letting 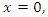 it follows from (3) that
it follows from (3) that 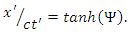 But
But 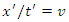 is the velocity of
is the velocity of 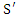 relative to the
relative to the 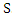 . Thus,
. Thus, 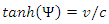 | (4) |
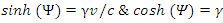 | (5) |
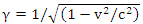 is known as the Lorentz factor.Substituting (5) into (3) yields the familiar LT. The drawback of this approach is that there’s still no guarantee that
is known as the Lorentz factor.Substituting (5) into (3) yields the familiar LT. The drawback of this approach is that there’s still no guarantee that 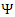 is independent of x and t. For example, in choosing
is independent of x and t. For example, in choosing 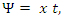 the above argument can be implemented to draw the same conclusion.
the above argument can be implemented to draw the same conclusion. 2.3. Special Relativity & Classical Field Theory
- Next, we discuss [4] which is one of four books of Susskind and Friendman’s “The Theoretical Minimum” series. They begin by pointing out that
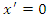 if and only if
if and only if 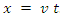 . This is certainly true in the way we described the frames
. This is certainly true in the way we described the frames 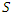 and
and 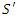 . Then they claim that
. Then they claim that 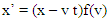 | (6) |
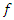 is a function to be determined. Clearly, (6) certainly implies that
is a function to be determined. Clearly, (6) certainly implies that 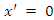 if and only if
if and only if 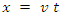 . The converse, however, is not true. As a random example,
. The converse, however, is not true. As a random example, 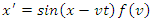 also ensures that
also ensures that 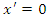 if and only if
if and only if 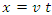 . Yet again we have a situation in which prior knowledge of the LT is used to derive the LT.
. Yet again we have a situation in which prior knowledge of the LT is used to derive the LT. 2.4. On the Electrodynamics of Moving Bodies
- On page 6 of [5], it is written “In the first place it is clear that the equations must be linear on account of the properties of homogeneity which we attribute to space and time.” There are two points to be made about this assertion. The first is that Einstein is now going beyond his two postulates to support his claim. Secondly, it isn’t immediately clear how homogeneity guarantees that two inertial reference frames are related linearly. A common definition of the term homogeneous is that there is no special place in the universe. More precisely, at any given point in time, the universe is everywhere the same assuming that we consider sufficiently large spatial regions. In my best effort to put this in mathematical terms, let
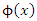 denote a physical quantity of some kind at a spatial location
denote a physical quantity of some kind at a spatial location 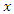 . Homogeneity requires the function
. Homogeneity requires the function 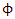 to be invariant under spatial translations,
to be invariant under spatial translations, 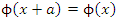 . How this implies that two inertial reference frames are related by a linear transformation is unclear.
. How this implies that two inertial reference frames are related by a linear transformation is unclear. 3. A Rigorous Derivation of the Lorentz Transformation
- In this section we will derive the Lorentz Transformation using only the two postulates of special relativity. We will do so without making the presupposition that the transformation has any particular form.For easy reference, let’s state the two postulates. 1. The Principle of Relativity: The laws of physics are the same in all inertial reference frames.2. Invariance of the Speed of Light: The speed of light in a vacuum is constant and independent of the motion of the light source or the observer. The length contraction and time dilation formulas are easily and rigorously derived in essentially any source on the topic. Thus, we will simply state these two formulas.The time between two distinct events that occur at the same spatial location in the
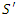 frame is related to the time in the
frame is related to the time in the 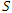 frame by the equation
frame by the equation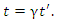 | (7) |
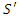 frame, and is of length
frame, and is of length 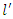 as measured by an observer who is at rest in that frame. An observer in the
as measured by an observer who is at rest in that frame. An observer in the 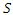 frame will determine the length of the rod to be
frame will determine the length of the rod to be 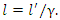 | (8) |
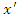 can be written in terms of
can be written in terms of 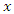 and
and 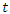 . As asserted in Section 2,
. As asserted in Section 2, 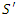 travels in the direction of increasing values of
travels in the direction of increasing values of 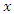 at a speed
at a speed 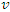 . That is, given an arbitrary constant
. That is, given an arbitrary constant 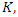 the plane
the plane 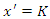 in the
in the 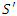 frame travels in the direction of increasing values of
frame travels in the direction of increasing values of 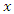 at speed
at speed 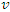 . So a stationary observer in
. So a stationary observer in 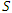 will describe the motion of such a traveling plane via the kinematic equation
will describe the motion of such a traveling plane via the kinematic equation 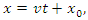 where
where 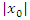 is the distance between the traveling plane and the plane
is the distance between the traveling plane and the plane 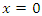 at
at 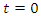 according to the observer in
according to the observer in 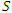 .Let us consider a specific example in which
.Let us consider a specific example in which 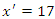 .
.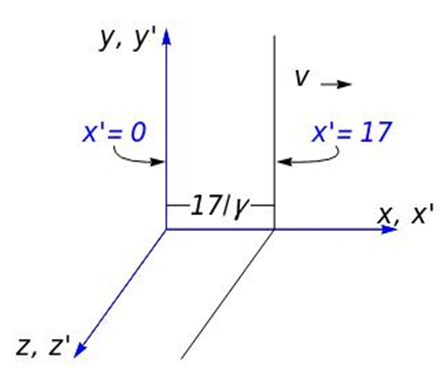 | Figure 1. The plane 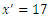 at time at time 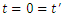 |
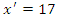 at
at 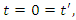 the moment in which the planes
the moment in which the planes 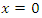 and
and 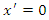 align. While a stationary observer in
align. While a stationary observer in 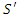 at
at 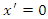 will see the plane
will see the plane 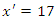 as stationary and 17 units away, a stationary observer in
as stationary and 17 units away, a stationary observer in 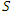 at
at 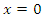 will see the plane at a contracted length of
will see the plane at a contracted length of 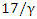 units away at that moment. Thus, we substitute
units away at that moment. Thus, we substitute 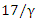 for
for 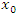 in the kinematic equation. Doing so yields
in the kinematic equation. Doing so yields 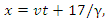 which can be rewritten as
which can be rewritten as 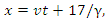 Of course there is nothing special about the number 17. An arbitrary but fixed value of
Of course there is nothing special about the number 17. An arbitrary but fixed value of 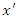 refers to a stationary plane in
refers to a stationary plane in 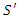 and a plane traveling at speed
and a plane traveling at speed 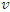 in
in 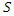 . Thus, the very same argument can be applied to
. Thus, the very same argument can be applied to 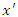 that was applied to 17 to obtain
that was applied to 17 to obtain 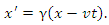 | (9) |
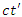 in terms of
in terms of 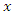 and
and 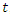 . In proving (9) we viewed planes of the form
. In proving (9) we viewed planes of the form 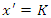 as traveling in the direction of increasing values of
as traveling in the direction of increasing values of 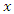 at speed
at speed 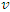 . It is equally legitimate to consider
. It is equally legitimate to consider 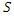 as the moving frame and
as the moving frame and 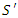 as the stationary frame. That is, we can repeat the same method that we used to obtain (9) to deduce
as the stationary frame. That is, we can repeat the same method that we used to obtain (9) to deduce 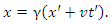 | (10) |
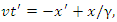 or equivalently
or equivalently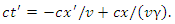 By (9), we can substitute
By (9), we can substitute 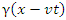 for
for 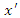 in the above equation. Doing this and a little algebra yields
in the above equation. Doing this and a little algebra yields 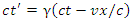 | (11) |
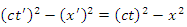 which holds whenever
which holds whenever 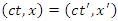 .
.4. Conclusions
- We have presented several textbook examples of how the LT is derived. In every case, the author took advantage of their prior knowledge regarding the LT’s form. This raises the question of whether the LT must be of the stated form. In particular, on the topic of whether the transformation must be linear, a hand-waving argument is presented at best. We also discussed the shortcomings of Einstein’s reasoning of why the LT is linear as presented in [5]. Next, we provided a rigorous derivation of the Lorentz transform without presupposing that it has any particular form from the start.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML