Naveed Hussain 1, Hassnain Abdullah Hussain 2, Ather Qayyum 3, Muhammad Ali Shaukat Rao 4
1Department of Physics, Punjab College Abdul Hakeem, Multan Division, Pakistan
2Institute of Physics, Bahauddin Zakerya University, Multan, Pakistan
3QFBA-Northumbria University Doha-Qatar
4RMIT University - Mechanical Engineering Department, Australia
Correspondence to: Ather Qayyum , QFBA-Northumbria University Doha-Qatar.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A frame of reference that is accelerating or rotating or accelerating and rotating is known as noninertial frame of reference. The transformation matrix for noninertial frame of reference is universal in the sense that all the spacetime laws of physics remain same for all observers in their original form after transformation which is the basic requirement of Einstein’s principle of relativity (EPR). Electrodynamics in universal noninertial frame based on single transformation law for 4-vectrors and tensors (STL) under universal Lorentz transformation matrix (ULTM) predicts zero-point electrodynamics within usual electrodynamics. As a consequence of transformation of electromagnetic field (EMF), Maxwell’s equations (ME) and conservation law in tensor form gave rise to zero-point or new symmetry terms of EMF, ME and conservation law along their corresponding diagonals. Zero- point terms or Singularities 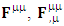 and
and 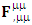 are the representatives of zero-point EMF, Maxwell’s equations and conservation law respectively. Matrix method and Einstein’s summation method are employed. Both methods give the same results up to the transformation of EMF and ME but they differ in the transformation of conservation law. Matrix method obeys usual conservation law but Einstein’s method gives zero-point origin of 4D electromagnetic wave and conservation law becomes 7D wave. The most beautiful consequence of STL is the emergence of complete structure of zero-pint electrodynamics without affecting the usual form of electrodynamics. The model completely obeys EPR, conservation law and symmetry. Besides this, electrodynamics, inertia and gravitation in noninertial coordinate metric predict zero-point energy, zero-point Maxwell’s equations as power-force and zero-point conservation law as 4D wave of energy. These results are also predicted by Lorenz transformation in 2D as well as in 4D but with Lorentz factor given in appendix. These discoveries will provide an unending source of power for space vehicles. An independent theory of zero-point electrodynamics is also developed where complete electrodynamics is obtained.
are the representatives of zero-point EMF, Maxwell’s equations and conservation law respectively. Matrix method and Einstein’s summation method are employed. Both methods give the same results up to the transformation of EMF and ME but they differ in the transformation of conservation law. Matrix method obeys usual conservation law but Einstein’s method gives zero-point origin of 4D electromagnetic wave and conservation law becomes 7D wave. The most beautiful consequence of STL is the emergence of complete structure of zero-pint electrodynamics without affecting the usual form of electrodynamics. The model completely obeys EPR, conservation law and symmetry. Besides this, electrodynamics, inertia and gravitation in noninertial coordinate metric predict zero-point energy, zero-point Maxwell’s equations as power-force and zero-point conservation law as 4D wave of energy. These results are also predicted by Lorenz transformation in 2D as well as in 4D but with Lorentz factor given in appendix. These discoveries will provide an unending source of power for space vehicles. An independent theory of zero-point electrodynamics is also developed where complete electrodynamics is obtained.
Keywords:
Universal Lorentz Transformation for Noninertial Frame, Single Transformation Law for 4-Vectors and Tensors, Purely Zero-Point Model of Electrodynamics, Inertia and Gravitation, Zero-Point Origin of 4D EM wave, Conservation Law as 7D EM Wave
Cite this paper: Naveed Hussain , Hassnain Abdullah Hussain , Ather Qayyum , Muhammad Ali Shaukat Rao , Electrodynamics in Universal Noninertial Frame Predicts Complete Structure of Zero-Point Electrodynamics, International Journal of Theoretical and Mathematical Physics, Vol. 14 No. 2, 2024, pp. 40-65. doi: 10.5923/j.ijtmp.20241402.02.
1. Introduction
Albert Einstein left a great treasure of knowledge as heritage for coming generations. He taught us the methodology of doing spacetime physics in the language of 4-vectors and tensors. His work is legendary. On the other hand, Maxwell’s work provided a physical interpretation of electromagnetic laws in unified framework. Einstein’s presentation of Maxwell’s theory in the language of tensors and 4-vectors has opened newer possibilities. Principle of relativity has been waiting for its complete validity and now it is getting its universal status for all observers in noninertial frame.In Einstein’s relativity theory, time and space, energy and momentum, Gauss’s law and Ampere’s law are relative but as a whole no explanation for spacetime, energy-momentum and Gauss’s law -Ampere’s law respectively. In principle, spacetime as a whole must appear same for all observers such that length contraction must be balanced by time dilation by the same amount. In the same manner, combination of energy and momentum, Gauss’s law and Ampere’s law must appear same for all observers independent of inertial and noninertial frame. According to EPR, all the spacetime laws of physics must remain same in every frame of reference. In other words, spacetime laws of physics must appear same for all observers. Time and space individually are relative but their combination must appear same to all observers. On investigation, it is found that 4-vetors and tensors as a whole do not remain same under usual Lorentz transformation (LT). The constancy of speed of light doesn’t imply the form invariance of all the spacetime laws of physics. Speed of light c is time component of 4-velocity that doesn’t remain same as a whole under LT. In principle, 4-velocity must appear same for all observers that doesn’t put any constraint on the constancy of speed of light. In the context of relativistic electrodynamics, Maxwell’s equations in tensor form must appear same to all observers with Gauss’s law and Ampere’s law as relative concepts. Actually, due to unavailability of ULTM and STL for 4-vectors and tensors, EPR remained in trouble. In the present paper, spacetime electrodynamics is developed in noninertial frame based on STL for 4-vectors and tensors and ULTM for noninertial frame of reference that is accelerating with constant acceleration and rotating with constant angular speed. In this framework, all the 4-vectors, tensors, inner product of 4-vectors, inner product of tensors and 4D wave operator remain same for all observers. In our previous paper [1], all of these relations remain same for all observers based on ULTM for inertial frame of reference. The results of both models are in complete agreement given in the table-1. It is to be noted that ULTM for inertial and noninertial frame are valid for both frame that provides us the actual spirit of EPR, conservation law and symmetry.The technique of STL for 4-vectors and tensors in spacetime physics is uncovering the hidden world of physical theories not only in electrodynamics but also in the theories of inertia and gravitation in the context of noninertial metrices [2]. Furthermore, application of STL is not confined only to ULTM for inertial and noninertial but for any transformation matrix e.g. in usual Lorentz transformation matrix in 2D and 4D. The validity of EPR, conservation law and symmetry principle depend upon the nature of transformation matrix.Spacetime physics in noninertial frame is needed to understand our physical world as the most of the natural systems are noninertial like our planet itself is a noninertial frame. Large Hadron Collider (LHC) setup is a noninertial. Particle accelerators are also noninertial systems. The accelerating expansion of our universe is the recent empirical evidence in this context. The most important thing about any physical theory in noninertial frame is to obey EPR, conservation law and symmetry principle. In the contemporary world of spacetime physics, there doesn’t exist a single model that fully obeys the above principles. In this paper, we shall mainly focus on the transformation of relations of electrodynamics as it is one of the well-understood physical theories and nicely fits in the framework of relativity. The earlier models [1-2] motivated to develop a framework for such situations where bodies are moving with constant acceleration a and rotating with constant angular velocity 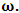 So ULTM for noninertial frame and STL is constructed to understand general relativity in a very simple language with which we are already familiar. This framework is valid for inertial as well as noninertial frame. The most difficult problem was to introduce acceleration and rotation in 4-position coordinate. Since speed of light c is taken as the time component of 4-velocity so its derivative with respect to time gave zero for time component of acceleration in the context of special relativity. In general relativity 4-acceleratin must contain its time component. Furthermore, special relativity and general relativity must appear as only theory of relativity. For this adventure, a consistent choice of coordinate is required. By choosing
So ULTM for noninertial frame and STL is constructed to understand general relativity in a very simple language with which we are already familiar. This framework is valid for inertial as well as noninertial frame. The most difficult problem was to introduce acceleration and rotation in 4-position coordinate. Since speed of light c is taken as the time component of 4-velocity so its derivative with respect to time gave zero for time component of acceleration in the context of special relativity. In general relativity 4-acceleratin must contain its time component. Furthermore, special relativity and general relativity must appear as only theory of relativity. For this adventure, a consistent choice of coordinate is required. By choosing 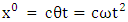 and
and 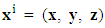 have the dimensions of distance so 4-position coordinate
have the dimensions of distance so 4-position coordinate 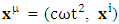 is considered such that 4-velocity
is considered such that 4-velocity 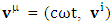 and 4-acceleration becomes
and 4-acceleration becomes 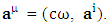 Here
Here 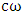 is time component of 4-acceleration. It has not only generalized special relativity to general but a jump towards the higher order effects like time varying acceleration or jerk
is time component of 4-acceleration. It has not only generalized special relativity to general but a jump towards the higher order effects like time varying acceleration or jerk 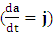 in modern mechanics. Electrodynamic relations viz. 4-current density, EMF, ME, conservation law and wave operator are transformed under ULTM and STL for 4-vectors and tensors. New symmetry terms are observed along the diagonal of EMF, ME and conservation law written in tensor components form. These symmetry terms contribute to validate conservation law and original form of the physical quantities after transformation. It is important to note that hidden structure of electrodynamics is affected by the frame of reference but the usual structure is independent of this effect. The results of our earlier model based on ULTM for inertial frame when reviewed recently [1] found in complete agreement with the results of present model.An extraordinary consequence of STL for 4-vectors and tensor is the existence of an independent model of purely zero-point theory of electrodynamics The results are presented in tale-2 and table-4. Our model is entirely different from the contemporary models on electrodynamics in noninertial frames [3-9]. Accelerating expansion of our universe and search for dark energy and matter are discussed in [10-12] but our approach will be different from them.The problem of zero-point energy, zero-point field (ZPF) Lorentz force (Magnetic Force) as the origin of inertia are very popular topics in contemporary world [13-14]. The applications of zero-point energy and ZPF is also interesting for future space vehicle propulsion addressed in [17-22]. In our models [1,2] and [23], zero-point world is naturally present as an integral part with definite origin.Model-1: Model of Electrodynamics in Universal Noninertial Frame Notations in this model are adopted according to modern approach of relativity. Greek alphabets
in modern mechanics. Electrodynamic relations viz. 4-current density, EMF, ME, conservation law and wave operator are transformed under ULTM and STL for 4-vectors and tensors. New symmetry terms are observed along the diagonal of EMF, ME and conservation law written in tensor components form. These symmetry terms contribute to validate conservation law and original form of the physical quantities after transformation. It is important to note that hidden structure of electrodynamics is affected by the frame of reference but the usual structure is independent of this effect. The results of our earlier model based on ULTM for inertial frame when reviewed recently [1] found in complete agreement with the results of present model.An extraordinary consequence of STL for 4-vectors and tensor is the existence of an independent model of purely zero-point theory of electrodynamics The results are presented in tale-2 and table-4. Our model is entirely different from the contemporary models on electrodynamics in noninertial frames [3-9]. Accelerating expansion of our universe and search for dark energy and matter are discussed in [10-12] but our approach will be different from them.The problem of zero-point energy, zero-point field (ZPF) Lorentz force (Magnetic Force) as the origin of inertia are very popular topics in contemporary world [13-14]. The applications of zero-point energy and ZPF is also interesting for future space vehicle propulsion addressed in [17-22]. In our models [1,2] and [23], zero-point world is naturally present as an integral part with definite origin.Model-1: Model of Electrodynamics in Universal Noninertial Frame Notations in this model are adopted according to modern approach of relativity. Greek alphabets 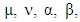 …runs from 0 to 3 and Latin letters i, j, k, … from 1 to 3. Comma (,) denote partial differentiation e. g.
…runs from 0 to 3 and Latin letters i, j, k, … from 1 to 3. Comma (,) denote partial differentiation e. g. 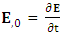 Partial derivative of electric field w. r. t. time,
Partial derivative of electric field w. r. t. time, 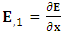 Partial derivative of electric field w. r. t. x-axis,
Partial derivative of electric field w. r. t. x-axis, 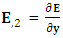 Partial derivative of electric field w. r. t. y-axis,
Partial derivative of electric field w. r. t. y-axis, 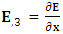 Partial derivative of electric field w. r. t. z-axis,
Partial derivative of electric field w. r. t. z-axis, 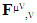 means 4-dimensional or spacetime partial derivative of EMF tensor.4 dimensional Coordinates
means 4-dimensional or spacetime partial derivative of EMF tensor.4 dimensional Coordinates 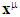 = (x0, x1, x2, x3) = (ct, x, y, z) =(ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that
= (x0, x1, x2, x3) = (ct, x, y, z) =(ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that 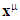 is the unification of time and space. The dimensions of all components are that of length.
is the unification of time and space. The dimensions of all components are that of length.
1.1. Development of ULTM in 2D and 4D in Noninertial Frame
The incompatibility of Lorentz transformation with EPR and is resolved by the development of a ULTM and UTL for 4-vectors and tensors in our recent paper [1]. Here, we get ULTM for noninertial frame just by replacing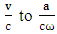 in equation (6) of [1].
in equation (6) of [1]. 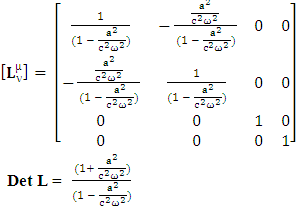 | (1) |
The above matrix acts as a 4 by 4 physical identity matrix. All the spacetime laws of physics (4-vectors and tensors including their inner product) remain same in their original form after transformation in a single step operation.Its inverse is 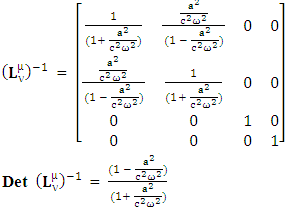 | (2) |
Its inverse matrix also behaves as physical identity matrix. Both equations (1) and (2) satisfy the requirement of EPR. The product of equation (1) and (2), results as an identity matrix to confirm the validity. 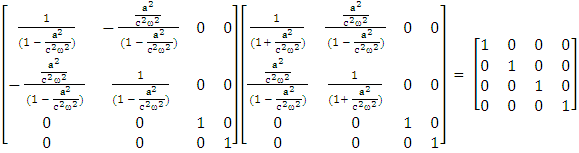 | (3) |
1.2. ULTM for Noninertial Frame in 4D
This matrix is nothing but 4 by 4 physical identity matrix for noninertial frame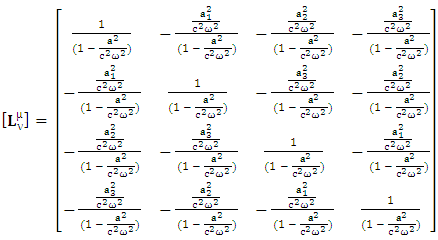 | (4) |
Its inverse again is a 4 by 4 physical identity matrix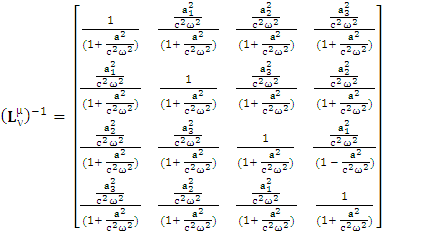 | (5) |
Equations (4) and (5) are ULTM for noninertial frame in 4D.
1.3. The Key Role of Single Transformation Law for 4-Vectors and Tensors
The need of a STL for 4-vectors and tensors is pointed out in [1], here, we mention them directly as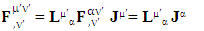 | (6) |
Both sides of equation are transformed under the same transformation law and the results are in complete agreement. This also implies the validity of transformation of electromagnetic field and conservation law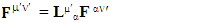 | (7) |
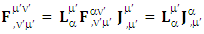 | (8) |
STL for 4-vectors and tensors is the decoder of zero-point physics when the tensors are transformed in their component form. It is valid for any 4 by 4 matrix but principle of relativity, conservation law and symmetry hold only for universal transformation matrices.
1.4. Application of ULTM and STL in Electrodynamics
ULTM in 2D and 4D give the same results that is all the spacetime laws of physics remain same in their original form after transformation. Only 2D matrix is used to save the space of expansion of expressions. Now we apply this transformation matrix transform one example of 4-vector and one for tensor to confirm the validity of ULTM.
1.5. Transformation of 4-Current Density under 4D ULTM in Noninertial Frame
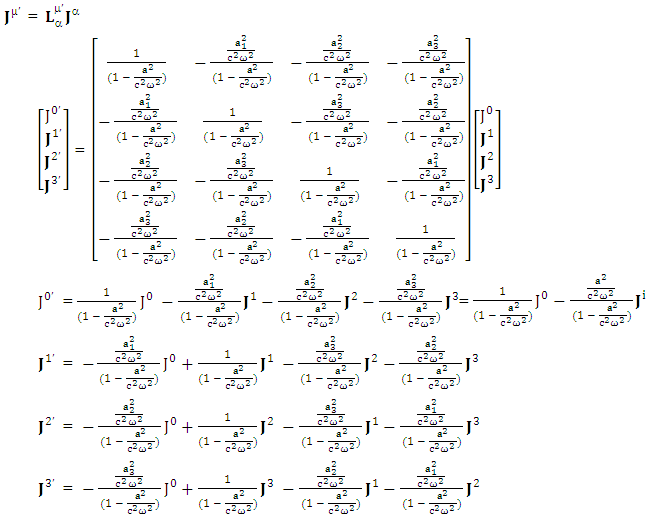 | (9) |
Adding all components on LHS and RHS and arranging common terms on RHS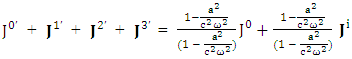 Since
Since 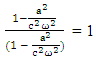 so, we have
so, we have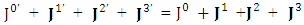
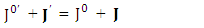 | (10) |
 | (11) |
The transformation is also true for covariant 4-position 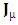
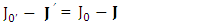 | (12) |
 | (13) |
Cotravariant and covariant 4-current density densities remain universal for all observers.
1.6. Transformation of Electromagnetic Field Tensor
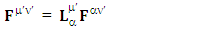 | (14) |
Electromagnetic field tensor 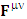 is related to its components electric field E and magnetic field B as follows
is related to its components electric field E and magnetic field B as follows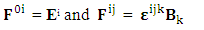 Electromagnetic field tensor in component form is needed to get new terms along the diagonal of Electromagnetic field. It is represented as 4 by 4 antisymmetric matrix
Electromagnetic field tensor in component form is needed to get new terms along the diagonal of Electromagnetic field. It is represented as 4 by 4 antisymmetric matrix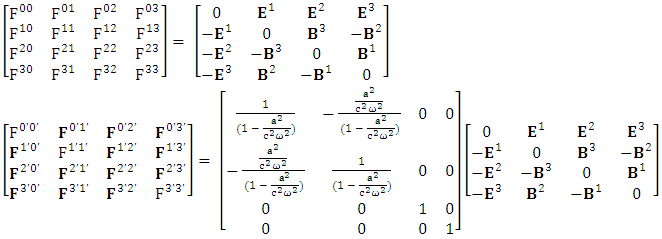 Zero-point terms are indicated by red color to understand their origin in the form of equations
Zero-point terms are indicated by red color to understand their origin in the form of equations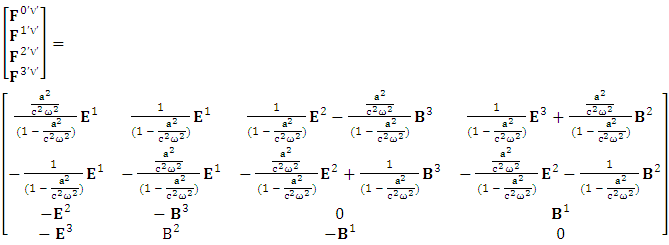 A new symmetry of electromagnetic field is emerged. Two terms of new symmetry along the diagonal areZero-point Term of Electric Field
A new symmetry of electromagnetic field is emerged. Two terms of new symmetry along the diagonal areZero-point Term of Electric Field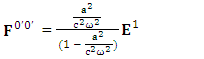 | (15) |
Zero-point term of Magnetic field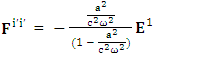 | (16) |
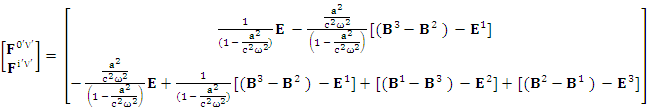 Electric Field:
Electric Field: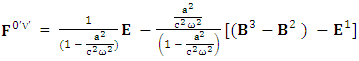 | (17) |
Magnetic Field: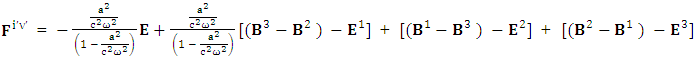 | (18) |
Adding all the terms on right hand side and combining common termsAdding (17) and (18) with the substitution 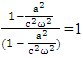 so the above relation simplifies to
so the above relation simplifies to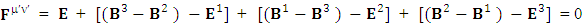 | (19) |
All the terms on right hand side cancel out due to opposite sign so electromagnetic field remains in its original form after transformation that satisfies completely EPR and symmetry principle.
1.7. Transformation of Maxwell’s Equations
Maxwell’s equations in tensor form is the sum of Gauss’s law and Ampere’s law. First row of the matrix is Gauss’s law and remaining three rows constitute Ampere’s law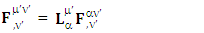 | (20) |
Maxwell’s equations in terms of tensor in matrix form are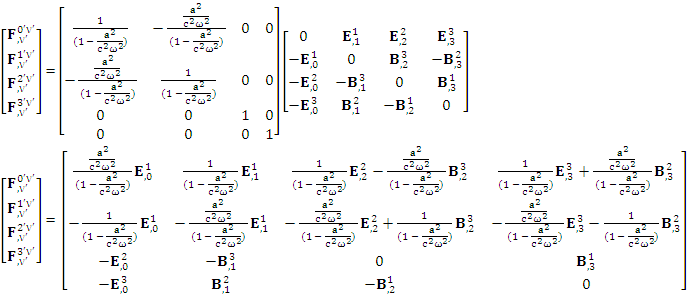 Zero-point terms of Maxwell’s equationsZero-point Term of Gauss’s Law
Zero-point terms of Maxwell’s equationsZero-point Term of Gauss’s Law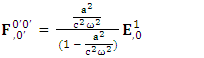 | (21) |
Zero-point Term of Ampere’s Law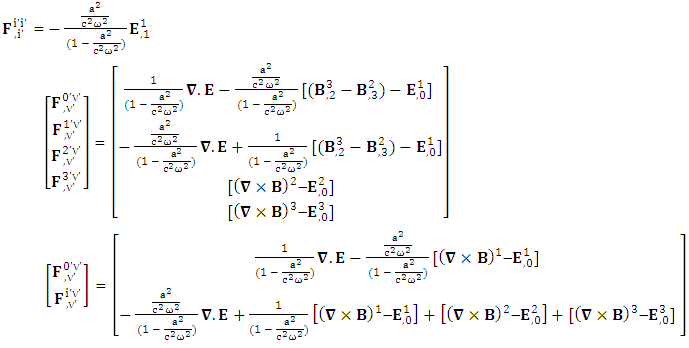 | (22) |
Gauss’s LawGauss’s law is affected by frame of reference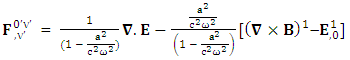 | (23) |
Ampere’s LawSimilarly, Ampere’s law is affected by frame of reference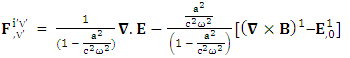 | (24) |
Combined Gauss’s Law and Ampere’s Law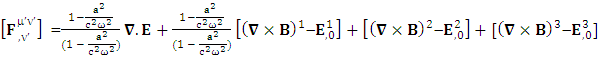 | (25) |
But the combination of gauss’s law and ampere’s law remains un-affected by the frame of reference.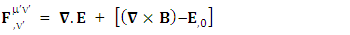 | (26) |
Maxwell’s equations in tensor form remain same.
1.8. Transformation of Conservation Law by Matrix Method
Conservation law can be written in tensor form is very simple but no one has ever noticed this simplicity. First row tells us about conservation of Gauss’s law and remaining three give conservation of Ampere’s law and their superposition results in conservation of both electromagnetic laws.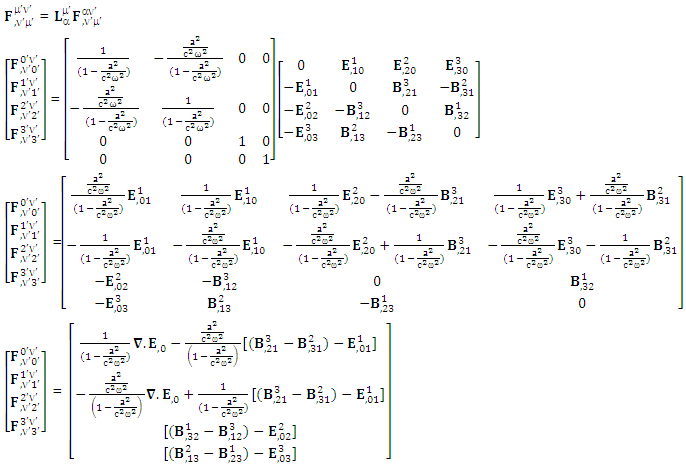 | (27) |
Zero-point Term of Conservation of Gauss’s Law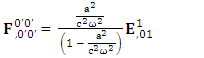 | (28) |
Zero-point Term of Conservation of Ampere’s Law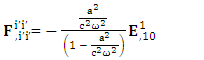 | (29) |
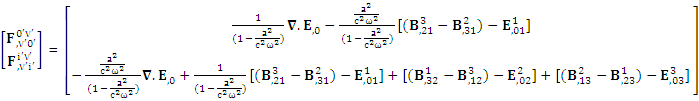 Conservation of Gauss’s LawConservation of Gauss’s law is affected by frame of reference
Conservation of Gauss’s LawConservation of Gauss’s law is affected by frame of reference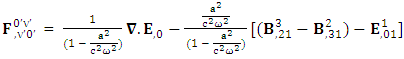 Conservation of Ampere’s is also affected by the frame of reference
Conservation of Ampere’s is also affected by the frame of reference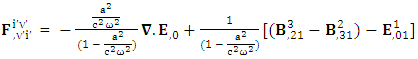
 Zero- point Conservation law
Zero- point Conservation law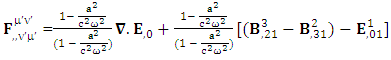
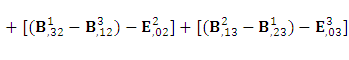 But the conservation law as a whole remains same for all observers
But the conservation law as a whole remains same for all observers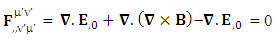 | (30) |
1.9. Transformation of Conservation Law by Einstein’s Summation Method
In the case of transformation of conservation law, 4D EM wave and higher order wave are affected by the frame of reference. 4D EM wave contains some extra terms that do not constitute a definite physical quantity showing the fragments of Laplacian wave of magnetic field. These terms contribute to complete the structure of conservation law in terms of higher order wave of electric field.Zero-point 4D EM Wave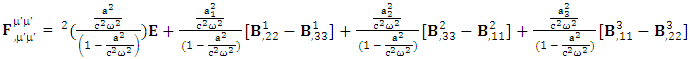 | (31) |
The nature of conservation law in terms of 7D wave with invariant character is very surprising indeed. It is affected by the frame of reference that seems to be responsible for the accelerating expansion of our universe [10-11].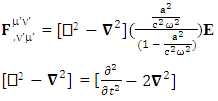 | (32) |
1.10. Transformation of Inner Product of Tensors 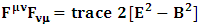
The inner product of cotravariant and covariant electromagnetic field tensor whose trace gives us scalar quantity called invariant of electromagnetic field as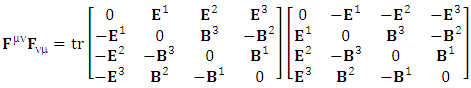 | (33) |
The product 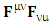 is decomposed in to 4 components that directly gives the trace of product
is decomposed in to 4 components that directly gives the trace of product 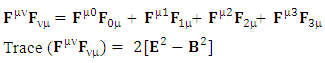 | (34) |
the transformation is now become very simple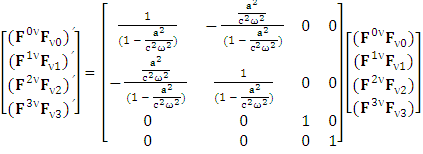 After multiplying, adding all the terms on left- and right-hand sides, we have
After multiplying, adding all the terms on left- and right-hand sides, we have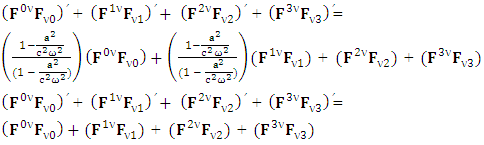 Now, putting the values of the terms in small brackets and of
Now, putting the values of the terms in small brackets and of 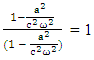 in above equation
in above equation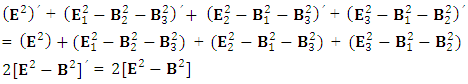 | (35) |
Inner product of Contravariant and covariant electromagnetic field tensor remains same.
1.11. Inner Product of EMF and Its Dual: 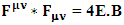
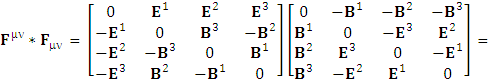 | (36) |
The above product is also decomposed in to 4 components that only represent the trace of the product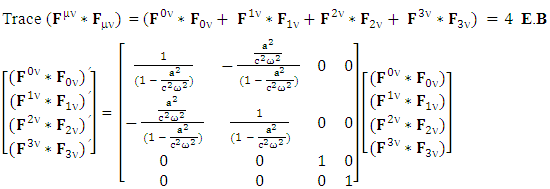 After multiplication, adding all the terms on left- and right-hand side
After multiplication, adding all the terms on left- and right-hand side 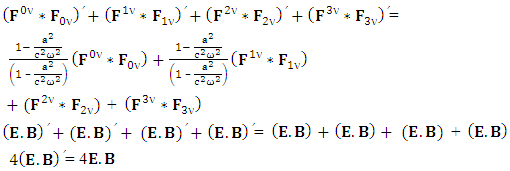 | (37) |
inner product of electromagnetic tensor with its duel remains same.
1.12. Electrodynamics in 4D Universal Noninertial and Inertial Frame
Zero-Point results of electrodynamics in universal inertial frame were not presented as a complete structure in [1]. Their physical significance was realized later on during the development of [2]. Now, here they are compared with the results of universal noninertial frame. Since transformation under 4D ULTM occupies a lot of space so the results are given in the table. The similarity between the models is as expected. | Table 1. Comparison of Results of Electrodynamics in 4D ULTM for and 4D ULTM for Inertial Frame of Reference |
1.13. Purely Zero-Point Electrodynamics in Universal Noninertial and Inertial Frame
After the development of above model, the need of an independent model of purely zero-point theory of electrodynamics is emerged. Table-2 represents zero-point electrodynamics in 4D ULTM for inertial and noninertial frame.Zero-point electrodynamics consists of transformation of EMF, ME and conservation law in tensor form given by three transformation laws.Transformation of Zero-Point Electromagnetic Field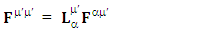 | (38) |
Transformation of Zero-Point Maxwell’s Equations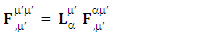 | (39) |
Transformation of Zero-Point Conservation Law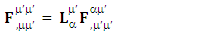 | (40) |
 | Table 2. Comparison of Results of Zero-Point Electrodynamics in 4D ULTM for noninertial and Inertial Frame of Reference |
2. Model-2: Zero-Point Results of Electrodynamics, Inertia and Gravitation in Noninertial Coordinate Metric Based on STL for 4-Vectors and Tensors
Quantum theory predicts existence of zero-point energy for ground state of harmonic oscillator 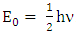 . Our model of electrodynamics, inertia and Gravitation in table-3, predicts outlandish results. The presence of zero-point energy via equation (1) in each column represents electrical energy, mechanical energy and gravitational energy respectively. They also incorporate the concept of Coulomb potential energy, inertial energy and Newtonian gravitational potential energy
. Our model of electrodynamics, inertia and Gravitation in table-3, predicts outlandish results. The presence of zero-point energy via equation (1) in each column represents electrical energy, mechanical energy and gravitational energy respectively. They also incorporate the concept of Coulomb potential energy, inertial energy and Newtonian gravitational potential energy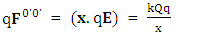 | (1) |
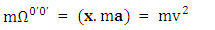 | (1) |
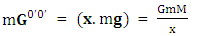 | (1) |
Other results can be seen in the table-3. Next, we consider the case of zero-point Maxwell’s equations for electrodynamics, inertia and gravitation theories via equations (6) of each column. 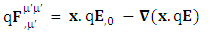 | (6) |
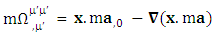 | (6) |
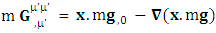 | (6) |
In mechanics, negative of gradient of potential energy is equal to force so the terms 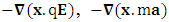 and
and 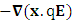 represent electric force, inertial force and gravitational force. The above equations represent power-force relation for electrodynamics, inertia and gravitation. As we know in special relativity that energy and momentum are unified. The next concept is power and force are unified. Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical energy, inertial energy and gravitational energy respectively via equation (7) of each column.
represent electric force, inertial force and gravitational force. The above equations represent power-force relation for electrodynamics, inertia and gravitation. As we know in special relativity that energy and momentum are unified. The next concept is power and force are unified. Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical energy, inertial energy and gravitational energy respectively via equation (7) of each column.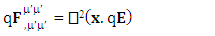 | (7) |
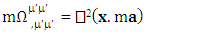 | (7) |
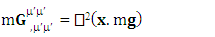 | (7) |
The set of equations (1), (6) and (7) show clearly that future space vehicles will be extracting energy and power-force from vacuum. The zero-point physical quantities are no more mysteries from now onward.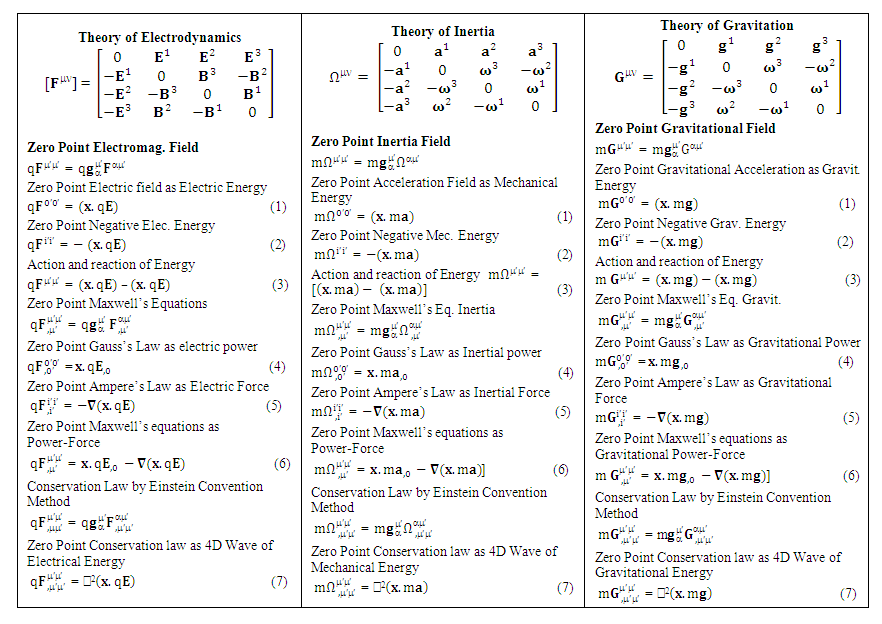 | Table 3. (Components of Noninertial Coordinate Metric: 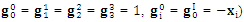 |
2.1. Zero-Point Electrodynamics, Inertia and Gravitation in Noninertial Metric
Quantum theory predicts existence of zero-point Casimir force. Our model of electrodynamics, inertia and Gravitation in table-4, predicts outlandish results. The presence of zero-point force via equation (1) in each column represents electrical force, Newton’s 2nd law and gravitational force respectively. Since forces appear equal and opposite so Newton’s third law is satisfied through equation (3) | (1) |
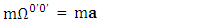 | (1) |
 | (1) |
Other results can be seen in the table. Next, we consider the case of zero-point Maxwell’s equations for electrodynamics, inertia and gravitation theories via equations (6) of each column. 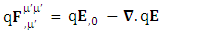 | (6) |
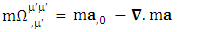 | (6) |
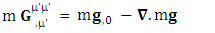 | (6) |
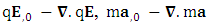 and
and 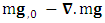 represent time varying electric force-Divergence of electric force, time varying inertial force-Divergence of force and time varying gravitational force-Divergence of gravitational force. Here time varying force and divergence of force are unified. In modern mechanics, time varying force is known as Yank.Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical force, Newton’s 2nd law and gravitational force respectively via equation (7) of each column.
represent time varying electric force-Divergence of electric force, time varying inertial force-Divergence of force and time varying gravitational force-Divergence of gravitational force. Here time varying force and divergence of force are unified. In modern mechanics, time varying force is known as Yank.Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical force, Newton’s 2nd law and gravitational force respectively via equation (7) of each column.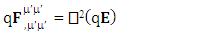 | (7) |
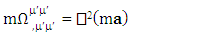 | (7) |
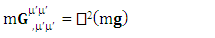 | (7) |
The set of equations (1), (6) and (7) show clearly that future space vehicles will be propelled by these forces. 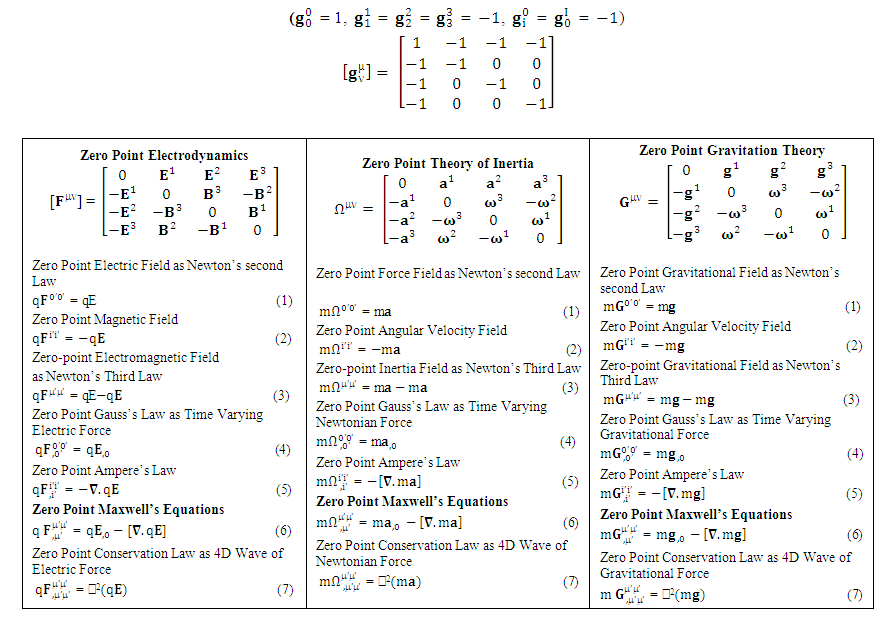 | Table 4 |
3. Model-3: Zero Point Spacetime Physics of Electrodynamics
In the above models via table-2 and table-4, zero-point relations of electrodynamics are not independent of effect of frame of reference. In other words, they contain the terms of transformation matrix.Is it possible to construct a model of zero-point electrodynamics that contains pure relations of electrodynamics consisting of electromagnetic field, Maxwell’s equations and conservation law in tensor form? The answer is yes. A transformation is constructed that gives us pure electrodynamics based on STL for 4-vectors and tensors. The process is very short and simple and the results are obtained in matrix form. All the results in final form remain same for all observers. 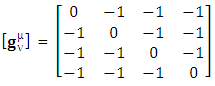 | (3.1) |
3.1. Derivation of Zero-Point Electromagnetic Field
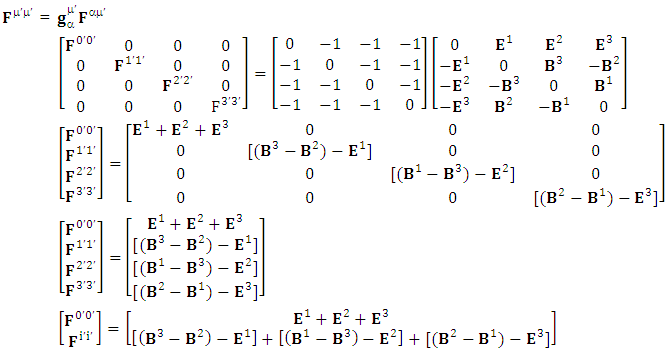 | (3.2) |
Zero-Point Electric Field | (3.3) |
Zero-Point Magnetic Field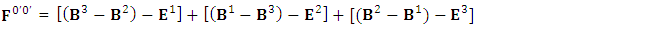 | (3.4) |
Zero-Point Electromagnetic Field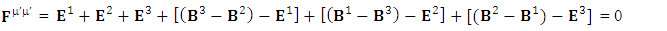 | (3.5) |
Zero-Point electromagnetic field remains same for all observers.
3.2. Derivation of Zero-Point Maxwell’s Equations
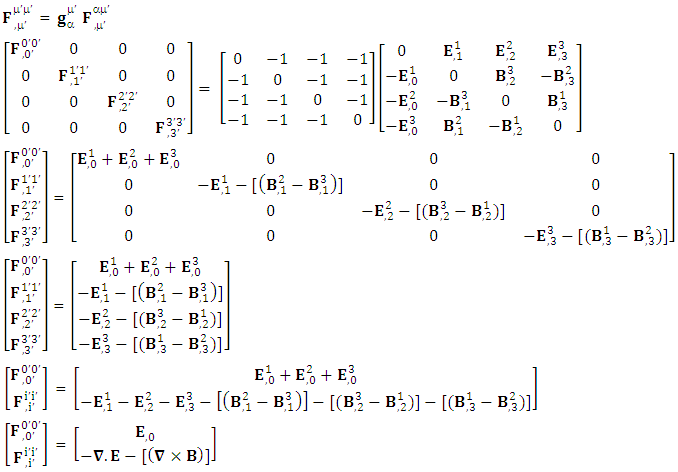 | (3.6) |
Zero-Point Gauss’s Law | (3.7) |
Zero-Point Ampere’s Law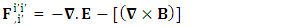 | (3.8) |
Zero-Point Maxwell’s Equations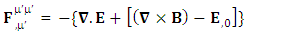 | (3.9) |
Zero-Point Maxwell’s equation remain same for all observers.
3.3. Derivation of Zero-Point Conservation Law
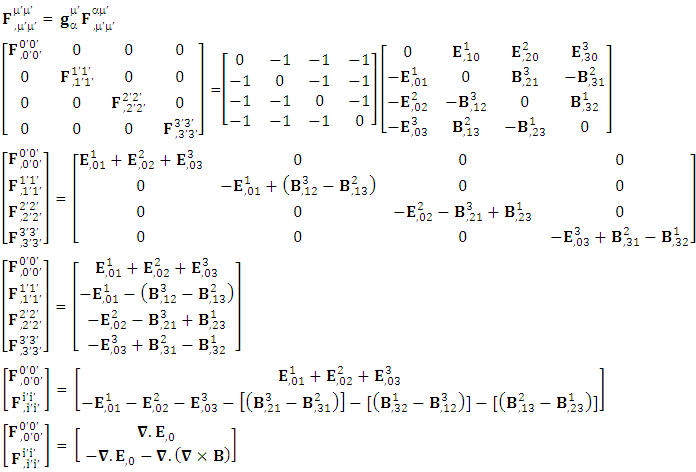 | (3.10) |
Zero-Point Conservation of Gauss’s Law | (3.11) |
Zero-Point Conservation of Ampere’s Law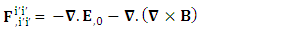 | (3.12) |
Zero-Point Conservation law 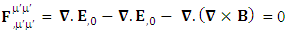 | (3.13) |
Zero-Point conservation law remains same for all observers.All the results consisting of electromagnetic field, Maxwell’s equations and conservation law via equations (3.5), (3.9) and (3.13) remain same for all observers in their original form after transformation.
4. Discussion and Comparison
Three models of electrodynamics are presented. The first model is related to universal noninertial frame and its consistency with the results of universal inertial frame of reference. The second model consists of electrodynamics in usual Lorentz transformation in 2D and in 4D Lorentz transformation. Both models contain usual electrodynamics and zero-point electrodynamics. Their zero-point results are presented in table-2 and table-4. The third model deals with the purely zero-point electrodynamics.Einstein’s relativity theory in ULTM for noninertial frame based on STL for 4-vectors and tensors is developed in the language of SR. It predicts very interesting results. STL has caused the emergence of complete zero-point structure of electrodynamics within usual electrodynamics. The zero-point structure is affected by frame of reference but the usual structure remains independent of this effect. It obeys conservation law, EPR and principle of symmetry. Conservation law by matrix method appears as usual but by Einstein’s method predicts two very strange results viz. 4D EM wave with zero-point origin and conservation law as a 7D EM wave having invariant property. The results of this model match with our earlier model completely that is based on ULTM for inertial frame [1]. The predictions of zero-point structure of electrodynamics in this model is unlike the search for dark matter and energy [10-12].Einstein’s SR only talk about the constancy of speed of light and invariance of inner product of 4-vectors and tensors. It doesn’t discuss the invariance of spacetime as a whole. In principle, if time and space are relative concept then spacetime must be the same for all observers. This inconsistency is actually due to unavailability of universal nature of Lorentz transformation and STL for 4-vectors and tensors. Our earlier model of ULTM for inertial frame and present model for noninertial frame resolves this issue within the domain of EPR and symmetry principle such that time and space are relative but their combination as spacetime remains same for all observers. This is the marvelous achievement of this adventure.RESULTS OF THE MODEL:
4.1. Form Invariance of 4-Vectors in Noninertial Frame
All 4-vectors remain same for all observers such that temporal and spatial components are relative but 4-vetor as a whole remains same. For example, 4-current density remains universal | (49) |
4.2. Zero-point Terms of Electromagnetic Field
Zero-point Terms of Electric Field | (50) |
Zero-point Terms of Magnetic Field 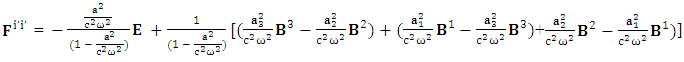 | (51) |
Zero-point Terms of Electromagnetic Field 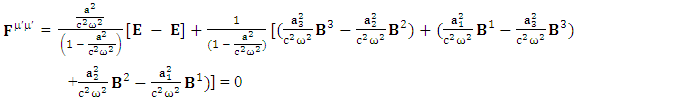 | (52) |
Usual Electromagnetic field remains same for all observers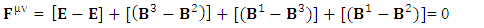 | (53) |
4.3. Zero-point Terms of Maxwell’s Equations
Zero-Point Term of Gauss’s Law represents time varying electric field | (54) |
Zero-point term of Ampere’s law consists of Gauss’s Law and curl of magnetic field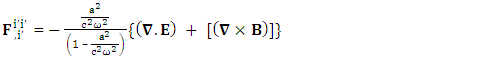 | (55) |
Zero-Point Maxwell’s Equations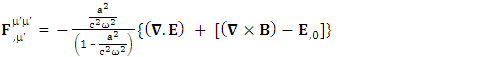 | (56) |
Gauss’s Law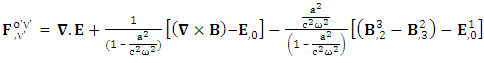 | (57) |
Ampere’s Law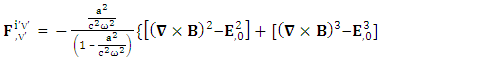 | (58) |
Zero-point Maxwell’s equations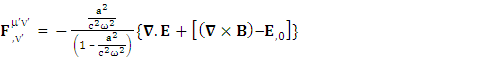 | (59) |
Usual Maxwell’s Equations remain universal for all observers | (60) |
Relation Between Zero-Point Maxwell’s Equations and Usual Maxwell’s Equations | (61) |
4.4. Zero-point Terms of Conservation Law by Matrix Method
Zero-Point Terms of conservation of Gauss’s law  | (62) |
Zero Point Terms of Conservation of Ampere’s Law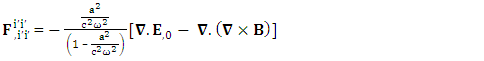 | (63) |
Zero-Point Conservation law holds along the diagonal. 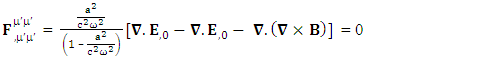 | (64) |
The combination of temporal and spatial singularities 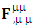 of conservation law constitutes, combination of conservation of Gauss’s law and Ampere’s law. Usual conservation law holds as it is
of conservation law constitutes, combination of conservation of Gauss’s law and Ampere’s law. Usual conservation law holds as it is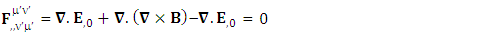 | (65) |
Relation Between Zero-Point and Usual Conservation Law | (66) |
4.5. Zero-point Terms of in Conservation Law by Einstein’s Method
By Einstein’s summation convention method, we get very strange results. The set of singularities of conservation law 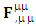 is transformed into 4D EM wave with some extra terms.Zero-Point 4D EM Wave
is transformed into 4D EM wave with some extra terms.Zero-Point 4D EM Wave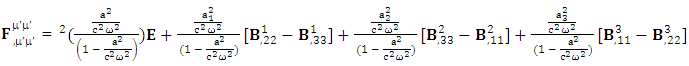 | (67) |
Zero-Point Conservation Law as 7D Wave Equation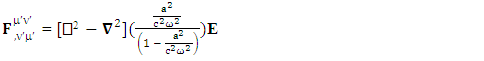 | (68) |
Whereas conservation law is transformed in to 4-times of usual conservation law and 7-dimensional wave of electric field. The 7D wave operator 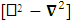 is the consequence of transformation of conservation law based on STL for 4-vectors and tensors. It is entirely new result. It possesses 6 dimensions of space and one dimension of time. As there are 4 dimensions of zero-point and 4 dimensions of usual electrodynamics so it represents 8D model of electrodynamics. Our previous models [1,2], also represent 8D models of electrodynamics, inertia and gravitation. It seems to be a string theory of electrodynamics where zero-point electrodynamics has a definite physical significance as each term has a clear source.The contemporary models on electrodynamics in noninertial frame by Scorgie [3] doesn’t possess the explanation of reference frame. Atwater [4] considers Galilean metric as the representative of noninertial metric that is a special case of our noninertial metric [2]. References [5] and [6] are based on differential forms and usual Lorentz transformation that are replaced by our ULTM. Fedosin’s model [7] Lorentz invariance of gravito-electromagnetism without STL for 4-vectors and tensors. Nicolie’s model [8] based on monad algebra and Costa [9] on Lie derivatives are of highly importance in accelerating and rotating systems but these models do not discuss the transformation of conservation law and the extra terms in Maxwell’s equations do not have clear origin like ours. Furthermore, wave equations are not discussed. Maxwell’s equations in accelerating metric have been developed in our earlier model [2], in model-4, page-210. The accelerating expansion of our universe [10-12] can be viewed in the light of our model. Maxwell’s equations in noninertial frame based on connection coefficients initiated the need of STL for 4-vectors and tensors and ULTM in 2D and 4D [13], case# 7, page-4.
is the consequence of transformation of conservation law based on STL for 4-vectors and tensors. It is entirely new result. It possesses 6 dimensions of space and one dimension of time. As there are 4 dimensions of zero-point and 4 dimensions of usual electrodynamics so it represents 8D model of electrodynamics. Our previous models [1,2], also represent 8D models of electrodynamics, inertia and gravitation. It seems to be a string theory of electrodynamics where zero-point electrodynamics has a definite physical significance as each term has a clear source.The contemporary models on electrodynamics in noninertial frame by Scorgie [3] doesn’t possess the explanation of reference frame. Atwater [4] considers Galilean metric as the representative of noninertial metric that is a special case of our noninertial metric [2]. References [5] and [6] are based on differential forms and usual Lorentz transformation that are replaced by our ULTM. Fedosin’s model [7] Lorentz invariance of gravito-electromagnetism without STL for 4-vectors and tensors. Nicolie’s model [8] based on monad algebra and Costa [9] on Lie derivatives are of highly importance in accelerating and rotating systems but these models do not discuss the transformation of conservation law and the extra terms in Maxwell’s equations do not have clear origin like ours. Furthermore, wave equations are not discussed. Maxwell’s equations in accelerating metric have been developed in our earlier model [2], in model-4, page-210. The accelerating expansion of our universe [10-12] can be viewed in the light of our model. Maxwell’s equations in noninertial frame based on connection coefficients initiated the need of STL for 4-vectors and tensors and ULTM in 2D and 4D [13], case# 7, page-4.
4.6. Comparison With Contemporary Models: The Case of ZPF
Haisch B. [13], page-682, equation (18), considers magnetic force as zero-point field (ZPF) effect of inertia due to reaction to acceleration. 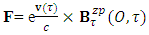 | (4.7.1) |
In our model [2], (page-220, equation (2)) magnetic component of Lorentz force is the consequence of transformation of electromagnetic field in noninertial velocity metric based on STL for 4-vectors and tensors where EMF appears as magnetic force.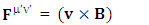 | (4.7.2) |
In our model [2], (page-222, equation (2)) magnetic component of Lorentz force is the consequence of transformation of electromagnetic field in Lorentz transformation in 4D based on STL for 4-vectors and tensors where EMF appears as Lorentz factor times magnetic force.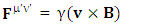 | (4.7.3) |
In an accelerating metric [2], page-226, electromagnetic field becomes time-varying magnetic force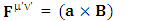 | (4.7.4) |
4.7. The Case of Zero-Point Energy
As compared to the concept of zero-point energy in quantum mechanics 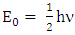 , we do have a very rich structure of zero-point electric energy in model-2, in noninertial coordinate metric via equation (1). Zero-point results are possible only by means of transformation of electrodynamics based on STL for 4-vectors and tensors where there is no extra assumptions or speculations. This relation is also obtained in 4D Lorentz transformation presented in appendix.
, we do have a very rich structure of zero-point electric energy in model-2, in noninertial coordinate metric via equation (1). Zero-point results are possible only by means of transformation of electrodynamics based on STL for 4-vectors and tensors where there is no extra assumptions or speculations. This relation is also obtained in 4D Lorentz transformation presented in appendix.
4.8. The Case of Zero-Point Force
Quantum theory predicts zero-point force as Casimir force. In model-2, via equation (6), we have obtained zero-point Maxwell’s equations as power-Force unified concept in noninertial coordinate metric. Lorentz transformation in 4D possesses zero-point Maxwell’s equations as power-Force with Lorentz factor, column-2, equation (6) in appendix A-1.
4.9. The Case of Zero-Point Conservation Law as 4D wave of Electrical Energy
The concept of zero-point conservation law as 4D wave of electrical energy is only the prediction of our model in noninertial coordinate metric.
4.10. Applications of Zero-Point Energy in Space Vehicles
Scientists of the day are proposing the possibility of space vehicles to be driven by the zero-point energy [15-21] Our cosmic world is so large that even light years appear very small scale. In order to explore cosmos, a natural and unending source of energy is needed that must be supplied by the vacuum. Zero-point energy and zero-point power-force of vacuum is expected to provide this technology.A complete framework of electrodynamics in 2D and 4D Lorentz transformation based on similarity transformation method is presented in appendix A-2. It was necessary to differentiate between the two methods viz. STL and STM. It is to be noted that, STM doesn’t provide zero-point results.
5. Conclusions
Single transformation law for 4-vectors and tensors has been proved as the decoder of zero-point physics in this model as well as in the previous two papers [1,2] and [23]. The discovery of zero-point electrodynamics and conservation law as 7D wave within usual electrodynamics in noninertial frame are the major consequences of STL for 4-vectors and tensors. Einstein’s principle of relativity has got its real universal status. In other words, spacetime laws of physics remain same for all observers has been achieved in inertial as well as in noninertial frame shown in the table-1. Quantum theory predicted zero-point energy but our present model predicts complete structure of zero-point electrodynamics, 4D EM wave and conservation law as 7D EM wave. Zero-point structure of electrodynamics is also predicted by usual Lorentz transformation in 2D and 4D but based on STL that confirms the validity of our methodology. An independent framework of zero-point complete electrodynamics is developed where we can see the zero-point results in three steps. Electrodynamics in noninertial coordinate metric has predicted zero-point energy, zero-point Maxwell’s equation as power-force and zero-point conservation law as 4D wave of electrical energy. These discoveries will help us to develop space vehicles propelled by zero-point energy and power-force. Our previous model [2] and recently [23] have predicted a series of zero-point physical concepts like electric power, time varying electric power etc. In the upcoming papers, framework of inertia and gravitation are expected to be related with quantum theory via simple equations are the topics of our future work.
Appendix
A-1. Zero-Point Electrodynamics under Usual Lorentz TransformationWhat kind of electrodynamics is emerged in usual Lorentz transformation based on single transformation law for 4-vectors and tensors? It is the most valid question because 117 years of spacetime physics is relying on it. Very interesting results are obtained in this context. Zero-point electrodynamics is present within the usual electrodynamics. In order to show the importance of this formulation, we transform Maxwell’s equations in tensor form and 4-current density under STL which gives us the same results.Maxwell’s equations in tensor form are represented by the divergence of electromagnetic field tensor equal to 4-current density | (A1) |
Now, we transform both sides of (2.1) under STL | (A2) |
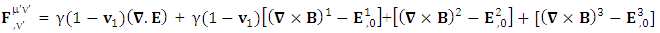 | (A3) |
 | (A4) |
 | (A5) |
Comparing the results of (2.3) and (2.5), we get the same results that establishes the validity of STL for 4-vectors and tensors.If we transform Maxwell’s equations by means of similarity transformation technique | (A6) |
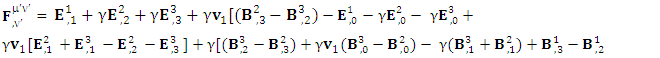 | (A7) |
Then the results of both sides of (A1) do not remain same as (A5) and (A7) are different. That is why we need STL for consistency. A-1.1: Transformation of Electromagnetic Field Tensor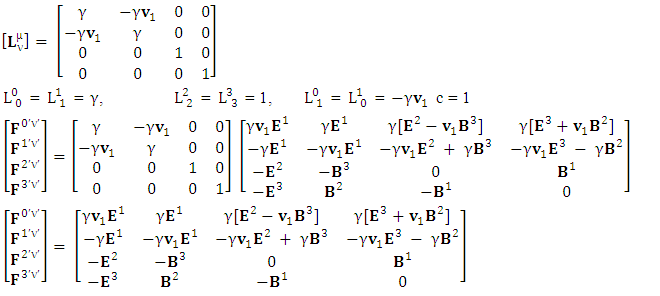 | (A8) |
Zero-point term of Electric Field | (A9) |
Zero-point term of Magnetic Field | (A10) |
4D Electric Field | (A11) |
Magnetic Field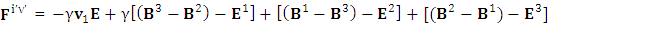 | (A12) |
Electromagnetic Field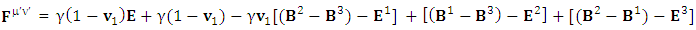 | (A13) |
Electromagnetic field doesn’t remain same in its original form after transformationA-1.2: Transformation of Maxwell’s Equations Based on STL Method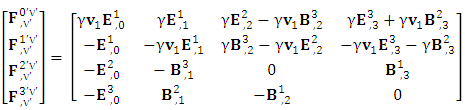 Zero-Point Term of Gauss’s Law
Zero-Point Term of Gauss’s Law | (A14) |
Zero-Point Term of Ampere’s Law | (A15) |
Gauss’s Law | (A16) |
Ampere’s Law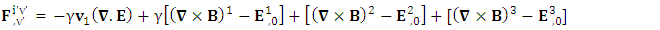 | (A17) |
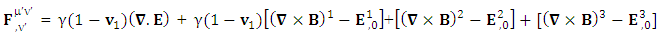 | (A18) |
Maxwell’s equations in tensor form do not remain same in its original form after transformation.A-1.3: Transformation of Conservation Law by Matrix Method 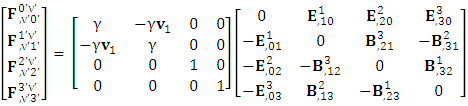
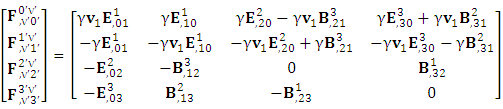 Zero-Point Term of Conservation of Gauss’s Law
Zero-Point Term of Conservation of Gauss’s Law | (A19) |
Zero-Point Term of Conservation of Ampere’s Law | (A20) |
 | (A21) |
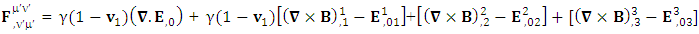 | (A22) |
Conservation law doesn’t remain same in its original form after transformation.A-1.4: Transformation of Conservation Law (Einstein’s Summation Convention Method)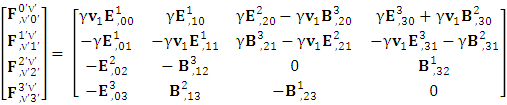 Zero-Point Term of Conservation of Gauss’s Law
Zero-Point Term of Conservation of Gauss’s Law | (A23) |
Zero-Point Term of Conservation of Ampere’s Law | (A24) |
Zero-Point Term of Conservation Law | (A25) |
It represents only one component of 4D wave equation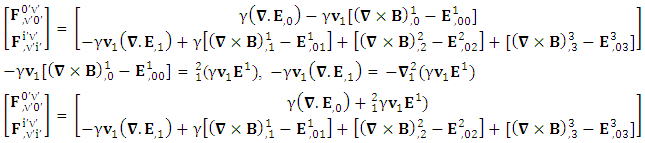 Conservation of Gauss’s Law
Conservation of Gauss’s Law | (A26) |
Conservation of Ampere’s Law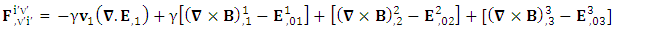 | (A27) |
Complete Conservation Law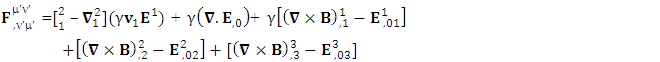 | (A28) |
 | Table 5. Electrodynamics in 2D and 4D Lorentz Transformation (Single Transformation Law Method) |
 | Table 6. Zero-Point Electrodynamics in 2D and 4D Lorentz Transformation (Single Transformation Method) |
A-2: Electrodynamics in 2D and 4D Lorentz Transformation (Similarity Transformation Method)What is the complete structure of electrodynamics under usual Lorentz transformation based on similarity transformation method (STM)? In order to remove all confusions about electrodynamics in Lorentz transformation in 2D and 4D, table-6 contains the complete formulation under STM. Similarity transformation is valid only for tensors not for 4-vectors which is the major difference between STM and STL for 4-vectors and tensors. In STM, zero-point quantities do not exist. The contemporary physicists are limited up to the transformation of EMF only under 2D Lorentz transformation based on STM. Transformation of Maxwell’s equations and conservation law under STM are entirely new results.The results of electrodynamics in 4D Lorentz transformation under STM are clear and comprehensiveElectric Field  | (1) |
Magnetic field | (2) |
Electromagnetic Field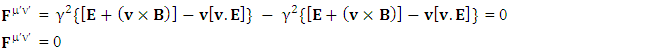 | (3) |
Electromagnetic field remains antisymmetric but not in its original form Maxwell’s EquationsGauss’s Law  | (4) |
Ampere’s Law 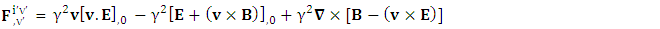 | (5) |
Maxwell’s Equations in Tensor Form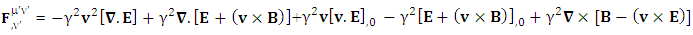 | (6) |
Conservation Law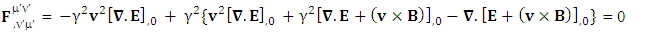 | (7) |
Conservation law holds but not in its original form.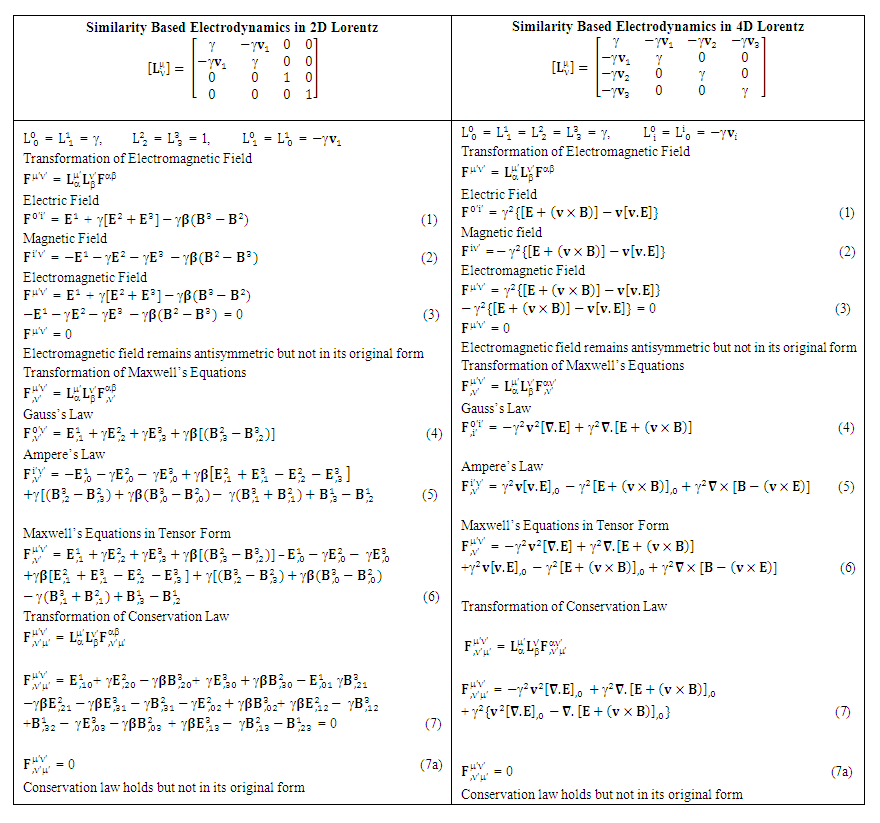 | Table 7. Electrodynamics in 2Dand 4D Lorentz Matrix (Similarity Transformation Method) |
Dedicated To Those Who Work and Live for Humanity.Declaration: This research work is not sponsored by any organization or grant agency. It is totally self-financed project.
ACKNOWLEDGEMENTS
There is a long list of moral supporters during 30 years of research but the least are mentioned. I am thankful to Prof. Dr. Jawaid Quamar from whom I learnt the art of thinking in research at the frontiers of physics and highly valuable discussions in the field of spacetime physics. I am also thankful to Dr. R. K. Ansari, Dr. Javed Iqbal, Dr. M. Ayub, Dr. Arif Kamal, Dr. Shahid Mehmood, M. Suhail, Dr. Naim Khan Canada, Ms. Shamsa, Asifa, Prof. Nafees A. Khan, Muddassir Manzoor, Tilawat Sher khan, Suhail Aslam, Khalid Siddiqi, Mr. Ahmar, Prof. Dr. S. A. Kamal Jaffery USA, Dr. Raja Khalid, Dr. Gulnaz, Dr. Imama, Awad and Saad Canada, Dr. Tariq, Ms. Huma, Adil, Umar, sara Australia, Computer Engineer Ms. Maryem Australia, Prof. Hafiz Ahmad USA, Dr. M. Ashfaq COMSAT University, Lahore, Dr. Junaid Iqbal B.Z. University, Multan, Prof. Kashif Mehmood Principal Punjab College, All of my Colleagues at Punjab college, All of my Students of BS physics, Math., Chemistry, Abdul Hakeem Ansari, Khan Abdusstar, Sqd. Ldr. GR Shahid, M. Ashraf Lahore, Dr. Masood Iqbal and M. Arif Pinstech, Islamabad, Malik Bashir Ahmad, Malik Maqbool A. Kamal, Radio Engineer Malik Shabbir A. Qaiser, Dr. Hashir, Prof. Ejaz Malik, Dr. Haseeb, Dr. Khadija, Shaheen Shabbir, Saqlain Abdulla, Ayesha Naveed, Nasir Aftab, Rao Imran Nasir, Prof. Iqra, Engineer Rao Faizan, Rao Rizwan, Laila, Humaira, Prof. Raheela, Abdul Momin, Noorul Huda, Abdul Wali, M. Arsal, Computer Scientist Rao Nazar Iqbal Islamabad, Engr. Khalid Munir, Engr. Kamran, Adnan Talib, Asif Murtaza, Marine Engr. Rao Furqan, M. Ahmad Advocate, Rao Inam -ul- Haq, Prof. Kanwar Javed, Rao Zubair, Yahya A. Qadir, Sayed Bhai Jan, Zulqarnain, Zainul Abideen, Malik Manzoor Atif, R. M. Sagheer, Cdr. Rao Abdul Jabbar, Computer Engr. Faisal Jabbar, Dr. Rao M. Siddique, Prof. Dr. Salim Raza, for their moral support and valuable suggestions.
References
| [1] | Hussain, N., et al. "Re Birth of Einstein’s Relativity via Unified Transformation Law." International Journal of Physics 11.1 (2023): 6-16. |
| [2] | Naveed Hussain, Hassnain Abdullah Hussain, Ather Qayum. "Electrodynamics in Noninertial Metrices Predicts Entirely New Origin of 4D Electromagnetic Wave." International Journal of Physics Vol.11. No .4 (2023): 193-230. DOI:10.12691/ijp-11-4-5. |
| [3] | Scorgie G. C. (1990), Electromagnetism in Noninertial Coordinates, Journal of Physics A: Mathematical and General, 1990/11 Vol 23: ISS 22. |
| [4] | H. A. Atwater (1974), Introduction to General Relativity, Pergamon Press. |
| [5] | Obukhov, Yuri N. "Electrodynamics in noninertial frames." The European Physical Journal C 81 (2021): 1-11. |
| [6] | Kurz, Stefan, Bernd Flemisch, and Barbara Wohlmuth. "A framework for Maxwells equations in non-inertial frames based on differential forms." Proceedings of ICAP. 2006. |
| [7] | Fedosin, Sergey G. "Electromagnetic and gravitational pictures of the world." (2007). Apeiron, Vol.14, No. 4, pp. 385-413. |
| [8] | Nikolie V M, (1996), Relativistic Physics in Arbitrary Reference Frames, General Relativity and Quantum Cosmology, Monad representation of Maxwell’s equations, pp. 78-79. |
| [9] | Costa, L. Filipe O., and José Natário. "Gravito-electromagnetic analogies." General Relativity and Gravitation 46 (2014): 1-57. Page-30, Max. equations 86-89. |
| [10] | Schmidt, Brian P. “Nobel Lecture: Accelerating expansion of the Universe through observations of distant supernovae.” Reviews of Modern Physics 84.3 (2012): 1151. |
| [11] | Padmanabhan, T. "Accelerated expansion of the universe driven by tachyonic matter." Physical Review D 66.2 (2002): 021301. |
| [12] | Jacquart, Melissa. "Dark matter and dark energy." The routledge companion to philosophy of physics. Routledge, 2021. 731-743. |
| [13] | Naveed Hussain (2001), “On the General Covariance of Maxwellian Electrodynamics” Science International, Lahore, 13(1), pg1-6. |
| [14] | Haisch, Bernhard, Alfonso Rueda, and Harold E. Puthoff. "Inertia as a zero-point-field Lorentz force." Physical Review A 49.2 (1994): 678. Equation (18), page-682. |
| [15] | Musha, Takaaki. Physics of the zero-point field and its applications to advanced technology. Nova Publishers, 2013. |
| [16] | Woodward, James F., and Thomas Mahood. "What is the Cause of Inertia?" Foundations of Physics 29.6 (1999): 899-930. |
| [17] | Robertson, Glen A., P. A. Murad, and Eric Davis. "New frontiers in space propulsion sciences." Energy Conversion and Management 49.3 (2008): 436-452. |
| [18] | Haisch, Bernhard, and Alfonso Rueda. "The Zero-Point Field and the NASA Challenge to Create the Space Drive." NASA Breakthrough Propulsion Physics Workshop Proceedings. 1999. |
| [19] | Puthoff, Harold E., S. R. Little, and M. Ibison. "Engineering the zero-point field and polarizable vacuum for interstellar flight." Journal of the British Interplanetary Society 55 (2002): 137-144. |
| [20] | Millis, Marc G. "Exploring the notion of space coupling propulsion." Vision 21 (1991): 307-316. |
| [21] | Musha, Takaaki. "Possibility of the Space Propulsion System Utilizing the ZPF Field." AIP Conference Proceedings. Vol. 1103. No. 1. American Institute of Physics, 2009. |
| [22] | Boyer, Timothy H. "Any classical description of nature requires classical electromagnetic zero-point radiation." American Journal of Physics 79.11 (2011): 1163-1167. |
| [23] | Naveed Hussain, Hassnain Abdullah Hussain, Ather Qayum. "Spacetime Exchange Method of Derivation of Electromagnetic Laws Based on Symmetry of Universal Lorentz Transformation Matrix" International Journal of Theoretical and Mathematical Physics 2024, 14(2): 17-39 DOI: 0.5923/j.ijtmp.20241402.01. |


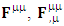 and
and 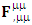 are the representatives of zero-point EMF, Maxwell’s equations and conservation law respectively. Matrix method and Einstein’s summation method are employed. Both methods give the same results up to the transformation of EMF and ME but they differ in the transformation of conservation law. Matrix method obeys usual conservation law but Einstein’s method gives zero-point origin of 4D electromagnetic wave and conservation law becomes 7D wave. The most beautiful consequence of STL is the emergence of complete structure of zero-pint electrodynamics without affecting the usual form of electrodynamics. The model completely obeys EPR, conservation law and symmetry. Besides this, electrodynamics, inertia and gravitation in noninertial coordinate metric predict zero-point energy, zero-point Maxwell’s equations as power-force and zero-point conservation law as 4D wave of energy. These results are also predicted by Lorenz transformation in 2D as well as in 4D but with Lorentz factor given in appendix. These discoveries will provide an unending source of power for space vehicles. An independent theory of zero-point electrodynamics is also developed where complete electrodynamics is obtained.
are the representatives of zero-point EMF, Maxwell’s equations and conservation law respectively. Matrix method and Einstein’s summation method are employed. Both methods give the same results up to the transformation of EMF and ME but they differ in the transformation of conservation law. Matrix method obeys usual conservation law but Einstein’s method gives zero-point origin of 4D electromagnetic wave and conservation law becomes 7D wave. The most beautiful consequence of STL is the emergence of complete structure of zero-pint electrodynamics without affecting the usual form of electrodynamics. The model completely obeys EPR, conservation law and symmetry. Besides this, electrodynamics, inertia and gravitation in noninertial coordinate metric predict zero-point energy, zero-point Maxwell’s equations as power-force and zero-point conservation law as 4D wave of energy. These results are also predicted by Lorenz transformation in 2D as well as in 4D but with Lorentz factor given in appendix. These discoveries will provide an unending source of power for space vehicles. An independent theory of zero-point electrodynamics is also developed where complete electrodynamics is obtained.
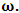 So ULTM for noninertial frame and STL is constructed to understand general relativity in a very simple language with which we are already familiar. This framework is valid for inertial as well as noninertial frame. The most difficult problem was to introduce acceleration and rotation in 4-position coordinate. Since speed of light c is taken as the time component of 4-velocity so its derivative with respect to time gave zero for time component of acceleration in the context of special relativity. In general relativity 4-acceleratin must contain its time component. Furthermore, special relativity and general relativity must appear as only theory of relativity. For this adventure, a consistent choice of coordinate is required. By choosing
So ULTM for noninertial frame and STL is constructed to understand general relativity in a very simple language with which we are already familiar. This framework is valid for inertial as well as noninertial frame. The most difficult problem was to introduce acceleration and rotation in 4-position coordinate. Since speed of light c is taken as the time component of 4-velocity so its derivative with respect to time gave zero for time component of acceleration in the context of special relativity. In general relativity 4-acceleratin must contain its time component. Furthermore, special relativity and general relativity must appear as only theory of relativity. For this adventure, a consistent choice of coordinate is required. By choosing 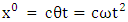 and
and 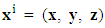 have the dimensions of distance so 4-position coordinate
have the dimensions of distance so 4-position coordinate 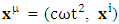 is considered such that 4-velocity
is considered such that 4-velocity 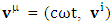 and 4-acceleration becomes
and 4-acceleration becomes 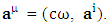 Here
Here 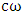 is time component of 4-acceleration. It has not only generalized special relativity to general but a jump towards the higher order effects like time varying acceleration or jerk
is time component of 4-acceleration. It has not only generalized special relativity to general but a jump towards the higher order effects like time varying acceleration or jerk 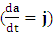 in modern mechanics. Electrodynamic relations viz. 4-current density, EMF, ME, conservation law and wave operator are transformed under ULTM and STL for 4-vectors and tensors. New symmetry terms are observed along the diagonal of EMF, ME and conservation law written in tensor components form. These symmetry terms contribute to validate conservation law and original form of the physical quantities after transformation. It is important to note that hidden structure of electrodynamics is affected by the frame of reference but the usual structure is independent of this effect. The results of our earlier model based on ULTM for inertial frame when reviewed recently [1] found in complete agreement with the results of present model.An extraordinary consequence of STL for 4-vectors and tensor is the existence of an independent model of purely zero-point theory of electrodynamics The results are presented in tale-2 and table-4. Our model is entirely different from the contemporary models on electrodynamics in noninertial frames [3-9]. Accelerating expansion of our universe and search for dark energy and matter are discussed in [10-12] but our approach will be different from them.The problem of zero-point energy, zero-point field (ZPF) Lorentz force (Magnetic Force) as the origin of inertia are very popular topics in contemporary world [13-14]. The applications of zero-point energy and ZPF is also interesting for future space vehicle propulsion addressed in [17-22]. In our models [1,2] and [23], zero-point world is naturally present as an integral part with definite origin.Model-1: Model of Electrodynamics in Universal Noninertial Frame Notations in this model are adopted according to modern approach of relativity. Greek alphabets
in modern mechanics. Electrodynamic relations viz. 4-current density, EMF, ME, conservation law and wave operator are transformed under ULTM and STL for 4-vectors and tensors. New symmetry terms are observed along the diagonal of EMF, ME and conservation law written in tensor components form. These symmetry terms contribute to validate conservation law and original form of the physical quantities after transformation. It is important to note that hidden structure of electrodynamics is affected by the frame of reference but the usual structure is independent of this effect. The results of our earlier model based on ULTM for inertial frame when reviewed recently [1] found in complete agreement with the results of present model.An extraordinary consequence of STL for 4-vectors and tensor is the existence of an independent model of purely zero-point theory of electrodynamics The results are presented in tale-2 and table-4. Our model is entirely different from the contemporary models on electrodynamics in noninertial frames [3-9]. Accelerating expansion of our universe and search for dark energy and matter are discussed in [10-12] but our approach will be different from them.The problem of zero-point energy, zero-point field (ZPF) Lorentz force (Magnetic Force) as the origin of inertia are very popular topics in contemporary world [13-14]. The applications of zero-point energy and ZPF is also interesting for future space vehicle propulsion addressed in [17-22]. In our models [1,2] and [23], zero-point world is naturally present as an integral part with definite origin.Model-1: Model of Electrodynamics in Universal Noninertial Frame Notations in this model are adopted according to modern approach of relativity. Greek alphabets 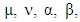 …runs from 0 to 3 and Latin letters i, j, k, … from 1 to 3. Comma (,) denote partial differentiation e. g.
…runs from 0 to 3 and Latin letters i, j, k, … from 1 to 3. Comma (,) denote partial differentiation e. g. 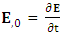 Partial derivative of electric field w. r. t. time,
Partial derivative of electric field w. r. t. time, 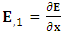 Partial derivative of electric field w. r. t. x-axis,
Partial derivative of electric field w. r. t. x-axis, 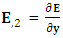 Partial derivative of electric field w. r. t. y-axis,
Partial derivative of electric field w. r. t. y-axis, 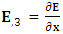 Partial derivative of electric field w. r. t. z-axis,
Partial derivative of electric field w. r. t. z-axis, 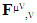 means 4-dimensional or spacetime partial derivative of EMF tensor.4 dimensional Coordinates
means 4-dimensional or spacetime partial derivative of EMF tensor.4 dimensional Coordinates 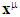 = (x0, x1, x2, x3) = (ct, x, y, z) =(ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that
= (x0, x1, x2, x3) = (ct, x, y, z) =(ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that 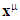 is the unification of time and space. The dimensions of all components are that of length.
is the unification of time and space. The dimensions of all components are that of length.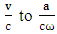 in equation (6) of [1].
in equation (6) of [1]. 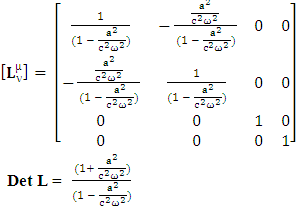
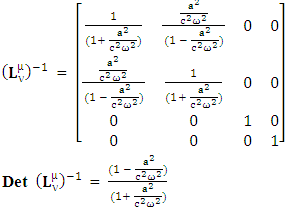
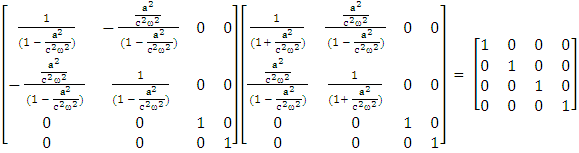
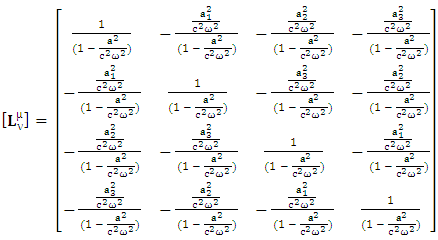
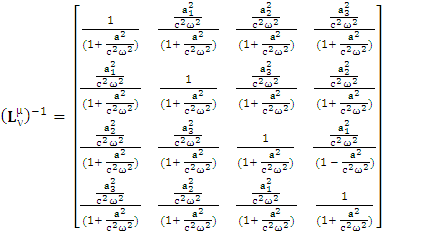
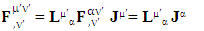
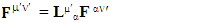
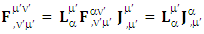

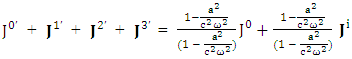 Since
Since 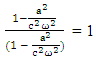 so, we have
so, we have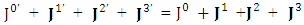
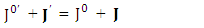

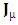
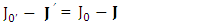

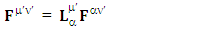
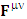 is related to its components electric field E and magnetic field B as follows
is related to its components electric field E and magnetic field B as follows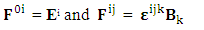 Electromagnetic field tensor in component form is needed to get new terms along the diagonal of Electromagnetic field. It is represented as 4 by 4 antisymmetric matrix
Electromagnetic field tensor in component form is needed to get new terms along the diagonal of Electromagnetic field. It is represented as 4 by 4 antisymmetric matrix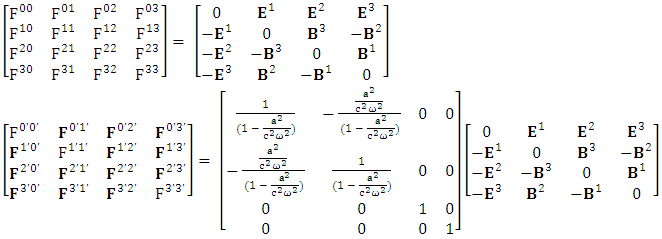 Zero-point terms are indicated by red color to understand their origin in the form of equations
Zero-point terms are indicated by red color to understand their origin in the form of equations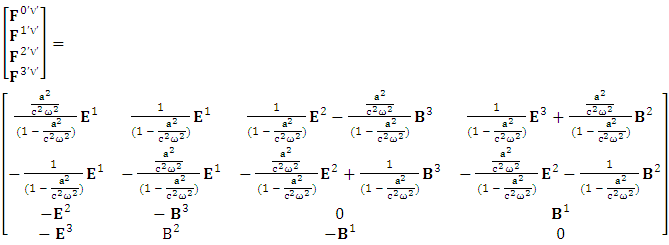 A new symmetry of electromagnetic field is emerged. Two terms of new symmetry along the diagonal areZero-point Term of Electric Field
A new symmetry of electromagnetic field is emerged. Two terms of new symmetry along the diagonal areZero-point Term of Electric Field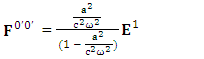
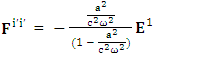
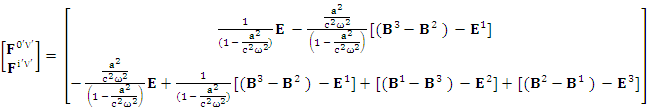 Electric Field:
Electric Field: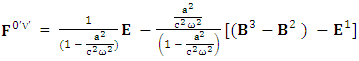
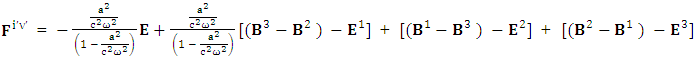
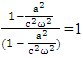 so the above relation simplifies to
so the above relation simplifies to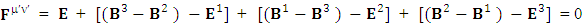
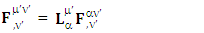
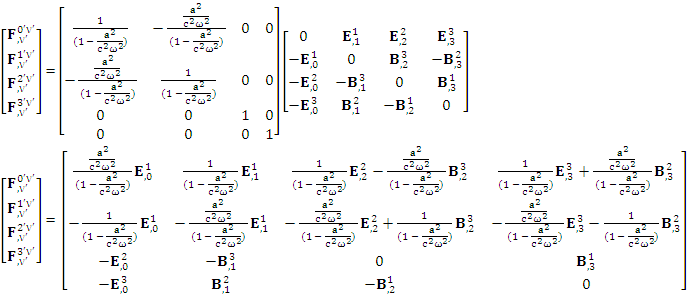 Zero-point terms of Maxwell’s equationsZero-point Term of Gauss’s Law
Zero-point terms of Maxwell’s equationsZero-point Term of Gauss’s Law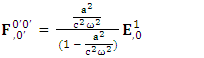
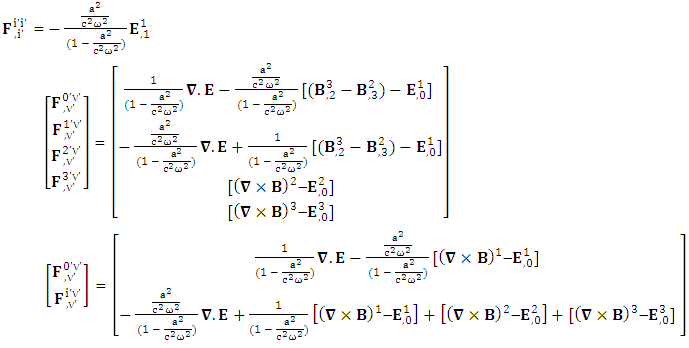
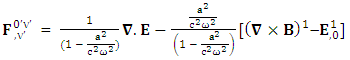
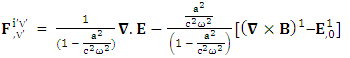
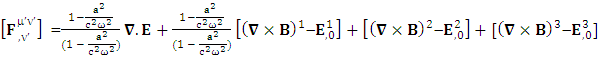
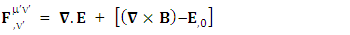

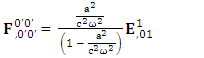
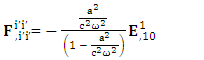
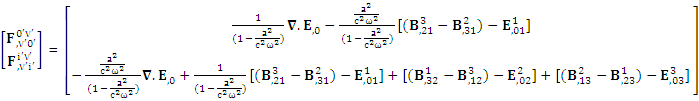 Conservation of Gauss’s LawConservation of Gauss’s law is affected by frame of reference
Conservation of Gauss’s LawConservation of Gauss’s law is affected by frame of reference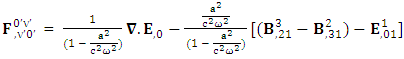 Conservation of Ampere’s is also affected by the frame of reference
Conservation of Ampere’s is also affected by the frame of reference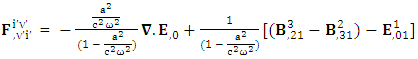
 Zero- point Conservation law
Zero- point Conservation law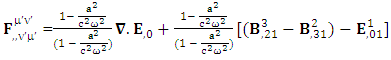
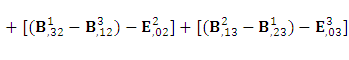 But the conservation law as a whole remains same for all observers
But the conservation law as a whole remains same for all observers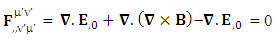
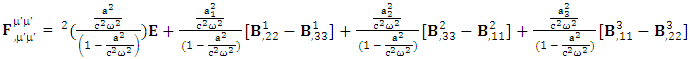
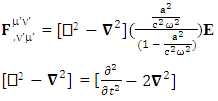
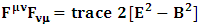
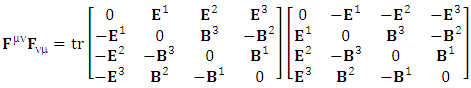
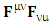 is decomposed in to 4 components that directly gives the trace of product
is decomposed in to 4 components that directly gives the trace of product 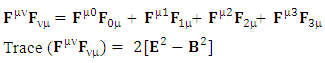
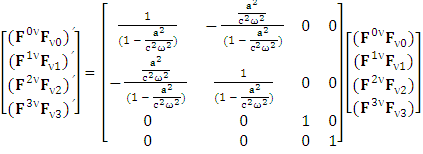 After multiplying, adding all the terms on left- and right-hand sides, we have
After multiplying, adding all the terms on left- and right-hand sides, we have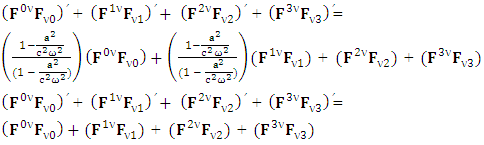 Now, putting the values of the terms in small brackets and of
Now, putting the values of the terms in small brackets and of 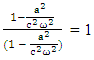 in above equation
in above equation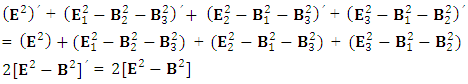
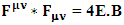
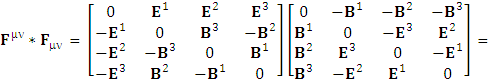
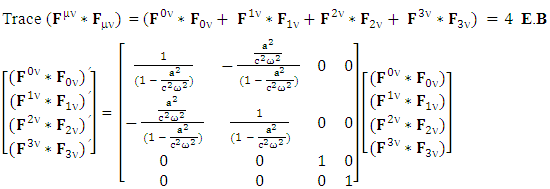 After multiplication, adding all the terms on left- and right-hand side
After multiplication, adding all the terms on left- and right-hand side 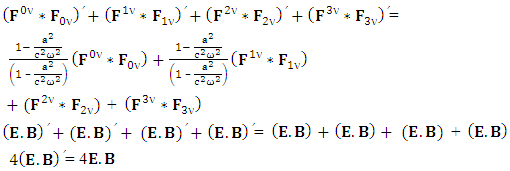

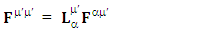
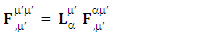
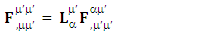

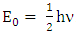 . Our model of electrodynamics, inertia and Gravitation in table-3, predicts outlandish results. The presence of zero-point energy via equation (1) in each column represents electrical energy, mechanical energy and gravitational energy respectively. They also incorporate the concept of Coulomb potential energy, inertial energy and Newtonian gravitational potential energy
. Our model of electrodynamics, inertia and Gravitation in table-3, predicts outlandish results. The presence of zero-point energy via equation (1) in each column represents electrical energy, mechanical energy and gravitational energy respectively. They also incorporate the concept of Coulomb potential energy, inertial energy and Newtonian gravitational potential energy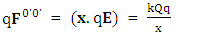
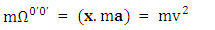
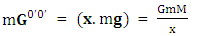
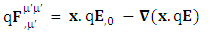
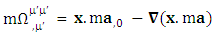
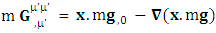
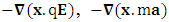 and
and 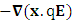 represent electric force, inertial force and gravitational force. The above equations represent power-force relation for electrodynamics, inertia and gravitation. As we know in special relativity that energy and momentum are unified. The next concept is power and force are unified. Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical energy, inertial energy and gravitational energy respectively via equation (7) of each column.
represent electric force, inertial force and gravitational force. The above equations represent power-force relation for electrodynamics, inertia and gravitation. As we know in special relativity that energy and momentum are unified. The next concept is power and force are unified. Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical energy, inertial energy and gravitational energy respectively via equation (7) of each column.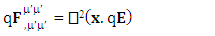
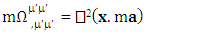
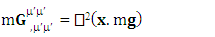

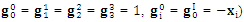

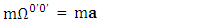

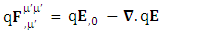
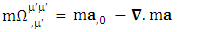
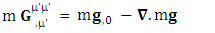
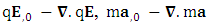 and
and 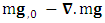 represent time varying electric force-Divergence of electric force, time varying inertial force-Divergence of force and time varying gravitational force-Divergence of gravitational force. Here time varying force and divergence of force are unified. In modern mechanics, time varying force is known as Yank.Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical force, Newton’s 2nd law and gravitational force respectively via equation (7) of each column.
represent time varying electric force-Divergence of electric force, time varying inertial force-Divergence of force and time varying gravitational force-Divergence of gravitational force. Here time varying force and divergence of force are unified. In modern mechanics, time varying force is known as Yank.Finally, we consider the case of conservation law by Einstein’s summation convention method where zero-point conservation law represent 4D wave of electrical force, Newton’s 2nd law and gravitational force respectively via equation (7) of each column.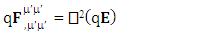
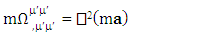
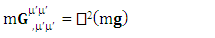

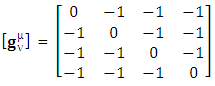
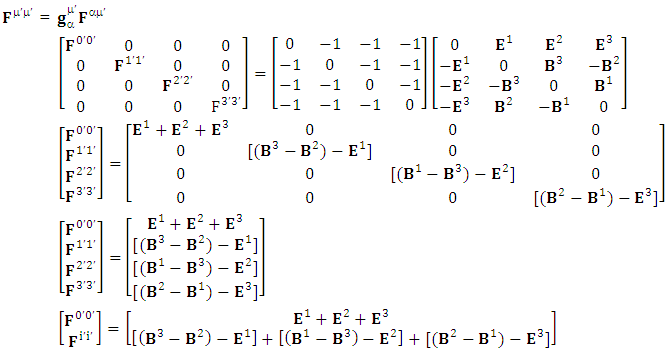

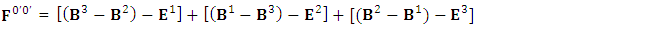
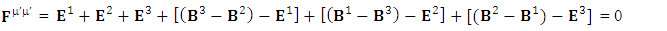
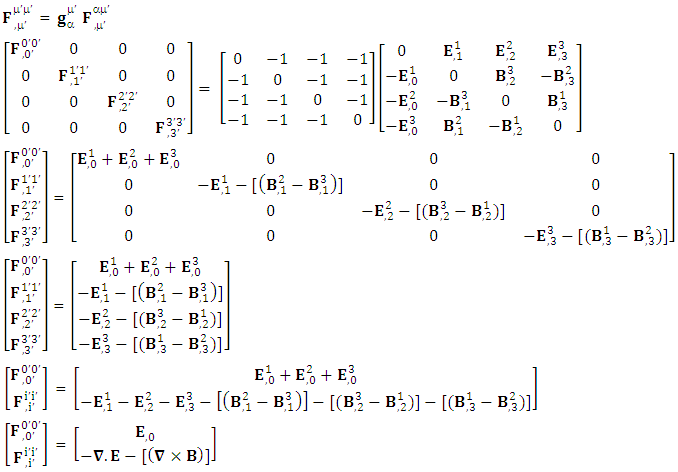

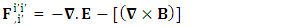
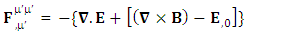
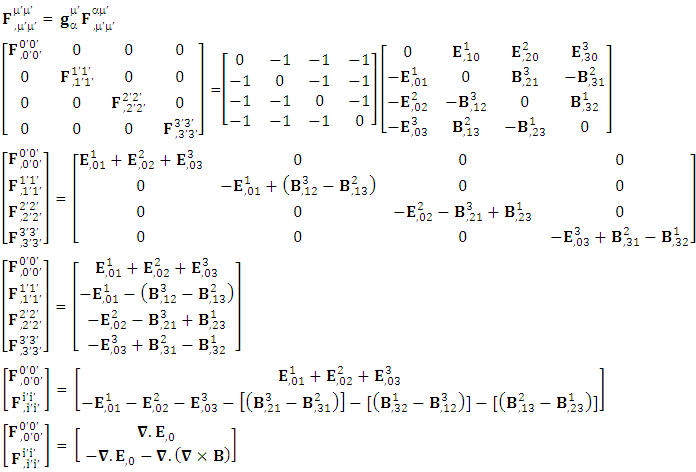

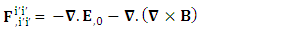
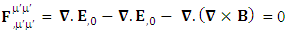


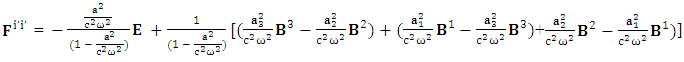
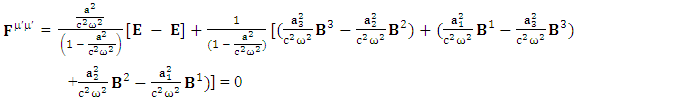
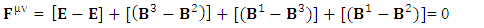

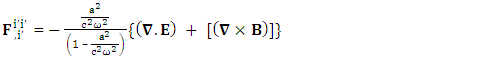
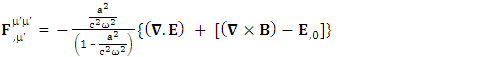
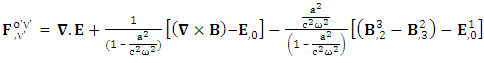
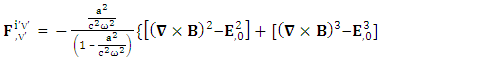
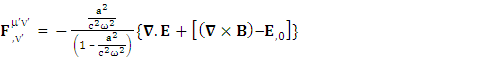



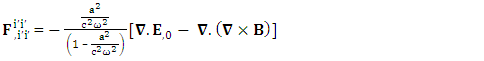
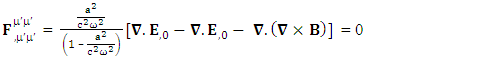
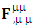 of conservation law constitutes, combination of conservation of Gauss’s law and Ampere’s law. Usual conservation law holds as it is
of conservation law constitutes, combination of conservation of Gauss’s law and Ampere’s law. Usual conservation law holds as it is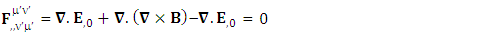

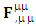 is transformed into 4D EM wave with some extra terms.Zero-Point 4D EM Wave
is transformed into 4D EM wave with some extra terms.Zero-Point 4D EM Wave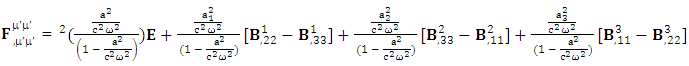
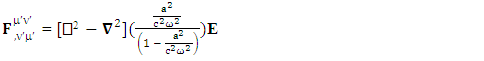
 is the consequence of transformation of conservation law based on STL for 4-vectors and tensors. It is entirely new result. It possesses 6 dimensions of space and one dimension of time. As there are 4 dimensions of zero-point and 4 dimensions of usual electrodynamics so it represents 8D model of electrodynamics. Our previous models [1,2], also represent 8D models of electrodynamics, inertia and gravitation. It seems to be a string theory of electrodynamics where zero-point electrodynamics has a definite physical significance as each term has a clear source.The contemporary models on electrodynamics in noninertial frame by Scorgie [3] doesn’t possess the explanation of reference frame. Atwater [4] considers Galilean metric as the representative of noninertial metric that is a special case of our noninertial metric [2]. References [5] and [6] are based on differential forms and usual Lorentz transformation that are replaced by our ULTM. Fedosin’s model [7] Lorentz invariance of gravito-electromagnetism without STL for 4-vectors and tensors. Nicolie’s model [8] based on monad algebra and Costa [9] on Lie derivatives are of highly importance in accelerating and rotating systems but these models do not discuss the transformation of conservation law and the extra terms in Maxwell’s equations do not have clear origin like ours. Furthermore, wave equations are not discussed. Maxwell’s equations in accelerating metric have been developed in our earlier model [2], in model-4, page-210. The accelerating expansion of our universe [10-12] can be viewed in the light of our model. Maxwell’s equations in noninertial frame based on connection coefficients initiated the need of STL for 4-vectors and tensors and ULTM in 2D and 4D [13], case# 7, page-4.
is the consequence of transformation of conservation law based on STL for 4-vectors and tensors. It is entirely new result. It possesses 6 dimensions of space and one dimension of time. As there are 4 dimensions of zero-point and 4 dimensions of usual electrodynamics so it represents 8D model of electrodynamics. Our previous models [1,2], also represent 8D models of electrodynamics, inertia and gravitation. It seems to be a string theory of electrodynamics where zero-point electrodynamics has a definite physical significance as each term has a clear source.The contemporary models on electrodynamics in noninertial frame by Scorgie [3] doesn’t possess the explanation of reference frame. Atwater [4] considers Galilean metric as the representative of noninertial metric that is a special case of our noninertial metric [2]. References [5] and [6] are based on differential forms and usual Lorentz transformation that are replaced by our ULTM. Fedosin’s model [7] Lorentz invariance of gravito-electromagnetism without STL for 4-vectors and tensors. Nicolie’s model [8] based on monad algebra and Costa [9] on Lie derivatives are of highly importance in accelerating and rotating systems but these models do not discuss the transformation of conservation law and the extra terms in Maxwell’s equations do not have clear origin like ours. Furthermore, wave equations are not discussed. Maxwell’s equations in accelerating metric have been developed in our earlier model [2], in model-4, page-210. The accelerating expansion of our universe [10-12] can be viewed in the light of our model. Maxwell’s equations in noninertial frame based on connection coefficients initiated the need of STL for 4-vectors and tensors and ULTM in 2D and 4D [13], case# 7, page-4.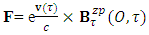
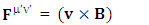
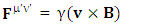
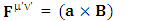
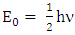 , we do have a very rich structure of zero-point electric energy in model-2, in noninertial coordinate metric via equation (1). Zero-point results are possible only by means of transformation of electrodynamics based on STL for 4-vectors and tensors where there is no extra assumptions or speculations. This relation is also obtained in 4D Lorentz transformation presented in appendix.
, we do have a very rich structure of zero-point electric energy in model-2, in noninertial coordinate metric via equation (1). Zero-point results are possible only by means of transformation of electrodynamics based on STL for 4-vectors and tensors where there is no extra assumptions or speculations. This relation is also obtained in 4D Lorentz transformation presented in appendix.

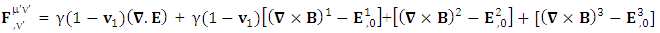



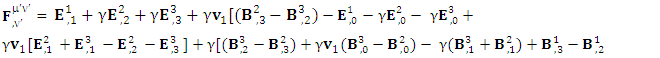
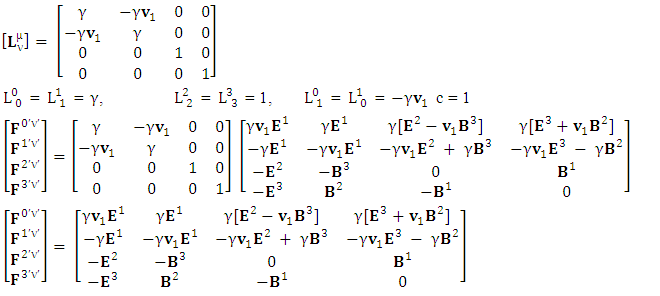



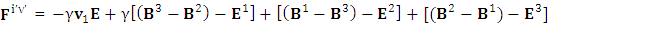
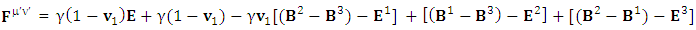
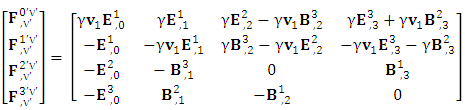 Zero-Point Term of Gauss’s Law
Zero-Point Term of Gauss’s Law


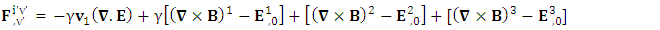
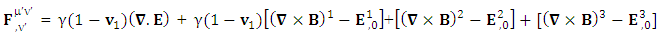
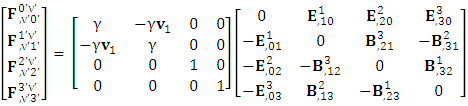
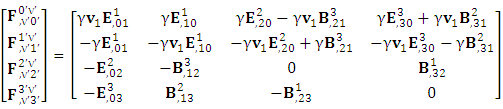 Zero-Point Term of Conservation of Gauss’s Law
Zero-Point Term of Conservation of Gauss’s Law


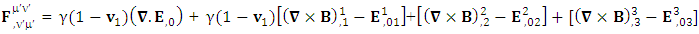
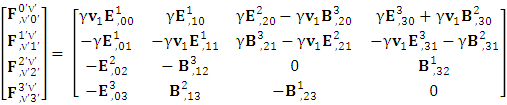 Zero-Point Term of Conservation of Gauss’s Law
Zero-Point Term of Conservation of Gauss’s Law


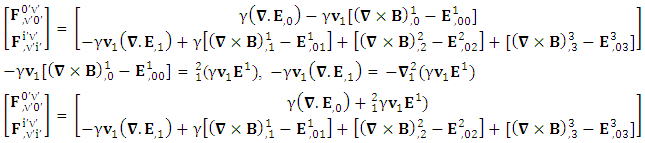 Conservation of Gauss’s Law
Conservation of Gauss’s Law
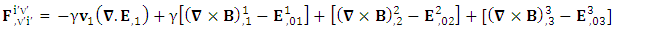
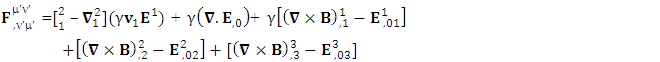




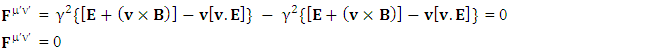

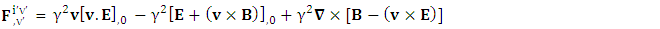
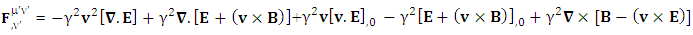
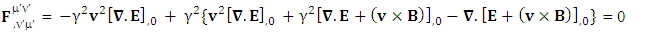

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML