Naveed Hussain 1, Hassnain Abdullah Hussain 2, Ather Qayyum 3
1Department of Physics, Punjab College Abdul Hakeem, Multan Division, Pakistan
2Institute of Physics, Bahauddin Zakaria University, Multan, Pakistan
3Department of Mathematics, ISP University, Multan, Pakistan
Correspondence to: Ather Qayyum , Department of Mathematics, ISP University, Multan, Pakistan.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
An un-orthdoxial and entirely different method of derivation of electromagnetic laws from each other based on universal spacetime exchanger matrices (USEM) are developed by the application of single transformation law (STL) for 4-vectors and tensors. Results are obtained in a single step operation as compared to contemporary approaches. The important property of these matrices is that they behave in such a way that space and time components are exchanged but the spacetime as a whole remains same that satisfies Einstein’s principle of relativity (EPR) as well as symmetry principle. As a result of transformation of electromagnetic field (EMF), Maxwell’s equations (ME) and conservation law written in matrix form gave rise to new symmetry along the diagonal of the matrix. Fortunately, these new symmetry terms or zero-point physical terms not only obey EPR, conservation law but also symmetry principle. This model is an entirely new framework, not only valid to derive electromagnetic laws in tensor form but also exchange of time and space components of 4-vectors such that 4-vector as a whole remains same. Four models are developed consisting of two physical USEM and two numerical. The existing models in this context, do not have such simplicity and clarification in a single step operation in the contemporary literature. These models are expected to explain the activities of hidden universe through zero-point relations. The outstanding consequence of this approach is that all the spacetime laws of physics remain same for all observers. Usual Lorentz transformation matrix in this new scheme also shows spacetime exchange but doesn’t validate conservation law to satisfy EPR and symmetry principle.
Keywords:
Universal Spacetime Exchanger Matrices, Derivation of Electromagnetic Laws, New Symmetry of EMF, Zero-Point Origin of Electric Field, Time varying Electric Field, Universality of Spacetime laws of physics
Cite this paper: Naveed Hussain , Hassnain Abdullah Hussain , Ather Qayyum , Spacetime Exchange Method of Derivation of Electromagnetic Laws Based on Symmetry of Universal Lorentz Transformation Matrix, International Journal of Theoretical and Mathematical Physics, Vol. 14 No. 2, 2024, pp. 17-39. doi: 10.5923/j.ijtmp.20241402.01.
1. Introduction
Even though, electrodynamics is one of the well-understood physical theories but still very interesting aspects of relativistic electrodynamics have not been appreciated in tensor notation. Almost all of the physicists are limited to the transformation of electromagnetic field only in tensor form whereas transformation of Maxwell’s equations and electromagnetic conservation law in components of tensor form provide far reaching consequences that have been un-noticed by the contemporary physicists. In this paper, we derive electromagnetic laws from each other in a very simple and straightforward method by using USEM such that space and time components are exchanged but the spacetime as a whole remains same in its original form. Here, electromagnetic laws are exchanged without altering the total result like exchange of electric and magnetic field where electromagnetic field as a whole remains same. Similarly, Gauss’s law and ampere’s law are exchanged but Maxwell’s equations in tensor form remain same. Exchange in conservation law also holds in the same way. The emergence of zero-point terms along the diagonals of EMF, ME and conservation law are the consequence of STL for 4-vectors and tensors. These terms responsible for the validity of conservation law and indicate the existence of hidden world. The presence of zero-point terms are predicted by our earlier models [1-2] where zero-point origin of 4D electromagnetic wave is obtained along the diagonal of the conservation law. Dual relations of electrodynamics are also presented where exchange of Gauss’s law for magnetism and Faraday’s law is of more importance that tells us about the zero-point source of magnetism. There is only one important model in the existing literature by Field J. H. [3] who has discussed about spacetime exchange invariance in the derivation of Ampere’s law and Faraday’s law but doesn’t possess such simplicity and generality. His results are compared in the form of table in the discussion and comparison section. It was legend Einstein who perceived the idea that magnetism is the relativistic consequence of motion of electric charge. He introduced the concept of 4-vector potential to link electrostatics with magnetism based on Lorentz transformation. Later on, many physicists started to derive Maxwell’ equations from electrostatics [4-13]. Melvin Shwartz work [14] to derive Maxwell’s equations from electrostatics by utilizing the concept of 4 vector potential and Lorentz transformation is no doubt very useful in the contemporary literature on relativistic electrodynamics and cited by enormous number of authors. His text book on principles of electrodynamics is a master piece on standard electrodynamics. There is only one model by H. A. Atwater [6] who perused the transformation of Maxwell’s equations in tensor form by using Galilean transformation but he also left the case of transformation of conservation law. Our approach is entirely different from the contemporary world. For this purpose, first USEM was constructed in terms of numbers. This matrix transformed Maxwell’s equations such that Ampere’s law transformed Gauss’s law and Gauss’s law to Ampere’s law. Similar behavior was observed in the transformation of 4-current density. The next challenge was to develop a physical USEM. The discovery of ULTM for inertial and noninertial frame in 2D served the purpose of USEM but in an unusual technique. Besides this, two more matrices in terms of numbers provided the same results one of which acts as a NOT GATE matrix in computer science. Our model is so straightforward that the required results are obtained in a single step operation. There are seven USEM at the moment. Only four cases will be presented with calculations and remaining three are applied on transformation of 4-current density as the mathematical framework is same for all.
1.1. Development of Electrodynamic Models Based on USEM
Notations in this model are adopted according to modern approach of relativity. Greek alphabets 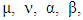 …runs from 0 to 3 and Latin letters i, j, k, .. from 1 to 3. Comma (,) denote partial differentiation e. g.
…runs from 0 to 3 and Latin letters i, j, k, .. from 1 to 3. Comma (,) denote partial differentiation e. g. 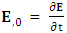 Partial derivative of electric field w. r. t. time,
Partial derivative of electric field w. r. t. time, 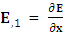 Partial derivative of electric field w. r. t. x-axis,
Partial derivative of electric field w. r. t. x-axis, 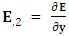 Partial derivative of electric field w. r. t. y-axis,
Partial derivative of electric field w. r. t. y-axis, 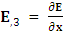 Partial derivative of electric field w. r. t. z-axis,
Partial derivative of electric field w. r. t. z-axis, 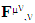 means 4-dimensional or spacetime partial derivative of EMF tensor.4-dimensional Coordinates
means 4-dimensional or spacetime partial derivative of EMF tensor.4-dimensional Coordinates 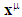 = (x0, x1, x2, x3) = (ct, x, y, z) = (ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that
= (x0, x1, x2, x3) = (ct, x, y, z) = (ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that 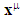 is the unification of time and space. The dimensions of all components are that of length.
is the unification of time and space. The dimensions of all components are that of length.
1.2. Universal Lorentz Transformation Matrix (ULTM) in 2D
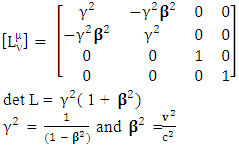 | (1) |
The inverse of matrix (1) is calculated as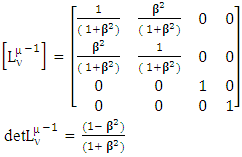 | (2) |
1.3. Adjusting ULTM in 2D as USEM
By adjusting a matrix along the secondary or anti-diagonal diagonal of a matrix becomes USEM. Such matrices exist in Pauli’s matrices as well as in Dirac matrices.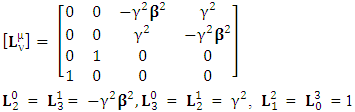 | (3) |
Model-1: Application of STL and USEM in Electrodynamics
1.4. Spacetime Exchange symmetry of 4-Current Density
The universal nature of 4-current density 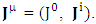 EPR demands universal nature of laws of physics independent of inertial and noninertial frame. Our approach is within the domain of EPR, symmetry principle and conservation law.Transformation of 4-Current Density
EPR demands universal nature of laws of physics independent of inertial and noninertial frame. Our approach is within the domain of EPR, symmetry principle and conservation law.Transformation of 4-Current Density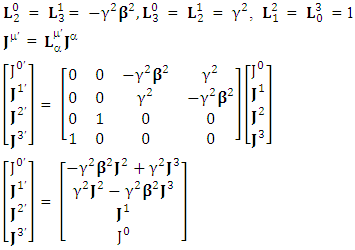 | (4) |
Adding the terms of space components on both sides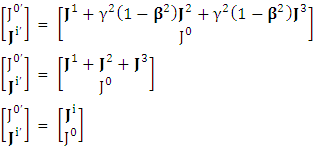
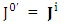 | (5) |
Charge density is transformed into current density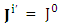 | (6) |
Current density is transformed into charge density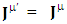 | (7) |
4-current density as a whole remains same. Covariant 4-current density remains same for all observers.
1.5. Spacetime Exchange Symmetry of Electromagnetic Field
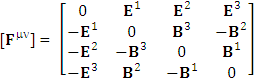 | (8) |
EMF tensor 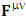 is related to its components electric field E and magnetic field B as follows
is related to its components electric field E and magnetic field B as follows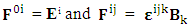 EMF tensor in component form is needed to get new terms along the diagonal of EMF. It is represented as 4 by 4 antisymmetric matrix
EMF tensor in component form is needed to get new terms along the diagonal of EMF. It is represented as 4 by 4 antisymmetric matrix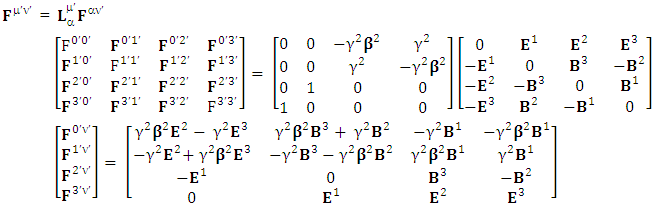 | (9) |
We can see the shifting of last three rows of EMF after multiplication to first three and first row goes to fourth row. In other words, magnetic field part goes to electric field and electric goes to magnetic field part with two zeroes appearing along the secondary diagonal. Two zeros are observed as the transformation matrix is two dimensional.Zero-point terms of Electric Field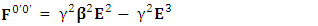 | (10) |
Zero-point terms of Magnetic Field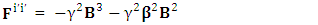 | (11) |
Zero-point terms of Electromagnetic Field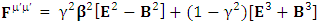 | (12) |
The set of singularities of EMF doesn’t constitute any definite physical law but they contribute in the structure of electric and magnetic field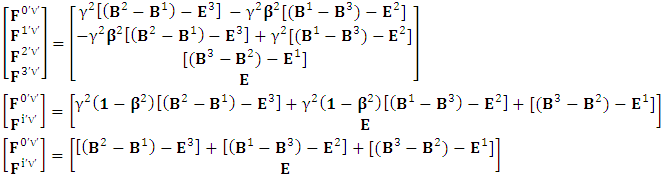 Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following
Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following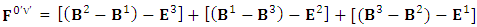 | (13) |
Electric field is transformed in to magnetic field in tensor form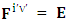 | (14) |
Magnetic field is transformed in to electric fieldIn other words, Electric field and magnetic field are exchanged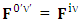 | (15) |
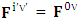 | (16) |
Electromagnetic field becomes zero due to anti-symmetry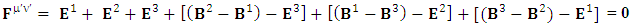 | (17) |
Right side of equation (17) can be written in tensor form in its original form as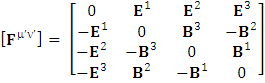 | (18) |
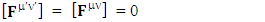 | (19) |
Antisymmetric EMF remains same after transformation in its original form.
1.6. Spacetime Exchange Symmetry of Maxwell’s Equations
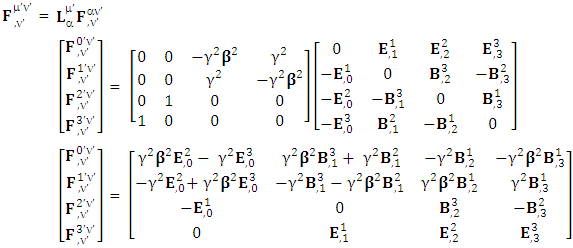 | (20) |
Zero-point terms of Gauss’s Law | (21) |
Zero-point terms of Ampere’s Law | (22) |
Zero-point terms of Maxwell’s equations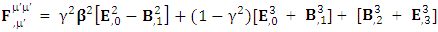 | (23) |
The zero-point terms do not constitute any definite physical law but they contribute for the validity of form invariance of maxwell’s equations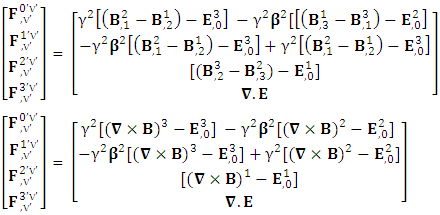 Adding space components on both sides
Adding space components on both sides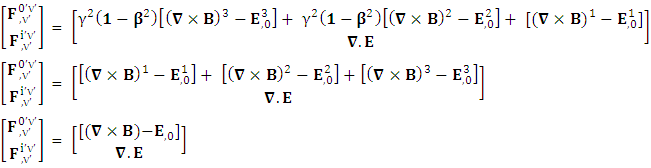 Gauss’s law is transformed into Ampere’s law
Gauss’s law is transformed into Ampere’s law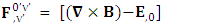 | (24) |
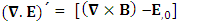 | (25) |
Ampere’s law is transformed into Gauss’s law | (26) |
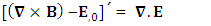 | (26a) |
Sum of Gauss’s law and Ampere’s law remains same for all observers as per required by EPR 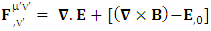 | (27) |
1.7. Spacetime Exchange Symmetry of Conservation Law
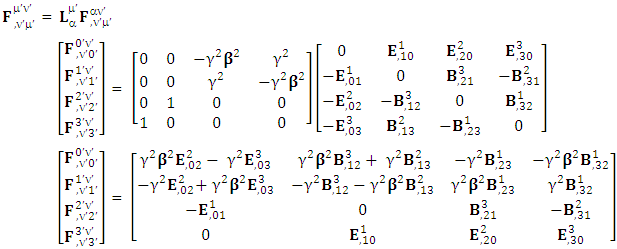 | (28) |
Zero-point terms of Conservation of Gauss’s Law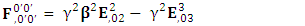 | (29) |
Zero-point terms of Conservation of Ampere’s Law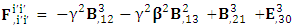 | (30) |
Zero-point terms of Total Conservation Law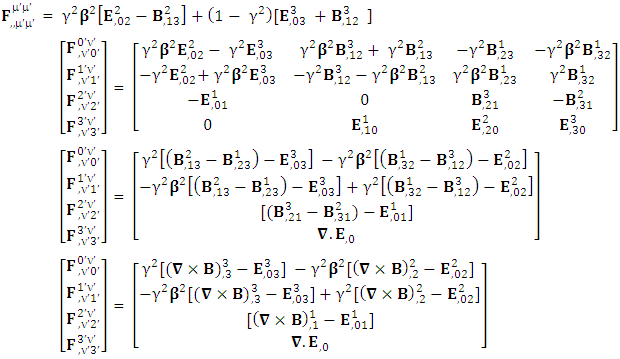 | (31) |
Adding space components on both sides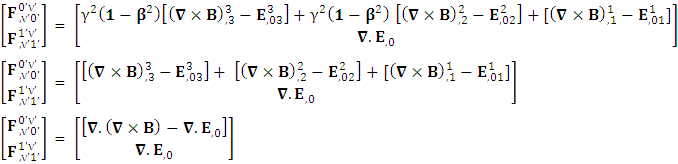 Conservation of Gauss’s law is transformed into conservation of Ampere’s law
Conservation of Gauss’s law is transformed into conservation of Ampere’s law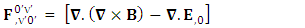 | (32) |
Conservation of Ampere’s law is transformed into conservation of Gauss’s law | (33) |
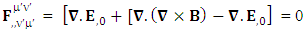 | (34) |
Conservation law remains same after transformation in its original form required by symmetry principle and EPR.
1.8. Dual of Electrodynamic Laws Under Physical USEM
There are two parts of electrodynamics consisting of source equations and field equations. Source equations consist of gauss’s law and Ampere’s law whereas field equations contain Gauss’s law for magnetism and Faraday’s law. There is a simple relation between source equations and field equations. Replacing electric field E by magnetic field B and magnetic field by negative of electric field – E. The dual of electromagnetic field tensor 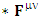 is denoted by putting star on it as
is denoted by putting star on it as 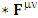 .Dual of Electromagnetic Field
.Dual of Electromagnetic Field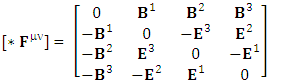 | (35) |
Dual EMF tensor 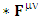 is related to its components electric field E and magnetic field B as follows
is related to its components electric field E and magnetic field B as follows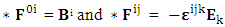
1.9. Spacetime Exchange Symmetry of Electromagnetic Field
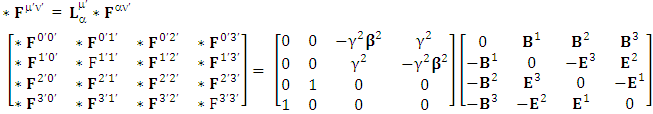 | (36) |
Since the mathematical framework for dual is same as above so we write the results directlyZero-point terms of dual Electric Field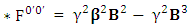 | (37) |
Zero-point terms of dual Magnetic Field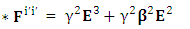 | (38) |
Zero-point terms of Dual Electromagnetic Field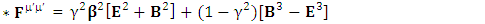 | (39) |
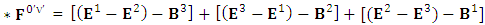 | (40) |
Dual Electric field is transformed in to dual of magnetic field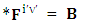 | (41) |
Dual of Magnetic field is transformed in to dual electric fieldIn other words, dual Electric field and dual magnetic field are exchanged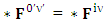 | (42) |
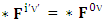 | (43) |
But the dual of electromagnetic field becomes zero due to anti-symmetry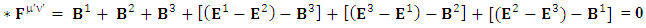 | (44) |
Right side of equation (17) can be written in tensor form in its original form as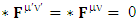 | (45) |
Antisymmetric EMF remains same after transformation in its original form.
1.10. Spacetime Exchange Symmetry of Dual of Maxwell’s Equations
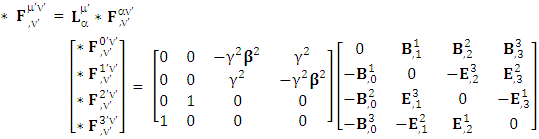 | (46) |
Zero-point terms of Gauss’s Law for magnetism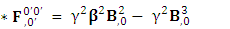 | (47) |
Zero-point terms of Faraday’s Law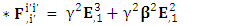 | (48) |
Zero-point terms of Dual of Maxwell’s equations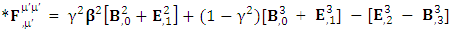 | (49) |
Gauss’s law for magnetism is transformed into Faraday’s law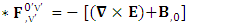 | (50) |
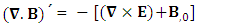 | (51) |
Faraday’s law is transformed into Gauss’s law for magnetism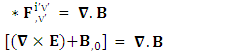 | (52) |
Sum of Gauss’s law for magnetism and Faraday’s law remains same for all observers. 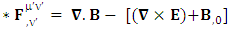 | (53) |
1.11. Spacetime Exchange Symmetry of dual Conservation Law
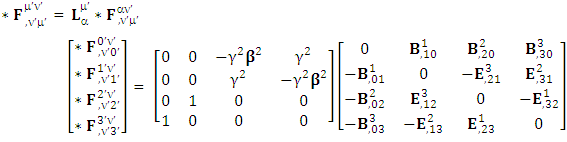 | (54) |
Zero-point terms of Conservation of Gauss’s Law for magnetism | (55) |
Zero-point terms of Conservation of Faraday’s Law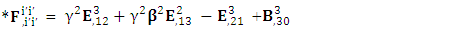 | (56) |
Zero-point terms of dual Conservation Law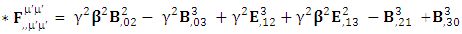 | (57) |
Conservation of Gauss’s law for magnetism is transformed into conservation of Faraday’s law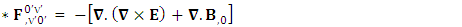 | (58) |
Conservation of Faraday’s law is transformed into conservation of Gauss’s law for magnetism | (59) |
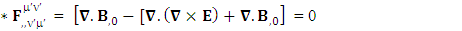 | (60) |
Dual conservation law remains same after transformation in its original form required by symmetry principle and EPR.
2. Model-2: Spacetime Exchange Symmetry of Electromagnetic Field (Potential Formulation)
2.1. Derivation of Electromagnetic Laws in Terms of 4-Vetor Potential
In the contemporary world, there is only one model by J.H. Field [2] that discusses spacetime exchange invariance and applies in the derivation of electromagnetic laws. We highly appreciate the work of JH Field who initiated this framework. There is always room for improvement. His adventure of re-derivation of Lorentz transformation matrix is actually looking for USEM that can fulfill the requirement of principle of relativity. Furthermore, his assertion on the use of 4-vector potential seems to be a necessary for the derivation of electromagnetic laws. We have found USEM without any assumption. In our model 4-velocity is same for all observers where speed of light c is the time component of 4-velocity. We have developed the framework for both cases viz. in terms of electric and magnetic field and in terms of 4-vector potential. STL for 4-vectors and tensors predicts zero-point results like 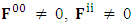 having no counter in the contemporary literature.The relation between electromagnetic field tensor
having no counter in the contemporary literature.The relation between electromagnetic field tensor 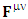 and 4-vector potential is given by
and 4-vector potential is given by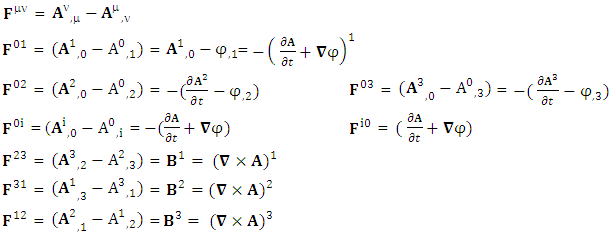 | (2.1) |
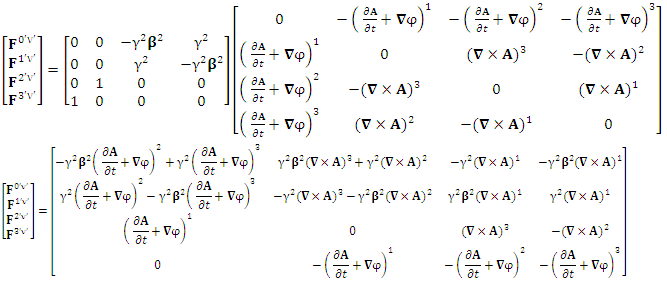 | (2.2) |
Zero-point new symmetry terms of Electric Field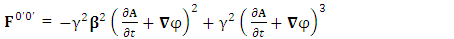 | (2.3) |
Zero-point new symmetry terms of Magnetic Field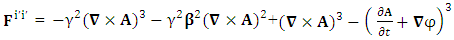 | (2.4) |
These terms are the consequence of STL for 4-vectors and tensors and contribute as an integral part of the theory.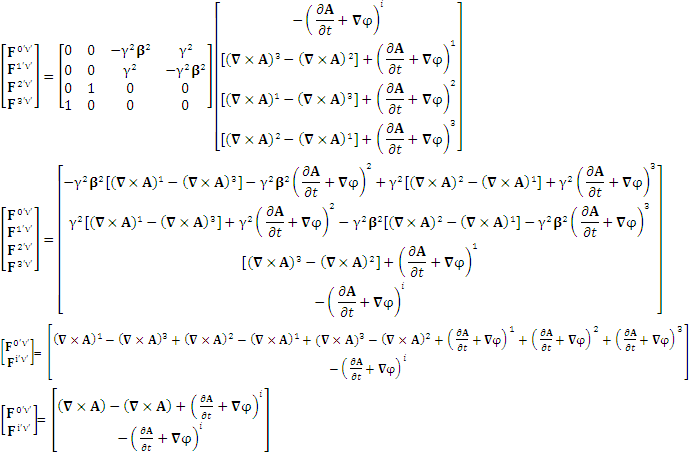 Electric field is transformed into magnetic field
Electric field is transformed into magnetic field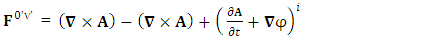 | (2.5) |
Magnetic field is transformed in to electric field | (2.6) |
Electromagnetic field remains same for all observers in its original anti-symmetric form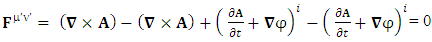 | (2.7) |
2.2. Spacetime Exchange Symmetry of Maxwell’s Equations
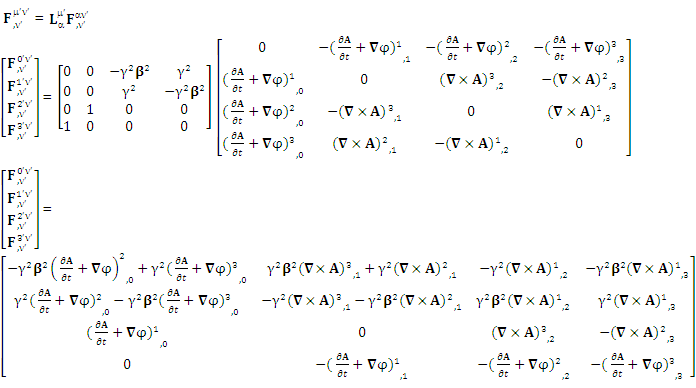 | (2.8) |
Zero-point new symmetry terms of Gauss’s Law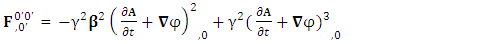 | (2.9) |
Zero-point new symmetry terms of Ampere’s Law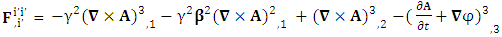 | (2.10) |
Zero-point new symmetry terms of Maxwell’s equations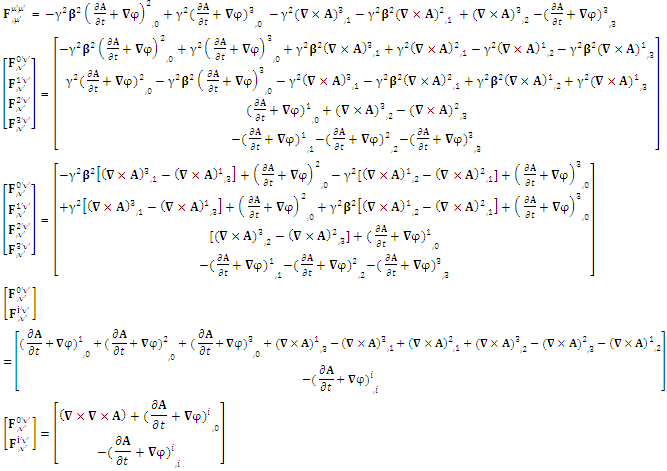 | (2.11) |
Gauss’s Law is transformed into Ampere’s law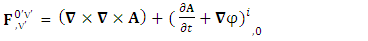 | (2.12) |
Ampere’s Law is transformed into Gauss’s law | (2.13) |
Maxwell’s equations in tensor form as the combination of Gauss’s law and Ampere’s law remain same for all observers 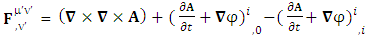 | (2.14) |
2.3. Spacetime Exchange Symmetry of Conservation Law
Zero-point terms of conservation of Gauss’s law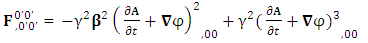 | (2.15) |
Zero-point terms of conservation of Ampere’s law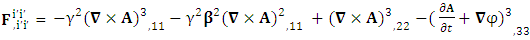 | (2.16) |
Zero-point of total conservation law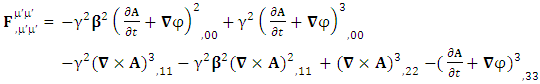 | (2.17) |
These new symmetry terms are necessary to validate the conservation law. Conservation of Gauss’s Law is transformed into conservation of Ampere’s law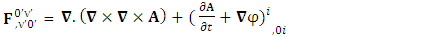 | (2.18) |
Conservation of Ampere’s Law is transformed into conservation of Gauss’s law | (2.19) |
Conservation law in tensor form as the combination of conservation of Gauss’s law and Ampere’s law remains same for all observers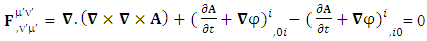 | (2.20) |
2.4. Spacetime Exchange symmetry of Spacetime Operator
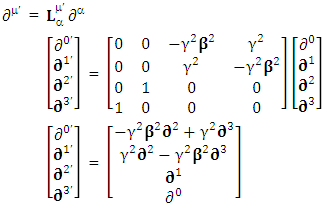 | (2.21) |
Adding the terms of space components on both sides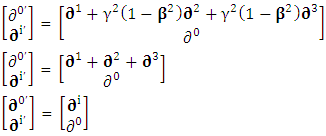 Time derivative operator is transformed into space operator
Time derivative operator is transformed into space operator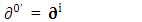 | (2.22) |
Space derivative operator is transformed into time derivative operator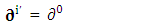 | (2.23) |
Spacetime derivative operator as a whole remains same for all observers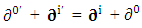 Contravariant spacetime derivative operator remains contravariant as a universal operator
Contravariant spacetime derivative operator remains contravariant as a universal operator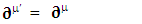 | (2.24) |
Similarly, covariant spacetime derivative operator 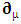 remains covariant as a universal operator
remains covariant as a universal operator 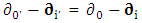 | (2.25) |
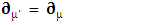 | (2.26) |
4-vector contravariant potential 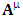 and covariant potential
and covariant potential 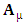 show the same spacetime exchange invariance.
show the same spacetime exchange invariance.
2.5. Spacetime Exchange Symmetry of Inner Product of 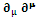 or 4D Wave Operator
or 4D Wave Operator 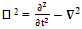
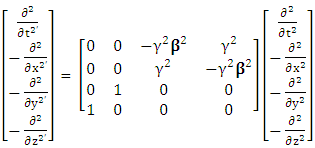 | (2.27) |
Rearranging all terms on left- and right-hand side, we get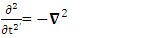 | (2.28) |
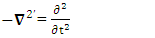 | (2.29) |
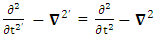 | (2.30) |
 | (2.31) |
4-D wave operator or de Alembertian operator remains same for all observers.
3. Model-3: Spacetime Exchange Symmetry of Electromagnetic Field (Circular Geometry)
The following matrix is a universal transformation that acts as a physical spacetime exchanger matrix under which all the spacetime laws of physics remain same for all observers in their original form after transformation.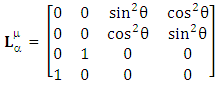 | (3.1) |
3.1. Spacetime Exchange Symmetry of Electromagnetic Field
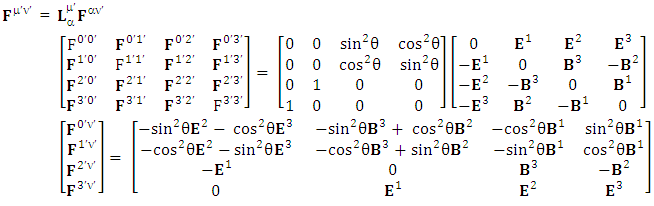 | (3.2) |
We can see the shifting of last three rows of EMF after multiplication to first three and first row goes to fourth row. In other words, magnetic field part goes to electric field and electric goes to magnetic field part with two zeroes appearing along the secondary diagonal. Two zeros are observed as the transformation matrix is two dimensional.Zero-point terms of Electric Field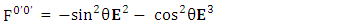 | (3.3) |
Zero-point terms of Magnetic Field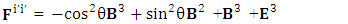 | (3.4) |
Zero-point terms of Electromagnetic Field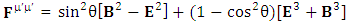 | (3.5) |
The set of singularities of EMF doesn’t constitute any definite physical law but they contribute in the structure of electric and magnetic field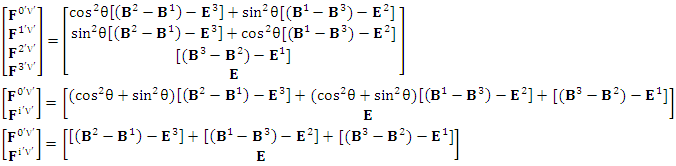 Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following
Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following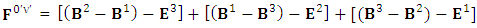 | (3.6) |
Electric field is transformed in to magnetic field | (3.7) |
Magnetic field is transformed in to electric fieldIn other words, Electric field and magnetic field are exchanged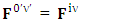 | (3.8) |
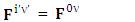 | (3.9) |
But electromagnetic field becomes zero due to anti-symmetry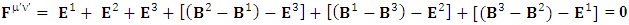 | (3.10) |
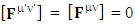 | (3.11) |
Antisymmetric EMF remains same after transformation in its original form.
3.2. Spacetime Exchange Symmetry of Maxwell’s Equations
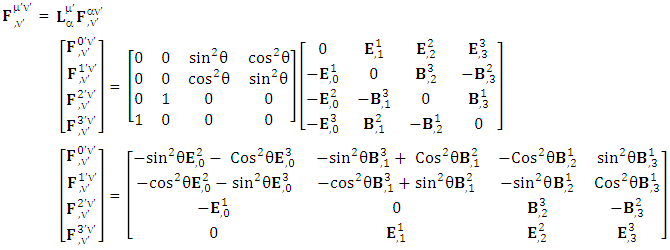 | (3.12) |
Zero-point terms of Gauss’s Law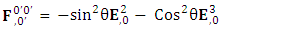 | (3.13) |
Zero-point terms of Ampere’s Law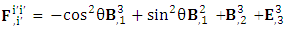 | (3.14) |
Zero-point terms of Maxwell’s equations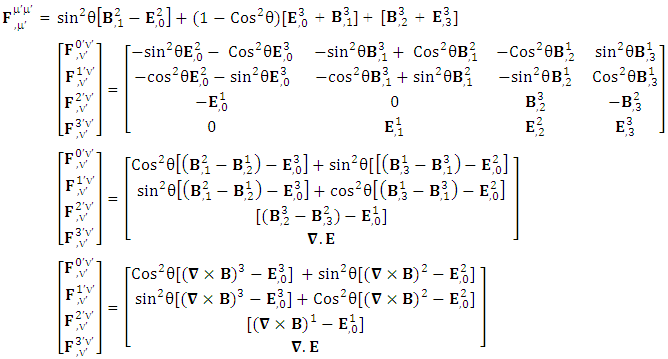 | (3.15) |
Adding space components on both sides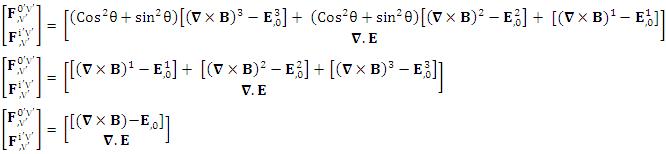 Gauss’s law is transformed into Ampere’s law
Gauss’s law is transformed into Ampere’s law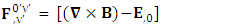 | (3.16) |
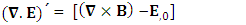 | (3.17) |
Ampere’s law is transformed into Gauss’s law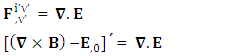 | (3.18) |
Sum of Gauss’s law and Ampere’s law remains same for all observers as per required by EPR 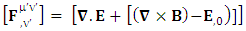 | (3.19) |
3.3. Spacetime Exchange Symmetry of Conservation Law
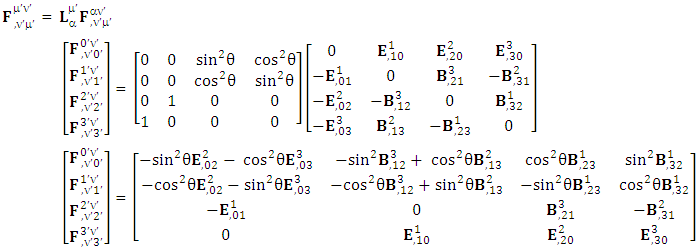 | (3.20) |
Zero-point terms of Conservation of Gauss’s Law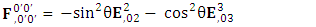 | (3.21) |
Zero-point terms of Conservation of Ampere’s Law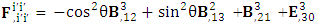 | (3.22) |
Zero-point terms of Total Conservation Law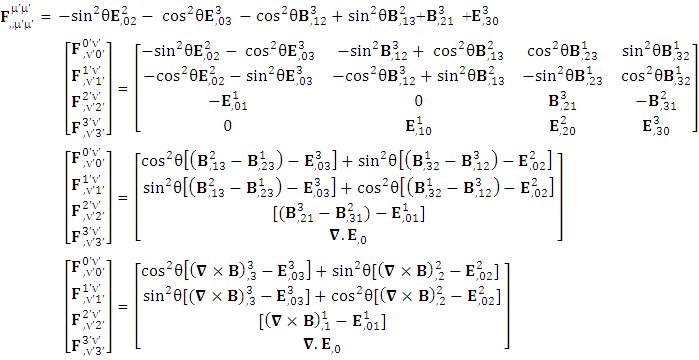 | (3.23) |
Adding space components on both sides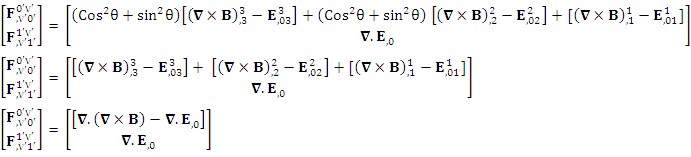 Conservation of Gauss’s law is transformed into conservation of Ampere’s law
Conservation of Gauss’s law is transformed into conservation of Ampere’s law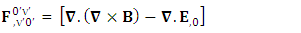 | (3.24) |
Conservation of Ampere’s law is transformed into conservation of Gauss’s law | (3.25) |
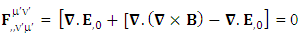 | (3.26) |
4. Model-4: Universal Spacetime Exchanger Matrix in 4D
This is one of the strange numerical matrices that acts as USEM such that its inverse also behaves as USEM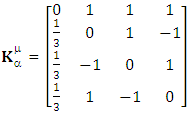 | (4.1) |
4.1. Transformation of EMF
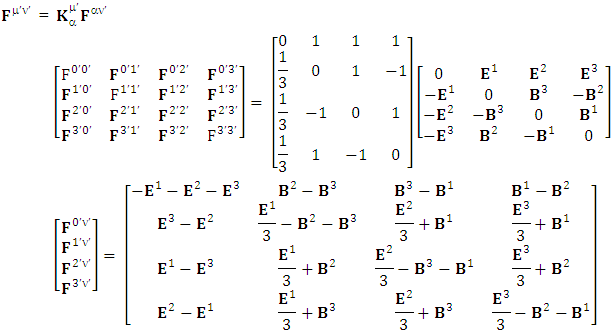 | (4.2) |
Origin of electric Field is the temporal singularity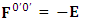 | (4.3) |
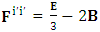 | (4.4) |
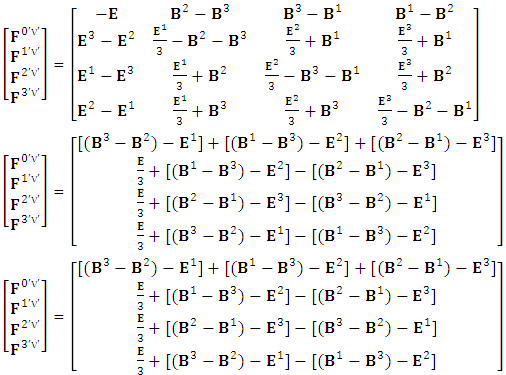 Adding space components on both sides
Adding space components on both sides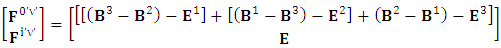
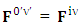 | (4.5) |
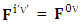 | (4.6) |
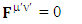 | (4.7) |
Electromagnetic field remains same for all observers in its original form after transformation.
4.2. Transformation of Maxwell’s Equations
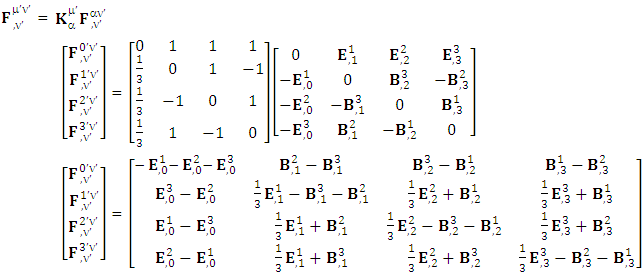 | (4.8) |
Zero-Point origin of Gauss’s as time varying electric field | (4.9) |
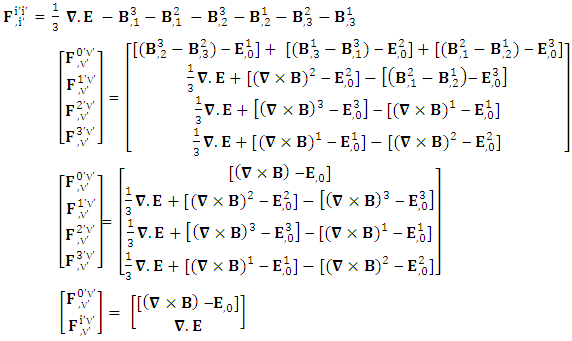 | (4.10) |
Gauss’s law is transformed into Ampere’s law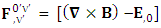 | (4.11) |
Ampere’s law is transformed into Gauss’s law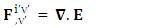 | (4.12) |
4.3. Transformation of Conservation Law
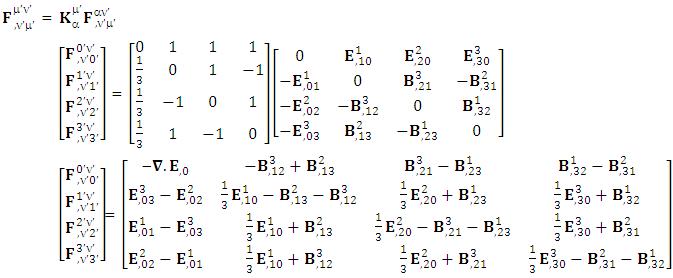 | (4.13) |
 | (4.14) |
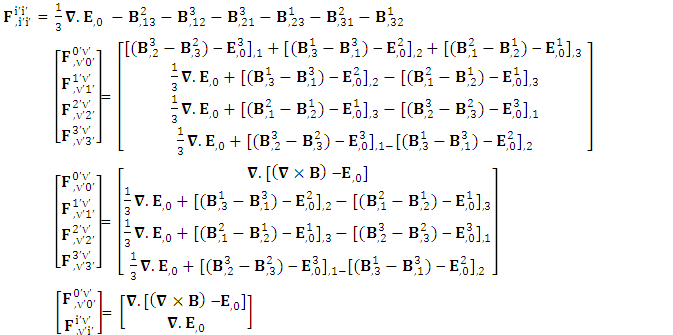 | (4.15) |
 | (4.16) |
 | (4.17) |
 | (4.18) |
All the results are true for dual of EMF, ME and conservation law for magnetism.
5. Derivation of Electromagnetic Laws by Other USEM
In order to avoid repetition of calculations, we only mention the USEM and one can easily obtain the same results by following the above method. Electromagnetic laws can be derived by the following USEM.
5.1. Physical USEM for Noninertial Frame
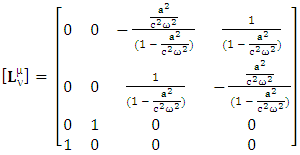 | (5.1) |
This matrix is universal Lorentz transformation in noninertial frame of reference that behaves as a physical identity matrix as well as USEM. The above model gives the same results as that of ULTM.Transformation of 4-current Density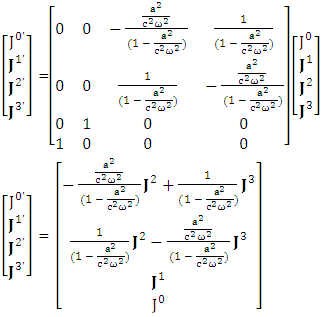 Adding the terms of space components on both sides
Adding the terms of space components on both sides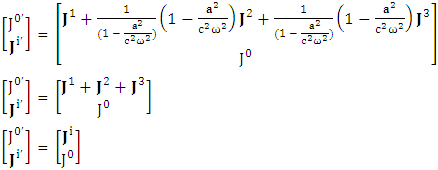 Charge density is transformed into current density
Charge density is transformed into current density  | (5.2) |
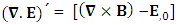 | (5,2a) |
Current density is transformed into charge density | (5.3) |
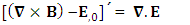 | (5.3a) |
4-current density as a whole remains same for all observers | (5.4) |
5.2. Numerical USEM in 2D
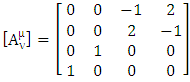 | (5.5) |
Transformation of 4-current Density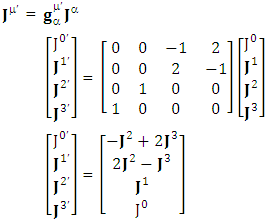 | (5.6) |
Adding the terms on 3 rows on right hand side and last 3 rows on left hand side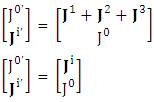 Charge density is transformed into current density
Charge density is transformed into current density  | (5.7) |
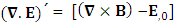 | (5,7a) |
Current density is transformed into charge density | (5.8) |
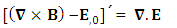 | (5.8a) |
4-current density as a whole remains same | (5.9) |
5.3. Anti-Identity Matrix as USEM
 | (5.10) |
The above matrix is one of the Dirac matrices that acts as the simplest USEM. On other hand, it inverts the output of OR GATE + AND GATE logic circuit in computer science. It behaves as a NOT GATE matrix.Transformation of 4-current Density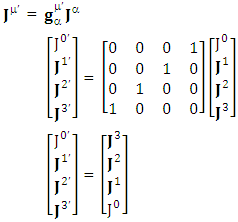 | (5.11) |
Adding the terms on 3 rows on right hand side and last 3 rows on left hand side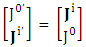 Charge density is transformed into current density
Charge density is transformed into current density  | (5.12) |
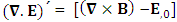 | (5,12a) |
Current density is transformed into charge density | (5.13) |
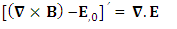 | (5.13a) |
4-current density as a whole remains same | (5.14) |
5.4. Application of Anti-Identity Matrix to OR Gate plus AND-GATE Output
The formula of OR Gate logic circuit is defined by | (5.15) |
Where A and B are the inputs and X is called its output so its output from truth table is given by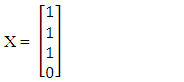 | (5.16) |
Now, we transform this output matrix by anti-identity matrix | (5.17) |
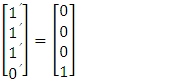 | (5.18) |
The result of this transformation matrix is NOR gate output matrix. It means that anti-identity matrix is playing the role of NOT gate matrix in logic gate mathematics.
6. Discussion and Comparison
Spacetime exchange symmetry of 4-vectors and tensors is an outstanding approach in the derivation of electromagnetic laws. The importance of this approach can be imagined that there is only model on this topic in the whole literature on spacetime electrodynamics concerning derivation of electromagnetic laws from electrostatics and magnetostatics. Our model represents simple and more general results in a single step having universal form of laws of physicsThe single transformation law for 4-vectors and tensors when applied on spacetime exchanger matrices, gave rise to the direct derivation of electromagnetic laws from each other in a single step operation. It is an entirely new method without any extra assumption. The new symmetry terms appeared along the diagonals of EMF, ME and conservation law. These terms help to sustain the symmetry and conservation law such that EMF, ME and conservation law remain same in their original form after transformation. It completely obeys EPR that makes this model valid and consistent with the standard theory of relativity. The first form of STL was observed in the derivation of Maxwell’s equations in noninertial frame based on connection coefficients [15]. References [4-13] are based on usual Lorentz transformation which do not discuss the exchange of spacetime and universality of laws of physics.There is only one viable model by J. F. Field [3] that can be compared with our model. It will be suitable to compare the results in the form of table to avoid confusion. First of all, we highly appreciate the work of J.H. Field in this context.  | Table 1. Comparison of Results of derivation of Electromagnetic Laws Based on Spacetime Exchange Symmetry |
The results of four models are same so we present the results of model-1 only. Equation numbers of results are as mentioned in the model.
6.1. Spacetime Exchange in 4-Vectors
 | (5) |
Charge density is transformed into current density | (6) |
Current density is transformed into charge density | (7) |
Such that 4-current density as a whole remains same
6.2. Spacetime Exchange of Electric and Magnetic Field
Electric field is transformed in to magnetic field | (15) |
Magnetic field is transformed in to electric field | (16) |
But electromagnetic field remains same and anti-symmetric | (17) |
6.3. Spacetime Exchange of Gauss’s and Ampere’s Law
This is the most beautiful part of the discovery where electromagnetic laws are derived from each other. It became possible due to STL and ULTM in 2D acting as USEM. Its simplicity lies in its single step operation.Gauss’s law is transformed into Ampere’s law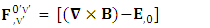 | (24) |
In usual 3D notation, we have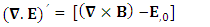 | (25) |
Ampere’s law is transformed into Gauss’s law | (26) |
Writing in usual notation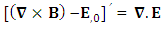 The combination of Gauss’s law and Ampere’s Law remains same as per required by EPR.
The combination of Gauss’s law and Ampere’s Law remains same as per required by EPR. 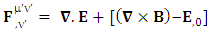 | (27) |
6.4. Spacetime Exchange of Conservation Law
Conservation of Gauss’s law is transformed into conservation of Ampere’s law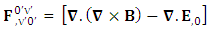 | (32) |
Conservation of Ampere’s law is transformed into conservation of Gauss’s law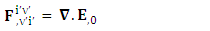 | (33) |
Conservation law remains same after transformation in its original form required by symmetry principle and EPR.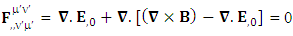 | (34) |
Results of Dual Electrodynamics
6.5. Spacetime Exchange of Dual Electric and Magnetic Field
Dual Electric field is transformed in to dual of magnetic field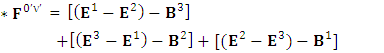 | (40) |
Dual of Magnetic field is transformed in to dual electric field | (41) |
The dual of electromagnetic field tensor becomes zero due to anti-symmetry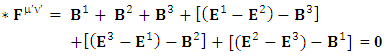 | (44) |
6.6. Spacetime Exchange of Dual Maxwell’s Equations
Gauss’s law for magnetism is transformed into Faraday’s law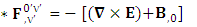 | (50) |
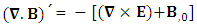 | (51) |
Faraday’s law is transformed into Gauss’s law for magnetism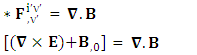 | (52) |
Sum of Gauss’s law for magnetism and Faraday’s law remains same for all observers. 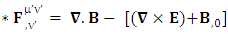 | (53) |
6.7. Spacetime Exchange of Dual Conservation Law
Conservation of Gauss’s law for magnetism is transformed into conservation of Faraday’s law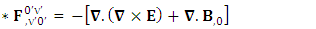 | (58) |
Conservation of Faraday’s law is transformed into conservation of Gauss’s law for magnetism | (59) |
Dual conservation law remains same after transformation in its original form required by symmetry principle and EPR.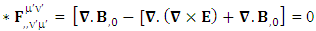 | (60) |
The results in terms of potential can be seen from equation (2.1) to (2.20) in model-2.From the above discussion and comparison, it is observed that universality of laws of physics appears when we look at them as a whole. In other words, partial response of laws of physics is relative but the collective behavior of laws of physics is universal. In the contemporary literature, time and space are relative but spacetime as a whole is discussed nowhere. In our framework, all the spacetime laws in terms of 4-vectors and tensors are universal.
7. Conclusions
The toolkit of STL for 4-vectors and tensors based on USEM has provided a single step derivation of electromagnetic laws from electrostatics and magnetostatics through spacetime exchange symmetry in universal form. The derivation of electromagnetic laws in terms of electric field, magnetic field as well as well as in terms of potentials has proved that both are equally valid. In our model, all the spacetime laws of physics remain same for all observers is the outstanding consequence of STL for 4-vectors and tensors based on physical and numerical USEM. STL for 4-vectors and tensors not only helping in spacetime exchanger methodology but also in discovering hidden world of physics like zero-point origin of 4D electromagnetic wave and conservation law as 7D wave in the recent paper [8]. ULTM in 2D as USEM made the derivation of electromagnetic laws from each other so simple and direct is a miraculous power of mathematics. ULTM in 2D for noninertial frame, in circular geometry and the numerical matrices show the same results. Spacetime exchange of physical quantities might help in quantum field theory and physical activity near the vicinity of black holes. It may help to understand happenings inside the LHC experiment where exchange of energy and matter is expected. Our future research is in process in the field of inertia and gravitation. Dedicated To the First Teacher of Humanity.Declaration: This research work is not sponsored by any organization or grant agency. It is totally self-financed project.
ACKNOWLEDGEMENTS
I am thankful to Prof. Dr. Jawaid Quamar for valuable discussions. I highly acknowledge the devotion and sacrifice of my all-family members specially, Saqlain Abdullah Hussain. I must acknowledge the moral support of my teachers, Research mates, university mates, colleagues, students at PAF College Sargodha, KPS Khanewal, Prof. Kashif Mehmood Punjab College Abdul Hakeem, Malik Manzoor Atif, Malik Maqbool, M. Ahmed who always encouraged me for my research activities.
References
| [1] | Hussain, N., et al. "Re Birth of Einstein’s Relativity via Unified Transformation Law." International Journal of Physics 11.1 (2023): 6-16. |
| [2] | Naveed Hussain, Hassnain Abdullah Hussain, Ather Qayum. "Electrodynamics in Noninertial Metrices Predicts Entirely New Origin of 4D Electromagnetic Wave." International Journal of Physics Vol.11. No .4 (2023): 193-230. DOI:10.12691/ijp-11-4-5. |
| [3] | Field, J. H. (2001). Space-time exchange invariance: Special relativity as a symmetry principle. American Journal of Physics, 69(5), 569-575. |
| [4] | Pierce, Allan D. "Derivation of Maxwell's equations via the covariance requirements of the special theory of relativity, starting with Newton's laws." arXiv preprint arXiv:0807.2557 (2008). |
| [5] | Peng, Hui. "Maxwell Equations Derived from Coulomb’s Law vs. Maxwell-type Gravity Derived from Newton’s Law." International Journal of Physics 9.1 (2021): 1-27. |
| [6] | H. A. Atwater (1974), Introduction to General Relativity, Pergamon Press. |
| [7] | Kobe, Donald H. "Generalization of Coulomb’s law to Maxwell’s equations using special relativity." American Journal of Physics 54.7 (1986): 631-636. |
| [8] | Heras, José A. "Can Maxwell’s equations be obtained from the continuity equation?" American Journal of Physics 75.7 (2007): 652-657. |
| [9] | König, Jürgen. "How to get from static to dynamic electromagnetism." European Journal of Physics 42.4 (2021): 045204. |
| [10] | Rȩbilas, Krzysztof. "A way to discover Maxwell's equations theoretically." Foundations of Physics Letters 19 (2006): 337-351. |
| [11] | Dodig, H. "Direct Derivation of Liénard–Wiechert Potentials, Maxwell’s Equations and Lorentz Force from Coulomb’s Law. Mathematics 2021, 9, 237." (2021). |
| [12] | Rosser, W. Geraint V., and W. Geraint V. Rosser. "Development of Maxwell’s equations from the expressions for the electric and magnetic fields due to a moving classical point charge." Interpretation of Classical Electromagnetism (1997): 108-165. |
| [13] | Burns, Michael E. "Maxwell's Equations from Electrostatics and Einstein's Gravitational Field Equation from Newton's Universal Law of Gravitation Using Tensors." (2004). |
| [14] | Melvin Schwartz (1987), Principles of Electrodynamics, Dover Publication, page 131, eqs. 3-5-13 to 3-5-17. |
| [15] | Naveed Hussain (2001), “On the General Covariance of Maxwellian Electrodynamics” Science International, Lahore, 13(1), pg1-6. |



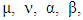 …runs from 0 to 3 and Latin letters i, j, k, .. from 1 to 3. Comma (,) denote partial differentiation e. g.
…runs from 0 to 3 and Latin letters i, j, k, .. from 1 to 3. Comma (,) denote partial differentiation e. g. 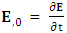 Partial derivative of electric field w. r. t. time,
Partial derivative of electric field w. r. t. time, 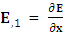 Partial derivative of electric field w. r. t. x-axis,
Partial derivative of electric field w. r. t. x-axis, 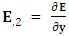 Partial derivative of electric field w. r. t. y-axis,
Partial derivative of electric field w. r. t. y-axis, 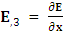 Partial derivative of electric field w. r. t. z-axis,
Partial derivative of electric field w. r. t. z-axis,  means 4-dimensional or spacetime partial derivative of EMF tensor.4-dimensional Coordinates
means 4-dimensional or spacetime partial derivative of EMF tensor.4-dimensional Coordinates  = (x0, x1, x2, x3) = (ct, x, y, z) = (ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that
= (x0, x1, x2, x3) = (ct, x, y, z) = (ct, xi) with x0 = ct and xi = (x, y, z). Time component ct is scalar while space components xi is vector such that 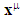 is the unification of time and space. The dimensions of all components are that of length.
is the unification of time and space. The dimensions of all components are that of length.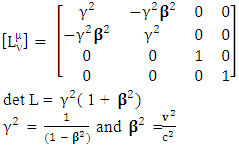
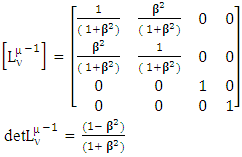
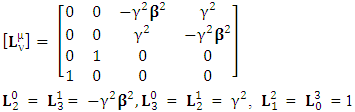
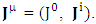 EPR demands universal nature of laws of physics independent of inertial and noninertial frame. Our approach is within the domain of EPR, symmetry principle and conservation law.Transformation of 4-Current Density
EPR demands universal nature of laws of physics independent of inertial and noninertial frame. Our approach is within the domain of EPR, symmetry principle and conservation law.Transformation of 4-Current Density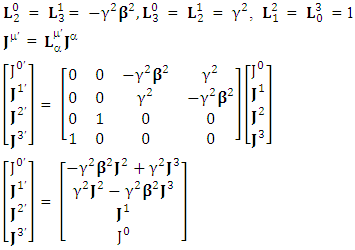
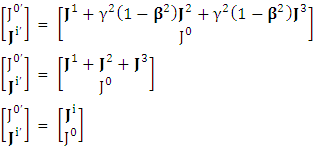
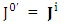
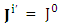
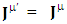
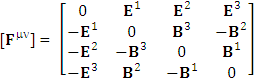
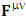 is related to its components electric field E and magnetic field B as follows
is related to its components electric field E and magnetic field B as follows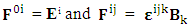 EMF tensor in component form is needed to get new terms along the diagonal of EMF. It is represented as 4 by 4 antisymmetric matrix
EMF tensor in component form is needed to get new terms along the diagonal of EMF. It is represented as 4 by 4 antisymmetric matrix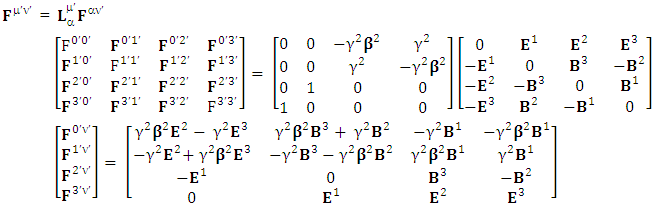
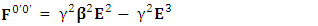
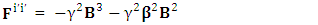
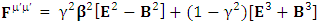
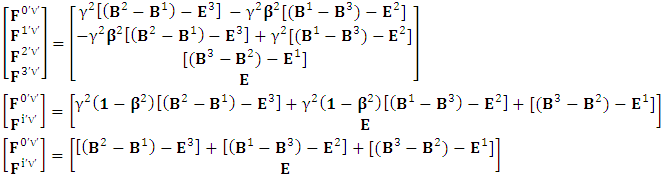 Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following
Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following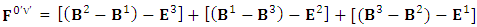
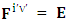
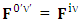
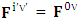
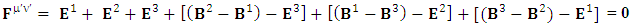
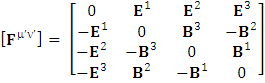
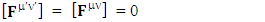
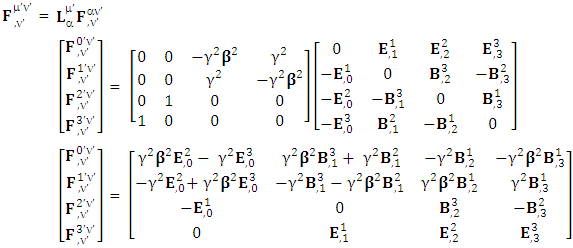


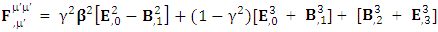
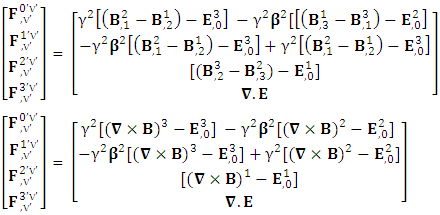 Adding space components on both sides
Adding space components on both sides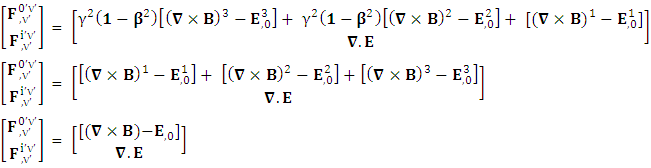 Gauss’s law is transformed into Ampere’s law
Gauss’s law is transformed into Ampere’s law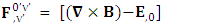
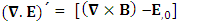

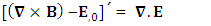
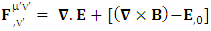
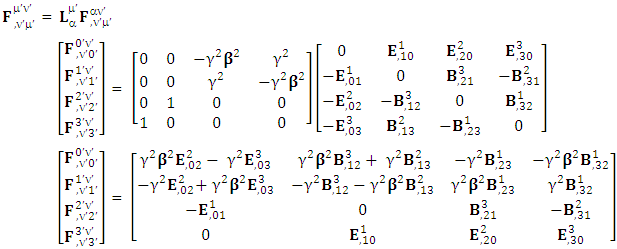
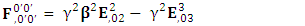
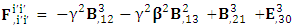
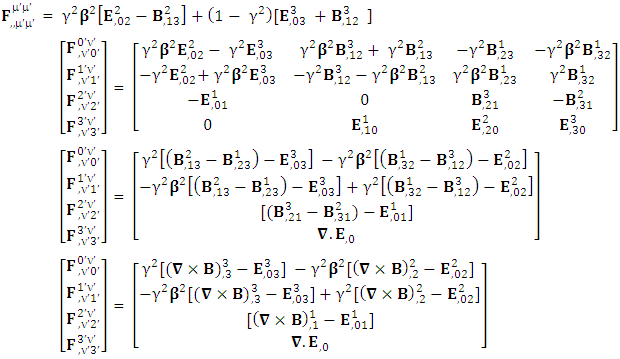
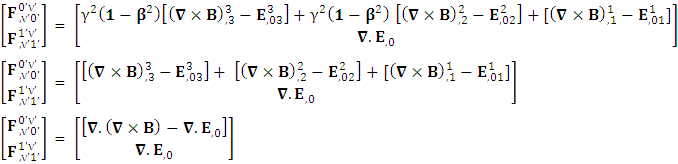 Conservation of Gauss’s law is transformed into conservation of Ampere’s law
Conservation of Gauss’s law is transformed into conservation of Ampere’s law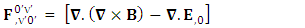

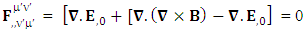
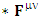 is denoted by putting star on it as
is denoted by putting star on it as 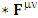 .Dual of Electromagnetic Field
.Dual of Electromagnetic Field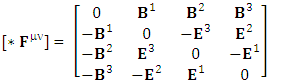
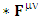 is related to its components electric field E and magnetic field B as follows
is related to its components electric field E and magnetic field B as follows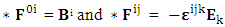
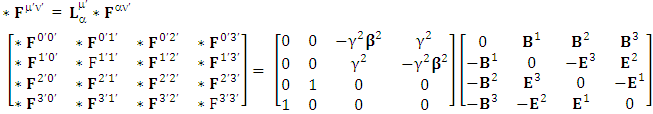
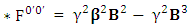
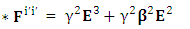
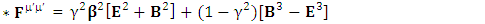
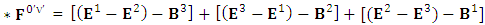
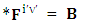
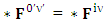
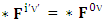
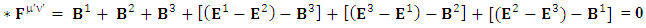
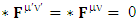
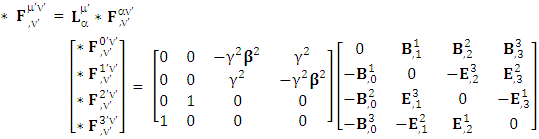
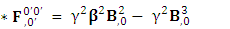
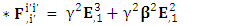
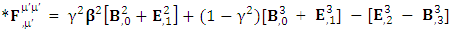
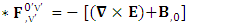
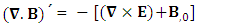
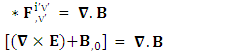
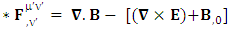
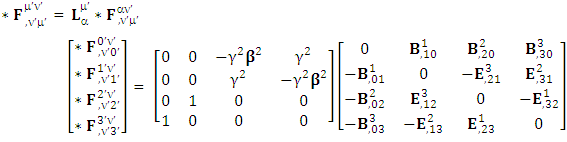

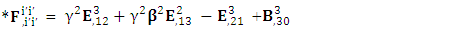
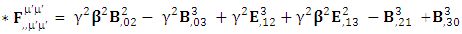
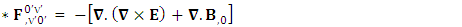

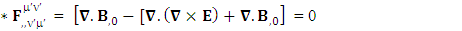
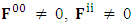 having no counter in the contemporary literature.The relation between electromagnetic field tensor
having no counter in the contemporary literature.The relation between electromagnetic field tensor 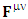 and 4-vector potential is given by
and 4-vector potential is given by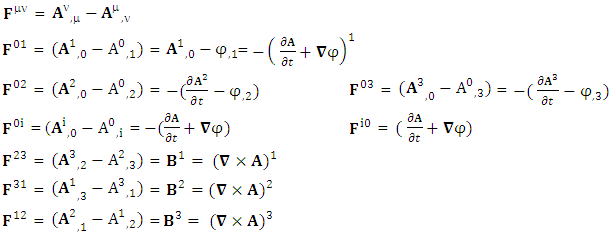
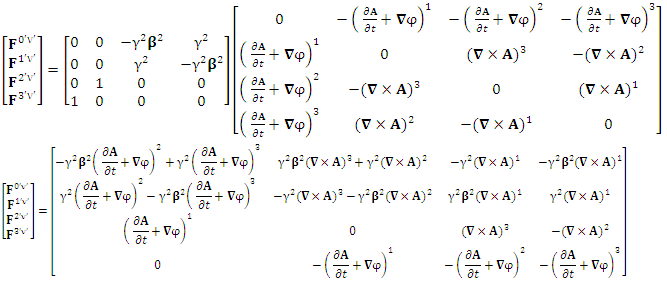
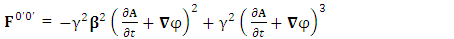
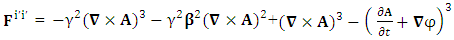
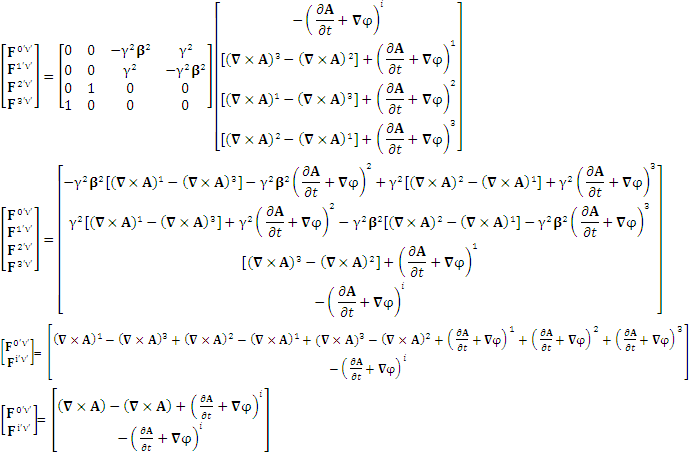 Electric field is transformed into magnetic field
Electric field is transformed into magnetic field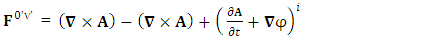

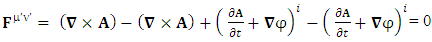
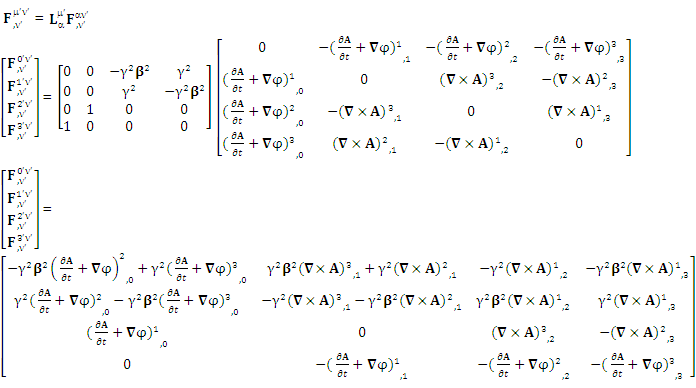
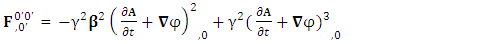
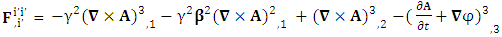
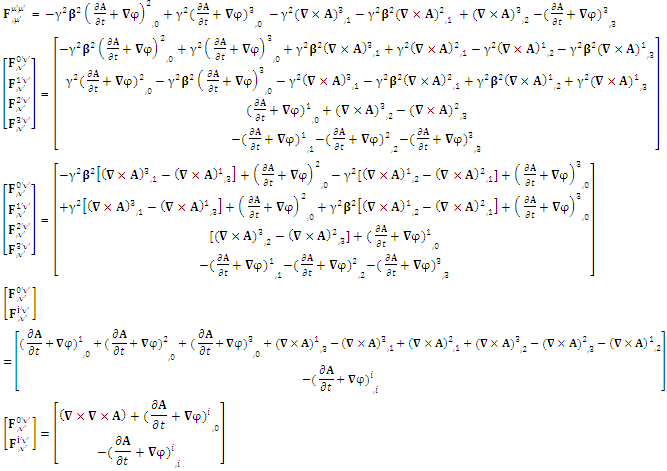
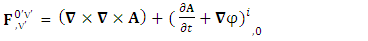

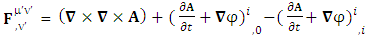
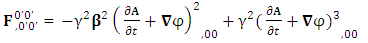
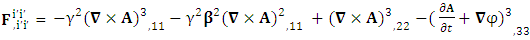
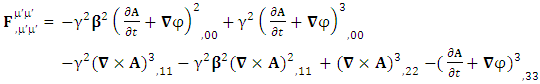
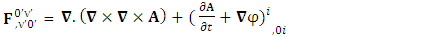

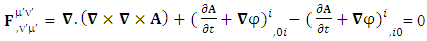
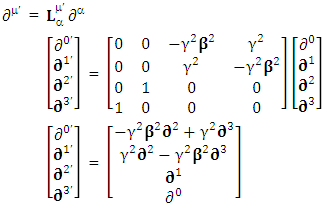
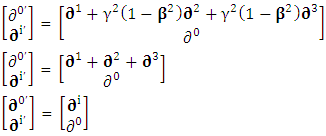 Time derivative operator is transformed into space operator
Time derivative operator is transformed into space operator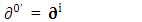
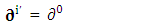
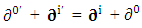 Contravariant spacetime derivative operator remains contravariant as a universal operator
Contravariant spacetime derivative operator remains contravariant as a universal operator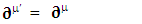
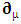 remains covariant as a universal operator
remains covariant as a universal operator 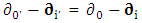
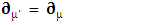
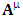 and covariant potential
and covariant potential 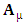 show the same spacetime exchange invariance.
show the same spacetime exchange invariance.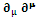 or 4D Wave Operator
or 4D Wave Operator 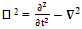
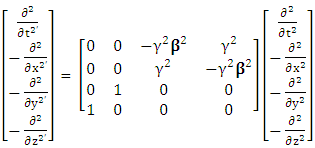
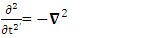
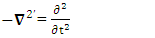
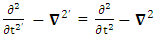

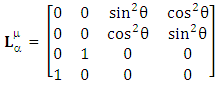
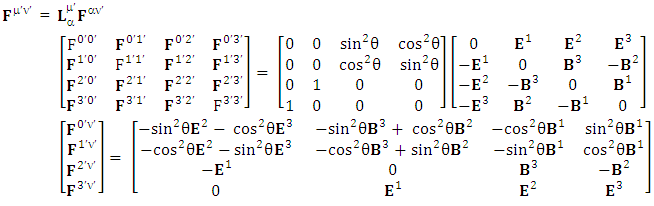
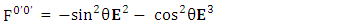
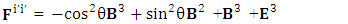
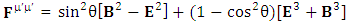
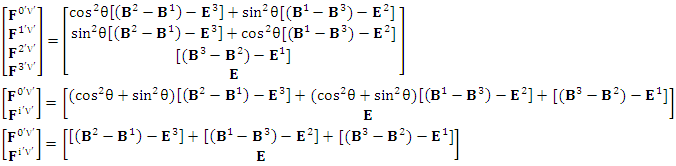 Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following
Electric field is transformed into mixture of electric and magnetic field while magnetic field is transformed into pure electric field.By simplification, we get the following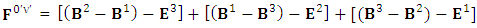

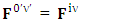
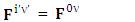
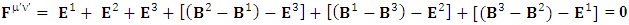
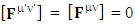
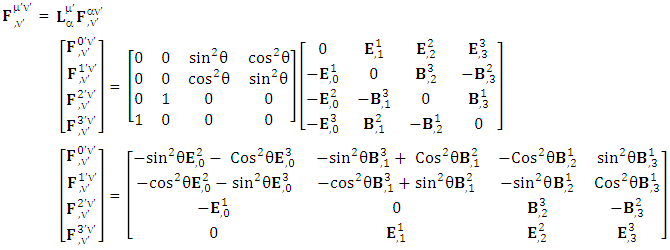
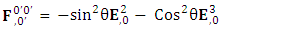
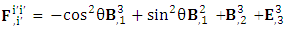
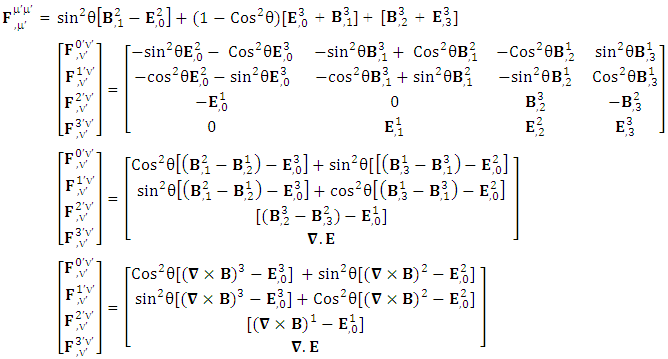
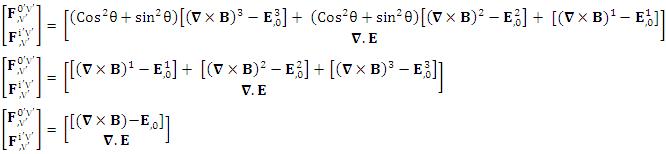 Gauss’s law is transformed into Ampere’s law
Gauss’s law is transformed into Ampere’s law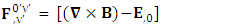
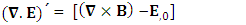
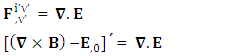
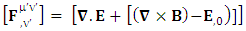
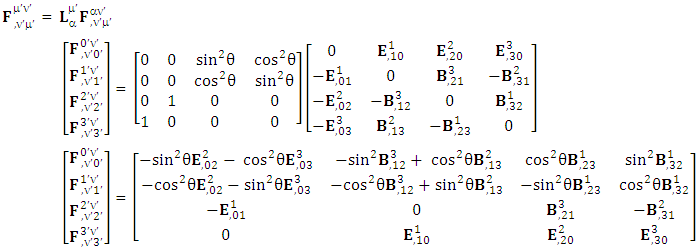
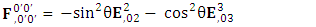
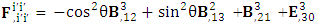
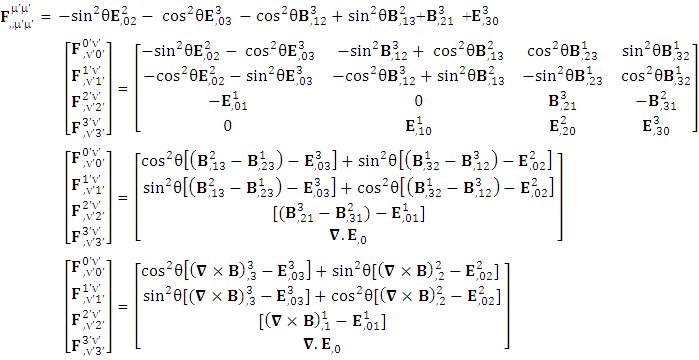
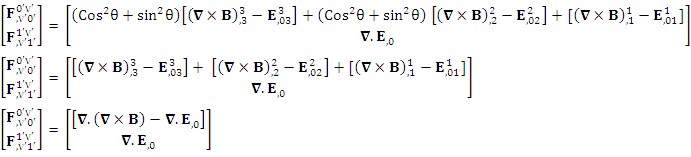 Conservation of Gauss’s law is transformed into conservation of Ampere’s law
Conservation of Gauss’s law is transformed into conservation of Ampere’s law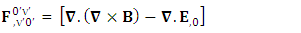

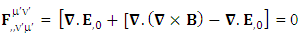
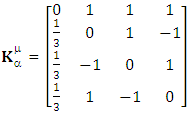
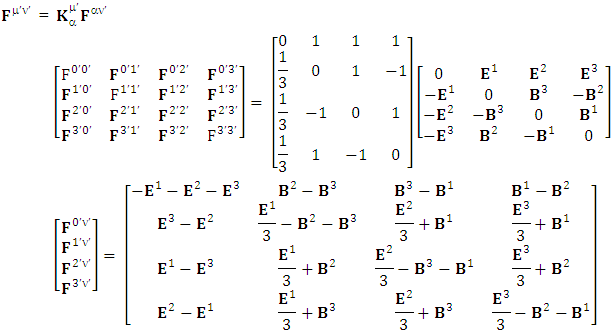
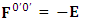
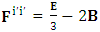
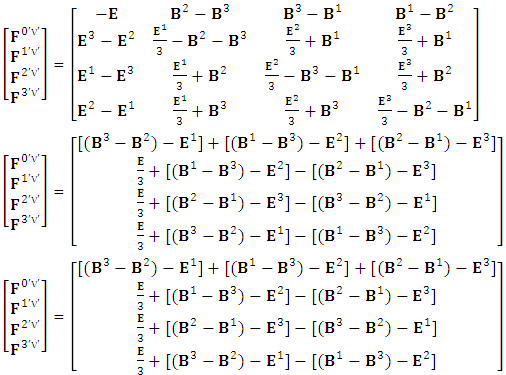 Adding space components on both sides
Adding space components on both sides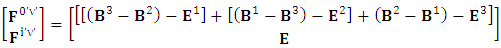
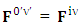
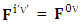
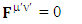
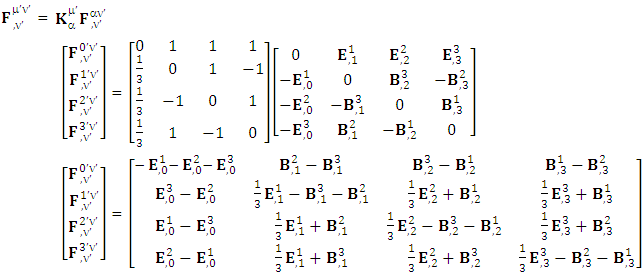

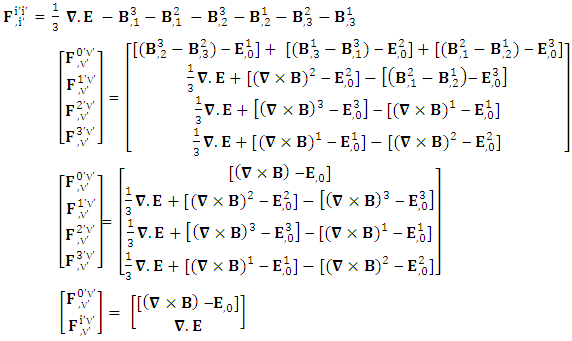
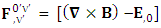
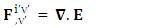
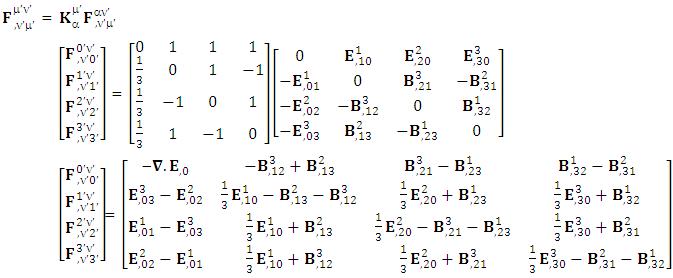

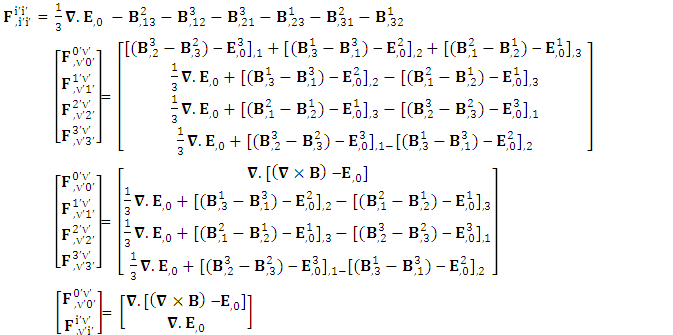



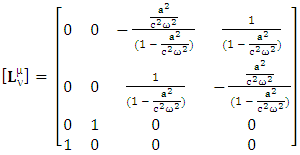
 Adding the terms of space components on both sides
Adding the terms of space components on both sides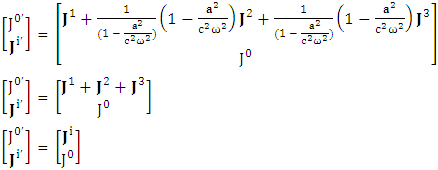 Charge density is transformed into current density
Charge density is transformed into current density 
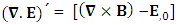

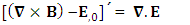

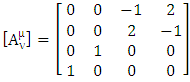
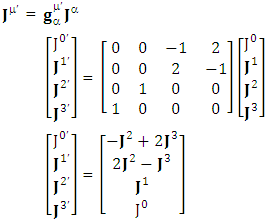
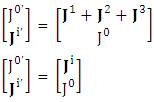 Charge density is transformed into current density
Charge density is transformed into current density 
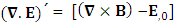

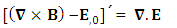


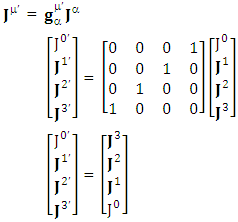
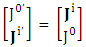 Charge density is transformed into current density
Charge density is transformed into current density 
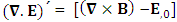

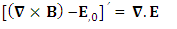


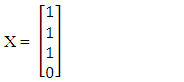

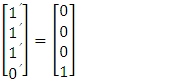







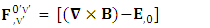
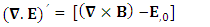

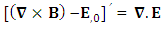 The combination of Gauss’s law and Ampere’s Law remains same as per required by EPR.
The combination of Gauss’s law and Ampere’s Law remains same as per required by EPR. 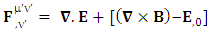
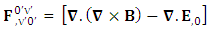
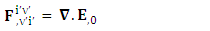
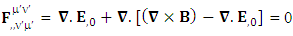
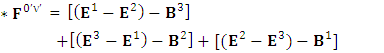

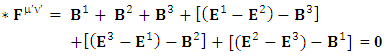
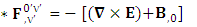
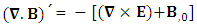
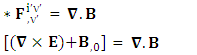
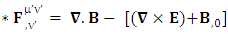
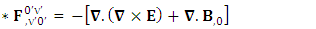

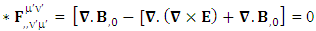
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML