-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2023; 13(5): 143-165
doi:10.5923/j.ijtmp.20231305.01
Received: Jun. 16, 2023; Accepted: Jun. 30, 2023; Published: Dec. 13, 2023

On the Entanglement Problem of the Space Time Continuum (Consideration of the Paradoxical Description of Physical Reality)
Nelson Blackie
College of Natural Sciences, Cuttington University, Liberia
Correspondence to: Nelson Blackie, College of Natural Sciences, Cuttington University, Liberia.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The theme we wish to present in following pages, results from our previous contribution on the problem we are faced in the view of the Paradoxical Description of physical Reality. In the previous consideration of the issue we want to discuss, certain transformation properties termed “Galilean-Lorentzian Transformation” were proposed. From them, one was led to answer question at issue regarding the Entanglement problem of systems in uniform translation with respect to one another in the affirmative. The previous consideration, although valid, does not really satisfy us by the extent of clarity to which the justification of the issues was there given. In the present matter, however, we provide a detail treatment of the theme, and with maximum clarity, so that the reader can now see from every rational point of view of reasoning, that our previous result really follows in a natural way. The present discussion has far-reaching consequence on the description of physical reality to the extent that it can be regarded as a generalized consideration of the problem in the paradoxical physics regarding the true nature of reality. One is then led to interesting results from which the entanglement problem is completely solved in a natural way, and without any hidden variable interpretation of the matter. Moreover, one naturally arrives at the Heisenberg principle of uncertainty, for spatial and temporal coordinates, in the dust-free continuum. The result does not change, however, if one were to take dust of zero pressure living inside that continuum. One is therefore looking at the possibility for a unified field theory from this paradoxical description of physical Reality. Lastly, the entanglement of space and time leads to an interesting discussion from which, from every rational point of view of the matter, the Maldacena’s AdS/CFT correspondence can be completely replaced, so that the result is valid in this 4-dimensional treatment of the space-time continuum. This is an interesting result because one is now able to see the natural possibility for a unified theory in which the introduction of an extra dimensionality of the space-time continuum is unnecessary.
Keywords: Paradoxical Physics, Fundamental postulate of Relativity, Galilean-Lorentzian Transformation, Space-Time Entanglement, Heisenberg’s Uncertainty Principal, Maldacena’s Correspondence, Dual-verse
Cite this paper: Nelson Blackie, On the Entanglement Problem of the Space Time Continuum (Consideration of the Paradoxical Description of Physical Reality), International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 5, 2023, pp. 143-165. doi: 10.5923/j.ijtmp.20231305.01.
Article Outline
1. Introduction
- In our previous contribution [1], a claim was made from which one was led to the conclusion that two coordinate systems, which are in uniform translation with respect to one another, could be described as composite systems (i.e., as entangled systems) having all the well-known properties of the quantum correlation. Then, the knowledge of any one of the systems so privileged precludes the knowledge of the other system, just as one meets in the atomic theory of quantum physics [2]. The argument from which this claim was made in the cited paper [1], in our opinion, does not provide a really convincing justification from which one can see that such description of physical reality is really possible. In this present paper, a justification is provided so that, from all rational view of the matter, one can see that our previous claim is material. It now seems obvious to us that there exists what we shall hereafter referred: —the fundamental postulate of relativity— whose validity leaves our claim justified in a satisfactory way. The Einstein’s consideration of the issue does not really satisfy this viewpoint as we will soon show. Throughout this paper, we shall continue to use, interchangeably, the words: system(s), coordinate(s) and coordinate system(s) to refer to “frame of reference(s)”, unless the otherwise is stated. The question to which we want to concern ourselves can be put forth as follow: to what extend can a Paradoxical Theory of physical Reality be justified, so that from all rational viewpoint of the matter, one can satisfactorily apply to uniformly translating systems (namely, K and K’) the quantum mechanical treatment of entanglement, in such a way that the result is a natural one? The term referred here as “paradoxical” is to intimate the point of view that, for a space-time description of process in the subject of relativity, one must (at a time) envision every event from exactly one of the systems which is chosen to be the privilege coordinate, so that in respect to this chosen coordinate, the latter system is looked upon to be in relative uniform motion. Nothing in this description must prohibit us from taking the reciprocal situation, so that the latter system is looked upon to be privileged, while the earlier is been looked taken as the one in uniform translation. However, both systems cannot be envisioned as the privileged system at the same time; the concept of simultaneity is therefore a necessary condition in our description of the subject, and the reader is advised to keep this in mind as we go along. At first sight, one will be inclined to say that the well-known treatment of the subject according to the Einstein’s consideration has put the matter according to the viewpoint we have stated above, and hence, according to the paradoxical description of nature. This however, is not the case. In the argument that follows below, we like to show, by easy example, that the ‘Einstein-Lorentz’ description of issue at hand does not really put the subject in the context which we have stated above, but only apparently does so. One will then see immediately that the answer at the question we have raised is in the affirmative under any purely paradoxical description of the theory of physical Reality, as long as one applies the fundamental postulate of relativity, the existence of which, we will also justify. It seems to us that as long as we describe nature in this paradoxical way, the laws of physics governing small things do not seem to differ from those describing classical things; one then obtains a unified theory. Observation from the Lorentzian TransformationThe well-known Lorentz transformation has described the theory of relativity in a way which leaves it incompatible with the paradoxical treatment of nature from which, we believe, the objective reality can really be justified. We have given a previous argument on this claim in earlier contribution [1] — we will assume that the main theme of that paper is already well-known. It was argued there (i.e. in [1]) that relativistic paradoxes such as length contraction, time dilation, as well as the well-known reciprocal relationship between the electro-magnetic fields of Maxwell theory, do not really follow from the viewpoint of any purely Lorentzian treatment of the issue at hand. We will justify this claim here by obvious argument to keep the discussion as easy to follow as possible:Let there exists two coordinate systems, (we will call them K and K’), so that in respect to the one which we regard as the privilege system, the latter system is in uniform translation with respect to the earlier. If in K, which we here choose as the privileged system, one measures the length of certain rod and gets the arbitrary value L, then, when envisioned from this privileged system (K), the rod appears to be shorten in the latter system (K’) according to the factor
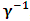 , where
, where 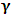 is a suitable number. It has been argued by Einstein [3] and by several (in fact all) textbooks [4-11] on this subject that this length contraction paradox really follows from the Lorentzian consequence of description of the matter. We like to disagree with this viewpoint. According to the definition we wish to assign to the term “paradoxical description”, it follows that, if one describes a physical event— by the help of clock systems and meter sticks— happening in K, and then again, describes the same event in the K’ system, but from the point of view of only one of the system which is so taken as the privileged one (in this case, K), only then will the process so described have any rational meaning of physical importance to the subject matter. This viewpoint is the train of thought which the paradoxical description has subjected the theory of relativity. [Indeed, one must take it that in the description we are making, exactly one of the system— at a given time— is taken as the privileged system, and from it, all the description of the two systems is there made]. However, the Lorentz transformation does not really satisfy this description of the issue. This can be showed easily by example. Let, envisioned from within the K system, there exists a current carrying coil, stationed in the K system [1,5,6]. Let it be that the current in the coil is caused by the motion of negatively charged particles, such that the direction of the magnetic field caused by the motion of the charges is along the
is a suitable number. It has been argued by Einstein [3] and by several (in fact all) textbooks [4-11] on this subject that this length contraction paradox really follows from the Lorentzian consequence of description of the matter. We like to disagree with this viewpoint. According to the definition we wish to assign to the term “paradoxical description”, it follows that, if one describes a physical event— by the help of clock systems and meter sticks— happening in K, and then again, describes the same event in the K’ system, but from the point of view of only one of the system which is so taken as the privileged one (in this case, K), only then will the process so described have any rational meaning of physical importance to the subject matter. This viewpoint is the train of thought which the paradoxical description has subjected the theory of relativity. [Indeed, one must take it that in the description we are making, exactly one of the system— at a given time— is taken as the privileged system, and from it, all the description of the two systems is there made]. However, the Lorentz transformation does not really satisfy this description of the issue. This can be showed easily by example. Let, envisioned from within the K system, there exists a current carrying coil, stationed in the K system [1,5,6]. Let it be that the current in the coil is caused by the motion of negatively charged particles, such that the direction of the magnetic field caused by the motion of the charges is along the 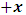 axis, for simplicity of things. One then sees that, in respect to K, the positive charges are at rest with respect to the coil and hence, with respect to himself (K), since the coil is stationary in this frame of reference. One may now ask: does the Lorentz’s transformation provide any way by which this privilege system is able to measure the speed of the negatively charged particles when looked upon in the K’ system? This question is a natural one, and the reader can easily convince himself that the answer has a deeper physical meaning. If we adopt the Lorentzian description of issue, the answer is clearly in the negative, since the Lorentz transformation does not provide to us any possible physical means by which the speed of the negatively charged particles can be measured in the K’ coordinate, if the measurement were really carried out by means of clocks and meter sticks at rest in K. Following this Lorentz view of things, one comes to admit that the privileged system is incapable of measuring the speed of the negatively charged particles in K’ by using clocks and meter sticks at rest in the privileged— K frame. Instead, the result which one obtains, in view of Lorentz, is pronounced as follows [5,6]: In view of K’, the negatively charged particles are considered stationary so that it is the positively charged particles which now move along the –x axis in respect to the K’ system.For if one follows in this line of thought, one sees that, in view of this latter though experiment, the description of the events in K and in K’ are carried out as though each observer were chosen as the privileged system simultaneously. It follows at once because, if one envisions the situation from K, one sees the negatively charged particles moving along the +x axis, and causing a magnetic field in that direction. However, if the situation is now view from the latter system K’, the negative charges are no longer in motion but rather, one finds the positively charged particles now moving in the opposing direction so that the magnetic field is now in the –x direction. One sees easily that K and K’ really envision the situation from their own respective frame of references by clocks and yard sticks at rest in their respective systems. That is, the two situations (in the two systems) were not view from one of the system which we can regard is the privileged system at the time.This description, as can be seen without any difficulty, is incompatible with the description which leads us to the length contraction paradox. For in the former treatment of issue (i.e., length contraction), one saw that the privilege observer in K measured the length of his rod, followed again by the length of a second rod in the latter system, by means of clocks and meter sticks at rest in the privileged (K) system. However, in the latter experiment, one sees that both systems measure the speed of the charges according as they view the situation in their respective systems; one easily sees that the systems behave as though both were taken as privilege systems, simultaneously. Indeed, in this latter experiment, one cannot say that the one system was privileged while the other was not privileged, such as we meet in the case of the length contraction paradox. As one can clearly see, the description of issues in Special relativity leads to certain inconsistency. If one were to measure the speed of the negatively charged particles in the K’ system, as it is viewed from the K system (i.e., by using clocks and yard stakes stationed in the K system), only then would said description really satisfy the view of things we have considered in the paradoxical description of reality. This would have been in the same view as the length contraction problem accordingly.The meaning of the theme “relativity”, as assigned by the usual Einstein-Lorentz consideration of the subject, does not in any way satisfy us. In fact, there appears to be a deeper and more fundamental postulate of physical reality— which we like to hereafter call, “The fundamental postulate”— whose effect has not really been considered in their treatment. We shall illustrate this important point by a very simple example so that a maximum clarity is achieved; the goal is to allow the reader to follow the trend of argument intuitively, and in all possible rational way.Let us take the coordinate systems, K and K’, into which we there perform a physical experiment. The goal of the experiment is to send light signals from one point (A) to another point (B) and then measure its velocity by means of clocks and yard sticks which, when brought to one location and there compare, do not differ. In the K system, let us send a light signal from the source (A) to the detector (B), followed by measurement of its velocity as it propagates in space; we will do this by clocks and meter rods which are at rest in respect to K. By obvious results, this observer gets the number c, the speed of light in vacuum according to Maxwell. The question then follows: does this result differ for the K’ system? Indeed, Einstein’s relativity has answered this question in the negative according to the justification of the invariant nature of the speed of light in vacuum. However, we like to show here that this is not the case. In fact, we shall see that the answer which one can provide to such question depends only upon the coordinate system from whose point of view one envisions the situation; this really follows from the very nature of relativity as the reader will soon see.Let one envisions the process above from the K’ coordinate; a trivial result is then obtained. This follows from all but the fact that an observer at rest in K’ does not see anything unusual in his frame, since he is at rest in that coordinate. The observer is therefore using clocks and rods that are at rest with respect to him according as we meet for any privileged choice of coordinate. This answer is also satisfied in the spirit of the Einstein-Lorentz consideration. However, we like to show here that, in view of the paradoxical description of physical reality, the given description of the issue does not permit us to look upon the systems as though they are in uniform motion as it is made to be view in the Einstein’s sense of things.Indeed, this follows naturally because, as long as both observers make measurements in their own coordinates in which they see themselves at rest, they can be seen as privileged systems in those coordinates independently and simultaneously. As each system will now use clocks and measuring sticks at rest in their respective frame of reference so that no one privileged system is seeing the situation for both systems, one sees easily that there can be no effect of relative motion on this description of the issue. An observer at rest in a Galilean frame of reference is, for this very reason, no different from those at rest in a reference frame in uniform translation with respect to the first, so long as we describe the situation from the frame of reference of that system. Actually, the uniform motion of any arbitrary system of reference can only be observed from a second reference system in such a way that the latter system is considered privileged, while the earlier is in uniform translation. Therefore, if the systems view themselves from their respective coordinates, the concept of relative motion cannot be material.Indeed, the justification follows easily since one can, with equal right, refer to any one of the coordinates as that in uniform translation with respect to the other. As one can then see, the description we have here given, does not really lead to the invariance of the speed of light, at least as made to be viewed from the Einstein-Lorentz sense of the issue. One obtains the number c for the speed of light in both systems for all reasons but the fact that the motion so described is no longer a relative one— since both systems use clocks and yardsticks that are at rest in their respective systems to make their measurements. Indeed, for any system in which the concept of relative motion does not apply, the result we have obtained is always true in that coordinate, and that the speed of light will be invariable from c in that system. We shall hereafter refer to this important result, the fundamental postulate of relativity, which is easily stated as follows:An observer at rest in a coordinate system so privileged does not see anything unusual in that space-time continuumThis result, as will soon be seen, plays an important role in the theory we want to write down here, and no less, the theory of the gravitational field which we shall write down shortly in our next contribution. We shall now proceed with the notion that the description we have given above does not imply the invariant nature of the speed of light, at least as justified by this paradoxical description of nature. There seems to be a deeper consideration from which the invariant behavior of the speed of light really follows in a satisfactory way in the view of the paradoxical theory of reality; we show this below.Suppose that an observer in the K system measures the speed of the light signal in respect to himself, and then again, in the K’ system, by the help of clocks and measuring yard sticks at rest in K. Clearly, the fundamental principle will no longer apply to one of the systems, in this case, the K’ system, since one is now describing the event in it (i.e., in K’) as it is envisioned from the privileged K system. One will then see the effect of the uniformly translated motion on the K’ system only if such description is really carried out. The extent to which we want to put forth this Paradoxical theory of reality is indeed a far-reaching consequence of the fundamental postulate. Let it be that, as envision from K, the speed of light signal is measured with rods and clock system at rest in K, and let one gets c in respect to himself (by virtue of the fundamental postulate). Then, because the clock systems in K’ will appear to be lagging behind when the situation is envisioned from K (by the fact that we are looking into K’ with measuring rods and clocks which are stationed in K rather than in K’), one gets
axis, for simplicity of things. One then sees that, in respect to K, the positive charges are at rest with respect to the coil and hence, with respect to himself (K), since the coil is stationary in this frame of reference. One may now ask: does the Lorentz’s transformation provide any way by which this privilege system is able to measure the speed of the negatively charged particles when looked upon in the K’ system? This question is a natural one, and the reader can easily convince himself that the answer has a deeper physical meaning. If we adopt the Lorentzian description of issue, the answer is clearly in the negative, since the Lorentz transformation does not provide to us any possible physical means by which the speed of the negatively charged particles can be measured in the K’ coordinate, if the measurement were really carried out by means of clocks and meter sticks at rest in K. Following this Lorentz view of things, one comes to admit that the privileged system is incapable of measuring the speed of the negatively charged particles in K’ by using clocks and meter sticks at rest in the privileged— K frame. Instead, the result which one obtains, in view of Lorentz, is pronounced as follows [5,6]: In view of K’, the negatively charged particles are considered stationary so that it is the positively charged particles which now move along the –x axis in respect to the K’ system.For if one follows in this line of thought, one sees that, in view of this latter though experiment, the description of the events in K and in K’ are carried out as though each observer were chosen as the privileged system simultaneously. It follows at once because, if one envisions the situation from K, one sees the negatively charged particles moving along the +x axis, and causing a magnetic field in that direction. However, if the situation is now view from the latter system K’, the negative charges are no longer in motion but rather, one finds the positively charged particles now moving in the opposing direction so that the magnetic field is now in the –x direction. One sees easily that K and K’ really envision the situation from their own respective frame of references by clocks and yard sticks at rest in their respective systems. That is, the two situations (in the two systems) were not view from one of the system which we can regard is the privileged system at the time.This description, as can be seen without any difficulty, is incompatible with the description which leads us to the length contraction paradox. For in the former treatment of issue (i.e., length contraction), one saw that the privilege observer in K measured the length of his rod, followed again by the length of a second rod in the latter system, by means of clocks and meter sticks at rest in the privileged (K) system. However, in the latter experiment, one sees that both systems measure the speed of the charges according as they view the situation in their respective systems; one easily sees that the systems behave as though both were taken as privilege systems, simultaneously. Indeed, in this latter experiment, one cannot say that the one system was privileged while the other was not privileged, such as we meet in the case of the length contraction paradox. As one can clearly see, the description of issues in Special relativity leads to certain inconsistency. If one were to measure the speed of the negatively charged particles in the K’ system, as it is viewed from the K system (i.e., by using clocks and yard stakes stationed in the K system), only then would said description really satisfy the view of things we have considered in the paradoxical description of reality. This would have been in the same view as the length contraction problem accordingly.The meaning of the theme “relativity”, as assigned by the usual Einstein-Lorentz consideration of the subject, does not in any way satisfy us. In fact, there appears to be a deeper and more fundamental postulate of physical reality— which we like to hereafter call, “The fundamental postulate”— whose effect has not really been considered in their treatment. We shall illustrate this important point by a very simple example so that a maximum clarity is achieved; the goal is to allow the reader to follow the trend of argument intuitively, and in all possible rational way.Let us take the coordinate systems, K and K’, into which we there perform a physical experiment. The goal of the experiment is to send light signals from one point (A) to another point (B) and then measure its velocity by means of clocks and yard sticks which, when brought to one location and there compare, do not differ. In the K system, let us send a light signal from the source (A) to the detector (B), followed by measurement of its velocity as it propagates in space; we will do this by clocks and meter rods which are at rest in respect to K. By obvious results, this observer gets the number c, the speed of light in vacuum according to Maxwell. The question then follows: does this result differ for the K’ system? Indeed, Einstein’s relativity has answered this question in the negative according to the justification of the invariant nature of the speed of light in vacuum. However, we like to show here that this is not the case. In fact, we shall see that the answer which one can provide to such question depends only upon the coordinate system from whose point of view one envisions the situation; this really follows from the very nature of relativity as the reader will soon see.Let one envisions the process above from the K’ coordinate; a trivial result is then obtained. This follows from all but the fact that an observer at rest in K’ does not see anything unusual in his frame, since he is at rest in that coordinate. The observer is therefore using clocks and rods that are at rest with respect to him according as we meet for any privileged choice of coordinate. This answer is also satisfied in the spirit of the Einstein-Lorentz consideration. However, we like to show here that, in view of the paradoxical description of physical reality, the given description of the issue does not permit us to look upon the systems as though they are in uniform motion as it is made to be view in the Einstein’s sense of things.Indeed, this follows naturally because, as long as both observers make measurements in their own coordinates in which they see themselves at rest, they can be seen as privileged systems in those coordinates independently and simultaneously. As each system will now use clocks and measuring sticks at rest in their respective frame of reference so that no one privileged system is seeing the situation for both systems, one sees easily that there can be no effect of relative motion on this description of the issue. An observer at rest in a Galilean frame of reference is, for this very reason, no different from those at rest in a reference frame in uniform translation with respect to the first, so long as we describe the situation from the frame of reference of that system. Actually, the uniform motion of any arbitrary system of reference can only be observed from a second reference system in such a way that the latter system is considered privileged, while the earlier is in uniform translation. Therefore, if the systems view themselves from their respective coordinates, the concept of relative motion cannot be material.Indeed, the justification follows easily since one can, with equal right, refer to any one of the coordinates as that in uniform translation with respect to the other. As one can then see, the description we have here given, does not really lead to the invariance of the speed of light, at least as made to be viewed from the Einstein-Lorentz sense of the issue. One obtains the number c for the speed of light in both systems for all reasons but the fact that the motion so described is no longer a relative one— since both systems use clocks and yardsticks that are at rest in their respective systems to make their measurements. Indeed, for any system in which the concept of relative motion does not apply, the result we have obtained is always true in that coordinate, and that the speed of light will be invariable from c in that system. We shall hereafter refer to this important result, the fundamental postulate of relativity, which is easily stated as follows:An observer at rest in a coordinate system so privileged does not see anything unusual in that space-time continuumThis result, as will soon be seen, plays an important role in the theory we want to write down here, and no less, the theory of the gravitational field which we shall write down shortly in our next contribution. We shall now proceed with the notion that the description we have given above does not imply the invariant nature of the speed of light, at least as justified by this paradoxical description of nature. There seems to be a deeper consideration from which the invariant behavior of the speed of light really follows in a satisfactory way in the view of the paradoxical theory of reality; we show this below.Suppose that an observer in the K system measures the speed of the light signal in respect to himself, and then again, in the K’ system, by the help of clocks and measuring yard sticks at rest in K. Clearly, the fundamental principle will no longer apply to one of the systems, in this case, the K’ system, since one is now describing the event in it (i.e., in K’) as it is envisioned from the privileged K system. One will then see the effect of the uniformly translated motion on the K’ system only if such description is really carried out. The extent to which we want to put forth this Paradoxical theory of reality is indeed a far-reaching consequence of the fundamental postulate. Let it be that, as envision from K, the speed of light signal is measured with rods and clock system at rest in K, and let one gets c in respect to himself (by virtue of the fundamental postulate). Then, because the clock systems in K’ will appear to be lagging behind when the situation is envisioned from K (by the fact that we are looking into K’ with measuring rods and clocks which are stationed in K rather than in K’), one gets  for the speed of light in this latter system, where
for the speed of light in this latter system, where 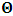 is a number proportional to the uniform relative velocity in an appropriate unit. Now, let it be that the same argument holds well if one were to envision the matter at hand, taking K’ as the privileged system instead; then, one gets the reciprocal results. Nothing must forbid us from getting this result from the fact that one is free to choose any coordinate as the privilege system so that one quickly sees that the entire description is symmetric. If one were to describe processes in K and K’, taking the latter system as privilege, one would see that the laws of physics do not differ in forms as one meets if the first system were the privileged. It is this point of view from which the paradoxical consideration really puts the theory of relativity. One will shortly see that interesting results can be obtained in a natural way.But, it should be noticed from easy argument that the speed of light will remain invariant under this latter description of issue, since it does not change in both K and K’, as long as one takes either of the systems as the privileged, and again by the fact that each system, with equal right, can be chosen as privileged. However, when we attempt to measure the speed of light in one coordinate system, envisioned from the other, one sees it obeying a Galilean addition of speed as in the ordinary theory of classical mechanics. This result has a physical meaning as it leads to the theory of retarded quantities; we shall see this point later on. We call the transformation laws which satisfy our description, the Galilean-Lorentzian Transformation. The meaning of the term “Galilean-Lorentzian” transformation, for the lack of better choice of word, is to satisfy the obvious condition that the speed of light also obeys a Galilean relation in certain unique way which, in fact, leads at once to the theory of retarded potentials in a satisfactory way. It must also be noticed that the invariance nature of the speed of light is also satisfied in a unique way. It follows that whichever system one selects as privileged, the speed of light does not differ from its value in vacuum, and that system is satisfied by the fundamental postulate. If one envisions the latter system from the former one (i.e., if one measures the speed of light in both systems, using clocks and yardsticks stationed only the privileged system), the speed of light differs from its Maxwell’s value in the latter system. This is the extent to which the paradoxical description has subjected the theory of physical reality. In our next presentation, it will be clear that a theory of Gravitation is obtainable under such description of the space-time Continuum.We now make the claim here that, there can be no other deeper meaning to the theme of “relativity” that is epistemologically correct if one describes physical reality according to the view of the well-known Einstein-Lorentz consideration of the issue. One must follow the path which this Paradoxical description has yielded us. In fact, the reader can see or can easily verify for himself that the so-called Lorentz length contraction, time dilation, and no less, the reciprocal relation of the electro-magnetic fields, follows only satisfactorily if nature is described from the point of view of this paradoxical consideration of the issue.We are face with an inherent limitation in the Special (and no less in the General) theory of Relativity, by its own nature, in such a way that, for the description of any physical event, one cannot, at the same time, regard two systems as the privileged choices of coordinates simultaneously. For if one chooses the earlier system as privileged, one regards the latter system as that which is in uniform translation with respect to the former [1,10,31]. By this condition, it is therefore seen at once that one cannot describe a single event from the point of view of the K and K’ systems as though both were chosen as privileged systems at the same time. In the later event (i.e., for the moving charges), if one were to view the motion of the negatively charged particles in K’, judging the situation as envisioned from K, only then would it really follow that such description is valid from the point of view of the paradoxical description of reality, and from which, the Lorentz transformation would have really satisfied this paradoxical consideration of the issue. This however, is not the case; we are led to answer in the affirmative at issue that the Lorentz transformation does not really satisfy this paradoxical description of nature. But, the dissatisfaction to which we like to call attention here is the farthest reaching consequence imaginable, which this paradoxical treatment of reality has subjected the theory of physical reality. In the forgoing discussion, one will soon see why the “Einstein-Lorentz” treatment of nature leads to an incomplete description of reality. We are of the view that this is the reason for the incompatibility of the atomic physics and the theory of gravitation. We consider this point here with maximum theoretical security. From here, we will be led to the general viewpoint that the paradoxical description of nature is the only consideration from which the description of physical reality is really justified; the reader will also see that the result follows naturally.Let us, in space and in time, choose two coordinate systems, K and K’, so that in respect to one system so chosen as the privileged coordinate, the second is in uniform translation, such that at the time
is a number proportional to the uniform relative velocity in an appropriate unit. Now, let it be that the same argument holds well if one were to envision the matter at hand, taking K’ as the privileged system instead; then, one gets the reciprocal results. Nothing must forbid us from getting this result from the fact that one is free to choose any coordinate as the privilege system so that one quickly sees that the entire description is symmetric. If one were to describe processes in K and K’, taking the latter system as privilege, one would see that the laws of physics do not differ in forms as one meets if the first system were the privileged. It is this point of view from which the paradoxical consideration really puts the theory of relativity. One will shortly see that interesting results can be obtained in a natural way.But, it should be noticed from easy argument that the speed of light will remain invariant under this latter description of issue, since it does not change in both K and K’, as long as one takes either of the systems as the privileged, and again by the fact that each system, with equal right, can be chosen as privileged. However, when we attempt to measure the speed of light in one coordinate system, envisioned from the other, one sees it obeying a Galilean addition of speed as in the ordinary theory of classical mechanics. This result has a physical meaning as it leads to the theory of retarded quantities; we shall see this point later on. We call the transformation laws which satisfy our description, the Galilean-Lorentzian Transformation. The meaning of the term “Galilean-Lorentzian” transformation, for the lack of better choice of word, is to satisfy the obvious condition that the speed of light also obeys a Galilean relation in certain unique way which, in fact, leads at once to the theory of retarded potentials in a satisfactory way. It must also be noticed that the invariance nature of the speed of light is also satisfied in a unique way. It follows that whichever system one selects as privileged, the speed of light does not differ from its value in vacuum, and that system is satisfied by the fundamental postulate. If one envisions the latter system from the former one (i.e., if one measures the speed of light in both systems, using clocks and yardsticks stationed only the privileged system), the speed of light differs from its Maxwell’s value in the latter system. This is the extent to which the paradoxical description has subjected the theory of physical reality. In our next presentation, it will be clear that a theory of Gravitation is obtainable under such description of the space-time Continuum.We now make the claim here that, there can be no other deeper meaning to the theme of “relativity” that is epistemologically correct if one describes physical reality according to the view of the well-known Einstein-Lorentz consideration of the issue. One must follow the path which this Paradoxical description has yielded us. In fact, the reader can see or can easily verify for himself that the so-called Lorentz length contraction, time dilation, and no less, the reciprocal relation of the electro-magnetic fields, follows only satisfactorily if nature is described from the point of view of this paradoxical consideration of the issue.We are face with an inherent limitation in the Special (and no less in the General) theory of Relativity, by its own nature, in such a way that, for the description of any physical event, one cannot, at the same time, regard two systems as the privileged choices of coordinates simultaneously. For if one chooses the earlier system as privileged, one regards the latter system as that which is in uniform translation with respect to the former [1,10,31]. By this condition, it is therefore seen at once that one cannot describe a single event from the point of view of the K and K’ systems as though both were chosen as privileged systems at the same time. In the later event (i.e., for the moving charges), if one were to view the motion of the negatively charged particles in K’, judging the situation as envisioned from K, only then would it really follow that such description is valid from the point of view of the paradoxical description of reality, and from which, the Lorentz transformation would have really satisfied this paradoxical consideration of the issue. This however, is not the case; we are led to answer in the affirmative at issue that the Lorentz transformation does not really satisfy this paradoxical description of nature. But, the dissatisfaction to which we like to call attention here is the farthest reaching consequence imaginable, which this paradoxical treatment of reality has subjected the theory of physical reality. In the forgoing discussion, one will soon see why the “Einstein-Lorentz” treatment of nature leads to an incomplete description of reality. We are of the view that this is the reason for the incompatibility of the atomic physics and the theory of gravitation. We consider this point here with maximum theoretical security. From here, we will be led to the general viewpoint that the paradoxical description of nature is the only consideration from which the description of physical reality is really justified; the reader will also see that the result follows naturally.Let us, in space and in time, choose two coordinate systems, K and K’, so that in respect to one system so chosen as the privileged coordinate, the second is in uniform translation, such that at the time 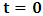 , the origins of the both systems coincide at some point. One can then assign to this point the origin of the coordinates of both systems of reference— call it Π. If we let the origin of the coordinate of K be
, the origins of the both systems coincide at some point. One can then assign to this point the origin of the coordinates of both systems of reference— call it Π. If we let the origin of the coordinate of K be 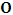 , and for K’, we call O’ (for mare distinction so as to avoid unnecessary confusion), then, at time
, and for K’, we call O’ (for mare distinction so as to avoid unnecessary confusion), then, at time 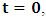 it is clear that
it is clear that 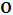 and
and 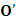 will both be at point Π. If we now envision that K is the privilege system, it is obvious that the fundamental postulate will be material in K but not in K’. Then, at time
will both be at point Π. If we now envision that K is the privilege system, it is obvious that the fundamental postulate will be material in K but not in K’. Then, at time 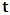 different from zero, the coordinate of K’ is observed to undergo uniform translation with velocity
different from zero, the coordinate of K’ is observed to undergo uniform translation with velocity 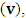 if one envisions the matter from K. Thus,
if one envisions the matter from K. Thus, 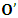 will no longer be at
will no longer be at 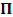 but rather, at some arbitrary point. We call this arbitrary point
but rather, at some arbitrary point. We call this arbitrary point 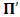 , which is distinct from Π by the factor
, which is distinct from Π by the factor 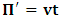 , according to reason of ordinary mechanics.We may now ask the question: where exactly does the origin of the K’ system lie just after the time
, according to reason of ordinary mechanics.We may now ask the question: where exactly does the origin of the K’ system lie just after the time 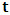 has elapsed? The answer to such question, as we saw above, depends upon the coordinate system from which one provides the answer according to our concept of description of issue in this paradoxical theory of reality. This constraint is imposed upon us by the fundamental postulate. For if one judges the issue from the point of view of the K’, one is led to answer that O’ is at the point Π after the time
has elapsed? The answer to such question, as we saw above, depends upon the coordinate system from which one provides the answer according to our concept of description of issue in this paradoxical theory of reality. This constraint is imposed upon us by the fundamental postulate. For if one judges the issue from the point of view of the K’, one is led to answer that O’ is at the point Π after the time 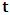 has elapsed (i.e., K’ has the coordinate
has elapsed (i.e., K’ has the coordinate 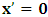 ). This is the case because, if one describes issue at hand from the point of view of the K’ system, one sees that there is no uniform motion in that system as view from itself according as to the justification of the fundamental postulate. However, if one envisions from the privileged system, K, one sees that the origin of K’ is really at Π’ after t time. In view of K, the new origin of K’, after the elapsed time, satisfies the equation
). This is the case because, if one describes issue at hand from the point of view of the K’ system, one sees that there is no uniform motion in that system as view from itself according as to the justification of the fundamental postulate. However, if one envisions from the privileged system, K, one sees that the origin of K’ is really at Π’ after t time. In view of K, the new origin of K’, after the elapsed time, satisfies the equation 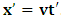 . This follows immediately from any rational consideration of the problem we are here faced, since it is indeed the case that, the fundamental postulate no longer applies to the K’ system, so long as we make the description from the K system. If we now describe issue at hand, purely from the perspective of the privileged K system, it is then straightforward to see that (judged from K), both observers will be at the common origin—at Π— if and only if the origin of K is described by the conditions
. This follows immediately from any rational consideration of the problem we are here faced, since it is indeed the case that, the fundamental postulate no longer applies to the K’ system, so long as we make the description from the K system. If we now describe issue at hand, purely from the perspective of the privileged K system, it is then straightforward to see that (judged from K), both observers will be at the common origin—at Π— if and only if the origin of K is described by the conditions 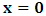 (since the fundamental postulate applies to K), and the K’, by the condition
(since the fundamental postulate applies to K), and the K’, by the condition 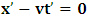 (i.e., the equation which brings the K’ coordinate to the origin). However, in view of the Lorentzian method of transformation, given in a well-known way [4-11,31,32,33], one gets, for K, the condition
(i.e., the equation which brings the K’ coordinate to the origin). However, in view of the Lorentzian method of transformation, given in a well-known way [4-11,31,32,33], one gets, for K, the condition 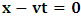 , and for K’, the condition
, and for K’, the condition  , as the conditions which are satisfied by the said description. This viewpoint, I cannot accept at all. As it is easy to see, this description of issue is clearly unacceptable from any rational view of the theory of Relativity (special or General). For if one follows this Einstein-Lorentzian description of the issue, one sees the following consequences which are immaterial in any rational valid theory of reality:α In the condition
, as the conditions which are satisfied by the said description. This viewpoint, I cannot accept at all. As it is easy to see, this description of issue is clearly unacceptable from any rational view of the theory of Relativity (special or General). For if one follows this Einstein-Lorentzian description of the issue, one sees the following consequences which are immaterial in any rational valid theory of reality:α In the condition 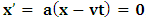 , for some number a, the systems (K and K’) will coincide at the point Π’ different from the origin, after the relative translation. Then, the first point of origin of coordinate of the systems (Π) is no longer maintained. From this, one sees that K and K’ really move to the new point Π’, so that distance of separation between the systems is immaterial. This must not cause any confusion to the reader since, both systems, after the time t, are now located at Π’ β For reason of simultaneity of choosing the privileged system, both K and K’ will be regarded as privileged systems in this description of issue such that one does not see any one of the systems as the privileged. That is, both systems will be seen as though they were, at the same time, the uniformly translated coordinates.The theoretical consequence of this viewpoint cannot be overly expressed. Indeed, if upon uniform translation, and at a later time
, for some number a, the systems (K and K’) will coincide at the point Π’ different from the origin, after the relative translation. Then, the first point of origin of coordinate of the systems (Π) is no longer maintained. From this, one sees that K and K’ really move to the new point Π’, so that distance of separation between the systems is immaterial. This must not cause any confusion to the reader since, both systems, after the time t, are now located at Π’ β For reason of simultaneity of choosing the privileged system, both K and K’ will be regarded as privileged systems in this description of issue such that one does not see any one of the systems as the privileged. That is, both systems will be seen as though they were, at the same time, the uniformly translated coordinates.The theoretical consequence of this viewpoint cannot be overly expressed. Indeed, if upon uniform translation, and at a later time 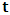 different from zero, statement (α) holds, we encounter the situation in which both systems move together to a different point Π’; the common point of origin, Π is no longer maintained, since the systems are both no longer at Π. Following this, one sees that the concept of distance can no longer be well-defined. On the other hands, if condition (β) holds, we are again faced with the natural inability of carrying out any valid description of event according as we meet from the theory of relativity. This follows because, according to our method of describing events in any valid theory of relativity, one takes a single coordinate system as the privileged observer at any given time so that, in respect to that system so chosen as the privileged, the other system is in uniform translation relative to the former system. Indeed, one cannot satisfactorily say that the one of the coordinate is stationary/privilege while the other is in uniform translation if we really view the situation from the Lorentz’s sense of things. Moreover, if, after the uniform translation, the systems really coincided at the new point Π’ according to the Lorentz view of things, it is not difficult to show that both Π and Π’ can be regarded as the origin of coordinate simultaneously (if one maintains the fact that Π is an origin at the time
different from zero, statement (α) holds, we encounter the situation in which both systems move together to a different point Π’; the common point of origin, Π is no longer maintained, since the systems are both no longer at Π. Following this, one sees that the concept of distance can no longer be well-defined. On the other hands, if condition (β) holds, we are again faced with the natural inability of carrying out any valid description of event according as we meet from the theory of relativity. This follows because, according to our method of describing events in any valid theory of relativity, one takes a single coordinate system as the privileged observer at any given time so that, in respect to that system so chosen as the privileged, the other system is in uniform translation relative to the former system. Indeed, one cannot satisfactorily say that the one of the coordinate is stationary/privilege while the other is in uniform translation if we really view the situation from the Lorentz’s sense of things. Moreover, if, after the uniform translation, the systems really coincided at the new point Π’ according to the Lorentz view of things, it is not difficult to show that both Π and Π’ can be regarded as the origin of coordinate simultaneously (if one maintains the fact that Π is an origin at the time 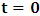 ). Such view however, has a far-reaching theoretical implication on the description of nature. A lengthy argument to this issue is not required; we put the argument simply. Let it be so imagined that the universe consists of two systems of dust which we referred, K and K’. Let the systems be chosen such that the one system does not influence any part of the other, but that the two are in uniform translation with respect to one another. At the initial time
). Such view however, has a far-reaching theoretical implication on the description of nature. A lengthy argument to this issue is not required; we put the argument simply. Let it be so imagined that the universe consists of two systems of dust which we referred, K and K’. Let the systems be chosen such that the one system does not influence any part of the other, but that the two are in uniform translation with respect to one another. At the initial time 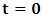 , we say that both systems are at Π as already stated. If we now allow the systems to evolve over time, t different from zero, we see that, following the Einstein-Lorentz view, both systems are now at Π’. The universe will now have two distinct points (namely Ⅱ and Ⅱ’) which we may describe as the origin of the universe at the same time. also, since there is no distance of separation between the systems (K and K’), one sees that the continuum vanished identically. This is physically not possible as the reader can easily see.
, we say that both systems are at Π as already stated. If we now allow the systems to evolve over time, t different from zero, we see that, following the Einstein-Lorentz view, both systems are now at Π’. The universe will now have two distinct points (namely Ⅱ and Ⅱ’) which we may describe as the origin of the universe at the same time. also, since there is no distance of separation between the systems (K and K’), one sees that the continuum vanished identically. This is physically not possible as the reader can easily see.2. Derivation of the Galilean-Lorentzian Transformation
- As we saw from the consideration above, the Lorentzian transformation does not provide to us any system of coordinate upon which, one may look at as privileged system accordingly as we meet in any rational relativistic description of the issue of reality. For if one starts, taking K as the privileged system, one soon sees that, after the uniform translation of the K’ system, the privileged system is no longer looked upon as being at rest according to our justification above. One cannot therefore say that the K system was really privileged, since one now sees that both systems really move to the new point Π’ after the uniform translation, and the common origin of coordinate is no longer maintained.It then appears to us that the only valid transformation properties which are really satisfied, according to the problem we are here faced, are those which, after the uniform translation of one of the coordinate in respect to the other, the common point, Π, does not change for both systems. The situation is then obvious that, upon the uniform translation of the latter system, the privileged system is maintained at the point Π and the later at Π’, so that the element of arc length, after any time different from zero, does not vanish. Nothing stops us from taking the reciprocal case so that in fact, the motion is really only a virtual one. For if one follows the line of thought that both systems really coincide at Π’, it is easy to see that, the element of arc length between K and K’ is immaterial according as we were to meet in Minkowski’s view of the issue. It must be emphasized here, the distinction which has been considered in this paradoxical theory of reality. In line of our discussion, it must be noticed that, as long as K is at the point Π, then, after the uniform translation, the element of length does not vanish, since in view of K, the later system (K’) will be at Π’, which is again connected to the origin, Π, by the transformation property which will soon be written down. But, notice that the reciprocal of the situation also holds well if one takes the latter system as the privileged. However, both systems are not at Π’ simultaneously according as we met in the Lorentz consideration of the problem. It will further be showed that the continuum of space and time is being created by the said description such that Π really describes the origin of space and of time according as the Big Band. We now find the transformation properties satisfying the consideration we have pointed out:Let, in relation to K, one has the coordinate
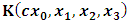 , and in K’, one has
, and in K’, one has 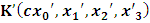 . We now consider a uniform translation along the
. We now consider a uniform translation along the 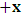 coordinate of both systems, for simplicity of the issue. Then, the transformation properties which holds between K and K’, in view of the paradoxical description of reality, is given here according as
coordinate of both systems, for simplicity of the issue. Then, the transformation properties which holds between K and K’, in view of the paradoxical description of reality, is given here according as 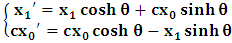 | (1) |
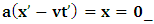 for some
for some 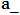 the validity of which we have showed from the discussion above— notice that it is different from that of Lorentz’s.Let
the validity of which we have showed from the discussion above— notice that it is different from that of Lorentz’s.Let 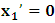 , so that the origin of K and K’ are at the common origin Π; then, from the first of the two equations in (1), one obtains the line which is parallel to the
, so that the origin of K and K’ are at the common origin Π; then, from the first of the two equations in (1), one obtains the line which is parallel to the 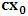 axis, with slope
axis, with slope 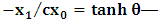 envisioned from K. We call this line, the
envisioned from K. We call this line, the 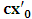 axis of K’, for our purpose Similarly, if one lets
axis of K’, for our purpose Similarly, if one lets 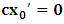 in the later of (1), one gets the line
in the later of (1), one gets the line 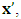 which is parallel to the
which is parallel to the 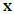 axis, with slope
axis, with slope 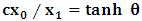 . We can therefore represent the space-time diagram of K and K’, in view of K as below (figure-1)
. We can therefore represent the space-time diagram of K and K’, in view of K as below (figure-1)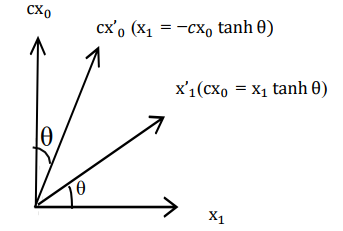 | Figure 1. Space time diagram of K and K’ |
 matrix which satisfies the transformation properties as
matrix which satisfies the transformation properties as 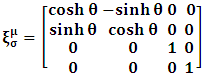 | (2) |
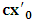 axis which, one sees without difficulty that, judged from K’, one is referring to the line on which the coordinate of K’ does not move, by reason of the fundamental postulate. Then, we obtain, for the slope of the same line,
axis which, one sees without difficulty that, judged from K’, one is referring to the line on which the coordinate of K’ does not move, by reason of the fundamental postulate. Then, we obtain, for the slope of the same line, 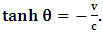 However, if one views the event from the privileged K coordinate, one sees that the line
However, if one views the event from the privileged K coordinate, one sees that the line 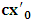 is the spatial interval which is covered by K’, after the time
is the spatial interval which is covered by K’, after the time 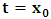 has elapsed. Then, while in respect to K’,
has elapsed. Then, while in respect to K’, 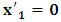 along the given axis, one sees that
along the given axis, one sees that 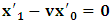 , if we envision the same line from the perspective of K. Then, since the fundamental postulate applies only to the privileged K, it follows at once that the equation
, if we envision the same line from the perspective of K. Then, since the fundamental postulate applies only to the privileged K, it follows at once that the equation 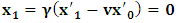 is the condition for which both K and K’ are at the common origin Π, for some suitable number
is the condition for which both K and K’ are at the common origin Π, for some suitable number 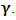 It must be emphasized here that, the relative velocity, after the interchanged
It must be emphasized here that, the relative velocity, after the interchanged 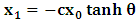 by
by 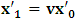 in respect to K does not cause us any physical problem. This is seen easily because, we are able to replace
in respect to K does not cause us any physical problem. This is seen easily because, we are able to replace 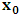 by
by 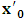 and
and 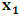 by
by 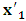 so that the relative velocity between the systems does not differ from
so that the relative velocity between the systems does not differ from 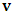 as desired. Now, substituting the slope
as desired. Now, substituting the slope 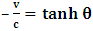 in either of the equations in (1), one gets
in either of the equations in (1), one gets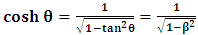 | (3) |
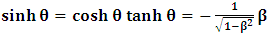 | (4) |
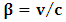 Letting
Letting 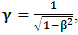 and substituting (3) and (4) into (1), and taking the parallel axes, we have the transformation properties
and substituting (3) and (4) into (1), and taking the parallel axes, we have the transformation properties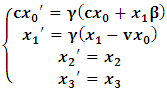 | (5) |
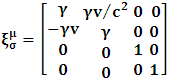 | (6) |
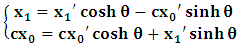 | (7) |
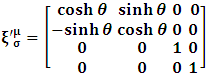 | (8) |
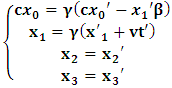 | (9) |
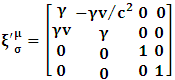 | (10) |
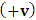 for all Lorentz boosts along the +x axis. As was argued from above however, if one assigns to the coordinate, a positive boost along the positive x-axis, one does not retain the origin Π, the element of arc length vanishes at once. However, from the argument we have given in (1) and (7), the justification follows that, we must assign –v for all Lorentz boosts along the positive x-axis and vice versa; the reverse argument holds because of the symmetry.We shall see that this plays an important role in the entangled state of K and K’ so that, the systems, when infinitely separated in space and in time, the separation does not play any physical role, just as we meet in Aspect’s Experiment. Indeed, it is the case that, upon choosing any arbitrary distance of separation of K and K’, the transformation serves no purpose other than retaining the common point of origin, Π. Moreover, since, by symmetry, we may just regard K’ as privileged, so that K is in uniform translation, one sees in a straightforward way that K’ is retained at the point Π after uniform translation of K_ if we take K’ as the privileged system. Equations (5) and (9) therefore satisfy the condition in which both K and K’ are really at the point, Π, in view of any coordinate system which is selected as the privileged; the separation and hence, the space-time continuum then becomes only a virtual one.From the consideration in view of which we have obtain these so-called “Galilean-Lorentzian transformation” relations, one can state here, in addition to the fundamental principle, two other postulates which are clearly satisfied according to the description which we here propose (Paradoxical description)1. Fundamental Postulate: An observer at rest in a coordinate system so privileged does not see anything unusual in the space-time continuum2. Galilean Relativity: The speed of Light is constant for every observer in their own coordinate system; it suffers a Galilean effect when measured from another coordinate system in uniform translation with respect to the first3. Modified Einstein’s Postulate of relativity (the Principle of Correspondence): The laws of physics are invariant when described independently in all coordinate systemThe modification of the third postulate is due to the use of the word “independently”, so that the condition holds only if a privilege observer so chosen, views the laws of physics from his own coordinate. Moreover, the third postulate is in fact, the single statement of the first two postulates in a unique way as the reader can easily see.
for all Lorentz boosts along the +x axis. As was argued from above however, if one assigns to the coordinate, a positive boost along the positive x-axis, one does not retain the origin Π, the element of arc length vanishes at once. However, from the argument we have given in (1) and (7), the justification follows that, we must assign –v for all Lorentz boosts along the positive x-axis and vice versa; the reverse argument holds because of the symmetry.We shall see that this plays an important role in the entangled state of K and K’ so that, the systems, when infinitely separated in space and in time, the separation does not play any physical role, just as we meet in Aspect’s Experiment. Indeed, it is the case that, upon choosing any arbitrary distance of separation of K and K’, the transformation serves no purpose other than retaining the common point of origin, Π. Moreover, since, by symmetry, we may just regard K’ as privileged, so that K is in uniform translation, one sees in a straightforward way that K’ is retained at the point Π after uniform translation of K_ if we take K’ as the privileged system. Equations (5) and (9) therefore satisfy the condition in which both K and K’ are really at the point, Π, in view of any coordinate system which is selected as the privileged; the separation and hence, the space-time continuum then becomes only a virtual one.From the consideration in view of which we have obtain these so-called “Galilean-Lorentzian transformation” relations, one can state here, in addition to the fundamental principle, two other postulates which are clearly satisfied according to the description which we here propose (Paradoxical description)1. Fundamental Postulate: An observer at rest in a coordinate system so privileged does not see anything unusual in the space-time continuum2. Galilean Relativity: The speed of Light is constant for every observer in their own coordinate system; it suffers a Galilean effect when measured from another coordinate system in uniform translation with respect to the first3. Modified Einstein’s Postulate of relativity (the Principle of Correspondence): The laws of physics are invariant when described independently in all coordinate systemThe modification of the third postulate is due to the use of the word “independently”, so that the condition holds only if a privilege observer so chosen, views the laws of physics from his own coordinate. Moreover, the third postulate is in fact, the single statement of the first two postulates in a unique way as the reader can easily see.3. Dynamical Consideration of the Paradoxical Description of the Space-Time Problem
- The transformation properties we have arrived at here are canonical in form and lead to a dynamical system. This is an important result because, from this, one has brought the theory of relativity in the same spirit as quantum physics, so that a compatible theory can be found for gravitation and atomic physics. We do not make this conclusion here however, but as the reader will see, the consequence is immediate.It must be noticed immediately that from this paradoxical description of issue at hand, one does not really find any dissatisfaction between the Special and General theories of Relativity as one sees in the usual Einstein’s treatment of the problem. One is then inclined to think that the gravitational field is indeed material in the background of a Minkowski’s space-time, so that a curved space-time description of the subject is really unnecessary in the paradoxical description of nature. We shall consider this point in the paper which follows this shortly. But, one will soon see that the fundamental postulate of relativity plays an important role in this dynamical consideration we have concern ourselves, and from which the gravitational field will follow easily.It was argued in [1] that, a single coordinate system does not really experience the effect of dilation on both its spatial and temporal axes simultaneously. We have again returned to this theme. If, in the K’ system which, in respect to the privilege K system, the earlier is in uniform translation, there exist a time dilation on its temporal axis, one sees that there is a corresponding increment of its spatial axis and vice versa, according to the argument provided in [1], which I have already assume to be well-known. One then arrives at a natural inability in which, one cannot determine both temporal and spatial dilations in any single coordinate system, whichever way one takes it. If we see one of the systems lagging behind in time, we see it leading in space (distance) and vice versa. A Hinesburg-like uncertainty seems to exist between the spatial and temporal axes of any single coordinate system in the 4-dimensional continuum; as one precisely measures a temporal dilation by clocks system, one sees his yard sticks stretching. This is indeed the main distinction which this paradoxical Galilean-Lorentzian transformation has really yielded us. One writes, formally, this space-time Heisenberg-like uncertainty for the continuum as follows: There can be no simultaneous dilation of spatial and temporal coordinates in respect to any single system of reference, however we choose that system. We have actually considered this result on our previous consideration, but it was un-named; we hereafter called this the Uncertainty principal of the continuum or Heisenberg’s principle, for short. We will return to this point again in the forgoing discussion. It follows that the space and time coordinates of a given reference frame are non-commuting parameters, just as we meet for the well-known principal of uncertainty; this can be verified by mare inspection of the matric in (2) or in (10). We then have before us, a canonical system of transformation from which, Hamilton’s dynamics follows immediately. We show here that this is indeed the case.Hamiltonian mechanics is already well-known in physics; there is no need for any deeper development of the subject matter. We shall only consider here, very shortly, the theme that will enable us write down two main results, namely: what we believe to be the Lagrangian of the system and indeed, Hamilton’s equations from which the dynamics of the continuum can be described; the procedure is no more than straightforward.Let us, for the purpose at hand, carry out the following slight changes of variables in eq. (1), so that things are really obvious. For the first equation in (1), let
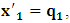
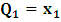 and
and 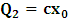 . In the second equation, let it be that
. In the second equation, let it be that 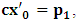
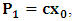 and
and 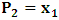 . This does not cause any confusion as soon as one keeps in mind that
. This does not cause any confusion as soon as one keeps in mind that 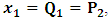 etc. We then obtain the order pair (q, p) as functions of some (Q, P) coordinate which, for our purpose at hand, are nothing but the variables in the privilege system. Following this, one rewrites (1) as
etc. We then obtain the order pair (q, p) as functions of some (Q, P) coordinate which, for our purpose at hand, are nothing but the variables in the privilege system. Following this, one rewrites (1) as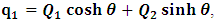
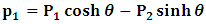 If one carries out the same process in relation to (7), one has
If one carries out the same process in relation to (7), one has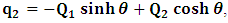
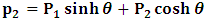 One then obtains the following relationship
One then obtains the following relationship 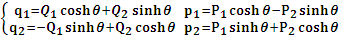 | (11a) |
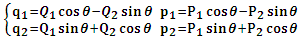 | (11b) |
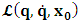 , where
, where 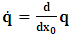 and the parameter x0 is the time coordinate envisioned from the rest or privilege system. The function
and the parameter x0 is the time coordinate envisioned from the rest or privilege system. The function 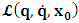 is the Lagrangian of the dynamics of the K’ coordinate, if one envisions the situation from the privileged K coordinate. This follows at once because, from the fundamental postulate, one is prohibited from writing down a dynamical equation for the privileged system, since the motion in it vanishes identically so that, only the relative motion of the latter system can be observed, if the situation is viewed from the privileged. Nothing forbids us from reversing the argument. The fact that
is the Lagrangian of the dynamics of the K’ coordinate, if one envisions the situation from the privileged K coordinate. This follows at once because, from the fundamental postulate, one is prohibited from writing down a dynamical equation for the privileged system, since the motion in it vanishes identically so that, only the relative motion of the latter system can be observed, if the situation is viewed from the privileged. Nothing forbids us from reversing the argument. The fact that 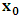 is the time parameter of the privileged (K) system is fundamental and leads to an interesting question as to the absoluteness of time such as we meet in the context of Newton. In fact, this has always been the problem in the general subject of relativity. For the sake of mare example, when one writes the Schwarzschild’s element of length, the term “Schwarzschild’s time” is used [12]. However, in the course of our discussion, one will soon see that there is really no such thing as Schwarzschild’s time, but rather, the absolute time (or in soft term, the time in the privileged system), controls the flow of the dynamics of the systems, and hence, the matrix of the continuum. Also, it will be seen that x0 plays a major role in the theory we which to present here and no less, the theory of gravitation (i.e. the theory of General Relativity), which results from this paradoxical discussion of reality. For now, our argument will only restrict itself to justifying our present choice of the use of
is the time parameter of the privileged (K) system is fundamental and leads to an interesting question as to the absoluteness of time such as we meet in the context of Newton. In fact, this has always been the problem in the general subject of relativity. For the sake of mare example, when one writes the Schwarzschild’s element of length, the term “Schwarzschild’s time” is used [12]. However, in the course of our discussion, one will soon see that there is really no such thing as Schwarzschild’s time, but rather, the absolute time (or in soft term, the time in the privileged system), controls the flow of the dynamics of the systems, and hence, the matrix of the continuum. Also, it will be seen that x0 plays a major role in the theory we which to present here and no less, the theory of gravitation (i.e. the theory of General Relativity), which results from this paradoxical discussion of reality. For now, our argument will only restrict itself to justifying our present choice of the use of 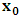 ; the reader will see that this follows from all but the fundamental postulate.From (11), we see that p is the time coordinate of the uniformly translating system K’, which is a function of x0 as already well-known. Indeed, if we take K’ as the coordinate system in uniform translation relative to K, then p defines to us, the time parameter in K’. Thus, since K is at rest, so that nothing is unusual with respect to it— by virtue of the fundamental postulate— we see that x0 is independent of p and of q in the K’ system, or in the system which is not privileged; this does not differ from the usual Lagrangian-Hamiltonian formalism. Moreover, to say that K’ is in uniform translation, one cannot describe the system by an observer who is at rest in it (K’). For example, to say that K’ is in uniform translation, the description can only have a satisfactory physical meaning if we see the situation from a privileged coordinate, K; this limitation is a natural one as we have already pointed out above. It then follows immediately that the spatial and temporal coordinates of the K’ system is measured from the point of view of the privileged system. Then, it follows that the time parameter here used does not depend upon any variable from K’. Then, one can say, for example, the privileged K system measures the time in the K’ system with clocks at rest in K, and finds K’ clocks lagging behind because, he compares the value, p (for K’) with x0 (for K) and finds some differential proportional to the uniform relative velocity; p behaves as a retarded quantity therefore.The x0 at hand plays an important role in all Hamiltonian systems; it determines a fixed time interval on which the variations can be carried out. In our case, it determines to what extent p and q change with change in the elapsed time within the K system. In order words, x0 controls the dynamics of the K’ coordinate according as stated.The independence of x0 presents an even further consequence to the theory which we want to write down; the reader can see immediately that this leads to a conclusion in which, the so called Twin paradox is really immaterial. We have argued this point in the previous consideration of the issue. This is immediate because, the Lagrangian we defined above is an invariant quantity in both K and K’ accordingly as argued above and from postulate 3. One then sees that, the x0 in both K and K’ must be identically equal, so that as long as we take one or the other coordinate systems as privileged, the Lagrangian does not differ. Then, once the travelling twin returns from his trip (or once he is regarded as the privilege brother), x0 does not change; he can consider his brother as the traveler.We write the Lagrangian of the system as
; the reader will see that this follows from all but the fundamental postulate.From (11), we see that p is the time coordinate of the uniformly translating system K’, which is a function of x0 as already well-known. Indeed, if we take K’ as the coordinate system in uniform translation relative to K, then p defines to us, the time parameter in K’. Thus, since K is at rest, so that nothing is unusual with respect to it— by virtue of the fundamental postulate— we see that x0 is independent of p and of q in the K’ system, or in the system which is not privileged; this does not differ from the usual Lagrangian-Hamiltonian formalism. Moreover, to say that K’ is in uniform translation, one cannot describe the system by an observer who is at rest in it (K’). For example, to say that K’ is in uniform translation, the description can only have a satisfactory physical meaning if we see the situation from a privileged coordinate, K; this limitation is a natural one as we have already pointed out above. It then follows immediately that the spatial and temporal coordinates of the K’ system is measured from the point of view of the privileged system. Then, it follows that the time parameter here used does not depend upon any variable from K’. Then, one can say, for example, the privileged K system measures the time in the K’ system with clocks at rest in K, and finds K’ clocks lagging behind because, he compares the value, p (for K’) with x0 (for K) and finds some differential proportional to the uniform relative velocity; p behaves as a retarded quantity therefore.The x0 at hand plays an important role in all Hamiltonian systems; it determines a fixed time interval on which the variations can be carried out. In our case, it determines to what extent p and q change with change in the elapsed time within the K system. In order words, x0 controls the dynamics of the K’ coordinate according as stated.The independence of x0 presents an even further consequence to the theory which we want to write down; the reader can see immediately that this leads to a conclusion in which, the so called Twin paradox is really immaterial. We have argued this point in the previous consideration of the issue. This is immediate because, the Lagrangian we defined above is an invariant quantity in both K and K’ accordingly as argued above and from postulate 3. One then sees that, the x0 in both K and K’ must be identically equal, so that as long as we take one or the other coordinate systems as privileged, the Lagrangian does not differ. Then, once the travelling twin returns from his trip (or once he is regarded as the privilege brother), x0 does not change; he can consider his brother as the traveler.We write the Lagrangian of the system as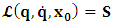 | (12) |
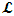 as the difference between the potential and kinetic energies of that system. However, this is not the case in our consideration, since the transformation properties only described to us the axis of space and time for the dust-free continuum. From §2, it was shown that, after the relative motion (or after a time
as the difference between the potential and kinetic energies of that system. However, this is not the case in our consideration, since the transformation properties only described to us the axis of space and time for the dust-free continuum. From §2, it was shown that, after the relative motion (or after a time 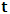 different from zero), K’ is at Π’, if the matter is viewed from K; the element of arc length does not vanished therefore. It is then straightforward to see that the Lagrangian defines, in our case, the element of arc length, or the separation of the system, as the constant of the motion. Now, since at
different from zero), K’ is at Π’, if the matter is viewed from K; the element of arc length does not vanished therefore. It is then straightforward to see that the Lagrangian defines, in our case, the element of arc length, or the separation of the system, as the constant of the motion. Now, since at 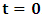 , K and K’ are both at the point Π, we see that the separation between Π and Π’ is nothing but the total observable dust-free continuum (just by the fact that we have not considered the matter field). We will come back to this point to justify our use of the term “Observable Continuum”, so that it can be clear to the reader as possible that the space-time continuum is really created from the separation resulting from this uniform translated motion of the systems. We are therefore referring to nothing different from the origin of the universe such as, for example, the Big Band.We can go even further then what we have discussed so far. Notice that the uniform translation of K’ with respect to K is symmetric about Π, so that one can, with equal validity, regard K as the system which is now in uniform translation relative to the latter, in the opposing direction; this is due to the choice of the Lorentz boost as desire. Following this line of thought, one sees immediately that a Universe is an unstable system; at least our space-time continuum should be a “DUALVERSE” in which we reside in half. We shall return to this theme more than once as we go along.Let
, K and K’ are both at the point Π, we see that the separation between Π and Π’ is nothing but the total observable dust-free continuum (just by the fact that we have not considered the matter field). We will come back to this point to justify our use of the term “Observable Continuum”, so that it can be clear to the reader as possible that the space-time continuum is really created from the separation resulting from this uniform translated motion of the systems. We are therefore referring to nothing different from the origin of the universe such as, for example, the Big Band.We can go even further then what we have discussed so far. Notice that the uniform translation of K’ with respect to K is symmetric about Π, so that one can, with equal validity, regard K as the system which is now in uniform translation relative to the latter, in the opposing direction; this is due to the choice of the Lorentz boost as desire. Following this line of thought, one sees immediately that a Universe is an unstable system; at least our space-time continuum should be a “DUALVERSE” in which we reside in half. We shall return to this theme more than once as we go along.Let 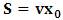 from reason of ordinary mechanics; eq. (12) then has the from
from reason of ordinary mechanics; eq. (12) then has the from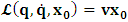 | (13) |
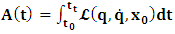 | (14) |
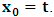 If one takes the variation of the action, in a well-known way, one sees that the integral vanishes identically. Eq. (14) will then be true only if its integrand vanishes identically according to
If one takes the variation of the action, in a well-known way, one sees that the integral vanishes identically. Eq. (14) will then be true only if its integrand vanishes identically according to 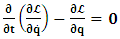 | (15) |
 we will again consider this point and the reader will see that important explanation of the quantum problem can be answered.What exactly is the Lagrangian of the system? Indeed, this question seems straightforward; in fact, the answer follows just as we meet in the mechanics of Newton and Maxwell. In the well-known Lagrangian-Hamiltonian dynamics, if one takes the pair of phase variables, (p, q) for generalize coordinate and conjugate momenta, one can define two functions, with each depending on exactly one of the variables as
we will again consider this point and the reader will see that important explanation of the quantum problem can be answered.What exactly is the Lagrangian of the system? Indeed, this question seems straightforward; in fact, the answer follows just as we meet in the mechanics of Newton and Maxwell. In the well-known Lagrangian-Hamiltonian dynamics, if one takes the pair of phase variables, (p, q) for generalize coordinate and conjugate momenta, one can define two functions, with each depending on exactly one of the variables as  and
and 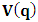 , so that one writes
, so that one writes 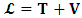 as the Lagrangian of the system, with T and V having their same meanings as the kinetic and potential of the system [13-15].However, as one is well aware, we are dealing with the dust free continuum in which, from the Heisenberg’s consideration above, follows the same rules as the functions T and V. That is to say, if one increases the Kinetic energy of a system so chosen, one sees that the potential of the same system is diminished with equal proportion, if the total energy of the system is invariable. We could have used position and momentum functions, but the result does not differ.Just as the Lagrangian leads to the total energy of the dynamical system as the constant of the motion, so too, the Lagrangian we are here concern, defines, in a well-known way, the total length element of the observable continuum. Trivial arguments can lead one to the quantization of space and time just as the invariable energy is treated in quantum mechanics; we will not investigate this interesting problem here any further, but we assume that the result is true for reason of mare comparison with the usual Hamiltonian treatment. In fact, it appears to us that the total energy of the universe has a direct relation to the total space-time continuum; the argument can be made easily. Several Lagrangian can be written down for the system; we shall take the simplest of all by taking functions of spatial axis (q) and the uniform velocity
as the Lagrangian of the system, with T and V having their same meanings as the kinetic and potential of the system [13-15].However, as one is well aware, we are dealing with the dust free continuum in which, from the Heisenberg’s consideration above, follows the same rules as the functions T and V. That is to say, if one increases the Kinetic energy of a system so chosen, one sees that the potential of the same system is diminished with equal proportion, if the total energy of the system is invariable. We could have used position and momentum functions, but the result does not differ.Just as the Lagrangian leads to the total energy of the dynamical system as the constant of the motion, so too, the Lagrangian we are here concern, defines, in a well-known way, the total length element of the observable continuum. Trivial arguments can lead one to the quantization of space and time just as the invariable energy is treated in quantum mechanics; we will not investigate this interesting problem here any further, but we assume that the result is true for reason of mare comparison with the usual Hamiltonian treatment. In fact, it appears to us that the total energy of the universe has a direct relation to the total space-time continuum; the argument can be made easily. Several Lagrangian can be written down for the system; we shall take the simplest of all by taking functions of spatial axis (q) and the uniform velocity 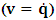 of the K’ system, envisioned from K as:
of the K’ system, envisioned from K as: 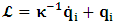 | (16) |
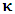 is some number having unit as the Hobble parameter (1/s), and q and
is some number having unit as the Hobble parameter (1/s), and q and 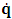 having their usual meanings as the spatial coordinate and velocity of the K’ system, and
having their usual meanings as the spatial coordinate and velocity of the K’ system, and 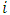 taking values from 1 to 3.Then, the evolution of the system can be described completely by (15) according to easy argument from Lagrangian formalism; the reader can check this by mare substitution. We will argue in a later paper that κ is indeed the Hobble’s parameter for the expansion of the universe; for now, we will just use the nomenclature here for the lack of better word and to keep the flow of argument. But, it follows at once that, for a non-varying
taking values from 1 to 3.Then, the evolution of the system can be described completely by (15) according to easy argument from Lagrangian formalism; the reader can check this by mare substitution. We will argue in a later paper that κ is indeed the Hobble’s parameter for the expansion of the universe; for now, we will just use the nomenclature here for the lack of better word and to keep the flow of argument. But, it follows at once that, for a non-varying 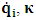 cannot be a constant number for any varying
cannot be a constant number for any varying 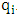 . We will see that κ is the strength of the field of acceleration which varied just as, for example, the magnetic field of Maxwell’s theory!Hamilton’s equation is also immediate. Suppose we take the total derivative of the Lagrangian (16), taking
. We will see that κ is the strength of the field of acceleration which varied just as, for example, the magnetic field of Maxwell’s theory!Hamilton’s equation is also immediate. Suppose we take the total derivative of the Lagrangian (16), taking 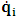 as an independent coordinate in the phase space. One obtains
as an independent coordinate in the phase space. One obtains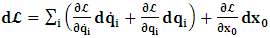 | (17-I) |
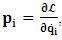 so that one gets, from (17-I)
so that one gets, from (17-I)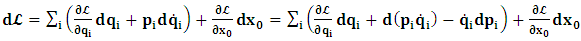 | (17-II) |
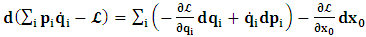 | (18) |
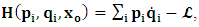 (18) becomes
(18) becomes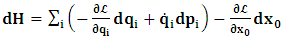 | (19) |
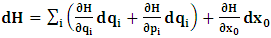 | (20) |
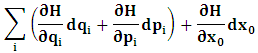
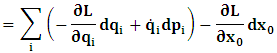 Notice that the
Notice that the  was chosen as though it were a phase variables; thus, upon equating respective coefficients, we have
was chosen as though it were a phase variables; thus, upon equating respective coefficients, we have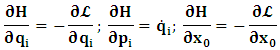 From our argument, one can explicitly write
From our argument, one can explicitly write  and
and  so that q and p are functions of x0. If one now takes
so that q and p are functions of x0. If one now takes  as a non-phase variable, one has
as a non-phase variable, one has 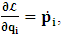 according to (15). We then obtain the 2n first order differential equations
according to (15). We then obtain the 2n first order differential equations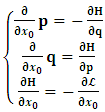 | (21) |
 , as we have already stated. Then, if one takes the matrices resulting from arbitrary selection of order pairs of differing choices, one obtains a family of 2n matrices satisfying the following determinant relations
, as we have already stated. Then, if one takes the matrices resulting from arbitrary selection of order pairs of differing choices, one obtains a family of 2n matrices satisfying the following determinant relations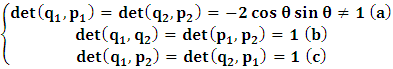 | (22) |
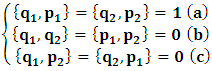 | (23) |
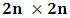 sympletic matrix can be defined by
sympletic matrix can be defined by 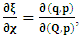 where
where  and
and 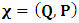 . From (23), one has the Jacobean relations
. From (23), one has the Jacobean relations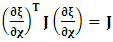 | (24) |
 is the
is the  identity matrix and
identity matrix and 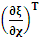 is the transpose of the sympletic matrix accordingly It is not hard to see that the determinant of the Jacobean is +1. It is also clear that the Hamiltonian is conserved for a change in choice of privileged system. In fact, by inspection, one can see that,
is the transpose of the sympletic matrix accordingly It is not hard to see that the determinant of the Jacobean is +1. It is also clear that the Hamiltonian is conserved for a change in choice of privileged system. In fact, by inspection, one can see that, 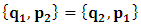 and so on; a Hamiltonian flow goes to a Hamiltonian flows and the systems are in complete involution with each other as desire. The inverse of
and so on; a Hamiltonian flow goes to a Hamiltonian flows and the systems are in complete involution with each other as desire. The inverse of 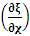 is also well defined. A non-rigorous proof follows if one takes it that the inverse matrix is that resulting if one were to choose the K’ as privilege system, so that it is now the K system which is uniformly translating with respect to the earlier. We shall not write this result here as it can be easily shown from above, and by trivial manipulation of (24). It follows that the system satisfies the
is also well defined. A non-rigorous proof follows if one takes it that the inverse matrix is that resulting if one were to choose the K’ as privilege system, so that it is now the K system which is uniformly translating with respect to the earlier. We shall not write this result here as it can be easily shown from above, and by trivial manipulation of (24). It follows that the system satisfies the  group. Now, since the canonical system satisfies the general
group. Now, since the canonical system satisfies the general 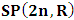 group which, for our 2-degree system, one has
group which, for our 2-degree system, one has 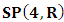 , one then sees easily that the system we are here concern is the intersecting
, one then sees easily that the system we are here concern is the intersecting 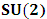 group. There is no need for a rigorous proof as the result flows from the argument we have already made. However, in our consideration, we shall be interested in the
group. There is no need for a rigorous proof as the result flows from the argument we have already made. However, in our consideration, we shall be interested in the 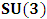 group for the 3-degree of freedom system and the argument is just the same Indeed, the conservation of space is immediate; it follows as we meet for the conservation law of energy according to Noether’s theorem [15]. Notice that (15) can be equivalently written as
group for the 3-degree of freedom system and the argument is just the same Indeed, the conservation of space is immediate; it follows as we meet for the conservation law of energy according to Noether’s theorem [15]. Notice that (15) can be equivalently written as 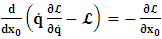 | (25) |
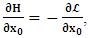 from the definition of the Hamiltonian above, and that
from the definition of the Hamiltonian above, and that 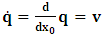 .But, from the time-independence of the Lagrangian, we see that
.But, from the time-independence of the Lagrangian, we see that 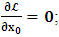 the result follows immediately as we wish.
the result follows immediately as we wish.3.1. Lorentz-like Transformation and the Entanglement Paradox
- As the reader can see, there is already a clear correlation between the quantum mechanical treatment and the theme we have here considered for the dust free continuum. In particular, the Heisenberg’s consideration, as well as the entangled correlation of K and K’ are immediate. This is an important result because, if it is really true, it follows that one is applying quantum mechanical treatment to the entire continuum; a unified field theory is therefore in sight. A question of concern can be put forth: what is the reason for the quantum-like correlating behavior of our systems. We wish to explain in a satisfactory way, the source of this relationship, so that one sees from all rational view that a Hidden Variable interpretation [16,36] of the situation is really immaterial; the same is also true for the quantum physics. It seems to us that all composite systems have certain important property which, one may assign to it, the cause of this correlating quantum behavior. That is, all entangled systems are related in a way such that they retain the information of their common origin of coordinate in their transformation laws at any future time and for any arbitrary separation. [The word “coordinate” here must be taken to refer to the actual space-time axes instead of the frame of reference]To see the reasoning involve, let one takes K as the privileged system; then, by the fundamental postulate, K is always looked at as being at the point of coordinate origin accordingly (i.e., at Ⅱ, so to speak). This is really no more different from Bell’s view of the Hidden Variable problem [37]. This must not cause any confusion to the reader because, it is the case that nothing is really unusual in any system chosen as privileged observer, when view from within that frame of reference. Then, viewed from K, the K’ system is in uniform translation with respect to the earlier. It then seems that the fundamental postulate has given us the natural security of the general nature of all privileged system such that, whichever way we take things, the result we have stated is always immediate. This is a special behavior to which, from all rational view point, one can assign to it, the actual reason for the quantum correlation which one observes within the systems. The matter then becomes strange if one noticed that we are free to choose the privilege system, and that any system which is taken as the privileged, it is always view to be at the origin of the space-time coordinate. One then sees that the motion is really only virtual, and the justification follows satisfactory without any Hidden variable interpretation of the issue— just by the application of the fundamental postulate of relativity. We put this argument in context by the lengthy discussion below.Consider here a 2 dimensional isotropic system defined by the Hamiltonian
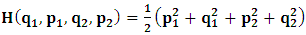 . We are interested in finding various constants of the motion other than the Hamiltonian itself. If we take the choices of the phase variable according as (q1, p1), or (q2, p2), one easily finds two unconnected constants of the motion, with each referring to exactly one part of the systems:
. We are interested in finding various constants of the motion other than the Hamiltonian itself. If we take the choices of the phase variable according as (q1, p1), or (q2, p2), one easily finds two unconnected constants of the motion, with each referring to exactly one part of the systems: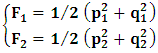 | (26) |
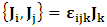 | (27) |
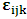 is the total anti-symmetric symbol with the usual definition, and the
is the total anti-symmetric symbol with the usual definition, and the 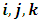 taking their appropriate range 1-3.One can then obtain, for a 3D system, a
taking their appropriate range 1-3.One can then obtain, for a 3D system, a  anti-symmetric matrix with entries obeying the relation:
anti-symmetric matrix with entries obeying the relation: 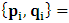
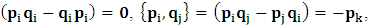 and so on. Let us define, for our purpose, a family of metrics
and so on. Let us define, for our purpose, a family of metrics 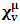 resulting only from the mixed choices (q1, p2) or (q2, p1) as all matrices satisfying a condition in which the isolating curve (or distance measurement) between the systems is not null, but that either one or the other system so privileged, is at the origin of coordinate, and the latter separated from the earlier by certain distance. We then see that
resulting only from the mixed choices (q1, p2) or (q2, p1) as all matrices satisfying a condition in which the isolating curve (or distance measurement) between the systems is not null, but that either one or the other system so privileged, is at the origin of coordinate, and the latter separated from the earlier by certain distance. We then see that 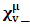 and hence, the choice of mixed variables_ is the only matrix in which distance measures are well defined. Then, by means of definition,
and hence, the choice of mixed variables_ is the only matrix in which distance measures are well defined. Then, by means of definition, 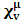 is a special subgroup of the general
is a special subgroup of the general  group, obtained by combination of only commuting parameters. All such matrices
group, obtained by combination of only commuting parameters. All such matrices 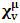 are pseudo-orthogonal and invariant under rotation and translation, as can be easily verified by the reader. We shall hereafter call the family
are pseudo-orthogonal and invariant under rotation and translation, as can be easily verified by the reader. We shall hereafter call the family 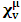 , the matrices of entanglement for the obvious reason that will soon be clear.We wish to now generalize things to the pseudo-4 dimensional space time continuum. From (27), we saw that, in a 3D system, one obtains
, the matrices of entanglement for the obvious reason that will soon be clear.We wish to now generalize things to the pseudo-4 dimensional space time continuum. From (27), we saw that, in a 3D system, one obtains  anti-symmetry matrix from the relationship of the phase variables according to the Poison structure. But, from obvious argument, it follows that, in place of the phase variables
anti-symmetry matrix from the relationship of the phase variables according to the Poison structure. But, from obvious argument, it follows that, in place of the phase variables 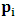 (which is nothing but the conjugate time parameter in the privilege system), one can write
(which is nothing but the conjugate time parameter in the privilege system), one can write 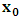 instead. This follows immediately from the fact that
instead. This follows immediately from the fact that 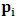 is the time coordinates of the other system which is so privileged. Besides, from the fundamental postulate when applied to K, it becomes obvious that the time in the K system is identically
is the time coordinates of the other system which is so privileged. Besides, from the fundamental postulate when applied to K, it becomes obvious that the time in the K system is identically  — since indeed, there is no relative motion in that system. This must not cause any confusion to the reader, as the justification follows from the very definition which this paradoxical theory has assigned to the theory of relativity. Then, all the conjugate phase variables, (pi) can be replaced by
— since indeed, there is no relative motion in that system. This must not cause any confusion to the reader, as the justification follows from the very definition which this paradoxical theory has assigned to the theory of relativity. Then, all the conjugate phase variables, (pi) can be replaced by  without any loss of generality of the argument. Also, since the fundamental postulate prohibits us from writing the dynamics of the K system, it is immediate that the
without any loss of generality of the argument. Also, since the fundamental postulate prohibits us from writing the dynamics of the K system, it is immediate that the 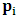 corresponding to the phase variables in K vanishes identically whenever one uses the time parameter
corresponding to the phase variables in K vanishes identically whenever one uses the time parameter 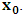 Then,
Then,  will vanish identically whereas
will vanish identically whereas  will now be non-zero; that is to say, view from the privilege system,
will now be non-zero; that is to say, view from the privilege system, 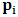 is a dynamical parameter whereas
is a dynamical parameter whereas 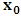 is not. Ϯ Attention must be call to the unique relationship we here obtained. It follows that whenever
is not. Ϯ Attention must be call to the unique relationship we here obtained. It follows that whenever 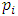 is non-vanishing,
is non-vanishing, 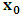 identically vanishes; in this case, an anti-symmetric metrics is obtained with vanishing diagonal element. If we take the reverse situation, the opposite happens, so that we are just changing roles,
identically vanishes; in this case, an anti-symmetric metrics is obtained with vanishing diagonal element. If we take the reverse situation, the opposite happens, so that we are just changing roles, 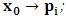 we then have a symmetric tensor in the latter interchange of variables. The symmetric metric then has zero off diagonal elements.This special relation has a far-reaching importance. Let us take
we then have a symmetric tensor in the latter interchange of variables. The symmetric metric then has zero off diagonal elements.This special relation has a far-reaching importance. Let us take 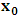 for K and the three spatial axes for the K’ system; one obtains a four vector
for K and the three spatial axes for the K’ system; one obtains a four vector 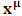 for
for  from which a
from which a 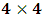 orthogonal matrix is defined upon multiplying
orthogonal matrix is defined upon multiplying 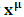 with itself accordingly. Then, one sees easily that the conjugate phase variable can be view as retarded function. This can be shown by complex process1 [17-20,35], but we shall show here that this process is greatly simplified if one follows the fundamental postulate. Let us writes the Maxwell’s equation for conserved quantity:
with itself accordingly. Then, one sees easily that the conjugate phase variable can be view as retarded function. This can be shown by complex process1 [17-20,35], but we shall show here that this process is greatly simplified if one follows the fundamental postulate. Let us writes the Maxwell’s equation for conserved quantity: 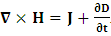 . One can easily identify the relationship
. One can easily identify the relationship 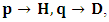 from obvious reason that H behaves like a conjugate momenta of the D. Then, from the fundamental postulate, H vanishes identically (since there is no variation in the privileged system K); one then has
from obvious reason that H behaves like a conjugate momenta of the D. Then, from the fundamental postulate, H vanishes identically (since there is no variation in the privileged system K); one then has 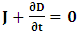 as the equation of motion of the system. The same solution follows from the divergence theorem, but it is easy to follow from the fundamental postulate instead. If one now takes the divergence, one gets the continuity equation identically in Maxwell’s field. The following relation becomes immediate:For if one takes x0, one gets the continuity equation as the only equation of motion_ the resulting
as the equation of motion of the system. The same solution follows from the divergence theorem, but it is easy to follow from the fundamental postulate instead. If one now takes the divergence, one gets the continuity equation identically in Maxwell’s field. The following relation becomes immediate:For if one takes x0, one gets the continuity equation as the only equation of motion_ the resulting  matrix is diagonal and symmetric; if, on the other hand, one takes the phase conjugate variables
matrix is diagonal and symmetric; if, on the other hand, one takes the phase conjugate variables 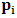 , one recovers all of Maxwell’s equations in an anti-symmetric matrix of the same rank and with vanishing diagonal element.We have used the word “Pseudo-4 dimensional continuum” to intimate that the phase space depends only on the three spatial coordinate and their corresponding three conjugate time parameters
, one recovers all of Maxwell’s equations in an anti-symmetric matrix of the same rank and with vanishing diagonal element.We have used the word “Pseudo-4 dimensional continuum” to intimate that the phase space depends only on the three spatial coordinate and their corresponding three conjugate time parameters 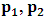 and
and 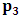 ; one is then referring to the
; one is then referring to the 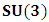 group. Then, in place of the conjugate variables
group. Then, in place of the conjugate variables 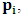 we can write
we can write 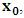 without loss of soundness of the argument, so long as we are now using the symmetric matrix with zero everywhere except the diagonal element. Following this, one sees that, for the 4-dimensional Minkowski’s matrix, the zeroth component is nothing but the time parameter of the privilege system. This does not cause us any trouble, since the Minkowski’s matrix is symmetric and diagonal as desired. If one were to take the phase conjugate variables, one would have obtained the desired
without loss of soundness of the argument, so long as we are now using the symmetric matrix with zero everywhere except the diagonal element. Following this, one sees that, for the 4-dimensional Minkowski’s matrix, the zeroth component is nothing but the time parameter of the privilege system. This does not cause us any trouble, since the Minkowski’s matrix is symmetric and diagonal as desired. If one were to take the phase conjugate variables, one would have obtained the desired 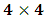 anti-symmetric matrix having zeros along the diagonal so that, instead of taking
anti-symmetric matrix having zeros along the diagonal so that, instead of taking 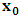 , one takes the three phase variables
, one takes the three phase variables 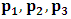 and the corresponding generalized coordinates.Let, for the sake of mare example in this pseudo-4 space, one takes a Lorentz boost along
and the corresponding generalized coordinates.Let, for the sake of mare example in this pseudo-4 space, one takes a Lorentz boost along 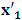 ; one obtains a
; one obtains a 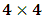 pseudo-orthogonal matrix with exactly the same properties as the well-known Lorentzian-like metric2; the reader is free to verify the claim easily by, for example, taking the metric resulting from choosing the q1 and p2 (and then including the parallel q2 and q3). The p2 as used here, refers to the second system which is privileged, whereas the q1, q2 and q3 refer to the spatial coordinate of the first system (which is not the privileged).It follows that, in this purely paradoxical theory of reality, a Lorentz-like matrix is obtained if one takes only commuting parameters of the two systems which are in uniform translation with each other; the knowledge of one of the system will then preclude the knowledge of the other, just as we meet in the atomistic theory of Quantum physics. Indeed, as the reader can see, the common origin of the systems (i.e., at Π) is now preserved, since, for the separating matrix, the one systems so privileged is at the common origin when viewed from itself, or precisely by our use of the variable
pseudo-orthogonal matrix with exactly the same properties as the well-known Lorentzian-like metric2; the reader is free to verify the claim easily by, for example, taking the metric resulting from choosing the q1 and p2 (and then including the parallel q2 and q3). The p2 as used here, refers to the second system which is privileged, whereas the q1, q2 and q3 refer to the spatial coordinate of the first system (which is not the privileged).It follows that, in this purely paradoxical theory of reality, a Lorentz-like matrix is obtained if one takes only commuting parameters of the two systems which are in uniform translation with each other; the knowledge of one of the system will then preclude the knowledge of the other, just as we meet in the atomistic theory of Quantum physics. Indeed, as the reader can see, the common origin of the systems (i.e., at Π) is now preserved, since, for the separating matrix, the one systems so privileged is at the common origin when viewed from itself, or precisely by our use of the variable 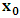 , or by application of the fundamental postulate. If we were to use the conjugate pi parameter, the result would not have changed except that the matrix would have been anti-symmetric, just as the Maxwell’s tensor in the theory of electrodynamics.We shall encounter this point again as we go alone. But, notice immediately that the matrix of entanglement differs from the well-known Lorentz type. This follows from the fact that the composite matrix
, or by application of the fundamental postulate. If we were to use the conjugate pi parameter, the result would not have changed except that the matrix would have been anti-symmetric, just as the Maxwell’s tensor in the theory of electrodynamics.We shall encounter this point again as we go alone. But, notice immediately that the matrix of entanglement differs from the well-known Lorentz type. This follows from the fact that the composite matrix 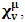 is made only of commuting variables of the two systems— this is not the case in the Lorentz formalism.We can go even further than what we have considered so far. Notice at once that, in a well-known way, the length of separation of the systems, or straightly speaking, the observable continuum can be given_ in Minkowski’s view, as
is made only of commuting variables of the two systems— this is not the case in the Lorentz formalism.We can go even further than what we have considered so far. Notice at once that, in a well-known way, the length of separation of the systems, or straightly speaking, the observable continuum can be given_ in Minkowski’s view, as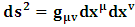 | (28) |
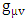 is the Minkowski’s matrix, defined from
is the Minkowski’s matrix, defined from 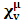 in a well-known way, with Greek symbols taking values 0, 1, 2, 3.The
in a well-known way, with Greek symbols taking values 0, 1, 2, 3.The 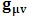 is symmetric and pseudo-orthogonal, by reason of definition of the
is symmetric and pseudo-orthogonal, by reason of definition of the 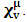 It then follows that
It then follows that 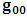 represents the privilege system, if one applies to that system, the fundamental postulate. The
represents the privilege system, if one applies to that system, the fundamental postulate. The 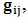 on the other hand, refers to the K’ system which is not privileged, and which is seen to be under uniform translation. Then,
on the other hand, refers to the K’ system which is not privileged, and which is seen to be under uniform translation. Then, 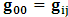 identically, where
identically, where  are the spatial coordinates of the K’ system, and that
are the spatial coordinates of the K’ system, and that 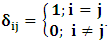 This follows since, in general, for the commuting variables, the continuum vanishes identically. Therefore,
This follows since, in general, for the commuting variables, the continuum vanishes identically. Therefore, 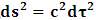 vanishes identically. The vanishing of ds2 must be understood from the condition of commuting of the variables in both K and K’, just as in atomic physics. The continuum (or the spatial separation ds) is therefore a virtual one.In fact, if one were to consider the dust content of the system, one would have seen that
vanishes identically. The vanishing of ds2 must be understood from the condition of commuting of the variables in both K and K’, just as in atomic physics. The continuum (or the spatial separation ds) is therefore a virtual one.In fact, if one were to consider the dust content of the system, one would have seen that  is a singularity point of dense material from which the outgoing Hawkins energy flows. Then,
is a singularity point of dense material from which the outgoing Hawkins energy flows. Then,  would have referred to all regions lying outside the horizon of
would have referred to all regions lying outside the horizon of 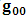 , and in which the pure energy appears as flux of pressure and stresses. However, in our consideration,
, and in which the pure energy appears as flux of pressure and stresses. However, in our consideration, 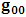 describes the point of origin Π, whereas
describes the point of origin Π, whereas 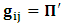 lies outside Π and, for our purpose, describes the observable continuum of the uniformly translated system (or the distance of separation); this will play an important role in our discussion of the Maldacena’s duality condition as the reader will soon see.
lies outside Π and, for our purpose, describes the observable continuum of the uniformly translated system (or the distance of separation); this will play an important role in our discussion of the Maldacena’s duality condition as the reader will soon see.3.2. Wave-like Treatment of the Space-time Continuum and the Klein-Gordon Equation
- Let, after any time different from zero, one of the systems which is not taken as the privileged, separates from the origin
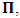 as a result of the uniform translation by desirable Lorentz boost. Suppose that we focus our attention on one of the systems—preferably K’ (just by the fact that we have been considering it as that in uniform motion). Let it be that the dynamics of the systems is govern by some function
as a result of the uniform translation by desirable Lorentz boost. Suppose that we focus our attention on one of the systems—preferably K’ (just by the fact that we have been considering it as that in uniform motion). Let it be that the dynamics of the systems is govern by some function 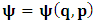 , where
, where 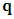 and
and 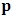 are some appropriate commuting variables. That is to say, one is using the pair
are some appropriate commuting variables. That is to say, one is using the pair 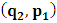 , so that
, so that 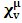 is the metric. The ψ-function is therefore pseudo-orthogonal as desired. We demand that
is the metric. The ψ-function is therefore pseudo-orthogonal as desired. We demand that 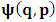 satisfies some arbitrary wave equation
satisfies some arbitrary wave equation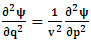 | (29) |
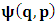 can be separated into two functions with each sub-function depending on exactly one of the variables in
can be separated into two functions with each sub-function depending on exactly one of the variables in 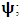 this follows from (11). One is then able to write ψ as a product of two functions according to:
this follows from (11). One is then able to write ψ as a product of two functions according to: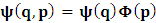 | (30) |
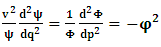 | (31) |
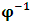 as the total observable continuum upon carrying out the operation; the justification will soon be obvious. Two separate equations can then be obtained from (31) accordingly
as the total observable continuum upon carrying out the operation; the justification will soon be obvious. Two separate equations can then be obtained from (31) accordingly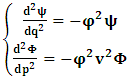 | (32) |
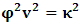 , so that
, so that  is the relative velocity of the system. This must be taken as the speed of expansion of the universe; we will have this discussion in a separate paper however. Then, the decrease in κ (cause by an increase in the age of the universe, by Hobble’s consideration of issue) leads to a corresponding decrease in φ (which also corresponds to increase in the total separation or observable continuum); this is satisfied by obvious observation and it is already well-known in string theory [12]Let it be that,
is the relative velocity of the system. This must be taken as the speed of expansion of the universe; we will have this discussion in a separate paper however. Then, the decrease in κ (cause by an increase in the age of the universe, by Hobble’s consideration of issue) leads to a corresponding decrease in φ (which also corresponds to increase in the total separation or observable continuum); this is satisfied by obvious observation and it is already well-known in string theory [12]Let it be that, 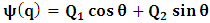 and
and 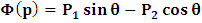 , where we have treated the Q’s and P’s as numbers. In order for (32) to hold well, the argument, θ must take the values
, where we have treated the Q’s and P’s as numbers. In order for (32) to hold well, the argument, θ must take the values  for ψ and
for ψ and  for Φ. One then obtains the functions
for Φ. One then obtains the functions 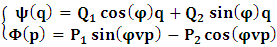 | (33) |
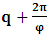 in
in 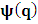 and
and 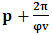 in
in 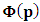 [21]Since the variables are commuting ones, we see that
[21]Since the variables are commuting ones, we see that 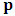 is the time coordinates of the privileged K system according to our use of the entangled (pseudo-orthogonal) metric,
is the time coordinates of the privileged K system according to our use of the entangled (pseudo-orthogonal) metric, 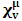 or, according to obvious rule in quantum physics [22-23]. Then, ψ carries all the information of the two systems, just as we would meet for quantum systems. By the fundamental postulate, one sees that ψ is independent of p. However, one may have obtained the same result from the obvious argument that the K’ system is in uniform translation relative to K, so that there is no differential of ψ in respect to p according to the fundamental postulate; the same result is still trivial. The differential of the wave-function depending on
or, according to obvious rule in quantum physics [22-23]. Then, ψ carries all the information of the two systems, just as we would meet for quantum systems. By the fundamental postulate, one sees that ψ is independent of p. However, one may have obtained the same result from the obvious argument that the K’ system is in uniform translation relative to K, so that there is no differential of ψ in respect to p according to the fundamental postulate; the same result is still trivial. The differential of the wave-function depending on 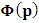 vanishes identically and (33) reduces to one equation, namely
vanishes identically and (33) reduces to one equation, namely 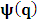 . From trivial algebra, the only useful equation in (32) becomes
. From trivial algebra, the only useful equation in (32) becomes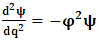 | (34) |
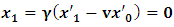 ; our result is not an arbitrary one. This defines the boundary condition of the continuum in a well-known way, as the reader can easily see. Taking
; our result is not an arbitrary one. This defines the boundary condition of the continuum in a well-known way, as the reader can easily see. Taking 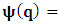
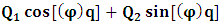 on the boundary
on the boundary 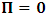 and
and 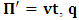 vanishes as desired. For the vanishing of ψ on the said condition, one then has
vanishes as desired. For the vanishing of ψ on the said condition, one then has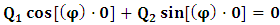 | (35) |
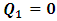 One now has, for the last condition and letting
One now has, for the last condition and letting 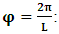
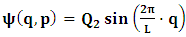 | (36) |
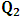 does not vanish for the entire continuum, since by this reason, the wave-function will vanish identically in places where the separation or, the observable continuum is material. Two observations can be made immediately:First, suppose that
does not vanish for the entire continuum, since by this reason, the wave-function will vanish identically in places where the separation or, the observable continuum is material. Two observations can be made immediately:First, suppose that 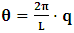 is some integer multiple of π according as
is some integer multiple of π according as 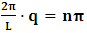 , then, the semi-classical quantization of space follows immediately. This is however a trivial argument because, as it is not hard to show, the quantization of energy actually leaves the said argument valid. Moreover, we will show later that the ratio,
, then, the semi-classical quantization of space follows immediately. This is however a trivial argument because, as it is not hard to show, the quantization of energy actually leaves the said argument valid. Moreover, we will show later that the ratio, 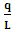 is always unity in the face of measurement, so that the argument of the function in (36) is always an integer multiple
is always unity in the face of measurement, so that the argument of the function in (36) is always an integer multiple 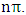 Second, one sees that the relative velocity, v is a constant; the universe is then expanding at constant velocity rather than exponentially. The expansion velocity of the early universe cannot therefore be different from that which we now observe. Does this cause us any trouble? Well, it turns out that this does not really prohibit the expansion of the universe, but that uniform acceleration has the remarkable property in which far away systems appear to recede faster with increasing distance; thus, giving the impression of accelerated/exponential expansion. Take
Second, one sees that the relative velocity, v is a constant; the universe is then expanding at constant velocity rather than exponentially. The expansion velocity of the early universe cannot therefore be different from that which we now observe. Does this cause us any trouble? Well, it turns out that this does not really prohibit the expansion of the universe, but that uniform acceleration has the remarkable property in which far away systems appear to recede faster with increasing distance; thus, giving the impression of accelerated/exponential expansion. Take 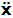 as some parameter corresponding to the acceleration of the universe. Suppose it is trivial that
as some parameter corresponding to the acceleration of the universe. Suppose it is trivial that 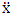 depends upon time, so that one writes
depends upon time, so that one writes 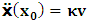 as the acceleration of the observable continuum; we are taking it that all the terms have their usual meanings and
as the acceleration of the observable continuum; we are taking it that all the terms have their usual meanings and 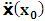 is the acceleration as function of time. If one now let
is the acceleration as function of time. If one now let 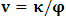 , one sees that the variation of
, one sees that the variation of 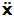 depends upon the variation of κ and φ, the result follows at once. We shall discuss the theme in greater detail and one will see that an expansion satisfying a characteristic
depends upon the variation of κ and φ, the result follows at once. We shall discuss the theme in greater detail and one will see that an expansion satisfying a characteristic 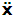 still leads to red-shift of circle per second of light ray as already observed. This discussion is actually two papers away from our current treatment, so we will not expand on it any further in this present paper.We end this discussion by finding the Klein-Gordon Operator for the system which is already immediate from (29) and (31). Indeed, one can proceed in several ways, but we choose the simplest of them. Notice that from (29), one may re-write (31) in the form
still leads to red-shift of circle per second of light ray as already observed. This discussion is actually two papers away from our current treatment, so we will not expand on it any further in this present paper.We end this discussion by finding the Klein-Gordon Operator for the system which is already immediate from (29) and (31). Indeed, one can proceed in several ways, but we choose the simplest of them. Notice that from (29), one may re-write (31) in the form 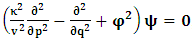 , where we have use the function
, where we have use the function 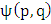 rather than the one depending only on the q’s. It then follows easily that
rather than the one depending only on the q’s. It then follows easily that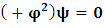 | (37) |
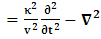 , and the change of variable
, and the change of variable  does not hurt us, from obvious argument above. Eq. (37) satisfactorily describes the space-time continuum (and no less the gravitational field), so that one gets a single equation capable of describing the space time continuum and again the quantum system!Interesting commutative relationships are also immediate.Take the non-commuting pair of variables,
does not hurt us, from obvious argument above. Eq. (37) satisfactorily describes the space-time continuum (and no less the gravitational field), so that one gets a single equation capable of describing the space time continuum and again the quantum system!Interesting commutative relationships are also immediate.Take the non-commuting pair of variables, 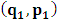 corresponding to the uniformly translating system, K’. From (21), one may write the operators of q and p according to
corresponding to the uniformly translating system, K’. From (21), one may write the operators of q and p according to 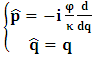 | (A) |
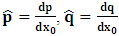 Notice that we have used the imaginary number—i, as a result of our definition of the proper time according to the relationship
Notice that we have used the imaginary number—i, as a result of our definition of the proper time according to the relationship  so that the resulting matrix has the signature
so that the resulting matrix has the signature  .If one defines an operation,
.If one defines an operation, 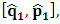 on the phase variables, one sees that the commutator
on the phase variables, one sees that the commutator 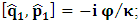 where it is obvious that
where it is obvious that 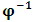 is the total continuum and
is the total continuum and 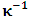 the time/ total age of the K’ system respectively [23,24]. This follows because, one sees only the motion of K’ from Π to Π’, if one considers the given pair of commuting variable; the reciprocal situation is also true. This is consistent with the non-commuting relation of the position and momentum of the usual Hamiltonian system in quantum physics. Accordingly also, if one takes the commuting pair
the time/ total age of the K’ system respectively [23,24]. This follows because, one sees only the motion of K’ from Π to Π’, if one considers the given pair of commuting variable; the reciprocal situation is also true. This is consistent with the non-commuting relation of the position and momentum of the usual Hamiltonian system in quantum physics. Accordingly also, if one takes the commuting pair 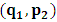 in the same way, one sees that the commutator
in the same way, one sees that the commutator 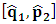 vanishes identically, so that K and K’ are at the common point Π as desired. One then sees immediately that (28) is valid for the vanishing of the Minkowski’s matrix.
vanishes identically, so that K and K’ are at the common point Π as desired. One then sees immediately that (28) is valid for the vanishing of the Minkowski’s matrix.3.2.1. Heisenberg’s Uncertainty of the Space-Time Continuum
- As has already been clearly pointed out, taking both the space and time coordinates of any chosen system (K or K’) together form a non-commuting relationship. Then, if one gets a time dilation of any system so chosen, one sees that there is a spatial increment of that same system and vice versa; one cannot therefore know, with certainty, the dilation of space and time together in any given coordinate system taken at will. This is indeed not strange to us from results already obtained. Take two arbitrary observables A and B; one can then write, following Schwarz’s inequality in a well-known way:
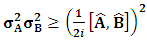 | (38) |
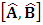 is the commutator of the two observablesLet it be that, for the observable corresponding to spatial coordinate, one writes
is the commutator of the two observablesLet it be that, for the observable corresponding to spatial coordinate, one writes 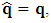 and let, for temporal observable, one writes the operator
and let, for temporal observable, one writes the operator 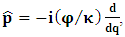 where, as stated above, the imaginary number results for the use of the matrix with signature
where, as stated above, the imaginary number results for the use of the matrix with signature 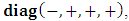 and κ and φ are already well-known. This, as the reader will easily agree, does not cause us any trouble, since it follows that the element of length vanishes if one takes commuting parameters. For it follows that, if one uses the pair of variables
and κ and φ are already well-known. This, as the reader will easily agree, does not cause us any trouble, since it follows that the element of length vanishes if one takes commuting parameters. For it follows that, if one uses the pair of variables 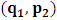 , corresponding to the temporal coordinate of K and spatial coordinate of K’, one gets the vanishing commutator
, corresponding to the temporal coordinate of K and spatial coordinate of K’, one gets the vanishing commutator 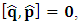 identically. However, if one uses the pair
identically. However, if one uses the pair 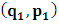 , so that one is taking only spatial and temporal coordinates of the same system, K’ say, one gets a non-vanishing commutator
, so that one is taking only spatial and temporal coordinates of the same system, K’ say, one gets a non-vanishing commutator 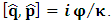 Substituting this into (38), one gets
Substituting this into (38), one gets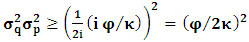 | (39A) |
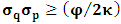 | (39B) |
3.3. On the Probabilistic Nature of the Systems
- In the atomic physics, the wave function is believed to carry with it, all the elements of physical reality regarding the quantum system; this is also the case for the dust free continuum in this paradoxical theory of reality. In order to know the physical state of the uniformly translating system, one must perform measurement on the system at some instant in time; only then can one find the system in one definite state or the other. When applied to the observable continuum, the meaning is again the same. By this way of reasoning, ψ is therefore a probability function. To this point, we may ask the following question: to what cause can one really assign as the reason of this probabilistic description of the system? This question is a necessary one because, throughout our consideration above, both systems have been taken in such a way that their states are purely deterministic according to method of ordinary classical mechanics. However, if one now describes the uniformly translating system by ψ, one can no longer know the exact state of that system, unless one makes appropriate measurement and finds it lying in some arbitrary observable state. In the forgoing argument, we wish to show here, without any hidden variable interpretation, that this cause is really a natural consequence. From it, the measurement problem will be completely solved.From (36), we may write
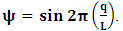 Let it be that the uniform translation of K’ is along one spatial direction— in the
Let it be that the uniform translation of K’ is along one spatial direction— in the 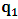 coordinate for example— with the Lorentz boost v. If we now view things, taking K as the privileged system, the K’ system will have the coordinate
coordinate for example— with the Lorentz boost v. If we now view things, taking K as the privileged system, the K’ system will have the coordinate 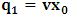 at any later time x0 distinct from zero. Therefore, by obvious argument from ordinary mechanics, we must regard q1 as the length of separation of the K’ system from K after time has elapsed. This must not, to any extend, cause confusion to the reader; it follows because, if we take the uniform translation along q1, one becomes satisfy with the fact that K is at Π and K’ at Π’ by reason of the validity of the fundamental postulate in the privileged system. Thus, it follows easily that the unprivileged system is separated from the origin (Π) by exactly the amount q1. This point will still be considered very shortly. Then, in an obvious way, we can now put our previous question in the following context:1. How does one assign physical meanings to the variable L, and 2. what is the physical difference between the space L and q? We like to argue here that L is not really a physical or material space of the K’ system. It has now become clear to us that, according to the language of ordinary probability theory, L is actually a probability space (or a sample space) of possible state into which we can find the system when measurement is made. Then, the wave-function will collapse immediately upon measurement of the system to produce one and only one outcome in the sample space, just as we meet in the atomic theory; the probabilistic nature of ψ is, by this reason, due only to the space variable L.To really understand the issue we like to point out here, the reader must see that, from our consideration of L and q, there may arise a natural confusion as follows: what is the real/ physical separation of the system when it is been observed? For our purpose, we will regard this as the actual observable continuum. The answer to this question is of theoretical importance as to the theme we want to consider here. Let it be, for example that, at
at any later time x0 distinct from zero. Therefore, by obvious argument from ordinary mechanics, we must regard q1 as the length of separation of the K’ system from K after time has elapsed. This must not, to any extend, cause confusion to the reader; it follows because, if we take the uniform translation along q1, one becomes satisfy with the fact that K is at Π and K’ at Π’ by reason of the validity of the fundamental postulate in the privileged system. Thus, it follows easily that the unprivileged system is separated from the origin (Π) by exactly the amount q1. This point will still be considered very shortly. Then, in an obvious way, we can now put our previous question in the following context:1. How does one assign physical meanings to the variable L, and 2. what is the physical difference between the space L and q? We like to argue here that L is not really a physical or material space of the K’ system. It has now become clear to us that, according to the language of ordinary probability theory, L is actually a probability space (or a sample space) of possible state into which we can find the system when measurement is made. Then, the wave-function will collapse immediately upon measurement of the system to produce one and only one outcome in the sample space, just as we meet in the atomic theory; the probabilistic nature of ψ is, by this reason, due only to the space variable L.To really understand the issue we like to point out here, the reader must see that, from our consideration of L and q, there may arise a natural confusion as follows: what is the real/ physical separation of the system when it is been observed? For our purpose, we will regard this as the actual observable continuum. The answer to this question is of theoretical importance as to the theme we want to consider here. Let it be, for example that, at 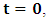 both coordinate systems are at Π (which have the same meaning as above); one sees that there is no physical space outside of Π, in view of both K and K’— since both systems coincide at that point. Now, if we allow the uniform translation of K’ to occur, the question we put forth becomes a necessary one, since the uniform translation of K’ must happen in some entity— let’s call it “a void” for convenience, since it must be distinct from the physical entity which we will litter on call, “space”. To keep the problem as simple, we make the following mare comparison so that the reader can easily follow. Consider a quantum system of single particle in a one dimensional box. Let the linear length element of the box be L. Let it be taken that the potential wall of the box is so infinite so that no contribution of the energy is taken from there, and that the particle is not allowed to interact with anything outside the walls of the box. Then, the only part of the Hamiltonian which contributes to the energy of the system is that resulting from the motion of the particle according to Schrodinger’s equation. Obvious result from atomic physics tells us that, prior to measurement, the particle can be envisioned to occupy all of L with variable probability [22-23]; the chance of finding the particle then depends upon the length element L, of the box, by reason of easy argument. We now start the system at some initial state
both coordinate systems are at Π (which have the same meaning as above); one sees that there is no physical space outside of Π, in view of both K and K’— since both systems coincide at that point. Now, if we allow the uniform translation of K’ to occur, the question we put forth becomes a necessary one, since the uniform translation of K’ must happen in some entity— let’s call it “a void” for convenience, since it must be distinct from the physical entity which we will litter on call, “space”. To keep the problem as simple, we make the following mare comparison so that the reader can easily follow. Consider a quantum system of single particle in a one dimensional box. Let the linear length element of the box be L. Let it be taken that the potential wall of the box is so infinite so that no contribution of the energy is taken from there, and that the particle is not allowed to interact with anything outside the walls of the box. Then, the only part of the Hamiltonian which contributes to the energy of the system is that resulting from the motion of the particle according to Schrodinger’s equation. Obvious result from atomic physics tells us that, prior to measurement, the particle can be envisioned to occupy all of L with variable probability [22-23]; the chance of finding the particle then depends upon the length element L, of the box, by reason of easy argument. We now start the system at some initial state 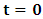 , which we allow to correspond to the point
, which we allow to correspond to the point 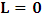 —i.e., the origin of the coordinate (or one corner of the experimental box). Let the system be allowed to evolve in time and in space. Because the box has the finite length L, and infinite potential barrier, the particle must be restricted only to the linear element L, with energy given by the appropriate Hamiltonian. Let, after the measurement at some arbitrary time t different from zero, one finds the particle in the state corresponding exactly to the point
—i.e., the origin of the coordinate (or one corner of the experimental box). Let the system be allowed to evolve in time and in space. Because the box has the finite length L, and infinite potential barrier, the particle must be restricted only to the linear element L, with energy given by the appropriate Hamiltonian. Let, after the measurement at some arbitrary time t different from zero, one finds the particle in the state corresponding exactly to the point 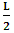 (i.e., halfway to the other end of the box). When this happens, one says that the particle is in the observable state
(i.e., halfway to the other end of the box). When this happens, one says that the particle is in the observable state 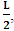 although one could not tell exactly where the particle was just prior to the measurement, according to the nature of
although one could not tell exactly where the particle was just prior to the measurement, according to the nature of 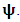 Suppose we wish to observe the particle from its own frame of reference. To facilitate this observation, we will assign to the particle’s frame, the name K’, for obvious reason. The fundamental postulate has prohibited us from obtaining any ambiguous state of the system, as long as the observation is done in that frame. Then, for an observer at rest in respect to the reference frame of the particle (K’ in this case), the particle will have a well determined point along L at all time, if we were to really view things from that frame. In fact, the argument can be made that the particle has always been in the state
Suppose we wish to observe the particle from its own frame of reference. To facilitate this observation, we will assign to the particle’s frame, the name K’, for obvious reason. The fundamental postulate has prohibited us from obtaining any ambiguous state of the system, as long as the observation is done in that frame. Then, for an observer at rest in respect to the reference frame of the particle (K’ in this case), the particle will have a well determined point along L at all time, if we were to really view things from that frame. In fact, the argument can be made that the particle has always been in the state 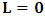 —by reason of lack of the privileged system; this is because the particle sees itself to always be at rest. This is not our main point of argument however.Thus, by reason of the fundamental postulate, it is clear that we are incapable of describing the particle (which we have taken to be in K’) from within its own frame of reference. This inability is a natural consequence; it is due to all reasons but the constraint imposed upon us that, for any system into which the fundamental postulate holds well, the observer in that frame cannot record any effect of uniform translated motion of any kind— the particle cannot therefore be viewed from its own reference frame. One then sees that the measuring apparatus then plays a crucial role in our definition of the physical reality of the particle (in K’). By the consideration of the matter here discussed, the description of the particle must be taken only from within the privilege system, with respect to which, the latter system (or the particle) is in uniform translation. Therefore, quantum mechanical description becomes the only satisfactory means by which one can rely upon for any element of physical reality of the K’ system. Then, one can conveniently place the measuring apparatus in the privileged system without loss of the sense of the argument— the physical reality of K’ must therefore be measured by clocks and yardsticks stationed in K. Actually, it is only within the privileged (K) system does the probabilistic description of the physical reality of K’ has with it, any physical meaning. That is because, if we were to really take things from the K’ system itself, the fundamental postulate would have applied at once. Then, as the particle does not really cover all of L, or is in a definite position on L when viewed from within itself, L cannot, in anyway, be a space of physical reality prior to any form of measurement on the system. Let the first measurement be made; the probabilistic description of the wave-function will then vanish identically. This follows merely from the theory of probability. Then, it becomes apparent to see that, it is only upon measurement that L can be assigned any physical meaning.Upon measurement, let one finds the particle in a state corresponding to L/2. We say that the total observable space of K’, viewed from the privileged system K, is from the coordinate origin to
—by reason of lack of the privileged system; this is because the particle sees itself to always be at rest. This is not our main point of argument however.Thus, by reason of the fundamental postulate, it is clear that we are incapable of describing the particle (which we have taken to be in K’) from within its own frame of reference. This inability is a natural consequence; it is due to all reasons but the constraint imposed upon us that, for any system into which the fundamental postulate holds well, the observer in that frame cannot record any effect of uniform translated motion of any kind— the particle cannot therefore be viewed from its own reference frame. One then sees that the measuring apparatus then plays a crucial role in our definition of the physical reality of the particle (in K’). By the consideration of the matter here discussed, the description of the particle must be taken only from within the privilege system, with respect to which, the latter system (or the particle) is in uniform translation. Therefore, quantum mechanical description becomes the only satisfactory means by which one can rely upon for any element of physical reality of the K’ system. Then, one can conveniently place the measuring apparatus in the privileged system without loss of the sense of the argument— the physical reality of K’ must therefore be measured by clocks and yardsticks stationed in K. Actually, it is only within the privileged (K) system does the probabilistic description of the physical reality of K’ has with it, any physical meaning. That is because, if we were to really take things from the K’ system itself, the fundamental postulate would have applied at once. Then, as the particle does not really cover all of L, or is in a definite position on L when viewed from within itself, L cannot, in anyway, be a space of physical reality prior to any form of measurement on the system. Let the first measurement be made; the probabilistic description of the wave-function will then vanish identically. This follows merely from the theory of probability. Then, it becomes apparent to see that, it is only upon measurement that L can be assigned any physical meaning.Upon measurement, let one finds the particle in a state corresponding to L/2. We say that the total observable space of K’, viewed from the privileged system K, is from the coordinate origin to 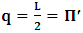 (i.e., one can then say that the particle travelled from L = 0 to L = L/2). Clearly, it follows that portion of L lies outside the physical space of the particle. That is, there is portion of the space L into which the K’ system has not covered, and thus lie outside the space of physical reality of the K’ system. But, the reader must see easily that an observer performing the measurement on K’ is incapable of really regarding any portion of L as a non-physical space, and can therefore conclude that the particle was really everywhere in space with varying probability.That the probabilistic function, ψ really vanishes/collapses upon measurement of the sample space, L is very easy to see. To make this point clear, notice that the argument of ψ is chosen so that
(i.e., one can then say that the particle travelled from L = 0 to L = L/2). Clearly, it follows that portion of L lies outside the physical space of the particle. That is, there is portion of the space L into which the K’ system has not covered, and thus lie outside the space of physical reality of the K’ system. But, the reader must see easily that an observer performing the measurement on K’ is incapable of really regarding any portion of L as a non-physical space, and can therefore conclude that the particle was really everywhere in space with varying probability.That the probabilistic function, ψ really vanishes/collapses upon measurement of the sample space, L is very easy to see. To make this point clear, notice that the argument of ψ is chosen so that 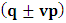 vanishes. Thus, only a certain portion of L, namely those satisfying
vanishes. Thus, only a certain portion of L, namely those satisfying 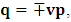 can be regarded as part of the observable space, for some p. We could choose L as large as infinity according to our wish, but upon measurement of the system,
can be regarded as part of the observable space, for some p. We could choose L as large as infinity according to our wish, but upon measurement of the system,  identically. This is made possible by boundary condition of the space, which is set down by q, forced upon us by measurement. The argument is even simplified if we take it from the point of view of the usual probability theory. As one is already well-aware, upon choosing any outcome in the sample space, the probabilities of all possible states/outcomes in the sample-space vanish, except the one so chosen. Then, in view of our question above, we can say that the K’ system moves in an entity which is not a reality space in our universe_ a void so to speak. The “void” becomes a reality space only upon finding the system there after measurement, just as we see in atomic physics. This viewpoint is also valid for the measurement problem of quantum physics so that the matter is completely solved. Ϯ Therefore, instead of the so-called “parallel universe” interpretation, one must assign to the cause of the collapsing wave-function, the fact that the sample space of possible outcome is not a space of physical reality of the particle on which bears the measurement, but only a mare state of possible outcomes. Once measurement is performed on the system, all other possible outcomes collapse, except the favorable one; one gets a deterministic state of the particle. We hereafter refer to q, in line of probability theory, the event or possible outcome, and to L, we shall call, the sample space. In ordinary mechanics, however, q is nothing but the material space of the particle, and to L we call, any arbitrary space.It is also clear that after measurement, L= q, so that the argument of
identically. This is made possible by boundary condition of the space, which is set down by q, forced upon us by measurement. The argument is even simplified if we take it from the point of view of the usual probability theory. As one is already well-aware, upon choosing any outcome in the sample space, the probabilities of all possible states/outcomes in the sample-space vanish, except the one so chosen. Then, in view of our question above, we can say that the K’ system moves in an entity which is not a reality space in our universe_ a void so to speak. The “void” becomes a reality space only upon finding the system there after measurement, just as we see in atomic physics. This viewpoint is also valid for the measurement problem of quantum physics so that the matter is completely solved. Ϯ Therefore, instead of the so-called “parallel universe” interpretation, one must assign to the cause of the collapsing wave-function, the fact that the sample space of possible outcome is not a space of physical reality of the particle on which bears the measurement, but only a mare state of possible outcomes. Once measurement is performed on the system, all other possible outcomes collapse, except the favorable one; one gets a deterministic state of the particle. We hereafter refer to q, in line of probability theory, the event or possible outcome, and to L, we shall call, the sample space. In ordinary mechanics, however, q is nothing but the material space of the particle, and to L we call, any arbitrary space.It is also clear that after measurement, L= q, so that the argument of  is always an integer. Semi-classical quantization then follows at once. One is now justified to define the probability of finding K’ on the probability space L as
is always an integer. Semi-classical quantization then follows at once. One is now justified to define the probability of finding K’ on the probability space L as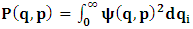 | (40) |
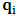 in (40) is now taken over all the 3-dimensional spatial axis. Then, for the entire continuum (or over all of L), the probability sums up to unity as
in (40) is now taken over all the 3-dimensional spatial axis. Then, for the entire continuum (or over all of L), the probability sums up to unity as 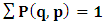 , and that
, and that 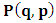 is normalizable to unity in a usual way [22-23]. We define, in a well-known way, a probability density matrix
is normalizable to unity in a usual way [22-23]. We define, in a well-known way, a probability density matrix 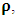 which depends on ψ according to the relationship
which depends on ψ according to the relationship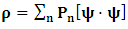 | (41) |
 is some operator which can be carried out on ψ, then, one obtains, if one carries out the operation
is some operator which can be carried out on ψ, then, one obtains, if one carries out the operation  on ψ, one of the eigenvalue as the observable state of the system according to
on ψ, one of the eigenvalue as the observable state of the system according to 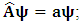 where ‘a’ is the eigenvalue (or the observable of the system). The expectation values of
where ‘a’ is the eigenvalue (or the observable of the system). The expectation values of 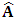 then becomes, from (41)
then becomes, from (41)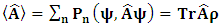 | (42) |
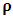 having all of the following properties [12,23,22]:a.
having all of the following properties [12,23,22]:a. 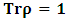 b.
b. 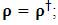
 is Harmitianc.
is Harmitianc.  One should also notice that according to how we have defined the pairs (q, p), the system can be in an entirely random state, just as we meet in the case of the quantum process. Consider now, a scalar field denoted by ς. One is then able to form a complete set of commuting operators for the field at each part of the hyperspace,
One should also notice that according to how we have defined the pairs (q, p), the system can be in an entirely random state, just as we meet in the case of the quantum process. Consider now, a scalar field denoted by ς. One is then able to form a complete set of commuting operators for the field at each part of the hyperspace, 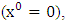 which are decomposed into the subsets/subspace
which are decomposed into the subsets/subspace  and
and  To see this point as clear as possible, let the coordinates of K and K’ are represented by
To see this point as clear as possible, let the coordinates of K and K’ are represented by 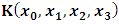 and
and 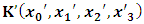 respectively. Then, the combine system can be divided into two congruent halves of the hyperspace at the point
respectively. Then, the combine system can be divided into two congruent halves of the hyperspace at the point 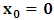 (or
(or 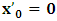 , according to our choice of privileged system). Then, by our choice of the Lorentz boost,
, according to our choice of privileged system). Then, by our choice of the Lorentz boost,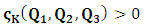 | (43A) |
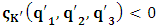 | (43B) |
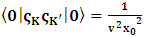 | (44) |
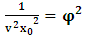 from (44), so that one has
from (44), so that one has 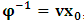 , as the total observable Space-time continuum as desired. The wave-function can then be written as
, as the total observable Space-time continuum as desired. The wave-function can then be written as 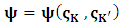 | (45) |
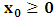 . Thus, (43A-B) are clearly arbitrary conditions which result merely from our choice of the privileged system, or the Lorentz boost. The matrix of the continuum, by this reasoning, is semi-definite, and the time reversal parity (i.e., interchange
. Thus, (43A-B) are clearly arbitrary conditions which result merely from our choice of the privileged system, or the Lorentz boost. The matrix of the continuum, by this reasoning, is semi-definite, and the time reversal parity (i.e., interchange 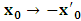 ) is immaterial. For the dynamics of any system which is not chosen as the privileged, we define the action by the semi-definite integral
) is immaterial. For the dynamics of any system which is not chosen as the privileged, we define the action by the semi-definite integral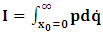 | (46) |
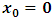 . That is, the K system appears to play the role as the singularity point for the moving K’ system, since it will see itself at the coordinate origin (Π) at any later time t, so long as we see the situation from that frame of reference. We will relook at this point shortly as it leads to the Maldacena’s conjecture.We end this section by an interesting observation. Consider the composite systems, K and K’; it is obvious that the probability density matrix is Harmitian, with all of its eigenvalues lying between zero and one. Suppose in one of the systems, say K’, one obtains unity
. That is, the K system appears to play the role as the singularity point for the moving K’ system, since it will see itself at the coordinate origin (Π) at any later time t, so long as we see the situation from that frame of reference. We will relook at this point shortly as it leads to the Maldacena’s conjecture.We end this section by an interesting observation. Consider the composite systems, K and K’; it is obvious that the probability density matrix is Harmitian, with all of its eigenvalues lying between zero and one. Suppose in one of the systems, say K’, one obtains unity 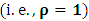 ; we say that K’ is in its pure state, and that all other probabilities vanish identically. In general, such state is possible if the wave function is factorizable according to
; we say that K’ is in its pure state, and that all other probabilities vanish identically. In general, such state is possible if the wave function is factorizable according to 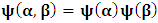 ; this is the case here according to (30) and (45). In the pure state of K’, the K system is also taken to be in a pure state with equal eigenvalues. In fact, the probabilistic nature of the systems vanishes so that one is now using the space q, rather than L; that is,
; this is the case here according to (30) and (45). In the pure state of K’, the K system is also taken to be in a pure state with equal eigenvalues. In fact, the probabilistic nature of the systems vanishes so that one is now using the space q, rather than L; that is, 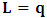 identically whenever the systems are in their pure states. The entanglement entropy can then be written as [12,23,25]
identically whenever the systems are in their pure states. The entanglement entropy can then be written as [12,23,25]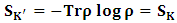 | (47) |
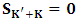 | (48) |
 , the length element,
, the length element,  vanished identically. This follows because the
vanished identically. This follows because the 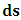 leaves the two systems at the common Π, so that the uniform translation and hence the spatial separation, is completely a virtual one. We wish to show that this is an immediate consequence from (48) according to the vanishing entropy of the systems. It can be observed that, at
leaves the two systems at the common Π, so that the uniform translation and hence the spatial separation, is completely a virtual one. We wish to show that this is an immediate consequence from (48) according to the vanishing entropy of the systems. It can be observed that, at 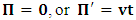 the wave function (29) vanishes trivially. Then, Π becomes distinct from Π’ only by reason according to our choice of the privileged coordinate, but that both systems cannot be at Π’ simultaneously. If we now define the probability density matrix by (41), one sees without difficulty that
the wave function (29) vanishes trivially. Then, Π becomes distinct from Π’ only by reason according to our choice of the privileged coordinate, but that both systems cannot be at Π’ simultaneously. If we now define the probability density matrix by (41), one sees without difficulty that 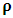 vanishes identically at Π and Π’ according to the vanishing of
vanishes identically at Π and Π’ according to the vanishing of 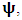 and by our choice of privileged system. Substituting (41) into (48), it follows at once that (48) vanishes as desired. One can therefore say that the universe had zero entropy at the origin of the universe (i.e. at the big band). Moreover, any system into which the fundamental postulate holds well, the entropy of that system must vanish according to obvious argument.This must not cause us any confusion. Indeed, it can be noticed that if we take K as the privileged observer, then the point
and by our choice of privileged system. Substituting (41) into (48), it follows at once that (48) vanishes as desired. One can therefore say that the universe had zero entropy at the origin of the universe (i.e. at the big band). Moreover, any system into which the fundamental postulate holds well, the entropy of that system must vanish according to obvious argument.This must not cause us any confusion. Indeed, it can be noticed that if we take K as the privileged observer, then the point 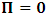 corresponds to location of the K system, and
corresponds to location of the K system, and 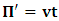 for the K’ system. Then, one sees at once that Ⅱ and Ⅱ’ are clearly equal (symmetric), and differ only by our choice of privileged system so that
for the K’ system. Then, one sees at once that Ⅱ and Ⅱ’ are clearly equal (symmetric), and differ only by our choice of privileged system so that 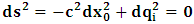 identically. Notice also that the vanishing of ψ at Π and Π’ does not follow from the interpretation of the usual Lorentzian sense of issue which we have already discussed above regarding to origin of the universe. It follows that, in the earlier argument (i.e., according to Lorentz), both Π and Π’ can be regarded as the origin simultaneously. In the latter sense of things however, exactly one of the systems is always chosen as been privileged and hence always sees itself at the origin of the coordinate system, and that the latter system is in uniform translation; in this way, the spatial separation is only but a virtual one. This is the extent to which the paradoxical description has presented space-time continuum, and hence, the true nature of physical reality.
identically. Notice also that the vanishing of ψ at Π and Π’ does not follow from the interpretation of the usual Lorentzian sense of issue which we have already discussed above regarding to origin of the universe. It follows that, in the earlier argument (i.e., according to Lorentz), both Π and Π’ can be regarded as the origin simultaneously. In the latter sense of things however, exactly one of the systems is always chosen as been privileged and hence always sees itself at the origin of the coordinate system, and that the latter system is in uniform translation; in this way, the spatial separation is only but a virtual one. This is the extent to which the paradoxical description has presented space-time continuum, and hence, the true nature of physical reality.3.4. Paradox in the Consideration of the Problem of Physical Reality
- It is obvious that the dynamics of the systems is govern by some function; we like to call it,
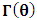 — with the definition
— with the definition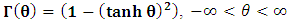 | (49) |
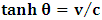 Along the given interval,
Along the given interval,  is allowed to take values ranging from -1 to 1, so that the relative translated velocity (v) takes values
is allowed to take values ranging from -1 to 1, so that the relative translated velocity (v) takes values  If one sketches the graph of
If one sketches the graph of 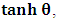 one sees that it is completely symmetric about the origin. We afterward interpret this as each part representing exactly one of the composite systems. However, from our way of defining the dynamical function (49), the square of
one sees that it is completely symmetric about the origin. We afterward interpret this as each part representing exactly one of the composite systems. However, from our way of defining the dynamical function (49), the square of 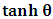 is never negative; hence,
is never negative; hence, 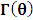 is semi-definite, with values lying on the interval
is semi-definite, with values lying on the interval  . In fact, in all ordinary sense of reasoning, one must take
. In fact, in all ordinary sense of reasoning, one must take 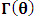 in the same sense as the so-called cosmological constant. For if one takes any one of the systems as the privileged coordinate,
in the same sense as the so-called cosmological constant. For if one takes any one of the systems as the privileged coordinate, 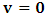 according to the fundamental principle; one then has
according to the fundamental principle; one then has 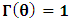 in this system. Let one now envisions K’ from the privilege system K; one sees that, as K’ falls towards K,
in this system. Let one now envisions K’ from the privilege system K; one sees that, as K’ falls towards K, 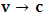 and
and 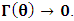 Indeed, that
Indeed, that  is not an arbitrary condition; an easy argument follows at once because, one is now using the advancing time-function
is not an arbitrary condition; an easy argument follows at once because, one is now using the advancing time-function 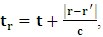 rather than retarded function— in this way, the matrix appears “light-like”. It will then appear as though K is a real gravitational field whose effect increases the acceleration of K’. The gravitational field is then produced in a nature way. We shall consider this point in our next treatment. The reciprocal situation of the problem (i.e., K’ moves away from K so that v→0) also has a physical meaning; indeed it will appear from K as though K’ is slowing down at increasing spatial separation, so that
rather than retarded function— in this way, the matrix appears “light-like”. It will then appear as though K is a real gravitational field whose effect increases the acceleration of K’. The gravitational field is then produced in a nature way. We shall consider this point in our next treatment. The reciprocal situation of the problem (i.e., K’ moves away from K so that v→0) also has a physical meaning; indeed it will appear from K as though K’ is slowing down at increasing spatial separation, so that 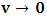 on account of retarding time function
on account of retarding time function 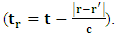 Therefore, the in-falling or outgoing K’ system behaves just as it does in ordinary Newtonian mechanics (such as an apple thrown upward would do in a real gravitational field). However, we will show in a later paper that in the case expansion of the universe,
Therefore, the in-falling or outgoing K’ system behaves just as it does in ordinary Newtonian mechanics (such as an apple thrown upward would do in a real gravitational field). However, we will show in a later paper that in the case expansion of the universe,  never goes to zero, and the expansion continues forever. However, since uniform motion has the natural effect of making far-away things to appear to recede faster with separation, it appears from earth that the expansion of the universe is accelerating. Now, suppose that the situation is described from the point of view of a third observer— to this purpose, we introduce another privileged system, K0. It follows that, as K’ falls towards K, he [K’] moves faster and faster towards K as though it were a real gravitational field. If the maximum allowed speed is c, then, in respect to K0,
never goes to zero, and the expansion continues forever. However, since uniform motion has the natural effect of making far-away things to appear to recede faster with separation, it appears from earth that the expansion of the universe is accelerating. Now, suppose that the situation is described from the point of view of a third observer— to this purpose, we introduce another privileged system, K0. It follows that, as K’ falls towards K, he [K’] moves faster and faster towards K as though it were a real gravitational field. If the maximum allowed speed is c, then, in respect to K0,  . We now define the gamma function by
. We now define the gamma function by  Then, as
Then, as 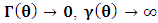 and K’ never falls to the singularity point, (Π) when the matter is viewed from the standby observer in K0. Suppose we now describe K’ by some wave-function ψ, then, an observer in the K0 system will see the in-falling wave-function spreading to infinity. This prediction is already well-known in String theory [12,26], but we obtain it here in this 4-dimensional consideration of the continuum.It must be emphasized that an observer in K does not actually see this spreading effect of ψ. In fact, the function
and K’ never falls to the singularity point, (Π) when the matter is viewed from the standby observer in K0. Suppose we now describe K’ by some wave-function ψ, then, an observer in the K0 system will see the in-falling wave-function spreading to infinity. This prediction is already well-known in String theory [12,26], but we obtain it here in this 4-dimensional consideration of the continuum.It must be emphasized that an observer in K does not actually see this spreading effect of ψ. In fact, the function 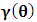 is not well defined in the K system, even though
is not well defined in the K system, even though 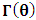 has a physical meaning in respect to K. The argument is really straightforward; it follows because, in the privilege K system, the dynamics of the K’ system is defined by (49); however, their inverses are not well-defined since, if it were really the case, it would imply that K is now in uniform translation. The fundamental postulate will no longer hold in K when view from itself. Since this is not the case, the claim is proven.Now, since
has a physical meaning in respect to K. The argument is really straightforward; it follows because, in the privilege K system, the dynamics of the K’ system is defined by (49); however, their inverses are not well-defined since, if it were really the case, it would imply that K is now in uniform translation. The fundamental postulate will no longer hold in K when view from itself. Since this is not the case, the claim is proven.Now, since 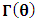 converges to unity, and the gamma function is not define in K, it follows— envisioned from K— that the in-falling observer will really reach the horizon and burn up identically at Π as though it [Ⅱ] were really a firewall, just as we meet in the AMPS paradox [27]. Thus, for some isolated observer K0, the in-falling particle never reaches the horizon, whereas, for the privileged system, the horizon behaves like a firewall. From the point of view of the in-falling observer itself, nothing is unusual to him; but his event horizon will behave like a firewall just as we meet for K— the latter claim follows because of lack of preferred frame of reference. Then, K and K’ will burn up identically if the situation is viewed only from either K’ or K respectively. In principle, however, this is the only situation which occur, contrary to the string theory argument of the spreading wave-function. Indeed, it follows easily from the monogamy of entangle, since by this principle, there cannot be a three-way entanglement, so that it is only the K and K’ systems which are entangled with one another, and from each of which, the observation is there made.The strong phrase “burning up” is misleading, and must not be taken too literal. It only means that, when K’ falls to K, clocks in the K’ system now ticks according to the clocks of the privileged K system so that no differential occurs for the both clock systems. This is no different from our argument we have given to the twin paradox. If Ⅱ is a real coordinate singularity such as the point of the big band, the meaning of the phrase is to intimate that space and time vanish (such as the big crush prediction).
converges to unity, and the gamma function is not define in K, it follows— envisioned from K— that the in-falling observer will really reach the horizon and burn up identically at Π as though it [Ⅱ] were really a firewall, just as we meet in the AMPS paradox [27]. Thus, for some isolated observer K0, the in-falling particle never reaches the horizon, whereas, for the privileged system, the horizon behaves like a firewall. From the point of view of the in-falling observer itself, nothing is unusual to him; but his event horizon will behave like a firewall just as we meet for K— the latter claim follows because of lack of preferred frame of reference. Then, K and K’ will burn up identically if the situation is viewed only from either K’ or K respectively. In principle, however, this is the only situation which occur, contrary to the string theory argument of the spreading wave-function. Indeed, it follows easily from the monogamy of entangle, since by this principle, there cannot be a three-way entanglement, so that it is only the K and K’ systems which are entangled with one another, and from each of which, the observation is there made.The strong phrase “burning up” is misleading, and must not be taken too literal. It only means that, when K’ falls to K, clocks in the K’ system now ticks according to the clocks of the privileged K system so that no differential occurs for the both clock systems. This is no different from our argument we have given to the twin paradox. If Ⅱ is a real coordinate singularity such as the point of the big band, the meaning of the phrase is to intimate that space and time vanish (such as the big crush prediction). 3.4.1. On the Impossibility of Time Travel
- The commuting relationship of spatial and temporal coordinates immediately leads to the impossibility for time travel in a natural way. But even without this viewpoint, one can easily convince himself that the argument of time travel cannot be an element of physical reality. Several arguments can be proposed to support our claim, but the simplest is to take it that the entropy of any real system is a non-negative real number. The change in entropy of an observer traveling backward in time will turn to negative on approaching the singularity point
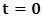 , if we judge the travelling system (K’) from the point of view of a privileged system, K. At once, we see that this is physically impossible. One could make the argument we have made earlier that an in-falling observer does not see anything unusual while falling; in this case, one appears to achieve the mentioned without violating entropy requirement. For that argument, it must be pointed out that, when we view the in-falling observer from his own frame of reference, one soon sees it satisfying the fundamental postulate so that it is now the privileged system. It is not hard to now see that any system into which the fundamental postulate is satisfied, the concept of entropy cannot be well defined— i.e., the entropy of that system vanishes identically. The argument that this is the case can be made in a number of ways, but the statement: (nothing is unusual in said system) is a sufficient and necessary justification for our claim. One then sees that the privileged system always has vanishing entropy in respect to itself at any time not necessarily zero. The in-falling observer (in this case, the K’ system), when taken as the privileged coordinate, soon starts to see the K system as that under uniform translation, so that one is referring to nothing but the reciprocal situation of the issue. The result will make no difference as can be showed easily by the lack of preferred choices of reference system.We like to make the argument as formal as possible that time travel is not an element of physical reality. But, from the forgoing discussion, one will soon come to realize that it is physically impossible to travel “backwards in space”. This argument is sample; it follows as soon as we distinguish the probability space from the physical space of the uniformly translated system according as was shown above. For the time independent solution of the uniformly translating coordinate, one writes (34) as
, if we judge the travelling system (K’) from the point of view of a privileged system, K. At once, we see that this is physically impossible. One could make the argument we have made earlier that an in-falling observer does not see anything unusual while falling; in this case, one appears to achieve the mentioned without violating entropy requirement. For that argument, it must be pointed out that, when we view the in-falling observer from his own frame of reference, one soon sees it satisfying the fundamental postulate so that it is now the privileged system. It is not hard to now see that any system into which the fundamental postulate is satisfied, the concept of entropy cannot be well defined— i.e., the entropy of that system vanishes identically. The argument that this is the case can be made in a number of ways, but the statement: (nothing is unusual in said system) is a sufficient and necessary justification for our claim. One then sees that the privileged system always has vanishing entropy in respect to itself at any time not necessarily zero. The in-falling observer (in this case, the K’ system), when taken as the privileged coordinate, soon starts to see the K system as that under uniform translation, so that one is referring to nothing but the reciprocal situation of the issue. The result will make no difference as can be showed easily by the lack of preferred choices of reference system.We like to make the argument as formal as possible that time travel is not an element of physical reality. But, from the forgoing discussion, one will soon come to realize that it is physically impossible to travel “backwards in space”. This argument is sample; it follows as soon as we distinguish the probability space from the physical space of the uniformly translated system according as was shown above. For the time independent solution of the uniformly translating coordinate, one writes (34) as 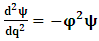 , where φ is defined to take values in the 3-spatial continuum. Writing
, where φ is defined to take values in the 3-spatial continuum. Writing 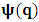 in the complex form, one has
in the complex form, one has 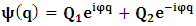 | (50) |
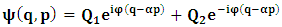 | (51) |
 , the constant relative velocity of K’. One then sees that
, the constant relative velocity of K’. One then sees that  depends on the combination
depends on the combination  , where the uniform translated coordinate travels in the
, where the uniform translated coordinate travels in the 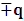 direction with speed,
direction with speed, 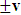 . This is in agreement with our argument for the choice of the Lorentz boost. Now, choose any fixed point on the waveform of the traveling wave, the maximum or minimum for example; This, by obvious result from quantum mechanics, corresponds to fixed values of q and p such that
. This is in agreement with our argument for the choice of the Lorentz boost. Now, choose any fixed point on the waveform of the traveling wave, the maximum or minimum for example; This, by obvious result from quantum mechanics, corresponds to fixed values of q and p such that 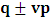 is always constant, or that the spatial separation
is always constant, or that the spatial separation 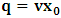 is a constant. Then, the diminishing of p immediately leads to the diminishing of q and vice versa. One then arrives at a condition in which one cannot change p without changing q. Moreover, it is immediate that
is a constant. Then, the diminishing of p immediately leads to the diminishing of q and vice versa. One then arrives at a condition in which one cannot change p without changing q. Moreover, it is immediate that 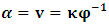 . If one moves backwards in time, one sees
. If one moves backwards in time, one sees  as
as  , where
, where  is the time at the singularity point. The expansion velocity of the universe (or more precisely, the velocity with which K’ is translating) will become infinitely large. One will require a system of infinite speed to carry the universe backwards in time. The situation then suggests itself that time travel is impossible without affecting the entire observable continuum; we are led to answer in the negative as to the possibility of such a description of nature. The impossibility of time travel leads to the impossibility of space trivial according to commuting relationship. This is not hard to show as soon as we distinguish the probability space from the physical space of the moving system. For a particle traveling between two points A and B, we have argued that the length element
is the time at the singularity point. The expansion velocity of the universe (or more precisely, the velocity with which K’ is translating) will become infinitely large. One will require a system of infinite speed to carry the universe backwards in time. The situation then suggests itself that time travel is impossible without affecting the entire observable continuum; we are led to answer in the negative as to the possibility of such a description of nature. The impossibility of time travel leads to the impossibility of space trivial according to commuting relationship. This is not hard to show as soon as we distinguish the probability space from the physical space of the moving system. For a particle traveling between two points A and B, we have argued that the length element 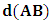 is not a real space, at least in the particle’s frame. For as long as the particle can be anywhere between
is not a real space, at least in the particle’s frame. For as long as the particle can be anywhere between 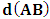 , the length element can only be regarded as a probability space rather than a real one. Thus, for a
, the length element can only be regarded as a probability space rather than a real one. Thus, for a 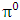 meson traveling from A to B, the distance between the two points is not an observable physical space in the frame of reference of the moving particle, but rather a probability space into which we may find the particle when measurement is made. As the reader can then see, the particle is not traveling in space, at least if one considers only the reality space, since it is the case that the physical space of the particle is produced only after the separation for A to B. This result might be confusing, but one can easily understand the main theme if the prior knowledge of the distance between A and B is not known to the observer. One will see that the space
meson traveling from A to B, the distance between the two points is not an observable physical space in the frame of reference of the moving particle, but rather a probability space into which we may find the particle when measurement is made. As the reader can then see, the particle is not traveling in space, at least if one considers only the reality space, since it is the case that the physical space of the particle is produced only after the separation for A to B. This result might be confusing, but one can easily understand the main theme if the prior knowledge of the distance between A and B is not known to the observer. One will see that the space 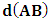 is a total void and only become part of the reality frame of the particle by means of measurement performed on the system after some elapsed time; the result follows at once.
is a total void and only become part of the reality frame of the particle by means of measurement performed on the system after some elapsed time; the result follows at once. 3.4.2. On the Dual-verse Problem
- From (51), we see that the waveform of the propagating wave does not change. It follows because the uniformly translated system does so at constant velocity. This actually leads to the prediction that the universe is expanding at some constant expansion velocity as we have already argued. We shall investigate this point in detail in a later paper, and the result is a nature one. However, it follows at once that (51) represents two congruent waveforms in which the first term represents one of the waveforms propagating in the positive direction, and the second term, a second waveform propagating to the negative direction. Nothing forbids such interpretation as ψ is pseudo-orthogonal according to our consideration of the composite systems. Then, it follows that
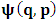 divides the continuum into two congruent halves, just as we meet for the Einstein-Rosen bridges in the gravitational field [28].We can write (51) into a single term as
divides the continuum into two congruent halves, just as we meet for the Einstein-Rosen bridges in the gravitational field [28].We can write (51) into a single term as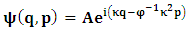 | (52) |
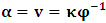 , and that, κ is proportional to the age and hence the total continuum, and A is a number. If we now focus our attention only to the congruent halves, κ takes on the values satisfying
, and that, κ is proportional to the age and hence the total continuum, and A is a number. If we now focus our attention only to the congruent halves, κ takes on the values satisfying For
For  is a number, and hence the differential equation in (34) vanishes. It then follows that the two waves begin at
is a number, and hence the differential equation in (34) vanishes. It then follows that the two waves begin at 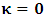 and propagate to infinity. As the argument readily suggest itself, one can then regard each half of ψ as the waveform corresponding to exactly one of the universes; one then obtains two congruent universes as the only possibility for a stable system. We will take on this task in more detail in a later paper.
and propagate to infinity. As the argument readily suggest itself, one can then regard each half of ψ as the waveform corresponding to exactly one of the universes; one then obtains two congruent universes as the only possibility for a stable system. We will take on this task in more detail in a later paper. 3.5. Maldacena’s Consideration of the AdS/CFT Correspondence
- Maldacena has called our attention to special duality criteria termed, the AdS/CFT correspondence theory. In it, one is led to a theory in which the laws of physics on the background of a ten dimensional
 space can be exactly equivalent, under a certain duality relation, to those on the four dimensional Minkowski space-time. The Minkowski’s background has been termed, the conformal field theory (CFT) [29-30]. In what follows, however, we wish to argue that the same result is obtained in this paradoxical description of physical reality. It appears to us that any well-chosen AdS space satisfying Maldacena’s conjecture can be replaced by the coordinate system into which the fundamental postulate of relativity holds well. Then, in this paradoxical theory, one completely solves the problem, free of any extra dimensionality of the continuum. The duality relation therefore lies in the commuting relation of space and time. We show the main idea by the following discussion:For a pair
space can be exactly equivalent, under a certain duality relation, to those on the four dimensional Minkowski space-time. The Minkowski’s background has been termed, the conformal field theory (CFT) [29-30]. In what follows, however, we wish to argue that the same result is obtained in this paradoxical description of physical reality. It appears to us that any well-chosen AdS space satisfying Maldacena’s conjecture can be replaced by the coordinate system into which the fundamental postulate of relativity holds well. Then, in this paradoxical theory, one completely solves the problem, free of any extra dimensionality of the continuum. The duality relation therefore lies in the commuting relation of space and time. We show the main idea by the following discussion:For a pair 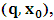 of the commuting variables, let
of the commuting variables, let 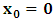 — notice that the use of the variable
— notice that the use of the variable 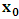 does not cause us any trouble as we have already seen from previous argument. Then, one is talking about a special state of the privileged K system in which it is identically at the origin of coordinate Π. This must not cause any difficulty of understanding because, as long as we apply the fundamental postulate to the K system, the result is immediate, and that
does not cause us any trouble as we have already seen from previous argument. Then, one is talking about a special state of the privileged K system in which it is identically at the origin of coordinate Π. This must not cause any difficulty of understanding because, as long as we apply the fundamental postulate to the K system, the result is immediate, and that 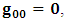 for obvious reason from the argument we have already made. In fact, the argument is true even if
for obvious reason from the argument we have already made. In fact, the argument is true even if 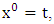 for any arbitrary time, so long as the fundamental postulate is satisfied. However, notice that the K’ system lies in the subspace
for any arbitrary time, so long as the fundamental postulate is satisfied. However, notice that the K’ system lies in the subspace 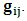 Notice also that
Notice also that 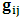 does not necessarily vanish, so long as, envisioned from the privileged, K, the K’ system is in uniform translation. However, if
does not necessarily vanish, so long as, envisioned from the privileged, K, the K’ system is in uniform translation. However, if 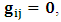 the physical meaning follows immediately that one is referring to the condition in which K and K’ are identically at Π, such that there is no separation of the system, and the space and time completely vanish. If we take it that
the physical meaning follows immediately that one is referring to the condition in which K and K’ are identically at Π, such that there is no separation of the system, and the space and time completely vanish. If we take it that 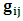 does not vanish, one has a 3-dimensional space into which K’ is present. Then, for the condition
does not vanish, one has a 3-dimensional space into which K’ is present. Then, for the condition 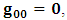 K will be at Π, so that it is now the privileged system. Since nothing prohibits us from taking the reciprocal situation, we arrive at a result which is no different from Einstein-Rosen treatment of the problem [28]. It then follows that, for a 4- dimensional space-time continuum,
K will be at Π, so that it is now the privileged system. Since nothing prohibits us from taking the reciprocal situation, we arrive at a result which is no different from Einstein-Rosen treatment of the problem [28]. It then follows that, for a 4- dimensional space-time continuum, 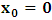 (satisfying
(satisfying 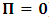 ) is a 2-dimensional space-like hyper-surface on the matrix
) is a 2-dimensional space-like hyper-surface on the matrix 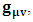 if one take the special coordinate according as in [28]. Eq. (28) then takes a solution in which the entire continuum consists of two equal halves separated about the surface of symmetry
if one take the special coordinate according as in [28]. Eq. (28) then takes a solution in which the entire continuum consists of two equal halves separated about the surface of symmetry 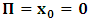 with the two congruent halves,
with the two congruent halves, 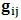 having only the 3-spatial variable
having only the 3-spatial variable 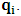 Notice that the same solution is obtained by carrying out a Lorentz boost of the two systems about Π just by mare change of privileged system; one easily gets the same result even without following the usual argument of Einstein-Rosen Bridge. Let, from the separation, K and K’ be represented as
Notice that the same solution is obtained by carrying out a Lorentz boost of the two systems about Π just by mare change of privileged system; one easily gets the same result even without following the usual argument of Einstein-Rosen Bridge. Let, from the separation, K and K’ be represented as 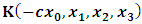 and
and 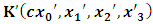 , where the minus sign in K occurs by mare choice of the Lorentz boost, or by the condition of the constant κ in the wave-function. Then, for the interval
, where the minus sign in K occurs by mare choice of the Lorentz boost, or by the condition of the constant κ in the wave-function. Then, for the interval 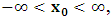 one has K going from
one has K going from 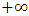 to 0 and K’ going as 0 to
to 0 and K’ going as 0 to 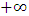 in space. But, if one applies the fundamental postulate to the privileged (K) system, one can take the entire part of the congruent space of K (i.e., the part
in space. But, if one applies the fundamental postulate to the privileged (K) system, one can take the entire part of the congruent space of K (i.e., the part 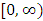 ) as the 2-dimensional hyper-surface
) as the 2-dimensional hyper-surface 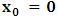 by obvious argument. Then, one can be justified to assign to the privileged system, the AdS space, whereas, to the system in uniform translation, we call it the conformal space; Maldacena’s conjecture is then immediate. It must be noticed that the conformal space, which we have now considered, is taken to be 3-dimensional,
by obvious argument. Then, one can be justified to assign to the privileged system, the AdS space, whereas, to the system in uniform translation, we call it the conformal space; Maldacena’s conjecture is then immediate. It must be noticed that the conformal space, which we have now considered, is taken to be 3-dimensional, 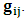 It follows because, we have allowed the commutation to occur between the time parameter of the K system and the 3-spatial parameter of the K’ system. But this does not cause us any trouble because, from the Maldacena’s view of things, one can see that the AdS space manifest as a 2-dimensional hyper-surface that is the time boundary of the Minkowski’s space [29]. We can go beyond Maldacena’s result and argue that the AdS space can also be regarded as the conformal space by our choice of the privileged system. This is a far reaching consequence as it allows our result to be testable in our solar system as easily as possible. The reader can already see that, following the fundamental postulate, as well as the natural principle of relativity, the argument is already valid. For as long as we take any of the system as privileged, the result follows accordingly. Then, since there is no preferred choice of reference system, the claim is proved at once. Instead of the fundamental postulate, however, we introduce Mach’s principle of non-absolute space, which is no different from the third postulate of relativity. Let us take it that K is the rest coordinate and K’ be the coordinate system in uniform translation with respect to the former. It follows immediately that K is a 2-D hyper-surface at Π. As the reciprocal situation is well-defined, the result follows at once. We then make the general claim that any system into which the fundamental postulate is material, we call it, the AdS space; otherwise, we call it the conformal space; Maldacena’s duality is then replaced by the space-time entanglement relation in a natural way. This is the extent to which the paradoxical theory of reality has put the Maldacena’s correspondence and the result, as the reader can see, is satisfied.An interesting result must also be called to attention immediately. It must be noticed that the paradoxical treatment of Maldacena’s consideration is testable in our solar system as one can be convinced by easy argument. In fact, the proof is no more different from Gauss’s theorem, which is already well-known. However, if this is really the case, one sees that the Holographic principle cannot have any deeper meaning other than the well-known divergence theorem according to Gauss. An observer in a far-away 2-dimensional hyper-surface can just as well be regarded as a 3-D space if the situation is viewed from that frame of reference. We are not in the position to argue this interesting problem any further, although the solution is really trivial. After a couple of papers, we shall again consider this theme, and the reader will see that the result follows naturally without any effort.
It follows because, we have allowed the commutation to occur between the time parameter of the K system and the 3-spatial parameter of the K’ system. But this does not cause us any trouble because, from the Maldacena’s view of things, one can see that the AdS space manifest as a 2-dimensional hyper-surface that is the time boundary of the Minkowski’s space [29]. We can go beyond Maldacena’s result and argue that the AdS space can also be regarded as the conformal space by our choice of the privileged system. This is a far reaching consequence as it allows our result to be testable in our solar system as easily as possible. The reader can already see that, following the fundamental postulate, as well as the natural principle of relativity, the argument is already valid. For as long as we take any of the system as privileged, the result follows accordingly. Then, since there is no preferred choice of reference system, the claim is proved at once. Instead of the fundamental postulate, however, we introduce Mach’s principle of non-absolute space, which is no different from the third postulate of relativity. Let us take it that K is the rest coordinate and K’ be the coordinate system in uniform translation with respect to the former. It follows immediately that K is a 2-D hyper-surface at Π. As the reciprocal situation is well-defined, the result follows at once. We then make the general claim that any system into which the fundamental postulate is material, we call it, the AdS space; otherwise, we call it the conformal space; Maldacena’s duality is then replaced by the space-time entanglement relation in a natural way. This is the extent to which the paradoxical theory of reality has put the Maldacena’s correspondence and the result, as the reader can see, is satisfied.An interesting result must also be called to attention immediately. It must be noticed that the paradoxical treatment of Maldacena’s consideration is testable in our solar system as one can be convinced by easy argument. In fact, the proof is no more different from Gauss’s theorem, which is already well-known. However, if this is really the case, one sees that the Holographic principle cannot have any deeper meaning other than the well-known divergence theorem according to Gauss. An observer in a far-away 2-dimensional hyper-surface can just as well be regarded as a 3-D space if the situation is viewed from that frame of reference. We are not in the position to argue this interesting problem any further, although the solution is really trivial. After a couple of papers, we shall again consider this theme, and the reader will see that the result follows naturally without any effort. 4. Conclusions
- We are led to the conclusion that the paradoxical description of physical reality satisfies the atomistic theory of quantum Physics in a well-known way. While the result at hand, one may argue, does not describe, to a satisfactory extend, a unified field theory, the view is expressed that such theoretical description is possible if one looks upon nature from this purely paradoxical consideration of issue.
Notes
- 1. Maxwell’s equations are recoverable from the continuity equation in a well-known way; however, the task is not easy! To do this, one introduces a specialized function term ‘retarded function’ δ [17-20,35]. The introduction of δ leads to an apparent delay in the propagation of the signal from the source to another point of detection in the space. For the electromagnetic fields, one may write
 and
and  representing the retarding charge density and current element respectively, where
representing the retarding charge density and current element respectively, where 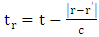 is the retarded time. If one now substitutes ω and δ in the continuity equation, followed by few but painstaking efforts, one recovers all of Maxwell’s equation [19]. But, we like to point out the following question: what is the physical justification for the use of the retarded time function? Indeed, the only answer epistemologically satisfying is to take it that the retarded time function allows a delay of propagating signals so that, even though the field propagates at the speed of light, one does not get a light-like matrix. One must notice that the delay is only apparent.The interpretation of the result is therefore straightforward; it follows that the retarded time is indeed a conjugate time parameter and hence allows one to replace the absolute time (x0) with the phase variable without any loss of generality. However, notice immediately that the method we present here (i.e. using the fundamental postulate) has greatly simplified the unnecessarily complication. We now make the bold claim that one can easily re-writes the anti-symmetric Maxwell’s tensor as a symmetric one by taking the diagonal metrics corresponding to the continuity equation (advanced time); the same is also true if one uses the stress-energy tensor in general relativity_ we shall show this point in our next presentation.2. We are taking the condition in which
is the retarded time. If one now substitutes ω and δ in the continuity equation, followed by few but painstaking efforts, one recovers all of Maxwell’s equation [19]. But, we like to point out the following question: what is the physical justification for the use of the retarded time function? Indeed, the only answer epistemologically satisfying is to take it that the retarded time function allows a delay of propagating signals so that, even though the field propagates at the speed of light, one does not get a light-like matrix. One must notice that the delay is only apparent.The interpretation of the result is therefore straightforward; it follows that the retarded time is indeed a conjugate time parameter and hence allows one to replace the absolute time (x0) with the phase variable without any loss of generality. However, notice immediately that the method we present here (i.e. using the fundamental postulate) has greatly simplified the unnecessarily complication. We now make the bold claim that one can easily re-writes the anti-symmetric Maxwell’s tensor as a symmetric one by taking the diagonal metrics corresponding to the continuity equation (advanced time); the same is also true if one uses the stress-energy tensor in general relativity_ we shall show this point in our next presentation.2. We are taking the condition in which 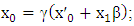 the justification follows similarly as in the case of the retarded function which is already well-known.
the justification follows similarly as in the case of the retarded function which is already well-known. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML