-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2023; 13(4): 85-91
doi:10.5923/j.ijtmp.20231304.01
Received: Oct. 26, 2023; Accepted: Nov. 20, 2023; Published: Nov. 23, 2023

Non-inertial Special Relativity Theory for the Real Frames (Objects)
Manhar L. Shah
MVM Electronics, Inc., 3410 N Harbor City Blvd., Suite E, Melbourne, FL, USA
Correspondence to: Manhar L. Shah, MVM Electronics, Inc., 3410 N Harbor City Blvd., Suite E, Melbourne, FL, USA.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Einstein’s Special Relativity Theory (ESRT) deals with the inertial frames. Connection between non-inertial and ESRT needs to be established for real physical cases. Kinematic Special Relativity (KSR) theory, (non-inertial Special Relativity), was developed earlier with the central theme of simultaneity providing an integral formula for the Space-Time Relation (STR) between two frames. Switching computation from one frame to other also switches the reference frame. That is OK for two inertial frames but it is in error for two real frames. Without realization of this fact and the real length contraction concept prevailing for a long time (over a century) have generated many paradoxes and misconceptions. Further research revealed that ESRT itself contains length expansion along the velocity direction when an object gains velocity. The moving inertial frame in ESRT is shown to be fictitious and a real object’s length expansion and contraction associated with it makes dimensions of objects appear the same regardless of the relative velocity. This paper describes Special Relativity for real physical frames or objects in detail. Earlier publications, one for KSR theory and other dealing with length contraction were scrutinized by computing data for various scenarios. In one scenario non-physical time relation occurred suggesting some deficiency in the model. Minor modifications of the earlier results are presented and discussed in this paper to eliminate non-physical outcome.
Keywords: Special Relativity, Non-inertial Special Relativity, Accelerated frame, Hyperbolic trajectory, Fermi coordinates, Infinitesimal Lorentz transformation, Twin paradox, Rotating frame, Length contraction
Cite this paper: Manhar L. Shah, Non-inertial Special Relativity Theory for the Real Frames (Objects), International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 4, 2023, pp. 85-91. doi: 10.5923/j.ijtmp.20231304.01.
Article Outline
1. Introduction
- Einstein’s Special Relativity Theory (ESRT) deals with the inertial frames. In real physical cases a frame needs to gain velocity from 0 to v at least once. This requires a theory to connect between non-inertial cases and ESRT. Kinematic Special Relativity (KSR) theory, (non-inertial special relativity), [1] was developed earlier to appropriately describe Special Relativity (SR) in non-inertial conditions. KSR theory was developed by establishing the Space-Time Relation (STR) between two frames in relative motion with simultaneity condition. This was done using the propagation time for the light signal of an event occurring at the synchronization position in the reference frame being simultaneously detected by the traveler and coincident observer in the stationary frame. The simultaneity condition is natural and central to ESRT. The final result of the KSR theory was an integral formula for the STR between two frames.ESRT uses inertial frames. One of the two frames with relative velocity can be inertial and designated as reference with label F and assumed stationary. The other frame with relative velocity to the previous one either would have gained velocity after being at rest in F or may have the relative velocity from eternity. For the inertial traveling frame F’ case an observer in the stationary frame obtains the STR in the other frame with reference to his own through synchronization. ESRT uses the frames resynchronization after F’ has gained constant velocity. Synchronization with real object or frame FR that will be moving with F’ is done in KSR when there is no relative velocity between F and FR. In this case the observed clock times of FR in F won’t agree with ESRT time in F’ but the incremental time of clocks in FR and F’ will be identical.Transition to non-inertial theory can be made with a real frame FR in F gaining velocity to co-move with an inertial frame F’. Each position of FR is matched to the position of F’ as it appears in F. Further discussion is presented in Sec. 4 to establish the special relativity theory for real frames or objects.More research was carried out on the subject of previously published KSR theory and the length contraction concept [2]. In a scenario of a traveler stopping after traveling some duration at constant velocity, the clock in F and one carried by the traveler (t and tR) didn’t increment equally for some duration. This is a non-physical condition requiring rectification of KSR theory. Discussion on this subject is provided in section 2. A minor modification was needed in KSR theory to prevent a non-physical outcome.The length contraction in SR theory has been accepted as real [3-7] for a long time (for about a century). But the publication [2] shows the contracted length is really the expanded space of the real frame when it gained velocity. This paper revels ESRT itself contains the length expansion along the direction of velocity for a real frame and the expanded length is observed contracted in the stationary frame. The space expansion as mentioned in the publication [2] over all three dimensions (3D) with clock sped-up, however, generated a problem when light propagation in the direction orthogonal to the direction of velocity was considered. Further research revealed that the space expansion should be only along the direction of the velocity of real frame FR and co-moving inertial frame F’. More discussion on this topic is presented in section 3 along with the explanation why the reference frame needs to be the stationary (inertial) frame. Length expansion-contraction is further discussed in this section. Explanation of why the space expansion in the direction of velocity alone doesn’t make space anisotropic is given there. Special Relativity (meaning flat space-time and no effect on STR due to acceleration) theory for real frames or objects is presented in section 4. A traveling real frame cannot be inertial so the special relativity theory for real frames or objects is synonymous to KSR theory and ESRT can be considered a subset of constant velocity interval in KSR. Misconceptions of ESRT have stemmed from the improper use of the reference frame. Switching frames without its implication on STR is the main reason. Section 5 elaborates on the reference frame designation. Resynchronization of clocks in a constant velocity interval in ESTR results in the out-of-sync clocks and simultaneity issue. Section 6 is devoted to this resynchronization issue. Conclusion follows thereafter.
2. More about Kinematic Special Relativity (KSR) Theory
- KSR theory is the basis for ESRT applications in the real physical environment. This theory was further scrutinized to make sure that all conceivable velocity trajectories produce real physical STR data. Some earlier part of the previously published KSR theory is repeated here for proper understanding on the subject. The nomenclature used here can be found in the earlier paper [1]. KSR theory is used to relate space-time data of an inertial frame to space-time data of a non-inertial frame with a non-constant velocity trajectory in general. Basically, that entails finding the simultaneity time relation between coincident observers to observe occurrence of an event and its detection at some spatially separated position of those frames. It should be noted that the expanded positions of FR coincide with F’ along with the positions x’=xR=0. The time increment
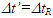 applies, so F’ can be used for this discussion. The parameters involved in this case are event time t0 and t’0, observation time t and t’, distance between the event and the observation point
applies, so F’ can be used for this discussion. The parameters involved in this case are event time t0 and t’0, observation time t and t’, distance between the event and the observation point 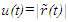 and u’, information propagation track length L and L’ and event to observer’s point propagation time tp and t’p in stationary and traveling frame F and F’, respectively. Computation of t’ involves finding L’, so t’p = L’/c can be added to t’0 to obtain t’. In the previous paper t’p was computed using the incremental time relation between
and u’, information propagation track length L and L’ and event to observer’s point propagation time tp and t’p in stationary and traveling frame F and F’, respectively. Computation of t’ involves finding L’, so t’p = L’/c can be added to t’0 to obtain t’. In the previous paper t’p was computed using the incremental time relation between 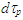 and
and  for a pulse of light traveling from
for a pulse of light traveling from 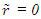 originating at time t0 and traveling distance L=u. The relation between
originating at time t0 and traveling distance L=u. The relation between  and
and  is,
is,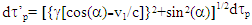 | (1) |
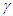 and v are
and v are 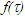 and
and 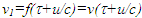 with
with 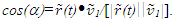 The final time relation becomes,
The final time relation becomes,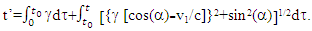 | (2) |
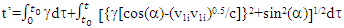 | (3) |
 In one scenario, t’ was computed for a traveler taking off with constant velocity and stopping at time tS. According to the previous publication, when
In one scenario, t’ was computed for a traveler taking off with constant velocity and stopping at time tS. According to the previous publication, when  was used in Eq. 2, the result showed t’ and t incrementing unequally for some duration after stop time tS. This non-physical result required rethinking about Eq. 2. The narrative of the first paragraph of this section was scrutinized further. Two different time, t and t0 are involved in the integration in Eq. 2. ESRT theory uses
was used in Eq. 2, the result showed t’ and t incrementing unequally for some duration after stop time tS. This non-physical result required rethinking about Eq. 2. The narrative of the first paragraph of this section was scrutinized further. Two different time, t and t0 are involved in the integration in Eq. 2. ESRT theory uses 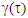 at the synchronization position. The light signal starts at t0 at the synchronization position so we need to use
at the synchronization position. The light signal starts at t0 at the synchronization position so we need to use  at the synchronization position. The incremental light propagation path length
at the synchronization position. The incremental light propagation path length  and
and 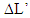 doesn’t occur until the light signal reaches the traveler’s destination at distance u. Therefore, the incremental path length calculation must use the traveler’s velocity at time t+u/c as light signal arrives at his position after traveling distance u. That means we must use
doesn’t occur until the light signal reaches the traveler’s destination at distance u. Therefore, the incremental path length calculation must use the traveler’s velocity at time t+u/c as light signal arrives at his position after traveling distance u. That means we must use  instead of
instead of  in Eq. 1 and 2. Since ESRT connects time relation between observers in relative motion any attempt to formulate a theory based upon the parameters of one observer (data at either x=0 or x’=0) won’t be correct and requirement of
in Eq. 1 and 2. Since ESRT connects time relation between observers in relative motion any attempt to formulate a theory based upon the parameters of one observer (data at either x=0 or x’=0) won’t be correct and requirement of  confirms that.Plots involving travel for time t=1 at constant velocity corresponding to
confirms that.Plots involving travel for time t=1 at constant velocity corresponding to 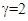 and then stop were made with the functionality of
and then stop were made with the functionality of 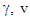 and v1 in Eq. 2 as
and v1 in Eq. 2 as  and
and  in all possible combinations to validate the model of the previous paragraph. Plots in Fig. 1 show the results for the combinations involving
in all possible combinations to validate the model of the previous paragraph. Plots in Fig. 1 show the results for the combinations involving 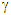 and v1 only. Other combinations involving
and v1 only. Other combinations involving 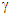 and v produced non-physical result such as t’ decreasing with increasing t for some duration in certain scenario.
and v produced non-physical result such as t’ decreasing with increasing t for some duration in certain scenario.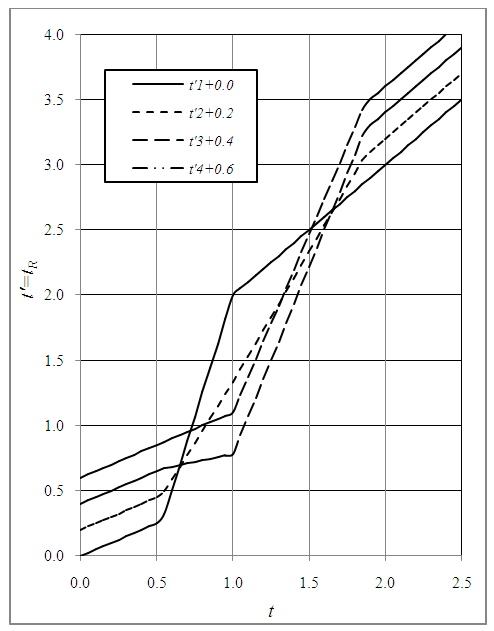 | Figure 1. Plots showing the time relation between t and t’ for t’1 having γ(τ) and v1(τ+u/c); t’2 having γ(τ+u/c) and v1(τ+u/c); t’3 having γ(τ+u/c) and v1(τ); and t’4 having γ(τ) and v1(τ) |
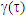 and
and 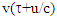 in Eq. 2 the clocks in F and F’ incremented equally after t=1 as the frames FR (same as F’ here) stopped. All other plots show non-equal time increment approximately up to time t=2 between clocks of F and FR even when there is no relative motion between frames. Clock in FR speeds-up after about t=0.5 due to FR stopping at t=1. Earlier theories of non-inertial frames do not show any such properties between the time relations and produce unacceptable physical conditions. Plot also shows
in Eq. 2 the clocks in F and F’ incremented equally after t=1 as the frames FR (same as F’ here) stopped. All other plots show non-equal time increment approximately up to time t=2 between clocks of F and FR even when there is no relative motion between frames. Clock in FR speeds-up after about t=0.5 due to FR stopping at t=1. Earlier theories of non-inertial frames do not show any such properties between the time relations and produce unacceptable physical conditions. Plot also shows 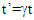 for F’ stopping at t=1. For the inertial case
for F’ stopping at t=1. For the inertial case 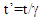 at t=1 was computed agreeing with ESRT because of the continuing of the relative velocity. Computations for round trip, speed decrease, speed increase and constant acceleration trajectory were performed with the modification as discussed for the KSR theory. The plots t’ vs t relation were somewhat shifted compared to the reported in the earlier publication but adhered to the proper physical behavior.
at t=1 was computed agreeing with ESRT because of the continuing of the relative velocity. Computations for round trip, speed decrease, speed increase and constant acceleration trajectory were performed with the modification as discussed for the KSR theory. The plots t’ vs t relation were somewhat shifted compared to the reported in the earlier publication but adhered to the proper physical behavior. 3. Discussion on the Length Contraction
- The current length contraction concept was first advanced by G. Fitzgerald in 1889 [8]. It was hypothesized as the length contraction in the direction of velocity and remained embedded ever since in ESRT. A moving rod not only appears shorter but it is accepted as real effect. It means the rod just doesn’t appear shorter but all physical aspects of the moving rod have to be based upon this shortened length [6-8]. This led to the notion that a moving rod (or axes) will appear rotated if it changed the relative velocity direction. A vast number of notions and publications based on this erroneous shortened length concept exist at present. However, a simple observation can prove that ESRT cannot have real length contraction. In the prevailing SR concept a rod of length L’ in the moving inertial frame F’ is observed contracted as
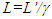 in the stationary “reference” frame F. Length contraction, if real then as the rod stops at time tS the length L’ will collapse to L in F according this concept. Furthermore, in F’ the rod has out-of sync times so the sections of the rods will continue to move and L’ will collapse to
in the stationary “reference” frame F. Length contraction, if real then as the rod stops at time tS the length L’ will collapse to L in F according this concept. Furthermore, in F’ the rod has out-of sync times so the sections of the rods will continue to move and L’ will collapse to  in F’. Such an outcome has no theoretical basis and appears non-physical.Further reasoning for the absence of length contraction can be provided with the Lorentz Transform (LT) itself which states
in F’. Such an outcome has no theoretical basis and appears non-physical.Further reasoning for the absence of length contraction can be provided with the Lorentz Transform (LT) itself which states  If we consider an object at x’=X’ a large value and v=0 then x=X’ at t’=0. Change,
If we consider an object at x’=X’ a large value and v=0 then x=X’ at t’=0. Change,  for a small time interval,
for a small time interval, 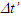 after t’=0 for F’ gaining sudden velocity v would be
after t’=0 for F’ gaining sudden velocity v would be 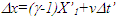 according to LT. For a small
according to LT. For a small  and
and 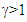 LT gives
LT gives  a large spatial change in a small time interval. That is impossible to achieve for a real object. This implies no length expansion or contraction of real frames or objects can be expected in SR.Synchronization of F and F’ with a constant relative velocity makes F’ a perpetual moving inertial frame. Such perpetual motion is non-physical so F’ cannot be a real frame but it should be designated as a fictitious frame. With this logic a rod of length L1 will correspond to length
a large spatial change in a small time interval. That is impossible to achieve for a real object. This implies no length expansion or contraction of real frames or objects can be expected in SR.Synchronization of F and F’ with a constant relative velocity makes F’ a perpetual moving inertial frame. Such perpetual motion is non-physical so F’ cannot be a real frame but it should be designated as a fictitious frame. With this logic a rod of length L1 will correspond to length 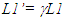 in F’ as it gains velocity. The length L1’ in F’ will be observed contracted by a factor
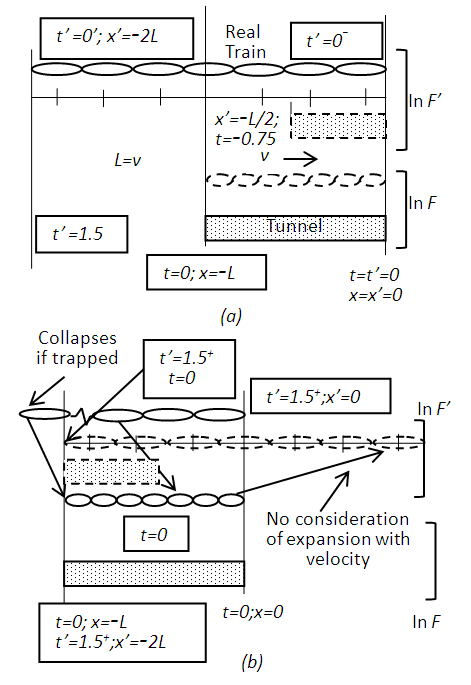
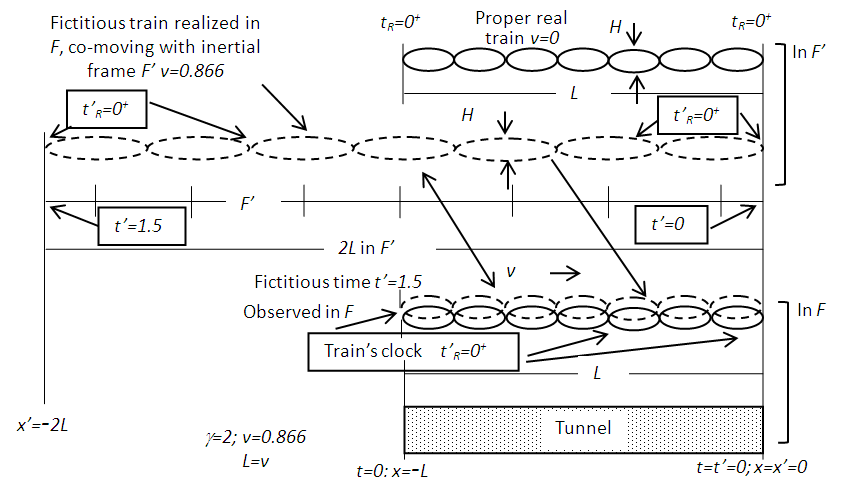
in F’ as it gains velocity. The length L1’ in F’ will be observed contracted by a factor 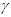 so the rod itself will be observed having length L1 in F. Thus a rod will be observed of the same length even when it has relative motion. Contrary to the prevailing concept no real length contraction or expansion should be conceptualized in SR.In the previous publication [2] the real length contraction was shown to be non-physical. The space expansion coupled with the clock sped-up and then length contraction was proposed for more appropriate special relativity theory. Further research showed the space expansion along the velocity direction can be explained within ESRT. Additionally, the space expansion for all directions (3D) stipulated in that publication was found to be in error. 3D expansion produced wrong results for light propagation orthogonal to the velocity direction. 3D expansion and sped-up clock were stipulated to make the space isotropic. Since the inertial space F’ is fictitious it can be anisotropic. However, the out-of-sync time terms in F’ makes it isotropic anyway overcoming the concern of anisotropic space. The length expansion of real objects in F’ coupled with contraction in F make observed dimensions of objects the same regardless of the relative velocity (except some optical illusion with shift of light rays due to velocity). Observed real rod’s length would be same with or without relative velocity due to its virtual space expansion in F’ and then observed contraction (along rod’s length) in F.The erroneous length contraction concept evolved due to three factors: (i) not recognizing that the moving inertial frame F’ is fictitious while confusing it as a real object or real frame FR (ii) not properly analyzing the relation between a real and inertial frame if start and stop were included and (iii) casual switching of the reference frame between F and F’ without corresponding STR correction as was pointed out previously [1]. Synchronization of clocks in two frames after one gains relative velocity is obviously going to produce out of synch time. If clocks of both frames were set to zero everywhere when there was no relative velocity then resynchronizing after relative velocity would require varying times in one frame. How can a clocks’ time jump? Such inquiry led to the realization that there is no real length contraction or expansion of length in ESRT.Representation of FR as expanded length in co-moving inertial frame F’ can be well illustrated using the reverse process of many prevailing explanation of length contraction such as used with trapping a train in a shorter tunnel. A graphical representation in Fig. 2 illustrates the reasoning. The parameters used for Fig. 2 are
so the rod itself will be observed having length L1 in F. Thus a rod will be observed of the same length even when it has relative motion. Contrary to the prevailing concept no real length contraction or expansion should be conceptualized in SR.In the previous publication [2] the real length contraction was shown to be non-physical. The space expansion coupled with the clock sped-up and then length contraction was proposed for more appropriate special relativity theory. Further research showed the space expansion along the velocity direction can be explained within ESRT. Additionally, the space expansion for all directions (3D) stipulated in that publication was found to be in error. 3D expansion produced wrong results for light propagation orthogonal to the velocity direction. 3D expansion and sped-up clock were stipulated to make the space isotropic. Since the inertial space F’ is fictitious it can be anisotropic. However, the out-of-sync time terms in F’ makes it isotropic anyway overcoming the concern of anisotropic space. The length expansion of real objects in F’ coupled with contraction in F make observed dimensions of objects the same regardless of the relative velocity (except some optical illusion with shift of light rays due to velocity). Observed real rod’s length would be same with or without relative velocity due to its virtual space expansion in F’ and then observed contraction (along rod’s length) in F.The erroneous length contraction concept evolved due to three factors: (i) not recognizing that the moving inertial frame F’ is fictitious while confusing it as a real object or real frame FR (ii) not properly analyzing the relation between a real and inertial frame if start and stop were included and (iii) casual switching of the reference frame between F and F’ without corresponding STR correction as was pointed out previously [1]. Synchronization of clocks in two frames after one gains relative velocity is obviously going to produce out of synch time. If clocks of both frames were set to zero everywhere when there was no relative velocity then resynchronizing after relative velocity would require varying times in one frame. How can a clocks’ time jump? Such inquiry led to the realization that there is no real length contraction or expansion of length in ESRT.Representation of FR as expanded length in co-moving inertial frame F’ can be well illustrated using the reverse process of many prevailing explanation of length contraction such as used with trapping a train in a shorter tunnel. A graphical representation in Fig. 2 illustrates the reasoning. The parameters used for Fig. 2 are 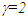 and the tunnel length L in F equal to v (t=1). The train and its length is currently accepted real in F’ and is equal to
and the tunnel length L in F equal to v (t=1). The train and its length is currently accepted real in F’ and is equal to 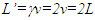 so the train is expected to fit in the tunnel due to length contraction. According to the prevailing narrative [4] the whole train is inside the tunnel in F at t=t’=0 and the exit door position is designated as x=x’=0. But in F’ at t’=0 the caboose position is at x’=-2 and the tunnel’s entrance door at x’=-0.5 value. An observer in F’ sees tunnel too short and doesn’t expect to fit it in the tunnel. For the whole train to be inside the tunnel caboose has to be at the entrance door of the tunnel. This will happen at t’=1.5 at that time t=0 as shown in Fig. 2a satisfying the SR results. The prevailing concept at present to fit a long train in a short tunnel as it trapped is explained by arguing that the train is composed of microscopic sections and each section would enter tunnel at different time in F’ and result in compressed train to fit in the tunnel as shown in Fig. 2b. The trapped compressed train’s length in F is L. In the reverse of trapping the train the compressed train gains velocity at t=0 in F. Fig. 2b depicts the situation. The whole trains gains velocity v at time t=0. The time in F’ at x=x’=0 will be t’=0. The time at x’=-2L in F’ will be t’=1.5 as was the case when the train was stopping. When the caboose is at the entrance of the tunnel at t’=1.5 the exit of the tunnel will be at half the length of the expanded train in F’ with t=0; x=0; t’=1.5 and x’=-2L. The total train length in F’ would be 2L as expanded trapped train length of L.
so the train is expected to fit in the tunnel due to length contraction. According to the prevailing narrative [4] the whole train is inside the tunnel in F at t=t’=0 and the exit door position is designated as x=x’=0. But in F’ at t’=0 the caboose position is at x’=-2 and the tunnel’s entrance door at x’=-0.5 value. An observer in F’ sees tunnel too short and doesn’t expect to fit it in the tunnel. For the whole train to be inside the tunnel caboose has to be at the entrance door of the tunnel. This will happen at t’=1.5 at that time t=0 as shown in Fig. 2a satisfying the SR results. The prevailing concept at present to fit a long train in a short tunnel as it trapped is explained by arguing that the train is composed of microscopic sections and each section would enter tunnel at different time in F’ and result in compressed train to fit in the tunnel as shown in Fig. 2b. The trapped compressed train’s length in F is L. In the reverse of trapping the train the compressed train gains velocity at t=0 in F. Fig. 2b depicts the situation. The whole trains gains velocity v at time t=0. The time in F’ at x=x’=0 will be t’=0. The time at x’=-2L in F’ will be t’=1.5 as was the case when the train was stopping. When the caboose is at the entrance of the tunnel at t’=1.5 the exit of the tunnel will be at half the length of the expanded train in F’ with t=0; x=0; t’=1.5 and x’=-2L. The total train length in F’ would be 2L as expanded trapped train length of L.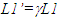 is the correct result and the length contraction of F’ observed in F makes the observed length of a rod same regardless of its relative velocity.
is the correct result and the length contraction of F’ observed in F makes the observed length of a rod same regardless of its relative velocity. 4. Special Relativity for Real Frames
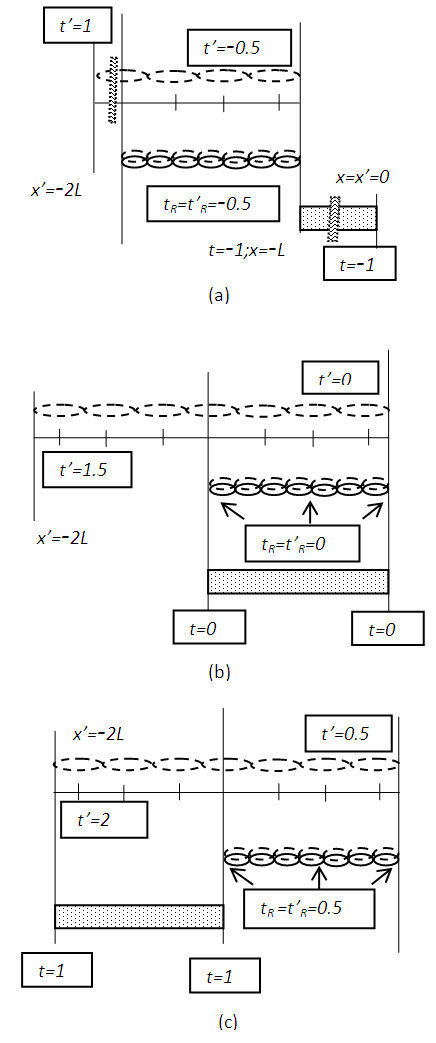
- The space expansion stated in [2] is in-line with the above explanation except 3D expansion was in error. Only the space expansion along the velocity direction is correct. In fact it is not the space expansion. It is the representation of a real frame FR as it gains relative velocity and co-moves with an inertial frame F’ in the reference frame F (usually a stationary frame). This is in contrast to the concept mentioned by Krane [9] as just observing a relatively moving object contracted. The object will be observed same regardless of its relative motion.For better understanding we introduce proper time, length and co-ordinates tR, LR and xR, respectively for a real frame FR in one dimensional case. Frames have x=x’=xR=0 with FR stationary in F at t=t’=tR=0. That sets clock times for all x and xR identical equal to zero. Frame F’ is inertial and is moving with constant velocity v so t’ observed in F will not be proper except at x’=0. Frame FR gains velocity v at time t=0+ and co-moves with F’. Since space and clocks in FR cannot jump, values xR=x and tR=t=0 will persists for t=0+. Because the proper length in F’ appears contracted in F a length LR would exactly match in F’ to the proper length
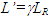 and no sudden change of co-ordinate of FR in F need to be contemplated. A moving object or frame FR would appear the same in F regardless of its relative velocity and no anisotropic space arises in the theory. Time increments equally at all positions in F’ so same will happen in FR and identical time tR in FR will be observed at all positions in F. Position x’=0 and xR=0 will be coincident and the moving observer will have x=vt value in F. These results suggest the Special Relativity theory and Lorentz transformation should be modified for the real frame FR gaining constant relative velocity in F after the start as:
and no sudden change of co-ordinate of FR in F need to be contemplated. A moving object or frame FR would appear the same in F regardless of its relative velocity and no anisotropic space arises in the theory. Time increments equally at all positions in F’ so same will happen in FR and identical time tR in FR will be observed at all positions in F. Position x’=0 and xR=0 will be coincident and the moving observer will have x=vt value in F. These results suggest the Special Relativity theory and Lorentz transformation should be modified for the real frame FR gaining constant relative velocity in F after the start as: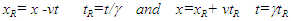 | (4) |
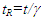 doesn’t provide the needed data to satisfy the simultaneity condition. The incremental light propagation path length and time relation for a given relative velocity as discussed for the KSR theory needs to be used in non-inertial situation.
doesn’t provide the needed data to satisfy the simultaneity condition. The incremental light propagation path length and time relation for a given relative velocity as discussed for the KSR theory needs to be used in non-inertial situation.5. Reference Frame Selection
- For the real frames the symmetric relations of Lorentz transformation doesn’t hold according to Eq. 4. With a constant relative velocity the stationary observers will see a clock’s time in FR as dilated (running slow) but the observers gaining velocity would see the clock’s time of F as contracted (running fast) according to Eq. 3. In general, in a non-inertial case the time relation between two frames will not be same over the duration of constant velocity as illustrated in Fig. 1.A question arises how the traveler would observe the stationary frame and obtain STR? For that, only the frame that doesn’t change velocity (like stationary frame) must be designated as the reference frame. This requirement is basic not appreciated in the prevailing understanding of ESRT. Frame F and FR must maintain the consistent time relation after synchronization without relative velocity. A wave-front generated at the synchronization is observed with the proper time at all places and all durations in F. This is not true in FR if it changes velocity. This means all computations of STR must be based upon the reference frame F. In that case the traveler with constant velocity must use the same computation as in Eq. 2 making
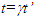 and then follow his trajectory in F. The symmetry of LT that makes STR symmetric also has symmetry for frames F and F’. Switching computation from one frame to other also switches the reference frame. That is OK for the two inertial frames but it is in error for two real frames. Without realization of this fact many paradoxes and misconceptions have occurred with ESRT.In ESRT both F and F’ are inertial so if we consider F as the stationary (no change of velocity or acceleration over time) real frame then length and time are well defined in F and that is why it is selected as the reference frame. However, with perpetual velocity of F’ or resynchronization after velocity gain the length and time of F’ cannot be compared to the same in F but can be observed only. Therefore, F’ cannot be considered as real frame; but it should be accepted as the virtual frame. Prevailing ESRT use same length data for F’ as was before gaining velocity and clocks are reset in F’. Why the data of FR need to change as it co-moves with F’ ? Only the positions of F’ and FR need to correspond properly like map or photo. Clocks in FR will maintain their value while going from no relative velocity to gaining velocity state. Identical time and position data of real frame FR before gaining velocity will persist at t=0+. The out-of-sync time terms of F’ used in ESRT has no real use in obtaining the STR when the KSR theory is considered. Clocks of both F and FR are synchronized when there is no relative velocity and the time increment in FR is same at all positions like in F’ according to the KSR theory and ESRT.The important point is the synchronization of clocks in F and FR must be done when there is no relative velocity, the frame that gains velocity is FR and the stationary frame is F in which clocks have the same time at all positions. Any attempt to find STR using same time at spatially separated positions in a frame makes that frame the reference frame and produces erroneous data if the frame is not stationary (inertial). All STR must be based upon the KSR theory with F as the reference frame. Incidentally, earth is used as the reference frame because it is not expected to gain velocity after synchronization. In that case only the earth can be the reference frame consequently the reciprocity of Lorentz transformation is not for the real world.
and then follow his trajectory in F. The symmetry of LT that makes STR symmetric also has symmetry for frames F and F’. Switching computation from one frame to other also switches the reference frame. That is OK for the two inertial frames but it is in error for two real frames. Without realization of this fact many paradoxes and misconceptions have occurred with ESRT.In ESRT both F and F’ are inertial so if we consider F as the stationary (no change of velocity or acceleration over time) real frame then length and time are well defined in F and that is why it is selected as the reference frame. However, with perpetual velocity of F’ or resynchronization after velocity gain the length and time of F’ cannot be compared to the same in F but can be observed only. Therefore, F’ cannot be considered as real frame; but it should be accepted as the virtual frame. Prevailing ESRT use same length data for F’ as was before gaining velocity and clocks are reset in F’. Why the data of FR need to change as it co-moves with F’ ? Only the positions of F’ and FR need to correspond properly like map or photo. Clocks in FR will maintain their value while going from no relative velocity to gaining velocity state. Identical time and position data of real frame FR before gaining velocity will persist at t=0+. The out-of-sync time terms of F’ used in ESRT has no real use in obtaining the STR when the KSR theory is considered. Clocks of both F and FR are synchronized when there is no relative velocity and the time increment in FR is same at all positions like in F’ according to the KSR theory and ESRT.The important point is the synchronization of clocks in F and FR must be done when there is no relative velocity, the frame that gains velocity is FR and the stationary frame is F in which clocks have the same time at all positions. Any attempt to find STR using same time at spatially separated positions in a frame makes that frame the reference frame and produces erroneous data if the frame is not stationary (inertial). All STR must be based upon the KSR theory with F as the reference frame. Incidentally, earth is used as the reference frame because it is not expected to gain velocity after synchronization. In that case only the earth can be the reference frame consequently the reciprocity of Lorentz transformation is not for the real world.6. Discussion on KSR’s Subset ESRT and Misconceptions
- A general non-inertial trajectory of a traveler AR in FR co-moving with A’ in frame F’ relative to a stationary (inertial) observer A in frame F is considered. In this trajectory one or more intervals may be with constant velocity. In a constant velocity interval ESRT and LT are applicable. Two items; (i) a constant position in a frame and other (ii) equal time at spatially separated positions in a frame are of significance. A large extent frame cannot be expected to gain high velocity making a frame like earth as the stationary (inertial) frame F as the reference frame. Traveler AR gains high velocity so his real frame FR cannot have large extent. The co-moving fictitious frame F’ can be of any extent but has no real physical significance for x’ except at x’=0. This means time relations between two frames for some interval with x’=0 has the significance. The short extent of FR makes the spatial separation in it meaningless so the physical significance of the item (ii) is with equal time t at spatially separated positions in F.The first item occurs in the case of observing the muon dilated life time. The important aspect in this item is the synchronization before or after has no impact on the theory. That is because the positions and clocks of AR, A and A’ match; xR=x=x’=0 and tR=t=t’=0 as AR gains velocity.The item (ii) is the part of misconceptions because it depends upon the clock synchronization process. In ESRT a prevailing concept is “two spatially separated simultaneous events in a frame are not simultaneous in the relatively moving frame [10].” This is true if the synchronization of the clocks in two frames was performed after AR gained velocity. If the synchronization of clocks was done when F and FR didn’t have relative velocity then those events will be observed simultaneous in both F and FR frames. Clarification of this point also shows, in ESRT if clocks time in F’ are set to match with F at synchronization t=t’=0 then non-simultaneous observation and out-of–synch clocks would not arise. Setting of clocks in F’ at the synchronization can be made with some different rule, such as identical to F for ESRT. In that case there will be no out-of sync time but the incremental time
 will still be related to
will still be related to 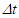 according to ESRT.
according to ESRT. 7. Conclusions
- Special relativity theory applicable to real frames or objects is presented in this paper. Because two real frames cannot have perpetual constant velocity non-inertial SR, as named KSR theory, is developed here. Minor modifications of the previously published results were required to eliminate non-physical time relation is some scenarios. A detailed discussion of the results of ESRT itself was provided to show length expansion of an object with the gain of velocity but the same expanded length being observed contracted in the stationary frame. This result shows the current concept of the real length contraction in ESRT is in error and objects would appear same with or without relative velocity. Importance of what constitutes the reference frame is highlighted.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML