Liu Ke Dian
New Tech Institute, China
Correspondence to: Liu Ke Dian, New Tech Institute, China.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper derives and clarifies the accurate physical meaning of Planck’s constant h through analyzing and calculating the integrals of energy over one wave cycle of various waves. Thus discover that the energy of one wavelength of any wave is proportional to distinctive constant and its frequency respectively. These constants are different respect to different waves, and the constant of EM wave is prevailingly called Planck’s constant h.
Keywords:
Planck’s constant, Quanta energy, hν, Quantum mechanics, Black body radiation
Cite this paper: Liu Ke Dian, Physical Meaning of Planck’s Constant h is the Integral of EM Wave Energy over One Cycle Per Wave Frequency ν, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 3, 2023, pp. 80-84. doi: 10.5923/j.ijtmp.20231303.03.
1. Introduction
The accurate physical meaning of Planck’s constant h must be foundSince Max Planck has proposed the new theory of quantum hypothesis and Planck’s constant h in 1904, until nowadays, the accurate physical meaning of Planck’s constant h has not yet been found or not properly explained, therefore it is always abused indiscriminately in many obvious unsuitable wave applications such as matter waves and even in some not wave matter subjects.Therefore, it is factually necessary to research, to seek and to clarify what is the accurate true nature physical meaning of the Planck’s constant h.To find or seek the true accurate physical meaning of Planck’s constant h, there two or three key viewpoints must be taken into account.The point 1 is that we must notice that the quanta energy E = hν of EM wave being produced or being absorbed by electrons is the measurable smallest energy unity. The point 2 is that we must be objectively aware of Planck’ constant h is originally generated from research of black radiation; it could be a same value and universally applicable in calculating energies of EM waves and light waves, however, before the accurate physical meaning has been found, it cannot be applied universally indiscriminately in some waves other than EM wave and light wave.The point 3 is the difference between the wave energy from the point mass energy lies in that the instantaneous measurable energy of a point mass is the total energy, whilst the instantaneously measured energy of a wave may not be the total energy of a wave, not be the mean energy of a wave, not be the average energy of a wave. Because wave energy generally is composed of at least two kinds of energy being transformed each other. Then, when we count the wave energy, we must measure the integral of one cycle energy (e.g., ET, E𝜆 or KT, K𝜆).Therefore, we will try to break through research and analyze on the true values of total energy over one cycle of different kinds of waves to try to find the accurate physical meaning of Planck’s constant h in the following sections.
1.1. Further Derivation of the Energy over One Wavelength of Sound Wave with Respect to Frequency
1.1.1. Briefing the Prevailing Description (Cited from the Book Fundamentals of Physics)
“As the sound wave propagates away from the piston, the displacement of any volume of air in front of the piston is given by Equation 17.2. To evaluate the kinetic energy of this volume of air, we need to know its speed. We find the speed by taking the time derivative of Equation 17.2: 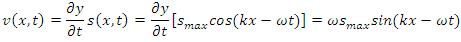 Imagine that we take a “snapshot” of the wave at the kinetic energy of a given volume of air at this time is
Imagine that we take a “snapshot” of the wave at the kinetic energy of a given volume of air at this time is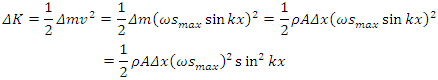 where A is the cross-sectional area of the moving air and A Δx is its volume. Now, as in Section 16.8, we integrate this expression over a full wavelength to find the total kinetic energy in one wavelength. Letting the volume of air shrink to infinitesimal thickness, so that
where A is the cross-sectional area of the moving air and A Δx is its volume. Now, as in Section 16.8, we integrate this expression over a full wavelength to find the total kinetic energy in one wavelength. Letting the volume of air shrink to infinitesimal thickness, so that 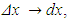 we have
we have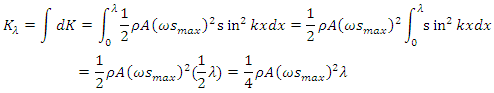 ”
”
1.1.2. Further Derivation of Energy with Respect to Frequency
Since the angular frequency is 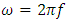 | (1.1) |
Substituting (1.1) into the energy expression of one wavelength 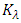 obtains
obtains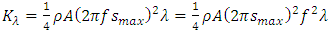 | (1.2) |
Since velocity v is 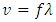 | (1.3) |
Substituting (1.3) into (1.2) we have the expression of energy in one wavelength 𝜆 as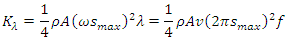 where
where 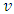 is the velocity of the sound wave.Let
is the velocity of the sound wave.Let 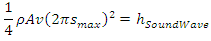 Therefore the total energy in one wavelength of sound wave is
Therefore the total energy in one wavelength of sound wave is 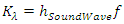 If we use ν to represent f then
If we use ν to represent f then 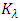 is written as
is written as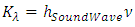 | (1.4) |
1.1.3. Remarks and Conclusion
It is worth noting that the above deduction never introduce any new variables and new parameters, therefore the deduced equation (1.4) has no difference with the conclusions, statements and descriptions of the cited book [1], the only difference lies in that the expressional form is changed. Since it is difficult to calculate the total energy of sound wave in an opened volume, we focus on the propagation in long narrow tube (as the cited book [1] discussed). Thus when the density 𝜌 of medium, A and v remain unchanged, the coefficient 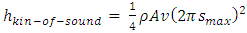 is a constant, the integral total kinetic energy of one cycle of sound wave is
is a constant, the integral total kinetic energy of one cycle of sound wave is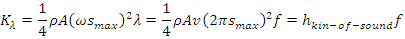 Therefore, theoretically, the total energy in one wavelength of one dimension sound wave is a constant
Therefore, theoretically, the total energy in one wavelength of one dimension sound wave is a constant 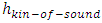 multiplying by the wave frequency f.
multiplying by the wave frequency f.
1.2. Further Derivation of the Energy over One Wavelength of String Wave with Respect to Frequency
1.2.1. Briefing the Prevailing Description (Cited from the Book Fundamentals of Physics)
“Let us focus our attention on a segment of the string of length Δx and mass Δm. Each such segment moves vertically with simple harmonic motion. Furthermore, all segments have the same angular frequency 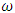 and the same amplitude A. The elastic potential energy U associated with a particle in simple harmonic motion is
and the same amplitude A. The elastic potential energy U associated with a particle in simple harmonic motion is 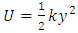 where the simple harmonic motion is in the y direction. Using the relationship
where the simple harmonic motion is in the y direction. Using the relationship 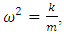 we can write this as
we can write this as 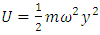 . If we apply this to the segment of mass Δm, the potential energy of this segment is
. If we apply this to the segment of mass Δm, the potential energy of this segment is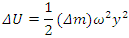 Because the mass per unit length of the string is
Because the mass per unit length of the string is 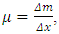 we can express the potential energy of the segment as
we can express the potential energy of the segment as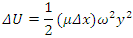 As the length of the segment shrinks to zero, Δx → dx, and this expression becomes a differential relationship:
As the length of the segment shrinks to zero, Δx → dx, and this expression becomes a differential relationship: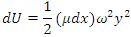 We replace the general displacement y of the segment with the wave function for a sinusoidal wave:
We replace the general displacement y of the segment with the wave function for a sinusoidal wave: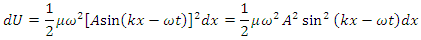 If we take a snapshot of the wave at time then the potential energy in a given segment is
If we take a snapshot of the wave at time then the potential energy in a given segment is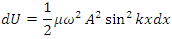 To obtain the total potential energy in one wavelength, we integrate this expression over all the string segments in one wavelength:
To obtain the total potential energy in one wavelength, we integrate this expression over all the string segments in one wavelength: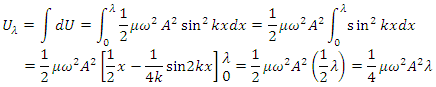 Because it is in motion, each segment of the string also has kinetic energy. When we use this procedure to analyze the total kinetic energy in one wavelength of the string, we obtain the same result:
Because it is in motion, each segment of the string also has kinetic energy. When we use this procedure to analyze the total kinetic energy in one wavelength of the string, we obtain the same result: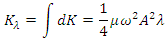 The total energy in one wavelength of the wave is the sum of the potential and kinetic energies:
The total energy in one wavelength of the wave is the sum of the potential and kinetic energies: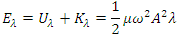 ”
”
1.2.2. Further Derivation of Energy with Respect to Frequency
Since the angular frequency is 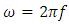 | (2.1) |
Substituting (2.3.1) into the energy in one wavelength expression 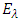 obtains
obtains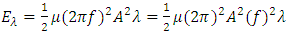 | (2.2) |
Since the velocity 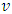 is
is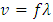 | (2.3) |
Substituting (3.2.3) into (3.2.2) we have the expression of energy in one wavelength 𝜆 as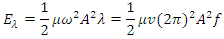 Let
Let 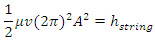 Therefore the total energy in one wavelength of string wave is
Therefore the total energy in one wavelength of string wave is 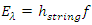 If f is represented by ν then the E𝜆 is expressed as
If f is represented by ν then the E𝜆 is expressed as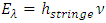 | (2.4) |
1.2.3. Remarks and Conclusion
It is worth noting that the above further deduction never introduce or create any new variables and parameters, therefore the deduced equation (2.4) has no difference with the conclusions, statements and descriptions of the cited book [1], the only difference lies in that the expressional form is changed. Since the integral total energy over one cycle carried by string wave is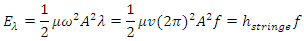 when the magnitudes of 𝜇, v and A remain unchanged, the coefficient
when the magnitudes of 𝜇, v and A remain unchanged, the coefficient 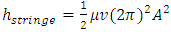 is a constant. Therefore, theoretically, the total energy in one wavelength of a string wave is a constant
is a constant. Therefore, theoretically, the total energy in one wavelength of a string wave is a constant 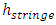 multiplying by its frequency f.
multiplying by its frequency f.
1.3. Analysis of Integral of EM Wave Energy over One Wavelength with Respect to Frequency
1.3.1. Calculating the EM Wave Energy over One Cycle
A prevailing assertion is that:“The rate of flow of energy in an electromagnetic wave is described by a vector S, called the Poynting vector, which is prevailingly defined by the expression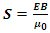 The magnitude of the Poynting vector represents the rate at which energy flows through a unit surface area perpendicular to the direction of wave propagation.”However, considering the definition of the equation
The magnitude of the Poynting vector represents the rate at which energy flows through a unit surface area perpendicular to the direction of wave propagation.”However, considering the definition of the equation 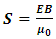 for S is “apply at any instant of time and represent the instantaneous rate at which energy is passing through a unit area” [1], the physical dimension unit of energy flow rate formula
for S is “apply at any instant of time and represent the instantaneous rate at which energy is passing through a unit area” [1], the physical dimension unit of energy flow rate formula 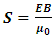 is W/m2, it sounds the flow rate with respect to area being not the function of variable time t, actually it is magnitude of energy density respect to area of spatial surface. Because the wave propagation speed c is constant, for different wavelength 𝜆 the spent time for flow the energy of one cycle wave is very different. For example, the wavelength of EM radiation can be 10-15 meter, also can be 10 meters; can both of the instantaneous flow rates be expressed as
is W/m2, it sounds the flow rate with respect to area being not the function of variable time t, actually it is magnitude of energy density respect to area of spatial surface. Because the wave propagation speed c is constant, for different wavelength 𝜆 the spent time for flow the energy of one cycle wave is very different. For example, the wavelength of EM radiation can be 10-15 meter, also can be 10 meters; can both of the instantaneous flow rates be expressed as 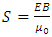 based on instantaneous amplitude?Then the wave with different wavelengths or with different frequencies will have very different instantaneous flow rates that are the frequency f or ω determined.Therefore we should redefine the formula of magnitudes of electric and magnetic fields energy of EM wave as
based on instantaneous amplitude?Then the wave with different wavelengths or with different frequencies will have very different instantaneous flow rates that are the frequency f or ω determined.Therefore we should redefine the formula of magnitudes of electric and magnetic fields energy of EM wave as 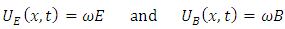 | (3.1) |
Or, we need to find the flow rate with respect to time t.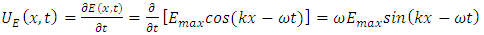 | (3.2) |
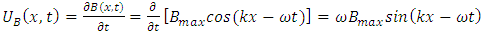 | (3.3) |
The energy flow rate with respect to time t should be expressed as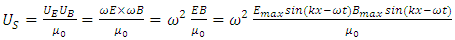 | (3.4) |
Thus we can calculate the total energy over one wavelength of the energy flow rate by integrating (3.4) over a full wavelength. If we take a snapshot of the wave at time then the energy flow rate in a wavelength 𝜆 is the integral of the expression respect with x over one wavelength 𝜆: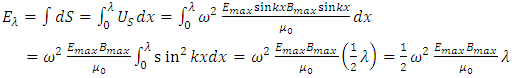 | (3.5) |
Since the angular frequency is 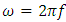 Substituting
Substituting 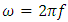 into (3.5) obtains
into (3.5) obtains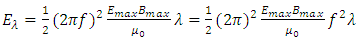 | (3.6) |
Since 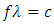 | (3.7) |
Substituting (3.6) into (3.5) we have the expression of energy in one wavelength as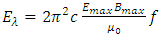 | (3.8) |
1.3.2. Analysis of EM Wave Energy with Respect to Frequency
We have found the total EM wave energy over one wavelength: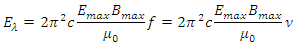 Where c as being light speed is constant; Emax and Bmax as being max amplitudes are constants; coefficient 𝜇0 as being permeability is constant. Then the coefficient
Where c as being light speed is constant; Emax and Bmax as being max amplitudes are constants; coefficient 𝜇0 as being permeability is constant. Then the coefficient 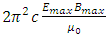 is constant.Notice that:• The quanta energy (hν) is Planck’ constant h multiplying by the wave frequency ν.• The integral of EM wave energy over one wavelength is also a constant
is constant.Notice that:• The quanta energy (hν) is Planck’ constant h multiplying by the wave frequency ν.• The integral of EM wave energy over one wavelength is also a constant 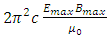 multiply by the wave frequency ν.• For any wave the total instantaneous energy is constant and equal to integral energy over one wavelength. • The quanta energy (E = hν) of EM wave is the measurable smallest energy unity. • Wave is normally composed of at least two kinds of energy being transformed each other. We cannot measure instantaneous EM wave energy. Instead, we can only measure the integral of one cycle energy (E𝜆). In fact, EM wave energy is existed only in a package being equal to integral over one cycle (the quanta energy). One can either measure the quanta energy package or he can measure the instantaneous wave energy in case of having the wave system destructed completely. Thus actually one doesn’t know what he is measuring when the wave system is destructed. He can measure nonsense of a destructed wave system actually.Therefore we can deduce that:1. The integral of EM wave energy over one wavelength E𝜆 must be equal to the quanta energy hν. Then the Planck’s constant
multiply by the wave frequency ν.• For any wave the total instantaneous energy is constant and equal to integral energy over one wavelength. • The quanta energy (E = hν) of EM wave is the measurable smallest energy unity. • Wave is normally composed of at least two kinds of energy being transformed each other. We cannot measure instantaneous EM wave energy. Instead, we can only measure the integral of one cycle energy (E𝜆). In fact, EM wave energy is existed only in a package being equal to integral over one cycle (the quanta energy). One can either measure the quanta energy package or he can measure the instantaneous wave energy in case of having the wave system destructed completely. Thus actually one doesn’t know what he is measuring when the wave system is destructed. He can measure nonsense of a destructed wave system actually.Therefore we can deduce that:1. The integral of EM wave energy over one wavelength E𝜆 must be equal to the quanta energy hν. Then the Planck’s constant 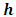 must be equal to the coefficient
must be equal to the coefficient 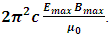 2. Thus the Planck’s constant h actually and factually is the energy over one wavelength of EM wave
2. Thus the Planck’s constant h actually and factually is the energy over one wavelength of EM wave 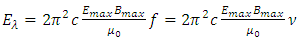 per frequency ν.i.e.:
per frequency ν.i.e.: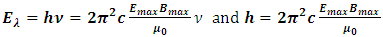 | (3.9) |
2. Conclusions
According to the deductions and conclusions of previous sections of this paper, we have seen clearly that:1. The integral total kinetic energy of one cycle of sound wave of one dimension (in a long tube) is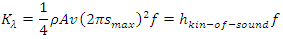 the coefficient
the coefficient 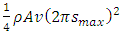 is a constant. Therefore, theoretically the total energy in one wavelength is a constant
is a constant. Therefore, theoretically the total energy in one wavelength is a constant 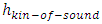 multiplying by the wave frequency f.2. The integral total energy over one cycle carried by string wave is
multiplying by the wave frequency f.2. The integral total energy over one cycle carried by string wave is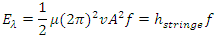 the coefficient
the coefficient 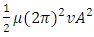 is a constant. Therefore, theoretically the total energy in one wavelength is a constant
is a constant. Therefore, theoretically the total energy in one wavelength is a constant 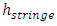 multiplying by its frequency f.3. The total energy over one wavelength of EM wave is
multiplying by its frequency f.3. The total energy over one wavelength of EM wave is 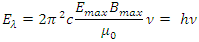 is a constant
is a constant 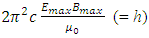 multiply by its frequency
multiply by its frequency 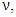 is the quanta energy of EM wave.Therefore we can conclude that the total energy of one cycle of any waves is proportional to the wave parameters determined a constant and is proportional to the wave frequency f or ν. In other words, the expression of total energy of one cycle of any wave is a constant hx multiplying by its wave frequency f or ν, i.e.,
is the quanta energy of EM wave.Therefore we can conclude that the total energy of one cycle of any waves is proportional to the wave parameters determined a constant and is proportional to the wave frequency f or ν. In other words, the expression of total energy of one cycle of any wave is a constant hx multiplying by its wave frequency f or ν, i.e.,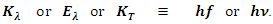 The footnote 𝜆 or T represents the energy in one wavelength 𝜆 or in one period T. However, for different waves the value of the constant hmatter is distinctively different and for EM wave, the constant h had been called Planck’s constant beforehand.Generally and conclusively, the physical meaning of Planck’s constant h is the integral of EM wave energy over one cycle per wave frequency ν.
The footnote 𝜆 or T represents the energy in one wavelength 𝜆 or in one period T. However, for different waves the value of the constant hmatter is distinctively different and for EM wave, the constant h had been called Planck’s constant beforehand.Generally and conclusively, the physical meaning of Planck’s constant h is the integral of EM wave energy over one cycle per wave frequency ν.
3. Postscript
If the deduction and conclusion of the physical meaning of Planck’s constant in this paper will be accurately understood and clarified by mainstream of physics community, It will provides an occasion for reforms, changes or revolutions of thinking mode of quantum mechanics. It will be a clue to further research of the possibility of existence and properties of the medium ether.
References
| [1] | David Halliday, Robert Resnick, Jearl Walker: Fundamental of Physics (8th edition). John Wiley & Sons, Inc 2008. |
| [2] | Wolfgang Demtröder: Atoms, Molecules and Photons. Springer 2010. |
| [3] | Beiser Arthur: Concepts of modern physics, 6th edition. McGraw-Hill Higher Education 2003. |
| [4] | Alan Jeffrey: Handbook of Mathematical formulas and integrals Second Edition. Academic Press 2000. |
| [5] | Liu Ke Dian: Correction of Fundamental Mistakes of Quantum Mechanics. American Academic Press 2023. |


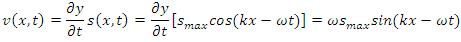 Imagine that we take a “snapshot” of the wave at the kinetic energy of a given volume of air at this time is
Imagine that we take a “snapshot” of the wave at the kinetic energy of a given volume of air at this time is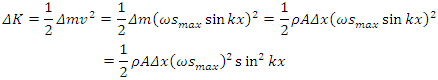 where A is the cross-sectional area of the moving air and A Δx is its volume. Now, as in Section 16.8, we integrate this expression over a full wavelength to find the total kinetic energy in one wavelength. Letting the volume of air shrink to infinitesimal thickness, so that
where A is the cross-sectional area of the moving air and A Δx is its volume. Now, as in Section 16.8, we integrate this expression over a full wavelength to find the total kinetic energy in one wavelength. Letting the volume of air shrink to infinitesimal thickness, so that 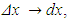 we have
we have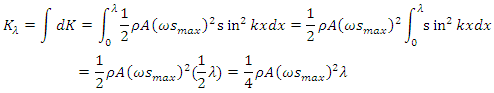 ”
”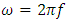
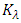 obtains
obtains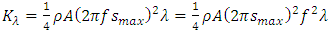
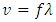
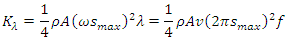 where
where 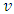 is the velocity of the sound wave.Let
is the velocity of the sound wave.Let 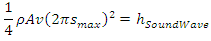 Therefore the total energy in one wavelength of sound wave is
Therefore the total energy in one wavelength of sound wave is 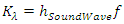 If we use ν to represent f then
If we use ν to represent f then 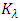 is written as
is written as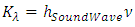
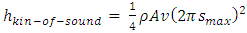 is a constant, the integral total kinetic energy of one cycle of sound wave is
is a constant, the integral total kinetic energy of one cycle of sound wave is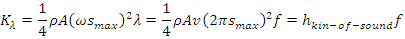 Therefore, theoretically, the total energy in one wavelength of one dimension sound wave is a constant
Therefore, theoretically, the total energy in one wavelength of one dimension sound wave is a constant 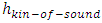 multiplying by the wave frequency f.
multiplying by the wave frequency f.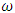 and the same amplitude A. The elastic potential energy U associated with a particle in simple harmonic motion is
and the same amplitude A. The elastic potential energy U associated with a particle in simple harmonic motion is 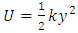 where the simple harmonic motion is in the y direction. Using the relationship
where the simple harmonic motion is in the y direction. Using the relationship 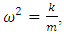 we can write this as
we can write this as 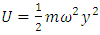 . If we apply this to the segment of mass Δm, the potential energy of this segment is
. If we apply this to the segment of mass Δm, the potential energy of this segment is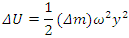 Because the mass per unit length of the string is
Because the mass per unit length of the string is 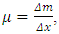 we can express the potential energy of the segment as
we can express the potential energy of the segment as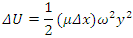 As the length of the segment shrinks to zero, Δx → dx, and this expression becomes a differential relationship:
As the length of the segment shrinks to zero, Δx → dx, and this expression becomes a differential relationship: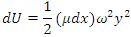 We replace the general displacement y of the segment with the wave function for a sinusoidal wave:
We replace the general displacement y of the segment with the wave function for a sinusoidal wave: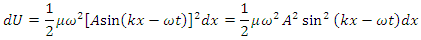 If we take a snapshot of the wave at time then the potential energy in a given segment is
If we take a snapshot of the wave at time then the potential energy in a given segment is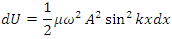 To obtain the total potential energy in one wavelength, we integrate this expression over all the string segments in one wavelength:
To obtain the total potential energy in one wavelength, we integrate this expression over all the string segments in one wavelength: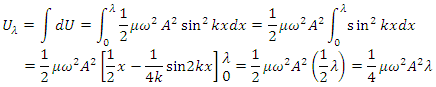 Because it is in motion, each segment of the string also has kinetic energy. When we use this procedure to analyze the total kinetic energy in one wavelength of the string, we obtain the same result:
Because it is in motion, each segment of the string also has kinetic energy. When we use this procedure to analyze the total kinetic energy in one wavelength of the string, we obtain the same result: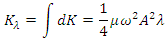 The total energy in one wavelength of the wave is the sum of the potential and kinetic energies:
The total energy in one wavelength of the wave is the sum of the potential and kinetic energies: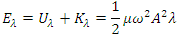 ”
”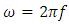
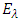 obtains
obtains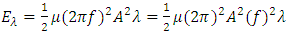
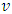 is
is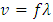
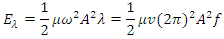 Let
Let 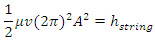 Therefore the total energy in one wavelength of string wave is
Therefore the total energy in one wavelength of string wave is 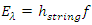 If f is represented by ν then the E𝜆 is expressed as
If f is represented by ν then the E𝜆 is expressed as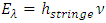
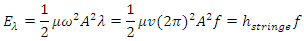 when the magnitudes of 𝜇, v and A remain unchanged, the coefficient
when the magnitudes of 𝜇, v and A remain unchanged, the coefficient 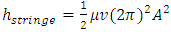 is a constant. Therefore, theoretically, the total energy in one wavelength of a string wave is a constant
is a constant. Therefore, theoretically, the total energy in one wavelength of a string wave is a constant 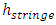 multiplying by its frequency f.
multiplying by its frequency f.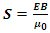 The magnitude of the Poynting vector represents the rate at which energy flows through a unit surface area perpendicular to the direction of wave propagation.”However, considering the definition of the equation
The magnitude of the Poynting vector represents the rate at which energy flows through a unit surface area perpendicular to the direction of wave propagation.”However, considering the definition of the equation 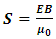 for S is “apply at any instant of time and represent the instantaneous rate at which energy is passing through a unit area” [1], the physical dimension unit of energy flow rate formula
for S is “apply at any instant of time and represent the instantaneous rate at which energy is passing through a unit area” [1], the physical dimension unit of energy flow rate formula 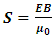 is W/m2, it sounds the flow rate with respect to area being not the function of variable time t, actually it is magnitude of energy density respect to area of spatial surface. Because the wave propagation speed c is constant, for different wavelength 𝜆 the spent time for flow the energy of one cycle wave is very different. For example, the wavelength of EM radiation can be 10-15 meter, also can be 10 meters; can both of the instantaneous flow rates be expressed as
is W/m2, it sounds the flow rate with respect to area being not the function of variable time t, actually it is magnitude of energy density respect to area of spatial surface. Because the wave propagation speed c is constant, for different wavelength 𝜆 the spent time for flow the energy of one cycle wave is very different. For example, the wavelength of EM radiation can be 10-15 meter, also can be 10 meters; can both of the instantaneous flow rates be expressed as 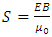 based on instantaneous amplitude?Then the wave with different wavelengths or with different frequencies will have very different instantaneous flow rates that are the frequency f or ω determined.Therefore we should redefine the formula of magnitudes of electric and magnetic fields energy of EM wave as
based on instantaneous amplitude?Then the wave with different wavelengths or with different frequencies will have very different instantaneous flow rates that are the frequency f or ω determined.Therefore we should redefine the formula of magnitudes of electric and magnetic fields energy of EM wave as 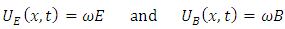
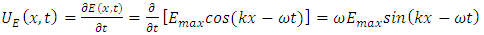
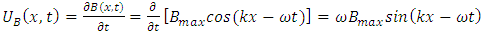
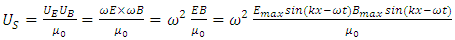
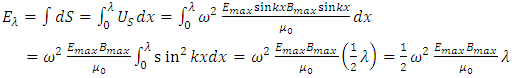
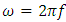 Substituting
Substituting 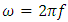 into (3.5) obtains
into (3.5) obtains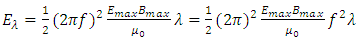
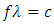
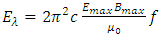
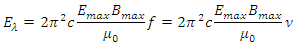 Where c as being light speed is constant; Emax and Bmax as being max amplitudes are constants; coefficient 𝜇0 as being permeability is constant. Then the coefficient
Where c as being light speed is constant; Emax and Bmax as being max amplitudes are constants; coefficient 𝜇0 as being permeability is constant. Then the coefficient 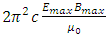 is constant.Notice that:• The quanta energy (hν) is Planck’ constant h multiplying by the wave frequency ν.• The integral of EM wave energy over one wavelength is also a constant
is constant.Notice that:• The quanta energy (hν) is Planck’ constant h multiplying by the wave frequency ν.• The integral of EM wave energy over one wavelength is also a constant 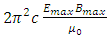 multiply by the wave frequency ν.• For any wave the total instantaneous energy is constant and equal to integral energy over one wavelength. • The quanta energy (E = hν) of EM wave is the measurable smallest energy unity. • Wave is normally composed of at least two kinds of energy being transformed each other. We cannot measure instantaneous EM wave energy. Instead, we can only measure the integral of one cycle energy (E𝜆). In fact, EM wave energy is existed only in a package being equal to integral over one cycle (the quanta energy). One can either measure the quanta energy package or he can measure the instantaneous wave energy in case of having the wave system destructed completely. Thus actually one doesn’t know what he is measuring when the wave system is destructed. He can measure nonsense of a destructed wave system actually.Therefore we can deduce that:1. The integral of EM wave energy over one wavelength E𝜆 must be equal to the quanta energy hν. Then the Planck’s constant
multiply by the wave frequency ν.• For any wave the total instantaneous energy is constant and equal to integral energy over one wavelength. • The quanta energy (E = hν) of EM wave is the measurable smallest energy unity. • Wave is normally composed of at least two kinds of energy being transformed each other. We cannot measure instantaneous EM wave energy. Instead, we can only measure the integral of one cycle energy (E𝜆). In fact, EM wave energy is existed only in a package being equal to integral over one cycle (the quanta energy). One can either measure the quanta energy package or he can measure the instantaneous wave energy in case of having the wave system destructed completely. Thus actually one doesn’t know what he is measuring when the wave system is destructed. He can measure nonsense of a destructed wave system actually.Therefore we can deduce that:1. The integral of EM wave energy over one wavelength E𝜆 must be equal to the quanta energy hν. Then the Planck’s constant 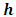 must be equal to the coefficient
must be equal to the coefficient 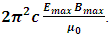 2. Thus the Planck’s constant h actually and factually is the energy over one wavelength of EM wave
2. Thus the Planck’s constant h actually and factually is the energy over one wavelength of EM wave 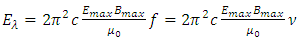 per frequency ν.i.e.:
per frequency ν.i.e.: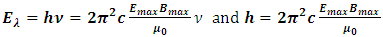
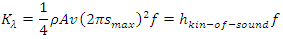 the coefficient
the coefficient 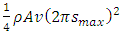 is a constant. Therefore, theoretically the total energy in one wavelength is a constant
is a constant. Therefore, theoretically the total energy in one wavelength is a constant 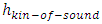 multiplying by the wave frequency f.2. The integral total energy over one cycle carried by string wave is
multiplying by the wave frequency f.2. The integral total energy over one cycle carried by string wave is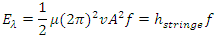 the coefficient
the coefficient 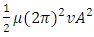 is a constant. Therefore, theoretically the total energy in one wavelength is a constant
is a constant. Therefore, theoretically the total energy in one wavelength is a constant 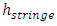 multiplying by its frequency f.3. The total energy over one wavelength of EM wave is
multiplying by its frequency f.3. The total energy over one wavelength of EM wave is 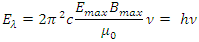 is a constant
is a constant 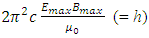 multiply by its frequency
multiply by its frequency 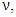 is the quanta energy of EM wave.Therefore we can conclude that the total energy of one cycle of any waves is proportional to the wave parameters determined a constant and is proportional to the wave frequency f or ν. In other words, the expression of total energy of one cycle of any wave is a constant hx multiplying by its wave frequency f or ν, i.e.,
is the quanta energy of EM wave.Therefore we can conclude that the total energy of one cycle of any waves is proportional to the wave parameters determined a constant and is proportional to the wave frequency f or ν. In other words, the expression of total energy of one cycle of any wave is a constant hx multiplying by its wave frequency f or ν, i.e.,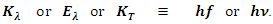 The footnote 𝜆 or T represents the energy in one wavelength 𝜆 or in one period T. However, for different waves the value of the constant hmatter is distinctively different and for EM wave, the constant h had been called Planck’s constant beforehand.Generally and conclusively, the physical meaning of Planck’s constant h is the integral of EM wave energy over one cycle per wave frequency ν.
The footnote 𝜆 or T represents the energy in one wavelength 𝜆 or in one period T. However, for different waves the value of the constant hmatter is distinctively different and for EM wave, the constant h had been called Planck’s constant beforehand.Generally and conclusively, the physical meaning of Planck’s constant h is the integral of EM wave energy over one cycle per wave frequency ν. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML