Thomas Erber1, 2, Porter W. Johnson3
1Distinguished Professor of Physics and Mathematics (Emeritus), Departments of Physics and of Applied Mathematics Lllinois Institute of Technology, Chicago IL, USA
2Research Associate, Department of Physics University of Chicago, Chicago IL, USA
3Professor of Physics (Emeritus), Department of Physics lllinois Institute of Technology, Chicago IL, USA
Correspondence to: Porter W. Johnson, Professor of Physics (Emeritus), Department of Physics lllinois Institute of Technology, Chicago IL, USA.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A previous quantum mechanical description of synchrotron radiation led to unphysical results. The reasons for this error were limitations in the Erdelyi- Swanson asymptotic approximation of the Whittaker functions. These problems were rectified with a new derivation of the asymptotic expansion. The most prominent feature of the new synchrotron spectrum is that under extreme conditions the maximum radiation is shifted upwards towards the tip.
Keywords:
Magnetor, Quantum, Synchrrotron, Asymptotic
Cite this paper: Thomas Erber, Porter W. Johnson, Quantum Theory of Synchrotron Radiation, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 3, 2023, pp. 75-79. doi: 10.5923/j.ijtmp.20231303.02.
1. Overview
With current equipment it is possible to accelerate electrons to energies of the order of 1012 eV. Also with high energy condenser banks and spiral generators pulsed magnetic fields in the range 1-10 MG (1 MG = 106 Gauss) can be produced.1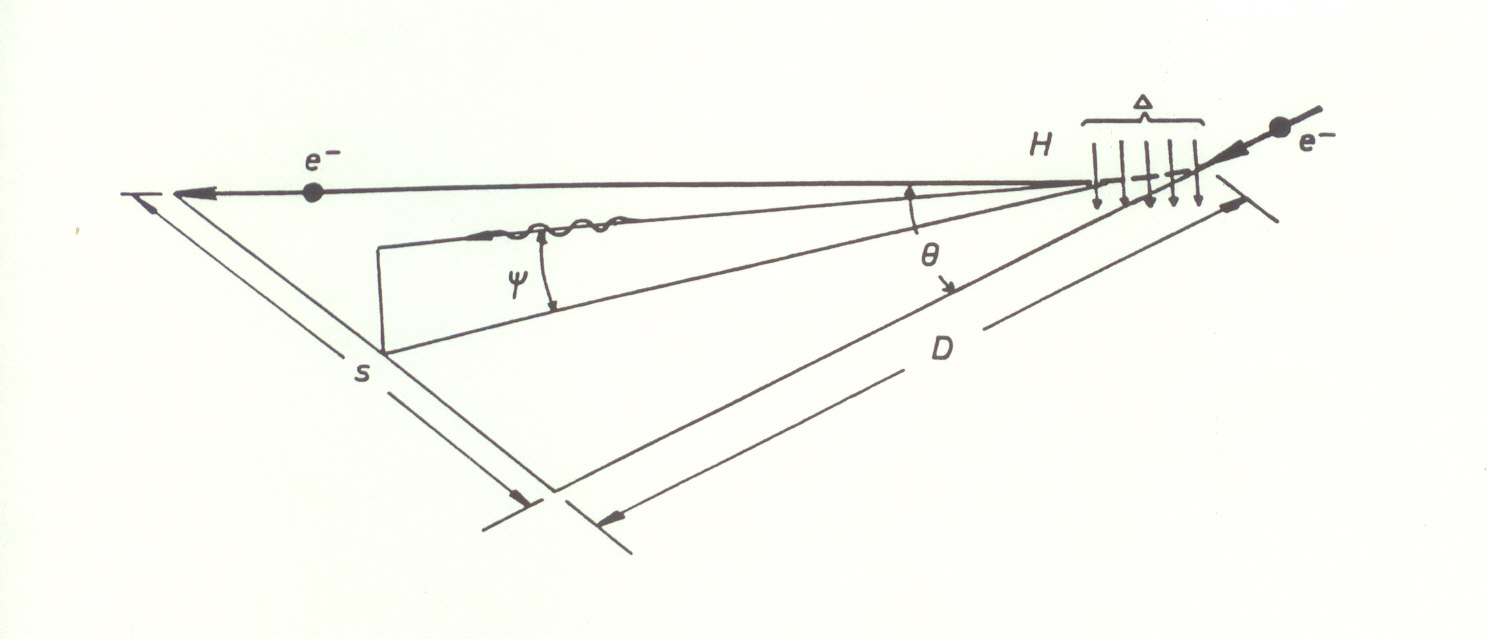 | Figure 1. Kinematics of magnetic bremsstrahlung |
Even more extreme conditions occur in astronomy. Electrons with energies of 1018 eV have been detected in cosmic ray showers, and it is surmised that `magnetars' can sustain magnetic fields up to 1015 Gauss. Under these circumstances the classical computation of synchrotron radiation leads to unphysical results. This error is due to identifying the synchrotron intensity spectrum with the Fourier resolution of the classical radiation field. Under extreme conditions the upper end of the radiation field includes photons whose energies exceed the energies of the incident electrons. Since the classical computations are not constrained by energy conservation this violation leads to unphysical results. Ironically, a previous attempt to resolve these issues with a complete quantum mechanical computation also led to unphysical results [1]. The general scheme of the quantum calculation is shown in Fig. 2. This depicts the situation where an electron in an initial state 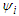 with energy
with energy 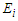 and momentum
and momentum 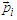 emits a photon
emits a photon 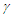 with energy
with energy 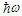 and momentum
and momentum 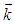 while transitioning to a final state
while transitioning to a final state 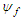 with energy
with energy 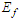 and momentum
and momentum 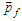 . In quantum mechanics energy and momentum conservation are built in from the outset:
. In quantum mechanics energy and momentum conservation are built in from the outset: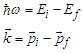 | (1) |
However, these constraints do not determine unique final states. Moreover, arbitrarily large momentum transfers can be absorbed by the magnetic fields: in principle this momentum is ultimately taken up by the macroscopic devices that generate the fields. The stochastic features enter in the overlap integral 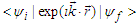 which, as indicated on Fig. 2, effectively determines the shape of the synchrotron radiation spectrum. The explicit evaluation of the overlap integral is given in Ref. [1]. The results are lengthy expressions whose essential components are the generalized Laguerre functions
which, as indicated on Fig. 2, effectively determines the shape of the synchrotron radiation spectrum. The explicit evaluation of the overlap integral is given in Ref. [1]. The results are lengthy expressions whose essential components are the generalized Laguerre functions 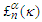 whose argument
whose argument 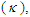 index
index 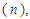 and order
and order 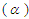 are given by
are given by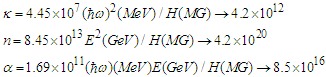 | (2) |
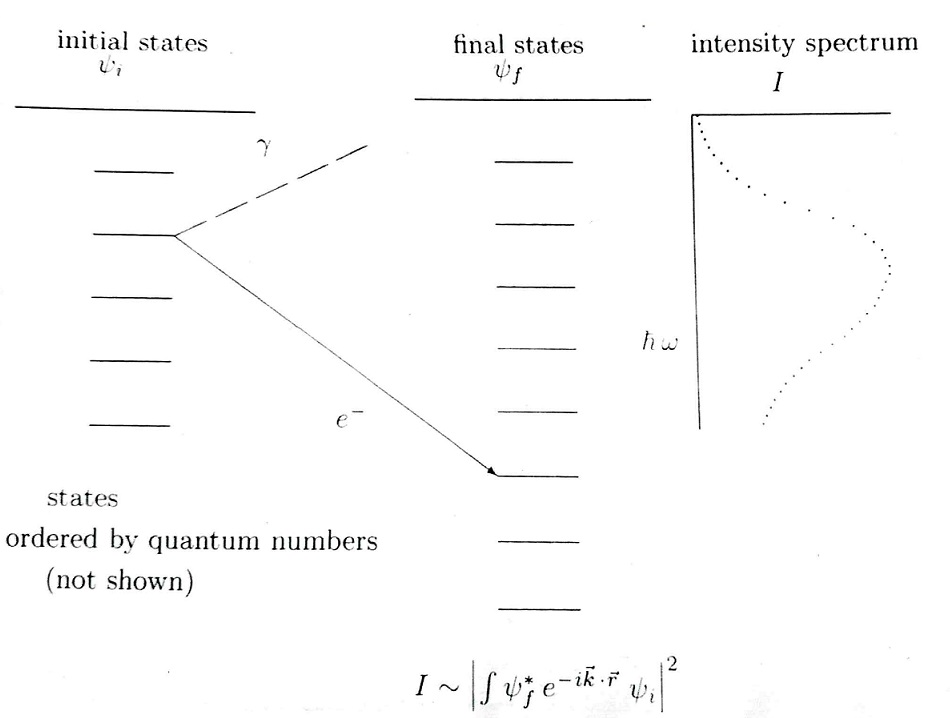 | Figure 2. Schematic for Photon Emission |
The special values correspond to the physical parameters 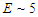 TeV,
TeV, 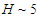 MG, and photon energies
MG, and photon energies 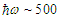 MeV. Clearly, a direct numerical evaluation of the Laguerre functions is not feasible and it is necessary to resort to asymptotic expansions. In Ref. [1] this next step utilized the expansions developed by Erdelyi and Swanson Ref. [2]. Unfortunately the end results also turned out to give unphysical predictions for the synchrotron radiation spectrum. A line-by-line check of the computations in [1] showed that errors occurred in the Erdelyi-Swanson asymptotic expansions. The situation is illustrated graphically in Fig. 3. The plots show the behavior of the Whittaker function
MeV. Clearly, a direct numerical evaluation of the Laguerre functions is not feasible and it is necessary to resort to asymptotic expansions. In Ref. [1] this next step utilized the expansions developed by Erdelyi and Swanson Ref. [2]. Unfortunately the end results also turned out to give unphysical predictions for the synchrotron radiation spectrum. A line-by-line check of the computations in [1] showed that errors occurred in the Erdelyi-Swanson asymptotic expansions. The situation is illustrated graphically in Fig. 3. The plots show the behavior of the Whittaker function 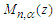 — which is closely related to the Laguerre function — for modest values of the index and order;
— which is closely related to the Laguerre function — for modest values of the index and order; 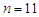 and
and 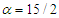 . Obviously, even for these small parameter values there is no useful resemblance between the Erdelyi-Swanson asymptotic expansion
. Obviously, even for these small parameter values there is no useful resemblance between the Erdelyi-Swanson asymptotic expansion  and the exact result
and the exact result  . Overcoming these difficulties required the development of new asymptotic expansions for the Whittaker functions, including rigorous error bounds [3]. Fig. 3 shows that the new expansion
. Overcoming these difficulties required the development of new asymptotic expansions for the Whittaker functions, including rigorous error bounds [3]. Fig. 3 shows that the new expansion  is a close fit to the exact result
is a close fit to the exact result 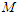 , and this improvement also holds for large parameter values such as those in Eq.(2). The complete calculation of the overlap integrals then yields new results for the synchrotron radiation spectrum.
, and this improvement also holds for large parameter values such as those in Eq.(2). The complete calculation of the overlap integrals then yields new results for the synchrotron radiation spectrum.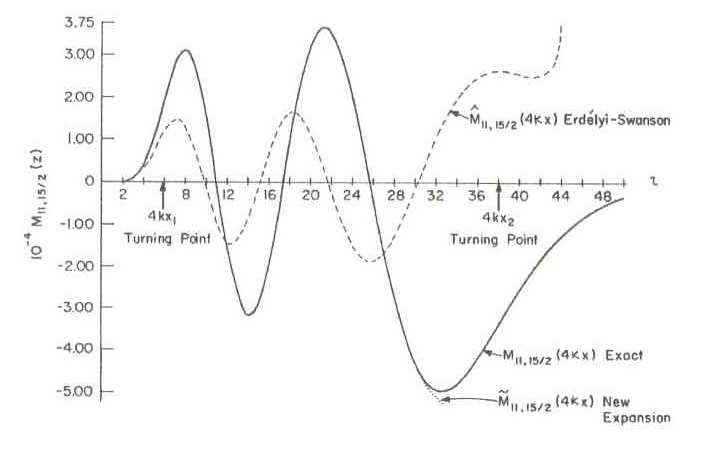 | Figure 3. Comparison of the exact value of M11,15/2 with the new and Erdelyi-Swanson Asymptotic Expression |
2. The Synchrotron Radiation Spectrum
The detailed derivation of the uniform Whittaker asymptotic expansion is given in Ref. [3]. Here it is sufficient to note that the essential idea is to use sequential or telescoping expansions. Specifically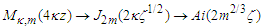 | (3) |
The argument of the Airy function contains the factor 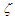 .
.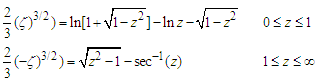 | (4) |
The auxiliary variable 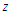 is determined by the argument of the Whittaker function. In principle this ‘double descent’ can be extended another step because the Airy function can be approximated by
is determined by the argument of the Whittaker function. In principle this ‘double descent’ can be extended another step because the Airy function can be approximated by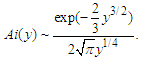 | (5) |
Extensive tabulations of the Airy function are also available. Fig. 4 gives an indication of the trend of the results by comparing the classical and quantum mechanical radiation rates as functions of the dimensionless parameter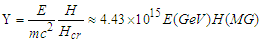 | (6) |
The quantum features enter the calculation through the scale of the magnetic field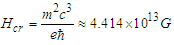 | (7) |
Earlier work attempted to gauge the deviations from the classical results by successive expansions in the quantum parameter 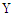 . As shown in Fig. 4 these computations were confused by the fact that the second order
. As shown in Fig. 4 these computations were confused by the fact that the second order 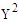 corrections appeared to dominate the first order
corrections appeared to dominate the first order 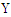 corrections. Clarity was eventually achieved by comparison with the ‘exact’ results, where ‘exact’ refers to spectral calculations utilizing the new asymptotic expansions.
corrections. Clarity was eventually achieved by comparison with the ‘exact’ results, where ‘exact’ refers to spectral calculations utilizing the new asymptotic expansions.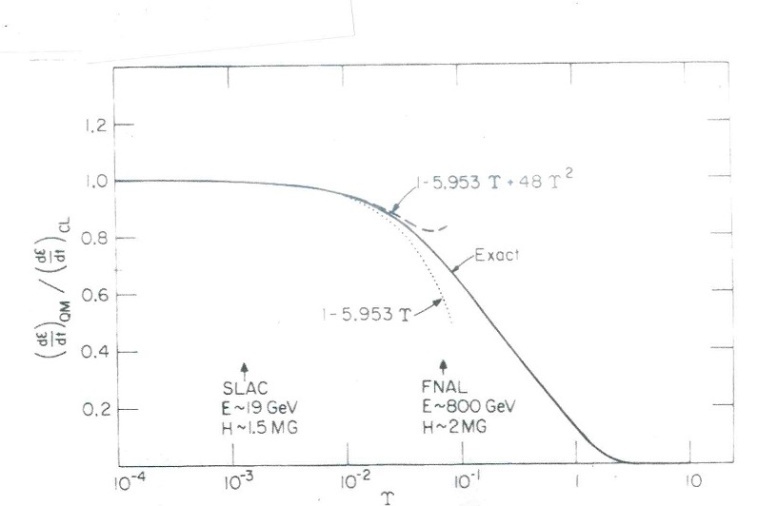 | Figure 4. Aftermaths of SLAC |
Fig. 5 shows the upper end of the synchrotron spectrum for fairly demanding technical conditions; i.e. 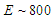 GeV,
GeV, 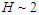 MG, and
MG, and 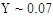 Evidently most of the classical result falls below 300 GeV and so there is no significant violation of energy conservation. The plot shows that it would be very difficult to distinguish between the classical and quantum mechanical spectral shapes.
Evidently most of the classical result falls below 300 GeV and so there is no significant violation of energy conservation. The plot shows that it would be very difficult to distinguish between the classical and quantum mechanical spectral shapes.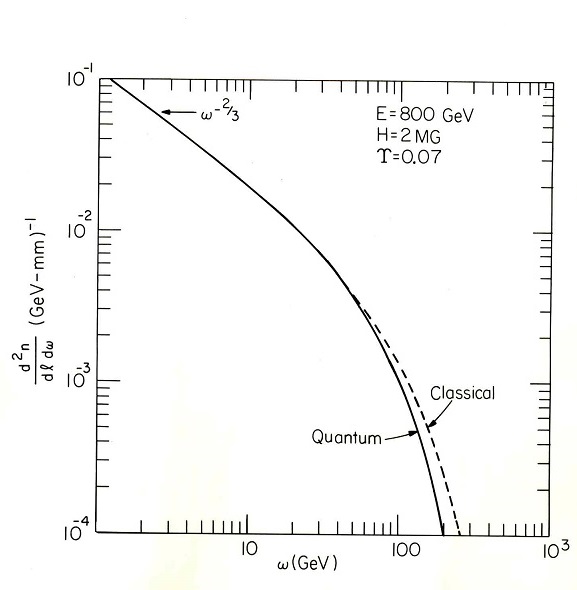 | Figure 5. Classical versus quantum radiation spectrum |
Fig. 6 displays the situation for still more extreme — but technically feasible — parameter values 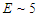 TeV,
TeV, 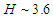 MG, and
MG, and 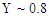 . Now a significant portion of the classical spectrum extends above the energy conservation limit
. Now a significant portion of the classical spectrum extends above the energy conservation limit 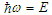 , and accordingly the classical predictions have to be discarded as unphysical. By contrast, the quantum mechanical spectrum (
, and accordingly the classical predictions have to be discarded as unphysical. By contrast, the quantum mechanical spectrum (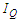 ) cuts off at
) cuts off at 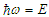 as it should. Furthermore, the maximun of the radiation rate has shifted upwards towards the tip.
as it should. Furthermore, the maximun of the radiation rate has shifted upwards towards the tip.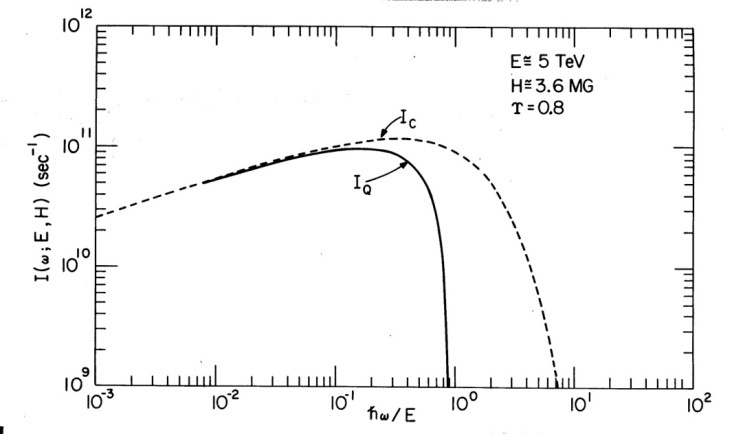 | Figure 6. Classical versus quantum spectra |
The character of the radiation is altered even more drastically in the extreme quantum regime.Fig. 7 shows that when 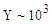 , which may occur in magnetars, the quantum radiation spectrum has increased monotonically with energy to a maximum at the tip
, which may occur in magnetars, the quantum radiation spectrum has increased monotonically with energy to a maximum at the tip 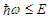 .
.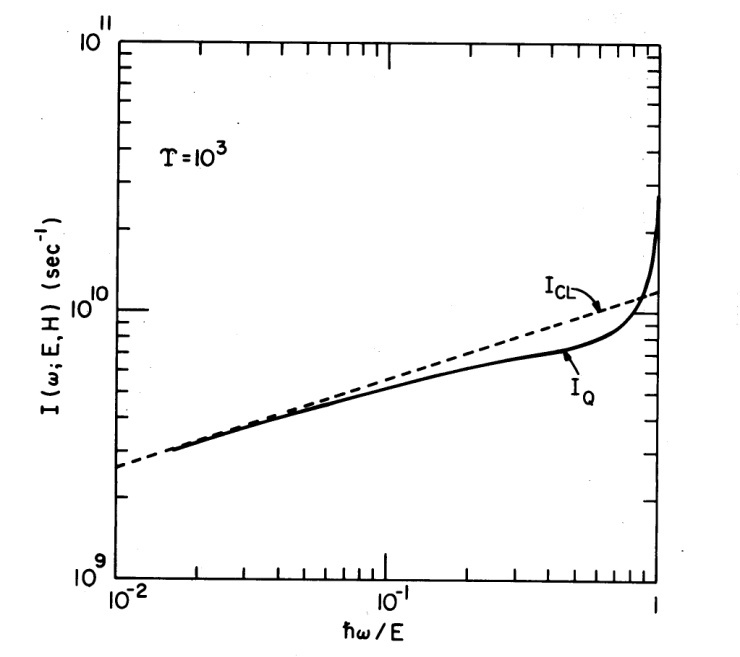 | Figure 7. Classical versus quantum radiation spectrum |
An overview of the various field and energy combinations determining the values of 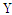 is given in Fig 8. The ‘VBA’ point refers to the parameter values associated with a ‘Very Big Accelerator’. To date this project has been approximated by the construction of the ‘Large Hadron Collider’ (
is given in Fig 8. The ‘VBA’ point refers to the parameter values associated with a ‘Very Big Accelerator’. To date this project has been approximated by the construction of the ‘Large Hadron Collider’ (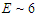 TeV) at CERN. Due to their speculative status magnetars have been omitted from the diagram Ref. [4].
TeV) at CERN. Due to their speculative status magnetars have been omitted from the diagram Ref. [4].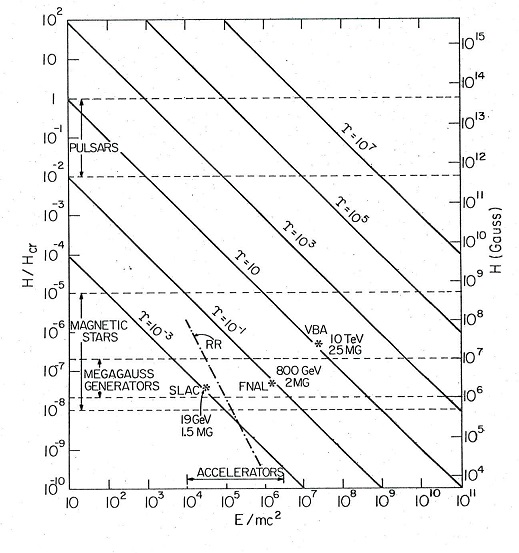 | Figure 8. Overview |
Synchrotron radiation is widely used in medicine and in industrial fabrication; but the SLAC point at 19 GeV, 1.5 MG, and 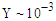 represents the only demonstration of the process under robust conditions. The details of this experiment are described in Refs. [5] and [6]. The essential point is to shoot a single compact beam pulse of width 1.3 mm containing 106 electrons through a coil with 2 mm entrance and exit holes.Fig. 9 shows that the timing sequence is arranged so that the beam pulse passes through the coil just as the magnetic field reaches its peak value of 1.5 MG. The resultant photon spray is incident on an Ilford G-5 nuclear emulsion target where about 0.5% of the photons convert into
represents the only demonstration of the process under robust conditions. The details of this experiment are described in Refs. [5] and [6]. The essential point is to shoot a single compact beam pulse of width 1.3 mm containing 106 electrons through a coil with 2 mm entrance and exit holes.Fig. 9 shows that the timing sequence is arranged so that the beam pulse passes through the coil just as the magnetic field reaches its peak value of 1.5 MG. The resultant photon spray is incident on an Ilford G-5 nuclear emulsion target where about 0.5% of the photons convert into 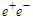 pairs. Microscopic measurements of the multiple scattering of the pairs in the emulsion can then be calibrated to yield the incident photon energies Ref. [7]. The final results for the synchrotron spectrum are shown in Fig. 10. There is satisfactory agreement between experiment and theory.
pairs. Microscopic measurements of the multiple scattering of the pairs in the emulsion can then be calibrated to yield the incident photon energies Ref. [7]. The final results for the synchrotron spectrum are shown in Fig. 10. There is satisfactory agreement between experiment and theory.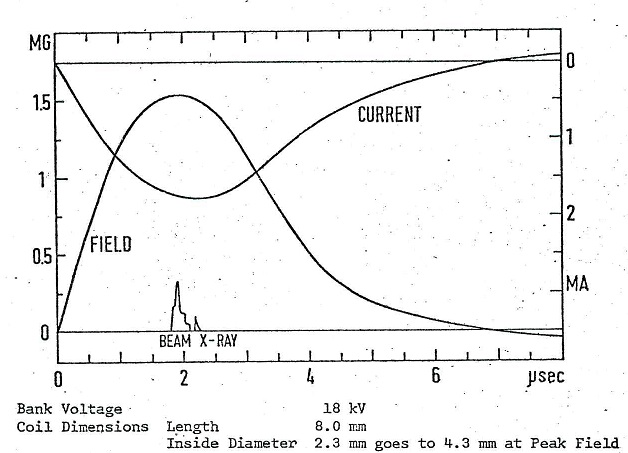 | Figure 9. Timing Sequence |
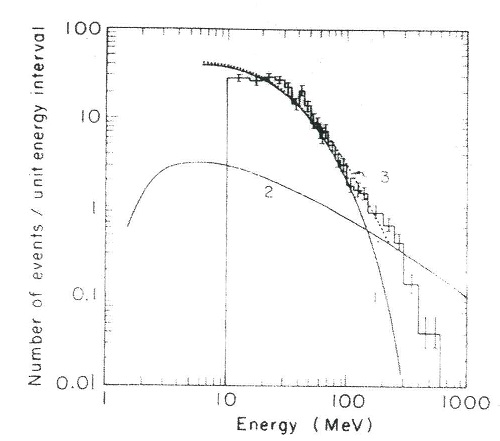 | Figure 10. 1. Theoretical prediction, 2. Beam Halo, 3. Measured Spectrum |
Note
1. The kinematics of the synchrotron radiation emitted when electrons traverse a magnetic field are shown in Fig. 1.
References
| [1] | Quantum Modifications in Magnetic Bremsstrahlung. H.G. Latal and T. Erber, Annals of Physics (NY) 108 No. 2, 408-442 (1977). |
| [2] | Asymptotic Form of Whittaker’s Confluent Hypergeometric Function. A. Erdelyi and C. A. Swanson, Mem. Am. Math. Soc. No. 25 (1957). |
| [3] | Uniform Asymptotic Approximations for the Whittaker Function Mκ,m(z). G. B. Baumgartner Jr. Ph.D. Dissertation, Illinois Institute of Technology (1980). |
| [4] | The Strongest Magnets in the Cosmos. S. Zane and R. Turolla, Physics World 16 No. 1 36-40 (2003). |
| [5] | Experiments with Megagauss Targets at SLAC. F. Herlach, R. McBroom, T. Erber, J. J. Murray, and R. Gearhart, IEEE Trans. Nucl. Sci. NS-18, No. 13 809-814 (1973). |
| [6] | Eigenschrift: The End of the Classical Theories of Radiation Reaction. T. Erber, Doing Physics, 255-279 (ed) P. W. Johnson, IIT Press (2010). |
| [7] | Measurement of Magnetic Bremsstrahlung Spectrum and Pair Production Cross Sections. M. Mashkour, Phys. Rev. A8 No.5, 2342-2347 (1973). |



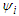 with energy
with energy 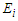 and momentum
and momentum 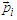 emits a photon
emits a photon 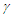 with energy
with energy 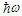 and momentum
and momentum 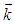 while transitioning to a final state
while transitioning to a final state 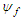 with energy
with energy 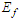 and momentum
and momentum 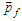 . In quantum mechanics energy and momentum conservation are built in from the outset:
. In quantum mechanics energy and momentum conservation are built in from the outset: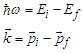
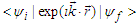 which, as indicated on Fig. 2, effectively determines the shape of the synchrotron radiation spectrum. The explicit evaluation of the overlap integral is given in Ref. [1]. The results are lengthy expressions whose essential components are the generalized Laguerre functions
which, as indicated on Fig. 2, effectively determines the shape of the synchrotron radiation spectrum. The explicit evaluation of the overlap integral is given in Ref. [1]. The results are lengthy expressions whose essential components are the generalized Laguerre functions 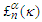 whose argument
whose argument 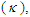 index
index 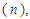 and order
and order 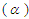 are given by
are given by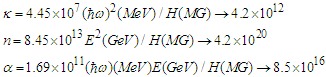

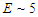 TeV,
TeV, 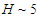 MG, and photon energies
MG, and photon energies 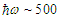 MeV. Clearly, a direct numerical evaluation of the Laguerre functions is not feasible and it is necessary to resort to asymptotic expansions. In Ref. [1] this next step utilized the expansions developed by Erdelyi and Swanson Ref. [2]. Unfortunately the end results also turned out to give unphysical predictions for the synchrotron radiation spectrum. A line-by-line check of the computations in [1] showed that errors occurred in the Erdelyi-Swanson asymptotic expansions. The situation is illustrated graphically in Fig. 3. The plots show the behavior of the Whittaker function
MeV. Clearly, a direct numerical evaluation of the Laguerre functions is not feasible and it is necessary to resort to asymptotic expansions. In Ref. [1] this next step utilized the expansions developed by Erdelyi and Swanson Ref. [2]. Unfortunately the end results also turned out to give unphysical predictions for the synchrotron radiation spectrum. A line-by-line check of the computations in [1] showed that errors occurred in the Erdelyi-Swanson asymptotic expansions. The situation is illustrated graphically in Fig. 3. The plots show the behavior of the Whittaker function 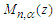 — which is closely related to the Laguerre function — for modest values of the index and order;
— which is closely related to the Laguerre function — for modest values of the index and order; 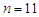 and
and 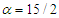 . Obviously, even for these small parameter values there is no useful resemblance between the Erdelyi-Swanson asymptotic expansion
. Obviously, even for these small parameter values there is no useful resemblance between the Erdelyi-Swanson asymptotic expansion 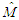 and the exact result
and the exact result 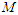 . Overcoming these difficulties required the development of new asymptotic expansions for the Whittaker functions, including rigorous error bounds [3]. Fig. 3 shows that the new expansion
. Overcoming these difficulties required the development of new asymptotic expansions for the Whittaker functions, including rigorous error bounds [3]. Fig. 3 shows that the new expansion 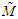 is a close fit to the exact result
is a close fit to the exact result 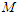 , and this improvement also holds for large parameter values such as those in Eq.(2). The complete calculation of the overlap integrals then yields new results for the synchrotron radiation spectrum.
, and this improvement also holds for large parameter values such as those in Eq.(2). The complete calculation of the overlap integrals then yields new results for the synchrotron radiation spectrum.
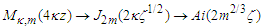
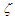 .
.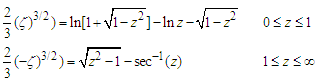
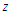 is determined by the argument of the Whittaker function. In principle this ‘double descent’ can be extended another step because the Airy function can be approximated by
is determined by the argument of the Whittaker function. In principle this ‘double descent’ can be extended another step because the Airy function can be approximated by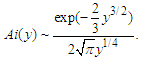
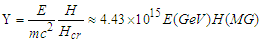
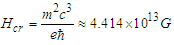
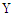 . As shown in Fig. 4 these computations were confused by the fact that the second order
. As shown in Fig. 4 these computations were confused by the fact that the second order 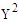 corrections appeared to dominate the first order
corrections appeared to dominate the first order 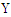 corrections. Clarity was eventually achieved by comparison with the ‘exact’ results, where ‘exact’ refers to spectral calculations utilizing the new asymptotic expansions.
corrections. Clarity was eventually achieved by comparison with the ‘exact’ results, where ‘exact’ refers to spectral calculations utilizing the new asymptotic expansions.
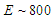 GeV,
GeV, 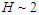 MG, and
MG, and 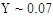 Evidently most of the classical result falls below 300 GeV and so there is no significant violation of energy conservation. The plot shows that it would be very difficult to distinguish between the classical and quantum mechanical spectral shapes.
Evidently most of the classical result falls below 300 GeV and so there is no significant violation of energy conservation. The plot shows that it would be very difficult to distinguish between the classical and quantum mechanical spectral shapes.
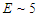 TeV,
TeV, 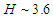 MG, and
MG, and 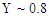 . Now a significant portion of the classical spectrum extends above the energy conservation limit
. Now a significant portion of the classical spectrum extends above the energy conservation limit 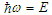 , and accordingly the classical predictions have to be discarded as unphysical. By contrast, the quantum mechanical spectrum (
, and accordingly the classical predictions have to be discarded as unphysical. By contrast, the quantum mechanical spectrum (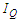 ) cuts off at
) cuts off at 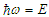 as it should. Furthermore, the maximun of the radiation rate has shifted upwards towards the tip.
as it should. Furthermore, the maximun of the radiation rate has shifted upwards towards the tip.
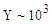 , which may occur in magnetars, the quantum radiation spectrum has increased monotonically with energy to a maximum at the tip
, which may occur in magnetars, the quantum radiation spectrum has increased monotonically with energy to a maximum at the tip 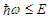 .
.
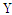 is given in Fig 8. The ‘VBA’ point refers to the parameter values associated with a ‘Very Big Accelerator’. To date this project has been approximated by the construction of the ‘Large Hadron Collider’ (
is given in Fig 8. The ‘VBA’ point refers to the parameter values associated with a ‘Very Big Accelerator’. To date this project has been approximated by the construction of the ‘Large Hadron Collider’ (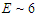 TeV) at CERN. Due to their speculative status magnetars have been omitted from the diagram Ref. [4].
TeV) at CERN. Due to their speculative status magnetars have been omitted from the diagram Ref. [4].
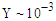 represents the only demonstration of the process under robust conditions. The details of this experiment are described in Refs. [5] and [6]. The essential point is to shoot a single compact beam pulse of width 1.3 mm containing 106 electrons through a coil with 2 mm entrance and exit holes.Fig. 9 shows that the timing sequence is arranged so that the beam pulse passes through the coil just as the magnetic field reaches its peak value of 1.5 MG. The resultant photon spray is incident on an Ilford G-5 nuclear emulsion target where about 0.5% of the photons convert into
represents the only demonstration of the process under robust conditions. The details of this experiment are described in Refs. [5] and [6]. The essential point is to shoot a single compact beam pulse of width 1.3 mm containing 106 electrons through a coil with 2 mm entrance and exit holes.Fig. 9 shows that the timing sequence is arranged so that the beam pulse passes through the coil just as the magnetic field reaches its peak value of 1.5 MG. The resultant photon spray is incident on an Ilford G-5 nuclear emulsion target where about 0.5% of the photons convert into 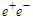 pairs. Microscopic measurements of the multiple scattering of the pairs in the emulsion can then be calibrated to yield the incident photon energies Ref. [7]. The final results for the synchrotron spectrum are shown in Fig. 10. There is satisfactory agreement between experiment and theory.
pairs. Microscopic measurements of the multiple scattering of the pairs in the emulsion can then be calibrated to yield the incident photon energies Ref. [7]. The final results for the synchrotron spectrum are shown in Fig. 10. There is satisfactory agreement between experiment and theory.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML