Liu Ke Dian
China
Correspondence to: Liu Ke Dian, China.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper aims to present the key points of the discovery of a universal static thermal repulsive force. The breaking through point is to clarify and verify the gas pressure being not caused by the collisions of gas molecule but by a universal static thermal repulsive conservative contact force. If collisions of gas molecules are really existed, they are not the decisive cause of producing gas pressure but the effect of the thermal repulsive force.
Keywords:
Gas pressure, Gas molecule collision, Atmosphere pressure, Stable of solar system, Boltzmann gas velocity distribution, Diffusion of small latex particles, Matter phase states
Cite this paper: Liu Ke Dian, Discovery of a Universal Static Thermal Repulsive Force, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 3, 2023, pp. 59-74. doi: 10.5923/j.ijtmp.20231303.01.
1. Introduction
The endeavors of research work of this paper are just following scientific methods and rules of science developments and scientific revolutions.1 Some rules of scientific revolutionThe emergence of a new theory breaks with one tradition of scientific practice and introduces a new one conducted under different rules and within a different universe of discourse, it occur only when the first tradition is felt to have gone badly astray. Anomaly appears only against the background provided by the paradigm; it provides an occasion for paradigm change. Discovery commences with the awareness of anomaly, i.e., with the recognition that nature has somehow violated the paradigm-induced expectations that govern normal science.Awareness of anomaly and the consequent change of paradigm often accompanies by resistance. An anomaly may evoke crisis. In scientific development the sense of malfunction that can lead to crisis is prerequisite to revolution.-Thames Kuhn. The Structure of Scientific Revolution2 Crucial anomalies of existed paradigm of kinetic theory of gasDaniel Bernoulli explained the experimental results of Boyle-Marriott Law, where PV = constant at constant temperature or PV = nRT by assuming that gas pressure is caused by the direct impact of particles on the walls of their container. Maxwell explained the properties of gas by assuming that the molecules undergo elastic collisions.The above explanations had been unchallenged, widely accepted ideas and paradigm.However, in practice, gas shows that it is a continuum medium with bulk modulus B. In adiabatic process, the energy of gas system manifests property of potential energy rather than kinetic energy and the forces of the molecules exerted each other manifest conservative force rather than momentum or impulse of collision.Gas molecule collision assertion and Boltzmann’s distribution function cannot directly explain any gas phenomena. Instead, almost every macroscopic and microscopic physical phenomena and principle of gas can be explained by the newly discovered universal thermal repulsive force (field).3 New rules to conduct innovative research and breaking through points of anomaliesThis paper verifies and corroborates the discovery of a universal static thermal repulsive force through analyzing the following main points (of anomalies or discrepancies):1. Based on general laws of elastic collision, the gas molecules motions must be oblique collisions that cannot maintain Maxwell-Boltzmann distribution function rather than head-on collisions.2. According to Rutherford’s experiment, molecules are not elastic rigid ball, only the nucleus of atom is elastic ball, so the so called Mean-Free-Path is pseudo science.3. Bernoulli Equation and its applications contradict and factually falsify the energy equations of kinetic theory of gas which are derived from Boltzmann’s velocity distribution law.4. Dalton’s law of partial pressures and Amagat’s law of partial volumes imply the gas molecules are point source of (thermal) repulsive force.5. The fact of the sound wave of gases being as longitudinal wave is contradictory to (and falsifies) Boltzmann’s distribution.6. Applications of dynamic gas bearing and static gas bearing in industries falsify the gas collision notion and the Boltzmann distribution law.7. Decisive causal of atmospheric pressure being weight of gases molecule layers contradicts the gas molecule collision assertion and implies existence of thermal repulsive contact force.8. If there are only the centrifugal forces to balance the universal gravitational forces between the Sun and planets, then the solar system will be in an unstable equilibrium. This implies that a repulsive conservative force between the Sun and planets is ignored or overlooked.9. Black hole and plasma can be explained as another two matter phase states other than the existed three phase states corroborate the existence of a universal static thermal repulsive force.10. Diffusion effect corroborates the thermal repulsive force.11. Peltier effect of semiconductor refrigeration can be re-explained by the discovery of thermal repulsive force theory corroborates electrons are also point source of thermal repulsive force.12. Solar wind corroborates that a thermal repulsive force of Sun is exerting on its surrounding plasmas.13. The universal thermal repulsive force can explain the reason why the Earth is orbiting the Sun in an elliptical orbit.
2. Theoretically and Practically Refuting the Assertion of Gas Molecule Collisions Causing Pressure and the Maxwell-Boltzmann Gas Velocity Distribution Function
Section 1 Briefing the Maxwell-Boltzmann gas velocity distribution functionThe Maxwell-Boltzmann distribution function is 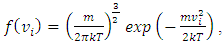 i = x, y, z (- ∞ < vi < + ∞), where k is the Boltzmann constant, v is the molecular speed of a molecule, m is the mass of the molecule, and T is the temperature of the gas. The mean molecular speed
i = x, y, z (- ∞ < vi < + ∞), where k is the Boltzmann constant, v is the molecular speed of a molecule, m is the mass of the molecule, and T is the temperature of the gas. The mean molecular speed 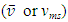 is the mathematical average of the speed distribution
is the mathematical average of the speed distribution 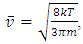 the root-mean-square speed
the root-mean-square speed 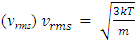 . The total force exerted by the molecules can be expressed in
. The total force exerted by the molecules can be expressed in 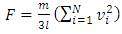 . The total force on the wall of the container then can be written as
. The total force on the wall of the container then can be written as 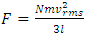 . The pressure then be written as
. The pressure then be written as 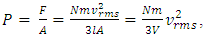 where A = the area on which force is exerted, V = the volume. Since Nm stands for the total mass of the gas, then the density of the gas is ρ = Nm/V and
where A = the area on which force is exerted, V = the volume. Since Nm stands for the total mass of the gas, then the density of the gas is ρ = Nm/V and 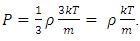 Equation
Equation 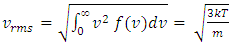 can be rewritten as
can be rewritten as 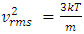 or
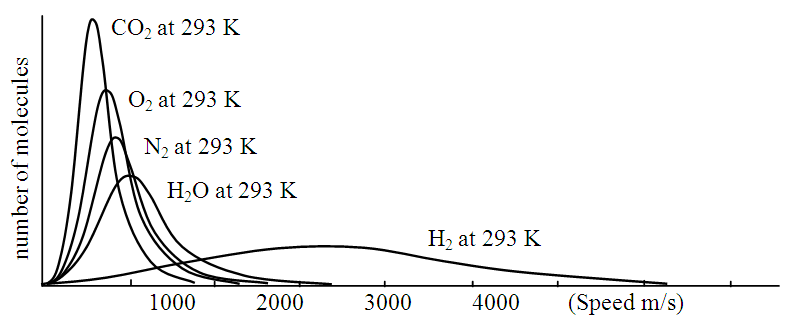
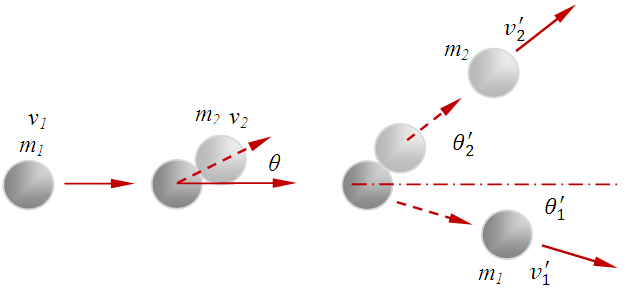
or 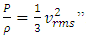 .Section 2 General laws of elastic collision contradict and falsify Maxwell-Boltzmann gas velocity distribution functionAccording to Boltzmann’s distribution function, different gas molecules in a mixture have varying speed distributions, as shown in Fig.1.1. However, in reality, the collisions of gases molecules (if really occur) must be oblique collisions rather than head-on collision, as shown in Fig.1.2. Study of universal situations of oblique elastic collisions, when m2 = m1, then
.Section 2 General laws of elastic collision contradict and falsify Maxwell-Boltzmann gas velocity distribution functionAccording to Boltzmann’s distribution function, different gas molecules in a mixture have varying speed distributions, as shown in Fig.1.1. However, in reality, the collisions of gases molecules (if really occur) must be oblique collisions rather than head-on collision, as shown in Fig.1.2. Study of universal situations of oblique elastic collisions, when m2 = m1, then 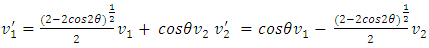 | (1.2.1) |
When m2 ≠ m1, for example m2 = 𝜷m1, then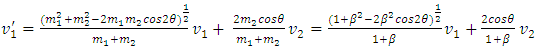 | (1.2.2) |
 | Figure 1.1. Mixture gases speed distribution |
 | Figure 1.2 |
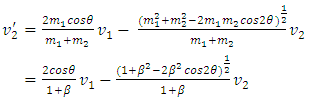 | (1.2.3) |
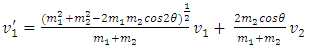 | (1.2.4) |
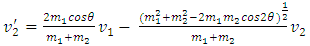 | (1.2.5) |
2.2. Analysis and conclusionFrom (1.2.1) to (1.2.5), since 𝜷 can be any value (1 < 𝜷 < 100), and cos2θ can be any value in a range of -1 to 1, therefore the values of 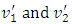 will be any value. Assuming that the gas molecules are colliding continuously, the final result is that all the velocities of the gas molecules will tend to equal, and is equal to the mean speed i.e.,
will be any value. Assuming that the gas molecules are colliding continuously, the final result is that all the velocities of the gas molecules will tend to equal, and is equal to the mean speed i.e., 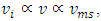 (0<i<∞). Thus the oblique collisions of gas molecules must spoil the Boltzmann’s distribution.This is one anomaly that shows the Boltzmann’s velocity distribution function can never be maintained.Therefore, there are no elastic collisions between gas molecules, if some collision is really existed, it must not be the decisive factor of air pressure.Section 3 Rutherford’s gold foil experiment (1911) show that atoms and molecules are not elastic rigid balls and have no chance to undergo elastic collision According to Rutherford’s gold foil experiment (1911), the atomic volume of the gold is about VA =10-29 m3 and that of its nucleus is only VN = 10-42 m3.The atom diameter of gold compared to the diameter of its nucleus is DA / DN = (VA /VN)1/3=21,544.3.Diameter of the soft shell (electron cloudy) of the atom is 21,544.3 times bigger than its hardcore nucleus.Therefore the atoms and molecules are not rigid balls! The so-called gas molecule collisions (if they occur) only happen between the outer shells of electron clouds of atoms, which are definitely not elastic collisions. It is important to note that the speed of atoms or molecules of gases cannot be (the speed in Rutherford’ experiment) 2*107 m/s.Firstly, it is worthwhile to notice that the effective diameter of molecules d used to calculate effective collision area is 104 times much larger than the Rutherford’s gold foil experimental data of nucleus diameter. Then the so called mean-free-path of nucleus (hardcore) is almost infinite, therefore there is no chance for gas molecules to collide each other.Secondly, when temperature is in the range of 200 -1000K, the relative velocities are at most
(0<i<∞). Thus the oblique collisions of gas molecules must spoil the Boltzmann’s distribution.This is one anomaly that shows the Boltzmann’s velocity distribution function can never be maintained.Therefore, there are no elastic collisions between gas molecules, if some collision is really existed, it must not be the decisive factor of air pressure.Section 3 Rutherford’s gold foil experiment (1911) show that atoms and molecules are not elastic rigid balls and have no chance to undergo elastic collision According to Rutherford’s gold foil experiment (1911), the atomic volume of the gold is about VA =10-29 m3 and that of its nucleus is only VN = 10-42 m3.The atom diameter of gold compared to the diameter of its nucleus is DA / DN = (VA /VN)1/3=21,544.3.Diameter of the soft shell (electron cloudy) of the atom is 21,544.3 times bigger than its hardcore nucleus.Therefore the atoms and molecules are not rigid balls! The so-called gas molecule collisions (if they occur) only happen between the outer shells of electron clouds of atoms, which are definitely not elastic collisions. It is important to note that the speed of atoms or molecules of gases cannot be (the speed in Rutherford’ experiment) 2*107 m/s.Firstly, it is worthwhile to notice that the effective diameter of molecules d used to calculate effective collision area is 104 times much larger than the Rutherford’s gold foil experimental data of nucleus diameter. Then the so called mean-free-path of nucleus (hardcore) is almost infinite, therefore there is no chance for gas molecules to collide each other.Secondly, when temperature is in the range of 200 -1000K, the relative velocities are at most 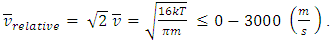 The relative velocities:
The relative velocities: 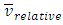 is (<<) much lower than 2*107 m/s, the velocity of the protons in Rutherford’s gold foil experiment.This is one anomaly that verifies there being no elastic collisions between gas molecules at all. Factually, the gas molecules are laid in a relative static equilibrium, they never have free path.Therefore, there is no elastic collision between gas molecules at all, if there is some collision, their velocities are very low and MFP is almost infinite, therefore it must not be the decisive factor of air pressure.Section 4 Bernoulli Equation contradicts the gas kinetic energy formula derived from Boltzmann’s velocity distributionThe Bernoulli equation is based on the energy conservation law and mass conservation law and has been a verified truth by scientific research and industrial technologies in macroscopic domain for hundreds of years. The energy of gas flow in pipe of Bernoulli equation is
is (<<) much lower than 2*107 m/s, the velocity of the protons in Rutherford’s gold foil experiment.This is one anomaly that verifies there being no elastic collisions between gas molecules at all. Factually, the gas molecules are laid in a relative static equilibrium, they never have free path.Therefore, there is no elastic collision between gas molecules at all, if there is some collision, their velocities are very low and MFP is almost infinite, therefore it must not be the decisive factor of air pressure.Section 4 Bernoulli Equation contradicts the gas kinetic energy formula derived from Boltzmann’s velocity distributionThe Bernoulli equation is based on the energy conservation law and mass conservation law and has been a verified truth by scientific research and industrial technologies in macroscopic domain for hundreds of years. The energy of gas flow in pipe of Bernoulli equation is 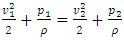 . The equation applied in pressure sensor and flow meter is expressed as
. The equation applied in pressure sensor and flow meter is expressed as 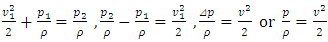 . The expression
. The expression 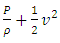 is total energy. Expressions
is total energy. Expressions 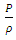 and
and 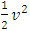 are partial energies which can be converted reversible. However, in gas molecules collision theory, gas pressure is expressed as
are partial energies which can be converted reversible. However, in gas molecules collision theory, gas pressure is expressed as 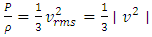 and
and 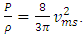 The problems are:1. In practical sense, being in any direction with equal probability, the velocities vrms and vms of the microscopic kinetic energies
The problems are:1. In practical sense, being in any direction with equal probability, the velocities vrms and vms of the microscopic kinetic energies 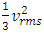 and
and 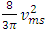 cannot automatically immediately convert to the velocities v (being in one direction along the delta pressure Δ P difference) of the macroscopic dynamic energy
cannot automatically immediately convert to the velocities v (being in one direction along the delta pressure Δ P difference) of the macroscopic dynamic energy 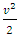 .2. Based on the assumption of kinetic theory “the forces between molecules are negligible except during a collision,” thus there will be no force between the molecules to transmit the Δ P each other in Bernoulli equation.3. If the masses of gas molecules are same, then the value of the microscopic mean speed
.2. Based on the assumption of kinetic theory “the forces between molecules are negligible except during a collision,” thus there will be no force between the molecules to transmit the Δ P each other in Bernoulli equation.3. If the masses of gas molecules are same, then the value of the microscopic mean speed 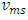 must be equal to the value of the macroscopic speed
must be equal to the value of the macroscopic speed 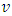 . When the microscopic energy
. When the microscopic energy  is converted to macroscopic energy
is converted to macroscopic energy 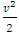 in Bernoulli equation, there is an energy difference between
in Bernoulli equation, there is an energy difference between 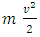 and
and 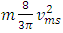 . This is theoretically and practically contrary to the energy conservation law! This is one anomaly that falsifies the Boltzmann’s distribution.4. The practicable industry technologies of pressure sensors such as the Pitot tube and the Venturi tube being the application of Bernoulli equation are the direct evidences that falsifies the assertion of pressure being caused by collision. Section 5 Dalton’s law of partial pressures actually imply the existence of thermal repulsive forces between gas molecules Dalton’s law of partial pressure states that the total pressure is the sum of the partial pressures of the individual gases.5.1. Analysis and re-explanation of Dalton’s law with conclusionSubstituting Dalton’s law of partial pressures is
. This is theoretically and practically contrary to the energy conservation law! This is one anomaly that falsifies the Boltzmann’s distribution.4. The practicable industry technologies of pressure sensors such as the Pitot tube and the Venturi tube being the application of Bernoulli equation are the direct evidences that falsifies the assertion of pressure being caused by collision. Section 5 Dalton’s law of partial pressures actually imply the existence of thermal repulsive forces between gas molecules Dalton’s law of partial pressure states that the total pressure is the sum of the partial pressures of the individual gases.5.1. Analysis and re-explanation of Dalton’s law with conclusionSubstituting Dalton’s law of partial pressures is 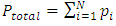 into ideal gas equation
into ideal gas equation 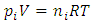 and
and 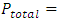
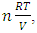 yields
yields 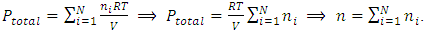 The mole numbers of individual gases can be any number (0 < ni < n), can approach to 0.Thus, ni can be 1 (a single molecule). The
The mole numbers of individual gases can be any number (0 < ni < n), can approach to 0.Thus, ni can be 1 (a single molecule). The 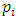 in the equation
in the equation 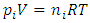 is representing the static pressure of any numbers even one single gas molecule.Therefore, every gas molecule is an independent pressure source that must be in a force equilibrium state with same size of mechanical radius on which the molecules have same static pressure interacting each other to form the total pressure of the mixture of gases. 5.2. Dalton’s partial pressures law manifests a static mechanical repulsive force molecule modelConspicuously, the Dalton’s law of partial gas pressure clearly and accurately shows us that:1. Every gas molecule is a point source of repulsive force field which is a mechanical pressure ball supporting the total pressure just as molecules of a liquid does. 2. Every molecule is acting and reacting with other molecules in static repulsive forces equilibrium statically. Section 6 Amagat’s partial volume law imply the gas molecules are point source of repulsive force 6.1. Amagat’s law contradicts the gas molecule collision notion and the Boltzmann’s distributionAmagat’s law states that the partial volume, vi, of an ideal gas (i) in a mixture of ideal gases is equal to the volume that gas (i) would occupy if it were alone and was at the pressure and temperature of the gas mixture. Substituting
is representing the static pressure of any numbers even one single gas molecule.Therefore, every gas molecule is an independent pressure source that must be in a force equilibrium state with same size of mechanical radius on which the molecules have same static pressure interacting each other to form the total pressure of the mixture of gases. 5.2. Dalton’s partial pressures law manifests a static mechanical repulsive force molecule modelConspicuously, the Dalton’s law of partial gas pressure clearly and accurately shows us that:1. Every gas molecule is a point source of repulsive force field which is a mechanical pressure ball supporting the total pressure just as molecules of a liquid does. 2. Every molecule is acting and reacting with other molecules in static repulsive forces equilibrium statically. Section 6 Amagat’s partial volume law imply the gas molecules are point source of repulsive force 6.1. Amagat’s law contradicts the gas molecule collision notion and the Boltzmann’s distributionAmagat’s law states that the partial volume, vi, of an ideal gas (i) in a mixture of ideal gases is equal to the volume that gas (i) would occupy if it were alone and was at the pressure and temperature of the gas mixture. Substituting 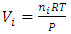 and
and 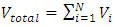 into ideal gas equation we have:
into ideal gas equation we have: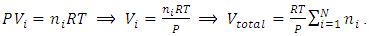 Amagat’s law shows that the total volume is proportional to the total number of molecules of gases. The mole numbers, ni, of an individual gas can be any number (0 < ni < n), can approach to 0. Therefore, ni = 0, 1, 2, 3, and etc. This implies that the total gas volume is the sum of volumes of every single molecule of gas.6.2. The Amagat’s law manifests and depicts the thermal repulsive force molecule modelConspicuously, with
Amagat’s law shows that the total volume is proportional to the total number of molecules of gases. The mole numbers, ni, of an individual gas can be any number (0 < ni < n), can approach to 0. Therefore, ni = 0, 1, 2, 3, and etc. This implies that the total gas volume is the sum of volumes of every single molecule of gas.6.2. The Amagat’s law manifests and depicts the thermal repulsive force molecule modelConspicuously, with 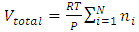 , the Amagat’s law of partial gas volume clearly and accurately tells us that every gas molecule is an independent point source of repulsive force.Every molecule is a mechanical force field (pressure) ball with mechanical radius, r, and effective static mechanical volume
, the Amagat’s law of partial gas volume clearly and accurately tells us that every gas molecule is an independent point source of repulsive force.Every molecule is a mechanical force field (pressure) ball with mechanical radius, r, and effective static mechanical volume 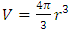 . In atmosphere and in practical calculation, the average volume or effect volume is
. In atmosphere and in practical calculation, the average volume or effect volume is 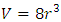 . The mechanical volume is proportional on its temperature, T, and does not depend on the mass of the molecule. Conclusions of analysis of Amagat’s law are exactly same as Dalton’s law, they are not repeated stating here.Section 7 Direct evidence of above deductionsOne assumption of the kinetic theory of gas is: “The number of molecules is large and the volume of the molecules is negligible when compared with the volume of the container.” This assumption is interpreted as that there must be adequate enough numbers of gas molecules to maintain a probability of Boltzmann’s distribution. Therefore there are three practical evidences at least.The first evidence is: when a gas container has a micrometer even nanometer scale crack, the pressure inside the crack is exact same as or identical to the pressure of the container. There is no enough numbers of gas molecules to maintain a Boltzmann’s distribution inside a micrometer or nanometers crack which is also a gas volume! Hence it is contact forces of the molecules acting as point sources of repulsive force just as Dalton’s partial pressure law and Amagat’ partial volume law described that produce and transmit the pressure inside and into the micrometer or nanometer scale crack!The second evidence is: inside a space suit, the air must be maintained an adequate pressure. As we know, the volume of space suit is very small, there is no enough volume of molecules to maintain Boltzmann’s distribution!The third evidence is: the clearances of applicable gas bearings are always in micrometer even nanometer scale, there are not enough molecules to maintain Boltzmann’s distribution. There is no molecules collision there at all; however, there is gas pressure much higher than ambient pressure in the gas bearing clearance. (We will discuss the details of gas bearings in Chapter Three of this paper).Therefore we know that it is the gas molecules acting as point source of repulsive contact force to transmit and maintain gas pressure into and inside the micro gas volumes rather than groundless momentums of collisions.These are anomalies that falsify gas molecules collision assertion.Therefore, there are no elastic collisions between gases molecules at all, if there is some, it must not be the decisive factor of air pressure.
. The mechanical volume is proportional on its temperature, T, and does not depend on the mass of the molecule. Conclusions of analysis of Amagat’s law are exactly same as Dalton’s law, they are not repeated stating here.Section 7 Direct evidence of above deductionsOne assumption of the kinetic theory of gas is: “The number of molecules is large and the volume of the molecules is negligible when compared with the volume of the container.” This assumption is interpreted as that there must be adequate enough numbers of gas molecules to maintain a probability of Boltzmann’s distribution. Therefore there are three practical evidences at least.The first evidence is: when a gas container has a micrometer even nanometer scale crack, the pressure inside the crack is exact same as or identical to the pressure of the container. There is no enough numbers of gas molecules to maintain a Boltzmann’s distribution inside a micrometer or nanometers crack which is also a gas volume! Hence it is contact forces of the molecules acting as point sources of repulsive force just as Dalton’s partial pressure law and Amagat’ partial volume law described that produce and transmit the pressure inside and into the micrometer or nanometer scale crack!The second evidence is: inside a space suit, the air must be maintained an adequate pressure. As we know, the volume of space suit is very small, there is no enough volume of molecules to maintain Boltzmann’s distribution!The third evidence is: the clearances of applicable gas bearings are always in micrometer even nanometer scale, there are not enough molecules to maintain Boltzmann’s distribution. There is no molecules collision there at all; however, there is gas pressure much higher than ambient pressure in the gas bearing clearance. (We will discuss the details of gas bearings in Chapter Three of this paper).Therefore we know that it is the gas molecules acting as point source of repulsive contact force to transmit and maintain gas pressure into and inside the micro gas volumes rather than groundless momentums of collisions.These are anomalies that falsify gas molecules collision assertion.Therefore, there are no elastic collisions between gases molecules at all, if there is some, it must not be the decisive factor of air pressure.
3. Sound Wave of Gases Falsifies the Gas Molecule Collision Assertion and Boltzmann’s Distribution (Kinetic Theory of Gases)
Section 1 Bulk Modulus B of gases applying in calculation of sound wave velocity contradicts Boltzmann’s distribution and manifests the existence of a conservative repulsive force between gas molecules1.1. Prevailing descriptionsBulk modulus characterizes the response of a substance to uniform squeezing or to a reduction in pressure when the object is placed in a partial vacuum. The elastic modulus is the ratio of the stress to the resulting strain 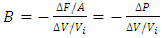 .The speed of sound waves depends on the compressibility and inertia of the medium. If the medium has a bulk modulus B and density ρ, the speed of sound waves in that medium is
.The speed of sound waves depends on the compressibility and inertia of the medium. If the medium has a bulk modulus B and density ρ, the speed of sound waves in that medium is 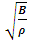 . A sound wave can be considered as either a displacement wave or a pressure wave. 1.2. DiscrepancyThe above descriptions of sound wave contradict and falsify the Boltzmann’s distribution and gas molecule collision assertion.The sound wave of gas of its media (gas) having bulk modulus B that manifests gas is continuum medium and pressure is effect of elasticity (conservative) contact repulsive forces of the medium.Force and pressure are instantaneous values to produce wave and propagate wave that cannot be cumulated by momentums during a time intervals. And the cumulative forces or cumulative momentums do not have instantaneous elastic property of bulk modulus B. Being wave energy, the sound of gases must be potential energy, however chaotic motion collisions of the gas molecules with each other are not conservative forces and do not result in potential energy, this is contradictory to that gases have bulk modulus B.Therefore there must be a repulsive conservative contact force or field of the continuum medium gas (with bulk modulus B,) i.e. there must be a universal (thermal) repulsive force (field) to transfer the compression and expansion of gas medium to propagate sound wave.Section 2 Sound wave being a longitudinal wave contradicts Boltzmann’s distribution and manifests the existence of a thermal repulsive force of gas molecules2.1. Prevailing descriptionsIf the gas molecules move randomly so that any molecule can move in any direction with equal probability as Boltzmann’s distribution described, then sound wave of gas will not be longitudinal wave, rather, it will be spherical wave that propagate in any directions including transversal direction!A sound wave of air is oscillator of compression and expansion of air element and is propagating in longitudinal direction.Both compressed regions of condensation and expanded rarefaction regions are continuously set up and move with a speed equal to the speed of sound in the medium.If Boltzmann’s distribution law or the kinetic theory of gases is tenable, the gas molecules will move randomly mean that any molecule can move in any direction with equal probability and their motion is extremely chaotic. Then the average value of v2 for all the molecules is related to the average values of
. A sound wave can be considered as either a displacement wave or a pressure wave. 1.2. DiscrepancyThe above descriptions of sound wave contradict and falsify the Boltzmann’s distribution and gas molecule collision assertion.The sound wave of gas of its media (gas) having bulk modulus B that manifests gas is continuum medium and pressure is effect of elasticity (conservative) contact repulsive forces of the medium.Force and pressure are instantaneous values to produce wave and propagate wave that cannot be cumulated by momentums during a time intervals. And the cumulative forces or cumulative momentums do not have instantaneous elastic property of bulk modulus B. Being wave energy, the sound of gases must be potential energy, however chaotic motion collisions of the gas molecules with each other are not conservative forces and do not result in potential energy, this is contradictory to that gases have bulk modulus B.Therefore there must be a repulsive conservative contact force or field of the continuum medium gas (with bulk modulus B,) i.e. there must be a universal (thermal) repulsive force (field) to transfer the compression and expansion of gas medium to propagate sound wave.Section 2 Sound wave being a longitudinal wave contradicts Boltzmann’s distribution and manifests the existence of a thermal repulsive force of gas molecules2.1. Prevailing descriptionsIf the gas molecules move randomly so that any molecule can move in any direction with equal probability as Boltzmann’s distribution described, then sound wave of gas will not be longitudinal wave, rather, it will be spherical wave that propagate in any directions including transversal direction!A sound wave of air is oscillator of compression and expansion of air element and is propagating in longitudinal direction.Both compressed regions of condensation and expanded rarefaction regions are continuously set up and move with a speed equal to the speed of sound in the medium.If Boltzmann’s distribution law or the kinetic theory of gases is tenable, the gas molecules will move randomly mean that any molecule can move in any direction with equal probability and their motion is extremely chaotic. Then the average value of v2 for all the molecules is related to the average values of 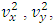 and
and 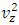 according to the expression
according to the expression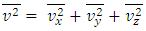 Because the motion is completely random, the average
Because the motion is completely random, the average 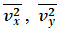 values and
values and 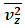 are equal to each other. The average molecular speed increase with increase of temperature, increase of temperature in turn produces an increase in pressure
are equal to each other. The average molecular speed increase with increase of temperature, increase of temperature in turn produces an increase in pressure 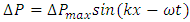 , where the pressure amplitude ΔPmax is the maximum change in pressure from the equilibrium value.2.2. ContradictionIf above prevailing assertions and descriptions of Boltzmann and kinetic theory are tenable, the sound wave of gas will propagate in a way like this:The compressed regions and expanded regions are continuously set up; therefore, result in temperature increasing and decreasing continuously accordingly that in turn produces an increase and decrease in pressure.If so, there are discrepancies:The gas molecules will move in any direction with equal probability, then the average values of
, where the pressure amplitude ΔPmax is the maximum change in pressure from the equilibrium value.2.2. ContradictionIf above prevailing assertions and descriptions of Boltzmann and kinetic theory are tenable, the sound wave of gas will propagate in a way like this:The compressed regions and expanded regions are continuously set up; therefore, result in temperature increasing and decreasing continuously accordingly that in turn produces an increase and decrease in pressure.If so, there are discrepancies:The gas molecules will move in any direction with equal probability, then the average values of 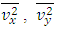 and
and 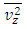 in equation
in equation 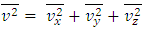 are equal to each other, which will result in equal temperature increase-decrease of molecules in x, y and z directions regions, thus in turn produces an increase-decrease in pressure in x, y and z directions regions.Thus it will produce
are equal to each other, which will result in equal temperature increase-decrease of molecules in x, y and z directions regions, thus in turn produces an increase-decrease in pressure in x, y and z directions regions.Thus it will produce 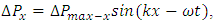
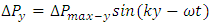 and
and 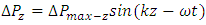 in x, y and z directions.Thus the sound wave will propagate not only in x (longitudinal) directions but also in all directions including y and z directions and any transversal direction.Hence, the phenomenon that the sound wave of gas being a longitudinal wave, is discrepancy or anomaly that theoretically and factually contradicts and falsifies the Boltzmann’s distribution law and the assertion of gas molecules collisions.
in x, y and z directions.Thus the sound wave will propagate not only in x (longitudinal) directions but also in all directions including y and z directions and any transversal direction.Hence, the phenomenon that the sound wave of gas being a longitudinal wave, is discrepancy or anomaly that theoretically and factually contradicts and falsifies the Boltzmann’s distribution law and the assertion of gas molecules collisions.
4. Practical Gas Bearings Technologies in Scientific Research and Industry Contradict the Gas Molecule Collision Theory
Section 1 Application of dynamic gas bearing in industries contradicts the gas collision notion and the Boltzmann’s velocity distribution functionDynamic gas bearing had been working well and has played a critical role in many industries for hundreds of years where gases are treated and considered as a continuum medium like other fluids. According to Reynolds, the fluid (gas) obeys Newton’s law of viscosity. The pressure is constant in the direction perpendicular to the laminar flow 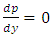 . The shearing stress can be defined as
. The shearing stress can be defined as 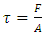 where A is the area of gas film, thus shear stress can be expressed:
where A is the area of gas film, thus shear stress can be expressed: 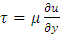 .1.1. Acting forces and pressure distribution analysisThe equation of the equilibrium of the forces in the direction of the flow is as follows
.1.1. Acting forces and pressure distribution analysisThe equation of the equilibrium of the forces in the direction of the flow is as follows 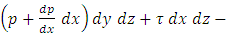
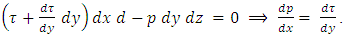 Substitution of τ from Newton’s law of viscosity,
Substitution of τ from Newton’s law of viscosity, 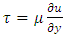 results in
results in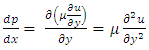 | (3.1.1) |
The velocity function is obtained by integrating the equation (3.1.1) twice with respect to y: 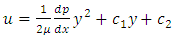 | (3.1.2) |
The constants of integration c1 and c2 can be determined from the boundary conditions,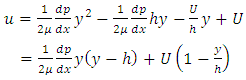 | (3.1.3) |
The total flow of the lubricant is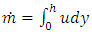 | (3.1.4) |
Substituting (3.1.3) and 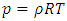 into (3.1.4) yields
into (3.1.4) yields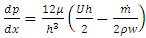 | (3.1.5) |
According to the assumption about compressibility of the lubricant, the flow 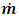 does not change in x direction
does not change in x direction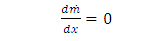 | (3.1.6) |
Differentiating the equation (3.1.5) with respect x and combining with (3.1.6) and ideal gas equation 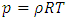 , results in:
, results in: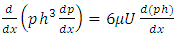 | (3.1.7) |
This is the Reynolds equation for one dimensional flow.1.2. Reynolds number of typical dynamic gas bearingRe is defined as Re = ρvL / μ, where ρ = density (kg/m3), v = velocity (m/s), L = characteristic length (m), μ = viscosity (N s/m2, Pa s). A Reynolds number less than or equal to 2100 indicates laminar flow.For a typical dynamic gas bearing application, the Reynolds number Re = 1.017, therefore it is laminar flow.1.3. Analysis and conclusion1) It is only the viscosity (μ) of a gas that causes the pressure gradient in a circumferential direction 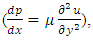 which is the basis and basic working conditions of the dynamic gas bearing. There is energy loss due to friction, then, there will be no Boltzmann’s velocity distribution!2) It is the journal speed, u, that generates the shear stress; therefore, the shear stress generates the pressure gradient. The pressure gradient, i.e., the pressure difference between the (gaps), clearance generates load capacity!If there are velocities of the Boltzmann distribution, the laminar flow of the gas will be spoilt, then, the air bearing will not work! Section 2 Static gas bearing technology contradicts the gas molecule collision notion2.1. Theoretical basic of static gas bearingThere is a significant disparity in the length scale which causes the fluids to flow in a geometry in which one dimension is significantly smaller than others. This is called thin film flow. According to Newton’s Law of Viscosity, the Stokes equation of a Newtonian fluid in Cartesian coordinates is expressed as
which is the basis and basic working conditions of the dynamic gas bearing. There is energy loss due to friction, then, there will be no Boltzmann’s velocity distribution!2) It is the journal speed, u, that generates the shear stress; therefore, the shear stress generates the pressure gradient. The pressure gradient, i.e., the pressure difference between the (gaps), clearance generates load capacity!If there are velocities of the Boltzmann distribution, the laminar flow of the gas will be spoilt, then, the air bearing will not work! Section 2 Static gas bearing technology contradicts the gas molecule collision notion2.1. Theoretical basic of static gas bearingThere is a significant disparity in the length scale which causes the fluids to flow in a geometry in which one dimension is significantly smaller than others. This is called thin film flow. According to Newton’s Law of Viscosity, the Stokes equation of a Newtonian fluid in Cartesian coordinates is expressed as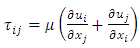 | (3.2.1) |
where μ is the viscosity of the fluid.The shearing stress can be defined as 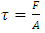 , shear stress can be expressed
, shear stress can be expressed 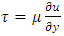 .The pressurized gas is fed from a central orifice into the central recess bearing. The shear stress balancing equation for the central recess bearing is
.The pressurized gas is fed from a central orifice into the central recess bearing. The shear stress balancing equation for the central recess bearing is 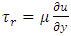 . The Reynolds equation reduces to
. The Reynolds equation reduces to 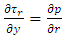 , where p is the pressure and τr is the shear stress in the radial direction.Assuming the element is in equilibrium, the fluid is Newtonian and
, where p is the pressure and τr is the shear stress in the radial direction.Assuming the element is in equilibrium, the fluid is Newtonian and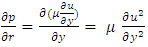 | (3.2.2) |
Also, the pressure is constant in the height and axi-symmetric 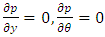 .Integrating in y twice time, obtains
.Integrating in y twice time, obtains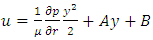 | (3.2.3) |
Substituting the boundary condition into (3.2.3), obtain: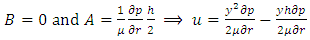 | (3.2.4) |
Mass flow rate is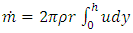 | (3.2.5) |
Substituting (3.2.4) into (3.2.5), yields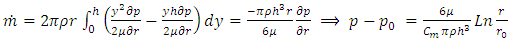 | (3.2.6) |
2.2. The above equation is contradicts the gas molecule collision notionIf assuming viscosity μ = 0, (according to gas molecule collision notion and Boltzmann’s velocity distribution function.) the right side of the equation 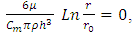 i.e., left side
i.e., left side 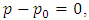 means either p = p0 or p = pambient = 0. Thus, the stiffness of the bearing is zero, the loading capacity is zero, and the bearing will not work at all.For a typical static gas bearing application, the Reynolds number is Re = 2πr*h*ρ*v/μ = 5.76.The Re is less than 2100. Therefore, it is laminar flow. Section 3 Conclusion1) Since gases have viscosity μ = 1.98E-5 (Pa s), there is no elastic collision between molecules of gas! 2) If there is chaotic motion, the gas fluid cannot form laminar flow. If there is no laminar flow, gas flow should not form or generate pressure gradient in radial direction, the derivative of pressure will be zero, thus there is no stiffness, no load capacity, and gas bearing will completely do not work at all! The practicable applications of gas bearings provide direct evidences that the air pressure can be maintained in the clearance of gas bearing without enough volume of molecules to maintain collisions.Therefore, there is no collision between molecules of gas at all. If there is some collision of gas molecules, it must not be the decisive factor of air pressure.These are anomalies that contradictory to and falsify the basic assumption of kinetic theory of gas thus directly falsify Boltzmann’s distribution law and the assertion of gas molecules collisions.
means either p = p0 or p = pambient = 0. Thus, the stiffness of the bearing is zero, the loading capacity is zero, and the bearing will not work at all.For a typical static gas bearing application, the Reynolds number is Re = 2πr*h*ρ*v/μ = 5.76.The Re is less than 2100. Therefore, it is laminar flow. Section 3 Conclusion1) Since gases have viscosity μ = 1.98E-5 (Pa s), there is no elastic collision between molecules of gas! 2) If there is chaotic motion, the gas fluid cannot form laminar flow. If there is no laminar flow, gas flow should not form or generate pressure gradient in radial direction, the derivative of pressure will be zero, thus there is no stiffness, no load capacity, and gas bearing will completely do not work at all! The practicable applications of gas bearings provide direct evidences that the air pressure can be maintained in the clearance of gas bearing without enough volume of molecules to maintain collisions.Therefore, there is no collision between molecules of gas at all. If there is some collision of gas molecules, it must not be the decisive factor of air pressure.These are anomalies that contradictory to and falsify the basic assumption of kinetic theory of gas thus directly falsify Boltzmann’s distribution law and the assertion of gas molecules collisions.
5. Decisive Causal of Atmospheric Pressure Contradicts the Gas Molecule Collision Assertion and Implies the Existence of Thermal Repulsive Force
Section 1 Depiction of element of air columnThe atmosphere of earth is formed of layers of gases due to gravitational force of earth. The analysis of an element of an air column is shown in Fig.4.1.“A given layer (element) of air must support the weight of the atmosphere all above it, the greater the altitude, the less the weight of the air above that layer, and the lower the pressure. Because the air is in static equilibrium, the magnitude of the upward force exerted on the bottom of this layer must exceed the magnitude of the downward force on the top of the layer, by an amount equal to the weight of gas in this thin layer.” [1] (21.1 MOLECULAR MODEL OF AN IDEAL GAS.)The weight of the element is 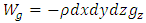 , the force between dz is
, the force between dz is 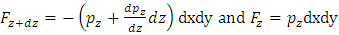 | (4.1) |
where Wg is the weight of the element, gz is the gravitation at the height z, and pz is the pressure at the height of z. In balancing the equation of forces, we obtain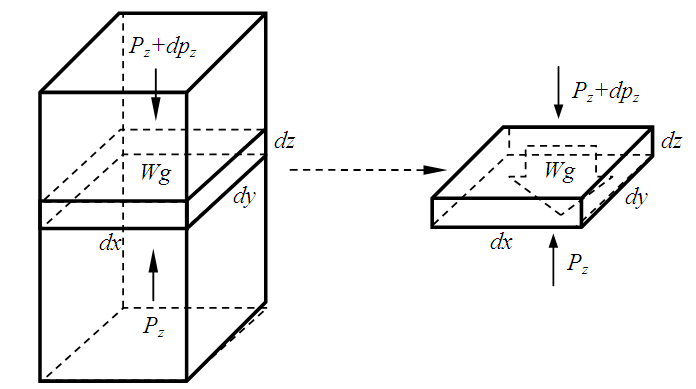 | Figure 4.1 |
 | (4.2) |
Simplifing (4.1) reduces to 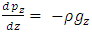 .The temperature T(h) at height h is given by
.The temperature T(h) at height h is given by 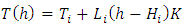 and the changes in gravitational force are less than 5% of height from 0km (sea level) to 100km. However, to pursue the most accurate results, we will still use the data from local gravity and temperatures.Taking different values of temperature and gravitational force of different altitudes into account, for convenience, z in the equation is replaced by altitude h, therefore, the equation is expressed as
and the changes in gravitational force are less than 5% of height from 0km (sea level) to 100km. However, to pursue the most accurate results, we will still use the data from local gravity and temperatures.Taking different values of temperature and gravitational force of different altitudes into account, for convenience, z in the equation is replaced by altitude h, therefore, the equation is expressed as 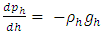 . Substituting
. Substituting 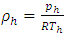 into
into 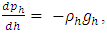 obtains
obtains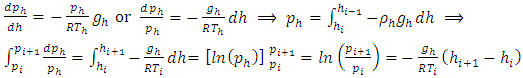 | (4.3) |
Calculation results of pressure for every layers is listed as below table
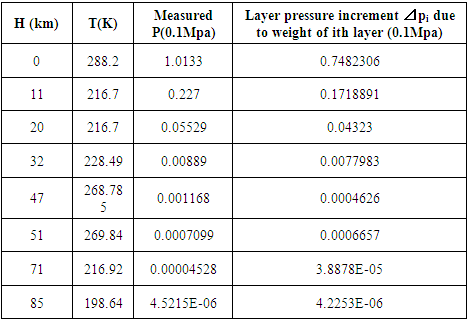 |
| |
|
Sum up all the ⊿pi results in the total pressure Pw at sea level caused by weight of gas layer: 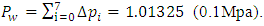 According to previous analysis, we can see clearly that the ideal gas equation is a manifestation of potential energy of the thermal repulsive force of gas. Considering gi ≈ constant g, calculating exponent of both side of the equation (5.3). From ideal gas equation we have
According to previous analysis, we can see clearly that the ideal gas equation is a manifestation of potential energy of the thermal repulsive force of gas. Considering gi ≈ constant g, calculating exponent of both side of the equation (5.3). From ideal gas equation we have 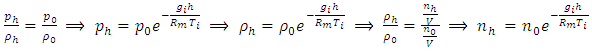 This expression means that gas molecules are cumulated layer by layer over the surface of earth in equilibrium of repulsive forces and gravitational forces result in the exponential form shown as Fig.4.2.
This expression means that gas molecules are cumulated layer by layer over the surface of earth in equilibrium of repulsive forces and gravitational forces result in the exponential form shown as Fig.4.2. | Figure 4.2. Atmosphere gas molecules distribution is in static equilibrium by mechanical volumes and in exponential form |
4.6. Analysis and conclusionThe value of measured pressure at sea level is: Pmeasured = 1.0133 (0.1Mpa).Compared to the calculated pressure caused by weight: Pweight = 1.01325(0.1Mpa).We can clearly see that the measured sea level pressure is exactly equal to the pressure being due to weight of atmosphere or gravitational force of earth. Therefore we see that: 1. At sea water surface of oceans of earth, if the gas molecules are colliding onto sea water; there should be inelastic collisions. Thus the gas molecules should be adhering to water, however, in fact not. Therefore the gas molecules do not collide onto the sea water but interact with the sea water and with each other by contact repulsive conservative force (field).2. It is the contact repulsive force sustains (reacts) and transmits pressure of the atmosphere in between sea water surface and gas molecules.The sea water support the weight of the atmosphere all above it, the lowest layer floating on the surface of sea water interact with sea water by contact repulsive force and interact with upper layers of air all above it. The layer above the lowest layer in turn interacts with the lowest layer and interacts with the layer above it and so on to form exponential distribution. 3. The pressure exponential form distribution of atmosphere is caused by density distribution; the density distribution is caused by weight (static macroscopic gravitational force) of gas layers. If the pressure is decided by collisions of molecules then there will be no the exponential distribution but a distribution only being proportional to temperature.4. Anywhere, anytime, the air is in static equilibrium between gravitational force and thermal repulsive contact force.5. Of course there are winds and air flow, but they are the effect of the conservative gravitational force and conservative repulsive force. In the wind, air flow and the exponential distribution, there is only energy transformation between macroscopic kinetic energy of wind speed and potential energy of the two conservative forces. The wind, air flow and the exponential distribution are all in macroscopic dynamic equilibrium and do nothing with so called microscopic collisions.This is one anomaly or discrepancy that falsifies the gas collision assertion.Therefore, there are no collisions between molecules of atmosphere and onto sea water surface. If there is some collision, it must not be the decisive factor of atmospheric pressure.
6. The stability of the solar system implies the existence of a static universal thermal repulsive force
Section 1 Briefing general laws (mathematical expressions) of the equilibrium of forces and conditionsAssume a system having one degree of freedom, r, evaluate the potential energy function V.1. Stable equilibrium: If an object is in a stable equilibrium, the center of gravity of the object will be altered when a disruptive force (i.e. pushing or pulling) is applied, but will return to its initial state upon the removal of the force. Mathematically, if V= V(r) is a minimum then 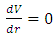 and
and 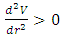 then the system is stable equilibrium.2. Unstable equilibrium: If an object is in an unstable equilibrium, the center of gravity will be altered when a disturbing force is applied, but cannot return to the original position upon removal of the force. Mathematically, if V= V(r) is a maximum then
then the system is stable equilibrium.2. Unstable equilibrium: If an object is in an unstable equilibrium, the center of gravity will be altered when a disturbing force is applied, but cannot return to the original position upon removal of the force. Mathematically, if V= V(r) is a maximum then 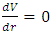 and
and 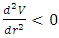 , then the system is unstable equilibrium.3. Neutral equilibrium: If an object is in neutral equilibrium, the center of gravity is unchanged when a disturbing force is applied and the object does not move when the disturbing force is removed. Mathematically, if V= V(r) is a minimum
, then the system is unstable equilibrium.3. Neutral equilibrium: If an object is in neutral equilibrium, the center of gravity is unchanged when a disturbing force is applied and the object does not move when the disturbing force is removed. Mathematically, if V= V(r) is a minimum 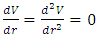 , then the system is in neutral equilibrium.Section 2 Analyzing the equilibrium of the Sun-Earth systemThe potential gravitational force energy of Earth is
, then the system is in neutral equilibrium.Section 2 Analyzing the equilibrium of the Sun-Earth systemThe potential gravitational force energy of Earth is 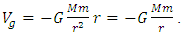 Total energy of earth is Ekinetic + Epotential where
Total energy of earth is Ekinetic + Epotential where 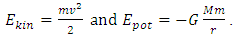 Since Ekin is the energy of motion, is constant and derivative of Ekin = 0. Then the derivative of potential energy is
Since Ekin is the energy of motion, is constant and derivative of Ekin = 0. Then the derivative of potential energy is 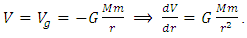 Only when r ∝ ∞, the derivative of potential energy V is equal to zero:
Only when r ∝ ∞, the derivative of potential energy V is equal to zero: 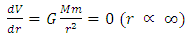 The second derivative of V is
The second derivative of V is 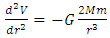 , where the item
, where the item 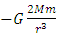 is less than 0 (< 0), then the system will be unstable.This analysis concludes that the current dominant depiction of the Sun-Earth system is an unstable equilibrium. Section 3 ConclusionWhy the dominant model of the solar system is unstable under accurate theoretical analysis? Because the centrifugal force is non-conservative force, it does not result in potential energy and is irreversible. However, the Sun-Earth system seems being in stable equilibrium. Therefore, there must be another conservative repulsive force (opposite to or cancel the conservative gravitational force) between Sun and Earth that is ignored or overlooked by the dominant model, i.e., there must be equilibrium of a conservative repulsive force and the gravitational force between Sun and Earth.Thus the systematic potential energy is the sum of (thermal) repulsive force energy and gravitational force energy.
is less than 0 (< 0), then the system will be unstable.This analysis concludes that the current dominant depiction of the Sun-Earth system is an unstable equilibrium. Section 3 ConclusionWhy the dominant model of the solar system is unstable under accurate theoretical analysis? Because the centrifugal force is non-conservative force, it does not result in potential energy and is irreversible. However, the Sun-Earth system seems being in stable equilibrium. Therefore, there must be another conservative repulsive force (opposite to or cancel the conservative gravitational force) between Sun and Earth that is ignored or overlooked by the dominant model, i.e., there must be equilibrium of a conservative repulsive force and the gravitational force between Sun and Earth.Thus the systematic potential energy is the sum of (thermal) repulsive force energy and gravitational force energy.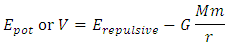 The
The 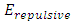 is inversely proportional to the distance r
is inversely proportional to the distance r 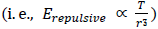 Therefore, when
Therefore, when 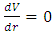 and
and 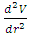 is larger than zero (> 0), the solar system thus can be in stable equilibrium.This is an anomaly could evoke crisis of dominant model of solar system.
is larger than zero (> 0), the solar system thus can be in stable equilibrium.This is an anomaly could evoke crisis of dominant model of solar system.
7. Innovative Discovery of the Universal Static Thermal Repulsive Force Gas Molecule Mechanical Model
Section 1 General correction of the misconception and misinterpretation of kinetic theory of gas and general clarification of the essential truth of gas pressure1.1. Briefing of potential energy and conservative forceŸ Potential energy is associated with objects that exert conservative forces on each other. Potential energy is the stored energy that can either do work or be converted to kinetic energy.Ÿ Potential energy is the work done by a conservative force equals the decrease in the potential energy of the system. Ÿ A force is conservative if the work it does on a particle moving between any two points is independent of the path taken by the particle.Ÿ When conservative energy is changed from one form to another, the energy disappears in one object and appears in another object. Ÿ When conservative forces act within an isolated system, the kinetic energy gained or lost by the system as its members change their relative positions is balanced by an equal loss or gain in potential energy. Ÿ The energy of conservative forces transformation is reversible. Ÿ Gravitational force is conservative force. 1.2. Key points can be clarified and conclusions can be reached upon analysis in previous chapters1. An adiabatic process refers to a change in a system that occurs without any heat or particle exchange with the surroundings, but with other forms of energy exchange. Therefore when the ideal gas equation 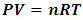 or
or 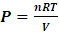 is applied to express an adiabatic process, manifests that the energy transformation is reversible and is potential energy. The forces exerted on gas molecules each other are conservative repulsive forces but not the collision momentums which are not conservative forces and not reversible. Therefore in adiabatic process, the pressure P in
is applied to express an adiabatic process, manifests that the energy transformation is reversible and is potential energy. The forces exerted on gas molecules each other are conservative repulsive forces but not the collision momentums which are not conservative forces and not reversible. Therefore in adiabatic process, the pressure P in 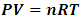 is directly caused by a thermal repulsive conservative contact force of gas molecule.2. General laws of elastic collision disprove the Boltzmann gas velocity distribution.3. Bernoulli Equation and its applications in scientific research and industry contradict and actually falsify Boltzmann’s distribution and gas molecule collision notion.4. Dalton’s law of partial pressures and Amagat’s law of partial volumes imply that the gas molecules are point source of repulsive conservative force and the gas pressure is produced by the repulsive conservative forces exerted on molecules each other rather than chaotic motion of collision.5. Sound wave of gases being as longitudinal wave proves gas is continuum medium with bulk modulus B. It disproves and falsifies Boltzmann’s distribution and the gas molecule collision assertion. It proves that the energy of sound of air is potential energy and the restoring force of sound wave of air is conservative force i.e. a static (thermal) repulsive conservative contact force.6. Practical industry technologies of dynamic gas bearing and static gas bearing falsify the gas collision notion and the Boltzmann’s velocity distribution function.7. Bernoulli Equation and weight deciding atmospheric pressure show us that the motions of gas molecules are produced by macroscopic contact forces and gravitational forces rather than something of unsubstantiated microscopic momentum.The weight of gas molecule layers being decisive factors of atmospheric pressure manifests that there are repulsive contact forces exerted on each other and on surface of earth including water surface of oceans rather than being microscopic momentums.8. Since the centripetal force is not conservative force and is irreversible, therefore the stability of the solar system must be an equilibrium of a conservative repulsive force and the gravitational force between the Sun and planets, i.e. there must be a conservative static universal thermal repulsive force to balance or cancel the gravitational force. Section 2 Discrepancy being worth noting and preliminary conclusions2.1. Discrepancy or contradiction between two descriptions in physics bookContact forces and field forces are two classes of force in classic mechanics, the former forces involve physical contact between two objects, and the later do not involve physical contact between two objects but instead act through empty space. “Other examples of contact forces are the force exerted by gas molecules on the walls of a container.” “The distinction between contact forces and field forces is not as sharp as you may have been led to believe by the previous discussion.” [1] (5.1 THE CONCEPT OF FORCE.)“The model shows that the pressure that a gas exerts on the walls of its container is a consequence of the collisions of the gas molecules with the walls.” [1] (21.1 MOLECULAR MODEL OF AN IDEAL GAS.)It is worth noting that the force of gas molecule exerts on the wall of container is described as “contact force” in 5.1 of reference [1], and is also described as “a consequence of the collisions of the gas molecules” in 21.1 of reference [1].This is obviously an awareness of anomaly or discrepancy by mainstream of physics community that is contradictory to and falsies the basic assumption of kinetic theory of gas thus directly falsifies Boltzmann’s distribution law and the assertion of gas molecules collisions.2.2. Discrepancy between theoretical pressure and sensing pressureBoltzmann’s distribution describes the force and pressure of gas as
is directly caused by a thermal repulsive conservative contact force of gas molecule.2. General laws of elastic collision disprove the Boltzmann gas velocity distribution.3. Bernoulli Equation and its applications in scientific research and industry contradict and actually falsify Boltzmann’s distribution and gas molecule collision notion.4. Dalton’s law of partial pressures and Amagat’s law of partial volumes imply that the gas molecules are point source of repulsive conservative force and the gas pressure is produced by the repulsive conservative forces exerted on molecules each other rather than chaotic motion of collision.5. Sound wave of gases being as longitudinal wave proves gas is continuum medium with bulk modulus B. It disproves and falsifies Boltzmann’s distribution and the gas molecule collision assertion. It proves that the energy of sound of air is potential energy and the restoring force of sound wave of air is conservative force i.e. a static (thermal) repulsive conservative contact force.6. Practical industry technologies of dynamic gas bearing and static gas bearing falsify the gas collision notion and the Boltzmann’s velocity distribution function.7. Bernoulli Equation and weight deciding atmospheric pressure show us that the motions of gas molecules are produced by macroscopic contact forces and gravitational forces rather than something of unsubstantiated microscopic momentum.The weight of gas molecule layers being decisive factors of atmospheric pressure manifests that there are repulsive contact forces exerted on each other and on surface of earth including water surface of oceans rather than being microscopic momentums.8. Since the centripetal force is not conservative force and is irreversible, therefore the stability of the solar system must be an equilibrium of a conservative repulsive force and the gravitational force between the Sun and planets, i.e. there must be a conservative static universal thermal repulsive force to balance or cancel the gravitational force. Section 2 Discrepancy being worth noting and preliminary conclusions2.1. Discrepancy or contradiction between two descriptions in physics bookContact forces and field forces are two classes of force in classic mechanics, the former forces involve physical contact between two objects, and the later do not involve physical contact between two objects but instead act through empty space. “Other examples of contact forces are the force exerted by gas molecules on the walls of a container.” “The distinction between contact forces and field forces is not as sharp as you may have been led to believe by the previous discussion.” [1] (5.1 THE CONCEPT OF FORCE.)“The model shows that the pressure that a gas exerts on the walls of its container is a consequence of the collisions of the gas molecules with the walls.” [1] (21.1 MOLECULAR MODEL OF AN IDEAL GAS.)It is worth noting that the force of gas molecule exerts on the wall of container is described as “contact force” in 5.1 of reference [1], and is also described as “a consequence of the collisions of the gas molecules” in 21.1 of reference [1].This is obviously an awareness of anomaly or discrepancy by mainstream of physics community that is contradictory to and falsies the basic assumption of kinetic theory of gas thus directly falsifies Boltzmann’s distribution law and the assertion of gas molecules collisions.2.2. Discrepancy between theoretical pressure and sensing pressureBoltzmann’s distribution describes the force and pressure of gas as 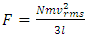 and
and 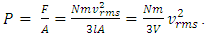 However, the actual gas pressure P is instantaneous value and the molecules have different velocities, 2l/vix and ⊿ti, and various collision frequencies. The consequence of the collisions
However, the actual gas pressure P is instantaneous value and the molecules have different velocities, 2l/vix and ⊿ti, and various collision frequencies. The consequence of the collisions 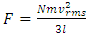 and the momentums of gas molecules need time interval to be cumulated. The container wall of volume gas has no way to accumulate the forces with very different longer and shorter interval time of collisions! Elastic deformations (of feeling of instantaneous pressure) of container wall or diaphragm of sensor cannot be cumulated.Additionally, the molecules with lower velocity should not cause container wall or sensor diaphragm to deform to feel the pressure or force that will reduce the total integral value over the Boltzmann’s distribution accordingly. Being as a better laboratory of gas, the atmosphere in where, the parameters of (thermal repulsive force of) temperature T, density ρ and pressure p can be measured directly; the parameters such as vrms and vms of gas molecule collision theory and Boltzmann distribution function are immeasurable and do not have practical utilities.2.3. Deductions of vrms and vms and further deductions based on them are circular reasoningAll deductions and discussions dealing with or involve in the parameters of vrms and vms of gas molecule are actually circular reasoning. In the argument of kinetic theory of gas, the premise “the average translational kinetic energy E per molecule is
and the momentums of gas molecules need time interval to be cumulated. The container wall of volume gas has no way to accumulate the forces with very different longer and shorter interval time of collisions! Elastic deformations (of feeling of instantaneous pressure) of container wall or diaphragm of sensor cannot be cumulated.Additionally, the molecules with lower velocity should not cause container wall or sensor diaphragm to deform to feel the pressure or force that will reduce the total integral value over the Boltzmann’s distribution accordingly. Being as a better laboratory of gas, the atmosphere in where, the parameters of (thermal repulsive force of) temperature T, density ρ and pressure p can be measured directly; the parameters such as vrms and vms of gas molecule collision theory and Boltzmann distribution function are immeasurable and do not have practical utilities.2.3. Deductions of vrms and vms and further deductions based on them are circular reasoningAll deductions and discussions dealing with or involve in the parameters of vrms and vms of gas molecule are actually circular reasoning. In the argument of kinetic theory of gas, the premise “the average translational kinetic energy E per molecule is 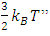 is just as much in need of proof or evidence as the conclusion
is just as much in need of proof or evidence as the conclusion 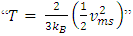 or the premise
or the premise 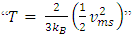 is just the conclusion “E per molecule is
is just the conclusion “E per molecule is 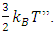 The statement of the kinetic theory is: “the internal energy of an ideal gas depends only on the temperature” because “the temperature is a direct measure of average molecular kinetic energy.”“Temperature is proportional to average kinetic energy” because “The total translational kinetic energy of N molecules of gas is simply N times the average energy per molecule
The statement of the kinetic theory is: “the internal energy of an ideal gas depends only on the temperature” because “the temperature is a direct measure of average molecular kinetic energy.”“Temperature is proportional to average kinetic energy” because “The total translational kinetic energy of N molecules of gas is simply N times the average energy per molecule 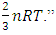 2.4. Preliminary conclusions1. Based on above analysis, we can see clearly that there are no elastic collisions of Boltzmann’s distribution between gas molecules.Anytime and anywhere, with any longer or shorter distance, there are only static stable equilibriums between (thermal) repulsive contact force fields with mechanical radius of gas molecules. The static stable equilibrium of the repulsive force field forms the total pressure of the volume gas.2. Of course, every gas molecule has six degrees of freedom, motion is inevitable. However, the motions of gas molecules are not the causes of gas pressure but the effect of the pressure (thermal repulsive forces). Although the molecules are moving, they are moving slowly not in Boltzmann’s velocity distribution function but in a static equilibrium of conservative contact force. 3. Boltzmann’s distribution function and gas molecule collision assertion actually are substitutes for some transitional science development stages. They are expedient measures in a sense of something better than nothing and a pragmatic tactic as well!The parameters such as vrms and vms of gas molecule collision theory are dummy variables or virtual variables that are of no use but being used only in circular reasoning and boring involution! Section 3 General description and definition of elementary point source particle of thermal repulsive force field of the universal thermal repulsive force (field)1. Every atom or molecule of gas is a point or particle source of the universal static thermal repulsive force field. 2. The magnitude of the thermal repulsive force is proportional to its temperature, T, and is inversely proportional to the distance or its mechanics radii, r, from the point heat source. It is not a function of molecule size and particle mass. 3. When a size of particle (including electron) is equal to or smaller than any molecule size, it acts as a point source of the thermal repulsive force (field).For example, for a gas mixture of H2, He, N2, O2 and CO2 the temperature and pressure are the same, their mechanical radius or force equilibrium radius is identical. 4. The general form of the equation can be written as
2.4. Preliminary conclusions1. Based on above analysis, we can see clearly that there are no elastic collisions of Boltzmann’s distribution between gas molecules.Anytime and anywhere, with any longer or shorter distance, there are only static stable equilibriums between (thermal) repulsive contact force fields with mechanical radius of gas molecules. The static stable equilibrium of the repulsive force field forms the total pressure of the volume gas.2. Of course, every gas molecule has six degrees of freedom, motion is inevitable. However, the motions of gas molecules are not the causes of gas pressure but the effect of the pressure (thermal repulsive forces). Although the molecules are moving, they are moving slowly not in Boltzmann’s velocity distribution function but in a static equilibrium of conservative contact force. 3. Boltzmann’s distribution function and gas molecule collision assertion actually are substitutes for some transitional science development stages. They are expedient measures in a sense of something better than nothing and a pragmatic tactic as well!The parameters such as vrms and vms of gas molecule collision theory are dummy variables or virtual variables that are of no use but being used only in circular reasoning and boring involution! Section 3 General description and definition of elementary point source particle of thermal repulsive force field of the universal thermal repulsive force (field)1. Every atom or molecule of gas is a point or particle source of the universal static thermal repulsive force field. 2. The magnitude of the thermal repulsive force is proportional to its temperature, T, and is inversely proportional to the distance or its mechanics radii, r, from the point heat source. It is not a function of molecule size and particle mass. 3. When a size of particle (including electron) is equal to or smaller than any molecule size, it acts as a point source of the thermal repulsive force (field).For example, for a gas mixture of H2, He, N2, O2 and CO2 the temperature and pressure are the same, their mechanical radius or force equilibrium radius is identical. 4. The general form of the equation can be written as 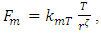 where the kmT is the coefficient constant,
where the kmT is the coefficient constant, 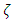 is power of r.5. The atom or molecule of gases is in equilibrium with environmental pressure (or repulsive force field of other molecules).6. In the extreme circumstance of the plasma state, the electrons are separated from nucleus. They act the same as a point source of the thermal repulsive force field like other plasma nuclei or ions.Section 4 Deduction of the accurate rational gas molecule model from physics laws and physical phenomenonBased on the ideal gas equation,
is power of r.5. The atom or molecule of gases is in equilibrium with environmental pressure (or repulsive force field of other molecules).6. In the extreme circumstance of the plasma state, the electrons are separated from nucleus. They act the same as a point source of the thermal repulsive force field like other plasma nuclei or ions.Section 4 Deduction of the accurate rational gas molecule model from physics laws and physical phenomenonBased on the ideal gas equation, 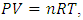 and the above conclusions about point source thermal repulsive force (field), the equation of single gas molecule can be written as
and the above conclusions about point source thermal repulsive force (field), the equation of single gas molecule can be written as 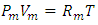 , where Rm is single gas molecule constant, Pm is partial pressure of molecule particle ball, Vm is volume of single gas molecule, T is temperature of the molecule in Kelvin.The Rm is then
, where Rm is single gas molecule constant, Pm is partial pressure of molecule particle ball, Vm is volume of single gas molecule, T is temperature of the molecule in Kelvin.The Rm is then 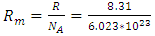 . The volume of single molecule is
. The volume of single molecule is 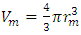 , where rm is force equilibrium radius of gas molecule, or mechanical radius of gas molecule. Partial gas molecule pressure is then
, where rm is force equilibrium radius of gas molecule, or mechanical radius of gas molecule. Partial gas molecule pressure is then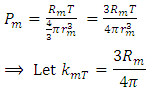 | (6.4.1) |
Pm reduces to (or mathematically expresses as):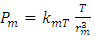 | (6.4.2) |
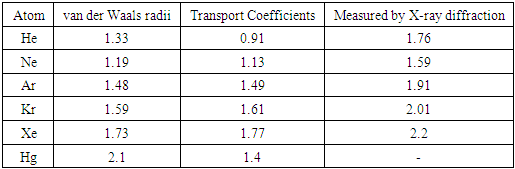
Therefore, we know Pm is proportional to the temperature, T, and is inversely proportional to 3rd power of rm, i.e., inversely proportional to the 3 times power of the rm, i.e., Pm ∝ 1/rm3. Section 5 Radius under the definition of the thermal repulsive force and compared to the gas molecule radius of other definitionsCurrently, the gas molecule radius of an atom or molecule is based on the liquid state volume of the molecule where molecules are densely packed or could be compressed further. However, the radius values are variable based on the method.For example, the atom radius measured or calculated by the following methods: a) van der Waals equation, b) transport coefficient of collision and c) X-ray diffraction, are quite different. Table 6 is the datasheet list of atoms radius of He, Ne, Ar, Kr, Xe and Hg by different methods. Table 6. Atom radii (10-10 m)
 |
| |
|
Therefore, based on the data of the Table and Rutherford’s gold foil experiment, we see that there is no real radius of the hard shell of a molecule or atom!There is only a mechanical radius, force equilibrium radius, or pressure equilibrium radius of molecule or atom. This is true no matter what the phase state is, such as solid, liquid, and gas.Atoms or molecules have no physical hardware radius but have only temporary equilibrium mechanical radii, force equilibrium radii, effective force equilibrium radii, or functional force equilibrium radii.What can be currently estimated or experimentally determined for the hardcore radius is only the radius of nuclei (by Rutherford’s experiments).It is supported by effective force dynamic equilibrium of the thermal repulsive force field and attractive forces field. The force fields of molecules or atoms are attracting and repelling mutually such that the molecules or atom maintain a rough (dynamic equilibrium) distance between one another that is around the value of the effective mechanical diameter of the gas or liquid molecule.Experimentally, the effective mechanical force equilibrium radius is proportional to its temperature, T, due to thermal repulsive forces. Heat expansion and cold contraction of liquids and solids are a prime example of this phenomenon.Section 6 Deduction of the thermal repulsive force calculus formula of a single moleculeThe ideal gas equation is 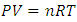 , considering one single gas molecule, the equation can be written as
, considering one single gas molecule, the equation can be written as 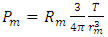 . There is an integral algorithm that can be used to calculate the thermal repulsive force in a certain direction. Integrating with respect to plane areaA plane surface integral of the pressure, Pm, component, is perpendicular to the plane. The calculation is respect to plane area, S. The distance between the central point of the particle (molecule) and the plane is r, as shown in Fig.6.
. There is an integral algorithm that can be used to calculate the thermal repulsive force in a certain direction. Integrating with respect to plane areaA plane surface integral of the pressure, Pm, component, is perpendicular to the plane. The calculation is respect to plane area, S. The distance between the central point of the particle (molecule) and the plane is r, as shown in Fig.6.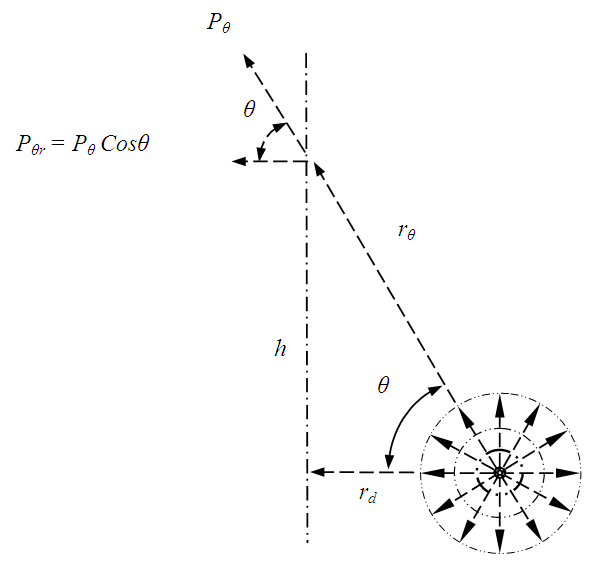 | Figure 6. Analysis and integral of a molecule |
Integrating (6.6.1) with respect to area, S, is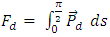 | (6.6.2) |
In the angular, θ, direction, the pressure is 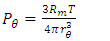 | (6.6.3) |
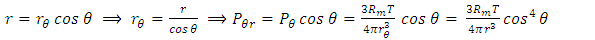 | (6.6.4) |
 | (6.6.5) |
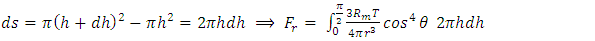 | (6.6.6) |
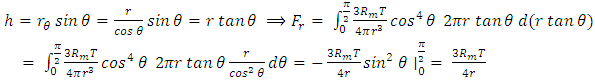 | (6.6.7) |
Thus, we know that the thermal repulsive force is proportional to the temperature, T, and is inversely proportional to mechanical radius, r.
8. Re-Understanding and Re-Explanation of Matter Phase States by the Universal Static Thermal Repulsive Force Theory
The universal thermal repulsive force is the major decisive factor that supports the existence of matter or substance; otherwise, matter will collapse into a black hole state.Section 1 Redefinition of matter phase statesBased on the new discovery of the universal static thermal repulsive force, we can divide the phases of matter into five states: as temperature increases, the phase state of matter changes from black hole to solid, liquid, gas, and plasma. The effective radius or mechanical radius of atoms (Rea) or molecules of matter in a certain state are proportional to their temperature, T. The higher the temperature is, the larger the mechanical radius of the atom or molecule.In the extreme condition, when the temperature is approaching to 0 K, matter will exist in the black hole state. On the other extreme condition, when the temperature is extremely high (higher enough to approach to tens of thousands K), matter will exist in the plasma state. Hence, all the electrons escape from the nucleus to become independent point sources of the static thermal repulsive force field.As shown in Fig.7 and Table.7.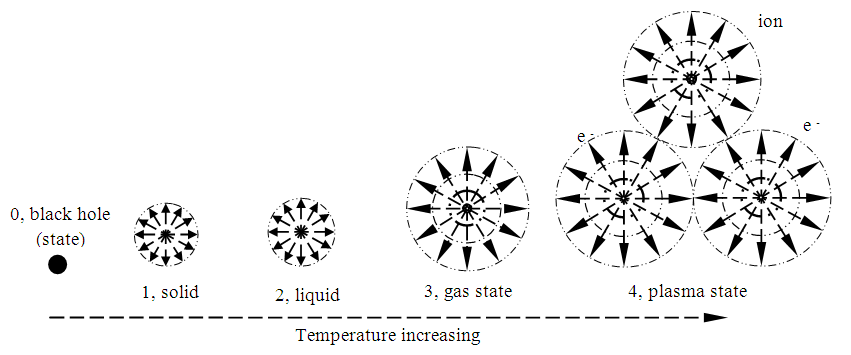 | Figure 7. Matter state changes along temperature |
Table 7. Matter state and size changes along temperature
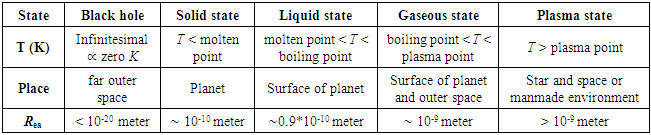 |
| |
|
Section 2 Re-explanation of nucleus-electrons structureElectrons and the nucleus must be interlocked by the thermal repulsive and attractive force when they are in equilibrium.Based on the results and conclusions of the previous investigations, the force to support electrons do not fall into nucleus must only be the universal thermal repulsive force!According to prevalent explanation, the directions of velocities of kinetic energy of the electrons are random. Therefore, the motions of electrons (if really occurring) have no way to automatically balance the Coulomb attractive forces. Instead, without the thermal repulsive force, the electrons are inevitably falling into the nucleus, because the nucleus and the electrons are an unstable system.It is the action and reaction of the thermal repulsive forces (field) and the attractive force (Coulomb attractive and universal attractive force) that keep the electrons and the nuclei (protons) in stable equilibrium.
9. Re-Clarifying and Re-Explaining Some Crucial Physical Phenomenon to Corroborate the Novel Universal Static Thermal Repulsive Force Theory
Section 2 Diffusion is the effect of the universal thermal repulsive force2.1. Calculating the thermal repulsive force on the interface (boundaries) of two phases of matterWe can calculate out that the total thermal repulsive force is the total pressure multiplying the effective overlapping area of exerted matter,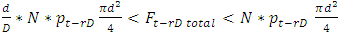 | (8.1) |
2.2. Questioning the measurement method of the Boltzmann constant2.2.1. Dominant descriptionAccording to description in the book of Atoms, Molecules and Photons (Wolfgang Demtröder ): “Measurement of Boltzmann constant is done through observation of a vertical density distribution of small latex particles in a liquid within a glass cylinder.At equilibrium the Boltzmann distribution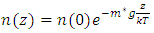 is obtained, where m*g = (m - ρlVp)g is the effective weight of a particle with volume Vp . This gives the gradient
is obtained, where m*g = (m - ρlVp)g is the effective weight of a particle with volume Vp . This gives the gradient 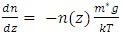 Counting the number of n(z) yields dn/dz and Boltzmann constant. Due to gravity the particles sink down. If the gravity force
Counting the number of n(z) yields dn/dz and Boltzmann constant. Due to gravity the particles sink down. If the gravity force 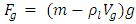 is just compensated by the friction force
is just compensated by the friction force 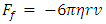 which spherical particle of radius r experience when they fall with velocity v in a medium with viscosity η, the net force is zero. The constant velocity is then
which spherical particle of radius r experience when they fall with velocity v in a medium with viscosity η, the net force is zero. The constant velocity is then 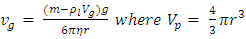 The downward flux of particles jg = vg n creates a concentration gradient dn/dz, which leads to an upward diffusion flux
The downward flux of particles jg = vg n creates a concentration gradient dn/dz, which leads to an upward diffusion flux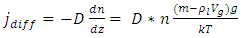 where D is the diffusion coefficient.Finally stationary conditions are reached when both fluxes just cancel. This means
where D is the diffusion coefficient.Finally stationary conditions are reached when both fluxes just cancel. This means 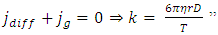 2.2.2. Remarks and questions1. The equation
2.2.2. Remarks and questions1. The equation 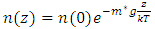 is obtained by observations and not is derived theoretically. Therefore, this is not an effect of equilibrium of kinetic motion, instead of, equilibrium of static forces should be considered first. 2. In equilibrium state, the velocity of small latex particle is zero, therefore friction force due to viscosity, η, of the liquid is zero, the deduction of that “both fluxes
is obtained by observations and not is derived theoretically. Therefore, this is not an effect of equilibrium of kinetic motion, instead of, equilibrium of static forces should be considered first. 2. In equilibrium state, the velocity of small latex particle is zero, therefore friction force due to viscosity, η, of the liquid is zero, the deduction of that “both fluxes 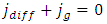 just cancel” is a pseudo-event when friction force is zero.2.3. Comparing with the atmospheric pressure distribution to verify that the vertical density distribution of small particles is an effect of thermal repulsive force fieldThe vertical density distribution of small latex particles is
just cancel” is a pseudo-event when friction force is zero.2.3. Comparing with the atmospheric pressure distribution to verify that the vertical density distribution of small particles is an effect of thermal repulsive force fieldThe vertical density distribution of small latex particles is 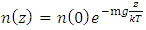 , compare with the molecule number distribution of the atmosphere due to thermal repulsive force
, compare with the molecule number distribution of the atmosphere due to thermal repulsive force 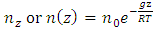 , we can see clearly that both distribution functions are exactly same. Both work on the same physical law of the universal thermal repulsive force, as shown in Fig.8.The back ground difference lies in that the small latex particles have a higher density and a higher thermal repulsive pressure than the liquid. If the small latex particles are not in liquid, the thermal repulsive force is not big enough to distribute in the form of
, we can see clearly that both distribution functions are exactly same. Both work on the same physical law of the universal thermal repulsive force, as shown in Fig.8.The back ground difference lies in that the small latex particles have a higher density and a higher thermal repulsive pressure than the liquid. If the small latex particles are not in liquid, the thermal repulsive force is not big enough to distribute in the form of 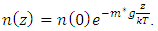 However, the buoyancy force of liquid cancels the partial earth gravitational force and is equivalent to the decrease in the density of solid particles, therefore, the particle distribution is only the equilibrium of the universal thermal repulsive force and the gravitational force of earth which thus is the same situation as the atmosphere on surface of the Earth distributed in exponential form.Therefore we can conclude that the vertical density distribution of small particles is an effect of thermal repulsive force field.Section 2 the earlier air cycle refrigeration can be re-explained by the thermal repulsive force theoryIn the thermodynamic system of gases, any work done by gas system is either done at the expense of the potential energy of thermal repulsive force or done on system to increase the potential energy of thermal repulsive force. The total thermal repulsive force potential energy of a volume of gas is the sum of thermal repulsive force potential energy of every single gas molecule.When the gas system is working, it is the every single gas molecule to transfer or recharge potential energy of thermal repulsive force through changes of temperature T and changes of mechanical volume of molecule Vm or mechanical radius rm of molecule.
However, the buoyancy force of liquid cancels the partial earth gravitational force and is equivalent to the decrease in the density of solid particles, therefore, the particle distribution is only the equilibrium of the universal thermal repulsive force and the gravitational force of earth which thus is the same situation as the atmosphere on surface of the Earth distributed in exponential form.Therefore we can conclude that the vertical density distribution of small particles is an effect of thermal repulsive force field.Section 2 the earlier air cycle refrigeration can be re-explained by the thermal repulsive force theoryIn the thermodynamic system of gases, any work done by gas system is either done at the expense of the potential energy of thermal repulsive force or done on system to increase the potential energy of thermal repulsive force. The total thermal repulsive force potential energy of a volume of gas is the sum of thermal repulsive force potential energy of every single gas molecule.When the gas system is working, it is the every single gas molecule to transfer or recharge potential energy of thermal repulsive force through changes of temperature T and changes of mechanical volume of molecule Vm or mechanical radius rm of molecule. | Figure 8. Distribution of latex particles in liquid |
Thermal repulsive force potential energy can lose energy in two ways:1) The system work done by volume expanding.2) Heat transfer from the molecules to the other matter so that the temperature of molecule is decreased.Similarly, thermal repulsive force potential energy can gain energy in two ways: 1) Compression of the system.2) Direct heat transfer to the gas molecules to increase the molecule temperature.Section 3 Peltier effect of semiconductor refrigeration can be re-explained by the thermal repulsive force theoryIn the Peltier refrigeration cycle works, electrons (the refrigerant) are the point source of the thermal repulsive force, just like gas molecules for the air cycle process of the earlier air refrigeration. To complete a Peltier refrigeration cycle, the processes work as follows: 1, the electrons flow out from the negative electrode to a p-type semiconductor, the mechanical volumes of electrons are compressed (mechanical radius of electrons are decreased), and heat is rejected and transmitted to a heat sinking plate.2, the volumes of electrons are expanded to a lower temperature and cold is transmitted; 3, the electrons flow out from the p-type materials to an n-type semiconductor material and the electron volume is expanded to a lower temperature and cold is transmitted.4, the mechanical volumes of electrons are compressed (contracting back to original volume) and heat has been rejected and transmitted to heat sinking plate.Electron cycle inside n-type material in Peltier refrigeration is similar to p-type semiconductor inversely. Therefore we know that the working principles of earlier air cycle refrigeration and Peltier effect of semiconductor refrigeration are same, both are working based on conservative thermal repulsive forces. The only difference lies in different point source of the thermal repulsive force being used as refrigerants, the former is air molecule and the later is electron.Section 4 Solar wind of plasma is caused by the thermal repulsive force of Sun and plasmaIn the universal thermal repulsive force of Sun and plasma with high temperatures, the thermal repulsive force is much larger than gravitational attractive force, thus the thermal repulsive force will repel the plasma cluster to form a plasma solar wind to move away from the Sun centrifugally toward outer space, including toward earth and other planets.Section 5 Re-explanation of why the Earth is orbiting the Sun in an elliptical orbitThe prevalent explanation of the elliptical orbit of earth and other planets are due to the attractive force of solar system (and attractive forces of galaxy), but no more details are provided. The contradiction is that the changes of the attractive forces of Sun and planets to earth is not an elliptical orbit, because the motion cycles of other planets of the solar system are very different from that of the earth cycle. Therefore, the sum of the attractive forces of other planets is irregularly changed and different from the earth elliptical model.It is the thermal repulsive force to cause earth orbiting Sun in elliptic orbit.The reason is that the northern hemisphere has significantly more land mass than the southern hemisphere. In summer season in the north hemisphere, the sunlight shines vertically on the Tropic of Cancer and the average temperature of earth is higher due to more land being heated. Therefore, the thermal repulsive force between the Sun and earth is increased. Under the influence of an imbalance of the thermal repulsive force and attractive force, the distance between Sun and earth increases to balance the longer distance position. This is the opposite for the southern hemisphere, where has significantly more ocean area than the northern hemisphere.
10. Conclusions
1. The so called collision between gas molecules, (the author has proven it being not existed), if it is really existed, it must not be the decisive cause of producing gas pressure, instead, it is effect of thermal repulsive force.2. Gas molecules are point sources of thermal repulsive force; they are in equilibrium of thermal repulsive forces between gases molecules by their mechanical radius of thermal repulsive forces field. Gas pressure is thus produced by gas molecules being as point sources of thermal repulsive force.3. The universal static thermal repulsive force is conservative contact force; it is the basic decisive foundation of existence of matter world.4. Without the thermal repulsive force, or when the temperature approaches extreme low or approaches zero K, the thermal repulsive force will approaches infinitesimal, the matter will lie in black hole state, the earth and other planets will fall onto the Sun, the electrons will fall in nucleus.
References
| [1] | D. Halliday, R. Resnick, J. Walker: Fundamental of Physics (8th edition). John Wiley & Sons 2008. |
| [2] | Wolfgang Demtröder: Atoms, Molecules and Photons. Springer 2010. |
| [3] | Beiser Arthur: Concepts of modern physics, 6th edition. McGraw-Hill Higher Education 2003. |
| [4] | Alan Jeffrey: Handbook of Mathematical formulas and integrals Second Edition Academic Press 2000. |
| [5] | Karl R Popper: Conjecture and Refutation. Basic Books, Publisher. 1962. |
| [6] | Thames S. Kuhn: The Structure of Scientific Revolutions. The University of Chicago Press 1970. |
| [7] | Liu Kedian: Improvements on Some Scientific Methods. American Academic Press 2021. |


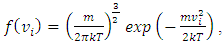 i = x, y, z (- ∞ < vi < + ∞), where k is the Boltzmann constant, v is the molecular speed of a molecule, m is the mass of the molecule, and T is the temperature of the gas. The mean molecular speed
i = x, y, z (- ∞ < vi < + ∞), where k is the Boltzmann constant, v is the molecular speed of a molecule, m is the mass of the molecule, and T is the temperature of the gas. The mean molecular speed 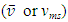 is the mathematical average of the speed distribution
is the mathematical average of the speed distribution 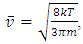 the root-mean-square speed
the root-mean-square speed 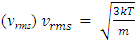 . The total force exerted by the molecules can be expressed in
. The total force exerted by the molecules can be expressed in 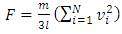 . The total force on the wall of the container then can be written as
. The total force on the wall of the container then can be written as 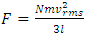 . The pressure then be written as
. The pressure then be written as 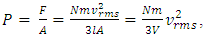 where A = the area on which force is exerted, V = the volume. Since Nm stands for the total mass of the gas, then the density of the gas is ρ = Nm/V and
where A = the area on which force is exerted, V = the volume. Since Nm stands for the total mass of the gas, then the density of the gas is ρ = Nm/V and 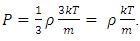 Equation
Equation 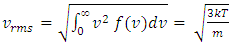 can be rewritten as
can be rewritten as 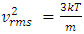 or
or 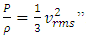 .Section 2 General laws of elastic collision contradict and falsify Maxwell-Boltzmann gas velocity distribution functionAccording to Boltzmann’s distribution function, different gas molecules in a mixture have varying speed distributions, as shown in Fig.1.1. However, in reality, the collisions of gases molecules (if really occur) must be oblique collisions rather than head-on collision, as shown in Fig.1.2. Study of universal situations of oblique elastic collisions, when m2 = m1, then
.Section 2 General laws of elastic collision contradict and falsify Maxwell-Boltzmann gas velocity distribution functionAccording to Boltzmann’s distribution function, different gas molecules in a mixture have varying speed distributions, as shown in Fig.1.1. However, in reality, the collisions of gases molecules (if really occur) must be oblique collisions rather than head-on collision, as shown in Fig.1.2. Study of universal situations of oblique elastic collisions, when m2 = m1, then 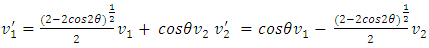
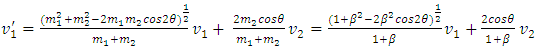


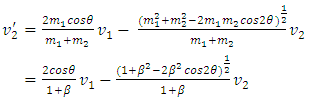
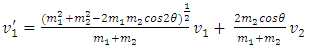
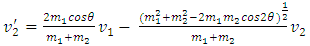
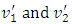 will be any value. Assuming that the gas molecules are colliding continuously, the final result is that all the velocities of the gas molecules will tend to equal, and is equal to the mean speed i.e.,
will be any value. Assuming that the gas molecules are colliding continuously, the final result is that all the velocities of the gas molecules will tend to equal, and is equal to the mean speed i.e., 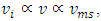 (0<i<∞). Thus the oblique collisions of gas molecules must spoil the Boltzmann’s distribution.This is one anomaly that shows the Boltzmann’s velocity distribution function can never be maintained.Therefore, there are no elastic collisions between gas molecules, if some collision is really existed, it must not be the decisive factor of air pressure.Section 3 Rutherford’s gold foil experiment (1911) show that atoms and molecules are not elastic rigid balls and have no chance to undergo elastic collision According to Rutherford’s gold foil experiment (1911), the atomic volume of the gold is about VA =10-29 m3 and that of its nucleus is only VN = 10-42 m3.The atom diameter of gold compared to the diameter of its nucleus is DA / DN = (VA /VN)1/3=21,544.3.Diameter of the soft shell (electron cloudy) of the atom is 21,544.3 times bigger than its hardcore nucleus.Therefore the atoms and molecules are not rigid balls! The so-called gas molecule collisions (if they occur) only happen between the outer shells of electron clouds of atoms, which are definitely not elastic collisions. It is important to note that the speed of atoms or molecules of gases cannot be (the speed in Rutherford’ experiment) 2*107 m/s.Firstly, it is worthwhile to notice that the effective diameter of molecules d used to calculate effective collision area is 104 times much larger than the Rutherford’s gold foil experimental data of nucleus diameter. Then the so called mean-free-path of nucleus (hardcore) is almost infinite, therefore there is no chance for gas molecules to collide each other.Secondly, when temperature is in the range of 200 -1000K, the relative velocities are at most
(0<i<∞). Thus the oblique collisions of gas molecules must spoil the Boltzmann’s distribution.This is one anomaly that shows the Boltzmann’s velocity distribution function can never be maintained.Therefore, there are no elastic collisions between gas molecules, if some collision is really existed, it must not be the decisive factor of air pressure.Section 3 Rutherford’s gold foil experiment (1911) show that atoms and molecules are not elastic rigid balls and have no chance to undergo elastic collision According to Rutherford’s gold foil experiment (1911), the atomic volume of the gold is about VA =10-29 m3 and that of its nucleus is only VN = 10-42 m3.The atom diameter of gold compared to the diameter of its nucleus is DA / DN = (VA /VN)1/3=21,544.3.Diameter of the soft shell (electron cloudy) of the atom is 21,544.3 times bigger than its hardcore nucleus.Therefore the atoms and molecules are not rigid balls! The so-called gas molecule collisions (if they occur) only happen between the outer shells of electron clouds of atoms, which are definitely not elastic collisions. It is important to note that the speed of atoms or molecules of gases cannot be (the speed in Rutherford’ experiment) 2*107 m/s.Firstly, it is worthwhile to notice that the effective diameter of molecules d used to calculate effective collision area is 104 times much larger than the Rutherford’s gold foil experimental data of nucleus diameter. Then the so called mean-free-path of nucleus (hardcore) is almost infinite, therefore there is no chance for gas molecules to collide each other.Secondly, when temperature is in the range of 200 -1000K, the relative velocities are at most 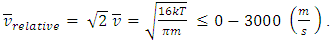 The relative velocities:
The relative velocities:  is (<<) much lower than 2*107 m/s, the velocity of the protons in Rutherford’s gold foil experiment.This is one anomaly that verifies there being no elastic collisions between gas molecules at all. Factually, the gas molecules are laid in a relative static equilibrium, they never have free path.Therefore, there is no elastic collision between gas molecules at all, if there is some collision, their velocities are very low and MFP is almost infinite, therefore it must not be the decisive factor of air pressure.Section 4 Bernoulli Equation contradicts the gas kinetic energy formula derived from Boltzmann’s velocity distributionThe Bernoulli equation is based on the energy conservation law and mass conservation law and has been a verified truth by scientific research and industrial technologies in macroscopic domain for hundreds of years. The energy of gas flow in pipe of Bernoulli equation is
is (<<) much lower than 2*107 m/s, the velocity of the protons in Rutherford’s gold foil experiment.This is one anomaly that verifies there being no elastic collisions between gas molecules at all. Factually, the gas molecules are laid in a relative static equilibrium, they never have free path.Therefore, there is no elastic collision between gas molecules at all, if there is some collision, their velocities are very low and MFP is almost infinite, therefore it must not be the decisive factor of air pressure.Section 4 Bernoulli Equation contradicts the gas kinetic energy formula derived from Boltzmann’s velocity distributionThe Bernoulli equation is based on the energy conservation law and mass conservation law and has been a verified truth by scientific research and industrial technologies in macroscopic domain for hundreds of years. The energy of gas flow in pipe of Bernoulli equation is 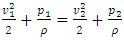 . The equation applied in pressure sensor and flow meter is expressed as
. The equation applied in pressure sensor and flow meter is expressed as 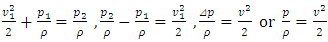 . The expression
. The expression 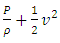 is total energy. Expressions
is total energy. Expressions 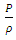 and
and 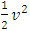 are partial energies which can be converted reversible. However, in gas molecules collision theory, gas pressure is expressed as
are partial energies which can be converted reversible. However, in gas molecules collision theory, gas pressure is expressed as 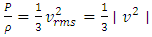 and
and 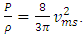 The problems are:1. In practical sense, being in any direction with equal probability, the velocities vrms and vms of the microscopic kinetic energies
The problems are:1. In practical sense, being in any direction with equal probability, the velocities vrms and vms of the microscopic kinetic energies 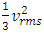 and
and 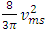 cannot automatically immediately convert to the velocities v (being in one direction along the delta pressure Δ P difference) of the macroscopic dynamic energy
cannot automatically immediately convert to the velocities v (being in one direction along the delta pressure Δ P difference) of the macroscopic dynamic energy 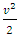 .2. Based on the assumption of kinetic theory “the forces between molecules are negligible except during a collision,” thus there will be no force between the molecules to transmit the Δ P each other in Bernoulli equation.3. If the masses of gas molecules are same, then the value of the microscopic mean speed
.2. Based on the assumption of kinetic theory “the forces between molecules are negligible except during a collision,” thus there will be no force between the molecules to transmit the Δ P each other in Bernoulli equation.3. If the masses of gas molecules are same, then the value of the microscopic mean speed 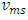 must be equal to the value of the macroscopic speed
must be equal to the value of the macroscopic speed 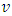 . When the microscopic energy
. When the microscopic energy  is converted to macroscopic energy
is converted to macroscopic energy 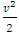 in Bernoulli equation, there is an energy difference between
in Bernoulli equation, there is an energy difference between 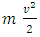 and
and 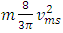 . This is theoretically and practically contrary to the energy conservation law! This is one anomaly that falsifies the Boltzmann’s distribution.4. The practicable industry technologies of pressure sensors such as the Pitot tube and the Venturi tube being the application of Bernoulli equation are the direct evidences that falsifies the assertion of pressure being caused by collision. Section 5 Dalton’s law of partial pressures actually imply the existence of thermal repulsive forces between gas molecules Dalton’s law of partial pressure states that the total pressure is the sum of the partial pressures of the individual gases.5.1. Analysis and re-explanation of Dalton’s law with conclusionSubstituting Dalton’s law of partial pressures is
. This is theoretically and practically contrary to the energy conservation law! This is one anomaly that falsifies the Boltzmann’s distribution.4. The practicable industry technologies of pressure sensors such as the Pitot tube and the Venturi tube being the application of Bernoulli equation are the direct evidences that falsifies the assertion of pressure being caused by collision. Section 5 Dalton’s law of partial pressures actually imply the existence of thermal repulsive forces between gas molecules Dalton’s law of partial pressure states that the total pressure is the sum of the partial pressures of the individual gases.5.1. Analysis and re-explanation of Dalton’s law with conclusionSubstituting Dalton’s law of partial pressures is 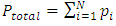 into ideal gas equation
into ideal gas equation 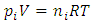 and
and 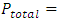
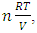 yields
yields 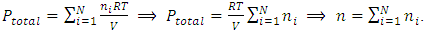 The mole numbers of individual gases can be any number (0 < ni < n), can approach to 0.Thus, ni can be 1 (a single molecule). The
The mole numbers of individual gases can be any number (0 < ni < n), can approach to 0.Thus, ni can be 1 (a single molecule). The 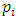 in the equation
in the equation 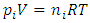 is representing the static pressure of any numbers even one single gas molecule.Therefore, every gas molecule is an independent pressure source that must be in a force equilibrium state with same size of mechanical radius on which the molecules have same static pressure interacting each other to form the total pressure of the mixture of gases. 5.2. Dalton’s partial pressures law manifests a static mechanical repulsive force molecule modelConspicuously, the Dalton’s law of partial gas pressure clearly and accurately shows us that:1. Every gas molecule is a point source of repulsive force field which is a mechanical pressure ball supporting the total pressure just as molecules of a liquid does. 2. Every molecule is acting and reacting with other molecules in static repulsive forces equilibrium statically. Section 6 Amagat’s partial volume law imply the gas molecules are point source of repulsive force 6.1. Amagat’s law contradicts the gas molecule collision notion and the Boltzmann’s distributionAmagat’s law states that the partial volume, vi, of an ideal gas (i) in a mixture of ideal gases is equal to the volume that gas (i) would occupy if it were alone and was at the pressure and temperature of the gas mixture. Substituting
is representing the static pressure of any numbers even one single gas molecule.Therefore, every gas molecule is an independent pressure source that must be in a force equilibrium state with same size of mechanical radius on which the molecules have same static pressure interacting each other to form the total pressure of the mixture of gases. 5.2. Dalton’s partial pressures law manifests a static mechanical repulsive force molecule modelConspicuously, the Dalton’s law of partial gas pressure clearly and accurately shows us that:1. Every gas molecule is a point source of repulsive force field which is a mechanical pressure ball supporting the total pressure just as molecules of a liquid does. 2. Every molecule is acting and reacting with other molecules in static repulsive forces equilibrium statically. Section 6 Amagat’s partial volume law imply the gas molecules are point source of repulsive force 6.1. Amagat’s law contradicts the gas molecule collision notion and the Boltzmann’s distributionAmagat’s law states that the partial volume, vi, of an ideal gas (i) in a mixture of ideal gases is equal to the volume that gas (i) would occupy if it were alone and was at the pressure and temperature of the gas mixture. Substituting 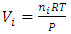 and
and 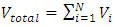 into ideal gas equation we have:
into ideal gas equation we have: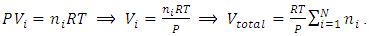 Amagat’s law shows that the total volume is proportional to the total number of molecules of gases. The mole numbers, ni, of an individual gas can be any number (0 < ni < n), can approach to 0. Therefore, ni = 0, 1, 2, 3, and etc. This implies that the total gas volume is the sum of volumes of every single molecule of gas.6.2. The Amagat’s law manifests and depicts the thermal repulsive force molecule modelConspicuously, with
Amagat’s law shows that the total volume is proportional to the total number of molecules of gases. The mole numbers, ni, of an individual gas can be any number (0 < ni < n), can approach to 0. Therefore, ni = 0, 1, 2, 3, and etc. This implies that the total gas volume is the sum of volumes of every single molecule of gas.6.2. The Amagat’s law manifests and depicts the thermal repulsive force molecule modelConspicuously, with 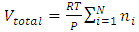 , the Amagat’s law of partial gas volume clearly and accurately tells us that every gas molecule is an independent point source of repulsive force.Every molecule is a mechanical force field (pressure) ball with mechanical radius, r, and effective static mechanical volume
, the Amagat’s law of partial gas volume clearly and accurately tells us that every gas molecule is an independent point source of repulsive force.Every molecule is a mechanical force field (pressure) ball with mechanical radius, r, and effective static mechanical volume 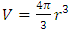 . In atmosphere and in practical calculation, the average volume or effect volume is
. In atmosphere and in practical calculation, the average volume or effect volume is 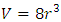 . The mechanical volume is proportional on its temperature, T, and does not depend on the mass of the molecule. Conclusions of analysis of Amagat’s law are exactly same as Dalton’s law, they are not repeated stating here.Section 7 Direct evidence of above deductionsOne assumption of the kinetic theory of gas is: “The number of molecules is large and the volume of the molecules is negligible when compared with the volume of the container.” This assumption is interpreted as that there must be adequate enough numbers of gas molecules to maintain a probability of Boltzmann’s distribution. Therefore there are three practical evidences at least.The first evidence is: when a gas container has a micrometer even nanometer scale crack, the pressure inside the crack is exact same as or identical to the pressure of the container. There is no enough numbers of gas molecules to maintain a Boltzmann’s distribution inside a micrometer or nanometers crack which is also a gas volume! Hence it is contact forces of the molecules acting as point sources of repulsive force just as Dalton’s partial pressure law and Amagat’ partial volume law described that produce and transmit the pressure inside and into the micrometer or nanometer scale crack!The second evidence is: inside a space suit, the air must be maintained an adequate pressure. As we know, the volume of space suit is very small, there is no enough volume of molecules to maintain Boltzmann’s distribution!The third evidence is: the clearances of applicable gas bearings are always in micrometer even nanometer scale, there are not enough molecules to maintain Boltzmann’s distribution. There is no molecules collision there at all; however, there is gas pressure much higher than ambient pressure in the gas bearing clearance. (We will discuss the details of gas bearings in Chapter Three of this paper).Therefore we know that it is the gas molecules acting as point source of repulsive contact force to transmit and maintain gas pressure into and inside the micro gas volumes rather than groundless momentums of collisions.These are anomalies that falsify gas molecules collision assertion.Therefore, there are no elastic collisions between gases molecules at all, if there is some, it must not be the decisive factor of air pressure.
. The mechanical volume is proportional on its temperature, T, and does not depend on the mass of the molecule. Conclusions of analysis of Amagat’s law are exactly same as Dalton’s law, they are not repeated stating here.Section 7 Direct evidence of above deductionsOne assumption of the kinetic theory of gas is: “The number of molecules is large and the volume of the molecules is negligible when compared with the volume of the container.” This assumption is interpreted as that there must be adequate enough numbers of gas molecules to maintain a probability of Boltzmann’s distribution. Therefore there are three practical evidences at least.The first evidence is: when a gas container has a micrometer even nanometer scale crack, the pressure inside the crack is exact same as or identical to the pressure of the container. There is no enough numbers of gas molecules to maintain a Boltzmann’s distribution inside a micrometer or nanometers crack which is also a gas volume! Hence it is contact forces of the molecules acting as point sources of repulsive force just as Dalton’s partial pressure law and Amagat’ partial volume law described that produce and transmit the pressure inside and into the micrometer or nanometer scale crack!The second evidence is: inside a space suit, the air must be maintained an adequate pressure. As we know, the volume of space suit is very small, there is no enough volume of molecules to maintain Boltzmann’s distribution!The third evidence is: the clearances of applicable gas bearings are always in micrometer even nanometer scale, there are not enough molecules to maintain Boltzmann’s distribution. There is no molecules collision there at all; however, there is gas pressure much higher than ambient pressure in the gas bearing clearance. (We will discuss the details of gas bearings in Chapter Three of this paper).Therefore we know that it is the gas molecules acting as point source of repulsive contact force to transmit and maintain gas pressure into and inside the micro gas volumes rather than groundless momentums of collisions.These are anomalies that falsify gas molecules collision assertion.Therefore, there are no elastic collisions between gases molecules at all, if there is some, it must not be the decisive factor of air pressure.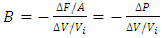 .The speed of sound waves depends on the compressibility and inertia of the medium. If the medium has a bulk modulus B and density ρ, the speed of sound waves in that medium is
.The speed of sound waves depends on the compressibility and inertia of the medium. If the medium has a bulk modulus B and density ρ, the speed of sound waves in that medium is 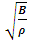 . A sound wave can be considered as either a displacement wave or a pressure wave. 1.2. DiscrepancyThe above descriptions of sound wave contradict and falsify the Boltzmann’s distribution and gas molecule collision assertion.The sound wave of gas of its media (gas) having bulk modulus B that manifests gas is continuum medium and pressure is effect of elasticity (conservative) contact repulsive forces of the medium.Force and pressure are instantaneous values to produce wave and propagate wave that cannot be cumulated by momentums during a time intervals. And the cumulative forces or cumulative momentums do not have instantaneous elastic property of bulk modulus B. Being wave energy, the sound of gases must be potential energy, however chaotic motion collisions of the gas molecules with each other are not conservative forces and do not result in potential energy, this is contradictory to that gases have bulk modulus B.Therefore there must be a repulsive conservative contact force or field of the continuum medium gas (with bulk modulus B,) i.e. there must be a universal (thermal) repulsive force (field) to transfer the compression and expansion of gas medium to propagate sound wave.Section 2 Sound wave being a longitudinal wave contradicts Boltzmann’s distribution and manifests the existence of a thermal repulsive force of gas molecules2.1. Prevailing descriptionsIf the gas molecules move randomly so that any molecule can move in any direction with equal probability as Boltzmann’s distribution described, then sound wave of gas will not be longitudinal wave, rather, it will be spherical wave that propagate in any directions including transversal direction!A sound wave of air is oscillator of compression and expansion of air element and is propagating in longitudinal direction.Both compressed regions of condensation and expanded rarefaction regions are continuously set up and move with a speed equal to the speed of sound in the medium.If Boltzmann’s distribution law or the kinetic theory of gases is tenable, the gas molecules will move randomly mean that any molecule can move in any direction with equal probability and their motion is extremely chaotic. Then the average value of v2 for all the molecules is related to the average values of
. A sound wave can be considered as either a displacement wave or a pressure wave. 1.2. DiscrepancyThe above descriptions of sound wave contradict and falsify the Boltzmann’s distribution and gas molecule collision assertion.The sound wave of gas of its media (gas) having bulk modulus B that manifests gas is continuum medium and pressure is effect of elasticity (conservative) contact repulsive forces of the medium.Force and pressure are instantaneous values to produce wave and propagate wave that cannot be cumulated by momentums during a time intervals. And the cumulative forces or cumulative momentums do not have instantaneous elastic property of bulk modulus B. Being wave energy, the sound of gases must be potential energy, however chaotic motion collisions of the gas molecules with each other are not conservative forces and do not result in potential energy, this is contradictory to that gases have bulk modulus B.Therefore there must be a repulsive conservative contact force or field of the continuum medium gas (with bulk modulus B,) i.e. there must be a universal (thermal) repulsive force (field) to transfer the compression and expansion of gas medium to propagate sound wave.Section 2 Sound wave being a longitudinal wave contradicts Boltzmann’s distribution and manifests the existence of a thermal repulsive force of gas molecules2.1. Prevailing descriptionsIf the gas molecules move randomly so that any molecule can move in any direction with equal probability as Boltzmann’s distribution described, then sound wave of gas will not be longitudinal wave, rather, it will be spherical wave that propagate in any directions including transversal direction!A sound wave of air is oscillator of compression and expansion of air element and is propagating in longitudinal direction.Both compressed regions of condensation and expanded rarefaction regions are continuously set up and move with a speed equal to the speed of sound in the medium.If Boltzmann’s distribution law or the kinetic theory of gases is tenable, the gas molecules will move randomly mean that any molecule can move in any direction with equal probability and their motion is extremely chaotic. Then the average value of v2 for all the molecules is related to the average values of 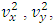 and
and 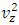 according to the expression
according to the expression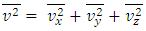 Because the motion is completely random, the average
Because the motion is completely random, the average 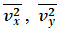 values and
values and 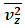 are equal to each other. The average molecular speed increase with increase of temperature, increase of temperature in turn produces an increase in pressure
are equal to each other. The average molecular speed increase with increase of temperature, increase of temperature in turn produces an increase in pressure 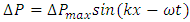 , where the pressure amplitude ΔPmax is the maximum change in pressure from the equilibrium value.2.2. ContradictionIf above prevailing assertions and descriptions of Boltzmann and kinetic theory are tenable, the sound wave of gas will propagate in a way like this:The compressed regions and expanded regions are continuously set up; therefore, result in temperature increasing and decreasing continuously accordingly that in turn produces an increase and decrease in pressure.If so, there are discrepancies:The gas molecules will move in any direction with equal probability, then the average values of
, where the pressure amplitude ΔPmax is the maximum change in pressure from the equilibrium value.2.2. ContradictionIf above prevailing assertions and descriptions of Boltzmann and kinetic theory are tenable, the sound wave of gas will propagate in a way like this:The compressed regions and expanded regions are continuously set up; therefore, result in temperature increasing and decreasing continuously accordingly that in turn produces an increase and decrease in pressure.If so, there are discrepancies:The gas molecules will move in any direction with equal probability, then the average values of 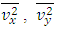 and
and 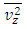 in equation
in equation 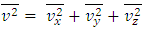 are equal to each other, which will result in equal temperature increase-decrease of molecules in x, y and z directions regions, thus in turn produces an increase-decrease in pressure in x, y and z directions regions.Thus it will produce
are equal to each other, which will result in equal temperature increase-decrease of molecules in x, y and z directions regions, thus in turn produces an increase-decrease in pressure in x, y and z directions regions.Thus it will produce 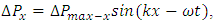
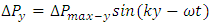 and
and 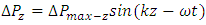 in x, y and z directions.Thus the sound wave will propagate not only in x (longitudinal) directions but also in all directions including y and z directions and any transversal direction.Hence, the phenomenon that the sound wave of gas being a longitudinal wave, is discrepancy or anomaly that theoretically and factually contradicts and falsifies the Boltzmann’s distribution law and the assertion of gas molecules collisions.
in x, y and z directions.Thus the sound wave will propagate not only in x (longitudinal) directions but also in all directions including y and z directions and any transversal direction.Hence, the phenomenon that the sound wave of gas being a longitudinal wave, is discrepancy or anomaly that theoretically and factually contradicts and falsifies the Boltzmann’s distribution law and the assertion of gas molecules collisions.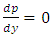 . The shearing stress can be defined as
. The shearing stress can be defined as 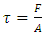 where A is the area of gas film, thus shear stress can be expressed:
where A is the area of gas film, thus shear stress can be expressed: 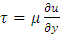 .1.1. Acting forces and pressure distribution analysisThe equation of the equilibrium of the forces in the direction of the flow is as follows
.1.1. Acting forces and pressure distribution analysisThe equation of the equilibrium of the forces in the direction of the flow is as follows 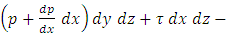
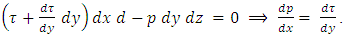 Substitution of τ from Newton’s law of viscosity,
Substitution of τ from Newton’s law of viscosity, 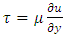 results in
results in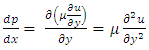
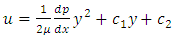
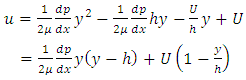
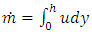
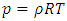 into (3.1.4) yields
into (3.1.4) yields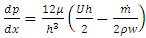
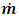 does not change in x direction
does not change in x direction
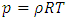 , results in:
, results in: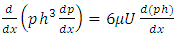
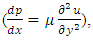 which is the basis and basic working conditions of the dynamic gas bearing. There is energy loss due to friction, then, there will be no Boltzmann’s velocity distribution!2) It is the journal speed, u, that generates the shear stress; therefore, the shear stress generates the pressure gradient. The pressure gradient, i.e., the pressure difference between the (gaps), clearance generates load capacity!If there are velocities of the Boltzmann distribution, the laminar flow of the gas will be spoilt, then, the air bearing will not work! Section 2 Static gas bearing technology contradicts the gas molecule collision notion2.1. Theoretical basic of static gas bearingThere is a significant disparity in the length scale which causes the fluids to flow in a geometry in which one dimension is significantly smaller than others. This is called thin film flow. According to Newton’s Law of Viscosity, the Stokes equation of a Newtonian fluid in Cartesian coordinates is expressed as
which is the basis and basic working conditions of the dynamic gas bearing. There is energy loss due to friction, then, there will be no Boltzmann’s velocity distribution!2) It is the journal speed, u, that generates the shear stress; therefore, the shear stress generates the pressure gradient. The pressure gradient, i.e., the pressure difference between the (gaps), clearance generates load capacity!If there are velocities of the Boltzmann distribution, the laminar flow of the gas will be spoilt, then, the air bearing will not work! Section 2 Static gas bearing technology contradicts the gas molecule collision notion2.1. Theoretical basic of static gas bearingThere is a significant disparity in the length scale which causes the fluids to flow in a geometry in which one dimension is significantly smaller than others. This is called thin film flow. According to Newton’s Law of Viscosity, the Stokes equation of a Newtonian fluid in Cartesian coordinates is expressed as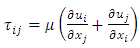
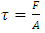 , shear stress can be expressed
, shear stress can be expressed 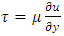 .The pressurized gas is fed from a central orifice into the central recess bearing. The shear stress balancing equation for the central recess bearing is
.The pressurized gas is fed from a central orifice into the central recess bearing. The shear stress balancing equation for the central recess bearing is 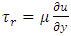 . The Reynolds equation reduces to
. The Reynolds equation reduces to 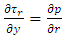 , where p is the pressure and τr is the shear stress in the radial direction.Assuming the element is in equilibrium, the fluid is Newtonian and
, where p is the pressure and τr is the shear stress in the radial direction.Assuming the element is in equilibrium, the fluid is Newtonian and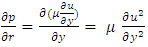
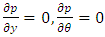 .Integrating in y twice time, obtains
.Integrating in y twice time, obtains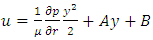
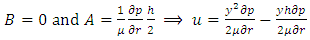
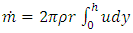
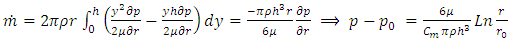
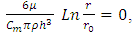 i.e., left side
i.e., left side 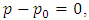 means either p = p0 or p = pambient = 0. Thus, the stiffness of the bearing is zero, the loading capacity is zero, and the bearing will not work at all.For a typical static gas bearing application, the Reynolds number is Re = 2πr*h*ρ*v/μ = 5.76.The Re is less than 2100. Therefore, it is laminar flow. Section 3 Conclusion1) Since gases have viscosity μ = 1.98E-5 (Pa s), there is no elastic collision between molecules of gas! 2) If there is chaotic motion, the gas fluid cannot form laminar flow. If there is no laminar flow, gas flow should not form or generate pressure gradient in radial direction, the derivative of pressure will be zero, thus there is no stiffness, no load capacity, and gas bearing will completely do not work at all! The practicable applications of gas bearings provide direct evidences that the air pressure can be maintained in the clearance of gas bearing without enough volume of molecules to maintain collisions.Therefore, there is no collision between molecules of gas at all. If there is some collision of gas molecules, it must not be the decisive factor of air pressure.These are anomalies that contradictory to and falsify the basic assumption of kinetic theory of gas thus directly falsify Boltzmann’s distribution law and the assertion of gas molecules collisions.
means either p = p0 or p = pambient = 0. Thus, the stiffness of the bearing is zero, the loading capacity is zero, and the bearing will not work at all.For a typical static gas bearing application, the Reynolds number is Re = 2πr*h*ρ*v/μ = 5.76.The Re is less than 2100. Therefore, it is laminar flow. Section 3 Conclusion1) Since gases have viscosity μ = 1.98E-5 (Pa s), there is no elastic collision between molecules of gas! 2) If there is chaotic motion, the gas fluid cannot form laminar flow. If there is no laminar flow, gas flow should not form or generate pressure gradient in radial direction, the derivative of pressure will be zero, thus there is no stiffness, no load capacity, and gas bearing will completely do not work at all! The practicable applications of gas bearings provide direct evidences that the air pressure can be maintained in the clearance of gas bearing without enough volume of molecules to maintain collisions.Therefore, there is no collision between molecules of gas at all. If there is some collision of gas molecules, it must not be the decisive factor of air pressure.These are anomalies that contradictory to and falsify the basic assumption of kinetic theory of gas thus directly falsify Boltzmann’s distribution law and the assertion of gas molecules collisions.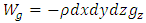 , the force between dz is
, the force between dz is 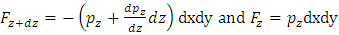


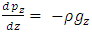 .The temperature T(h) at height h is given by
.The temperature T(h) at height h is given by 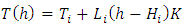 and the changes in gravitational force are less than 5% of height from 0km (sea level) to 100km. However, to pursue the most accurate results, we will still use the data from local gravity and temperatures.Taking different values of temperature and gravitational force of different altitudes into account, for convenience, z in the equation is replaced by altitude h, therefore, the equation is expressed as
and the changes in gravitational force are less than 5% of height from 0km (sea level) to 100km. However, to pursue the most accurate results, we will still use the data from local gravity and temperatures.Taking different values of temperature and gravitational force of different altitudes into account, for convenience, z in the equation is replaced by altitude h, therefore, the equation is expressed as 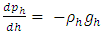 . Substituting
. Substituting 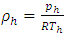 into
into 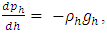 obtains
obtains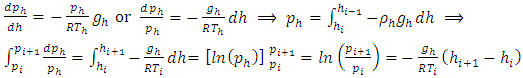
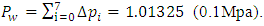 According to previous analysis, we can see clearly that the ideal gas equation is a manifestation of potential energy of the thermal repulsive force of gas. Considering gi ≈ constant g, calculating exponent of both side of the equation (5.3). From ideal gas equation we have
According to previous analysis, we can see clearly that the ideal gas equation is a manifestation of potential energy of the thermal repulsive force of gas. Considering gi ≈ constant g, calculating exponent of both side of the equation (5.3). From ideal gas equation we have 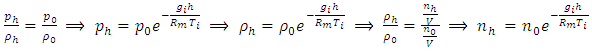 This expression means that gas molecules are cumulated layer by layer over the surface of earth in equilibrium of repulsive forces and gravitational forces result in the exponential form shown as Fig.4.2.
This expression means that gas molecules are cumulated layer by layer over the surface of earth in equilibrium of repulsive forces and gravitational forces result in the exponential form shown as Fig.4.2.
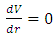 and
and 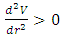 then the system is stable equilibrium.2. Unstable equilibrium: If an object is in an unstable equilibrium, the center of gravity will be altered when a disturbing force is applied, but cannot return to the original position upon removal of the force. Mathematically, if V= V(r) is a maximum then
then the system is stable equilibrium.2. Unstable equilibrium: If an object is in an unstable equilibrium, the center of gravity will be altered when a disturbing force is applied, but cannot return to the original position upon removal of the force. Mathematically, if V= V(r) is a maximum then 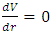 and
and 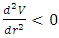 , then the system is unstable equilibrium.3. Neutral equilibrium: If an object is in neutral equilibrium, the center of gravity is unchanged when a disturbing force is applied and the object does not move when the disturbing force is removed. Mathematically, if V= V(r) is a minimum
, then the system is unstable equilibrium.3. Neutral equilibrium: If an object is in neutral equilibrium, the center of gravity is unchanged when a disturbing force is applied and the object does not move when the disturbing force is removed. Mathematically, if V= V(r) is a minimum 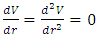 , then the system is in neutral equilibrium.Section 2 Analyzing the equilibrium of the Sun-Earth systemThe potential gravitational force energy of Earth is
, then the system is in neutral equilibrium.Section 2 Analyzing the equilibrium of the Sun-Earth systemThe potential gravitational force energy of Earth is 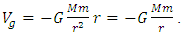 Total energy of earth is Ekinetic + Epotential where
Total energy of earth is Ekinetic + Epotential where 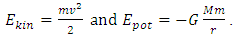 Since Ekin is the energy of motion, is constant and derivative of Ekin = 0. Then the derivative of potential energy is
Since Ekin is the energy of motion, is constant and derivative of Ekin = 0. Then the derivative of potential energy is 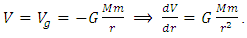 Only when r ∝ ∞, the derivative of potential energy V is equal to zero:
Only when r ∝ ∞, the derivative of potential energy V is equal to zero: 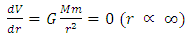 The second derivative of V is
The second derivative of V is 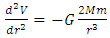 , where the item
, where the item 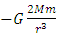 is less than 0 (< 0), then the system will be unstable.This analysis concludes that the current dominant depiction of the Sun-Earth system is an unstable equilibrium. Section 3 ConclusionWhy the dominant model of the solar system is unstable under accurate theoretical analysis? Because the centrifugal force is non-conservative force, it does not result in potential energy and is irreversible. However, the Sun-Earth system seems being in stable equilibrium. Therefore, there must be another conservative repulsive force (opposite to or cancel the conservative gravitational force) between Sun and Earth that is ignored or overlooked by the dominant model, i.e., there must be equilibrium of a conservative repulsive force and the gravitational force between Sun and Earth.Thus the systematic potential energy is the sum of (thermal) repulsive force energy and gravitational force energy.
is less than 0 (< 0), then the system will be unstable.This analysis concludes that the current dominant depiction of the Sun-Earth system is an unstable equilibrium. Section 3 ConclusionWhy the dominant model of the solar system is unstable under accurate theoretical analysis? Because the centrifugal force is non-conservative force, it does not result in potential energy and is irreversible. However, the Sun-Earth system seems being in stable equilibrium. Therefore, there must be another conservative repulsive force (opposite to or cancel the conservative gravitational force) between Sun and Earth that is ignored or overlooked by the dominant model, i.e., there must be equilibrium of a conservative repulsive force and the gravitational force between Sun and Earth.Thus the systematic potential energy is the sum of (thermal) repulsive force energy and gravitational force energy.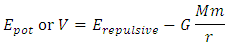 The
The 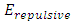 is inversely proportional to the distance r
is inversely proportional to the distance r 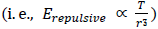 Therefore, when
Therefore, when 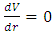 and
and 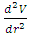 is larger than zero (> 0), the solar system thus can be in stable equilibrium.This is an anomaly could evoke crisis of dominant model of solar system.
is larger than zero (> 0), the solar system thus can be in stable equilibrium.This is an anomaly could evoke crisis of dominant model of solar system. 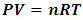 or
or 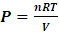 is applied to express an adiabatic process, manifests that the energy transformation is reversible and is potential energy. The forces exerted on gas molecules each other are conservative repulsive forces but not the collision momentums which are not conservative forces and not reversible. Therefore in adiabatic process, the pressure P in
is applied to express an adiabatic process, manifests that the energy transformation is reversible and is potential energy. The forces exerted on gas molecules each other are conservative repulsive forces but not the collision momentums which are not conservative forces and not reversible. Therefore in adiabatic process, the pressure P in 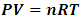 is directly caused by a thermal repulsive conservative contact force of gas molecule.2. General laws of elastic collision disprove the Boltzmann gas velocity distribution.3. Bernoulli Equation and its applications in scientific research and industry contradict and actually falsify Boltzmann’s distribution and gas molecule collision notion.4. Dalton’s law of partial pressures and Amagat’s law of partial volumes imply that the gas molecules are point source of repulsive conservative force and the gas pressure is produced by the repulsive conservative forces exerted on molecules each other rather than chaotic motion of collision.5. Sound wave of gases being as longitudinal wave proves gas is continuum medium with bulk modulus B. It disproves and falsifies Boltzmann’s distribution and the gas molecule collision assertion. It proves that the energy of sound of air is potential energy and the restoring force of sound wave of air is conservative force i.e. a static (thermal) repulsive conservative contact force.6. Practical industry technologies of dynamic gas bearing and static gas bearing falsify the gas collision notion and the Boltzmann’s velocity distribution function.7. Bernoulli Equation and weight deciding atmospheric pressure show us that the motions of gas molecules are produced by macroscopic contact forces and gravitational forces rather than something of unsubstantiated microscopic momentum.The weight of gas molecule layers being decisive factors of atmospheric pressure manifests that there are repulsive contact forces exerted on each other and on surface of earth including water surface of oceans rather than being microscopic momentums.8. Since the centripetal force is not conservative force and is irreversible, therefore the stability of the solar system must be an equilibrium of a conservative repulsive force and the gravitational force between the Sun and planets, i.e. there must be a conservative static universal thermal repulsive force to balance or cancel the gravitational force. Section 2 Discrepancy being worth noting and preliminary conclusions2.1. Discrepancy or contradiction between two descriptions in physics bookContact forces and field forces are two classes of force in classic mechanics, the former forces involve physical contact between two objects, and the later do not involve physical contact between two objects but instead act through empty space. “Other examples of contact forces are the force exerted by gas molecules on the walls of a container.” “The distinction between contact forces and field forces is not as sharp as you may have been led to believe by the previous discussion.” [1] (5.1 THE CONCEPT OF FORCE.)“The model shows that the pressure that a gas exerts on the walls of its container is a consequence of the collisions of the gas molecules with the walls.” [1] (21.1 MOLECULAR MODEL OF AN IDEAL GAS.)It is worth noting that the force of gas molecule exerts on the wall of container is described as “contact force” in 5.1 of reference [1], and is also described as “a consequence of the collisions of the gas molecules” in 21.1 of reference [1].This is obviously an awareness of anomaly or discrepancy by mainstream of physics community that is contradictory to and falsies the basic assumption of kinetic theory of gas thus directly falsifies Boltzmann’s distribution law and the assertion of gas molecules collisions.2.2. Discrepancy between theoretical pressure and sensing pressureBoltzmann’s distribution describes the force and pressure of gas as
is directly caused by a thermal repulsive conservative contact force of gas molecule.2. General laws of elastic collision disprove the Boltzmann gas velocity distribution.3. Bernoulli Equation and its applications in scientific research and industry contradict and actually falsify Boltzmann’s distribution and gas molecule collision notion.4. Dalton’s law of partial pressures and Amagat’s law of partial volumes imply that the gas molecules are point source of repulsive conservative force and the gas pressure is produced by the repulsive conservative forces exerted on molecules each other rather than chaotic motion of collision.5. Sound wave of gases being as longitudinal wave proves gas is continuum medium with bulk modulus B. It disproves and falsifies Boltzmann’s distribution and the gas molecule collision assertion. It proves that the energy of sound of air is potential energy and the restoring force of sound wave of air is conservative force i.e. a static (thermal) repulsive conservative contact force.6. Practical industry technologies of dynamic gas bearing and static gas bearing falsify the gas collision notion and the Boltzmann’s velocity distribution function.7. Bernoulli Equation and weight deciding atmospheric pressure show us that the motions of gas molecules are produced by macroscopic contact forces and gravitational forces rather than something of unsubstantiated microscopic momentum.The weight of gas molecule layers being decisive factors of atmospheric pressure manifests that there are repulsive contact forces exerted on each other and on surface of earth including water surface of oceans rather than being microscopic momentums.8. Since the centripetal force is not conservative force and is irreversible, therefore the stability of the solar system must be an equilibrium of a conservative repulsive force and the gravitational force between the Sun and planets, i.e. there must be a conservative static universal thermal repulsive force to balance or cancel the gravitational force. Section 2 Discrepancy being worth noting and preliminary conclusions2.1. Discrepancy or contradiction between two descriptions in physics bookContact forces and field forces are two classes of force in classic mechanics, the former forces involve physical contact between two objects, and the later do not involve physical contact between two objects but instead act through empty space. “Other examples of contact forces are the force exerted by gas molecules on the walls of a container.” “The distinction between contact forces and field forces is not as sharp as you may have been led to believe by the previous discussion.” [1] (5.1 THE CONCEPT OF FORCE.)“The model shows that the pressure that a gas exerts on the walls of its container is a consequence of the collisions of the gas molecules with the walls.” [1] (21.1 MOLECULAR MODEL OF AN IDEAL GAS.)It is worth noting that the force of gas molecule exerts on the wall of container is described as “contact force” in 5.1 of reference [1], and is also described as “a consequence of the collisions of the gas molecules” in 21.1 of reference [1].This is obviously an awareness of anomaly or discrepancy by mainstream of physics community that is contradictory to and falsies the basic assumption of kinetic theory of gas thus directly falsifies Boltzmann’s distribution law and the assertion of gas molecules collisions.2.2. Discrepancy between theoretical pressure and sensing pressureBoltzmann’s distribution describes the force and pressure of gas as 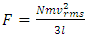 and
and 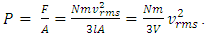 However, the actual gas pressure P is instantaneous value and the molecules have different velocities, 2l/vix and ⊿ti, and various collision frequencies. The consequence of the collisions
However, the actual gas pressure P is instantaneous value and the molecules have different velocities, 2l/vix and ⊿ti, and various collision frequencies. The consequence of the collisions 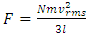 and the momentums of gas molecules need time interval to be cumulated. The container wall of volume gas has no way to accumulate the forces with very different longer and shorter interval time of collisions! Elastic deformations (of feeling of instantaneous pressure) of container wall or diaphragm of sensor cannot be cumulated.Additionally, the molecules with lower velocity should not cause container wall or sensor diaphragm to deform to feel the pressure or force that will reduce the total integral value over the Boltzmann’s distribution accordingly. Being as a better laboratory of gas, the atmosphere in where, the parameters of (thermal repulsive force of) temperature T, density ρ and pressure p can be measured directly; the parameters such as vrms and vms of gas molecule collision theory and Boltzmann distribution function are immeasurable and do not have practical utilities.2.3. Deductions of vrms and vms and further deductions based on them are circular reasoningAll deductions and discussions dealing with or involve in the parameters of vrms and vms of gas molecule are actually circular reasoning. In the argument of kinetic theory of gas, the premise “the average translational kinetic energy E per molecule is
and the momentums of gas molecules need time interval to be cumulated. The container wall of volume gas has no way to accumulate the forces with very different longer and shorter interval time of collisions! Elastic deformations (of feeling of instantaneous pressure) of container wall or diaphragm of sensor cannot be cumulated.Additionally, the molecules with lower velocity should not cause container wall or sensor diaphragm to deform to feel the pressure or force that will reduce the total integral value over the Boltzmann’s distribution accordingly. Being as a better laboratory of gas, the atmosphere in where, the parameters of (thermal repulsive force of) temperature T, density ρ and pressure p can be measured directly; the parameters such as vrms and vms of gas molecule collision theory and Boltzmann distribution function are immeasurable and do not have practical utilities.2.3. Deductions of vrms and vms and further deductions based on them are circular reasoningAll deductions and discussions dealing with or involve in the parameters of vrms and vms of gas molecule are actually circular reasoning. In the argument of kinetic theory of gas, the premise “the average translational kinetic energy E per molecule is 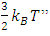 is just as much in need of proof or evidence as the conclusion
is just as much in need of proof or evidence as the conclusion 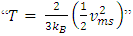 or the premise
or the premise 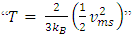 is just the conclusion “E per molecule is
is just the conclusion “E per molecule is 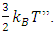 The statement of the kinetic theory is: “the internal energy of an ideal gas depends only on the temperature” because “the temperature is a direct measure of average molecular kinetic energy.”“Temperature is proportional to average kinetic energy” because “The total translational kinetic energy of N molecules of gas is simply N times the average energy per molecule
The statement of the kinetic theory is: “the internal energy of an ideal gas depends only on the temperature” because “the temperature is a direct measure of average molecular kinetic energy.”“Temperature is proportional to average kinetic energy” because “The total translational kinetic energy of N molecules of gas is simply N times the average energy per molecule 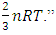 2.4. Preliminary conclusions1. Based on above analysis, we can see clearly that there are no elastic collisions of Boltzmann’s distribution between gas molecules.Anytime and anywhere, with any longer or shorter distance, there are only static stable equilibriums between (thermal) repulsive contact force fields with mechanical radius of gas molecules. The static stable equilibrium of the repulsive force field forms the total pressure of the volume gas.2. Of course, every gas molecule has six degrees of freedom, motion is inevitable. However, the motions of gas molecules are not the causes of gas pressure but the effect of the pressure (thermal repulsive forces). Although the molecules are moving, they are moving slowly not in Boltzmann’s velocity distribution function but in a static equilibrium of conservative contact force. 3. Boltzmann’s distribution function and gas molecule collision assertion actually are substitutes for some transitional science development stages. They are expedient measures in a sense of something better than nothing and a pragmatic tactic as well!The parameters such as vrms and vms of gas molecule collision theory are dummy variables or virtual variables that are of no use but being used only in circular reasoning and boring involution! Section 3 General description and definition of elementary point source particle of thermal repulsive force field of the universal thermal repulsive force (field)1. Every atom or molecule of gas is a point or particle source of the universal static thermal repulsive force field. 2. The magnitude of the thermal repulsive force is proportional to its temperature, T, and is inversely proportional to the distance or its mechanics radii, r, from the point heat source. It is not a function of molecule size and particle mass. 3. When a size of particle (including electron) is equal to or smaller than any molecule size, it acts as a point source of the thermal repulsive force (field).For example, for a gas mixture of H2, He, N2, O2 and CO2 the temperature and pressure are the same, their mechanical radius or force equilibrium radius is identical. 4. The general form of the equation can be written as
2.4. Preliminary conclusions1. Based on above analysis, we can see clearly that there are no elastic collisions of Boltzmann’s distribution between gas molecules.Anytime and anywhere, with any longer or shorter distance, there are only static stable equilibriums between (thermal) repulsive contact force fields with mechanical radius of gas molecules. The static stable equilibrium of the repulsive force field forms the total pressure of the volume gas.2. Of course, every gas molecule has six degrees of freedom, motion is inevitable. However, the motions of gas molecules are not the causes of gas pressure but the effect of the pressure (thermal repulsive forces). Although the molecules are moving, they are moving slowly not in Boltzmann’s velocity distribution function but in a static equilibrium of conservative contact force. 3. Boltzmann’s distribution function and gas molecule collision assertion actually are substitutes for some transitional science development stages. They are expedient measures in a sense of something better than nothing and a pragmatic tactic as well!The parameters such as vrms and vms of gas molecule collision theory are dummy variables or virtual variables that are of no use but being used only in circular reasoning and boring involution! Section 3 General description and definition of elementary point source particle of thermal repulsive force field of the universal thermal repulsive force (field)1. Every atom or molecule of gas is a point or particle source of the universal static thermal repulsive force field. 2. The magnitude of the thermal repulsive force is proportional to its temperature, T, and is inversely proportional to the distance or its mechanics radii, r, from the point heat source. It is not a function of molecule size and particle mass. 3. When a size of particle (including electron) is equal to or smaller than any molecule size, it acts as a point source of the thermal repulsive force (field).For example, for a gas mixture of H2, He, N2, O2 and CO2 the temperature and pressure are the same, their mechanical radius or force equilibrium radius is identical. 4. The general form of the equation can be written as 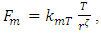 where the kmT is the coefficient constant,
where the kmT is the coefficient constant,  is power of r.5. The atom or molecule of gases is in equilibrium with environmental pressure (or repulsive force field of other molecules).6. In the extreme circumstance of the plasma state, the electrons are separated from nucleus. They act the same as a point source of the thermal repulsive force field like other plasma nuclei or ions.Section 4 Deduction of the accurate rational gas molecule model from physics laws and physical phenomenonBased on the ideal gas equation,
is power of r.5. The atom or molecule of gases is in equilibrium with environmental pressure (or repulsive force field of other molecules).6. In the extreme circumstance of the plasma state, the electrons are separated from nucleus. They act the same as a point source of the thermal repulsive force field like other plasma nuclei or ions.Section 4 Deduction of the accurate rational gas molecule model from physics laws and physical phenomenonBased on the ideal gas equation, 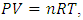 and the above conclusions about point source thermal repulsive force (field), the equation of single gas molecule can be written as
and the above conclusions about point source thermal repulsive force (field), the equation of single gas molecule can be written as 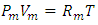 , where Rm is single gas molecule constant, Pm is partial pressure of molecule particle ball, Vm is volume of single gas molecule, T is temperature of the molecule in Kelvin.The Rm is then
, where Rm is single gas molecule constant, Pm is partial pressure of molecule particle ball, Vm is volume of single gas molecule, T is temperature of the molecule in Kelvin.The Rm is then 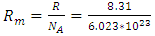 . The volume of single molecule is
. The volume of single molecule is 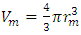 , where rm is force equilibrium radius of gas molecule, or mechanical radius of gas molecule. Partial gas molecule pressure is then
, where rm is force equilibrium radius of gas molecule, or mechanical radius of gas molecule. Partial gas molecule pressure is then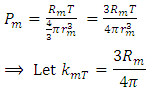
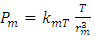
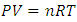 , considering one single gas molecule, the equation can be written as
, considering one single gas molecule, the equation can be written as 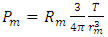 . There is an integral algorithm that can be used to calculate the thermal repulsive force in a certain direction. Integrating with respect to plane areaA plane surface integral of the pressure, Pm, component, is perpendicular to the plane. The calculation is respect to plane area, S. The distance between the central point of the particle (molecule) and the plane is r, as shown in Fig.6.
. There is an integral algorithm that can be used to calculate the thermal repulsive force in a certain direction. Integrating with respect to plane areaA plane surface integral of the pressure, Pm, component, is perpendicular to the plane. The calculation is respect to plane area, S. The distance between the central point of the particle (molecule) and the plane is r, as shown in Fig.6.
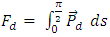
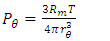
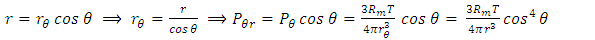

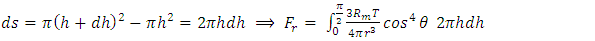
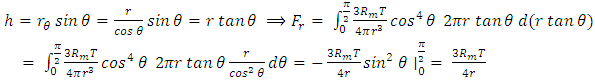

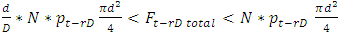
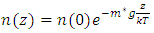 is obtained, where m*g = (m - ρlVp)g is the effective weight of a particle with volume Vp . This gives the gradient
is obtained, where m*g = (m - ρlVp)g is the effective weight of a particle with volume Vp . This gives the gradient 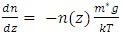 Counting the number of n(z) yields dn/dz and Boltzmann constant. Due to gravity the particles sink down. If the gravity force
Counting the number of n(z) yields dn/dz and Boltzmann constant. Due to gravity the particles sink down. If the gravity force 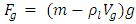 is just compensated by the friction force
is just compensated by the friction force 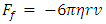 which spherical particle of radius r experience when they fall with velocity v in a medium with viscosity η, the net force is zero. The constant velocity is then
which spherical particle of radius r experience when they fall with velocity v in a medium with viscosity η, the net force is zero. The constant velocity is then 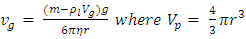 The downward flux of particles jg = vg n creates a concentration gradient dn/dz, which leads to an upward diffusion flux
The downward flux of particles jg = vg n creates a concentration gradient dn/dz, which leads to an upward diffusion flux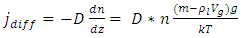 where D is the diffusion coefficient.Finally stationary conditions are reached when both fluxes just cancel. This means
where D is the diffusion coefficient.Finally stationary conditions are reached when both fluxes just cancel. This means 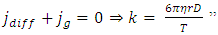 2.2.2. Remarks and questions1. The equation
2.2.2. Remarks and questions1. The equation 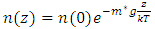 is obtained by observations and not is derived theoretically. Therefore, this is not an effect of equilibrium of kinetic motion, instead of, equilibrium of static forces should be considered first. 2. In equilibrium state, the velocity of small latex particle is zero, therefore friction force due to viscosity, η, of the liquid is zero, the deduction of that “both fluxes
is obtained by observations and not is derived theoretically. Therefore, this is not an effect of equilibrium of kinetic motion, instead of, equilibrium of static forces should be considered first. 2. In equilibrium state, the velocity of small latex particle is zero, therefore friction force due to viscosity, η, of the liquid is zero, the deduction of that “both fluxes 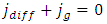 just cancel” is a pseudo-event when friction force is zero.2.3. Comparing with the atmospheric pressure distribution to verify that the vertical density distribution of small particles is an effect of thermal repulsive force fieldThe vertical density distribution of small latex particles is
just cancel” is a pseudo-event when friction force is zero.2.3. Comparing with the atmospheric pressure distribution to verify that the vertical density distribution of small particles is an effect of thermal repulsive force fieldThe vertical density distribution of small latex particles is 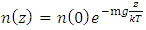 , compare with the molecule number distribution of the atmosphere due to thermal repulsive force
, compare with the molecule number distribution of the atmosphere due to thermal repulsive force 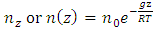 , we can see clearly that both distribution functions are exactly same. Both work on the same physical law of the universal thermal repulsive force, as shown in Fig.8.The back ground difference lies in that the small latex particles have a higher density and a higher thermal repulsive pressure than the liquid. If the small latex particles are not in liquid, the thermal repulsive force is not big enough to distribute in the form of
, we can see clearly that both distribution functions are exactly same. Both work on the same physical law of the universal thermal repulsive force, as shown in Fig.8.The back ground difference lies in that the small latex particles have a higher density and a higher thermal repulsive pressure than the liquid. If the small latex particles are not in liquid, the thermal repulsive force is not big enough to distribute in the form of 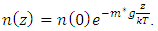 However, the buoyancy force of liquid cancels the partial earth gravitational force and is equivalent to the decrease in the density of solid particles, therefore, the particle distribution is only the equilibrium of the universal thermal repulsive force and the gravitational force of earth which thus is the same situation as the atmosphere on surface of the Earth distributed in exponential form.Therefore we can conclude that the vertical density distribution of small particles is an effect of thermal repulsive force field.Section 2 the earlier air cycle refrigeration can be re-explained by the thermal repulsive force theoryIn the thermodynamic system of gases, any work done by gas system is either done at the expense of the potential energy of thermal repulsive force or done on system to increase the potential energy of thermal repulsive force. The total thermal repulsive force potential energy of a volume of gas is the sum of thermal repulsive force potential energy of every single gas molecule.When the gas system is working, it is the every single gas molecule to transfer or recharge potential energy of thermal repulsive force through changes of temperature T and changes of mechanical volume of molecule Vm or mechanical radius rm of molecule.
However, the buoyancy force of liquid cancels the partial earth gravitational force and is equivalent to the decrease in the density of solid particles, therefore, the particle distribution is only the equilibrium of the universal thermal repulsive force and the gravitational force of earth which thus is the same situation as the atmosphere on surface of the Earth distributed in exponential form.Therefore we can conclude that the vertical density distribution of small particles is an effect of thermal repulsive force field.Section 2 the earlier air cycle refrigeration can be re-explained by the thermal repulsive force theoryIn the thermodynamic system of gases, any work done by gas system is either done at the expense of the potential energy of thermal repulsive force or done on system to increase the potential energy of thermal repulsive force. The total thermal repulsive force potential energy of a volume of gas is the sum of thermal repulsive force potential energy of every single gas molecule.When the gas system is working, it is the every single gas molecule to transfer or recharge potential energy of thermal repulsive force through changes of temperature T and changes of mechanical volume of molecule Vm or mechanical radius rm of molecule.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

