Liu Ke Dian
China
Correspondence to: Liu Ke Dian, China.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The prevailing formula of time dilation assertion of Einstein's SRT is physically and mathematically proven invalid and untenable based on accurate analysis from decisive points of view. This article theoretically and practically falsifies the time dilation formula 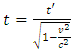 through analyzing and clarifying the exact actual physical situations. Concretely, the article falsifies the formula through two decisive points of view: Point 1: the derivation of the prevailing time dilation formula is based solely on a particular situation; hence the formula is incompatible with and contradicting to any other formulas that are deduced based on universal situations. Point 2: when considering wave property and particle property of the light pulse, the geometrical relationship that meet the Pythagorean Theorem between the two measured light speeds by stationary observer and moving observer which being based to derive the time dilation formula is not existed.
through analyzing and clarifying the exact actual physical situations. Concretely, the article falsifies the formula through two decisive points of view: Point 1: the derivation of the prevailing time dilation formula is based solely on a particular situation; hence the formula is incompatible with and contradicting to any other formulas that are deduced based on universal situations. Point 2: when considering wave property and particle property of the light pulse, the geometrical relationship that meet the Pythagorean Theorem between the two measured light speeds by stationary observer and moving observer which being based to derive the time dilation formula is not existed.
Keywords:
Time dilation, Special relativity theory, Einstein, Frame of reference, Length contraction
Cite this paper: Liu Ke Dian, The Prevailing Time Dilation Formula 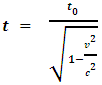 of Einstein’s SRT is Proven Invalid and Untenable Based on Accurate Analysis, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 1, 2023, pp. 20-25. doi: 10.5923/j.ijtmp.20231301.04.
of Einstein’s SRT is Proven Invalid and Untenable Based on Accurate Analysis, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 1, 2023, pp. 20-25. doi: 10.5923/j.ijtmp.20231301.04.
1. Briefing the Derivation of Time Dilation Formula
1.1. Extraction of Book Fundamental of Physics, 8th Edition
“A vehicle moving to the right with a speed v is shown in Figure 1.1a. A mirror is fixed to the ceiling of the vehicle, and observer O’ at rest in this system holds a laser a distance d below the mirror. At some instant, the laser emits a pulse of light directed toward the mirror (event 1), and at some later time after reflecting from the mirror, the pulse arrives back at the laser (event 2). Observer O’ carries a clock C’ and uses it to measure the time interval ⊿t p between these two events.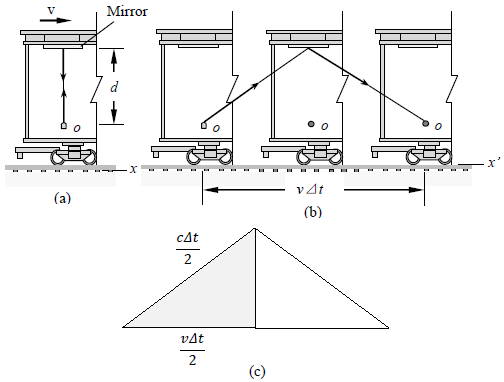 | Figure 1.1. (a) A mirror is fixed to a moving vehicle, and a light pulse is sent out by observer O’ at rest in the vehicle. (b) Relative to a stationary observer O standing alongside the vehicle, the mirror and O’ move with a speed v. Note that what observer O measures for the distance the pulse travels is greater than 2d. (c) The right triangle for calculating the relationship between ⊿t and ⊿t p |
The Pythagorean Theorem gives Solving for ⊿t gives 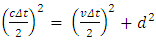 Solving for Δt gives
Solving for Δt gives 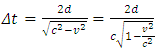 Because ⊿t p = 2d/c, we can express this result as
Because ⊿t p = 2d/c, we can express this result as 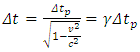 Where
Where 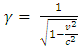 The final report briefly rewritten as
The final report briefly rewritten as 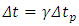 is, in fact, called ‘dilation of time’.”
is, in fact, called ‘dilation of time’.”
1.2. Extraction of Book Concepts of Modern Physics, Sixth Edition
“To see how time dilation comes about, let us consider two clocks shown in Fig.1.2. In each clock a pulse of light is reflected back and forth between two mirrors L0 apart.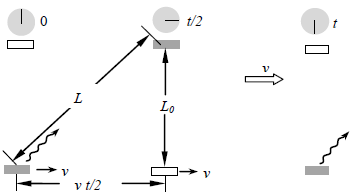 | Figure 1.2 |
One clock is at rest on the ground and the other is in a spacecraft that moves at the speed v. An observer in the laboratory watches both clocks:The time interval between ticks is the proper time t0 and the time needed for the light pulse to travel between the mirrors at the speed of light c is t0 /2. Hence t0/2 = L0/c.Since L0 is the vertical distance between the mirrors, then proper time is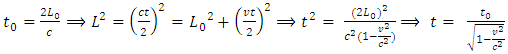
2. (Point of View 1): Derives Based on Universal Situation Manifest Time Dilation Formulas are Self-Confliction and Untenable
No matter whether it is right or wrong actually, the prevailing time dilation formula 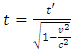 was not derived based on or covering universal situations; it was merely based on a particular motion relationship between light pulse speed and moving vehicle speed.
was not derived based on or covering universal situations; it was merely based on a particular motion relationship between light pulse speed and moving vehicle speed.
2.1. Depiction of Universal Situation
According to the time dilation thinking in above two citations, Einstein and his proponents considered only a particular situation that the propagation direction of light pulse is perpendicular to the direction of moving v. They did not consider the universal situation that the direction of light pulse always has an arbitrary angle φ to the mirrors and moving speed v, as shown in Fig.2.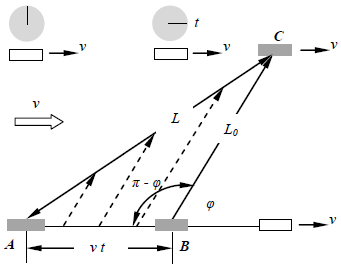 | Figure 2 |
Considering universal situation (we represent 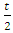 as t for convenient), from the triangle ABC of Fig.2, we have
as t for convenient), from the triangle ABC of Fig.2, we have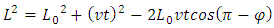 | (2.1) |
Since 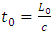 is the time interval t0 between ticks on the clock on the ground, so
is the time interval t0 between ticks on the clock on the ground, so 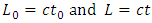 | (2.2) |
Substituting (2.2) into (2.1) obtains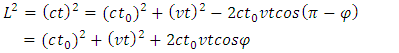 | (2.3) |
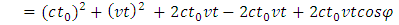 | (2.4) |
Simplified, then the universal relationship of t and t0 is expressed as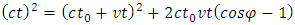 | (2.5) |
2.2. Analyzing the Case When φ = 0
When φ approaches zero, the limiting value of 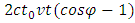 is zero or 0, therefore (2.5) is reduced to Find the square root of both sides, obtains
is zero or 0, therefore (2.5) is reduced to Find the square root of both sides, obtains 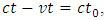 i. e.,
i. e.,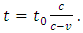 | (2.6) |
2.3. Analyzing the Case When 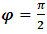
When φ approaches 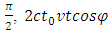 equals zero (0), (2.3) is reduced to
equals zero (0), (2.3) is reduced to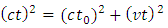 Thus Einstein obtained his time dilation formula,
Thus Einstein obtained his time dilation formula, 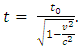 | (2.7) |
2.4. Analyzing the Case When φ = π
When φ approaches π, the limiting value of 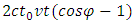 is
is 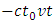 therefore (2.5) is reduced to
therefore (2.5) is reduced to 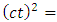
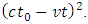 Find the square root of both sides, obtains
Find the square root of both sides, obtains 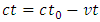 , i.e.,
, i.e.,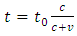 | (2.8) |
2.5. Summarize the All Cases of Extreme Conditions
The time dilation formulas manifest completely different and self-confliction as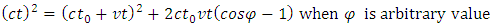 | (2.9) |
 | (2.10) |
 | (2.11) |
 | (2.12) |
The prevailing formula 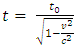 is only account of a particular relationship of the directions of the light pulse and motion of the moving vehicle (light source); it is not general formula of universal situation and is contradicting to other formulas of altered arbitrary situations. This self-confliction completely and firmly falsifies Einstein’s time dilation assertion. Therefore, the prevailing time dilation formula of Einstein’s SRT is invalid and untenable, i.e.,
is only account of a particular relationship of the directions of the light pulse and motion of the moving vehicle (light source); it is not general formula of universal situation and is contradicting to other formulas of altered arbitrary situations. This self-confliction completely and firmly falsifies Einstein’s time dilation assertion. Therefore, the prevailing time dilation formula of Einstein’s SRT is invalid and untenable, i.e.,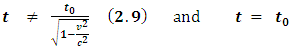 | (2.13) |
(The conclusive formulas of situations when 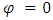 and when
and when 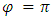 are also contradicting the formulas of Einstein’s Lorentz –Transformation, we do not discuss the details in this paper.)
are also contradicting the formulas of Einstein’s Lorentz –Transformation, we do not discuss the details in this paper.)
3. (Point of view 2): The Two Measured Light Speeds by Stationary Observer and Moving Observer have no Geometrical Relationship to Meet the Pythagorean Theorem
3.1. Slope Direction or Hypotenuse Light Pulse for Stationary Observer is not Existed
As a light pulse, suppose it consists of N wave cycles, its duration time must last a time interval say NΔt which is larger than zero (0 < Δt < NT) and before end of the emission, the light source moves away from the initial 0 time position. As shown in Fig.3.1a and Fig.3.1b. | Figure 3.1a |
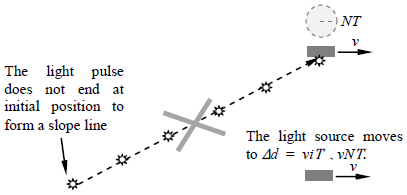 | Figure 3.1b |
The light pulse should not continue to emit wave cycles from a position which is not or no more a light source. After ith cycles or Nth cycles are emitted, the light pulse must be continuously emitted from the moved position a distance Δd = viT or vNT away from the initial position. Therefore, the imagined slope (or hypotenuse) direction light pulse is not existed for stationary no matter wave property or particle property is considered.Therefore, there is no a geometrics relationship of hypotenuse and opposite sides of a right triangular to apply Pythagorean’s theorem to derive the formula 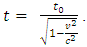
3.2. Accurate Analyses Considering Wave Property of the Light Pulse
Suppose the light pulse consists of N wave cycles, as shown in Fig.3.2. 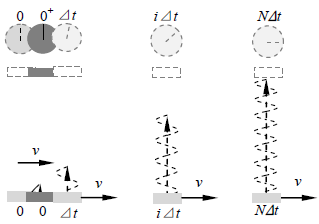 | Figure 3.2 |
In NΔt time interval, the N cycles of light pulse complete the emission and the head of the first cycle approaches the up mirror.3.2.1When the pulse starts off from the down light source it is born with horizontal speed v, due to the moving speed v of light source. Hence, whenever we begin to calculate the propagation distance of the light pulse, the light source is moving away from the initial position concretely.When time is Δt, iΔt, and NΔt successively, the down light source moves forward to new positions with the concrete delta distances away from the initial 0 time position,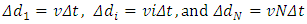 respectively.After the first cycle is emitted, there is a time interval Δt = T delay, the light source is moved to position of
respectively.After the first cycle is emitted, there is a time interval Δt = T delay, the light source is moved to position of 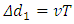 to emit the second cycle.After the ith cycle is emitted, there is a time interval Δt =iT delay, the light source is moved to position of
to emit the second cycle.After the ith cycle is emitted, there is a time interval Δt =iT delay, the light source is moved to position of 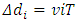 to emit next cycle and so on. Thus, the successive wave cycle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.2.Therefore, both the stationary observer and moving observer measure vertically light pulse. Thus, there is no a right triangular to apply Pythagorean’s theorem to derive the formula
to emit next cycle and so on. Thus, the successive wave cycle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.2.Therefore, both the stationary observer and moving observer measure vertically light pulse. Thus, there is no a right triangular to apply Pythagorean’s theorem to derive the formula 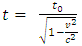 and thus
and thus 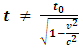 . The prevailing time dilation formula
. The prevailing time dilation formula 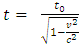 is invalid.Therefore, for the light pulse, the light speeds measured by stationary observer and moving observer are the same
is invalid.Therefore, for the light pulse, the light speeds measured by stationary observer and moving observer are the same 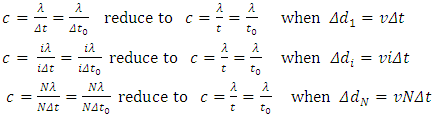 Hence all the equations of light pulse speed (for both stationary observer and moving observer) are the same
Hence all the equations of light pulse speed (for both stationary observer and moving observer) are the same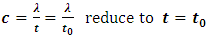 Therefore
Therefore 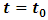 (for the whole light pulse emitting time interval of Δ t > 0)
(for the whole light pulse emitting time interval of Δ t > 0)
3.3. Accurate Analyses Considering Particle Property of the Light Pulse
As a light pulse, suppose it consists of N particles, the light pulse (particles) must continuously moves position away a distance Δdi = viΔt from the initial position.The particles of light pulse must be continuously emitted from a moved position a distance Δdi = viΔt (1< i <N) away from the initial position of the light source when Δ t > 0 as shown in Fig.3.3.3.3.1When the pulse starts off from the down light source, it is born with horizontal speed v, due to the moving of light source in speed v. As shown in Fig.3.3.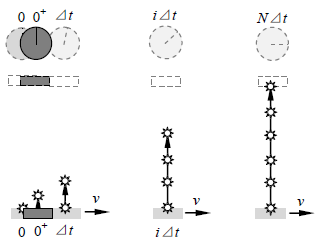 | Figure 3.3 |
When time = Δt, = iΔt, and = NΔt, successively, the down light source moves forward to new positions with the concrete delta distances or displacements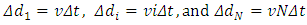 respectively.3.3.2The first particle is starting off from the initial 0 time position. As shown in Fig.3.3.The second particle is starting off from the
respectively.3.3.2The first particle is starting off from the initial 0 time position. As shown in Fig.3.3.The second particle is starting off from the 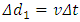 position away from the 0 time position. It is no way for the 2th particle to start off from the initial 0 time position since the light source is moving away. As shown in Fig.3.3.Inductively, the ith particle must be starting off from the position of
position away from the 0 time position. It is no way for the 2th particle to start off from the initial 0 time position since the light source is moving away. As shown in Fig.3.3.Inductively, the ith particle must be starting off from the position of 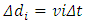 away from the 0 time position. The Nth particle must be starting off from the position of
away from the 0 time position. The Nth particle must be starting off from the position of 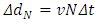 away from the 0 time position respectively. Of course, it is no way for the Nth particle to start off from the initial 0 time position to form a hypotenuse direction light pulse speed at all. Thus, the successive particle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.3.Hence, there is no a geometrics relationship of hypotenuse and opposite sides to form a right triangular to apply Pythagorean’s theorem to derive the formula
away from the 0 time position respectively. Of course, it is no way for the Nth particle to start off from the initial 0 time position to form a hypotenuse direction light pulse speed at all. Thus, the successive particle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.3.Hence, there is no a geometrics relationship of hypotenuse and opposite sides to form a right triangular to apply Pythagorean’s theorem to derive the formula 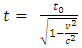 . Therefore, for all the light pulse emitting time interval of Δt, iΔt and NΔ t > 0,
. Therefore, for all the light pulse emitting time interval of Δt, iΔt and NΔ t > 0, 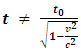 and
and 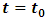 .The prevailing time dilation formula
.The prevailing time dilation formula 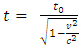 is invalid.
is invalid.
4. Conclusions
From decisive points of view to accurately reanalyze and re-clarify the details of derivation of the time dilation formula, the conclusions and deduced formulas show that the prevailing time dilation formula 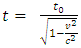 of Einstein’s SRT is self-confliction, untenable and invalid.
of Einstein’s SRT is self-confliction, untenable and invalid.
References
| [1] | B. Arthur: Concepts of Modern Physics, 6th edition. McGraw-Hill Higher Education. |
| [2] | J. Walker: Fundamental of Physics, 8th edition. HALLIDAY·RESNICK. |
| [3] | Einstein, Albert: Relativity, the Special and the General Theory. The Project Gutenberg eBook. |
| [4] | K. Liu: Refuting Einstein’s special relativity theory systematically. American Academic Press. |

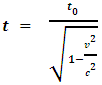 of Einstein’s SRT is Proven Invalid and Untenable Based on Accurate Analysis
of Einstein’s SRT is Proven Invalid and Untenable Based on Accurate Analysis

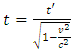 through analyzing and clarifying the exact actual physical situations. Concretely, the article falsifies the formula through two decisive points of view: Point 1: the derivation of the prevailing time dilation formula is based solely on a particular situation; hence the formula is incompatible with and contradicting to any other formulas that are deduced based on universal situations. Point 2: when considering wave property and particle property of the light pulse, the geometrical relationship that meet the Pythagorean Theorem between the two measured light speeds by stationary observer and moving observer which being based to derive the time dilation formula is not existed.
through analyzing and clarifying the exact actual physical situations. Concretely, the article falsifies the formula through two decisive points of view: Point 1: the derivation of the prevailing time dilation formula is based solely on a particular situation; hence the formula is incompatible with and contradicting to any other formulas that are deduced based on universal situations. Point 2: when considering wave property and particle property of the light pulse, the geometrical relationship that meet the Pythagorean Theorem between the two measured light speeds by stationary observer and moving observer which being based to derive the time dilation formula is not existed.
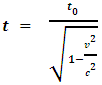 of Einstein’s SRT is Proven Invalid and Untenable Based on Accurate Analysis, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 1, 2023, pp. 20-25. doi: 10.5923/j.ijtmp.20231301.04.
of Einstein’s SRT is Proven Invalid and Untenable Based on Accurate Analysis, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 1, 2023, pp. 20-25. doi: 10.5923/j.ijtmp.20231301.04.
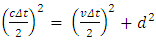 Solving for Δt gives
Solving for Δt gives 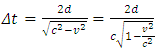 Because ⊿t p = 2d/c, we can express this result as
Because ⊿t p = 2d/c, we can express this result as 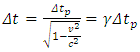 Where
Where 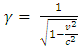 The final report briefly rewritten as
The final report briefly rewritten as 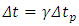 is, in fact, called ‘dilation of time’.”
is, in fact, called ‘dilation of time’.”
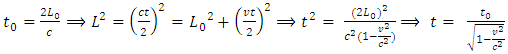
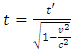 was not derived based on or covering universal situations; it was merely based on a particular motion relationship between light pulse speed and moving vehicle speed.
was not derived based on or covering universal situations; it was merely based on a particular motion relationship between light pulse speed and moving vehicle speed. 
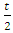 as t for convenient), from the triangle ABC of Fig.2, we have
as t for convenient), from the triangle ABC of Fig.2, we have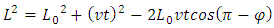
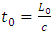 is the time interval t0 between ticks on the clock on the ground, so
is the time interval t0 between ticks on the clock on the ground, so 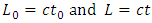
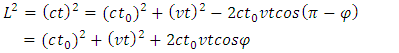
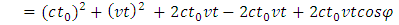
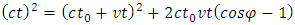
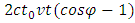 is zero or 0, therefore (2.5) is reduced to Find the square root of both sides, obtains
is zero or 0, therefore (2.5) is reduced to Find the square root of both sides, obtains 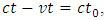 i. e.,
i. e.,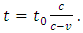
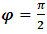
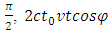 equals zero (0), (2.3) is reduced to
equals zero (0), (2.3) is reduced to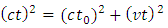 Thus Einstein obtained his time dilation formula,
Thus Einstein obtained his time dilation formula, 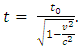
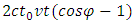 is
is 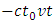 therefore (2.5) is reduced to
therefore (2.5) is reduced to 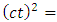
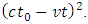 Find the square root of both sides, obtains
Find the square root of both sides, obtains 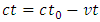 , i.e.,
, i.e.,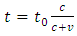
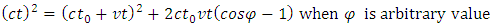



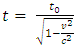 is only account of a particular relationship of the directions of the light pulse and motion of the moving vehicle (light source); it is not general formula of universal situation and is contradicting to other formulas of altered arbitrary situations. This self-confliction completely and firmly falsifies Einstein’s time dilation assertion. Therefore, the prevailing time dilation formula of Einstein’s SRT is invalid and untenable, i.e.,
is only account of a particular relationship of the directions of the light pulse and motion of the moving vehicle (light source); it is not general formula of universal situation and is contradicting to other formulas of altered arbitrary situations. This self-confliction completely and firmly falsifies Einstein’s time dilation assertion. Therefore, the prevailing time dilation formula of Einstein’s SRT is invalid and untenable, i.e.,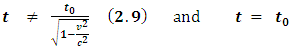
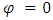 and when
and when 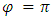 are also contradicting the formulas of Einstein’s Lorentz –Transformation, we do not discuss the details in this paper.)
are also contradicting the formulas of Einstein’s Lorentz –Transformation, we do not discuss the details in this paper.)

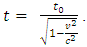

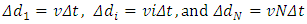 respectively.After the first cycle is emitted, there is a time interval Δt = T delay, the light source is moved to position of
respectively.After the first cycle is emitted, there is a time interval Δt = T delay, the light source is moved to position of 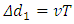 to emit the second cycle.After the ith cycle is emitted, there is a time interval Δt =iT delay, the light source is moved to position of
to emit the second cycle.After the ith cycle is emitted, there is a time interval Δt =iT delay, the light source is moved to position of 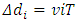 to emit next cycle and so on. Thus, the successive wave cycle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.2.Therefore, both the stationary observer and moving observer measure vertically light pulse. Thus, there is no a right triangular to apply Pythagorean’s theorem to derive the formula
to emit next cycle and so on. Thus, the successive wave cycle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.2.Therefore, both the stationary observer and moving observer measure vertically light pulse. Thus, there is no a right triangular to apply Pythagorean’s theorem to derive the formula 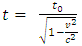 and thus
and thus 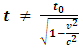 . The prevailing time dilation formula
. The prevailing time dilation formula 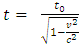 is invalid.Therefore, for the light pulse, the light speeds measured by stationary observer and moving observer are the same
is invalid.Therefore, for the light pulse, the light speeds measured by stationary observer and moving observer are the same 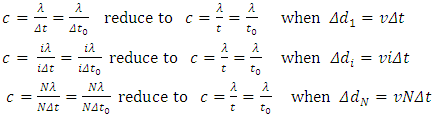 Hence all the equations of light pulse speed (for both stationary observer and moving observer) are the same
Hence all the equations of light pulse speed (for both stationary observer and moving observer) are the same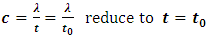 Therefore
Therefore 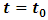 (for the whole light pulse emitting time interval of Δ t > 0)
(for the whole light pulse emitting time interval of Δ t > 0)
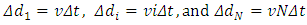 respectively.3.3.2The first particle is starting off from the initial 0 time position. As shown in Fig.3.3.The second particle is starting off from the
respectively.3.3.2The first particle is starting off from the initial 0 time position. As shown in Fig.3.3.The second particle is starting off from the 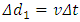 position away from the 0 time position. It is no way for the 2th particle to start off from the initial 0 time position since the light source is moving away. As shown in Fig.3.3.Inductively, the ith particle must be starting off from the position of
position away from the 0 time position. It is no way for the 2th particle to start off from the initial 0 time position since the light source is moving away. As shown in Fig.3.3.Inductively, the ith particle must be starting off from the position of 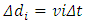 away from the 0 time position. The Nth particle must be starting off from the position of
away from the 0 time position. The Nth particle must be starting off from the position of 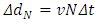 away from the 0 time position respectively. Of course, it is no way for the Nth particle to start off from the initial 0 time position to form a hypotenuse direction light pulse speed at all. Thus, the successive particle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.3.Hence, there is no a geometrics relationship of hypotenuse and opposite sides to form a right triangular to apply Pythagorean’s theorem to derive the formula
away from the 0 time position respectively. Of course, it is no way for the Nth particle to start off from the initial 0 time position to form a hypotenuse direction light pulse speed at all. Thus, the successive particle series of the light pulse form a vertical line rather than any slope line to the stationary observer, as shown in Fig.3.3.Hence, there is no a geometrics relationship of hypotenuse and opposite sides to form a right triangular to apply Pythagorean’s theorem to derive the formula 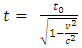 . Therefore, for all the light pulse emitting time interval of Δt, iΔt and NΔ t > 0,
. Therefore, for all the light pulse emitting time interval of Δt, iΔt and NΔ t > 0, 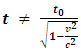 and
and 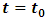 .The prevailing time dilation formula
.The prevailing time dilation formula 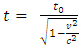 is invalid.
is invalid.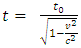 of Einstein’s SRT is self-confliction, untenable and invalid.
of Einstein’s SRT is self-confliction, untenable and invalid.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML