-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2023; 13(1): 15-19
doi:10.5923/j.ijtmp.20231301.03
Received: Jun. 29, 2023; Accepted: Jul. 12, 2023; Published: Jul. 24, 2023

Some New MDS LCD Codes and Entanglement-Assisted Quantum Codes from Constacyclic Codes
Xiaomeng Li, Shibo Wang, Wenting Chen, Jiantao Li
School of Mathematics and Statistics, Liaoning University, Shenyang, China
Correspondence to: Jiantao Li, School of Mathematics and Statistics, Liaoning University, Shenyang, China.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, several classes of linear complementary dual codes and entanglement-assisted quantum codes with good parameters are constructed. The parameters of these codes are not covered by existing results.
Keywords: Linear complementary dual codes, Entanglement-assisted quantum MDS codes, Constacyclic codes
Cite this paper: Xiaomeng Li, Shibo Wang, Wenting Chen, Jiantao Li, Some New MDS LCD Codes and Entanglement-Assisted Quantum Codes from Constacyclic Codes, International Journal of Theoretical and Mathematical Physics, Vol. 13 No. 1, 2023, pp. 15-19. doi: 10.5923/j.ijtmp.20231301.03.
Article Outline
1. Introduction
- Linear complementary dual (LCD) codes are widely used in communication systems, storage systems, cryptography, and consumer electronics. In 1992, Massey [1] introduced the concept of LCD codes. In [2], Sendrier proved that LCD codes meet the asymptotic Gilbert-Varshamov bound. In [3], Yang and Massey provided a sufficient and necessary condition for a cyclic code to be an LCD code. In [4], Dinh showed that if
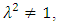 then any λ−constacyclic code over F_q is an LCD code. In [5], J. Qian et al. constructed MDS LCD codes of length q^2+1 and so on. Extensive work has been done on the construction of LCD codes using different methods (see, for example, [6,7]).In addition, there is a close connection between LCD codes and entanglement-assisted quantum codes. If the intersection of a nontrivial α−constacyclic code and its Hermitian dual code is empty, then maximal entanglement EAQEC codes can be constructed and achieve the EA-hashing bound asymptotically [8]. For more information on EAQEC codes, see [9-14].In this paper, based on the above results, we first construct three types of maximal distance separable (MDS) linear complementary dual codes. Then we construct some maximal entanglement MDS EAQEC codes from LCD codes.The paper is organized as follows. In Section 2, some basic definitions and properties of linear codes and constacyclic codes are given. In Section 3, the constructions of MDS LCD codes are presented. In Section 4, some MDS EAQEC codes with maximal entanglement are constructed. Section 5 gives a summary.
then any λ−constacyclic code over F_q is an LCD code. In [5], J. Qian et al. constructed MDS LCD codes of length q^2+1 and so on. Extensive work has been done on the construction of LCD codes using different methods (see, for example, [6,7]).In addition, there is a close connection between LCD codes and entanglement-assisted quantum codes. If the intersection of a nontrivial α−constacyclic code and its Hermitian dual code is empty, then maximal entanglement EAQEC codes can be constructed and achieve the EA-hashing bound asymptotically [8]. For more information on EAQEC codes, see [9-14].In this paper, based on the above results, we first construct three types of maximal distance separable (MDS) linear complementary dual codes. Then we construct some maximal entanglement MDS EAQEC codes from LCD codes.The paper is organized as follows. In Section 2, some basic definitions and properties of linear codes and constacyclic codes are given. In Section 3, the constructions of MDS LCD codes are presented. In Section 4, some MDS EAQEC codes with maximal entanglement are constructed. Section 5 gives a summary.2. Preliminaries
- Let
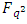 be a finite field with
be a finite field with 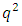 elements, where
elements, where 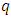 is a power of a prime
is a power of a prime 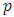 . Now, we present some basic notions and facts about linear codes and constacyclic codes.Definition 2.1 A code
. Now, we present some basic notions and facts about linear codes and constacyclic codes.Definition 2.1 A code 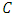 is cyclic if for any cyclic shift of a codeword is also a codeword, i.e.,
is cyclic if for any cyclic shift of a codeword is also a codeword, i.e.,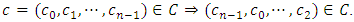 It is well-known that a cyclic code of length
It is well-known that a cyclic code of length 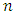 over
over 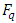 can be identified with an ideal in the residue ring
can be identified with an ideal in the residue ring 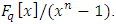 It follows that
It follows that 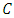 is generated by a monic polynomial
is generated by a monic polynomial 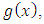 of lowest degree in
of lowest degree in 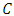 . This polynomial
. This polynomial 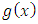 is called the generator polynomial of
is called the generator polynomial of 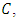 and
and 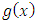 is a monic divisor of
is a monic divisor of 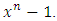 The dimension of
The dimension of 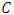 is
is 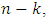 where
where 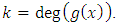 A code
A code 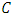 is called a
is called a 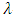 -constacyclic code if
-constacyclic code if 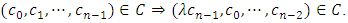 It is well known that the
It is well known that the 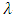 -constacyclic code
-constacyclic code 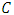 of length
of length 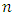 over
over 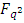 is an ideal of the quotient ring
is an ideal of the quotient ring 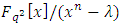 . Let
. Let 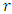 be the order of
be the order of 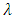 in the multiplicative group
in the multiplicative group 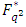 . Then, there exists a primitive
. Then, there exists a primitive 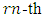 root
root 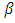 of unity in some extension field of
of unity in some extension field of 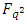 such that
such that 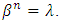 Therefore, the roots of
Therefore, the roots of 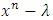 are precisely the elements
are precisely the elements 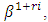 where
where 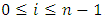 . Define
. Define 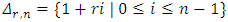 . Let
. Let 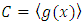 be an
be an 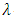 -constacyclic code of length
-constacyclic code of length 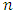 Then the set
Then the set 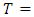
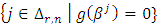 is called the defining set of
is called the defining set of 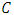 . Let
. Let 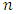 be a positive integer with
be a positive integer with 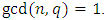 For
For 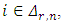 the
the 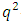 -cyclotomic coset modulo
-cyclotomic coset modulo 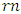 containing an element
containing an element 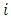 is defined as
is defined as 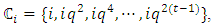 where
where 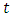 is the smallest positive integer such that
is the smallest positive integer such that 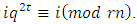 It is easy to see that the defining set
It is easy to see that the defining set 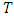 is a union of some
is a union of some 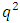 -cyclotomic cosets. The cyclotomic cosets are very important in constructing cyclic codes [15,16].Definition 2.2 For any
-cyclotomic cosets. The cyclotomic cosets are very important in constructing cyclic codes [15,16].Definition 2.2 For any 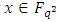 , the conjugate
, the conjugate 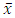 of
of 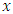 is defined as
is defined as 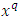 . For two vectors
. For two vectors 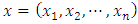 and
and 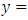
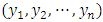 in
in 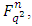 their Hermitian inner product is defined as
their Hermitian inner product is defined as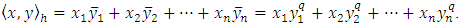 And
And 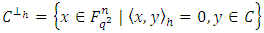 is called the Hermitian dual code of
is called the Hermitian dual code of 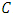 .Definition 2.3 If
.Definition 2.3 If 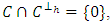 then the linear code
then the linear code 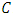 is called a Hermitian linear complementary dual code.The following results are often used to construct LCD codes, see [4,5] for example.Lemma 2.1 Let
is called a Hermitian linear complementary dual code.The following results are often used to construct LCD codes, see [4,5] for example.Lemma 2.1 Let 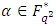 be a primitive
be a primitive 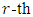 root of unity and
root of unity and 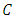 be a nontrivial
be a nontrivial 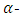 constacyclic code of length
constacyclic code of length 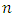 over
over 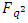 . If
. If 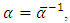 i.e.,
i.e., 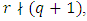 then
then 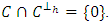 Proposition 2.1 (Singleton bound) If an
Proposition 2.1 (Singleton bound) If an 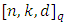 linear code
linear code 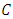 exists,
exists, 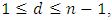 then
then 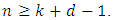 If
If 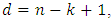 then
then 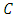 is called a maximum distance separable (MDS, for short) code.Proposition 2.2 (BCH bound) Assume that
is called a maximum distance separable (MDS, for short) code.Proposition 2.2 (BCH bound) Assume that 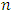 and
and 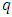 are relatively prime. Let
are relatively prime. Let 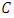 be an
be an 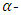 constacyclic code of length
constacyclic code of length 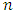 over
over 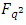 . If the generator polynomial
. If the generator polynomial 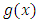 of
of 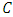 has roots
has roots 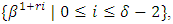 where
where 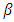 is a primitive
is a primitive 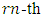 root of unity, then the minimum distance of
root of unity, then the minimum distance of 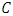 is at least
is at least 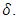
3. Constructions of MDS LCD Codes
3.1. MDS LCD Codes for q ≡ 1 (mod 4)
- In this subsection, assume that
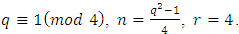 Obviously,
Obviously, 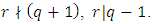 Let
Let 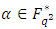 be a primitive
be a primitive 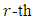 root of unity. Notice that
root of unity. Notice that 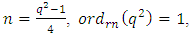 so the
so the 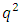 -cyclotomic coset modulo
-cyclotomic coset modulo 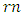 contains only one element. Let
contains only one element. Let 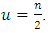 Then
Then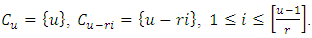 Theorem 3.1 Let
Theorem 3.1 Let 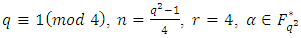 be a primitive
be a primitive 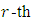 root of unity. Then there exists an
root of unity. Then there exists an 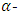 constacyclic MDS LCD code with parameters
constacyclic MDS LCD code with parameters 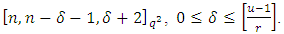 Proof Let
Proof Let 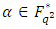 be a primitive
be a primitive 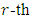 root of unity. Let
root of unity. Let 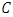 be an
be an 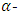 constacyclic code with defining set
constacyclic code with defining set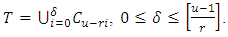 It follows from
It follows from 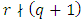 that
that 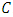 is an LCD code. Note that
is an LCD code. Note that 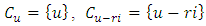 . So, the dimension
. So, the dimension 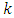 of
of 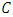 is
is 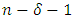 . According to Proposition 2.2, the minimum distance
. According to Proposition 2.2, the minimum distance 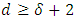 . It follows from Proposition 2.1 that
. It follows from Proposition 2.1 that 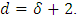 Hence
Hence 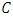 is an MDS LCD code with parameters
is an MDS LCD code with parameters 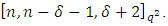 Example 3.1 Let
Example 3.1 Let 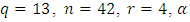 be a primitive 4-th root of unity. Let
be a primitive 4-th root of unity. Let 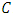 be an
be an 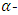 constacyclic code with defining set
constacyclic code with defining set 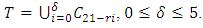 Then there exists MDS LCD codes with parameters
Then there exists MDS LCD codes with parameters 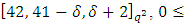
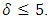 In particular, let
In particular, let 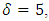 we can obtain MDS LCD codes with parameters
we can obtain MDS LCD codes with parameters 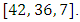
3.2. MDS LCD Codes for q ≡ 3 (mod 4), q ≠ 3
- In this subsection, let
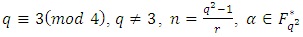 be a primitive
be a primitive 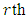 root of unity. Let
root of unity. Let 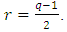 Then
Then 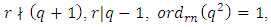 so the
so the 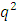 -cyclotomic coset modulo
-cyclotomic coset modulo 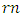 contains only one element. Let
contains only one element. Let 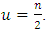 Then
Then 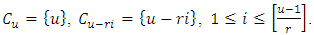 Theorem 3.2 Let
Theorem 3.2 Let 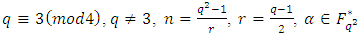 be a primitive
be a primitive 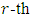 root of unity. Then there exists an
root of unity. Then there exists an 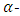 constacyclic MDS LCD code with parameters
constacyclic MDS LCD code with parameters 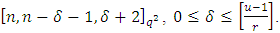 Proof Let
Proof Let 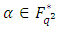 be a primitive
be a primitive 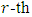 root of unity. Let
root of unity. Let 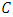 be an
be an 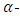 constacyclic code with defining set
constacyclic code with defining set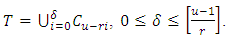 It follows from
It follows from 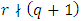 that
that 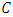 is a LCD code. Note that
is a LCD code. Note that 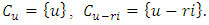 So, the dimension
So, the dimension 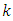 of
of 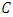 is
is 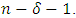 According to Proposition 2.2, the minimum distance
According to Proposition 2.2, the minimum distance 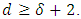 It follows from Proposition 2.1 that
It follows from Proposition 2.1 that 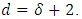 Hence
Hence  is an MDS LCD code with parameters
is an MDS LCD code with parameters 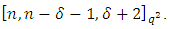
3.3. MDS LCD Codes for q = 3m (m ≥ 2)
- In this subsection, let
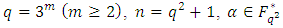 be a primitive
be a primitive 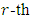 root of unity. Let
root of unity. Let 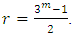 Then
Then 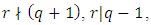 and
and 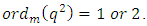 So, the
So, the 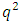 -cyclotomic coset modulo
-cyclotomic coset modulo 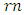 contains one or two elements. Let
contains one or two elements. Let 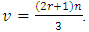 Then
Then 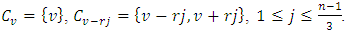 Theorem 3.3 Let
Theorem 3.3 Let 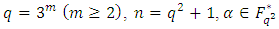 be a primitive
be a primitive 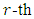 root of unity. Let
root of unity. Let 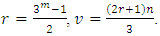 Then there exists an
Then there exists an 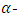 constacyclic MDS LCD code with parameters
constacyclic MDS LCD code with parameters 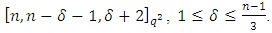 Proof Let
Proof Let 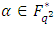 be a primitive
be a primitive 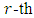 root of unity. Let
root of unity. Let 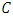 be an
be an 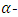 constacyclic code with defining set
constacyclic code with defining set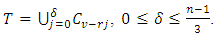 It follows from
It follows from 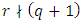 that
that 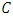 is a LCD code. Note that
is a LCD code. Note that 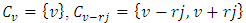 . So, the dimension
. So, the dimension 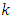 of
of 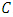 is
is 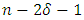 . According to proposition 2.2, the minimum distance
. According to proposition 2.2, the minimum distance 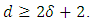 It follows from Proposition 2.1 that
It follows from Proposition 2.1 that 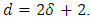 Hence
Hence 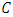 is an MDS LCD code with parameters
is an MDS LCD code with parameters 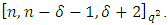 Example 3.2 Let
Example 3.2 Let 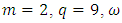 be a primitive
be a primitive 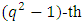 root of unity.
root of unity. 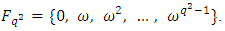 Assume that
Assume that 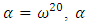 is a primitive 4-th root of unity. Let
is a primitive 4-th root of unity. Let 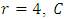 be an
be an 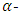 constacyclic code of length
constacyclic code of length 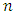 over
over 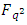 with defining set
with defining set 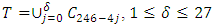 Then we can get MDS LCD codes with parameters
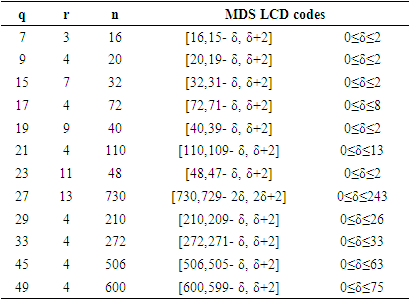
Then we can get MDS LCD codes with parameters 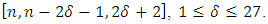 In Table 1, some examples of MDS LCD codes from the above three theorems are given.
In Table 1, some examples of MDS LCD codes from the above three theorems are given.
|
4. Constructions of Entanglement-Assisted Quantum MDS Codes
- In this section, we will use the MDS LCD codes in section 3 to construct entanglement-assisted quantum MDS codes. Basic concepts and facts about entanglement-assisted quantum error-correcting codes can be referred to [5,9,17-18,20].Definition 4.1 An EAQEC code, denoted by
 encodes
encodes 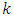 logical qubits into
logical qubits into 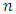 physical qubits using
physical qubits using 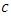 copies of maximally entangled Bell states, and
copies of maximally entangled Bell states, and 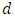 is the minimum distance of the code. Suppose that
is the minimum distance of the code. Suppose that 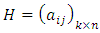 is a
is a 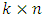 matrix,
matrix, 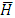 is defined as
is defined as 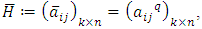 and
and 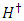 is the transpose matrix of
is the transpose matrix of 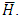 Lemma 4.1 If
Lemma 4.1 If 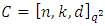 is a linear code over
is a linear code over 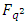 with a parity check matrix
with a parity check matrix 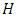 , then there exists an
, then there exists an 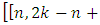
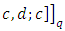 MDS EAQEC code, where
MDS EAQEC code, where 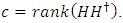 Proposition 4.1 Assume that
Proposition 4.1 Assume that 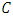 is an entanglement-assisted quantum code with parameters
is an entanglement-assisted quantum code with parameters 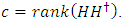 If
If 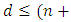
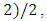 then
then 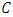 satisfies the entanglement-assisted Singleton bound
satisfies the entanglement-assisted Singleton bound 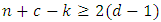 . If
. If 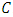 satisfies the equality
satisfies the equality 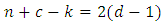 for
for 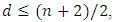 then it is called an entanglement-assisted quantum MDS code.Lemma 4.2 If
then it is called an entanglement-assisted quantum MDS code.Lemma 4.2 If 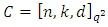 is a linear code over
is a linear code over 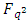 with parity check matrix
with parity check matrix 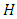 , generator matrix
, generator matrix 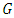 , then
, then 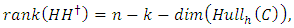 where
where 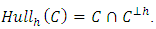 Lemma 4.3 Let
Lemma 4.3 Let 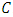 is an LCD code over
is an LCD code over 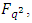 then
then 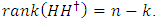 Definition 4.2 Let
Definition 4.2 Let 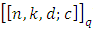 be a
be a 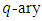 EAQEC code. Then the parameters satisfy the Singleton bound for EAQEC codes:
EAQEC code. Then the parameters satisfy the Singleton bound for EAQEC codes: 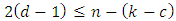 . An EAQEC code meeting this bound is called an MDS EAQEC code.Definition 4.3 A
. An EAQEC code meeting this bound is called an MDS EAQEC code.Definition 4.3 A 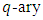 EAQEC code
EAQEC code 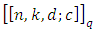 with
with 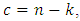 is called a maximal entanglement EAQEC code.Such quantum codes have better properties and efficiency, and can gradually reach the EA-hashing bound [19].
is called a maximal entanglement EAQEC code.Such quantum codes have better properties and efficiency, and can gradually reach the EA-hashing bound [19].4.1. MDS EAQEC Codes for q ≡ 1 (mod 4)
- Theorem 4.1 Let
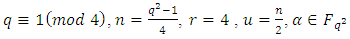 be a primitive
be a primitive 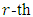 root of unity. Then there exists a maximal entanglement MDS EAQEC code with parameters
root of unity. Then there exists a maximal entanglement MDS EAQEC code with parameters 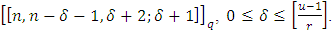 Proof According to Theorem 3.1, there exists an
Proof According to Theorem 3.1, there exists an 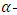 constacyclic MDS LCD code
constacyclic MDS LCD code 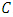 with parameters
with parameters 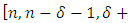
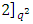 . Assume the check matrix is
. Assume the check matrix is 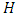 . So,
. So, 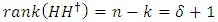 . Then there exists an EAQEC code with parameters
. Then there exists an EAQEC code with parameters 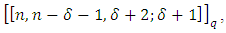
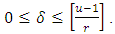
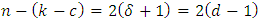 reaches the Singleton bound for EAQEC code, and
reaches the Singleton bound for EAQEC code, and 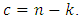
4.2. MDS EAQEC Codes for q ≡ 3 (mod 4), q ≠ 3
- Theorem 4.2 Let
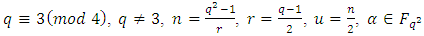 be a primitive
be a primitive 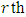 root of unity. Then there exists a maximal entanglement MDS EAQEC code with parameters
root of unity. Then there exists a maximal entanglement MDS EAQEC code with parameters 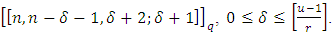 Proof According to Theorem 3.2, there exists an
Proof According to Theorem 3.2, there exists an 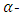 constacyclic MDS LCD code
constacyclic MDS LCD code 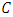 with parameters
with parameters 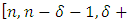
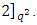 Assume the check matrix is
Assume the check matrix is 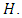 Then
Then 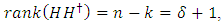 there exists an EAQEC code with parameters
there exists an EAQEC code with parameters 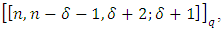
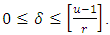
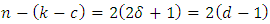 reaches the Singleton bound for EAQEC code, and
reaches the Singleton bound for EAQEC code, and 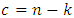 .
.4.3. MDS EAQEC Codes for q = 3m (m ≥ 2)
- Theorem 4.3 Let
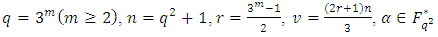 be a primitive
be a primitive 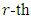 root of unity. Then there exists a maximal entanglement MDS EAQEC code with parameters
root of unity. Then there exists a maximal entanglement MDS EAQEC code with parameters 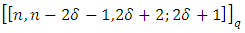
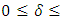
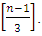 Proof According to Theorem 3.3, there exists an
Proof According to Theorem 3.3, there exists an 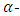 constacyclic MDS LCD code
constacyclic MDS LCD code 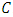 with parameters
with parameters 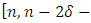
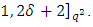 Assume the check matrix is
Assume the check matrix is 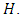 . Then
. Then 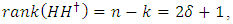 there exists an EAQEC code with parameters
there exists an EAQEC code with parameters 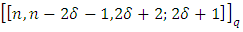 ,
, 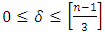 .
. 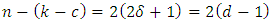 reaches the Singleton bound for EAQEC code, and
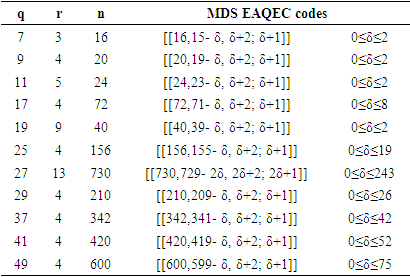
reaches the Singleton bound for EAQEC code, and 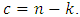 In Table 2, Some examples of maximal entanglement MDS EAQEC codes from the above theorems are given.
In Table 2, Some examples of maximal entanglement MDS EAQEC codes from the above theorems are given.
|
5. Conclusions
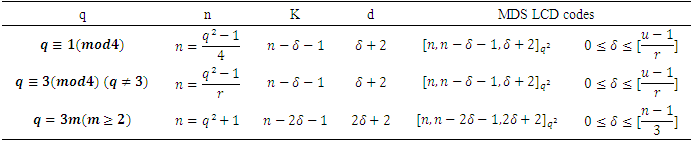
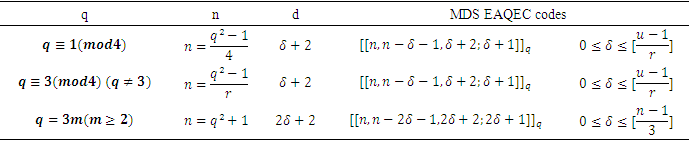
- In this paper, three types of maximal distance separable linear complementary dual codes are constructed as follows:
|
|
ACKNOWLEDGEMENTS
- The research was supported by the general project for the department of Liaoning Education [Grant number: LJKZ0096].
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML