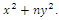-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2022; 12(2): 63-78
doi:10.5923/j.ijtmp.20221202.03
Received: Oct. 30, 2022; Accepted: Nov. 16, 2022; Published: Nov. 24, 2022

Riemann Hypothesis, Birch.S-Dyer, and Navier Stokes Conjectures Solved. Platonian Theory of Everything
Salahdin Daouairi
Research Scientist, USA
Correspondence to: Salahdin Daouairi , Research Scientist, USA.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

An extension to my previous articles [1] & [2], articles that I was credited and awarded in December 2019 with the Cockburn memorial medal by the European and Australian art & science organization for proving the 400 B.C Plato’s conjecture “Our Universe structure is simply a projection of the mathematical universe structure! The aim of this mathematical physical research paper is to prove the validity and the consistency of my Platonian Theory of Everything by solving Riemann Hypothesis, Birch-Swinnerton-Dyer BSD conjectures, and the Navier Stokes based on the equation of the T.o.E [1] & [2]! Where the physical Navier stokes is just an application to this Platonian T.o.E! A theory that describes the mathematical foundation of general system’s structures & distributions. First, we solve the concept of infinity, which is a primordial problem confronted by mathematicians & physicists! Link algebraic number theory to algebraic geometry & topology, and harmonic analysis, by building bridge between analytical L-functions and hyperbolical geometry of low dimension through algebraic variety! The paper consists of describing the packing of the sets  and its extensions, based on an irregular sphere packing method, then describes the geometrical & topological representation of these sets, describes the structure & the modular dynamical discrete system that is based on an infinite fractal horocycle flow expanding hyperbolically “Big Bang in Number Theory”, solves the splitting & the density volume of the prime numbers, then determines the singularity of the fractal connected hyperspace manifold system to solve R.H & BSD, and based on we prove as an application to the theory: the Navier Stokes conjecture, that shows its footprint in the structure and dynamical structure of the invariant mathematical system!. This mathematical model is considered as the foundation of mathematics & science to disclose the hidden truth behind the mathematical universe by analyzing its physical structure and its dynamical system. An Ultimate Grand Unification Theory of Mathematics & Theory of Everything Model. A theory of winding and intertwining based on the mathematical invariants: Legendre symbol in Algebraic number theory, linking number in knot theory & winding number in analysis that show similarity for an asymmetrical entangled system! A model that will ease the understanding of the structure of many natural & artificial physical systems and its chaotic distributions! A theory that contradicts Gödel’s incompleteness theorem due to the periodical fractal properties of the mathematical invariant universe system! At the end of the paper, I will be providing the shortest Equation for the T.o.E!
and its extensions, based on an irregular sphere packing method, then describes the geometrical & topological representation of these sets, describes the structure & the modular dynamical discrete system that is based on an infinite fractal horocycle flow expanding hyperbolically “Big Bang in Number Theory”, solves the splitting & the density volume of the prime numbers, then determines the singularity of the fractal connected hyperspace manifold system to solve R.H & BSD, and based on we prove as an application to the theory: the Navier Stokes conjecture, that shows its footprint in the structure and dynamical structure of the invariant mathematical system!. This mathematical model is considered as the foundation of mathematics & science to disclose the hidden truth behind the mathematical universe by analyzing its physical structure and its dynamical system. An Ultimate Grand Unification Theory of Mathematics & Theory of Everything Model. A theory of winding and intertwining based on the mathematical invariants: Legendre symbol in Algebraic number theory, linking number in knot theory & winding number in analysis that show similarity for an asymmetrical entangled system! A model that will ease the understanding of the structure of many natural & artificial physical systems and its chaotic distributions! A theory that contradicts Gödel’s incompleteness theorem due to the periodical fractal properties of the mathematical invariant universe system! At the end of the paper, I will be providing the shortest Equation for the T.o.E!
Keywords: Riemann Hypothesis Birch Swinnerton Dyer Navier Stokes conjectures Theory of Everything Entanglement Number Theory Algebraic geometric
Cite this paper: Salahdin Daouairi , Riemann Hypothesis, Birch.S-Dyer, and Navier Stokes Conjectures Solved. Platonian Theory of Everything, International Journal of Theoretical and Mathematical Physics, Vol. 12 No. 2, 2022, pp. 63-78. doi: 10.5923/j.ijtmp.20221202.03.
Article Outline
1. Introduction
- In the year 1990 while I was studying in the college “Mathematique Superieur, Nice, France”, I was inspired by this paradox idea that came to my mind “Numbers are in dynamic, but numbers are independent from spacetime” [1] & [2]. My second intrigued question is about the concept of infinity that confronted mathematicians and physicist to solve many problems. This paper from biggening to the end is a formulated step by step to answer and solve the equation of Navier Stokes, which is an application to the Platonian T.o.E, based on Riemann Hypothesis, and Birch.S-Dyer conjectures. This paper is a continuation to my previous papers to unveil the mystery hidden behind the structure of the discrete system defined by integers and their extensions. The manufacturing process system of mathematics: That describes the representation geometric, topologic & analytic of the numbers by its analogous: points, loops, or volume. A diagram that shows the physical structure & the flow of the invariant mathematical system. A model to ease the understanding of all kinds of natural & artificial systems evolution, through this manufacturing process system, where the discrete system represents the products in this manufacturing system, a giant abstract machine!
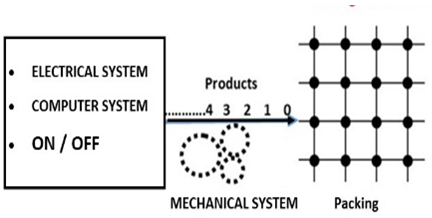 The concept of manufacturing system discovered by humankind in the industrial field, existed already in the abstract invariant mathematical system. A very interesting fact about the sequence 1,2,3…. Set of ℤ & Its extensions is that the sequence is simply the product of a machinery process system lined on a belt as a strict line on a 1- dimensional lattice, but in the reality the transformation or the sequence results from an abstract manufacturing numerical system process with multiple generators or symmetry transformations like the Rubik cube that describe a lattice in dynamic in higher dimension! The numerical system is generated by an intelligent super-computer system that codes, decodes and corrects error codes, combined with general systems for a manufacturing process: from mechanical, electrical, thermodynamical, communication system through optimal packing process to distributing, a cyclic periodical process of transformations. A model that will lead us to unify fields of mathematics and interconnect it with physics and other science & art fields by describing its technical process and physical functionality. The invariant mathematical system is in dynamic that we are not aware off, a giant abstract intelligent machine! An abstract conscious living natural system that exists and self-aware of any error in its system, while logic steers and control its cybernetic system “The Universe of Information”.
The concept of manufacturing system discovered by humankind in the industrial field, existed already in the abstract invariant mathematical system. A very interesting fact about the sequence 1,2,3…. Set of ℤ & Its extensions is that the sequence is simply the product of a machinery process system lined on a belt as a strict line on a 1- dimensional lattice, but in the reality the transformation or the sequence results from an abstract manufacturing numerical system process with multiple generators or symmetry transformations like the Rubik cube that describe a lattice in dynamic in higher dimension! The numerical system is generated by an intelligent super-computer system that codes, decodes and corrects error codes, combined with general systems for a manufacturing process: from mechanical, electrical, thermodynamical, communication system through optimal packing process to distributing, a cyclic periodical process of transformations. A model that will lead us to unify fields of mathematics and interconnect it with physics and other science & art fields by describing its technical process and physical functionality. The invariant mathematical system is in dynamic that we are not aware off, a giant abstract intelligent machine! An abstract conscious living natural system that exists and self-aware of any error in its system, while logic steers and control its cybernetic system “The Universe of Information”.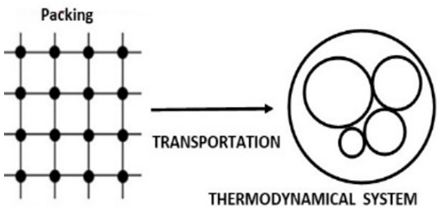 The mathematical universe is an entangled, bipolar asymmetrical system that doesn’t tangle, with structure magnetic “Hopf’s fibration”. Gravity exists even in the numerical system, defined by curvature of the modular lattices while in dynamics! We mentioned in the previous papers that the equation of spacetime is embedded in the mathematical universe, defined by two intertwining modular lattices that swaps roots & fixed points.
The mathematical universe is an entangled, bipolar asymmetrical system that doesn’t tangle, with structure magnetic “Hopf’s fibration”. Gravity exists even in the numerical system, defined by curvature of the modular lattices while in dynamics! We mentioned in the previous papers that the equation of spacetime is embedded in the mathematical universe, defined by two intertwining modular lattices that swaps roots & fixed points. 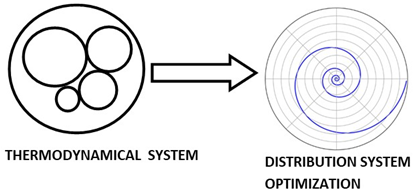 Once we introduce the concept of motion in mathematics, we discover those hidden properties. In this article we going to discover the mechanism of the frequencies of the heartbeat of the mathematical universe and its template projection, through a special modular knot analogous to frequencies to define the hyperbolic volume determined by the flow of its respiratory system, an analogous property to solve Navier Stokes equation which is naturally & abstractly live in the realm of the mathematical invariant system. The Code of our Reality This article is writing with simple mathematical methods, to ease the understanding for everyone the concept of our reality, since the truth based on simple equations. Our inspiration by the code of creation, gave us no choice but to choose the red pill to discover that hidden matrix: The magnificent wonderland of our reality! Mathematic is elegantly beautiful by nature but by uncovering its hidden secret then there is more to discover, from elegancy of its structure to divine truth to it! The beauty here is defined by the flow of its projected artistic geometric picture. A challenging tour for our mind to explore the realm of the mathematical ideal universe; a marvelous place where we will indulge the melody and the rhythmic harmony of the physical abstract Mathematical universe! A colorful tapestry which is seen as an artistic piece of art that shows beauty in its infinite fractal flow of coded patterns with abstract rhythmic musical beats that unfold in time [10]. A true philosophical metaphor that I proved in this comparison theory between the concrete universe and the abstract ideal universe where I attempt to show similitude of properties between the two holographic realms of universes. This theory finally will disclose that hidden bridge between the school of philosophical thoughts to prove the consistency of the 400 BC Plato’s conjecture and defeat Aristotle’s school of concrete narrowed thought. Our spacetime equation is hidden theoretically in the structure and the flow of the mathematical system! Our universe and its embedding fractal cosmic systems reality are simply a copy of the projection of the mathematical universe reality. The Asymmetrical entangled Mathematical Universe: Mathematic is asymmetrical by nature, defined by 3 kinds of asymmetries: Invariant/variant, internal asymmetry, and external asymmetry. 1- invariant/variant mathematics: Invariant mathematics described by a chain of interconnected invariant mathematical systems under symmetry transformations, generated by cyclic transformations, while variant mathematical systems are changeable that degenerate into the invariant systems. Although invariant theories are of two kinds: Abelian and Non-Abelian then you have solvable & non solvable groups. 2- Internal asymmetry seen in its asymmetrical mathematical abstract entities: binary system 0/1, +/-,
Once we introduce the concept of motion in mathematics, we discover those hidden properties. In this article we going to discover the mechanism of the frequencies of the heartbeat of the mathematical universe and its template projection, through a special modular knot analogous to frequencies to define the hyperbolic volume determined by the flow of its respiratory system, an analogous property to solve Navier Stokes equation which is naturally & abstractly live in the realm of the mathematical invariant system. The Code of our Reality This article is writing with simple mathematical methods, to ease the understanding for everyone the concept of our reality, since the truth based on simple equations. Our inspiration by the code of creation, gave us no choice but to choose the red pill to discover that hidden matrix: The magnificent wonderland of our reality! Mathematic is elegantly beautiful by nature but by uncovering its hidden secret then there is more to discover, from elegancy of its structure to divine truth to it! The beauty here is defined by the flow of its projected artistic geometric picture. A challenging tour for our mind to explore the realm of the mathematical ideal universe; a marvelous place where we will indulge the melody and the rhythmic harmony of the physical abstract Mathematical universe! A colorful tapestry which is seen as an artistic piece of art that shows beauty in its infinite fractal flow of coded patterns with abstract rhythmic musical beats that unfold in time [10]. A true philosophical metaphor that I proved in this comparison theory between the concrete universe and the abstract ideal universe where I attempt to show similitude of properties between the two holographic realms of universes. This theory finally will disclose that hidden bridge between the school of philosophical thoughts to prove the consistency of the 400 BC Plato’s conjecture and defeat Aristotle’s school of concrete narrowed thought. Our spacetime equation is hidden theoretically in the structure and the flow of the mathematical system! Our universe and its embedding fractal cosmic systems reality are simply a copy of the projection of the mathematical universe reality. The Asymmetrical entangled Mathematical Universe: Mathematic is asymmetrical by nature, defined by 3 kinds of asymmetries: Invariant/variant, internal asymmetry, and external asymmetry. 1- invariant/variant mathematics: Invariant mathematics described by a chain of interconnected invariant mathematical systems under symmetry transformations, generated by cyclic transformations, while variant mathematical systems are changeable that degenerate into the invariant systems. Although invariant theories are of two kinds: Abelian and Non-Abelian then you have solvable & non solvable groups. 2- Internal asymmetry seen in its asymmetrical mathematical abstract entities: binary system 0/1, +/-,  12/21.3- External asymmetry described by the asymmetrical system {math/logic}, where math is an extension to logic while logic is mathematical that derive from mathematics seen as feedback loops that control the mathematical input statements of the system. Logic acts as the consciousness or generator that control the entropy of the mathematical cybernetic system.
12/21.3- External asymmetry described by the asymmetrical system {math/logic}, where math is an extension to logic while logic is mathematical that derive from mathematics seen as feedback loops that control the mathematical input statements of the system. Logic acts as the consciousness or generator that control the entropy of the mathematical cybernetic system.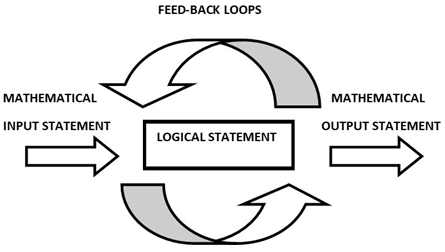 The mathematical loop network system: Loops and feedback loops are one of the characteristic primordial to define the action or reaction of an abstract or concrete system related indirectly to time and motion, it encompasses our everyday life activities from communication, transportation, friendship to feeling described by a graph, network or by web. Which give birth to Category Theory In mathematics, where we define loops by functors, maps, functions, transformations, relations, array, string, fibers, knot, edge, strands, step, and word categorized by a mathematical input statement and a mathematical output statement while between the two there is a logical argument as a feedback loop that control the mathematical statements. Structure of the mathematical Universe Template: The foundation of the invariant mathematical system is based on a stack of fibers, an asymmetrical fibered space described as a fractal of asymmetrical embedded fibered spaces. By cutting through a hyper-plan the asymmetrical stacked fibers, the cross section then describes a discrete lattice, an asymmetrical granular space which is the dual of the fibered space with discrete structure that generates a lattice field corresponding to an n-simplex
The mathematical loop network system: Loops and feedback loops are one of the characteristic primordial to define the action or reaction of an abstract or concrete system related indirectly to time and motion, it encompasses our everyday life activities from communication, transportation, friendship to feeling described by a graph, network or by web. Which give birth to Category Theory In mathematics, where we define loops by functors, maps, functions, transformations, relations, array, string, fibers, knot, edge, strands, step, and word categorized by a mathematical input statement and a mathematical output statement while between the two there is a logical argument as a feedback loop that control the mathematical statements. Structure of the mathematical Universe Template: The foundation of the invariant mathematical system is based on a stack of fibers, an asymmetrical fibered space described as a fractal of asymmetrical embedded fibered spaces. By cutting through a hyper-plan the asymmetrical stacked fibers, the cross section then describes a discrete lattice, an asymmetrical granular space which is the dual of the fibered space with discrete structure that generates a lattice field corresponding to an n-simplex 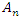 a set of regular polytopes. There exists an interesting connection between prime numbers, points, loops & volume of polytopes that we going to prove in this article to describe the mathematical modular coded asymmetrical template to solve Riemann Hypothesis & Navier Stokes conjecture. The Entangled Mathematical system: To study the macro mathematical system, we need first to analyze the structure and the flow of its micro mathematical system based on the set of two asymmetrical loops with cases that split, splice, inert or ramify, properties that are common between its embedding mathematical systems defined by the family of moduli spaces. By introducing a coded binary relation to the system to describe the coded hyper-graph of the mathematical micro-system, and through an asymmetrical hyper-invariant discrete lattice it will generate the macro mathematical system, which is the infinite cyclic flow generated by torus knots with hyperbolic modular flow. The micro asymmetrical mathematical system is analogous to the logical system which is defined by the basic foundation set
a set of regular polytopes. There exists an interesting connection between prime numbers, points, loops & volume of polytopes that we going to prove in this article to describe the mathematical modular coded asymmetrical template to solve Riemann Hypothesis & Navier Stokes conjecture. The Entangled Mathematical system: To study the macro mathematical system, we need first to analyze the structure and the flow of its micro mathematical system based on the set of two asymmetrical loops with cases that split, splice, inert or ramify, properties that are common between its embedding mathematical systems defined by the family of moduli spaces. By introducing a coded binary relation to the system to describe the coded hyper-graph of the mathematical micro-system, and through an asymmetrical hyper-invariant discrete lattice it will generate the macro mathematical system, which is the infinite cyclic flow generated by torus knots with hyperbolic modular flow. The micro asymmetrical mathematical system is analogous to the logical system which is defined by the basic foundation set 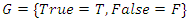 with the elements defined by the loop logical statements true or false analogous to the binary system
with the elements defined by the loop logical statements true or false analogous to the binary system 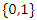 described sometimes by
described sometimes by 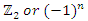 through an alternate oscillation.The Hidden dimension of the truth: One of the important elements of
through an alternate oscillation.The Hidden dimension of the truth: One of the important elements of 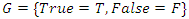 is the axis of the system, since our theory based on motion, the two asymmetrical abstract entities considered as loops
is the axis of the system, since our theory based on motion, the two asymmetrical abstract entities considered as loops 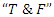 are orbiting in opposite direction around an axis! Here we represent the continuous system by the dynamical of the discrete system, extension of two asymmetrical points! The vector field then defined by a rotation, translation, or a twist, defined either in a hyperbolic space, analytic, or combined. The axis is with great importance, a reason why qubit system such as “quantum qubit system” is with great performance to detect the path between initial state and output final state, rather than our classic computer system which is based on binary system. Eventually the mystery is hidden in the axis of the system the backbone of the mathematical system! By unveiling the hidden properties of the axis, we going to discover the hidden dimensions, the geometrical shape, and the code of this micro system defined by 2 asymmetrical entities, properties that will lead us to analysis Navier Stokes to define the flow of the fluid & gas systems. Let’s denote by the micro asymmetrical system defined by the set
are orbiting in opposite direction around an axis! Here we represent the continuous system by the dynamical of the discrete system, extension of two asymmetrical points! The vector field then defined by a rotation, translation, or a twist, defined either in a hyperbolic space, analytic, or combined. The axis is with great importance, a reason why qubit system such as “quantum qubit system” is with great performance to detect the path between initial state and output final state, rather than our classic computer system which is based on binary system. Eventually the mystery is hidden in the axis of the system the backbone of the mathematical system! By unveiling the hidden properties of the axis, we going to discover the hidden dimensions, the geometrical shape, and the code of this micro system defined by 2 asymmetrical entities, properties that will lead us to analysis Navier Stokes to define the flow of the fluid & gas systems. Let’s denote by the micro asymmetrical system defined by the set 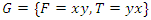 of two inverse loops with opposite orientation and by
of two inverse loops with opposite orientation and by 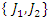 the axis of symmetry for each loop. Consider that the loop
the axis of symmetry for each loop. Consider that the loop  orbiting around the axis
orbiting around the axis 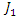 and the loop
and the loop 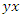 orbiting around
orbiting around 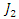 with a cyclic transformation. For a connected closed system, the 2 loops create a vortex ring model, orbiting oppositely around the axis with different periods
with a cyclic transformation. For a connected closed system, the 2 loops create a vortex ring model, orbiting oppositely around the axis with different periods 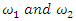 mapping a torus shape. the system is continuous, closed and connected, then entangled and in dynamic that we just discovered in the abstract universe. The question is why the system does not tangle? What is the nature and topological structure of those loops then? To resolve this problem first we going to analyze experimentally with an interesting transformation that results from how the axis of the system splits to two loops
mapping a torus shape. the system is continuous, closed and connected, then entangled and in dynamic that we just discovered in the abstract universe. The question is why the system does not tangle? What is the nature and topological structure of those loops then? To resolve this problem first we going to analyze experimentally with an interesting transformation that results from how the axis of the system splits to two loops 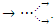 take a ribbon, glue its extremities, and cut longitudinally in the middle by trying the 4 cases of the ribbon twists
take a ribbon, glue its extremities, and cut longitudinally in the middle by trying the 4 cases of the ribbon twists 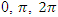 and
and 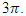 When
When 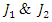 are strictly connected with 0 twist then the two loops
are strictly connected with 0 twist then the two loops 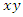 and
and 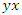 are trivial loops with 0 intersection. But when
are trivial loops with 0 intersection. But when 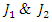 connected by
connected by 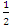 twist with an angular transformation of π the two loops are connected and generate a mobius strip with argument
twist with an angular transformation of π the two loops are connected and generate a mobius strip with argument 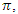 equivalent to a twisted cylinder topologically with no boundary, then by 1 twist or 2π the two loops
equivalent to a twisted cylinder topologically with no boundary, then by 1 twist or 2π the two loops 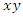 and
and 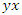 generate a special knot defined by Hopf link with argument
generate a special knot defined by Hopf link with argument 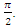 By a third twist or 3π the loops
By a third twist or 3π the loops 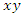 and
and 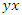 describe a trefoil knot with argument
describe a trefoil knot with argument 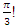 As a result, we come up to determine the shape of the asymmetrical loops that orbit along and map a torus known by torus knots
As a result, we come up to determine the shape of the asymmetrical loops that orbit along and map a torus known by torus knots 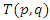 fibered knots. Although mobius strip can be contracted to a circle, while a torus knot degenerates to the product of 2 circles. But how many twists we can proceed? Topologically it shows how the set through different axis ramifies and splits into two asymmetrical loops “invariant knots“ torus knots that describe the fibers of a torus with short range and long range from trivial knot, Hopf’s links to a trefoil knots “ the 4 cases of the axis of symmetries described are relevant to a 4d-Torus. A dimension that we can also prove by the determining the Betti numbers based on Pascal’s triangle through cross section and the genus formulate for a 5-simplex polytope related to the dihedral groups. To determine the number of the twists we should base on Conway Hexad of invertible loops! There is an interesting hidden concept in the construction generalized by Conway [17], along the hexad system for the inverse loops that we are going to describe! An interesting concept with a solid mathematical interconnection defined in an invariant system that relate mathematical fields from knot theory, number theory, combinatory, algebraic curves, symmetry transformations, simplex geometry, graph theory and analysis! A path that leaded Conway to describe the path to the quaternions and octonions through the group automorphism generated by the orthogonal groups O(n) and SO(n) & the exceptional Lie groups
fibered knots. Although mobius strip can be contracted to a circle, while a torus knot degenerates to the product of 2 circles. But how many twists we can proceed? Topologically it shows how the set through different axis ramifies and splits into two asymmetrical loops “invariant knots“ torus knots that describe the fibers of a torus with short range and long range from trivial knot, Hopf’s links to a trefoil knots “ the 4 cases of the axis of symmetries described are relevant to a 4d-Torus. A dimension that we can also prove by the determining the Betti numbers based on Pascal’s triangle through cross section and the genus formulate for a 5-simplex polytope related to the dihedral groups. To determine the number of the twists we should base on Conway Hexad of invertible loops! There is an interesting hidden concept in the construction generalized by Conway [17], along the hexad system for the inverse loops that we are going to describe! An interesting concept with a solid mathematical interconnection defined in an invariant system that relate mathematical fields from knot theory, number theory, combinatory, algebraic curves, symmetry transformations, simplex geometry, graph theory and analysis! A path that leaded Conway to describe the path to the quaternions and octonions through the group automorphism generated by the orthogonal groups O(n) and SO(n) & the exceptional Lie groups 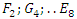 that relate the 4 division algebras[c] along the hexad. Giving a binary relation
that relate the 4 division algebras[c] along the hexad. Giving a binary relation 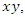 neutral element e & an inverse , with
neutral element e & an inverse , with 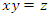 then
then 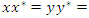
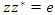 . The elements
. The elements 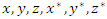 map a hexad. The asymmetrical system is characterized by duality
map a hexad. The asymmetrical system is characterized by duality 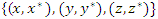 and triality
and triality 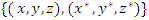 Elements orbiting around an axis system defined by the set
Elements orbiting around an axis system defined by the set 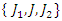 that are the analogue of the inverse loops. By introducing the isotopies, monotopies and their companions that preserve the relation: if
that are the analogue of the inverse loops. By introducing the isotopies, monotopies and their companions that preserve the relation: if 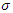 is a monotopy there exist
is a monotopy there exist 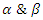 so that
so that 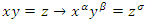 and by defining the left and right ideals of the loop companions
and by defining the left and right ideals of the loop companions 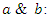 with
with 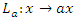 and
and 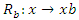 Then
Then 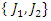 coincide with
coincide with 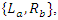 for more detail see Conway [17] The left and right ideals for the group automorphism that generates invertible loops along the axis characterized by twists. As a conclusion due to the triality and to the asymmetrical properties of the system, the number of the twists is 3. The system is entangled but not tangled dues to the effect of Paul Dirac belt trick generalized by the quaternions along the transformation of SO(3), more detail see Kauffman [2] But we will discover the rest of the flow by analyzing the hyperbolic dynamical of the discrete system in algebraic number theory! Since this dynamic is limited to elliptic modular only. In this paper we going to define integers by points representation and loops representation to describe its algebraic, geometric & topological structure while in dynamic.
for more detail see Conway [17] The left and right ideals for the group automorphism that generates invertible loops along the axis characterized by twists. As a conclusion due to the triality and to the asymmetrical properties of the system, the number of the twists is 3. The system is entangled but not tangled dues to the effect of Paul Dirac belt trick generalized by the quaternions along the transformation of SO(3), more detail see Kauffman [2] But we will discover the rest of the flow by analyzing the hyperbolic dynamical of the discrete system in algebraic number theory! Since this dynamic is limited to elliptic modular only. In this paper we going to define integers by points representation and loops representation to describe its algebraic, geometric & topological structure while in dynamic.  The equation [1] & [2] was defined and based on the following sequences: The set
The equation [1] & [2] was defined and based on the following sequences: The set 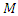 composed of 99 elements, has 25 prime numbers, 73 composites and number 1. A mysterious triangular sequences that call for the distribution of the primes, and integers inside the sphere
composed of 99 elements, has 25 prime numbers, 73 composites and number 1. A mysterious triangular sequences that call for the distribution of the primes, and integers inside the sphere 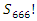 Sequences that generate an analytical function that we going to discover:
Sequences that generate an analytical function that we going to discover: 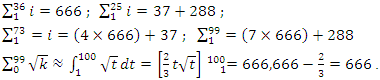 Generalization of the equation & The Concept of Infinity: In the previous papers [1] & [2], we did analyze the structure & the flow of the 2 sets:
Generalization of the equation & The Concept of Infinity: In the previous papers [1] & [2], we did analyze the structure & the flow of the 2 sets: 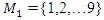 &
& 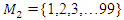 . Let’s denote by
. Let’s denote by 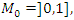 and by
and by 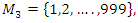
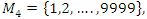

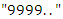 with n digits, and by
with n digits, and by 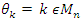 . It follows that the sequences
. It follows that the sequences 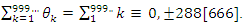 Interpretation: To find out the period of the system, we need to evaluate the sequence:
Interpretation: To find out the period of the system, we need to evaluate the sequence: 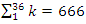 , since
, since 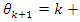
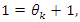 it shows 666 represent
it shows 666 represent 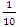 of
of 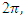 then period
then period 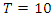 and
and 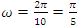 The sets of triangular sequences
The sets of triangular sequences 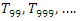 Expand by oscillating
Expand by oscillating 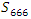 with the angle
with the angle 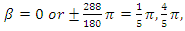 points that are considered vertices of a fractal tetrahedral mapped to
points that are considered vertices of a fractal tetrahedral mapped to  We have then 2 glued asymmetrical tetrahedral in
We have then 2 glued asymmetrical tetrahedral in 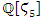 the abelian cyclotomic group. Tetrahedral that we consider with coordinates the points
the abelian cyclotomic group. Tetrahedral that we consider with coordinates the points 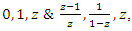 related to
related to 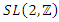 and the symmetry group
and the symmetry group 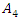 . This dynamical is based on a
. This dynamical is based on a 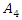 tetrahedral rotation, and
tetrahedral rotation, and 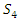 reflexion group for the twist transformation, a transformation that will allow us to go from
reflexion group for the twist transformation, a transformation that will allow us to go from 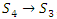 , to describe the transformation of an hyperelliptic curve to a elliptic curve. Orbital defined by a spiral of Fibonacci curve, that orbits along a fractal dodecahedral space dual of an icosahedral, that results from a quintic algebraic curve singularity. A homology sphere, an interconnection related to hyperbolic modular flow & volume of polytopes at singularity [1] & [2]. Let’s denote now by
, to describe the transformation of an hyperelliptic curve to a elliptic curve. Orbital defined by a spiral of Fibonacci curve, that orbits along a fractal dodecahedral space dual of an icosahedral, that results from a quintic algebraic curve singularity. A homology sphere, an interconnection related to hyperbolic modular flow & volume of polytopes at singularity [1] & [2]. Let’s denote now by 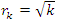 with
with 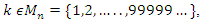 then since
then since 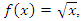 monotone increasing, we have the following: with
monotone increasing, we have the following: with 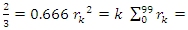
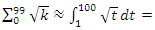
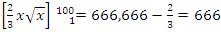
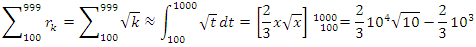
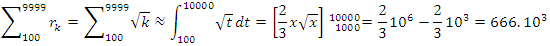 Interpretation: The sphere expands by
Interpretation: The sphere expands by 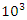 , by
, by 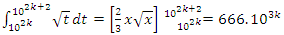 with radius:
with radius: 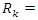
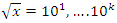 to pack the sets
to pack the sets 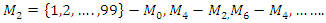
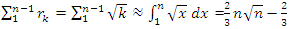 just volume of a sphere of radius
just volume of a sphere of radius 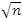 minus volume of a sphere unity of radius 1. The interesting thing about this sequence is that for each radius of
minus volume of a sphere unity of radius 1. The interesting thing about this sequence is that for each radius of 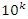 the integral
the integral 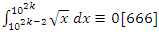 for even powers …. -2,2,4…. It also generates a fractal expansion that extend in
for even powers …. -2,2,4…. It also generates a fractal expansion that extend in 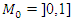 for the values in the interval
for the values in the interval 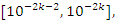 a concept that is seen also in the Riemann trivial zeros, which is due to the modular asymmetrical flow that we will describe later. Which also prove the packing of
a concept that is seen also in the Riemann trivial zeros, which is due to the modular asymmetrical flow that we will describe later. Which also prove the packing of 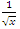 with a hyperbolical flow related to a translation transformation, and due to the optimal density of this irregular spheres packing “A fractal dynamical system of packing”, it follows then the convergence of the sequence. The Sphere expand then by
with a hyperbolical flow related to a translation transformation, and due to the optimal density of this irregular spheres packing “A fractal dynamical system of packing”, it follows then the convergence of the sequence. The Sphere expand then by 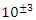 with a rate of
with a rate of 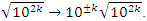 A periodical expansion of the radius defined by the period
A periodical expansion of the radius defined by the period 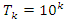 , similar to the hyperbolical function
, similar to the hyperbolical function 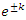 , since:
, since: 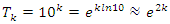 since
since 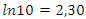 . Note that
. Note that 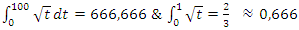 volume of unit sphere by multiplying with
volume of unit sphere by multiplying with 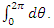 This rational sequence has an expansion to p-adic extension:
This rational sequence has an expansion to p-adic extension: 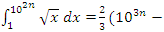
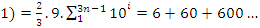 Conclusion: Let’s denote by the quadratic equation
Conclusion: Let’s denote by the quadratic equation 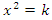 with
with 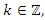 then this packing is related to the an irregular spheres packing of the set
then this packing is related to the an irregular spheres packing of the set 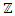 inside the sphere
inside the sphere 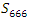 . Our goal in this paper is to define the spectrum
. Our goal in this paper is to define the spectrum 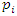 of the prime numbers and determine the packing of the set
of the prime numbers and determine the packing of the set 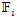 of the prime numbers, also the packing of the set of rational numbers
of the prime numbers, also the packing of the set of rational numbers  and its abelian extensions based on the quadratic equation, to solve R.H & B.S.D conjectures.System Model: Therefore, our system is a closed compact manifold, a fractal periodical space endowed with a metric space, defined by combining these 2 dynamical flows of a homogenous space & time with proportional parameters, that give a rise to a vector field with rotation, twist, and translation, both dynamical are periodic with common period
and its abelian extensions based on the quadratic equation, to solve R.H & B.S.D conjectures.System Model: Therefore, our system is a closed compact manifold, a fractal periodical space endowed with a metric space, defined by combining these 2 dynamical flows of a homogenous space & time with proportional parameters, that give a rise to a vector field with rotation, twist, and translation, both dynamical are periodic with common period 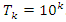 . Let’s denote by:
. Let’s denote by: 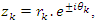 the flow described as a hyperbolic Fibonacci modular flow of an infinite cyclic covering of linked torus knots with a horocycle flow! To analyze such a flow, we need to determine the properties of the following parameters
the flow described as a hyperbolic Fibonacci modular flow of an infinite cyclic covering of linked torus knots with a horocycle flow! To analyze such a flow, we need to determine the properties of the following parameters 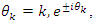
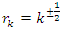 and
and 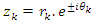 with an expansion by
with an expansion by 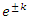 generated by the following matrix transformations:
generated by the following matrix transformations: 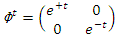 & by
& by 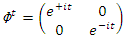 for the vector field defined by the matrix,
for the vector field defined by the matrix, 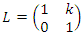 and
and 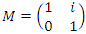 . Before we start describing the flow of the system we need to make some quite connection between the structure & the path of the prime numbers and our modeling system! Prime Numbers Distribution: Prime numbers are the building block of the integers, any composite number can be written as a product of prime numbers,
. Before we start describing the flow of the system we need to make some quite connection between the structure & the path of the prime numbers and our modeling system! Prime Numbers Distribution: Prime numbers are the building block of the integers, any composite number can be written as a product of prime numbers, 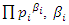 integer. Some primes ramify, some inert, and some split in the ring of integers. Any integer including primes is a trans-palindrome, or is a palindrome self-symmetric, like number 11 in the set
integer. Some primes ramify, some inert, and some split in the ring of integers. Any integer including primes is a trans-palindrome, or is a palindrome self-symmetric, like number 11 in the set 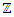 , while in
, while in 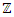 extensions it splits as conjugate elements. Following Dirichlet theorem for the arithmetic progression of the primes, any prime number
extensions it splits as conjugate elements. Following Dirichlet theorem for the arithmetic progression of the primes, any prime number 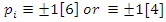 except the 2 primes 2 & 3. Then the product
except the 2 primes 2 & 3. Then the product 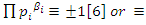
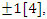 we can locate the primes then following the square & hexagram diagram! From these 2 diagrams we can conclude the existence of two sort of prime numbers: Eisenstein primes and Gaussian primes related to the modular hexagonal & square lattices defined by
we can locate the primes then following the square & hexagram diagram! From these 2 diagrams we can conclude the existence of two sort of prime numbers: Eisenstein primes and Gaussian primes related to the modular hexagonal & square lattices defined by 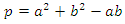 in the ring
in the ring 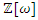 and
and 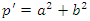 in the ring
in the ring 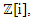 although there is other form of prime numbers, for detail see Daniel Chong for quadratic reciprocity [12], where
although there is other form of prime numbers, for detail see Daniel Chong for quadratic reciprocity [12], where 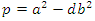 when discriminant
when discriminant 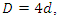 where
where 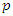 is quadratic residue mod[d], related to the quadratic equation:
is quadratic residue mod[d], related to the quadratic equation: 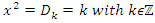 an extension of
an extension of 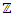 defined by the field
defined by the field 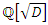 . Since the integers are in dynamic, then we need to find the exact path of the spectrum
. Since the integers are in dynamic, then we need to find the exact path of the spectrum 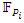 prime’s orbital, by finding the shape geometric of the curve dynamical, for this reason we need to analyze the structure, the flow, and the singularity of the curve according to the discriminant
prime’s orbital, by finding the shape geometric of the curve dynamical, for this reason we need to analyze the structure, the flow, and the singularity of the curve according to the discriminant 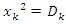 to determine the packing & the distribution of the integers and prime numbers related to our discovered periodical manifold Space defined by
to determine the packing & the distribution of the integers and prime numbers related to our discovered periodical manifold Space defined by 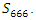 In the class field theory, we know that there exists a coherent relationship between, law of quadratic reciprocity, split & density of primes along the Galois extension of
In the class field theory, we know that there exists a coherent relationship between, law of quadratic reciprocity, split & density of primes along the Galois extension of  . Every finite abelian extension of
. Every finite abelian extension of  lie in some cyclotomic abelian field
lie in some cyclotomic abelian field 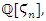 and for any finite abelian extension of
and for any finite abelian extension of 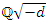 there is special values of automorphic functions over it, and there is a unique lattice
there is special values of automorphic functions over it, and there is a unique lattice 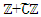 of an imaginary quadratic field. Let’s consider the following polynomials:
of an imaginary quadratic field. Let’s consider the following polynomials: 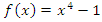 with roots
with roots 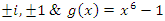 with roots
with roots 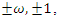 and
and 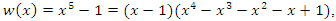 with
with 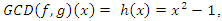 and since
and since 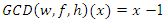 then all this polynomial degenerate at the point
then all this polynomial degenerate at the point 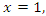 polynomials that are related to the cyclic polynomial defined in the abelian cyclotomic field
polynomials that are related to the cyclic polynomial defined in the abelian cyclotomic field 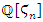 extension of
extension of 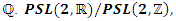 the Trefoil Knot, Hopf’s link, and the space rings of
the Trefoil Knot, Hopf’s link, and the space rings of 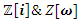 An interesting interconnection is that
An interesting interconnection is that 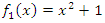 and
and 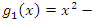
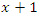 interchange roots and fixed points, for the units values
interchange roots and fixed points, for the units values 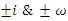 but
but 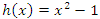 interchanges roots and fixed points with
interchanges roots and fixed points with 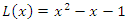 for the values
for the values 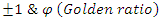 . Per stereography projection for
. Per stereography projection for 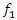 we have:
we have: 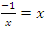 and for
and for 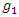 we have
we have 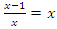 with matrix:
with matrix: 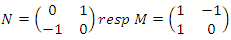 with
with 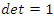 elements of
elements of 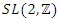 for more details see [20], while
for more details see [20], while 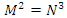 . Since
. Since 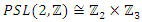 related to the elements
related to the elements 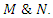 We notice the 2 units of the Rings
We notice the 2 units of the Rings 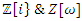 connected by the relation:
connected by the relation: 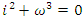 &
& 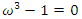 then
then 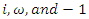 elements of the torus knot
elements of the torus knot 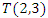 a trefoil knot, also since
a trefoil knot, also since 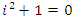 then
then 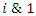 are elements of the Hopf’s link, defined by the 2 linked circles in
are elements of the Hopf’s link, defined by the 2 linked circles in 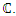 The map:
The map: 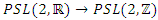 in the Poincare half disk shows that the flow is generated by a translation & a rotation transformation in the space of
in the Poincare half disk shows that the flow is generated by a translation & a rotation transformation in the space of 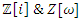 that describe a discrete subgroup of an infinite co-volume space [15], defined by Seifert surfaces through a hyperbolic flow generated by the compliment of the hyperbolic 8 knot
that describe a discrete subgroup of an infinite co-volume space [15], defined by Seifert surfaces through a hyperbolic flow generated by the compliment of the hyperbolic 8 knot 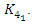 Now for an algebraic curve:
Now for an algebraic curve: 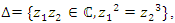 the trefoil
the trefoil 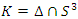 then
then 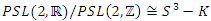 and
and 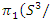
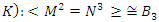 Braid group, for more details see Birman [14]. Trefoil Knot
Braid group, for more details see Birman [14]. Trefoil Knot 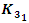 8 knot
8 knot 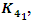 and Hopf’s link: Let
and Hopf’s link: Let 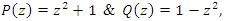 for
for 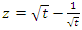 then we have then the Jones polynomials
then we have then the Jones polynomials 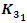 and
and 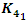
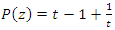 and
and 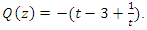 While Hopf’s link with polynomial:
While Hopf’s link with polynomial: 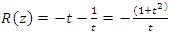 . Extension Polynomials, [9] that are related to the cyclotomic polynomial
. Extension Polynomials, [9] that are related to the cyclotomic polynomial 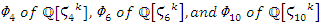 . The hyperbolic knot
. The hyperbolic knot 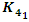 also constructed by gluing 2 ideal tetrahedral with the points:
also constructed by gluing 2 ideal tetrahedral with the points: 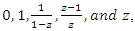 related to
related to 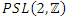 . We can conclude then that Hopf’s link and trefoil knot are connected and swaps root with fixed point for the values:
. We can conclude then that Hopf’s link and trefoil knot are connected and swaps root with fixed point for the values: 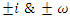 and the 8 knot
and the 8 knot 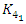 swaps roots with
swaps roots with 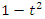 for values:
for values: 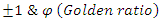 transformations that involve polynomial characteristic and Seifert surface defined by
transformations that involve polynomial characteristic and Seifert surface defined by 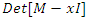 and
and 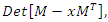 while polynomial characteristic involves the discriminant of the quadratic equation. Flow of the system: This dynamical system generated by 2 types of flows, one is related to infinite cyclic covering of a linked torus knots, where the Seifert surface related to the complement of the trefoil knot and Hop’f link a fibered knots, that give rise to a elliptic modular curves, which expand exponentially to create a hyperbolic Fibonacci modular flow, this combination of flows is related to the correspondence of the trefoil knot, Hopf’s link, trivial knots and the 8 knot. It shows that the convergence of the sequences defined by
while polynomial characteristic involves the discriminant of the quadratic equation. Flow of the system: This dynamical system generated by 2 types of flows, one is related to infinite cyclic covering of a linked torus knots, where the Seifert surface related to the complement of the trefoil knot and Hop’f link a fibered knots, that give rise to a elliptic modular curves, which expand exponentially to create a hyperbolic Fibonacci modular flow, this combination of flows is related to the correspondence of the trefoil knot, Hopf’s link, trivial knots and the 8 knot. It shows that the convergence of the sequences defined by 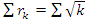 and
and 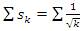 is trivial for even powers, a similar case of the R.H trivial zeros. This is seen in its distribution as irregular sphere packing with optimal density in the sphere
is trivial for even powers, a similar case of the R.H trivial zeros. This is seen in its distribution as irregular sphere packing with optimal density in the sphere 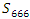 . Our aim is to define an analytical function or Serie
. Our aim is to define an analytical function or Serie 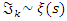 with common properties to describe the condition of convergence and the zeros of the R, for this reason we need to analyze the flow and the convergence of the following sequences: •
with common properties to describe the condition of convergence and the zeros of the R, for this reason we need to analyze the flow and the convergence of the following sequences: • 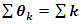 •
• 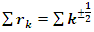 •
• 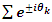 •
• 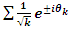 Evaluation of the twist & rotation transformations of the system: We know:
Evaluation of the twist & rotation transformations of the system: We know: 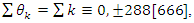 related to 0,
related to 0, 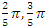 for the period T=10. Let’s denote by the number of twists
for the period T=10. Let’s denote by the number of twists 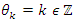 for the torus knots
for the torus knots 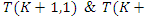
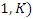 defined by the rational tangles:
defined by the rational tangles: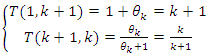 Due to our closed system, the flow describes 2 asymmetrical dynamics, with opposite directions, with stable & instable curves, for this reason, we are going also to analyze the asymmetrical twists.The flow of the system is defined in
Due to our closed system, the flow describes 2 asymmetrical dynamics, with opposite directions, with stable & instable curves, for this reason, we are going also to analyze the asymmetrical twists.The flow of the system is defined in 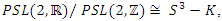 for an horocycle with stable flow determined by the right multiplication of the nilpotent group
for an horocycle with stable flow determined by the right multiplication of the nilpotent group 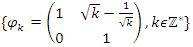 by the matrix of the hyperbolic flow defined by the diagonal group
by the matrix of the hyperbolic flow defined by the diagonal group 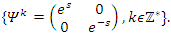
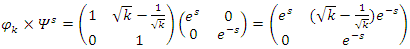
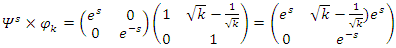 We have then:
We have then: 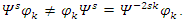 Which shows that the flow is asymmetrical, non-abelian with stable and instable flow, a flow which was analyzed by Birman & Ghys to solve the Lorenz modular flow for detail see [15] & [14]• Twist
Which shows that the flow is asymmetrical, non-abelian with stable and instable flow, a flow which was analyzed by Birman & Ghys to solve the Lorenz modular flow for detail see [15] & [14]• Twist 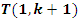 , the matrix correspondent
, the matrix correspondent 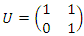 , with
, with 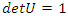 , then its polynomial characteristic
, then its polynomial characteristic 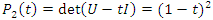 that degenerates for
that degenerates for 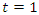 & its Seifert surface:
& its Seifert surface: 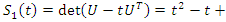
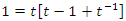 compliment of a trefoil knot
compliment of a trefoil knot 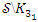 .• Twist
.• Twist 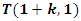 the matrix correspondent
the matrix correspondent 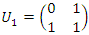 with
with 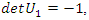 we recognize this Fibonacci fraction defined by:
we recognize this Fibonacci fraction defined by: 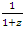 where
where 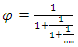 the rational tangle. Due to Cassini identity:
the rational tangle. Due to Cassini identity: 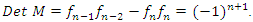 Modular when
Modular when 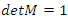 .Then its polynomial characteristic
.Then its polynomial characteristic 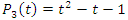 degenerates at the Golden ratio
degenerates at the Golden ratio 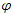 .And its Seifert surface:
.And its Seifert surface: 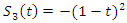 complement of the trivial knot.Since our twist defined by
complement of the trivial knot.Since our twist defined by 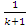 with
with 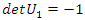 element of
element of 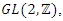 then due to continuity of the system, the twist going to ramify to combine with the modular flow. Hence
then due to continuity of the system, the twist going to ramify to combine with the modular flow. Hence 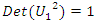 defined by the fraction:
defined by the fraction: 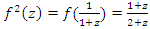 with the matrix correspondent:
with the matrix correspondent: 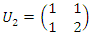 , the polynomial characteristic is:
, the polynomial characteristic is: 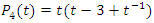 related to a hyperbolic 8 knot
related to a hyperbolic 8 knot 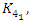 while its Seifert surface
while its Seifert surface 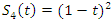 complement of the trivial knot.• Twist
complement of the trivial knot.• Twist 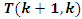 we have the matrix correspondent
we have the matrix correspondent 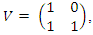 with
with 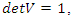 its polynomial characteristic
its polynomial characteristic 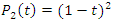 degenerates for
degenerates for 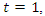 and its Seifert surface
and its Seifert surface  compliment of a trefoil knot
compliment of a trefoil knot 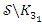 . Notice that the matrix
. Notice that the matrix 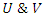 are products of the previous matrix
are products of the previous matrix 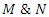 elements of
elements of 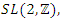 we have
we have 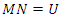 and
and 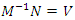 .• Twist
.• Twist 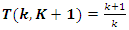 with the correspondent matrix
with the correspondent matrix 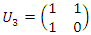 with
with 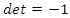 element of the
element of the 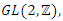 The polynomial characteristic then:
The polynomial characteristic then: 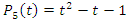 that converge toward the golden ratio
that converge toward the golden ratio 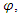 and its Sifert surface:
and its Sifert surface: 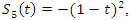 then also for this flow to combine with our modular flow, its twist going to ramify.
then also for this flow to combine with our modular flow, its twist going to ramify. 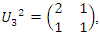 with
with 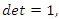 Then the polynomial characteristic
Then the polynomial characteristic 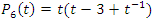 related to
related to 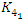 knot, and its Seifert Surface
knot, and its Seifert Surface 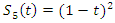 .Interpretation: The flow defined by 2 asymmetrical reverse flows determined by 2 Seifert surfaces compliment of a trefoil knot & compliment of the 8 knot that swaps & interchange path through roots & fixed points system, while the trefoil knot related to the cyclic modular torus knot flow and the 8-knot related to the modular hyperbolic flow that converge toward the golden ration. This is not a Fibonacci iteration flow, only
.Interpretation: The flow defined by 2 asymmetrical reverse flows determined by 2 Seifert surfaces compliment of a trefoil knot & compliment of the 8 knot that swaps & interchange path through roots & fixed points system, while the trefoil knot related to the cyclic modular torus knot flow and the 8-knot related to the modular hyperbolic flow that converge toward the golden ration. This is not a Fibonacci iteration flow, only 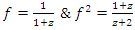 that are involved in our flow, there is a lot of modular knots with
that are involved in our flow, there is a lot of modular knots with 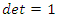 of their matrix that are not embedded or involved for this flow. Conclusion:
of their matrix that are not embedded or involved for this flow. Conclusion: 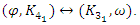 The asymmetrical flow degenerates alternatively for t=1 related alexander polynomial, one side of the flow degenerates, while the other side converges toward
The asymmetrical flow degenerates alternatively for t=1 related alexander polynomial, one side of the flow degenerates, while the other side converges toward 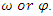 Since the hyperbolic flow is not limited only in
Since the hyperbolic flow is not limited only in 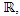 but also expand in
but also expand in 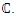 Then for the twist
Then for the twist 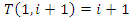 with the matrix correspondent:
with the matrix correspondent: 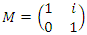 with
with 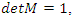 have a polynomial characteristic
have a polynomial characteristic 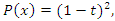 and a Seifert surface
and a Seifert surface 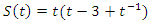 defined by the compliment of
defined by the compliment of  .Existence of other flows in our system: An interesting sequence that I will be decoding to determine the rest of the Seifert surface of our system.
.Existence of other flows in our system: An interesting sequence that I will be decoding to determine the rest of the Seifert surface of our system. 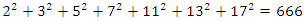 Equation of a hypersphere with radius
Equation of a hypersphere with radius 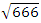 with origin the point
with origin the point 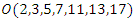 defined by the formal equation:
defined by the formal equation: 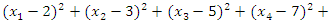
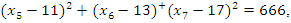 while
while 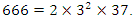 We are going then to calculate the Seifert Surfaces related to its origin point, the following discriminants
We are going then to calculate the Seifert Surfaces related to its origin point, the following discriminants 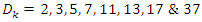 as the complement of the Alexander knot polynomial defined by:
as the complement of the Alexander knot polynomial defined by: 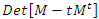 . Let’s denote by
. Let’s denote by 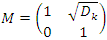 then
then 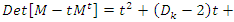
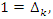 and due to the orientation of the flow, replacing
and due to the orientation of the flow, replacing 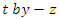 .Now we will recognize some of its Seifert surfaces:
.Now we will recognize some of its Seifert surfaces: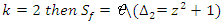 complement of Hopf’s Link.
complement of Hopf’s Link. 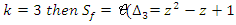 complement of a trefoil Knot
complement of a trefoil Knot 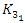 .
.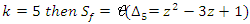 complement of an 8 knot
complement of an 8 knot 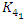 .
.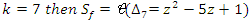 .
.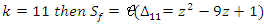 .
.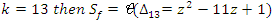 .
.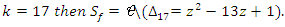 This quadratic equation defined by
This quadratic equation defined by 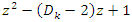 have a discriminant
have a discriminant 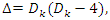 follows from Dirichlet theorem, although the factorization of
follows from Dirichlet theorem, although the factorization of 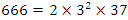 shows that for
shows that for 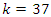 the discriminant of its complement Seifert surface is D = 37.11.3 connected to other discriminants. Now for
the discriminant of its complement Seifert surface is D = 37.11.3 connected to other discriminants. Now for 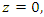 all polynomial degenerate to
all polynomial degenerate to 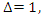 and the Seifert surface is then the complement of the circles, and from the Poincare conjecture, the complement of a circle is the sphere
and the Seifert surface is then the complement of the circles, and from the Poincare conjecture, the complement of a circle is the sphere 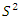 . The polynomial with
. The polynomial with 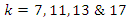 shown that are interconnected to other polynomials when solved in
shown that are interconnected to other polynomials when solved in 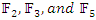 . Next we going to see that all the primes split in the complement of the hyperbolic space related to the hyperbolic eight knot
. Next we going to see that all the primes split in the complement of the hyperbolic space related to the hyperbolic eight knot 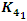 .The Splitting of all the prime numbers
.The Splitting of all the prime numbers 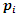 : For
: For 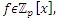 let’s denote by the quadratic equation:
let’s denote by the quadratic equation: 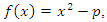 with
with 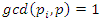 then for
then for 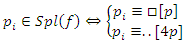 if
if 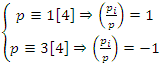 .Following law of reciprocity, [7] the split is based on the Legendre symbol
.Following law of reciprocity, [7] the split is based on the Legendre symbol 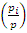 . Since
. Since 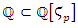 then
then 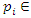
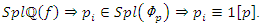 Now for
Now for 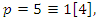 with
with 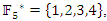 we notice 1 & 4 elements of
we notice 1 & 4 elements of 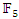 are square residues mod [5],
are square residues mod [5], 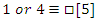 but not 2 & 3. By Fermat little theorem,
but not 2 & 3. By Fermat little theorem, 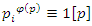 then
then 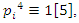 although some primes splits in
although some primes splits in 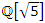 like 11, 31, 41…with the property
like 11, 31, 41…with the property 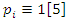 and some split in
and some split in 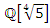 like 19, 29…. With the property
like 19, 29…. With the property 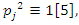 Then 5 does not split completely, but all primes
Then 5 does not split completely, but all primes 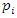 split completely in
split completely in 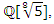 then split in
then split in 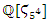 . Since
. Since 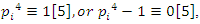 then
then 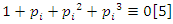 with
with 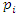 not splitting in
not splitting in 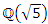 .Conclusion: By Little Fermat theorem, all the primes
.Conclusion: By Little Fermat theorem, all the primes 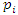 split in
split in 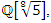 then split in
then split in 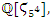 with
with 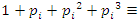
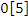 a formulate that will lead us to construct the algebraic variety for
a formulate that will lead us to construct the algebraic variety for 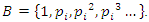 By Hensel’s lemma, the group of units
By Hensel’s lemma, the group of units 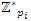 has
has 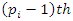 roots of unity. This splitting descends to the quotient rings
roots of unity. This splitting descends to the quotient rings 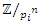 and its group of units, giving an isomorphism
and its group of units, giving an isomorphism 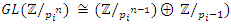 . Well in our case the units of
. Well in our case the units of 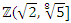 are the independent elements defined by:
are the independent elements defined by: 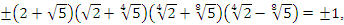 where the points
where the points 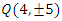 elements of the hyperelliptic curve with rank
elements of the hyperelliptic curve with rank 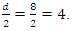 Since the period of our system is
Since the period of our system is 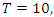 then for
then for 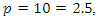 and since all
and since all 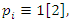 it follows that all the primes
it follows that all the primes 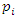 split in
split in 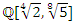 which is the quadratic extension of
which is the quadratic extension of 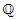 defined by
defined by 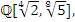 hence
hence 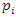 split in the cyclotomic abelian field
split in the cyclotomic abelian field 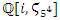 , and all those primes are unramified due to the discriminant
, and all those primes are unramified due to the discriminant 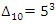 . For generalization with
. For generalization with 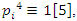 then
then 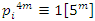 and all
and all 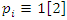 then for all
then for all 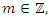 the quadratic equation
the quadratic equation 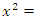
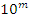 imply that
imply that 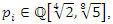 then all
then all 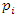 split in
split in 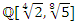 which is the extension of
which is the extension of 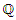 , hence
, hence 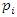 split in the cyclotomic abelian field defined by the abelian cyclotomic field
split in the cyclotomic abelian field defined by the abelian cyclotomic field 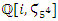 . Finite cyclic torus covering: We know that Alexander polynomial describes the homology of the infinite cyclic covering as
. Finite cyclic torus covering: We know that Alexander polynomial describes the homology of the infinite cyclic covering as 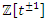 . Let’s denote by
. Let’s denote by 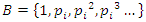 where
where 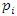 are prime numbers, and by
are prime numbers, and by 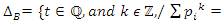
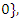 its algebraic variety associated to it, then
its algebraic variety associated to it, then 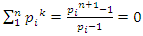 in our case the period
in our case the period 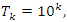 then for
then for 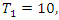
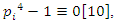 which proves that all the primes split in
which proves that all the primes split in 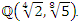 Then Let’s denote then by its extension in the cyclotomic field
Then Let’s denote then by its extension in the cyclotomic field 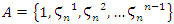 , with
, with 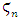 =
= 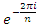 the abelian extension of
the abelian extension of 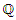 , and by
, and by 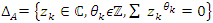 its algebraic variety, a cyclic covering of linked torus knots defined by the twists
its algebraic variety, a cyclic covering of linked torus knots defined by the twists 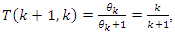 since
since 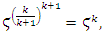 although the cyclic polynomial
although the cyclic polynomial 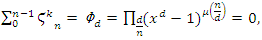 then
then 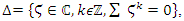 and the Seifert surface is the
and the Seifert surface is the 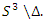 In our case the period of our dynamical system is
In our case the period of our dynamical system is 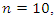 infinite cyclic linked torus knot is reduced due to the period of the system. Period defined by the Euler totient associated function:
infinite cyclic linked torus knot is reduced due to the period of the system. Period defined by the Euler totient associated function: 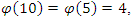 which is isomorphic to Mordell-Weil group
which is isomorphic to Mordell-Weil group 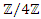 of order 4, the rank of the abelian variety related to the zero of the associated L-function related to Birch & Swinnerton-Dyer conjecture. The cyclotomic polynomial is then:
of order 4, the rank of the abelian variety related to the zero of the associated L-function related to Birch & Swinnerton-Dyer conjecture. The cyclotomic polynomial is then: 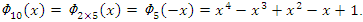 We recognize this polynomial by the Jones polynomial of the hyperbolic 8 knot
We recognize this polynomial by the Jones polynomial of the hyperbolic 8 knot 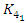 and the Seifert surface
and the Seifert surface 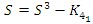 the complement of the hyperbolic 8 knot
the complement of the hyperbolic 8 knot 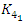 . A polynomial with discriminant
. A polynomial with discriminant 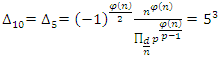 that shows 5 the only ramified prime number in the cyclotomic field
that shows 5 the only ramified prime number in the cyclotomic field 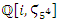 . We notice for
. We notice for 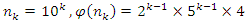 and
and 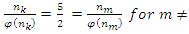
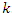 . Now let’s denote by
. Now let’s denote by 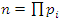 product off all unramified primes. Then
product off all unramified primes. Then 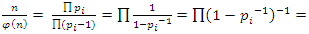
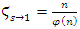 . Riemann function when
. Riemann function when 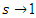 related to prime numbers. Algebraic & Geometric variety structure: It shows the system is related to the quintic algebraic equation:
related to prime numbers. Algebraic & Geometric variety structure: It shows the system is related to the quintic algebraic equation: 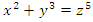 . Let
. Let 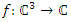 the complex polynomial
the complex polynomial 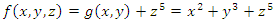 then
then 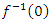 is the complex variety. By extending the line of singular algebraic variety to
is the complex variety. By extending the line of singular algebraic variety to 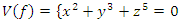 &
& 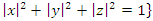 then we have per projection a
then we have per projection a 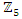 regular cover, where
regular cover, where 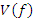 is the branched cover of
is the branched cover of 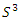 with branch locus
with branch locus 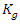 over the variety
over the variety 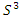 . It generates the equation of a dodecahedral. Let’s denote by
. It generates the equation of a dodecahedral. Let’s denote by 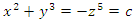 that when
that when 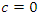 then
then 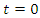 variety with cusp 0 at the origin, and when
variety with cusp 0 at the origin, and when 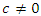 then the equation has 5 roots and the fixed points form the cone of the trefoil knot, we have then
then the equation has 5 roots and the fixed points form the cone of the trefoil knot, we have then 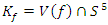 sits inside the dodecahedral for a 5 fold by symmetry. A particular case that corresponds to the homology 3- sphere “Brieskorn”
sits inside the dodecahedral for a 5 fold by symmetry. A particular case that corresponds to the homology 3- sphere “Brieskorn” 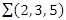 known by the Poincare dodecahedral space with finite fundamental group the binary icosahedral group defined by
known by the Poincare dodecahedral space with finite fundamental group the binary icosahedral group defined by 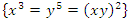 of order 120 double cover of the regular icosahedral group (alternating group) determined by the quotient space or simply by the double cover that can be constructed from Dehn surgery on knot from a right handed trefoil knot. In our case as a generalization, the construction is based then on the Brieskorn algebraic variety that are associated with polynomial
of order 120 double cover of the regular icosahedral group (alternating group) determined by the quotient space or simply by the double cover that can be constructed from Dehn surgery on knot from a right handed trefoil knot. In our case as a generalization, the construction is based then on the Brieskorn algebraic variety that are associated with polynomial 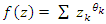 with
with 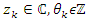 , with the variety
, with the variety 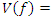
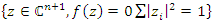 where the knot associated as the intersection of the variety algebraic and the sphere of dim
where the knot associated as the intersection of the variety algebraic and the sphere of dim 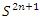 defined by
defined by 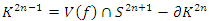 where
where 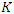 has an intersection form
has an intersection form 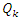 on
on 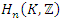 and if
and if 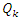 is unimodular then the boundary
is unimodular then the boundary 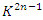 is a homology, exotic sphere. In our case for
is a homology, exotic sphere. In our case for 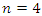 the knot associated to a manifold of dim 7 defined by
the knot associated to a manifold of dim 7 defined by 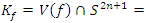
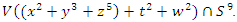 We have then:
We have then: 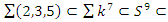
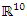 . And since the homology 3- sphere determined by the quotient
. And since the homology 3- sphere determined by the quotient 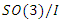 and the Milnor 7 sphere acts transitively on the group of the quaternions
and the Milnor 7 sphere acts transitively on the group of the quaternions 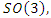 we have
we have 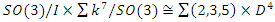 . Shows that SO(3) act between the icosahedral and the 7 dim Milnor sphere through Paul Dirac belt trick, a construction to prove which is based on using J-homomorphism and Hopf’s fibration for a higher dim to describe the fundamental group, for more detail see Kauffman [8]. This reason the asymmetrical flow in our system defined by the asymmetrical cyclic of linked torus knots with hyperbolic flow that doesn’t tangle. It shows then the dynamical of the orthogonal system defined by the trans-palindromes in
. Shows that SO(3) act between the icosahedral and the 7 dim Milnor sphere through Paul Dirac belt trick, a construction to prove which is based on using J-homomorphism and Hopf’s fibration for a higher dim to describe the fundamental group, for more detail see Kauffman [8]. This reason the asymmetrical flow in our system defined by the asymmetrical cyclic of linked torus knots with hyperbolic flow that doesn’t tangle. It shows then the dynamical of the orthogonal system defined by the trans-palindromes in 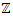 and the conjugates elements in
and the conjugates elements in 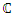 are linked and orbit in opposite directions without tangle, an asymmetrical flow controlled by Paul Dirac belt trick, including quaternions and their conjugates. The Alexander polynomial torus knot
are linked and orbit in opposite directions without tangle, an asymmetrical flow controlled by Paul Dirac belt trick, including quaternions and their conjugates. The Alexander polynomial torus knot 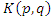 defined by:
defined by: 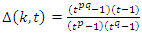 for
for 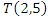 we have
we have 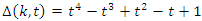 the 8 knot hyperbolic knot, a construction of the homology sphere
the 8 knot hyperbolic knot, a construction of the homology sphere 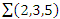 that is based on
that is based on 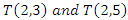 .
.2. Solution to Riemann Hypothesis Conjecture
- Riemann Hypothesis sequence related to the Jacobi Theta function & Gaussian distribution function: To solve R.H, we are interested in analyzing the case when the radius
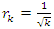 related to an analytical modular function & distribution function
related to an analytical modular function & distribution function 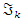 that we going to determine so that
that we going to determine so that 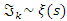 , but we end up discovering more solutions for s for its convergence related also to
, but we end up discovering more solutions for s for its convergence related also to 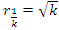 . We already showed the system is fractal for the series defined by:
. We already showed the system is fractal for the series defined by: 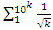 and
and 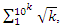 and with
and with 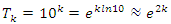 since
since 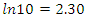 which will lead us to evaluate and analyze the Riemann sequence. Riemann’s condition of convergence: Let’s denote by the hyperbolic expansion of
which will lead us to evaluate and analyze the Riemann sequence. Riemann’s condition of convergence: Let’s denote by the hyperbolic expansion of 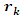 defined by
defined by 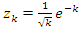 and by
and by 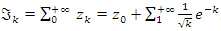 , with
, with 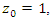 then the sequence defined by the integral
then the sequence defined by the integral 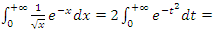
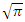 the Gaussian distribution of
the Gaussian distribution of 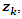 and by the prime theorem number:
and by the prime theorem number: 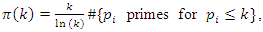 evaluating
evaluating 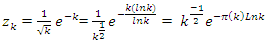
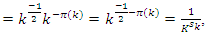 with
with 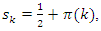 then
then 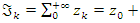
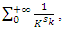 the sequence converge, and since Riemann sequence defined by
the sequence converge, and since Riemann sequence defined by 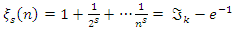 then since
then since 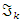 C.V and with
C.V and with 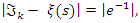 it follows that for the Riemann function sequence to converge the condition
it follows that for the Riemann function sequence to converge the condition 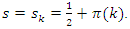 The same for
The same for 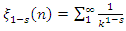 with
with 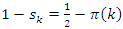 . Then a condition of R.H to convergence for this hyperbolic flow, is
. Then a condition of R.H to convergence for this hyperbolic flow, is 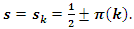 We notice also a missing part of the convergence related to
We notice also a missing part of the convergence related to 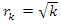 for
for 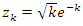 since
since 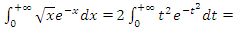
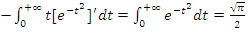 which proves the convergence of
which proves the convergence of 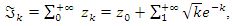 it follows that the Riemann sequence defined by
it follows that the Riemann sequence defined by 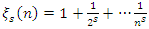 also converges with the condition
also converges with the condition 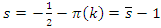 . Now let’s denote by the rotation & twist transformation of
. Now let’s denote by the rotation & twist transformation of 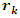 defined by:
defined by: 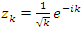 , with
, with 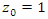 , then
, then 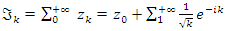 its sum defined by the integral
its sum defined by the integral 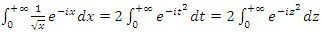
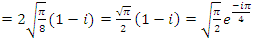 . And by the prime theorem number:
. And by the prime theorem number: 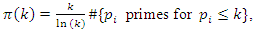 evaluating then
evaluating then 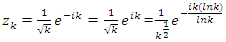
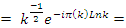
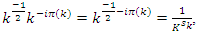 with
with 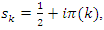 then
then 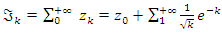
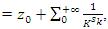 the sequence converge, and since Riemann sequence defined by
the sequence converge, and since Riemann sequence defined by 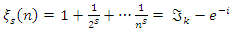 then since
then since 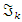 C.V and with
C.V and with 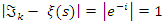 it follows for the Riemann sequence
it follows for the Riemann sequence 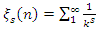 to converge the condition if and only
to converge the condition if and only 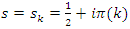 with
with 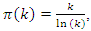 and this also valid for
and this also valid for 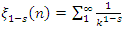 for
for 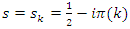 . Conclusion:
. Conclusion: 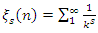 shows properties related to the Gaussian distribution or bump function, if
shows properties related to the Gaussian distribution or bump function, if 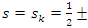
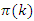 and
and 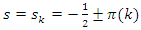 with
with 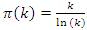 . The convergence follows since the system is fractal hyperbolic with period
. The convergence follows since the system is fractal hyperbolic with period 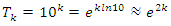 since
since 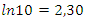 . Also Riemann Hypothesis for the other case is related to the analytical modular Theta function defined by the Fourier series
. Also Riemann Hypothesis for the other case is related to the analytical modular Theta function defined by the Fourier series 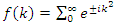 , and converge if for
, and converge if for 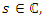 if
if 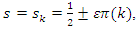 or
or 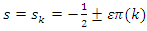 with
with 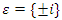 and
and 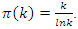 Gama Function:
Gama Function: 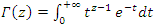 by replacing
by replacing 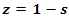 and
and 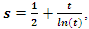 then Gama is just a Gaussian distribution:
then Gama is just a Gaussian distribution: 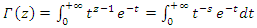
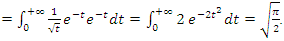 Evaluation of the twist: For the sequence
Evaluation of the twist: For the sequence 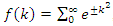 , let’s denote by
, let’s denote by 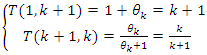 then by replacing
then by replacing 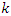 by
by 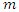 such that
such that 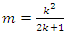 a rational tangle then
a rational tangle then 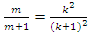 which also carry the same properties of
which also carry the same properties of 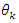 of the modular horocycle flow defined in the previous twists for the horocycle defined by
of the modular horocycle flow defined in the previous twists for the horocycle defined by 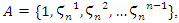 with
with 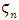 =
= 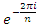 the abelian extension of
the abelian extension of 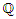 , and by
, and by 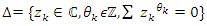 the algebraic variety. The number of integers
the algebraic variety. The number of integers 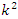 coprime to
coprime to 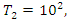 for example is the Euler Totient function
for example is the Euler Totient function 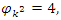 since
since 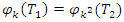 where
where 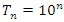 , with points element of a fractal dodecahedral, or 2 glued asymmetrical tetrahedral that go to
, with points element of a fractal dodecahedral, or 2 glued asymmetrical tetrahedral that go to 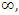 that define a hyperbolic 8 knot
that define a hyperbolic 8 knot 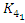 . Then we see a generalization of the flow defined by the function:
. Then we see a generalization of the flow defined by the function: 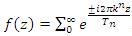 , with properties of an automorphic function, to solve and generalizes the
, with properties of an automorphic function, to solve and generalizes the 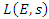 functions. Infinite Zeros of
functions. Infinite Zeros of 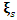 : It is trivial that all the zeros of
: It is trivial that all the zeros of 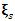 lie on
lie on 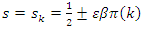 with
with 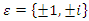 and due to condition of its convergence, and due to our periodic system, defined by the cyclotomic polynomials of the algebraic varieties defined by
and due to condition of its convergence, and due to our periodic system, defined by the cyclotomic polynomials of the algebraic varieties defined by 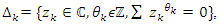 by
by 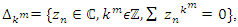 that show similar properties for their cyclotomic polynomial
that show similar properties for their cyclotomic polynomial 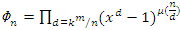 . Then when such a polynomial degenerates, we have infinite of solutions, and when is
. Then when such a polynomial degenerates, we have infinite of solutions, and when is 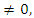 then finitely generated, and since
then finitely generated, and since 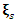 related to
related to 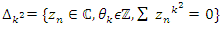 which proves that when
which proves that when 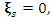 the
the 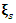 has infinite of solutions and when
has infinite of solutions and when 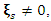 then
then 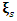 generated by a finite set. Volume Hyperbolic of the dynamical system: A problem of volume that was analyzed by Thurston describing hyperbolic structure on
generated by a finite set. Volume Hyperbolic of the dynamical system: A problem of volume that was analyzed by Thurston describing hyperbolic structure on 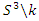 that degenerate by deforming ideal tetrahedral, also a reference to the hyperbolic volume conjecture by Michio Fuji. We notice this dynamical is in the form of 2 Laurent polynomials
that degenerate by deforming ideal tetrahedral, also a reference to the hyperbolic volume conjecture by Michio Fuji. We notice this dynamical is in the form of 2 Laurent polynomials 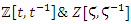 that swaps roots with coefficients, although we know by Seifert theorem
that swaps roots with coefficients, although we know by Seifert theorem 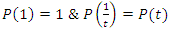 for symmetric polynomial. In this part we going to show that Riemann sequence related to Gaussian distribution & Riemann sequence related to the analytical function are connected to the hyperbolic volume. swap roots with coefficients based on the symmetric Laurent polynomial, where
for symmetric polynomial. In this part we going to show that Riemann sequence related to Gaussian distribution & Riemann sequence related to the analytical function are connected to the hyperbolic volume. swap roots with coefficients based on the symmetric Laurent polynomial, where 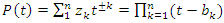 . Hence for a closed loop
. Hence for a closed loop 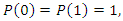 and with the condition of symmetric polynomial and Seifert theorem, with
and with the condition of symmetric polynomial and Seifert theorem, with 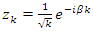 , with
, with 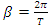 . then
. then 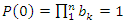 since
since 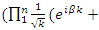
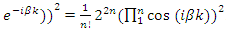 . Although we know the normal distribution is when
. Although we know the normal distribution is when 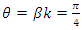 . Then
. Then 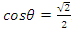 , which proves the equality
, which proves the equality 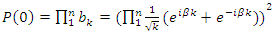
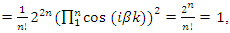 that corresponds to a volume of a polytope when the system degenerate to n=0. In our case the volume correspond to
that corresponds to a volume of a polytope when the system degenerate to n=0. In our case the volume correspond to 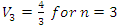 , and
, and 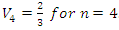 . Volume that we can prove it through distance
. Volume that we can prove it through distance 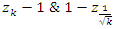 and then by summing:
and then by summing: 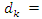
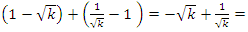 represents the distances between radiuses so we can calculate the volume of the polytope
represents the distances between radiuses so we can calculate the volume of the polytope 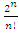 in the unity sphere:
in the unity sphere: 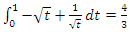 that shows n=3. Prime number theorem: We will terminate these parts by providing the density volume, the best and better approximation prime theorem defined through volume:
that shows n=3. Prime number theorem: We will terminate these parts by providing the density volume, the best and better approximation prime theorem defined through volume: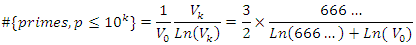
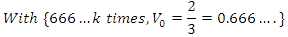
3. Solution Birch-Swinnerton-Dyer Conjecture
- First let’s give some background on the conjecture, the B.S-D conjecture is under many progresses developed by Gross & Zagier, Barry Mazur, Rubin, and Bhargava [16], and many other mathematicians with related works. The conjecture describes the set of rational solutions to the equations defining elliptic curves, that claims that the rank of the abelian group E(K) of point of E is the order of the zero of the Hass-Weil L-function
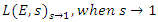 . From the Mordell theorem, the group of rational points on an elliptic curve has a finite basis, Helmut Hass conjectured that L(E,s) could converge not only when
. From the Mordell theorem, the group of rational points on an elliptic curve has a finite basis, Helmut Hass conjectured that L(E,s) could converge not only when 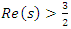 through an analytical continuation. Due to the modularity theorem that implies the analytical statement: to each elliptic curve over ℚ, we may attach a correspondent L-series, a Dirichlet series,
through an analytical continuation. Due to the modularity theorem that implies the analytical statement: to each elliptic curve over ℚ, we may attach a correspondent L-series, a Dirichlet series, 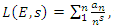 the generating function of the coefficient
the generating function of the coefficient 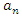 is then
is then 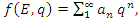 with
with 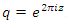 , [13].Prove: As a summary, we showed in this theory, which is based on a periodical fractal system, defined by an abelian algebraic variety described by a chain of finite cyclic covering of torus knots, with modular hyperbolic dynamical system. We defined the period of the system and showed that all the primes
, [13].Prove: As a summary, we showed in this theory, which is based on a periodical fractal system, defined by an abelian algebraic variety described by a chain of finite cyclic covering of torus knots, with modular hyperbolic dynamical system. We defined the period of the system and showed that all the primes 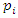 split in both in the abelian field of
split in both in the abelian field of 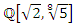 and in its cyclotomic abelian [11] extension
and in its cyclotomic abelian [11] extension 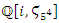 . Determined by the abelian variety defined by the complete split of all the prime numbers in the extensions,
. Determined by the abelian variety defined by the complete split of all the prime numbers in the extensions, 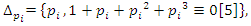 with
with 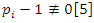 . In our case the period of our dynamical system is
. In our case the period of our dynamical system is 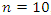 , infinite cyclic linked torus knot is reduced due to the period of the system. Number of roots defined by the Euler totient associated function:
, infinite cyclic linked torus knot is reduced due to the period of the system. Number of roots defined by the Euler totient associated function: 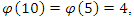 which is isomorphic to Mordel-Weil group
which is isomorphic to Mordel-Weil group  of order 4, is that the rank of the abelian variety related to the zero of the associated L-function related to Birch & Swinnerton-Dyer conjecture! We going to do more analysis to discover the right rank. By Hensel’s lemma, the group of units
of order 4, is that the rank of the abelian variety related to the zero of the associated L-function related to Birch & Swinnerton-Dyer conjecture! We going to do more analysis to discover the right rank. By Hensel’s lemma, the group of units  has
has 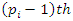 roots of unity. This splitting descends to the quotient rings
roots of unity. This splitting descends to the quotient rings 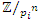 and its group of units, giving an isomorphism
and its group of units, giving an isomorphism 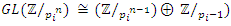 . Well in our case the units of
. Well in our case the units of 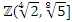 are the independent elements defined by:
are the independent elements defined by: 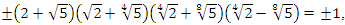 where the points
where the points 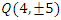 elements of the hyperelliptic curve with rank
elements of the hyperelliptic curve with rank 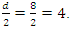 it shows that there is a correspondence between an hyperelliptic curve with genus 1 with degree defined by 2g+2, the Galois group is contained in the symmetric group
it shows that there is a correspondence between an hyperelliptic curve with genus 1 with degree defined by 2g+2, the Galois group is contained in the symmetric group 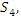 a double cover of
a double cover of 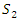 . Previously we proved the partial splitting of the primes in the field
. Previously we proved the partial splitting of the primes in the field 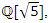 but a complete splitting of all the primes in the abelian extensions
but a complete splitting of all the primes in the abelian extensions 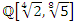 and the cyclotomic field
and the cyclotomic field 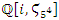 . Since for a curve of genus g and prime
. Since for a curve of genus g and prime 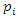 the extension of the curve generated by the points of the 5 torsion, then we have similar situation for the distribution of rational numbers as the prime numbers! the distribution of the rational points depend on the primes ramification! Then the ramification of the curves depends on the prime’s ramification in the field
the extension of the curve generated by the points of the 5 torsion, then we have similar situation for the distribution of rational numbers as the prime numbers! the distribution of the rational points depend on the primes ramification! Then the ramification of the curves depends on the prime’s ramification in the field 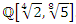 . Rational numbers lie partially on the elliptic curve, those elliptic curves embedded in the Seifert surfaces. Then after analyzing our system’s Seifert surfaces, we can conclude some rational points lie on the complement of the circle “the trivial knot”, some lie on the complement of the Hopf’s link, some lie on the complement of the trefoil knot, but all the rational points lie completely on the complement of the hyperbolic Eight Knot, describing then the Seifert surfaces defined by the complement of the algebraic varieties described before. Here we connect knots with elliptic & hyperelliptic curves through the quadratic equation. This hyperelliptic curve, is of
. Rational numbers lie partially on the elliptic curve, those elliptic curves embedded in the Seifert surfaces. Then after analyzing our system’s Seifert surfaces, we can conclude some rational points lie on the complement of the circle “the trivial knot”, some lie on the complement of the Hopf’s link, some lie on the complement of the trefoil knot, but all the rational points lie completely on the complement of the hyperbolic Eight Knot, describing then the Seifert surfaces defined by the complement of the algebraic varieties described before. Here we connect knots with elliptic & hyperelliptic curves through the quadratic equation. This hyperelliptic curve, is of 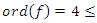
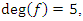 a reduced bilinear equation defined by
a reduced bilinear equation defined by 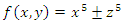 with degree 5, reduced to the quartic curve defined by:
with degree 5, reduced to the quartic curve defined by: 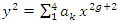
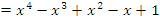 . There are no rational points for the case
. There are no rational points for the case 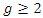 , (See [16]). Then we get 2 families of isotropic subspaces of the
, (See [16]). Then we get 2 families of isotropic subspaces of the 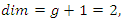 defined by the quadratic equations, generated by the symplectic matrices:
defined by the quadratic equations, generated by the symplectic matrices: 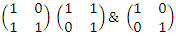 seen before, describing the modular twists.Let’s denote by the
seen before, describing the modular twists.Let’s denote by the 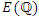 the Mordell-Weil group of rational on elliptic curve E,
the Mordell-Weil group of rational on elliptic curve E, 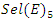 the 5 -Selmer group of
the 5 -Selmer group of 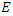 , and
, and 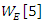 the 5-part of Tate-Shafarevich group of
the 5-part of Tate-Shafarevich group of 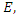 then we have the following sequence:
then we have the following sequence: 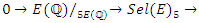
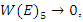 see detail for generalization [21]. The rank of
see detail for generalization [21]. The rank of 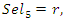 such that
such that 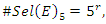 then if
then if 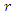 is the rank of the curve,
is the rank of the curve, 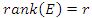 , and by the upper bound inequality we have:
, and by the upper bound inequality we have: 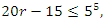 (See [16]). Then for
(See [16]). Then for 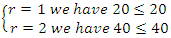 then
then 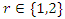 is an optimum bound. By The parity conjecture then concluded but for partial distribution, with less than 25% with rank 0 and less than 25% with rank 1 of the total rational points. And this is a perfect distribution since we see also as a prove the
is an optimum bound. By The parity conjecture then concluded but for partial distribution, with less than 25% with rank 0 and less than 25% with rank 1 of the total rational points. And this is a perfect distribution since we see also as a prove the 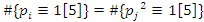 , defined by
, defined by 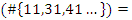
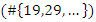 , while the remaining over 50% defined by
, while the remaining over 50% defined by 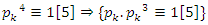 invertible elements through
invertible elements through 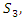 by the way
by the way 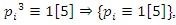 then the elements with
then the elements with 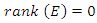 and elements with
and elements with 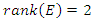 are equal. Now by observing the bound for the odd and even rank defined by
are equal. Now by observing the bound for the odd and even rank defined by 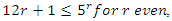 and
and 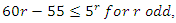 (See Bhargava details [16]) we have then
(See Bhargava details [16]) we have then 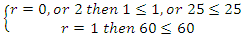 the rest of rational points by ramification will lie on the quartic equation defined by
the rest of rational points by ramification will lie on the quartic equation defined by 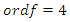 determined by the Seifert surface: the complement of the hyperbolic Eight-Knot. Conclusion: All rational lie completely on the quartic elliptic curve with
determined by the Seifert surface: the complement of the hyperbolic Eight-Knot. Conclusion: All rational lie completely on the quartic elliptic curve with 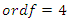 in the abelian extension
in the abelian extension 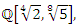 and lie partially on the elliptic curves with the
and lie partially on the elliptic curves with the 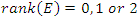 . Hence it shows an equidistributional of #{rational points} between
. Hence it shows an equidistributional of #{rational points} between 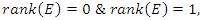 which prove the parity conjecture. While elliptic curve with rank 0 & 2 shows with symmetrical rational points with similar points. Then for this partial distribution, the elliptic curve of
which prove the parity conjecture. While elliptic curve with rank 0 & 2 shows with symmetrical rational points with similar points. Then for this partial distribution, the elliptic curve of 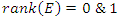 represent less than 50% of rational points, and the remaining over 50% lie on the hyperelliptic curve with
represent less than 50% of rational points, and the remaining over 50% lie on the hyperelliptic curve with 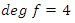 that we going to define. Now back to our Riemann sequence:
that we going to define. Now back to our Riemann sequence: 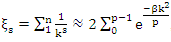 , related to Theta function, with
, related to Theta function, with 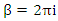 and
and 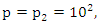 with
with 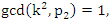 its Euler totient function
its Euler totient function 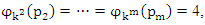 with
with 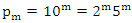 .
. 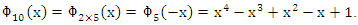 Now returning to our quartic polynomial, which is with discriminant
Now returning to our quartic polynomial, which is with discriminant 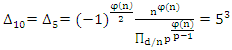 that shows 5 the only ramified prime number in the cyclotomic field
that shows 5 the only ramified prime number in the cyclotomic field  Since
Since 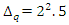 the discriminant of the quadratic equation, then the associate elliptic curve with discriminant
the discriminant of the quadratic equation, then the associate elliptic curve with discriminant 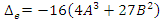
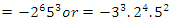 depends on 5 if divides
depends on 5 if divides 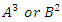 . Note since the system is fractal, modular, and periodic, then by the theorem of elliptic curve over rational set, for points
. Note since the system is fractal, modular, and periodic, then by the theorem of elliptic curve over rational set, for points  then
then 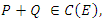 then all rational points are determined by the fractal system, defined by circles of radius
then all rational points are determined by the fractal system, defined by circles of radius 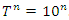 . For example from 2 rational points determined in
. For example from 2 rational points determined in 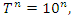 we can compute the third rational point in
we can compute the third rational point in 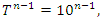 then the algebraic varieties stays the same analogous, with the same singular points, defined by rational points
then the algebraic varieties stays the same analogous, with the same singular points, defined by rational points 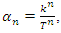 with
with 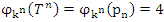 . Now returning to our quartic polynomial, which is with discriminant
. Now returning to our quartic polynomial, which is with discriminant 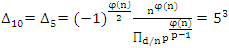 . The primes 2 & 3 are reversible symmetric in
. The primes 2 & 3 are reversible symmetric in  , by Fermat little theorem
, by Fermat little theorem 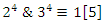
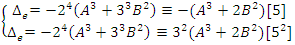 Since
Since 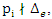 the same for
the same for 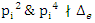 the discriminant of the elliptic curve, all the primes except 2 & 5 that are dividing the discriminant of the related elliptic curve, hence we have a good reduction, then
the discriminant of the elliptic curve, all the primes except 2 & 5 that are dividing the discriminant of the related elliptic curve, hence we have a good reduction, then 
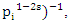 with
with 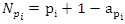 it follows:
it follows: 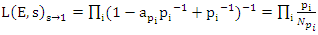 . Notice for the product of all ramified primes,
. Notice for the product of all ramified primes, 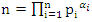 the Euler totient function
the Euler totient function 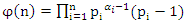 hence the fraction related to the prime density:
hence the fraction related to the prime density: 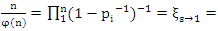
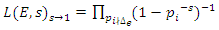 when
when  for bad reduction. To evaluate the rank, we need to find conditions on
for bad reduction. To evaluate the rank, we need to find conditions on 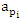 , the trace of the Frobenius, related to the density of the primes. We already know the distributions of the primes on the Seifert surfaces defined by our system, determined by the symplectic matrix, this examination will filtrate the values of
, the trace of the Frobenius, related to the density of the primes. We already know the distributions of the primes on the Seifert surfaces defined by our system, determined by the symplectic matrix, this examination will filtrate the values of 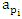 related to the discriminant of the quadratic equations. With
related to the discriminant of the quadratic equations. With 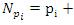
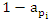 , we notice then in the following densities:
, we notice then in the following densities: 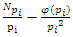 with giving
with giving 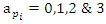 shows some interesting connections to Alexander knot polynomial, and the Seifert surfaces of our system:For
shows some interesting connections to Alexander knot polynomial, and the Seifert surfaces of our system:For  we have
we have 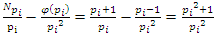 related to Hopf’s linkFor
related to Hopf’s linkFor 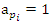 we have
we have 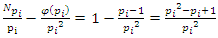 related to trefoil knotFor
related to trefoil knotFor 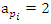 we have
we have 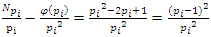 related to trivial knotsFor
related to trivial knotsFor 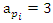 we have
we have 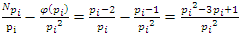 related to the hyperbolic Eight-Knot.Notice the interesting relation that links the knots of the system:
related to the hyperbolic Eight-Knot.Notice the interesting relation that links the knots of the system: 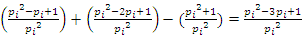 & by
& by 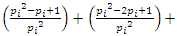
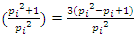 that shows the link of cyclic covering, describe an expanding trefoil knots, and expanding hyperbolically by changing the direction of the flow of the Hopf’s link. Hass proved the bound of
that shows the link of cyclic covering, describe an expanding trefoil knots, and expanding hyperbolically by changing the direction of the flow of the Hopf’s link. Hass proved the bound of 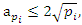 this bound is not sufficient to determine the rank of E, then a condition of the rank of an elliptic curve is
this bound is not sufficient to determine the rank of E, then a condition of the rank of an elliptic curve is 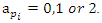 While
While 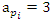 is related to the rank of the hyperelliptic curve of order 4, defined as a hyperbolic Seifert surface, complement of the hyperbolic 8-knot.Now we going to extend our analysis to prove the rank of the elliptic curve, by verifying the Zeta function of an elliptic curve over finite field
is related to the rank of the hyperelliptic curve of order 4, defined as a hyperbolic Seifert surface, complement of the hyperbolic 8-knot.Now we going to extend our analysis to prove the rank of the elliptic curve, by verifying the Zeta function of an elliptic curve over finite field 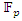 which is a generating function in the field extension
which is a generating function in the field extension 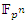 . The Zeta function defined by:
. The Zeta function defined by: 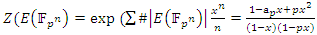 after evaluation. And for a finite field
after evaluation. And for a finite field 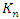 , the formula defined by:
, the formula defined by: 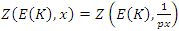
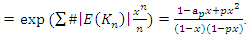 And since:
And since:  and
and  therefore:
therefore: 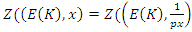
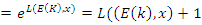 , and by approximating the rational fraction, with
, and by approximating the rational fraction, with  and condition
and condition 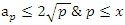 , notice the fraction:
, notice the fraction: 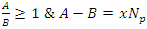 it follows then the approximation of the fraction for a max bound determined by:
it follows then the approximation of the fraction for a max bound determined by: 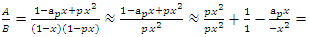
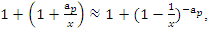 applying
applying 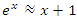 then
then 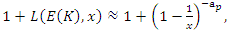 it follows
it follows 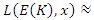
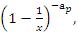 by using
by using 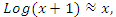 then
then 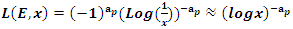 and since
and since 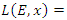
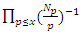 then
then 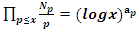 with:
with: 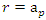 .Now the approximation for the inf bound of
.Now the approximation for the inf bound of 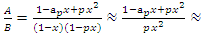
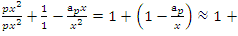
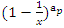 and with
and with 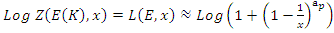 . Which shows that
. Which shows that 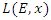 is analytical at the point
is analytical at the point 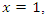 since
since 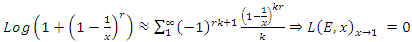 .Conclusion: The
.Conclusion: The 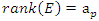 is the trace of the Frobenius, with conditions
is the trace of the Frobenius, with conditions 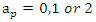 for elliptic curve and rank=3 for hyperelliptic curve of order 4 with genus 1. It also proves the parity conjecture that depends on
for elliptic curve and rank=3 for hyperelliptic curve of order 4 with genus 1. It also proves the parity conjecture that depends on 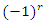 for
for 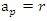 odd or even. An interesting conjecture that we going to use in connection to Riemann conjecture to solve Navier stokes conjecture.
odd or even. An interesting conjecture that we going to use in connection to Riemann conjecture to solve Navier stokes conjecture. 4. Solution to Navier Stokes Conjecture: Existence & Smoothness of the Navier Stokes Equation
- The analogous Physical parameters that described the mathematical system’s flow: As we notice from our previous analysis of the mathematical discrete system’s flow, that fundamentally Navier Stokes shows its footprint in the flow of the mathematical universe. Since we proved the duality between continuous systems & discrete system by analyzing Riemann hypothesis, which results from the flow of the discrete system, by proving the entangled representation of the asymmetrical set of integers and its extensions as points like for an N-Simplex, or as a loop for its analytical structure, or as a knot for its topological structure, or as a polytope volume for its geometric structure, and as an algorithm of string for its fundamental braid group structure. Let’s denote by the following analogous parameters of the mathematical universe system:
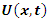 : field,
: field, 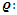 density,
density, 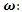 twist "frequency",
twist "frequency", 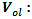 volume, E: energy, P: presure & by F force. We proved the dynamical system of integers is defined in a smooth fractal Manifold considered as the spacetime of 4 dimensions, in the Hilbert space, with metric space, endowed with inner product. The system is periodic, fractal, generated by two forces
volume, E: energy, P: presure & by F force. We proved the dynamical system of integers is defined in a smooth fractal Manifold considered as the spacetime of 4 dimensions, in the Hilbert space, with metric space, endowed with inner product. The system is periodic, fractal, generated by two forces 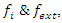 with
with 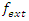 force exterior related to the hyperbolic expansion of the manifold as the packing sphere, that contains & covers the flow of the internal linked cyclic covering system generated by the hyperbolic force related to the 8-knot, and the other interior force
force exterior related to the hyperbolic expansion of the manifold as the packing sphere, that contains & covers the flow of the internal linked cyclic covering system generated by the hyperbolic force related to the 8-knot, and the other interior force 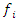 related to the link of the cyclic covering of the system generated by following 3 forces related to “Trivial knot, Hopf’s Link, and the Trefoil knot”, with a total then of 4 independent and unified forces in the Poincare group defined by symplectic group SO(3,1) related to the spacetime translation transformation and Lorentz transformation related to the rotation and reflection for its Dihedral group, while we notice in our system that the field
related to the link of the cyclic covering of the system generated by following 3 forces related to “Trivial knot, Hopf’s Link, and the Trefoil knot”, with a total then of 4 independent and unified forces in the Poincare group defined by symplectic group SO(3,1) related to the spacetime translation transformation and Lorentz transformation related to the rotation and reflection for its Dihedral group, while we notice in our system that the field 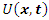 defined in
defined in 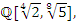 and its cyclotomic extension field
and its cyclotomic extension field 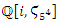 . Abelian group G, where its center Z(G)=G generated by the center groups
. Abelian group G, where its center Z(G)=G generated by the center groups 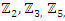 and the circle unity U(1), which is related to the Gauge field for the Yang Mills theory, normal subgroups that commute resp with SU(2), SU(3) and SU(5) or SO(10). While the flow of the vector field is asymmetrical generated by rotation, twist, and translation defined by a modular flow in a closed space, which imply the
and the circle unity U(1), which is related to the Gauge field for the Yang Mills theory, normal subgroups that commute resp with SU(2), SU(3) and SU(5) or SO(10). While the flow of the vector field is asymmetrical generated by rotation, twist, and translation defined by a modular flow in a closed space, which imply the  , defined by 2 asymmetrical curves, one stable related to the velocity
, defined by 2 asymmetrical curves, one stable related to the velocity 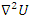 and the other flow related to
and the other flow related to 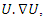 while
while 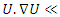
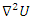 for a normal stable system flow. While the turbulence always exists but minimal, the flow is generated by the asymmetrical internal and external waves describing a vortex ring model, that we going to describe by the volume exterior
for a normal stable system flow. While the turbulence always exists but minimal, the flow is generated by the asymmetrical internal and external waves describing a vortex ring model, that we going to describe by the volume exterior 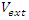 and its asymmetrical volume interior
and its asymmetrical volume interior 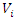 that flows in opposite direction, and while
that flows in opposite direction, and while 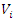 expands, it creates then an interior force from the inside described by the force of pressure, then the energy Kinetic exists and bounded since per definition knots are bounded! And the compliment of the knot is the Seifert surface! Our mathematical system describes all the parameters needed to describe Navier stokes equation. As parameters: we described our numerical flow based on the homogenous spacetime, where space & time have same period
expands, it creates then an interior force from the inside described by the force of pressure, then the energy Kinetic exists and bounded since per definition knots are bounded! And the compliment of the knot is the Seifert surface! Our mathematical system describes all the parameters needed to describe Navier stokes equation. As parameters: we described our numerical flow based on the homogenous spacetime, where space & time have same period 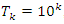 , defined by the analytical, or bump function
, defined by the analytical, or bump function 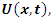 related to the convergence of Riemann series in a 4-dimensional spacetime analogous to Minkowski spacetime, defined by
related to the convergence of Riemann series in a 4-dimensional spacetime analogous to Minkowski spacetime, defined by 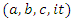 for its coordinates, with:
for its coordinates, with: 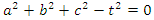 with
with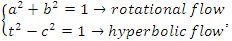 Then:
Then: 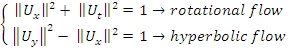 The space
The space 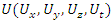 defined in
defined in  is an embedding, analogous space to Minkowski spacetime, since if we consider the relation between previous knots &
is an embedding, analogous space to Minkowski spacetime, since if we consider the relation between previous knots &  then with,
then with, 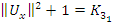 ,
, 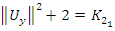 ”Hopf’s Link”,
”Hopf’s Link”, 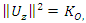 “Trivial knot”, and
“Trivial knot”, and 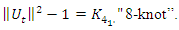 We notice the Seifert surfaces related to the vector spacetime
We notice the Seifert surfaces related to the vector spacetime 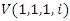 defined by the symplectic matrix:
defined by the symplectic matrix: 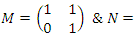
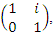 are the complement of the trefoil knot
are the complement of the trefoil knot 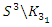 resp the complement of the hyperbolic 8-knot:
resp the complement of the hyperbolic 8-knot: 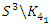 defined by:
defined by: 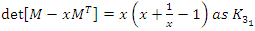 &
& 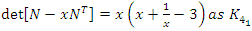 . Then for
. Then for  with:
with: 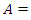
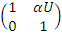 we have:
we have: 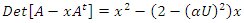
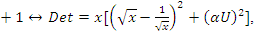 Then the Seifert surface covers the entire space if
Then the Seifert surface covers the entire space if 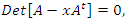 hence
hence 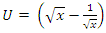 , with
, with 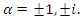 An equation that we are familiar in our paper, and already analyzed related to the convergence of Riemann Hypothesis series & B.S-Dyer rank conjecture. We described the density
An equation that we are familiar in our paper, and already analyzed related to the convergence of Riemann Hypothesis series & B.S-Dyer rank conjecture. We described the density  of the integers, and primes numbers by Euler totient function, also we defined the fractal volume of the packing related to the spheres packing
of the integers, and primes numbers by Euler totient function, also we defined the fractal volume of the packing related to the spheres packing 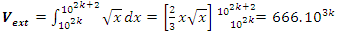 , and volume of its asymmetrical inverse flow by
, and volume of its asymmetrical inverse flow by 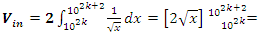
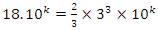 sphere of radius 3, that expands by
sphere of radius 3, that expands by 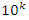 With
With 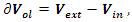 asymmetrical entities defined by volume that flow opposite direction, to create a vortex torus model, then in the interval [0,1] the volume is related to the polytope
asymmetrical entities defined by volume that flow opposite direction, to create a vortex torus model, then in the interval [0,1] the volume is related to the polytope 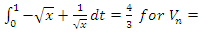
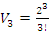 . The frequencies
. The frequencies  or the velocity of the system is defined by the modular twists related to the linking in the cyclic covering defined in the algebraic variety. Due to Riemann hypothesis convergences, then based on Fourier transform the series
or the velocity of the system is defined by the modular twists related to the linking in the cyclic covering defined in the algebraic variety. Due to Riemann hypothesis convergences, then based on Fourier transform the series 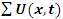 converge for both cases: analytic, modular & for Bump function related to the Gaussian distribution along the period and the expansion with
converge for both cases: analytic, modular & for Bump function related to the Gaussian distribution along the period and the expansion with 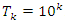 . The analytical modular function defined by the Laplacian function is to describe the behavior of the system along the eigen-values & eigen-function, which return to be a differential equation. Although, we know that the mathematical foundation of the wave, heat equation and the Schrodinger equation in quantum mechanics are based on Theta function. We proved also the singular points related to the algebraic variety in the Riemann Hypothesis section. The physical Navier Stokes equation is known by the equation that describes the chaotic flow of different systems! The foundation of such an equation is mathematical. We can then apply even Navier Stokes equation to describe the dynamical system of the discrete system! This analysis describes then the heartbeat of the mathematical universe flow, by describing the hyperbolic volume of its asymmetrical Seifert surfaces, and the singular points for such a fractal periodic system related to its twists “frequencies”. An abstract theoretical mathematical model that reflects reality, a consistent model to describe the flow of general systems, based on, then we can model the biological heartbeat system defined by sound to describe the air flow for the respiratory system, and blood flow system! The Platonian T.o.E then is just the fundamental mathematical structure of Navier Stokes equation. We proved that Navier Stokes equation which is defined for continuous system have a discrete dual representation based in Number Theory. We also showed the connection between cross polytopes, and the hyperbolic flow of the cyclic covering, properties that are related to the Poincare conjecture! Since we notice a similarity in the construction for the prove of the Poincare conjecture by Perlman, where he used in hyperbolic geometry Dehn surgery for a linked cyclic covering of the Seifert bundle that extent hyperbolically in a closed space! Both Perlman & Hamilton applied Ricci flow for a smooth differential manifold to prove the compact spaces diffeomorphic to spheres & to get a good understanding of the singularities. Here we showed the singularities are related to the blow up of the Alexander polynomial at
. The analytical modular function defined by the Laplacian function is to describe the behavior of the system along the eigen-values & eigen-function, which return to be a differential equation. Although, we know that the mathematical foundation of the wave, heat equation and the Schrodinger equation in quantum mechanics are based on Theta function. We proved also the singular points related to the algebraic variety in the Riemann Hypothesis section. The physical Navier Stokes equation is known by the equation that describes the chaotic flow of different systems! The foundation of such an equation is mathematical. We can then apply even Navier Stokes equation to describe the dynamical system of the discrete system! This analysis describes then the heartbeat of the mathematical universe flow, by describing the hyperbolic volume of its asymmetrical Seifert surfaces, and the singular points for such a fractal periodic system related to its twists “frequencies”. An abstract theoretical mathematical model that reflects reality, a consistent model to describe the flow of general systems, based on, then we can model the biological heartbeat system defined by sound to describe the air flow for the respiratory system, and blood flow system! The Platonian T.o.E then is just the fundamental mathematical structure of Navier Stokes equation. We proved that Navier Stokes equation which is defined for continuous system have a discrete dual representation based in Number Theory. We also showed the connection between cross polytopes, and the hyperbolic flow of the cyclic covering, properties that are related to the Poincare conjecture! Since we notice a similarity in the construction for the prove of the Poincare conjecture by Perlman, where he used in hyperbolic geometry Dehn surgery for a linked cyclic covering of the Seifert bundle that extent hyperbolically in a closed space! Both Perlman & Hamilton applied Ricci flow for a smooth differential manifold to prove the compact spaces diffeomorphic to spheres & to get a good understanding of the singularities. Here we showed the singularities are related to the blow up of the Alexander polynomial at  related to trivial knot “Unknot”, while prime number have this structure defined by the Unknot discovered by Barry Mazur, then the complement of a trivial knot defined by
related to trivial knot “Unknot”, while prime number have this structure defined by the Unknot discovered by Barry Mazur, then the complement of a trivial knot defined by  is the Seifert surface
is the Seifert surface 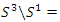
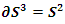 where
where  is the boundary of the Seifert surface, since by definition a knot is embedded in
is the boundary of the Seifert surface, since by definition a knot is embedded in  . Ricci flow here to describe the exterior forces related to curvature. Prove of Navier Stokes statement related to the existence of Smooth solution [18]: In our model we proved that Riemann hypothesis have two kind of distribution, analytical related to Fourier series, or Theta function, and discrete related to Poisson distribution, or Gaussian distribution for a probability normal distribution of the chaotic system, for this reason you can model any dynamical physical system from discrete to continuous system by a differential function of class
. Ricci flow here to describe the exterior forces related to curvature. Prove of Navier Stokes statement related to the existence of Smooth solution [18]: In our model we proved that Riemann hypothesis have two kind of distribution, analytical related to Fourier series, or Theta function, and discrete related to Poisson distribution, or Gaussian distribution for a probability normal distribution of the chaotic system, for this reason you can model any dynamical physical system from discrete to continuous system by a differential function of class 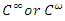 defined in our case by the bump function related to Gaussian distribution of class
defined in our case by the bump function related to Gaussian distribution of class 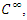 or by an analytical modular function of class
or by an analytical modular function of class 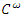 . Defined by:
. Defined by: 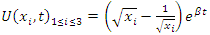 defined in
defined in 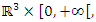 with
with 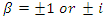 since the system is periodic & fractal! as defined for the condition of the Riemann Hypothesis sequence to converge to cover both the bump Gaussian function and the analytical, or the modular Theta function of the Riemann Hypothesis series. Then
since the system is periodic & fractal! as defined for the condition of the Riemann Hypothesis sequence to converge to cover both the bump Gaussian function and the analytical, or the modular Theta function of the Riemann Hypothesis series. Then 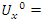
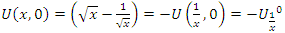 with
with 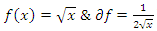 We already know the properties described for this function in our paper,
We already know the properties described for this function in our paper, 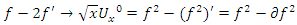 where we proved that
where we proved that  a fractal sequence related to the volume
a fractal sequence related to the volume  while
while 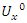 bounded since
bounded since 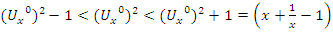 equation of a trefoil knot & 8-knots that are embedded in
equation of a trefoil knot & 8-knots that are embedded in 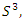 while knots are closed curves!
while knots are closed curves! 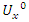 is of class
is of class 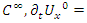
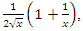 and for any
and for any  we have:
we have: 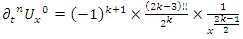
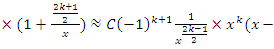
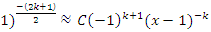
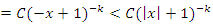 . Then
. Then 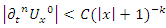 . The asymmetrical curves defined by the flows shows: The flow of the system is defined in
. The asymmetrical curves defined by the flows shows: The flow of the system is defined in 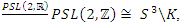 and since for
and since for 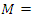
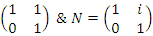 ,
, 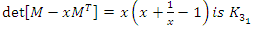 &
& 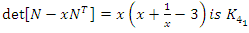 . And since
. And since 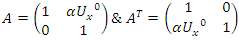 are connected by the Seifert matrix determinant, we have
are connected by the Seifert matrix determinant, we have 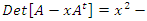
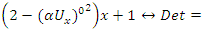
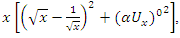 then for the Seifert surface to cover the entire space,
then for the Seifert surface to cover the entire space,  hence
hence 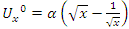 with
with  Since we are analyzing the hyperbolic horocycle flow based on
Since we are analyzing the hyperbolic horocycle flow based on 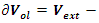
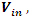 then we have the asymmetrical stable flows defined when
then we have the asymmetrical stable flows defined when 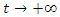 that converge toward the initial state, defined by stable curves determined by the right multiplication of the nilpotent group
that converge toward the initial state, defined by stable curves determined by the right multiplication of the nilpotent group 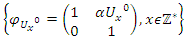 by the matrix of the hyperbolic flow, defined by the diagonal group
by the matrix of the hyperbolic flow, defined by the diagonal group 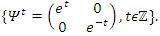
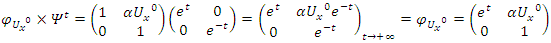 And for its asymmetrical flow by left multiplication of the matrix of the hyperbolic flow, defined by the diagonal group
And for its asymmetrical flow by left multiplication of the matrix of the hyperbolic flow, defined by the diagonal group 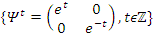 to its transpose matrix defined by the nilpotent group
to its transpose matrix defined by the nilpotent group 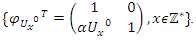 Otherwise, the asymmetrical flow is not stable. Then the asymmetrical flow is stable when
Otherwise, the asymmetrical flow is not stable. Then the asymmetrical flow is stable when 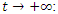
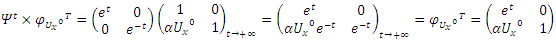 We notice the asymmetrical hyperbolical flows tend to be asymmetrical equal when
We notice the asymmetrical hyperbolical flows tend to be asymmetrical equal when 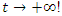 That tend to
That tend to 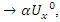 then the flow is with both directions ⇅ hence
then the flow is with both directions ⇅ hence 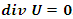 . Also I want to clarify for the hyperbolic flow
. Also I want to clarify for the hyperbolic flow 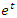 since we solved the problem of infinity based on the fractal manifold, that expand with a rate of
since we solved the problem of infinity based on the fractal manifold, that expand with a rate of 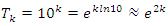 , then the parameter
, then the parameter 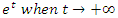 indicate in that direction the fractal flow of the system! The flow of the system is stable periodic and fractal. Also we proved in our system the connection of the distance
indicate in that direction the fractal flow of the system! The flow of the system is stable periodic and fractal. Also we proved in our system the connection of the distance 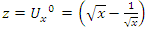 to the Alexander polynomial knots, described by: Trivial knot, Hopf’s link, trefoil knot & the hyperbolic 8-knot by the following equations:
to the Alexander polynomial knots, described by: Trivial knot, Hopf’s link, trefoil knot & the hyperbolic 8-knot by the following equations: 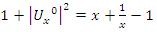 for
for 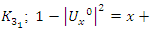
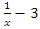 for
for 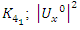 for the trivial knot
for the trivial knot 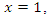 and
and 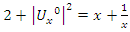 for Hopf’s link. Each of these knots related to a force, the system then described by 4 forces. With
for Hopf’s link. Each of these knots related to a force, the system then described by 4 forces. With  for a unit masse, hence the energy Kinetic
for a unit masse, hence the energy Kinetic 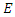 defined by
defined by 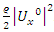 is then bounded since knots are closed curves, embedded in
is then bounded since knots are closed curves, embedded in 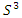 by definition, and the Seifert surfaces defined by the complement of the knots
by definition, and the Seifert surfaces defined by the complement of the knots 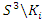 related to the fields
related to the fields 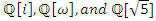 . And since all prime numbers split in
. And since all prime numbers split in 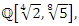 and its cyclotomic extension
and its cyclotomic extension 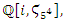 then all energy is distributed in this field of order 4. Now for the analytical, modular flow, described by Theta function in our theory for the Riemann series convergence,
then all energy is distributed in this field of order 4. Now for the analytical, modular flow, described by Theta function in our theory for the Riemann series convergence, 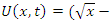
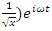 is of class
is of class 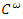 . We have the following analytical modular flow defined by the multiplication of the diagonal group
. We have the following analytical modular flow defined by the multiplication of the diagonal group 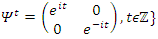 but this time by the nilpotent group
but this time by the nilpotent group  With
With 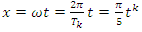 for a uniform velocity with period
for a uniform velocity with period 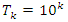 and for
and for 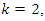 we have the convergence of the Riemann series defined by a Theta function as we described in this theory, and based on Fourier transform we determine the temporal and Spatial flow [19]. We also showed that the Euler Totient function is the same for the algebraic varieties of the fractal system
we have the convergence of the Riemann series defined by a Theta function as we described in this theory, and based on Fourier transform we determine the temporal and Spatial flow [19]. We also showed that the Euler Totient function is the same for the algebraic varieties of the fractal system 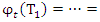
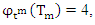 with
with 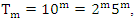 We have then:
We have then: 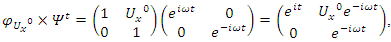 and for the asymmetrical flow:
and for the asymmetrical flow: 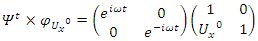
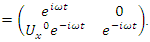 Hence this flow is periodic with order or period 5, known as the critical point.
Hence this flow is periodic with order or period 5, known as the critical point. 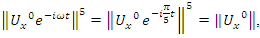 and
and 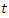 takes the discrete values in
takes the discrete values in 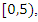 for the asymmetrical flow the 5 points are the conjugates, if we want to describe the geometric shape of these points, then these 12 points, including
for the asymmetrical flow the 5 points are the conjugates, if we want to describe the geometric shape of these points, then these 12 points, including  lie on the circumsphere of the icosahedral defined by the stereographic projection:
lie on the circumsphere of the icosahedral defined by the stereographic projection: 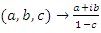 . The 12 vertices have complex coordinates: 0,
. The 12 vertices have complex coordinates: 0, 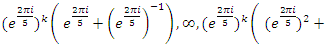
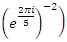 with
with  . We notice also when we add the 2 flows,
. We notice also when we add the 2 flows, 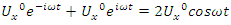 solution of the polynomial:
solution of the polynomial: 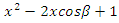 that represent the determinant of the Seifert surface defined by
that represent the determinant of the Seifert surface defined by 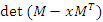 for the symplectic matrix
for the symplectic matrix 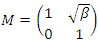 with
with 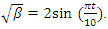 And since the system is fractal
And since the system is fractal 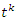 take the values in
take the values in 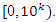 The energy E here also bounded as we proved for the hyperbolic bump function that connect
The energy E here also bounded as we proved for the hyperbolic bump function that connect 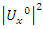 to the bounded knots described above in the fields
to the bounded knots described above in the fields 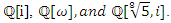 The pressure as a force its determination is related to the condition initial of
The pressure as a force its determination is related to the condition initial of 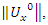 and
and 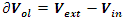 We have
We have 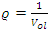 density per unit mass, and since
density per unit mass, and since 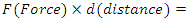
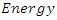 and
and 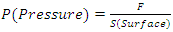 then:
then: 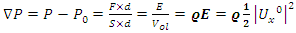 which show that the properties of the pressure are related to that of
which show that the properties of the pressure are related to that of 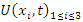 and
and 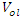 then
then 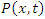 is of class
is of class  . We have then the following construction of Navier stokes eq defined by Newton’s 2nd law of motion
. We have then the following construction of Navier stokes eq defined by Newton’s 2nd law of motion 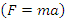 or momentum equation, within a controlled volume, the mass of the flow remains constant with time, and we have:
or momentum equation, within a controlled volume, the mass of the flow remains constant with time, and we have: 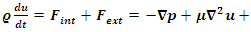
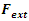 with
with 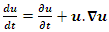 .Conclusion: Navier Stokes equation has its footprint in the mathematical invariant system for a smooth flow, which proves that the mathematical system is conscious! Also aware of non-smooth flows.
.Conclusion: Navier Stokes equation has its footprint in the mathematical invariant system for a smooth flow, which proves that the mathematical system is conscious! Also aware of non-smooth flows. 5. Platonian Theory of Everything Summary
 An Equation which provides & describes:- The sphere packing of the set
An Equation which provides & describes:- The sphere packing of the set 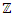 & its extensions.- The 4 unified forces: related to the 4 unified invariant knots described by trivial knot, Hopf’s link, trefoil knot & the hyperbolic 8-knot.- The probabilistic Quantum Mechanic: Described by Riemann Hypothesis, defined by Theta function, through Fourier transform [19]. - The yang Mills symmetries of transformations related to
& its extensions.- The 4 unified forces: related to the 4 unified invariant knots described by trivial knot, Hopf’s link, trefoil knot & the hyperbolic 8-knot.- The probabilistic Quantum Mechanic: Described by Riemann Hypothesis, defined by Theta function, through Fourier transform [19]. - The yang Mills symmetries of transformations related to 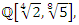 & its cyclotomic extension
& its cyclotomic extension 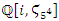 . - The Standard Model / Based on prime Numbers splitting defined in the set [1,100], since it is fractal. - The Chaotic distribution of general systems.The equation encompasses many fields and will answer many unsolved questions from: Multiverse ideas, existence of Aliens, wormholes, existence of life outside the earth, how the virology system works, Brain/Mind and consciousness, financial systems, and so on.…
. - The Standard Model / Based on prime Numbers splitting defined in the set [1,100], since it is fractal. - The Chaotic distribution of general systems.The equation encompasses many fields and will answer many unsolved questions from: Multiverse ideas, existence of Aliens, wormholes, existence of life outside the earth, how the virology system works, Brain/Mind and consciousness, financial systems, and so on.… ACKNOWLEDGEMENTS
- I want to thank Professor, and artist Robert Pope, “Director, Science-Art Research Centre of Australia, a great mind, who unveiled Plato’s hidden knowledge through arts & science”, for his encouragement to my research, and for opening me the door to view arts from different perspective, where Mathematics reflects its artistic structure in the reality! “The language of the Truth” Also, I don’t want to forget to thank the science & art community, especially the math community for their great achievements and tremendous progress seen along this journey of mathematical history, with a chain of connected mathematical discoveries that leaded us to discover puzzle after puzzle, the grand picture of the mathematical universe system. Also, I want to dedicate this paper for the memory of my deceased father Mohamed, the year 2012, because of his lost and other reasons, what pushed me to look for the truth and the foundation of the creation.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML