-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2022; 12(2): 25-31
doi:10.5923/j.ijtmp.20221202.01
Received: Aug. 30, 2022; Accepted: Sep. 16, 2022; Published: Sep. 23, 2022

Re-evaluating the Concept of Length Contraction to Reveal the True Nature of Special Relativity
Manhar L. Shah
MVM Electronics, Inc., 3410 N Harbor City Blvd., Suite E, Melbourne, FL, USA
Correspondence to: Manhar L. Shah , MVM Electronics, Inc., 3410 N Harbor City Blvd., Suite E, Melbourne, FL, USA.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The length contraction concept in Special Relativity (SR) is confounding and challenges one’s imagination and has generated many paradoxes and perplexing concepts in the past century. Perpetual constant relative velocity between two frames in SR and concepts based upon it are unrealistic. Constancy of light speed is the only connection between two inertial frames, hence allows length and time measures to differ in each by some factor 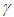 . SR so far has used identical measures. While developing Kinematic (non-inertial) SR (KSR) theory to connect inertial and non-inertial frames for physical reality the current SR concepts failed to provide consistent results. This paper shows SR, Lorentz Transformation and KSR will agree if the relatively moving inertial frame is regarded as space expanded and sped-up clock by a factor
. SR so far has used identical measures. While developing Kinematic (non-inertial) SR (KSR) theory to connect inertial and non-inertial frames for physical reality the current SR concepts failed to provide consistent results. This paper shows SR, Lorentz Transformation and KSR will agree if the relatively moving inertial frame is regarded as space expanded and sped-up clock by a factor 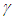 of the rest state. The prevailing concepts of SR using this frame with the inclusion of the start and stop considerations for such inertial frame also agrees with this new view and reveals the true nature of SR. The observed object’s dimensions would be unaffected due to its motion according to this new concept and spatially separated simultaneous events in one frame will be observed simultaneous in relatively moving other frames. As a result SR becomes easy to understand and settles many debated topics and issues such as twin paradox, Ehrenfest paradox, rigid body, stress with relative velocity, trapping a train in a shorter tunnel, etc.
of the rest state. The prevailing concepts of SR using this frame with the inclusion of the start and stop considerations for such inertial frame also agrees with this new view and reveals the true nature of SR. The observed object’s dimensions would be unaffected due to its motion according to this new concept and spatially separated simultaneous events in one frame will be observed simultaneous in relatively moving other frames. As a result SR becomes easy to understand and settles many debated topics and issues such as twin paradox, Ehrenfest paradox, rigid body, stress with relative velocity, trapping a train in a shorter tunnel, etc.
Keywords: Special Relativity, Non-inertial Special Relativity, Paradoxes in special relativity, Length contraction, Time dilation, KSR theory, Simultaneity, Space expansion, Sped-up clock
Cite this paper: Manhar L. Shah , Re-evaluating the Concept of Length Contraction to Reveal the True Nature of Special Relativity, International Journal of Theoretical and Mathematical Physics, Vol. 12 No. 2, 2022, pp. 25-31. doi: 10.5923/j.ijtmp.20221202.01.
Article Outline
1. Introduction
- The prevailing length contraction concept of Special Relativity (SR) stipulates that the contraction observed is real, meaning the relatively moving ruler of proper length L would appear shortened as
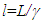 where
where 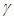 is the Lorentz contraction factor. Trapping a train in a shorter tunnel is extensively used in the past to illustrate this concept. On that thread, consider a train and platform of equal length L and
is the Lorentz contraction factor. Trapping a train in a shorter tunnel is extensively used in the past to illustrate this concept. On that thread, consider a train and platform of equal length L and 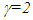 with the front, centre and the end of each marked A’, B’, and C’ for the train and A, B and C for the platform, respectively. Assume when A’ and A are aligned the clock time t’ at A’ and t at A is synchronized and set equal to zero (t=t’=0) and train stops. The train appears shortened on the platform so C’ is coincident to B while time of B is also t=0. For the train, according to the current concept of SR, C’ is nowhere near B at the time of C’ as t’=0 but at 2L from A and time of B equal to,
with the front, centre and the end of each marked A’, B’, and C’ for the train and A, B and C for the platform, respectively. Assume when A’ and A are aligned the clock time t’ at A’ and t at A is synchronized and set equal to zero (t=t’=0) and train stops. The train appears shortened on the platform so C’ is coincident to B while time of B is also t=0. For the train, according to the current concept of SR, C’ is nowhere near B at the time of C’ as t’=0 but at 2L from A and time of B equal to,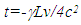 | (1) |
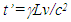 and that of B equals t=0. Additionally, the train is compressed on the platform with an argument that “no rigid body exist in SR.” In the prevailing literature on this subject there is no mention that in the train’s view B is at L/4 distance from A requiring B to jump to L/4 distance from A for the argument to hold. That means the platform has to compress as well. Thus we find that prevailing concept of length contraction requires revision.The concept of real length contraction in Special Relativity is confounding [1-2]. Perpetual constant relative velocity between two observers is not a reality, therefore, some paradoxes and concepts generated by SR may not be real either. The only connection between two inertial frames is the constancy of speed of light, c. As long as the ratio of the measure of length and time units is equal to c, different standards can prevail in different frames. The current SR theory is based upon identical length and time measures in two inertial frames with or without relative motion. No consideration has been given in the past to allow different length and time measures in two inertial frames. While developing Kinematic (non-inertial) SR (KSR) theory [3] to connect inertial and non-inertial frames for physical reality the current length contraction concept failed to provide consistent results. This paper shows SR, Lorentz Transformation (LT) and KSR can all be in agreement if the relatively moving inertial frame is regarded as space expanded by a factor
and that of B equals t=0. Additionally, the train is compressed on the platform with an argument that “no rigid body exist in SR.” In the prevailing literature on this subject there is no mention that in the train’s view B is at L/4 distance from A requiring B to jump to L/4 distance from A for the argument to hold. That means the platform has to compress as well. Thus we find that prevailing concept of length contraction requires revision.The concept of real length contraction in Special Relativity is confounding [1-2]. Perpetual constant relative velocity between two observers is not a reality, therefore, some paradoxes and concepts generated by SR may not be real either. The only connection between two inertial frames is the constancy of speed of light, c. As long as the ratio of the measure of length and time units is equal to c, different standards can prevail in different frames. The current SR theory is based upon identical length and time measures in two inertial frames with or without relative motion. No consideration has been given in the past to allow different length and time measures in two inertial frames. While developing Kinematic (non-inertial) SR (KSR) theory [3] to connect inertial and non-inertial frames for physical reality the current length contraction concept failed to provide consistent results. This paper shows SR, Lorentz Transformation (LT) and KSR can all be in agreement if the relatively moving inertial frame is regarded as space expanded by a factor 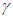 , the Lorentz contraction factor, with clock sped-up by the same factor
, the Lorentz contraction factor, with clock sped-up by the same factor 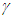 as compared to the values before gaining velocity. This view completely changes several current concepts and reveals the true nature of SR. The Space-time Transformation Relation (STR) between two frames as one frame gains velocity is simpler with this new concept. As a result issues such as the twin paradox, Ehrenfest paradox, rigid body, stress with relative velocity, trapping a train in a shorter tunnel, etc. do not arise once SR is properly understood.Abundant literature encompassing research papers, books on-line publications and youtube presentations exist describing those paradoxes and concepts [4-6]. The scientific community has shown intense interest in SR and its implication in the last century which generated a library of narratives, ad hoc theories and discussions to show resolution or validity of many paradoxes and concepts. This paper shows the observed length in any relatively moving frame is the same as the proper length. Moreover, it also shows ad hoc resolution of twin paradox as traveling twin younger is in error while predicting traveling twin older in agreeing with the result obtained using different approaches [3,7-8].How could one conceptualize immediate real length contraction of a long object in SR when it gains sudden relative velocity? The SR result: simultaneous events in one frame are not simultaneous in relatively moving other frames [9], is satisfactorily used to establish the length contraction concept for inertial frames. The out-of-sync clocks and objects consisting of movable microscopic sections instead of rigid bodies provide an acceptable explanation for trapping a train in a shorter tunnel. But, out-of-sync clocks may not exist if all body sections of an object start from rest with synchronized clocks. The acceptable explanation for the inertial case falls short for the non-inertial case. However, as shown in Sec. 3 if the same argument is used for the start and stop for the train in a same length platform or tunnel, the space expansion concept is revealed and the true nature of SR can be realized. Physical reality requires relatively moving objects to begin the journey with no relative motion. Inclusion of change in velocity results in several inconsistencies with SR. The simple fact that there cannot be a special observer rules out actual length contraction conceptualized in SR for so many years when the non-inertial condition is considered. The concept of each observer seeing length contraction of a relatively moving frame parallel to the direction of velocity is conditional for the inertial frames in SR. This paper provides the logical argument that observed relativistic length is same as zero relative velocity length in a realistic case and the observed objects’ dimensions are unaffected with relative motion. This point is elaborated in section 3.SR continued to-date to delve into the real length contraction concept without realizing the proper connection of the basic length and time units in the rest and the relatively moving state of a frame. That concept missed the point that observed length contraction of a ruler could be of the expanded length of the original ruler rendering no observational difference in length due to the relative velocity. There is no reason not to accept or regard the moving inertial frame as the transformed original frame before it gained velocity. Author of this paper finds this concept accurate and realistic and reveals the true nature of SR while remaining in agreement with the well-established time dilation results of LT, SR and KSR. Many paradoxes and mysterious concepts become nonissues with this understanding of the true nature of SR.The current concepts of real length contraction and out-of-sync clocks in the relatively moving frame are intertwined in SR. They explain how an observer can see two ends of a moving ruler contracted in length with the out-of-sync clocks. The real length contraction in SR can be explained for the inertial frames by invoking the simultaneity and non-rigid body idea but it is unacceptable for the non-inertial case.Section 2 is devoted to the discussion of the current concepts in SR and to show how they fail when a realistic non-inertial condition is encountered. The true nature of SR is established in section 3 with some analytical description to prove the time dilation but not the real length contraction is given in section 4. The discussion on the prevailing paradoxes and misconceptions is provided in section 5 with conclusions thereafter.
as compared to the values before gaining velocity. This view completely changes several current concepts and reveals the true nature of SR. The Space-time Transformation Relation (STR) between two frames as one frame gains velocity is simpler with this new concept. As a result issues such as the twin paradox, Ehrenfest paradox, rigid body, stress with relative velocity, trapping a train in a shorter tunnel, etc. do not arise once SR is properly understood.Abundant literature encompassing research papers, books on-line publications and youtube presentations exist describing those paradoxes and concepts [4-6]. The scientific community has shown intense interest in SR and its implication in the last century which generated a library of narratives, ad hoc theories and discussions to show resolution or validity of many paradoxes and concepts. This paper shows the observed length in any relatively moving frame is the same as the proper length. Moreover, it also shows ad hoc resolution of twin paradox as traveling twin younger is in error while predicting traveling twin older in agreeing with the result obtained using different approaches [3,7-8].How could one conceptualize immediate real length contraction of a long object in SR when it gains sudden relative velocity? The SR result: simultaneous events in one frame are not simultaneous in relatively moving other frames [9], is satisfactorily used to establish the length contraction concept for inertial frames. The out-of-sync clocks and objects consisting of movable microscopic sections instead of rigid bodies provide an acceptable explanation for trapping a train in a shorter tunnel. But, out-of-sync clocks may not exist if all body sections of an object start from rest with synchronized clocks. The acceptable explanation for the inertial case falls short for the non-inertial case. However, as shown in Sec. 3 if the same argument is used for the start and stop for the train in a same length platform or tunnel, the space expansion concept is revealed and the true nature of SR can be realized. Physical reality requires relatively moving objects to begin the journey with no relative motion. Inclusion of change in velocity results in several inconsistencies with SR. The simple fact that there cannot be a special observer rules out actual length contraction conceptualized in SR for so many years when the non-inertial condition is considered. The concept of each observer seeing length contraction of a relatively moving frame parallel to the direction of velocity is conditional for the inertial frames in SR. This paper provides the logical argument that observed relativistic length is same as zero relative velocity length in a realistic case and the observed objects’ dimensions are unaffected with relative motion. This point is elaborated in section 3.SR continued to-date to delve into the real length contraction concept without realizing the proper connection of the basic length and time units in the rest and the relatively moving state of a frame. That concept missed the point that observed length contraction of a ruler could be of the expanded length of the original ruler rendering no observational difference in length due to the relative velocity. There is no reason not to accept or regard the moving inertial frame as the transformed original frame before it gained velocity. Author of this paper finds this concept accurate and realistic and reveals the true nature of SR while remaining in agreement with the well-established time dilation results of LT, SR and KSR. Many paradoxes and mysterious concepts become nonissues with this understanding of the true nature of SR.The current concepts of real length contraction and out-of-sync clocks in the relatively moving frame are intertwined in SR. They explain how an observer can see two ends of a moving ruler contracted in length with the out-of-sync clocks. The real length contraction in SR can be explained for the inertial frames by invoking the simultaneity and non-rigid body idea but it is unacceptable for the non-inertial case.Section 2 is devoted to the discussion of the current concepts in SR and to show how they fail when a realistic non-inertial condition is encountered. The true nature of SR is established in section 3 with some analytical description to prove the time dilation but not the real length contraction is given in section 4. The discussion on the prevailing paradoxes and misconceptions is provided in section 5 with conclusions thereafter.2. Conflicts with Current SR Conceptions
- The true nature of SR is revealed when the relativistic inertial condition is analysed with the effect of start (and stop) from no relative motion. Explanation is provided here to show why real length contraction is not possible and the out-of-sync property of clocks in a relatively moving frame culminating in simultaneity concept is in error.A simple scenario is presented to show the limitation of SR for obtaining correct STR when a non-inertial condition exists. Consider two observers A’ and B’ separated by a vast distance in a traveling frame F’ and facing A and B in a stationary frame F with all positions x and x’ synchronized at time t=t’=0 when no relative motion exists at start. Let the origin of F and F’ be x=x’=0 at the position of A and A’ (According to the standard nomenclatures in SR, primed symbols are for the moving or traveling entities and un-primed for the stationary entities). At t=0+ both A’ and B’ attains equal constant relativistic velocity in a very short time. After t=0+ both F and F’ are inertial and SR can be applied. The movement of A’ and B’ in F at t=0+ would be very small. The length contraction in SR would require the vast distance between A’ and B’ shrink in F by the Lorentz contraction factor
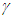 , requiring B’ to be quite close to A and A’. It is physically impossible for B’ to move such a vast distance in F in a short time. If F’ stops very quickly just after t=0+ then the opposite of the start condition needs to happen according to the current concept of SR. Thus SR presents unrealistic physical conditions if length contraction is assumed as real in a non-inertial travel condition. In the inertial frames case, A’ and B’ cannot start simultaneously at t=0 so the conflict doesn’t arise. This suggests some modification is necessary in the current SR concepts to include non-inertial frames in SR.Another way to present the above problem is to start with no relative motion between F and F’ and all clocks set to zero before quick velocity gain by all observers in F’. In SR some clocks should appear with negative time. No clock can run backward in F and F’ so SR produces unrealistic results with the current concepts when a non-inertial condition is present.Results predicted by one observer must agree with the results obtained by another observer in a similar situation. This principle is not followed in SR when a non-inertial condition is used. The scenario presented earlier is extended for more observers like ….A-2, A-1, A0, A1, A2, … in F and identically aligned ….A’-2, A’-1, A’0, A’1, A’2, … in F’ to make the point. Assume the velocity is such that
, requiring B’ to be quite close to A and A’. It is physically impossible for B’ to move such a vast distance in F in a short time. If F’ stops very quickly just after t=0+ then the opposite of the start condition needs to happen according to the current concept of SR. Thus SR presents unrealistic physical conditions if length contraction is assumed as real in a non-inertial travel condition. In the inertial frames case, A’ and B’ cannot start simultaneously at t=0 so the conflict doesn’t arise. This suggests some modification is necessary in the current SR concepts to include non-inertial frames in SR.Another way to present the above problem is to start with no relative motion between F and F’ and all clocks set to zero before quick velocity gain by all observers in F’. In SR some clocks should appear with negative time. No clock can run backward in F and F’ so SR produces unrealistic results with the current concepts when a non-inertial condition is present.Results predicted by one observer must agree with the results obtained by another observer in a similar situation. This principle is not followed in SR when a non-inertial condition is used. The scenario presented earlier is extended for more observers like ….A-2, A-1, A0, A1, A2, … in F and identically aligned ….A’-2, A’-1, A’0, A’1, A’2, … in F’ to make the point. Assume the velocity is such that 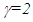 and the spacing at t=t’=0 of all observers is vt with t=1. Fig. 1(a). schematically shows the alignment and position of ….A’-2, A’-1, A’0, A’1, A’2, … as observed by A0 in F at t=0. Also shown are the same….A’-2, A’-1, A’0, A’1, A’2, … as they should be observed by A0 in F at t=0+ according to the current length contraction concept. In this case A0 faces A’0 and A1 faces A’2. Fig. 1(b). shows the same scenario as observed by A1 in F and the situation in F’. In this case A1 faces A’1 and A0 faces midway between A’-1 and A’0 while A’2 is away from A1. The results are contradictory suggesting the current concept of length contraction is inadequate when used with the non-inertial frames. Extension of this logic makes clear that real length contraction or expansion is not observable but such an effect can be present similar to observing the ground from a high flying plane.
and the spacing at t=t’=0 of all observers is vt with t=1. Fig. 1(a). schematically shows the alignment and position of ….A’-2, A’-1, A’0, A’1, A’2, … as observed by A0 in F at t=0. Also shown are the same….A’-2, A’-1, A’0, A’1, A’2, … as they should be observed by A0 in F at t=0+ according to the current length contraction concept. In this case A0 faces A’0 and A1 faces A’2. Fig. 1(b). shows the same scenario as observed by A1 in F and the situation in F’. In this case A1 faces A’1 and A0 faces midway between A’-1 and A’0 while A’2 is away from A1. The results are contradictory suggesting the current concept of length contraction is inadequate when used with the non-inertial frames. Extension of this logic makes clear that real length contraction or expansion is not observable but such an effect can be present similar to observing the ground from a high flying plane.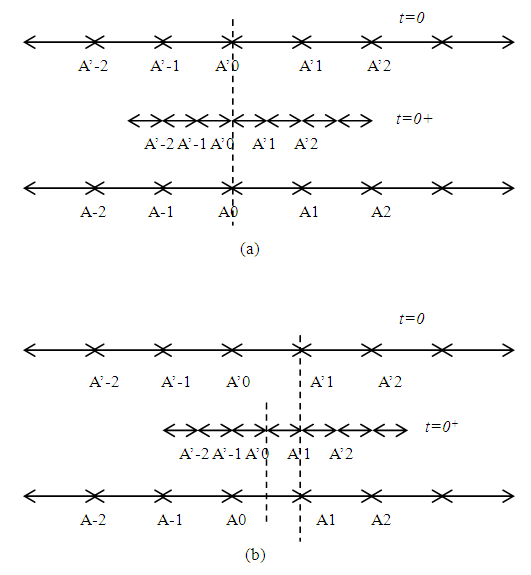 | Figure 1. Alignment of observers at t=0 and t=0+ according to the observer in F (a) at A0 and (b) at A1 with the current real length contraction concept in SR |
3. True Nature of Special Relativity
- Unrealistic concepts of SR will appear OK with the unrealistic inertial frames stipulation. Without injecting non-inertial conditions it is not possible to select physically realistic concepts. This is the case discussed here. Suppose a ruler of length L in F is moved to F’. According to LT the ruler in F’ should become, or regarded by an observer in F as either (i)
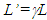 and match to another ruler, S’, of length L’ in F’ and observed with the original length L in F or (ii) it should be L in F’, not matched to S’ and observed with length
and match to another ruler, S’, of length L’ in F’ and observed with the original length L in F or (ii) it should be L in F’, not matched to S’ and observed with length 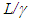 in F. The current length contraction concept in SR accepts the outcome (ii). Equally valid is the concept (i) but it has not received any attention in the past. In (ii) the ruler’s length appears shortening in F as it gains velocity. Just the same way in (i) the ruler’s spatial part is expanding or being regarded expanding by an observer in F as it gains velocity and appears of the same length in F due to length contraction. Which is the correct concept? Thinking of the proper length of ruler expanding in (i) being absurd may have caused the acceptance of the concept (ii) in the past. But it generated many paradoxes and unrealistic concepts. How to circumvent the ruler’s real length expansion and accept concept (i) is discussed below in this section.Objections were raised in Sec. 2 regarding the prevailing length contraction and out-of-sync clocks concepts in F’. This section shows length contraction is with regard to the inertial frame which is the transformed Meta-frame F’m of the real frame F’ when it was not moving. The Meta-frame meant here is really space expanded and sped-up clock frame synonymous to as regarded by an observer in F. An object or a frame appears in the original frame to transform to Mata-frame F’m when it gains velocity. In Meta-frame the space expands and clock speeds-up compared to its rest values. The Meta-frame space is observed contracted in the original frame making the space and objects’ size as observed in the original frame same as when there was no relative motion. This concept also differentiates the stationary and moving frame or observer. Light or information continuing to propagate through the velocity change of a non-inertial frame is obviously affected such as in stellar aberration. But in the stationary frame the propagation characteristic is unaffected. Such distinction is not possible in the current SR and it is the cause of the twin paradox. It is not unrealistic to think that the size of an object may appear different when it gains velocity. One observes objects contracted on ground from a high flying plane. However, all physical attributes need to use the real measures of the other frame when mapping between two frames. Time dilation and LT in SR cannot be disputed as it can be theorised several different ways and experimental proofs including muon observation has established its validity. According to LT when an object or frame F’ has relative velocity an observer at rest in F sees time t’ in F’ appear to him speed-up as
in F. The current length contraction concept in SR accepts the outcome (ii). Equally valid is the concept (i) but it has not received any attention in the past. In (ii) the ruler’s length appears shortening in F as it gains velocity. Just the same way in (i) the ruler’s spatial part is expanding or being regarded expanding by an observer in F as it gains velocity and appears of the same length in F due to length contraction. Which is the correct concept? Thinking of the proper length of ruler expanding in (i) being absurd may have caused the acceptance of the concept (ii) in the past. But it generated many paradoxes and unrealistic concepts. How to circumvent the ruler’s real length expansion and accept concept (i) is discussed below in this section.Objections were raised in Sec. 2 regarding the prevailing length contraction and out-of-sync clocks concepts in F’. This section shows length contraction is with regard to the inertial frame which is the transformed Meta-frame F’m of the real frame F’ when it was not moving. The Meta-frame meant here is really space expanded and sped-up clock frame synonymous to as regarded by an observer in F. An object or a frame appears in the original frame to transform to Mata-frame F’m when it gains velocity. In Meta-frame the space expands and clock speeds-up compared to its rest values. The Meta-frame space is observed contracted in the original frame making the space and objects’ size as observed in the original frame same as when there was no relative motion. This concept also differentiates the stationary and moving frame or observer. Light or information continuing to propagate through the velocity change of a non-inertial frame is obviously affected such as in stellar aberration. But in the stationary frame the propagation characteristic is unaffected. Such distinction is not possible in the current SR and it is the cause of the twin paradox. It is not unrealistic to think that the size of an object may appear different when it gains velocity. One observes objects contracted on ground from a high flying plane. However, all physical attributes need to use the real measures of the other frame when mapping between two frames. Time dilation and LT in SR cannot be disputed as it can be theorised several different ways and experimental proofs including muon observation has established its validity. According to LT when an object or frame F’ has relative velocity an observer at rest in F sees time t’ in F’ appear to him speed-up as 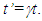 Since two frames in relative motion cannot have different velocities, it became necessary for the observer in F to see the space of F’ pass at a rate
Since two frames in relative motion cannot have different velocities, it became necessary for the observer in F to see the space of F’ pass at a rate 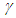 times his space as
times his space as 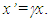 One couldn’t think of a change in proper length of an object with gain in velocity so the current concept of real length contraction provided the solution. Several paradoxes and unrealistic concepts developed with this solution, however.As explained earlier there are choices (i) and (ii) for the ruler’s length when it gains relative velocity. Length expansion, though seeming absurd at the first sight, is found to be physically realistic and reveals the true nature of SR. Once the length expansion and sped-up clock is combined the proper length of the ruler remains unchanged in F’m because it is characterized with the constancy of the speed of light. The connection between two inertial frames with velocity of light is reinforced in this manner. The occupants in F’m won’t have any clue of length expansion when it gains velocity because length expansion with sped-up clock would make ruler’s length change unrealizable when measured with light and all physical processes and measurements in F’m will be identical to the rest values. A problem arises with the length expansion concept of the previous paragraph. The dimensions orthogonal to the direction of velocity in F’m would be measured shrunk because of the expanded ruler length. Same shrinkage will be observed even with light measurements due to the sped-up clock. The solution lies in allowing the whole space to expand with gain in velocity of F’ and whole space, instead of just the length, observed contracted in F. This concept between F, F’ and F’m is almost identical to observing ground from a high flying plane. Mapping of F’m back to F involves space contraction while mapping of objects’ rest data to moving frame F’m involves space expansion. The overall effect is unobservable change in objects’ dimensions due to relative motion. The current real length contraction concept remains valid between F and F’m but it is distinctly different. The observed length, width and height of a moving train by an observer on ground would be identical to its zero relative velocity values (proper values) and no length contraction will be observed as currently believed.The above new concept is reinforced if the argument presented in connection with trapping a train in a shorter tunnel and similar scenarios are properly applied to start and stop conditions. If the start of the train is analysed in a similar manner as the stop for trapping of the train then the microscopic section of train will gain velocity over time expanding trains length and will be observed in the stationary frame to start at the same time. Thus, the train will expand in F’m when it gains velocity and contract when it stops or is trapped. But in F, the train is observed of the same length at all times as its proper length. In F the clocks of F’ will be observed with the same time over the entire train because the out-of-sync time is for F’m but actual clocks in F’ advance at the same rate
One couldn’t think of a change in proper length of an object with gain in velocity so the current concept of real length contraction provided the solution. Several paradoxes and unrealistic concepts developed with this solution, however.As explained earlier there are choices (i) and (ii) for the ruler’s length when it gains relative velocity. Length expansion, though seeming absurd at the first sight, is found to be physically realistic and reveals the true nature of SR. Once the length expansion and sped-up clock is combined the proper length of the ruler remains unchanged in F’m because it is characterized with the constancy of the speed of light. The connection between two inertial frames with velocity of light is reinforced in this manner. The occupants in F’m won’t have any clue of length expansion when it gains velocity because length expansion with sped-up clock would make ruler’s length change unrealizable when measured with light and all physical processes and measurements in F’m will be identical to the rest values. A problem arises with the length expansion concept of the previous paragraph. The dimensions orthogonal to the direction of velocity in F’m would be measured shrunk because of the expanded ruler length. Same shrinkage will be observed even with light measurements due to the sped-up clock. The solution lies in allowing the whole space to expand with gain in velocity of F’ and whole space, instead of just the length, observed contracted in F. This concept between F, F’ and F’m is almost identical to observing ground from a high flying plane. Mapping of F’m back to F involves space contraction while mapping of objects’ rest data to moving frame F’m involves space expansion. The overall effect is unobservable change in objects’ dimensions due to relative motion. The current real length contraction concept remains valid between F and F’m but it is distinctly different. The observed length, width and height of a moving train by an observer on ground would be identical to its zero relative velocity values (proper values) and no length contraction will be observed as currently believed.The above new concept is reinforced if the argument presented in connection with trapping a train in a shorter tunnel and similar scenarios are properly applied to start and stop conditions. If the start of the train is analysed in a similar manner as the stop for trapping of the train then the microscopic section of train will gain velocity over time expanding trains length and will be observed in the stationary frame to start at the same time. Thus, the train will expand in F’m when it gains velocity and contract when it stops or is trapped. But in F, the train is observed of the same length at all times as its proper length. In F the clocks of F’ will be observed with the same time over the entire train because the out-of-sync time is for F’m but actual clocks in F’ advance at the same rate 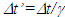 (for constant velocity case) from the initial synchronized value at rest. In a more general case involving varying velocities KSR theory needs to be used to find the relation between t and t’. The time t’ of the moving observer after synchronization at the origin is the time that will be observed in F for the entire frame F’. Thus spatially separated simultaneous events in one frame are also simultaneous in all frames regardless of their relative motion. The frame F’m can be considered as Meta-frame because no change in any physical process or measurements would be detectable between two states, at rest and moving. Its only purpose is for mapping the space-time between two frames and serving mathematical algorithms. The spatial relation between the positions of an object before and after it gains velocity is simply the standard product of velocity multiplied by time. As in the inertial frames case the time dilation occurs because the motion assists light or information to propagate a shorter distance between two points in F’m compared to F in the direction of the velocity.An observer gaining velocity with F’ could also claim the frame F has gained the velocity and its frame has space expanded and clock sped-up requiring
(for constant velocity case) from the initial synchronized value at rest. In a more general case involving varying velocities KSR theory needs to be used to find the relation between t and t’. The time t’ of the moving observer after synchronization at the origin is the time that will be observed in F for the entire frame F’. Thus spatially separated simultaneous events in one frame are also simultaneous in all frames regardless of their relative motion. The frame F’m can be considered as Meta-frame because no change in any physical process or measurements would be detectable between two states, at rest and moving. Its only purpose is for mapping the space-time between two frames and serving mathematical algorithms. The spatial relation between the positions of an object before and after it gains velocity is simply the standard product of velocity multiplied by time. As in the inertial frames case the time dilation occurs because the motion assists light or information to propagate a shorter distance between two points in F’m compared to F in the direction of the velocity.An observer gaining velocity with F’ could also claim the frame F has gained the velocity and its frame has space expanded and clock sped-up requiring 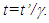 This is a symmetrical condition similar to the condition currently understood in SR. However, with the concept presented here F would have gained the velocity in F’ in later case and nothing would be wrong with the time relation
This is a symmetrical condition similar to the condition currently understood in SR. However, with the concept presented here F would have gained the velocity in F’ in later case and nothing would be wrong with the time relation 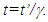 The frame gaining the velocity notices a change in the light propagation characteristics, particularly the light propagation direction orthogonal to the velocity direction, for a ray starting before the velocity gain or change. Thus, the space expansion and sped-up clock is associated only with the frame gaining the velocity.The distinction between a stationary and a traveling frame can also be made when light propagation in two frames is considered. Unlike non-inertial frames, light propagation distance between two points in an inertial frame is the same as the distance between them. In a non-inertial frame light propagation path length between two points is different if the velocity of the frame changes during the propagation. KSR provides the time relation between a traveling and stationary observer. In case of the twin paradox, light propagation path length in the travelling twin’s frame is much larger during the significant period of time near his return point, overtaking gain made during the other motion. This makes the travelling twin older and not younger upon the reunion.With concepts presented above, the effect of relative motion between two observers is chiefly on relative time between them. At the position of an observer in F time appears to speed-up by a factor
The frame gaining the velocity notices a change in the light propagation characteristics, particularly the light propagation direction orthogonal to the velocity direction, for a ray starting before the velocity gain or change. Thus, the space expansion and sped-up clock is associated only with the frame gaining the velocity.The distinction between a stationary and a traveling frame can also be made when light propagation in two frames is considered. Unlike non-inertial frames, light propagation distance between two points in an inertial frame is the same as the distance between them. In a non-inertial frame light propagation path length between two points is different if the velocity of the frame changes during the propagation. KSR provides the time relation between a traveling and stationary observer. In case of the twin paradox, light propagation path length in the travelling twin’s frame is much larger during the significant period of time near his return point, overtaking gain made during the other motion. This makes the travelling twin older and not younger upon the reunion.With concepts presented above, the effect of relative motion between two observers is chiefly on relative time between them. At the position of an observer in F time appears to speed-up by a factor 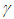 in F’. The frame F being the reference frame time is the same at all positions in it. The time and position of the moving observer is found with LT if the motion of the observer is inertial. In the general non-inertial case the moving observer’s path is just his trajectory in F and time is found using KSR theory. The frame time is the same as the moving observer’s time because the out-of-sync time in F’m is subtracted out in F’. For a non-coincident position of F’ at synchronization between F and F’ the out of sync time in F’m found using LT needs to be subtracted for that position in F’. This is similar to the situation of muon time when the earth surface is used for the synchronization. Muon time at the top of the atmosphere will be
in F’. The frame F being the reference frame time is the same at all positions in it. The time and position of the moving observer is found with LT if the motion of the observer is inertial. In the general non-inertial case the moving observer’s path is just his trajectory in F and time is found using KSR theory. The frame time is the same as the moving observer’s time because the out-of-sync time in F’m is subtracted out in F’. For a non-coincident position of F’ at synchronization between F and F’ the out of sync time in F’m found using LT needs to be subtracted for that position in F’. This is similar to the situation of muon time when the earth surface is used for the synchronization. Muon time at the top of the atmosphere will be 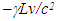 and on the surface of the earth it will be
and on the surface of the earth it will be 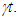 where t is the muon’s travel time and L the height of the top of the atmosphere. Muons don’t carry clock so the proper time of muons is set to zero when they are produced and
where t is the muon’s travel time and L the height of the top of the atmosphere. Muons don’t carry clock so the proper time of muons is set to zero when they are produced and 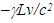 is subtracted out. This concept is also somewhat in line with the frame switching in which the proper time of an observer remains unchanged when he switches frame.The simultaneity concept, stating spatially separated events that are simultaneous in one frame are not simultaneous in other relatively moving frames, is already shown to be incorrect. Those events will appear simultaneous in both frames but observers in two frames won’t agree with the time of those events due to time dilation effect.The concepts developed in this section along with their implication are summarised below:1. A moving frame and objects therein are represented by a Meta-frame F’m in which the space is expanded and clock is sped-up by a factor
is subtracted out. This concept is also somewhat in line with the frame switching in which the proper time of an observer remains unchanged when he switches frame.The simultaneity concept, stating spatially separated events that are simultaneous in one frame are not simultaneous in other relatively moving frames, is already shown to be incorrect. Those events will appear simultaneous in both frames but observers in two frames won’t agree with the time of those events due to time dilation effect.The concepts developed in this section along with their implication are summarised below:1. A moving frame and objects therein are represented by a Meta-frame F’m in which the space is expanded and clock is sped-up by a factor 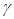 with respect to their original rest state values. This Meta-frame is the same as the inertial frame F’ used in SR. F’m is observed in the original rest frame F with space contracted by the same factor
with respect to their original rest state values. This Meta-frame is the same as the inertial frame F’ used in SR. F’m is observed in the original rest frame F with space contracted by the same factor 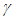 resulting in time relation (dilation for constant velocity) according to LT or KSR theory but no observable change in dimensions of objects due to relative motion.2. The space expansion and clock sped-up is associated with the frame changing the velocity. The stationary (relatively) frame is unique and used as the reference frame.3. All clocks in a frame advance at the same rate but the rate in each frame is dependent upon the relative velocity.4. Spatially separated simultaneous events in one frame are observed simultaneous in all frames but the time of observance may be different if there is relative motion.Although the observed dimensions of an object are unaltered due to the relative motion some optical illusion of observing an object could change due to time relation between two frames. A moving square appears distorted even without application of SR. Time dilation effect may add to such distortion.
resulting in time relation (dilation for constant velocity) according to LT or KSR theory but no observable change in dimensions of objects due to relative motion.2. The space expansion and clock sped-up is associated with the frame changing the velocity. The stationary (relatively) frame is unique and used as the reference frame.3. All clocks in a frame advance at the same rate but the rate in each frame is dependent upon the relative velocity.4. Spatially separated simultaneous events in one frame are observed simultaneous in all frames but the time of observance may be different if there is relative motion.Although the observed dimensions of an object are unaltered due to the relative motion some optical illusion of observing an object could change due to time relation between two frames. A moving square appears distorted even without application of SR. Time dilation effect may add to such distortion.4. Analytical Description
- This section analytically shows how time dilation is present with the concept of meta-frame and why real length contraction is not present between relatively moving frames. The parameters,
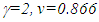 and the travel time t=1 is used for the illustration. Fig. 2a shows the stationary frame F, meta-frame F’m which is same as the inertial frame in SR and to be a relatively moving frame F’. Two rulers of equal length are used one in F and other in F’ with equal length L=vt (t=1) when there was no relative motion. All clocks in F, and F’ are set equal to zero (t=t’=0) as there is no relative velocity. The ruler ends are marked as A and B in F, A’ and B’ in F’. As F’ gains velocity it transitions or merges into co-moving inertial frame called meta-frame F’m. As F’ merges with F’m the space of F’ is expanded by a factor
and the travel time t=1 is used for the illustration. Fig. 2a shows the stationary frame F, meta-frame F’m which is same as the inertial frame in SR and to be a relatively moving frame F’. Two rulers of equal length are used one in F and other in F’ with equal length L=vt (t=1) when there was no relative motion. All clocks in F, and F’ are set equal to zero (t=t’=0) as there is no relative velocity. The ruler ends are marked as A and B in F, A’ and B’ in F’. As F’ gains velocity it transitions or merges into co-moving inertial frame called meta-frame F’m. As F’ merges with F’m the space of F’ is expanded by a factor 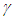 and clocks are sped-up by the same factor
and clocks are sped-up by the same factor 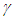 as compare to the values before gaining velocity. The coincident points in F’m for A’ and B’ after the space expansion are designated as A” and B” for F’m. Results of SR require length (actually space according to this manuscript) contraction in F with respect to F’m so there won’t be any spatial distinction between A’ and A” and B’ and B”. The origin of F, F’ and F’m denoted as as x=x’=x”=0 is selected at the position of A. Fig. 2b shows all frames at t=0+. From the true nature of SR presented here requiring space expansion the proper position of B’ in F’m designated as x”B’ will be,
as compare to the values before gaining velocity. The coincident points in F’m for A’ and B’ after the space expansion are designated as A” and B” for F’m. Results of SR require length (actually space according to this manuscript) contraction in F with respect to F’m so there won’t be any spatial distinction between A’ and A” and B’ and B”. The origin of F, F’ and F’m denoted as as x=x’=x”=0 is selected at the position of A. Fig. 2b shows all frames at t=0+. From the true nature of SR presented here requiring space expansion the proper position of B’ in F’m designated as x”B’ will be,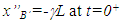 | (2) |
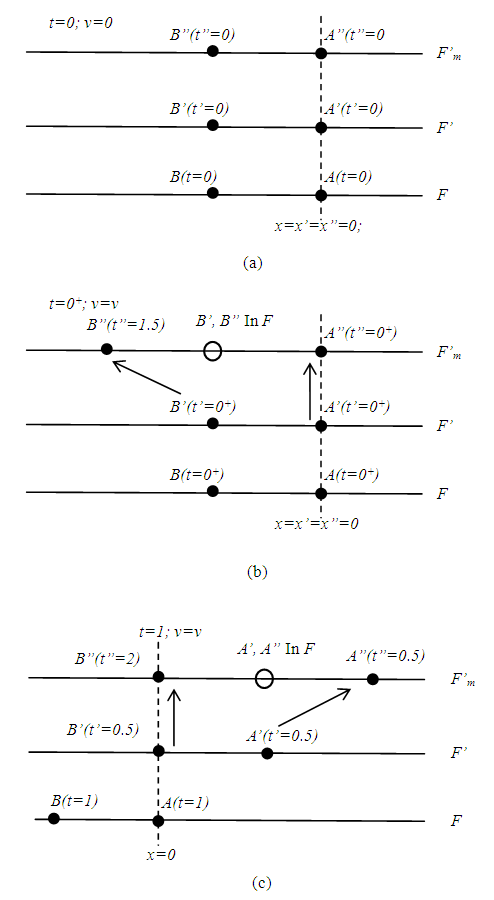 | Figure 2. Alignment and time of ruler’s ends in F, F’ and F’m at time (a) t=0 (b) t=0+ and (c) t=1 according to this manuscript |
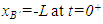 | (3) |
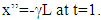 | (4) |
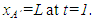 | (5) |
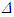 in F given as,
in F given as, 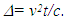 | (6) |
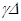 in F’m so the sped-up clock time
in F’m so the sped-up clock time 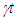 is reduced by the amount
is reduced by the amount 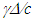 and we obtain t’ for A’ as,
and we obtain t’ for A’ as,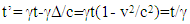 | (7) |
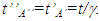 KSR theory as reported in [3] also provides the same result. Although, the time of A” and B” observed in F have out-of sync values the incremental time with respect to t for them and all positions in F’m is the same. Since the clock of B’ cannot jump its time must increment at the same rate as of A’ and needs to fallow the same relation resulting in,
KSR theory as reported in [3] also provides the same result. Although, the time of A” and B” observed in F have out-of sync values the incremental time with respect to t for them and all positions in F’m is the same. Since the clock of B’ cannot jump its time must increment at the same rate as of A’ and needs to fallow the same relation resulting in,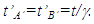 | (8) |
5. Paradoxes and Misconceptions
- Several paradoxes and currently prevailing misconceptions can be addressed with the true nature of SR developed in the previous section. Discussion on those issues follows:1. Twin Paradox:- There is no spatial separation when twins meet hence only the clocks need to be compared. The traveling twin’s clock in Meta-frame is sped-up by a factor
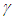 so he will be older by that factor compared to the stay home twin. Contrary to the well-entrenched belief held over a long period that the traveling twin will be younger. The stated result agrees with [9] and previously reported two articles by this author.2. Ehrenfest paradox:- As shown in Sec. 3 object size observed is the same regardless of its relative motion. A circular rotating rim’s circumference and diameter would be the same when it is not rotating making this paradox non-issue.3. Rigid body and velocity induced stress:- The out-of- sync clocks and real length contraction results made rigid body unacceptable even in principle in the prevailing SR theory. With both previous concepts changed rigid bodies can exist in principle and no stress can develop as no size change occurs.4. Trapping a train in a shorter tunnel:- It is shown that observed object size remains unaltered due to the relative motion. As a result the train cannot be observed to fit in a shorter tunnel. Though the expanded train size in the Meta-frame will fit into the shorter tunnel.Consideration of non-inertial motion led to re-examining the prevailing concepts of SR and to reveal the true nature of SR. Kinematic special relativity was developed to include non-inertial motion in SR [3]. When dealing with changing relative motion KSR theory needs to be used to find the time relation between two frames.
so he will be older by that factor compared to the stay home twin. Contrary to the well-entrenched belief held over a long period that the traveling twin will be younger. The stated result agrees with [9] and previously reported two articles by this author.2. Ehrenfest paradox:- As shown in Sec. 3 object size observed is the same regardless of its relative motion. A circular rotating rim’s circumference and diameter would be the same when it is not rotating making this paradox non-issue.3. Rigid body and velocity induced stress:- The out-of- sync clocks and real length contraction results made rigid body unacceptable even in principle in the prevailing SR theory. With both previous concepts changed rigid bodies can exist in principle and no stress can develop as no size change occurs.4. Trapping a train in a shorter tunnel:- It is shown that observed object size remains unaltered due to the relative motion. As a result the train cannot be observed to fit in a shorter tunnel. Though the expanded train size in the Meta-frame will fit into the shorter tunnel.Consideration of non-inertial motion led to re-examining the prevailing concepts of SR and to reveal the true nature of SR. Kinematic special relativity was developed to include non-inertial motion in SR [3]. When dealing with changing relative motion KSR theory needs to be used to find the time relation between two frames.6. Conclusions
- True nature of special relativity is revealed with the inclusion of general non-inertial frames. The frame or objects gaining velocity need to be represented in a Meta-frame with expanded space and sped-up clock by a factor
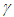 . Special Relativity results are consistent with the Meta-frame and the stationary frame designated as the inertial frames. The relative motion affects only the time relation and has no influence on the observed dimensions of the objects. Physically separated simultaneous events in one frame are simultaneous in all frames regardless of their relative motion. This innovative concept makes SR easy to understand and generates consistent results with LT, SR, and KSR. This concept is physically realistic and dismisses real length contraction settling many debated topics, paradoxes and issues.
. Special Relativity results are consistent with the Meta-frame and the stationary frame designated as the inertial frames. The relative motion affects only the time relation and has no influence on the observed dimensions of the objects. Physically separated simultaneous events in one frame are simultaneous in all frames regardless of their relative motion. This innovative concept makes SR easy to understand and generates consistent results with LT, SR, and KSR. This concept is physically realistic and dismisses real length contraction settling many debated topics, paradoxes and issues.Note
- The clocks carried by the travellers have time synchronized without relative velocity. They have the same time for all positions and have offset from times of moving space expanded and sped-up clocks frame. The simultaneity mentioned in Sec. 3 refers to these clocks. Events occurring in frames with relative motion are propagated according to the KSR theory and STR must be obtained in that manner (for an inertial frame using LT). The clocks will show times modified by the offset from the STR. Thus no conflict occurs with the simultaneity of SR theory.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML