Lucas W. L.1, Joseph I. K.2, Pius I. P.3, Ewa I. I.1, Sarki M. U.1
1Department of Physics, Nasarawa State University, Keffi, Keffi, Nigeria
2Department of Mathematics, Nasarawa State University, Keffi, Keffi, Nigeria
3University of Glasgow, School of Physics and Astronomy, Scotland UK
Correspondence to: Lucas W. L., Department of Physics, Nasarawa State University, Keffi, Keffi, Nigeria.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Despite the impressive success of the Newtonian dynamical theory of gravitation in explaining the observed gravitational phenomena, the theory reminds logically incomplete. In this article, the golden Riemannian geometry of space-time was applied to construct an extended Newton’s dynamical field equation and the gravitational scalar potential exterior and interior to the gravitational field of static homogeneous spherical mass. The obtained results reduce in the limit 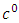 , to the corresponding pure Newtonian expressions. Results obtained contain post-Newton correction terms to the order of
, to the corresponding pure Newtonian expressions. Results obtained contain post-Newton correction terms to the order of 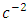 . The consequences of the additional correctional terms are that they can be applied to predict the existence of gravitational waves and their propagation in space and to derive the anomalous orbital precession of the orbit of the planet as well as the gravitational shift by the Sun as excellently as Einstein’s geometrical theory of gravitation. Also, it can be applied to examine the theoretical analysis of the motion of particles of non-zero rest masses and in a simple linear harmonic oscillator to determine its energy levels.
. The consequences of the additional correctional terms are that they can be applied to predict the existence of gravitational waves and their propagation in space and to derive the anomalous orbital precession of the orbit of the planet as well as the gravitational shift by the Sun as excellently as Einstein’s geometrical theory of gravitation. Also, it can be applied to examine the theoretical analysis of the motion of particles of non-zero rest masses and in a simple linear harmonic oscillator to determine its energy levels.
Keywords:
Newton’s Theory, Riemannian geometry, Scalar Potential, Precession, Red Shift, Harmonic Oscillator, and Energy Levels
Cite this paper: Lucas W. L., Joseph I. K., Pius I. P., Ewa I. I., Sarki M. U., Extention of Newton’s Dynamical Field Equation in the Gravitational Field of Spherical Mass, International Journal of Theoretical and Mathematical Physics, Vol. 12 No. 1, 2022, pp. 7-10. doi: 10.5923/j.ijtmp.20221201.02.
1. Introduction
Gravity is known to be the least understood of all the fundamental forces in nature. Interestingly, mass and space which are governed by gravitation are the basic building blocks of the universe [1,5].Around the year 300 BC, the Greek Philosopher and Mathematician called Euclid introduced his theory of geometry for space-time without the influence and interaction of gravitational fields which is popularly known today as Euclidian geometry [2,9,1,5,10].In the year 1854, the German Mathematician called George Friedrich Bernard Riemann introduced his principle of geometry for space-time with the influence and interaction of gravitational fields which is known today as the Riemannian geometry. This theory was formulated in terms of the mathematical quantity called the metric tensor of space-time with the influence and interaction of gravitational fields. It is important to note that George Friedrich Bernard Riemann never specified any explicit expression for the metric tensor or tensors for any given gravitational field [2,3,4,6].In the year 1686, Isaac Newton published his dynamical theory of gravitation based on Euclidean geometry. According to this theory, all interactions through nature manifest through force. This theory was successful in explaining the gravitational phenomena on earth and the experimental facts of the solar system. It is a well-known fact that Newton’s dynamical theory of gravitation (NDTG) could not explain the anomalous orbital precession of the orbit of the planet as well as the gravitational redshift by the Sun.In the year 1905, Einstein’s published his geometrical theory of gravitation (EGTG) which is popularly known today as General Relativity (GR). According to this theory, gravitation is not due to force but due to the geometrical curving of space and time. This theory offered the resolution of the anomalous orbital precession of the orbit of the planet as well as the gravitational redshift by the Sun. Despite the famous test of General Relativity (GR), several Physicists have continued to hold on to the view that Newton’s dynamical theory of gravitation can be extended in such a way as to account satisfactorily for the experimental data. Thus far, the General Theory of Relativity has been the most fundamental and successful theory of Physics that successfully explains the nature of gravity. If we better understand the nature of mass and space, we may be able to do things previously undreamed of, so far studies of General Relativity and Gravity have yielded atomic clocks, guidance systems for spacecraft, and the Global Positioning Systems (GPS). We cannot foresee all that can come from a better understanding of space-time and mass-energy, but a theory about these fundamental subjects must be thoroughly examined if we are to use it to our advantage [2,9,1,5,10].In the year 2010, Howusu, S. X. K. developed a hybrid theory of gravitation that combines Newton's dynamical theory and Einstein's geometrical theory into a Riemannian theory. He postulated that Newton’s dynamical theory of gravitation can be extended using the Great, Golden, and Super Golden Riemannian Laplacian operators [3,4].It is interesting and instructive to note that Howusu never showed how the Riemannian Laplacian operators can be applied to extend Newton’s dynamical theory of gravitation to account satisfactorily with experimental results and data.This research will substantially extend Newton’s dynamical theory of gravitation using a unique approach of golden Riemannian geometry of space-time to obtain an extended Newtonian dynamical field equation and the gravitational scalar potential exterior and interior in the gravitational field of static homogeneous spherical mass.
2. Theoretical Analysis
Consider a static homogeneous spherical body of radius 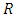 and total mass
and total mass 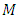 . The golden Riemannian metric tensor in the gravitational field exterior to a spherical mass is given explicitly by [3,4]
. The golden Riemannian metric tensor in the gravitational field exterior to a spherical mass is given explicitly by [3,4]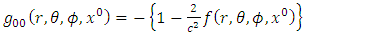 | (1) |
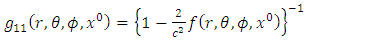 | (2) |
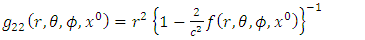 | (3) |
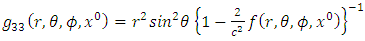 | (4) |
 | (5) |
where, 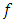 is an extended Riemannian gravitational scalar potential exterior to the spherical body and
is an extended Riemannian gravitational scalar potential exterior to the spherical body and 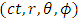 is the space- time coordinate with
is the space- time coordinate with 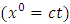 . The well - known Riemannian Laplacian operator
. The well - known Riemannian Laplacian operator 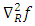 is given explicitly as [11,8]
is given explicitly as [11,8]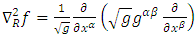 | (6) |
or more explicitly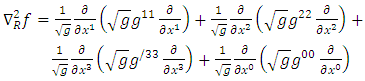 | (7) |
The covariant metric tensor for spherical polar coordinate is given explicitly by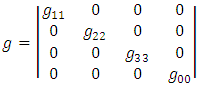 | (8) |
Substituting equations (1) - (5) into (8), we get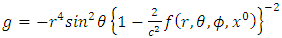 | (9) |
and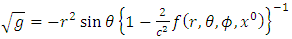 | (10) |
Similarly, the contravariant metric tensor is given as 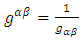 | (11) |
where 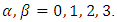 Hence, substituting (1) - (5) into (8), we obtain
Hence, substituting (1) - (5) into (8), we obtain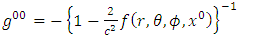 | (12) |
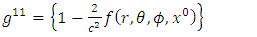 | (13) |
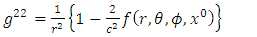 | (14) |
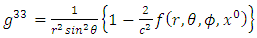 | (15) |
Substituting equation (10) and equations (12) – (15) into (7) we obtain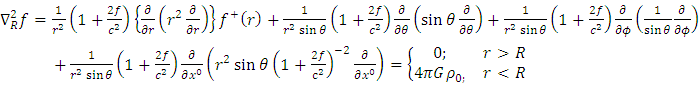 | (16) |
where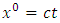 is the space time coordinate
is the space time coordinate 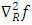 is the Riemannian Laplacian operator
is the Riemannian Laplacian operator 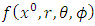 is the complete generalized gravitational scalar potential exterior to the body. By the symmetry of the distribution of mass, it follows that the gravitational field will depend only on the radial coordinate
is the complete generalized gravitational scalar potential exterior to the body. By the symmetry of the distribution of mass, it follows that the gravitational field will depend only on the radial coordinate 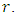 Therefore,
Therefore, 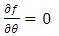 | (17) |
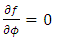 | (18) |
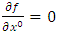 | (19) |
Consequently, equation (16) reduces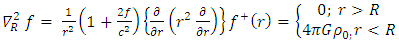 | (20) |
or more explicitly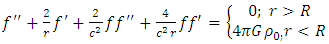 | (21) |
Equation (21) is an extended Newtonian dynamical gravitational field equation for spherical fields based on the golden Riemannian geometry of space - time. This equation: • Reduces in the limit of 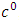 , to the corresponding pure Newton’s dynamical gravitational field equation and in the order of
, to the corresponding pure Newton’s dynamical gravitational field equation and in the order of 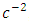 , it contains unknown post-Newton correction terms which are uncovered for theoretical development and experimental investigation s and applications.• Contain
, it contains unknown post-Newton correction terms which are uncovered for theoretical development and experimental investigation s and applications.• Contain 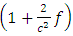 which are not found in the existing well-known Newtonian dynamical or Einstein geometrical field equations. • Contain the time - component which is not found in the existing well - known Newton’s dynamical field equation. The immediate consequences of the additional correction terms obtained in the extended Newtonian field equation are that it will predict:• Additional correction terms to the gravitational field of all massive bodies and by extension to the gravitational scalar potential exterior and interior.• Predict the existence of gravitational waves and their propagation in space with the phase velocity,
which are not found in the existing well-known Newtonian dynamical or Einstein geometrical field equations. • Contain the time - component which is not found in the existing well - known Newton’s dynamical field equation. The immediate consequences of the additional correction terms obtained in the extended Newtonian field equation are that it will predict:• Additional correction terms to the gravitational field of all massive bodies and by extension to the gravitational scalar potential exterior and interior.• Predict the existence of gravitational waves and their propagation in space with the phase velocity, 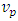 given by
given by 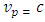 where,
where, 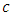 is the speed of light in vacuum.
is the speed of light in vacuum.
3. Construction of an Extended Newtonian Gravitational Scalar Potential Exterior and Interior for Static Homogeneous Spherical Mass
Let us seek the solution for the exterior field equation (21) as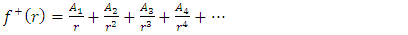 | (22) |
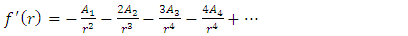 | (23) |
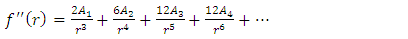 | (24) |
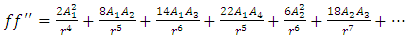 | (25) |
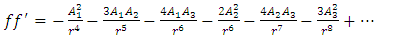 | (26) |
Substituting equations (22) - (26) into equation (21) and equating coefficients of 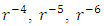 and
and 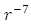 on both sides gives
on both sides gives 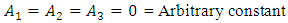 | (27) |
 | (28) |
Hence, the general solution for the exterior field equation (21) is given by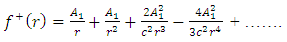 | (29) |
Let us seek the solution of the interior field equation (22) as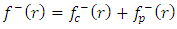 | (30) |
where, 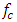 and
and 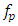 are complementary and particular solutions, respectively.The complementary solution of the interior field equation
are complementary and particular solutions, respectively.The complementary solution of the interior field equation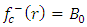 | (31) |
where, 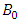 is an arbitrary constant.Seeking the solution in the form
is an arbitrary constant.Seeking the solution in the form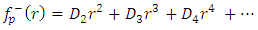 | (32) |
Differentiating equation (32) with respect to 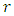 yields
yields 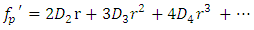 | (33) |
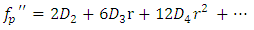 | (34) |
where 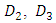 and
and 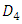 are arbitrary constants Putting equation (32), (33) and (34) into (21) and equating coefficients of
are arbitrary constants Putting equation (32), (33) and (34) into (21) and equating coefficients of 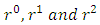 on both sides and using the well - known physical relationship between mass and density for a sphere of radius R we obtain equations which gives
on both sides and using the well - known physical relationship between mass and density for a sphere of radius R we obtain equations which gives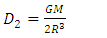 | (35) |
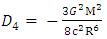 | (36) |
The general solution of the interior field equation (30) is given by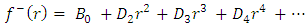 | (37) |
By the condition of continuity of gravitational scalar potential function across boundaries, 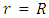
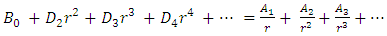 | (38) |
By the condition of continuity of normal derivatives of gravitational scalar potential function across all boundaries, 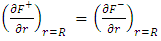
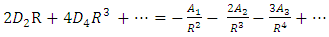 | (39) |
Solving equation (39) for 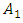 and using the well - known physical relationship between mass and density for a sphere of radius R gives
and using the well - known physical relationship between mass and density for a sphere of radius R gives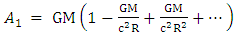 | (40) |
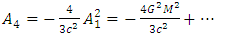 | (41) |
Solving equation (38) for 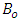 to the order of
to the order of 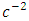 gives
gives | (42) |
Substituting equation (40) and (41) into the exterior field equation (22) gives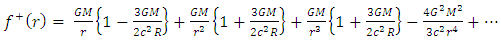 | (43) |
Similarly, substituting equations (35), (36) and (42) into (37) gives the interior field equation as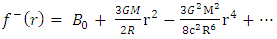 | (44) |
where 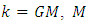 is the rest mass of the sun,
is the rest mass of the sun, 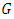 is the universal gravitational constant,
is the universal gravitational constant, 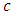 is the speed of light in vacuum,
is the speed of light in vacuum, 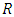 is the radius of the spherical astrophysical body and
is the radius of the spherical astrophysical body and 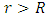 for the exterior field,
for the exterior field, 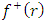 and
and 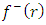 are the extended Newtonian gravitational scalar potential exterior and interior. Equations (43) and (44) are the extended exterior and interior Newtonian gravitational scalar potential based on the golden Riemannian geometry of space - time. It is interesting to note that these equations reduce in the limit of
are the extended Newtonian gravitational scalar potential exterior and interior. Equations (43) and (44) are the extended exterior and interior Newtonian gravitational scalar potential based on the golden Riemannian geometry of space - time. It is interesting to note that these equations reduce in the limit of 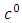 to the corresponding pure Newtonian expression and to the order of
to the corresponding pure Newtonian expression and to the order of 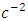 it contains post - Newton and post - Einstein correction terms. It is interesting to note that these results contain additional terms not found in [11]. The immediate consequences of the additional correction terms in the extended Newtonian gravitational scalar exterior and interior are that they can be:• Substituted into Newton’s, Einstein’s and General equations of motion to obtain generalizations of Newton’s, Einstein’s and General equations of motion to obtain corresponding revisions to the planetary equation of motion and hence the planetary parameter such the anomalous orbital precession in the solar, gravitational shift, orbital eccentricity, orbital period, orbital amplitude, perihelion and aphelion distance.• Applied to examine the theoretical analysis of the motion of particles of non-zero rest masses, gravitational length contraction and time dilation and in simple linear harmonic oscillator to determine its energy levels.• Applied to the motion of test particles in the gravitational fields of static homogeneous spherical bodies to give more accurate expression for the motion of test particles as it introduces hitherto unknown correction terms.• Can be substituted into the well - known Einstein’s (geodesic) equation of motion and the resulting equations of motion solved to obtain the corresponding post -Einstein and Newtonian generalizations and the physical effects.
it contains post - Newton and post - Einstein correction terms. It is interesting to note that these results contain additional terms not found in [11]. The immediate consequences of the additional correction terms in the extended Newtonian gravitational scalar exterior and interior are that they can be:• Substituted into Newton’s, Einstein’s and General equations of motion to obtain generalizations of Newton’s, Einstein’s and General equations of motion to obtain corresponding revisions to the planetary equation of motion and hence the planetary parameter such the anomalous orbital precession in the solar, gravitational shift, orbital eccentricity, orbital period, orbital amplitude, perihelion and aphelion distance.• Applied to examine the theoretical analysis of the motion of particles of non-zero rest masses, gravitational length contraction and time dilation and in simple linear harmonic oscillator to determine its energy levels.• Applied to the motion of test particles in the gravitational fields of static homogeneous spherical bodies to give more accurate expression for the motion of test particles as it introduces hitherto unknown correction terms.• Can be substituted into the well - known Einstein’s (geodesic) equation of motion and the resulting equations of motion solved to obtain the corresponding post -Einstein and Newtonian generalizations and the physical effects.
4. Conclusions
We have in this work shown one possible way to construct an extended Newtonian dynamical gravitational field equation and scalar potential exterior and interior for static homogeneous spherical massive bodies using the golden Riemannian geometry of space - time. It is interesting and instructive to note that these equations reduce in the limit of 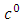 , to the corresponding pure Newtonian terms implying that it agrees with the well - known equivalence principles in Physics and to the order of
, to the corresponding pure Newtonian terms implying that it agrees with the well - known equivalence principles in Physics and to the order of 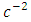 it contains unknown post - Newton and post - Einstein correction terms. The door is therefore open for the development and experimental investigations and possible applications of this theory.
it contains unknown post - Newton and post - Einstein correction terms. The door is therefore open for the development and experimental investigations and possible applications of this theory.
ACKNOWLEDGEMENTS
The authors wish to sincerely appreciate the effort of Tertiary Education Trust Fund (TETFUND), 2019/2020, for funding this research work from inception to the final stage.Source (s) of FundingThis research was funded by the Tertiary Education Trust Fund under the Institution Based Research grant.
References
| [1] | Einstein A. Relativity: the special and the general theory. General Press, 2016. |
| [2] | Anderson A. J. Principles of relativity physics, acad. Press, New York and London, 1967. |
| [3] | S. X .K. Howusu. Complete dynamical theory of physics. Jos University Press Ltd, pages 31–35, 2010. |
| [4] | S. X. K. Howusu. Riemannian revolution in physics and mathematics. Jos University Press Ltd, pages 1 – 190, 2013. |
| [5] | Foster J. A. and Nightingale J. D. A short course in General Relativity. Springer Science & Business Media, 2010. |
| [6] | Schwarzschild K. On the gravitational field of a point-mass, according to Einstein’s theory. American Association of Physics Teachers, page 19, 1982. |
| [7] | L.W. Lumbi, S. X. K. Howusu and M. S. Liman. Generalized dynamical gravitational field equation for static homogeneous spherical massive distribution of mass. International Journal of Modern Theoretical Physics 3 (1): 37, 43, 2014. |
| [8] | Y. Nura, S. X. K. Howusu, A. Musa N. Ibrahim, and A. Babakura. The general equation of motion in a gravitational field based upon the golden metric tensor. American Journal of Modern Physics, 6(6): 127–131, 2017. |
| [9] | Bergman P. G. Introduction to the theory of Relativity. Prentice Hall, India, 1987. |
| [10] | Weinberg S. Gravitation and cosmology: Principles and applications of general theory of relativity, copyright 1972 by john wiley & sons, 1972. |
| [11] | M.R. Spiegel and L. J. Stephens. Schaum’s Outline of Theory and Problems of. McGraw, 1961. |


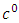 , to the corresponding pure Newtonian expressions. Results obtained contain post-Newton correction terms to the order of
, to the corresponding pure Newtonian expressions. Results obtained contain post-Newton correction terms to the order of 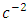 . The consequences of the additional correctional terms are that they can be applied to predict the existence of gravitational waves and their propagation in space and to derive the anomalous orbital precession of the orbit of the planet as well as the gravitational shift by the Sun as excellently as Einstein’s geometrical theory of gravitation. Also, it can be applied to examine the theoretical analysis of the motion of particles of non-zero rest masses and in a simple linear harmonic oscillator to determine its energy levels.
. The consequences of the additional correctional terms are that they can be applied to predict the existence of gravitational waves and their propagation in space and to derive the anomalous orbital precession of the orbit of the planet as well as the gravitational shift by the Sun as excellently as Einstein’s geometrical theory of gravitation. Also, it can be applied to examine the theoretical analysis of the motion of particles of non-zero rest masses and in a simple linear harmonic oscillator to determine its energy levels.
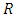 and total mass
and total mass 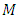 . The golden Riemannian metric tensor in the gravitational field exterior to a spherical mass is given explicitly by [3,4]
. The golden Riemannian metric tensor in the gravitational field exterior to a spherical mass is given explicitly by [3,4]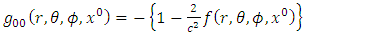
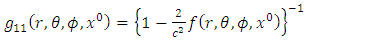
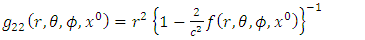
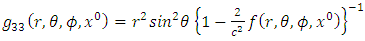

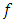 is an extended Riemannian gravitational scalar potential exterior to the spherical body and
is an extended Riemannian gravitational scalar potential exterior to the spherical body and 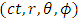 is the space- time coordinate with
is the space- time coordinate with 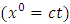 . The well - known Riemannian Laplacian operator
. The well - known Riemannian Laplacian operator 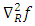 is given explicitly as [11,8]
is given explicitly as [11,8]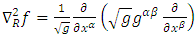
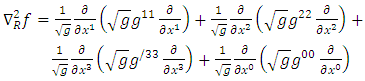
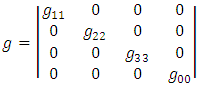
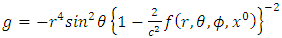
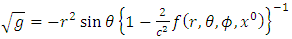
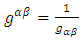
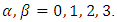 Hence, substituting (1) - (5) into (8), we obtain
Hence, substituting (1) - (5) into (8), we obtain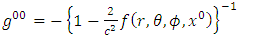
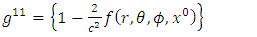
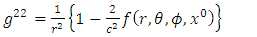
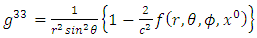
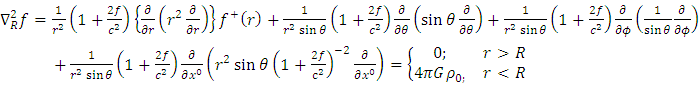
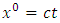 is the space time coordinate
is the space time coordinate 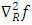 is the Riemannian Laplacian operator
is the Riemannian Laplacian operator 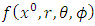 is the complete generalized gravitational scalar potential exterior to the body. By the symmetry of the distribution of mass, it follows that the gravitational field will depend only on the radial coordinate
is the complete generalized gravitational scalar potential exterior to the body. By the symmetry of the distribution of mass, it follows that the gravitational field will depend only on the radial coordinate 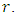 Therefore,
Therefore, 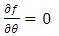
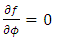
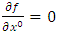
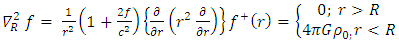
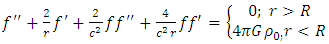
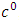 , to the corresponding pure Newton’s dynamical gravitational field equation and in the order of
, to the corresponding pure Newton’s dynamical gravitational field equation and in the order of 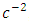 , it contains unknown post-Newton correction terms which are uncovered for theoretical development and experimental investigation s and applications.• Contain
, it contains unknown post-Newton correction terms which are uncovered for theoretical development and experimental investigation s and applications.• Contain 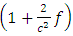 which are not found in the existing well-known Newtonian dynamical or Einstein geometrical field equations. • Contain the time - component which is not found in the existing well - known Newton’s dynamical field equation. The immediate consequences of the additional correction terms obtained in the extended Newtonian field equation are that it will predict:• Additional correction terms to the gravitational field of all massive bodies and by extension to the gravitational scalar potential exterior and interior.• Predict the existence of gravitational waves and their propagation in space with the phase velocity,
which are not found in the existing well-known Newtonian dynamical or Einstein geometrical field equations. • Contain the time - component which is not found in the existing well - known Newton’s dynamical field equation. The immediate consequences of the additional correction terms obtained in the extended Newtonian field equation are that it will predict:• Additional correction terms to the gravitational field of all massive bodies and by extension to the gravitational scalar potential exterior and interior.• Predict the existence of gravitational waves and their propagation in space with the phase velocity, 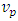 given by
given by 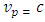 where,
where, 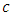 is the speed of light in vacuum.
is the speed of light in vacuum.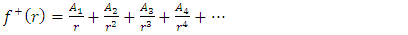
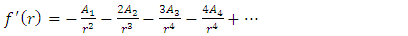
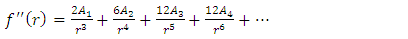
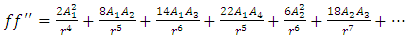
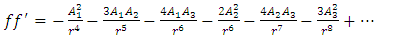
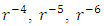 and
and 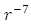 on both sides gives
on both sides gives 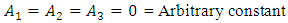

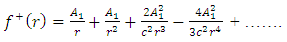
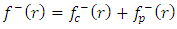
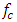 and
and 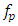 are complementary and particular solutions, respectively.The complementary solution of the interior field equation
are complementary and particular solutions, respectively.The complementary solution of the interior field equation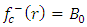
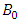 is an arbitrary constant.Seeking the solution in the form
is an arbitrary constant.Seeking the solution in the form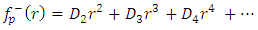
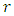 yields
yields 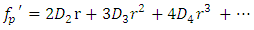
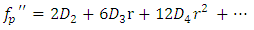
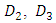 and
and 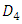 are arbitrary constants Putting equation (32), (33) and (34) into (21) and equating coefficients of
are arbitrary constants Putting equation (32), (33) and (34) into (21) and equating coefficients of 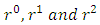 on both sides and using the well - known physical relationship between mass and density for a sphere of radius R we obtain equations which gives
on both sides and using the well - known physical relationship between mass and density for a sphere of radius R we obtain equations which gives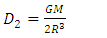
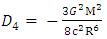
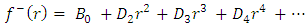
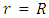
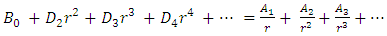
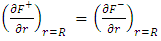
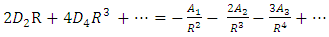
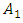 and using the well - known physical relationship between mass and density for a sphere of radius R gives
and using the well - known physical relationship between mass and density for a sphere of radius R gives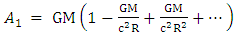
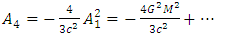
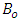 to the order of
to the order of 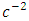 gives
gives
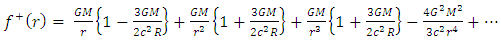
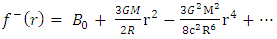
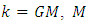 is the rest mass of the sun,
is the rest mass of the sun, 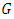 is the universal gravitational constant,
is the universal gravitational constant, 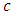 is the speed of light in vacuum,
is the speed of light in vacuum, 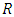 is the radius of the spherical astrophysical body and
is the radius of the spherical astrophysical body and 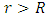 for the exterior field,
for the exterior field, 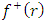 and
and 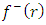 are the extended Newtonian gravitational scalar potential exterior and interior. Equations (43) and (44) are the extended exterior and interior Newtonian gravitational scalar potential based on the golden Riemannian geometry of space - time. It is interesting to note that these equations reduce in the limit of
are the extended Newtonian gravitational scalar potential exterior and interior. Equations (43) and (44) are the extended exterior and interior Newtonian gravitational scalar potential based on the golden Riemannian geometry of space - time. It is interesting to note that these equations reduce in the limit of 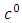 to the corresponding pure Newtonian expression and to the order of
to the corresponding pure Newtonian expression and to the order of 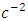 it contains post - Newton and post - Einstein correction terms. It is interesting to note that these results contain additional terms not found in [11]. The immediate consequences of the additional correction terms in the extended Newtonian gravitational scalar exterior and interior are that they can be:• Substituted into Newton’s, Einstein’s and General equations of motion to obtain generalizations of Newton’s, Einstein’s and General equations of motion to obtain corresponding revisions to the planetary equation of motion and hence the planetary parameter such the anomalous orbital precession in the solar, gravitational shift, orbital eccentricity, orbital period, orbital amplitude, perihelion and aphelion distance.• Applied to examine the theoretical analysis of the motion of particles of non-zero rest masses, gravitational length contraction and time dilation and in simple linear harmonic oscillator to determine its energy levels.• Applied to the motion of test particles in the gravitational fields of static homogeneous spherical bodies to give more accurate expression for the motion of test particles as it introduces hitherto unknown correction terms.• Can be substituted into the well - known Einstein’s (geodesic) equation of motion and the resulting equations of motion solved to obtain the corresponding post -Einstein and Newtonian generalizations and the physical effects.
it contains post - Newton and post - Einstein correction terms. It is interesting to note that these results contain additional terms not found in [11]. The immediate consequences of the additional correction terms in the extended Newtonian gravitational scalar exterior and interior are that they can be:• Substituted into Newton’s, Einstein’s and General equations of motion to obtain generalizations of Newton’s, Einstein’s and General equations of motion to obtain corresponding revisions to the planetary equation of motion and hence the planetary parameter such the anomalous orbital precession in the solar, gravitational shift, orbital eccentricity, orbital period, orbital amplitude, perihelion and aphelion distance.• Applied to examine the theoretical analysis of the motion of particles of non-zero rest masses, gravitational length contraction and time dilation and in simple linear harmonic oscillator to determine its energy levels.• Applied to the motion of test particles in the gravitational fields of static homogeneous spherical bodies to give more accurate expression for the motion of test particles as it introduces hitherto unknown correction terms.• Can be substituted into the well - known Einstein’s (geodesic) equation of motion and the resulting equations of motion solved to obtain the corresponding post -Einstein and Newtonian generalizations and the physical effects.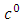 , to the corresponding pure Newtonian terms implying that it agrees with the well - known equivalence principles in Physics and to the order of
, to the corresponding pure Newtonian terms implying that it agrees with the well - known equivalence principles in Physics and to the order of 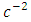 it contains unknown post - Newton and post - Einstein correction terms. The door is therefore open for the development and experimental investigations and possible applications of this theory.
it contains unknown post - Newton and post - Einstein correction terms. The door is therefore open for the development and experimental investigations and possible applications of this theory. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML