Toshiaki Ishikawa
Retired Seya-Ward, Yokohama-City, Kanagawa-Pref, Japan
Correspondence to: Toshiaki Ishikawa, Retired Seya-Ward, Yokohama-City, Kanagawa-Pref, Japan.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The Special Theory of Relativity and the Light-quantum Hypothesis were proposed in 1905 by Albert Einstein, who later introduced the General Theory of Relativity to supplement the Special Theory of Relativity’s shortcomings. The study reported here was conducted to address these shortcomings using the Light-quantum Hypothesis to improve the theory itself. Expansion of the improved Special Theory of Relativity enabled the discussion of motion equations for a light quantum and planet, which further led to a formula regarding planetary perihelion advancement. Related analysis has indicated that the General Theory of Relativity has no significance in physics.
Keywords:
Special Relativity Theory, General Relativity Theory, Motion Equation of Planet, Motion Equation of Light, Corpuscular Character of Light, Planetary Perihelion, Lorentz’s Ether Theory, Space Distortion, Escape from Gravity, Quantum Mechanics
Cite this paper: Toshiaki Ishikawa, Regarding the Special Theory of Relativity, International Journal of Theoretical and Mathematical Physics, Vol. 11 No. 4, 2021, pp. 135-140. doi: 10.5923/j.ijtmp.20211104.01.
1. Introduction
The Special Theory of Relativity (STR) and the Light-quantum Hypothesis were proposed by Albert Einstein in 1905. The STR suggests that time and space are interrelated, which is supported by results from a number of experiments.However, Einstein developed the General Theory of Relativity (GTR) because he considered the STR insufficient. As discussions on the STR usually start with the Special Principle of Relativity and the Principle of the Constancy of the Velocity of Light, the mathematical roles of the two principles need to be considered. The first principle (i.e., that of relativity) deals with the existence of a function maintained in a constant form via Lorentz transformation [1-6], and the second involves the determination of a function form. For the constancy of the velocity of light (as the second principle) to contain a function form, this velocity must not be tangible. This is clearly a self-contradiction. The constancy of the velocity of light has a sufficient condition to determine a function form, but does not have a necessary condition (i.e., it does not have to be the velocity of light). This study’s discussion is based on the relativity of space (premised on the concept that the recession velocity of the coordinate origins of two inertial systems are equal), which satisfies the necessary and sufficient conditions to determine a function form instead of the constancy of the velocity of light.Expanding the improved STR, which incorporates the Light-quantum Hypothesis, allows handling of the equations of motion for a light quantum and planet. It further highlights how a light quantum and particle can escape from any gravitational field, and allows derivation of the formula for the advance of the planetary perihelion. The subsequent detailed analysis indicated that the GTR lacks significance.
2. STR
The Theory of Relativity generally relates to the relationship between independent measurements of particle motion in two separate coordinate systems. The STR incorporates the static coordinate system K0 and the inertial coordinate system K1, which moves at a constant velocity 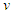 to K0. In line with the principle of special relativity, a function that always expresses the laws of physics in all inertial systems is needed. This is generally expressed as
to K0. In line with the principle of special relativity, a function that always expresses the laws of physics in all inertial systems is needed. This is generally expressed as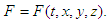 Here, the variants are time
Here, the variants are time 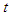 and the coordinates
and the coordinates 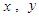 and
and 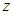 . With this, the Special Principle of Relativity is given as [7]
. With this, the Special Principle of Relativity is given as [7]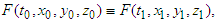 where the measured values of a particle in the K0 system are labeled 0, and 1 is used for those in the K1 system. When relativity in space is applied, differentiation of both sides of the equation with
where the measured values of a particle in the K0 system are labeled 0, and 1 is used for those in the K1 system. When relativity in space is applied, differentiation of both sides of the equation with 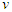 is necessary. The relationship between the time
is necessary. The relationship between the time 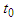 in the K0 system and the time
in the K0 system and the time 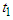 in the K1 system is expressed as
in the K1 system is expressed as 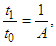 | (1) |
where 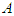 is a function of
is a function of 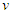 . The differential equation to be satisfied by
. The differential equation to be satisfied by 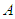 is determined as [8]
is determined as [8]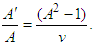 | (2) |
This is solved as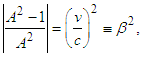 where
where 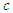 is a universal constant with the dimension of velocity, and is therefore referred to as universal velocity. Three conditions are set for the solution above: first, if
is a universal constant with the dimension of velocity, and is therefore referred to as universal velocity. Three conditions are set for the solution above: first, if 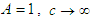 . Therefore,
. Therefore,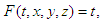 | (3) |
and if 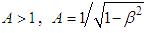 . Therefore,
. Therefore,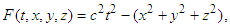 | (4) |
and if 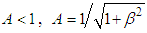 . Therefore,
. Therefore,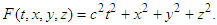 | (5) |
Einstein used the speed of light in a vacuum as the universal velocity (called the principle of the constancy of the velocity of light), expressed as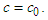 | (6) |
It is known that the STR can be used to explain experimental results effectively based on Equation 4. In fact, the theory became so historically entrenched that its validity was rarely questioned. This is because Equation 6 is somewhat self-contradictory; that is, the propagation speed of physical phenomena cannot reach universal velocity, with only the speed of light as an exception 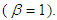 If this is accepted,
If this is accepted,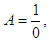 | (7) |
is true, or 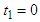 in Equation 1 is simply a remote action in and of itself (which would clearly be contradictory because there is no time lapse in light’s own coordinate system). This devalues the validity of Equation 4 and throws the theory’s raison d’être into question. To address the contradiction, discussion without exclusion of the speed of light as an exception is required.
in Equation 1 is simply a remote action in and of itself (which would clearly be contradictory because there is no time lapse in light’s own coordinate system). This devalues the validity of Equation 4 and throws the theory’s raison d’être into question. To address the contradiction, discussion without exclusion of the speed of light as an exception is required.
3. Mass and Speed of Light Quantum
In regard to the Light-quantum Hypothesis, a primary consideration is that the mass of a light quantum may not be zero, as light quantums and particles interact in reality. Here, the mass of a light quantum is provisionally labeled 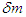 . The physical quantity opposing mass in the STR approaches the universal velocity
. The physical quantity opposing mass in the STR approaches the universal velocity 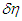 (known as the mass-conversion factor). When this is applied, the light quantum velocity
(known as the mass-conversion factor). When this is applied, the light quantum velocity 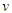 (
(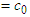 ) can be expressed as
) can be expressed as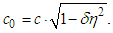 | (8) |
This replaces Equation 7 and gives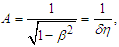 in which, to ensure validity,
in which, to ensure validity, 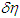 needs to be a limited definite value of a minute quantity and cannot be infinitesimal. The Theory of Relativity’s mass
needs to be a limited definite value of a minute quantity and cannot be infinitesimal. The Theory of Relativity’s mass 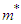 for a light quantum is expressed as [9]
for a light quantum is expressed as [9]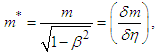 which can be further derived as
which can be further derived as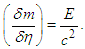 | (9) |
As the right-hand side of this formula is a settled value, neither 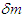 nor
nor 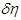 equates to zero. These values have the same sign and represent minute quantities with an order of the same degree. Thus, the following is true:
equates to zero. These values have the same sign and represent minute quantities with an order of the same degree. Thus, the following is true: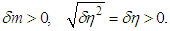 The former provides the theoretical basis for the Light-quantum Hypothesis (i.e., the light quantum is now material rather than hypothetical), and the mass-conversion factor of the latter is applied to Equation 8 to render the following true:
The former provides the theoretical basis for the Light-quantum Hypothesis (i.e., the light quantum is now material rather than hypothetical), and the mass-conversion factor of the latter is applied to Equation 8 to render the following true: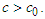 | (10) |
Here, Equation 9 is further examined. First, when 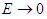 ,
, 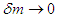 applies; as both
applies; as both 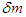 and
and 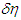 are minute quantities of the same degree,
are minute quantities of the same degree, 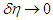 is true at the same time. Also, in accordance with the relational expression of an energy quantum, if
is true at the same time. Also, in accordance with the relational expression of an energy quantum, if 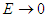 , then
, then 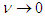 . Accordingly, when
. Accordingly, when 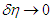 ,
, 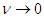 is true; using Equation 8, the principle of the constancy of the velocity of light is revised as follows:
is true; using Equation 8, the principle of the constancy of the velocity of light is revised as follows: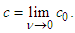 | (11) |
This equation also relates to the gravitation red-shift of light. Specifically, when a light quantum with mass is accelerated by gravity, its frequency decreases (i.e., its wavelength increases) as universal velocity approaches.Additionally, the relationship of energy momentum in the STR regarding light quantums is expressed as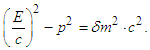 Previously, light quantums were considered to have no mass, so the solution for the right side of this formula was zero. The wave number
Previously, light quantums were considered to have no mass, so the solution for the right side of this formula was zero. The wave number 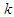 of a light quantum and the formula of an energy quantum derive
of a light quantum and the formula of an energy quantum derive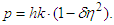
 here can be considered to represent the dispersion of momentum.
here can be considered to represent the dispersion of momentum.
4. Single-Dimension Motion Equation
Unlike the mass for a light quantum, the mass 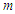 for a particle is a fixed-quantity value. Accordingly, the mass-conversion factor for a particle is greater than that for a light quantum. Therefore, applying
for a particle is a fixed-quantity value. Accordingly, the mass-conversion factor for a particle is greater than that for a light quantum. Therefore, applying 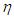 as the mass-conversion factor for a particle, the particle mass
as the mass-conversion factor for a particle, the particle mass 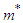 in the Theory of Relativity is expressed as
in the Theory of Relativity is expressed as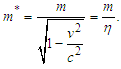 Additionally, the relationship between the mass-conversion factor and the velocity of the physical substance is expressed as
Additionally, the relationship between the mass-conversion factor and the velocity of the physical substance is expressed as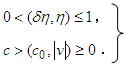 The single-dimension motion of a particle involves the issue of escape velocity. Here, a gravitational field with a mass
The single-dimension motion of a particle involves the issue of escape velocity. Here, a gravitational field with a mass  exists at the origin of the horizontal axis, and a particle placed at a positive coordinate
exists at the origin of the horizontal axis, and a particle placed at a positive coordinate  moves along the axis in the positive direction while being pulled by universal gravity from the particle at the origin. This motion is expressed by the equation of motion in the STR as
moves along the axis in the positive direction while being pulled by universal gravity from the particle at the origin. This motion is expressed by the equation of motion in the STR as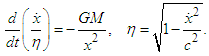 As the escape velocity of a particle varies with its position, if this velocity at the coordinate
As the escape velocity of a particle varies with its position, if this velocity at the coordinate 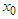 is labeled as
is labeled as 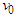 , the following is derived:
, the following is derived: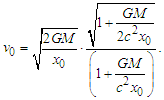 | (12) |
Next, for a light quantum, the equation of motion is expressed as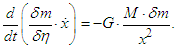 Due to the characteristic of
Due to the characteristic of 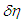 ,
, 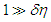 . Applying
. Applying 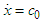 and Equation 8, and
and Equation 8, and 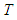 as the integral constant for integration with time, the following formula is derived:
as the integral constant for integration with time, the following formula is derived: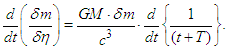 | (13) |
As the wavelengths of both 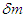 and
and 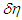 change together, iteration stops here.
change together, iteration stops here.
5. Motion Equation in Two Dimensions
Assuming that a source of gravity with a mass 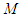 exists at the origin of a plane of coordinates, and the coordinates of the light quantum are labeled
exists at the origin of a plane of coordinates, and the coordinates of the light quantum are labeled 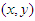 , the equation of motion for the light quantum is split into two coordinate components. They are developed by including the polar coordinate
, the equation of motion for the light quantum is split into two coordinate components. They are developed by including the polar coordinate 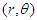 to give
to give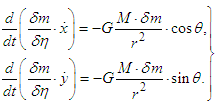 | (14) |
Also in this case, both 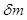 and
and 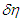 change together with wavelength.Next, particulate objects such as planets have constant mass, so the equation of motion is expressed as
change together with wavelength.Next, particulate objects such as planets have constant mass, so the equation of motion is expressed as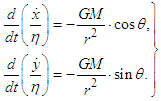 | (15) |
In Equation 15, placing 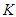 as the constant via integration leads to the derivation of
as the constant via integration leads to the derivation of 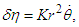 and
and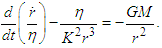 Using
Using 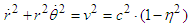 as the condition for the velocity of a particle also gives
as the condition for the velocity of a particle also gives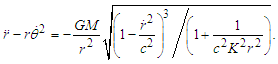 | (16) |
6. Advance of the Planetary Perihelion
In Newtonian mechanics, the perihelion advances due to gravitational interaction between planets and fluctuation of the vernal equinox. However, the advance is still observed even after correction for these factors; this is an issue with the advance of Mercury’s perihelion that astronomers discussed in the mid-19th century. Here, the issue of the advance of the planetary perihelion is examined using the equations of motion obtained.In Equation 16 relating to planetary motion, the value of the second term in each set of parentheses on the right-hand side is much smaller than 1. The three terms are therefore derived by an approximate expansion of the right-hand side. When the major radius of an orbit for a planet is expressed as 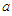 and the eccentricity of the orbit is expressed as
and the eccentricity of the orbit is expressed as 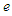 in the equation, the following is derived:
in the equation, the following is derived: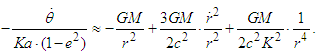 The initial term is associated with rotation based on Newtonian mechanics, and the other two are related to the advance of the perihelion for a planet. In consideration of the angular velocity of the left-hand side in terms of orbital motion and the advance of the perihelion, the angular velocity for the advance of the perihelion as an average value for one rotation is expressed as
The initial term is associated with rotation based on Newtonian mechanics, and the other two are related to the advance of the perihelion for a planet. In consideration of the angular velocity of the left-hand side in terms of orbital motion and the advance of the perihelion, the angular velocity for the advance of the perihelion as an average value for one rotation is expressed as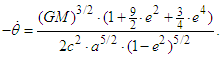 | (17) |
Based on this equation, the coordinate system associated with planetary rotation takes the direction opposite to that of rotation. Meanwhile, the coordinate system maintains a constant direction in space, so the planetary perihelion advances in the direction of rotation.In line with the GTR, applying 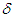 as the advance of the planetary perihelion for every rotation (where
as the advance of the planetary perihelion for every rotation (where 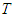 is an orbital period) gives the following [10-12]:
is an orbital period) gives the following [10-12]: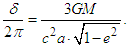 As the form of this equation is not appropriate for the expression of a total, an angular velocity is applied to express the advance of the planetary perihelion in the form of
As the form of this equation is not appropriate for the expression of a total, an angular velocity is applied to express the advance of the planetary perihelion in the form of 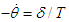 . This derives the following equation:
. This derives the following equation: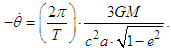 | (18) |
The two observation values for the advance of the planetary perihelion are angular velocity 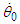 , which cannot be estimated in terms of Newtonian mechanics, and
, which cannot be estimated in terms of Newtonian mechanics, and 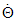 , which is the sum of an estimated angular velocity
, which is the sum of an estimated angular velocity 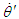 and
and 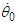 ; that is,
; that is, 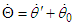 . The three variables share logical relations; this is expressed as
. The three variables share logical relations; this is expressed as 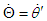 in Newtonian mechanics and as
in Newtonian mechanics and as 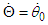 in other fields. Accordingly, no theory can be used to predict
in other fields. Accordingly, no theory can be used to predict 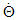 for the actual planet. The
for the actual planet. The 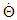 value for Mercury presented in the middle of the 19th century was around
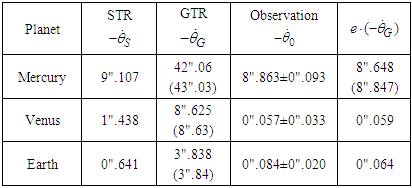
value for Mercury presented in the middle of the 19th century was around 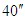 for a 100-year total.Examples of calculation with Equations 17 and 18 are shown in Table 1 for the three inner planets [10-16]. The angular velocity of the STR and the GTR labeled as
for a 100-year total.Examples of calculation with Equations 17 and 18 are shown in Table 1 for the three inner planets [10-16]. The angular velocity of the STR and the GTR labeled as 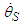 and
and 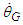 , respectively, and the column on the right shows the angular velocity
, respectively, and the column on the right shows the angular velocity 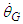 of the GTR multiplied by the orbital eccentricity
of the GTR multiplied by the orbital eccentricity 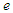 for the planet. Predicted values based on the GTR are shown in parentheses. The numerical values are 100-year totals.
for the planet. Predicted values based on the GTR are shown in parentheses. The numerical values are 100-year totals.Table 1
 |
| |
|
According to the GTR, the observation values in Table 1 are proportionate to planetary orbital eccentricity because the ratio of the observation value 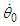 to the angular velocity value
to the angular velocity value 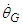 for Mercury was relatively close to the orbital eccentricity
for Mercury was relatively close to the orbital eccentricity 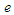 for Mercury. That is, orbital eccentricity appears only in the interaction between
for Mercury. That is, orbital eccentricity appears only in the interaction between 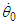 and (
and (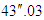 ). In other words, the observation value for Mercury is a physical quantity independent of orbital eccentricity.Focusing on the angular velocity of Mercury (
). In other words, the observation value for Mercury is a physical quantity independent of orbital eccentricity.Focusing on the angular velocity of Mercury (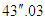 ) in terms of the GTR, no theory should exist (as previously mentioned) to predict this value, as it is close to
) in terms of the GTR, no theory should exist (as previously mentioned) to predict this value, as it is close to  for Mercury. Since Equation 18 therefore loses its significance, all values in the three columns in Table 1 are meaningless except the observation for Mercury.In conclusion, in fields other than Newtonian mechanics, the STR can be used to predict the observation value for the advance of Mercury’s perihelion; this value
for Mercury. Since Equation 18 therefore loses its significance, all values in the three columns in Table 1 are meaningless except the observation for Mercury.In conclusion, in fields other than Newtonian mechanics, the STR can be used to predict the observation value for the advance of Mercury’s perihelion; this value  and the angular value
and the angular value 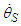 match to within 3%. This means that Equation 17 represents the first answer to the argument on the advance of the perihelion for Mercury since related discussions began in the mid-19th century.
match to within 3%. This means that Equation 17 represents the first answer to the argument on the advance of the perihelion for Mercury since related discussions began in the mid-19th century.
7. Discussion
The motion equation for a particle and a light quantum in a gravitational field was obtained by developing the improved STR via the incorporation of a new physical quantity (the mass-conversion factor) based on the light quantum hypothesis. As the equation cannot be solved for the light quantum in a strict sense, this section examines how the equation can be utilized.Motion in one dimension is an issue of escape velocity. This velocity for a particle is determined using Equation 12; in the region near 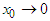 , it becomes
, it becomes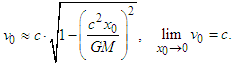 With this, the particle can escape from any gravitational field by approaching universal velocity.Motion for a light quantum is expressed by Equations 13 (one dimension) and 14 (two dimensions). Although
With this, the particle can escape from any gravitational field by approaching universal velocity.Motion for a light quantum is expressed by Equations 13 (one dimension) and 14 (two dimensions). Although 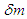 and
and 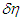 change with time, a light quantum whose velocity is infinitely close to universal velocity gives
change with time, a light quantum whose velocity is infinitely close to universal velocity gives 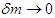 immediately regardless of temporal changes. Accordingly, for a light quantum with a velocity extremely close to universal velocity, the equation of motion can be transformed assuming that
immediately regardless of temporal changes. Accordingly, for a light quantum with a velocity extremely close to universal velocity, the equation of motion can be transformed assuming that 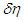 changes with time. With this, for one dimension, Equation 13 is derived as
changes with time. With this, for one dimension, Equation 13 is derived as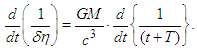 With the temporal differentiation of
With the temporal differentiation of 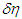 labeled
labeled 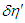 , and
, and 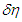 and
and 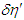 labeled as
labeled as 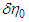 and
and 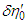 , respectively, when
, respectively, when 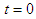 , the following is derived:
, the following is derived: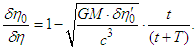 This equation shows the situation when a light quantum escapes from a gravitational field. That is,
This equation shows the situation when a light quantum escapes from a gravitational field. That is, 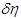 does not change greatly after the escape because a light quantum whose velocity is near universal velocity has an extremely small
does not change greatly after the escape because a light quantum whose velocity is near universal velocity has an extremely small 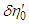 value. With very intense gravity, the light quantum may not be able to escape from the gravitational field in some cases. However, it is more likely that a light quantum with this velocity will escape.In similar analysis for a light quantum in two dimensions, motion is expressed by Equation 15 for a planet. Accordingly, by Equation 16 it is expressed as
value. With very intense gravity, the light quantum may not be able to escape from the gravitational field in some cases. However, it is more likely that a light quantum with this velocity will escape.In similar analysis for a light quantum in two dimensions, motion is expressed by Equation 15 for a planet. Accordingly, by Equation 16 it is expressed as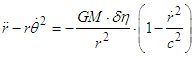 or
or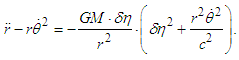 When a light quantum is distant from the gravity source,
When a light quantum is distant from the gravity source, 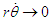 and
and 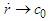 . Near the gravitational field
. Near the gravitational field 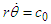 and
and 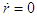 . When the variable
. When the variable 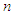 , which changes between 1 and 3 (including
, which changes between 1 and 3 (including 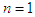 ) is applied, the equation of motion for a light quantum is expressed as
) is applied, the equation of motion for a light quantum is expressed as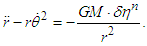 | (19) |
This equation of motion expresses how much the path of a light quantum near the surface of the Sun is bent (angle 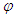 ) by the Sun’s gravity, with
) by the Sun’s gravity, with 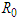 as the radius of the sun, as
as the radius of the sun, as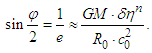 Here, as in the single-dimension analysis, the angle
Here, as in the single-dimension analysis, the angle 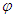 depends on the wavelength, and a light quantum moving at close to universal velocity is hardly affected (i.e., its orbit is a straight line).According to the differential Equation 2, the concept of common velocity for all inertial systems (universal velocity) supports the derivation of Equations 3 - 5 as transformation formulae. Among these, Equation 5 appears to represent the simplest solution when applied to the principle of the constancy of the speed of sound. However, as the speed of sound varies with the medium, universal velocity cannot be reached. That is, the existence of universal velocity itself puts an end to the argument regarding ether (the absolute rest system) that began in the 19th century.Next, Equations 3 and 4 remain as transform expressions, but the Galilei transformation for the former (universal velocity is equivalent to infinity) is not supported by any experimental evidence. As a result, only Equation 4 is left as a possible solution. Here the issue of universal velocity arises, and further development incorporating the following is needed; 1) consideration of universal velocity as the velocity of light (this practically means the principle of the constancy of the velocity of light as expressed by Equation 6); 2) consideration of universal velocity (which has no substance) as greater than the velocity of light for the derivation of Equation 10, or Equation 11, which is characterized by stricter expression. In the history of physics, as the GTR emerged during the first step, the second step has been left unaddressed.
depends on the wavelength, and a light quantum moving at close to universal velocity is hardly affected (i.e., its orbit is a straight line).According to the differential Equation 2, the concept of common velocity for all inertial systems (universal velocity) supports the derivation of Equations 3 - 5 as transformation formulae. Among these, Equation 5 appears to represent the simplest solution when applied to the principle of the constancy of the speed of sound. However, as the speed of sound varies with the medium, universal velocity cannot be reached. That is, the existence of universal velocity itself puts an end to the argument regarding ether (the absolute rest system) that began in the 19th century.Next, Equations 3 and 4 remain as transform expressions, but the Galilei transformation for the former (universal velocity is equivalent to infinity) is not supported by any experimental evidence. As a result, only Equation 4 is left as a possible solution. Here the issue of universal velocity arises, and further development incorporating the following is needed; 1) consideration of universal velocity as the velocity of light (this practically means the principle of the constancy of the velocity of light as expressed by Equation 6); 2) consideration of universal velocity (which has no substance) as greater than the velocity of light for the derivation of Equation 10, or Equation 11, which is characterized by stricter expression. In the history of physics, as the GTR emerged during the first step, the second step has been left unaddressed.
8. End Notes
Conditional on the velocity of light being less than universal velocity and changing with wavelength, and a particle being able to escape from any gravitational field at close-to-universal velocity, faster-than-light particles (tachyons) may exist.Analysis has yielded a motion equation for a light quantum, but conditions remain that do not allow its complete solution. However, related motion has been clarified by limiting the case to a light quantum moving at extremely close to universal velocity. This means that if visible rays meet such a condition (i.e., being significantly close to universal velocity), their motions in a gravitational field are clarified. In this case, the behavior of visible rays in the Solar System is expressed by Equation 19, which indicates that their motions are hardly influenced by the gravity of the Sun (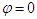 ) at all, suggesting that spatial distortion does not exist.
) at all, suggesting that spatial distortion does not exist.
References
| [1] | T. G. Pavlopoulos: Il Nuovo Cimento, Vol. 60B, No. 1, (1969) 93 – 106. |
| [2] | Jerrold Franklin: Found Phys, 43 (2013) 1489 – 1501. |
| [3] | Pablo Acuña: Studies in History and Philosophy of Modern Physics, 46 (2014) 283 – 302. |
| [4] | T. Lunghi, J. Kaniewski, F. Bussières, R. Houlmann, M. Tomamichel, A. Kent, N. Gisin, S. Wehner, and H. Zbinden: Physical Review Letters, 111 (2013) 180504 – 5. |
| [5] | Jorge Alfaro, Victor O. Rivelles: Physics Letters B, 734 (2014) 239 – 244. |
| [6] | Riccardo Junior Buonocore: Physical Review D, 89 (2014) 064013 – 14. |
| [7] | Karl Stiegler: Int. J. Theor. Phys., 5 (1972) 403 – 419. |
| [8] | T. Ishikawa: The Physics Education Society of Japan, Vol. 40, No. 1, (1992) 1 – 3. |
| [9] | A. S. Eddington: Phil. Mag., 35 (1918) 481 – 487. |
| [10] | P. G. Bergmann: Introduction to the Theory of Relativity, Prentice-Hall, Inc. Englewood Cliffs, N. J. (1942) 28 – 222. |
| [11] | T. Yamauchi, R. Uchiyama, T. Nakano: Theory of General Relativity and Gravitation, Shokabo (1975) 182 – 188. |
| [12] | G. M. Clemence: Rev. Mod. Physics, 19 (1947) 361 – 364. |
| [13] | G. M. Clemence: Astr. Papers Amer. Ephem., 11 (1943) 1 – 225. |
| [14] | H. R. Morgan: Astron. J., 51 (1945) 127 – 128. |
| [15] | G. M. Clemence, D. Brouwer: Astron. J., 60 (1955) 118 – 125. |
| [16] | R. L. Duncombe: Astron. J., 61 (1956) 174 – 175. |



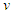 to K0. In line with the principle of special relativity, a function that always expresses the laws of physics in all inertial systems is needed. This is generally expressed as
to K0. In line with the principle of special relativity, a function that always expresses the laws of physics in all inertial systems is needed. This is generally expressed as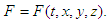 Here, the variants are time
Here, the variants are time 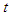 and the coordinates
and the coordinates 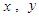 and
and 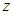 . With this, the Special Principle of Relativity is given as [7]
. With this, the Special Principle of Relativity is given as [7]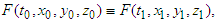 where the measured values of a particle in the K0 system are labeled 0, and 1 is used for those in the K1 system. When relativity in space is applied, differentiation of both sides of the equation with
where the measured values of a particle in the K0 system are labeled 0, and 1 is used for those in the K1 system. When relativity in space is applied, differentiation of both sides of the equation with 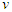 is necessary. The relationship between the time
is necessary. The relationship between the time 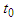 in the K0 system and the time
in the K0 system and the time 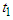 in the K1 system is expressed as
in the K1 system is expressed as 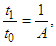
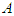 is a function of
is a function of 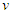 . The differential equation to be satisfied by
. The differential equation to be satisfied by 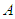 is determined as [8]
is determined as [8]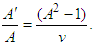
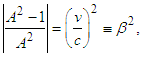 where
where 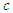 is a universal constant with the dimension of velocity, and is therefore referred to as universal velocity. Three conditions are set for the solution above: first, if
is a universal constant with the dimension of velocity, and is therefore referred to as universal velocity. Three conditions are set for the solution above: first, if 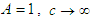 . Therefore,
. Therefore,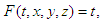
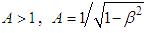 . Therefore,
. Therefore,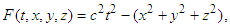
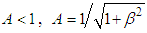 . Therefore,
. Therefore,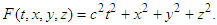
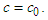
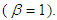 If this is accepted,
If this is accepted,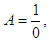
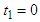 in Equation 1 is simply a remote action in and of itself (which would clearly be contradictory because there is no time lapse in light’s own coordinate system). This devalues the validity of Equation 4 and throws the theory’s raison d’être into question. To address the contradiction, discussion without exclusion of the speed of light as an exception is required.
in Equation 1 is simply a remote action in and of itself (which would clearly be contradictory because there is no time lapse in light’s own coordinate system). This devalues the validity of Equation 4 and throws the theory’s raison d’être into question. To address the contradiction, discussion without exclusion of the speed of light as an exception is required.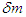 . The physical quantity opposing mass in the STR approaches the universal velocity
. The physical quantity opposing mass in the STR approaches the universal velocity 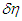 (known as the mass-conversion factor). When this is applied, the light quantum velocity
(known as the mass-conversion factor). When this is applied, the light quantum velocity 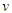 (
(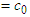 ) can be expressed as
) can be expressed as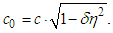
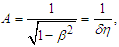 in which, to ensure validity,
in which, to ensure validity, 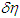 needs to be a limited definite value of a minute quantity and cannot be infinitesimal. The Theory of Relativity’s mass
needs to be a limited definite value of a minute quantity and cannot be infinitesimal. The Theory of Relativity’s mass 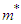 for a light quantum is expressed as [9]
for a light quantum is expressed as [9]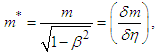 which can be further derived as
which can be further derived as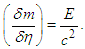
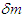 nor
nor 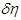 equates to zero. These values have the same sign and represent minute quantities with an order of the same degree. Thus, the following is true:
equates to zero. These values have the same sign and represent minute quantities with an order of the same degree. Thus, the following is true: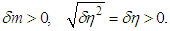 The former provides the theoretical basis for the Light-quantum Hypothesis (i.e., the light quantum is now material rather than hypothetical), and the mass-conversion factor of the latter is applied to Equation 8 to render the following true:
The former provides the theoretical basis for the Light-quantum Hypothesis (i.e., the light quantum is now material rather than hypothetical), and the mass-conversion factor of the latter is applied to Equation 8 to render the following true: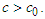
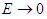 ,
, 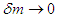 applies; as both
applies; as both 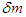 and
and 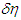 are minute quantities of the same degree,
are minute quantities of the same degree, 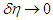 is true at the same time. Also, in accordance with the relational expression of an energy quantum, if
is true at the same time. Also, in accordance with the relational expression of an energy quantum, if 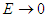 , then
, then 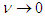 . Accordingly, when
. Accordingly, when 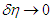 ,
, 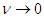 is true; using Equation 8, the principle of the constancy of the velocity of light is revised as follows:
is true; using Equation 8, the principle of the constancy of the velocity of light is revised as follows: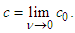
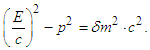 Previously, light quantums were considered to have no mass, so the solution for the right side of this formula was zero. The wave number
Previously, light quantums were considered to have no mass, so the solution for the right side of this formula was zero. The wave number 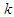 of a light quantum and the formula of an energy quantum derive
of a light quantum and the formula of an energy quantum derive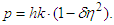
 here can be considered to represent the dispersion of momentum.
here can be considered to represent the dispersion of momentum.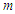 for a particle is a fixed-quantity value. Accordingly, the mass-conversion factor for a particle is greater than that for a light quantum. Therefore, applying
for a particle is a fixed-quantity value. Accordingly, the mass-conversion factor for a particle is greater than that for a light quantum. Therefore, applying 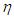 as the mass-conversion factor for a particle, the particle mass
as the mass-conversion factor for a particle, the particle mass 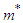 in the Theory of Relativity is expressed as
in the Theory of Relativity is expressed as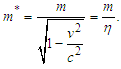 Additionally, the relationship between the mass-conversion factor and the velocity of the physical substance is expressed as
Additionally, the relationship between the mass-conversion factor and the velocity of the physical substance is expressed as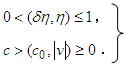 The single-dimension motion of a particle involves the issue of escape velocity. Here, a gravitational field with a mass
The single-dimension motion of a particle involves the issue of escape velocity. Here, a gravitational field with a mass 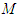 exists at the origin of the horizontal axis, and a particle placed at a positive coordinate
exists at the origin of the horizontal axis, and a particle placed at a positive coordinate 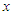 moves along the axis in the positive direction while being pulled by universal gravity from the particle at the origin. This motion is expressed by the equation of motion in the STR as
moves along the axis in the positive direction while being pulled by universal gravity from the particle at the origin. This motion is expressed by the equation of motion in the STR as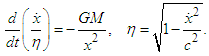 As the escape velocity of a particle varies with its position, if this velocity at the coordinate
As the escape velocity of a particle varies with its position, if this velocity at the coordinate 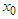 is labeled as
is labeled as 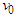 , the following is derived:
, the following is derived: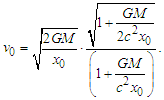
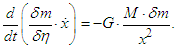 Due to the characteristic of
Due to the characteristic of 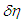 ,
, 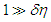 . Applying
. Applying 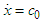 and Equation 8, and
and Equation 8, and 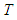 as the integral constant for integration with time, the following formula is derived:
as the integral constant for integration with time, the following formula is derived: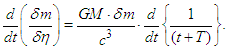
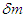 and
and 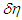 change together, iteration stops here.
change together, iteration stops here.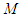 exists at the origin of a plane of coordinates, and the coordinates of the light quantum are labeled
exists at the origin of a plane of coordinates, and the coordinates of the light quantum are labeled 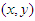 , the equation of motion for the light quantum is split into two coordinate components. They are developed by including the polar coordinate
, the equation of motion for the light quantum is split into two coordinate components. They are developed by including the polar coordinate 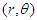 to give
to give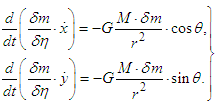
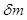 and
and 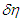 change together with wavelength.Next, particulate objects such as planets have constant mass, so the equation of motion is expressed as
change together with wavelength.Next, particulate objects such as planets have constant mass, so the equation of motion is expressed as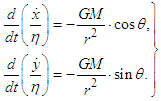
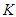 as the constant via integration leads to the derivation of
as the constant via integration leads to the derivation of 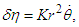 and
and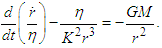 Using
Using 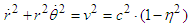 as the condition for the velocity of a particle also gives
as the condition for the velocity of a particle also gives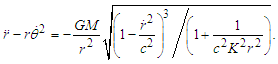
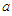 and the eccentricity of the orbit is expressed as
and the eccentricity of the orbit is expressed as 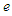 in the equation, the following is derived:
in the equation, the following is derived: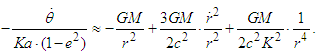 The initial term is associated with rotation based on Newtonian mechanics, and the other two are related to the advance of the perihelion for a planet. In consideration of the angular velocity of the left-hand side in terms of orbital motion and the advance of the perihelion, the angular velocity for the advance of the perihelion as an average value for one rotation is expressed as
The initial term is associated with rotation based on Newtonian mechanics, and the other two are related to the advance of the perihelion for a planet. In consideration of the angular velocity of the left-hand side in terms of orbital motion and the advance of the perihelion, the angular velocity for the advance of the perihelion as an average value for one rotation is expressed as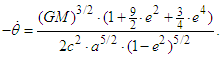
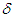 as the advance of the planetary perihelion for every rotation (where
as the advance of the planetary perihelion for every rotation (where 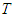 is an orbital period) gives the following [10-12]:
is an orbital period) gives the following [10-12]: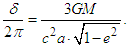 As the form of this equation is not appropriate for the expression of a total, an angular velocity is applied to express the advance of the planetary perihelion in the form of
As the form of this equation is not appropriate for the expression of a total, an angular velocity is applied to express the advance of the planetary perihelion in the form of 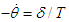 . This derives the following equation:
. This derives the following equation: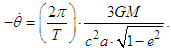
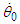 , which cannot be estimated in terms of Newtonian mechanics, and
, which cannot be estimated in terms of Newtonian mechanics, and 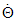 , which is the sum of an estimated angular velocity
, which is the sum of an estimated angular velocity 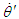 and
and 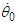 ; that is,
; that is, 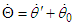 . The three variables share logical relations; this is expressed as
. The three variables share logical relations; this is expressed as 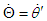 in Newtonian mechanics and as
in Newtonian mechanics and as 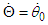 in other fields. Accordingly, no theory can be used to predict
in other fields. Accordingly, no theory can be used to predict 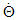 for the actual planet. The
for the actual planet. The 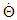 value for Mercury presented in the middle of the 19th century was around
value for Mercury presented in the middle of the 19th century was around 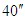 for a 100-year total.Examples of calculation with Equations 17 and 18 are shown in Table 1 for the three inner planets [10-16]. The angular velocity of the STR and the GTR labeled as
for a 100-year total.Examples of calculation with Equations 17 and 18 are shown in Table 1 for the three inner planets [10-16]. The angular velocity of the STR and the GTR labeled as 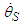 and
and 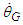 , respectively, and the column on the right shows the angular velocity
, respectively, and the column on the right shows the angular velocity 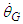 of the GTR multiplied by the orbital eccentricity
of the GTR multiplied by the orbital eccentricity 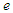 for the planet. Predicted values based on the GTR are shown in parentheses. The numerical values are 100-year totals.
for the planet. Predicted values based on the GTR are shown in parentheses. The numerical values are 100-year totals.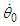 to the angular velocity value
to the angular velocity value 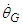 for Mercury was relatively close to the orbital eccentricity
for Mercury was relatively close to the orbital eccentricity 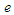 for Mercury. That is, orbital eccentricity appears only in the interaction between
for Mercury. That is, orbital eccentricity appears only in the interaction between 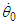 and (
and (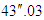 ). In other words, the observation value for Mercury is a physical quantity independent of orbital eccentricity.Focusing on the angular velocity of Mercury (
). In other words, the observation value for Mercury is a physical quantity independent of orbital eccentricity.Focusing on the angular velocity of Mercury (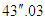 ) in terms of the GTR, no theory should exist (as previously mentioned) to predict this value, as it is close to
) in terms of the GTR, no theory should exist (as previously mentioned) to predict this value, as it is close to 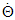 for Mercury. Since Equation 18 therefore loses its significance, all values in the three columns in Table 1 are meaningless except the observation for Mercury.In conclusion, in fields other than Newtonian mechanics, the STR can be used to predict the observation value for the advance of Mercury’s perihelion; this value
for Mercury. Since Equation 18 therefore loses its significance, all values in the three columns in Table 1 are meaningless except the observation for Mercury.In conclusion, in fields other than Newtonian mechanics, the STR can be used to predict the observation value for the advance of Mercury’s perihelion; this value 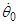 and the angular value
and the angular value 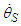 match to within 3%. This means that Equation 17 represents the first answer to the argument on the advance of the perihelion for Mercury since related discussions began in the mid-19th century.
match to within 3%. This means that Equation 17 represents the first answer to the argument on the advance of the perihelion for Mercury since related discussions began in the mid-19th century.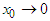 , it becomes
, it becomes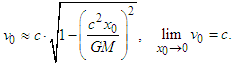 With this, the particle can escape from any gravitational field by approaching universal velocity.Motion for a light quantum is expressed by Equations 13 (one dimension) and 14 (two dimensions). Although
With this, the particle can escape from any gravitational field by approaching universal velocity.Motion for a light quantum is expressed by Equations 13 (one dimension) and 14 (two dimensions). Although 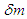 and
and 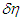 change with time, a light quantum whose velocity is infinitely close to universal velocity gives
change with time, a light quantum whose velocity is infinitely close to universal velocity gives 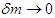 immediately regardless of temporal changes. Accordingly, for a light quantum with a velocity extremely close to universal velocity, the equation of motion can be transformed assuming that
immediately regardless of temporal changes. Accordingly, for a light quantum with a velocity extremely close to universal velocity, the equation of motion can be transformed assuming that 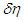 changes with time. With this, for one dimension, Equation 13 is derived as
changes with time. With this, for one dimension, Equation 13 is derived as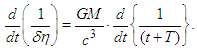 With the temporal differentiation of
With the temporal differentiation of 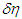 labeled
labeled 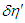 , and
, and 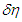 and
and 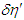 labeled as
labeled as 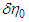 and
and 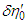 , respectively, when
, respectively, when 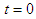 , the following is derived:
, the following is derived: This equation shows the situation when a light quantum escapes from a gravitational field. That is,
This equation shows the situation when a light quantum escapes from a gravitational field. That is, 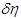 does not change greatly after the escape because a light quantum whose velocity is near universal velocity has an extremely small
does not change greatly after the escape because a light quantum whose velocity is near universal velocity has an extremely small 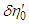 value. With very intense gravity, the light quantum may not be able to escape from the gravitational field in some cases. However, it is more likely that a light quantum with this velocity will escape.In similar analysis for a light quantum in two dimensions, motion is expressed by Equation 15 for a planet. Accordingly, by Equation 16 it is expressed as
value. With very intense gravity, the light quantum may not be able to escape from the gravitational field in some cases. However, it is more likely that a light quantum with this velocity will escape.In similar analysis for a light quantum in two dimensions, motion is expressed by Equation 15 for a planet. Accordingly, by Equation 16 it is expressed as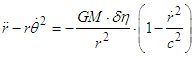 or
or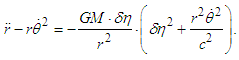 When a light quantum is distant from the gravity source,
When a light quantum is distant from the gravity source, 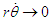 and
and 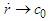 . Near the gravitational field
. Near the gravitational field 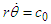 and
and 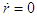 . When the variable
. When the variable 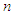 , which changes between 1 and 3 (including
, which changes between 1 and 3 (including 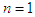 ) is applied, the equation of motion for a light quantum is expressed as
) is applied, the equation of motion for a light quantum is expressed as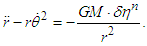
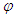 ) by the Sun’s gravity, with
) by the Sun’s gravity, with 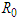 as the radius of the sun, as
as the radius of the sun, as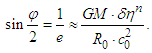 Here, as in the single-dimension analysis, the angle
Here, as in the single-dimension analysis, the angle 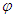 depends on the wavelength, and a light quantum moving at close to universal velocity is hardly affected (i.e., its orbit is a straight line).According to the differential Equation 2, the concept of common velocity for all inertial systems (universal velocity) supports the derivation of Equations 3 - 5 as transformation formulae. Among these, Equation 5 appears to represent the simplest solution when applied to the principle of the constancy of the speed of sound. However, as the speed of sound varies with the medium, universal velocity cannot be reached. That is, the existence of universal velocity itself puts an end to the argument regarding ether (the absolute rest system) that began in the 19th century.Next, Equations 3 and 4 remain as transform expressions, but the Galilei transformation for the former (universal velocity is equivalent to infinity) is not supported by any experimental evidence. As a result, only Equation 4 is left as a possible solution. Here the issue of universal velocity arises, and further development incorporating the following is needed; 1) consideration of universal velocity as the velocity of light (this practically means the principle of the constancy of the velocity of light as expressed by Equation 6); 2) consideration of universal velocity (which has no substance) as greater than the velocity of light for the derivation of Equation 10, or Equation 11, which is characterized by stricter expression. In the history of physics, as the GTR emerged during the first step, the second step has been left unaddressed.
depends on the wavelength, and a light quantum moving at close to universal velocity is hardly affected (i.e., its orbit is a straight line).According to the differential Equation 2, the concept of common velocity for all inertial systems (universal velocity) supports the derivation of Equations 3 - 5 as transformation formulae. Among these, Equation 5 appears to represent the simplest solution when applied to the principle of the constancy of the speed of sound. However, as the speed of sound varies with the medium, universal velocity cannot be reached. That is, the existence of universal velocity itself puts an end to the argument regarding ether (the absolute rest system) that began in the 19th century.Next, Equations 3 and 4 remain as transform expressions, but the Galilei transformation for the former (universal velocity is equivalent to infinity) is not supported by any experimental evidence. As a result, only Equation 4 is left as a possible solution. Here the issue of universal velocity arises, and further development incorporating the following is needed; 1) consideration of universal velocity as the velocity of light (this practically means the principle of the constancy of the velocity of light as expressed by Equation 6); 2) consideration of universal velocity (which has no substance) as greater than the velocity of light for the derivation of Equation 10, or Equation 11, which is characterized by stricter expression. In the history of physics, as the GTR emerged during the first step, the second step has been left unaddressed.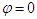 ) at all, suggesting that spatial distortion does not exist.
) at all, suggesting that spatial distortion does not exist. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML