-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2021; 11(2): 61-66
doi:10.5923/j.ijtmp.20211102.01
Received: Feb. 2, 2021; Accepted: Mar. 31, 2021; Published: Apr. 2, 2021

New Insights and the Development of an Appropriate Kinematic (Non-Inertial) Special Relativity Theory
Manhar L. Shah
MVM Electronics, Inc., 3410 N Harbor City Blvd., Suite E, Melbourne, FL, USA
Correspondence to: Manhar L. Shah, MVM Electronics, Inc., 3410 N Harbor City Blvd., Suite E, Melbourne, FL, USA.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Existing Special Relativity (SR) theories involving non-inertial frames are shown to produce erroneous Space-time Transformation Relations (STR). Formulation of SR shows that specifying the trajectory in the traveller’s proper time makes his frame the reference frame. Traveller velocity change implies a new reference frame requiring correction for STR. But commonly used Successive Incremental Lorentz Transformation (SILT) or equivalently the Fermi Coordinates (FC) principle with Lorentz Boost and earlier theories fail to include corrections and simultaneity. In stationary (inertial) frames the time for light propagation between two points is simply the distance divided by the speed of light, but with changing velocities in non-inertial frames that relation doesn’t hold. Establishing simultaneity, which relies upon the information propagation from an event to the observation points, is difficult when the trajectory is in the traveller’s time. For an appropriate Kinematic Special Relativity (KSR) theory, (non-inertial SR), inclusion of corrections in earlier theories without consideration of the simultaneity and the information propagation time is inadequate. Moreover, it would be paradoxical to designate who is the traveller in SILT and FC if both frames are non-inertial. Therefore, KSR theory is developed here using simultaneity which is central to SR with the trajectory in the stationary frame’s proper time.
Keywords: Special Relativity, Non-inertial Special Relativity, Accelerated frame, Hyperbolic trajectory, Fermi coordinates, Infinitesimal Lorentz transformation, Twin paradox, Rotating frame
Cite this paper: Manhar L. Shah, New Insights and the Development of an Appropriate Kinematic (Non-Inertial) Special Relativity Theory, International Journal of Theoretical and Mathematical Physics, Vol. 11 No. 2, 2021, pp. 61-66. doi: 10.5923/j.ijtmp.20211102.01.
Article Outline
1. Introduction
- Special Relativity (SR) theory is restricted to inertial frames but in real life situations a frame may travel with varying velocities, acceleration and rotation rendering it non-inertial. SR theory involving non-inertial frames in flat space-time (to exclude effects of acceleration, gravity and general relativity considerations) is referred to as Kinematic Special Relativity (KSR) theory. Several authors have developed KSR theory based upon Successive Infinitesimal Lorentz Transformation (SILT) as in [1] and its equivalent Fermi Coordinates (FC) principle as in [2-3] and the associated “Postulate of Locality”. The FC principle uses infinite co-moving inertial frames to match the velocity of a non-inertial observer. Frame switching is used in FC and incremental Space-time Transformation Relation (STR) that includes Time Transformation Relations (TTR) at the non-inertial traveller’s position is sequentially transformed from frame to frame by means of Lorentz Boost (LB). Mathematically, the procedure of FC is like the procedure of SILT. The infinitesimal change in STR between observers in SILT and FC is integrated and erroneously assumed in earlier theories as STR between stationary and travelling observers.It has been established that if the gravitational equivalent of acceleration requiring General Relativity effect is neglected then the acceleration has no effect on STR in SR like in Galilean frames. Therefore, one cannot distinguish with kinematic consideration alone who is the traveller and who is the stationary (inertial) observer in SR. However, in SR unlike in the Galilean case, time is relative and specifying the traveller’s trajectory in his proper time, as done in FC and SILT case, makes his frame the reference frame. In formulation of the SR theory, the reference frame is set to have a universal or global time independent of position in that frame while in non-reference frames it is not. In other words, if time is specified at one point in the reference frame then the same value can be used for all other places in that frame but that cannot be done in non-reference frames. STR is established in SR by having an event that takes place at the synchronization position and being observed simultaneously by the traveller and an observer at his position in the reference frame. Velocity of the traveller’s frame is considered positive if information flow is in the same direction. Both frames being inertial in SR, negative velocity is regarded as the interchange of traveller and stationary observers frame. Such interchange makes the event to take place at the traveller’s position but in SR no distinction exists between a stationary and travelling observer. First, the problems with specifying the trajectory in the traveller’s proper time will be discussed. Then, limitations of earlier theories are demonstrated with illustrations of inconsistent results when those theories are applied. Consideration for developing an appropriate KSR theory with simultaneity follows. Emphasis is placed upon developing the temporal part of KSR. The spatial part of KSR is not dependent upon simultaneity, so LB matrix can be used to transform the spatial coordinates of the stationary frame into the traveller’s frame or vice versa. Expression of the temporal part will be derived explicitly to complete KSR theory. Plots for several standard trajectories are shown using this theory. Finally, implications of the results of this novel KSR theory are discussed with a comparison to historically accepted TTR results and conclusions at the end. The nomenclature or designations used in this paper are as follows: stationary (meaning also inertial) frame F and non-inertial travelling frame F’; stationary observer A and traveller A’ at the origin of their respective frame; time t and position
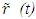 with parameters in F un-primed and corresponding parameters in F’ primed; velocity of light (also same as information propagation) as c with length unit in c=1; relative velocity between frames as
with parameters in F un-primed and corresponding parameters in F’ primed; velocity of light (also same as information propagation) as c with length unit in c=1; relative velocity between frames as 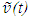 as observed in F with
as observed in F with 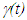 as Lorentz contraction factor and
as Lorentz contraction factor and 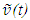 as a fraction of c; same in F’ designated as
as a fraction of c; same in F’ designated as 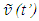 and
and 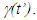 Synchronization of frames is set as
Synchronization of frames is set as 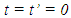 at
at 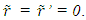
2. Problems with Specifying the Trajectory in the Traveller’s Proper Time
- When the trajectory is specified in the traveller’s proper time, his frame becomes the reference frame. SR provides time relation at the reference frame’s synchronization position as
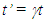 at
at 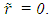 In SR stationary and travelling frame can be interchanged and
In SR stationary and travelling frame can be interchanged and 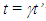 is true at
is true at 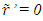 but the same can be obtained using the simultaneity condition without interchanging frames. In the non-inertial case, the event is assumed to occur at the synchronization position in the reference frame and the information flow direction is fixed from there to the traveller. It is shown in a later section that the relation between information (light) propagation path length in a stationary vs. a non-inertial frame depends upon the velocity direction relative to the information flow. Therefore, interchanging of frames is not possible. This means the reference frame needs to be stationary and
but the same can be obtained using the simultaneity condition without interchanging frames. In the non-inertial case, the event is assumed to occur at the synchronization position in the reference frame and the information flow direction is fixed from there to the traveller. It is shown in a later section that the relation between information (light) propagation path length in a stationary vs. a non-inertial frame depends upon the velocity direction relative to the information flow. Therefore, interchanging of frames is not possible. This means the reference frame needs to be stationary and 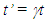 at the stationary observer’s position is the true relation and not
at the stationary observer’s position is the true relation and not 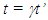 at the traveller’s position as used in SILT, FC and earlier theories. Besides, if both relations are true then no difference exists between inertial and non-inertial frames.An illustration is presented to show why the trajectory in the traveller’s proper time can lead to complications resulting in errors in earlier theories. Consider A and A’ in inertial frames with relative velocity, v~0.866, corresponding to
at the traveller’s position as used in SILT, FC and earlier theories. Besides, if both relations are true then no difference exists between inertial and non-inertial frames.An illustration is presented to show why the trajectory in the traveller’s proper time can lead to complications resulting in errors in earlier theories. Consider A and A’ in inertial frames with relative velocity, v~0.866, corresponding to 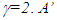 ravels 0.5 unit of his proper time so the distance of A in his frame would be 0.5x0.866=0.433. Now A’ switches into the frame of A and makes that frame his new reference frame. Though, he can keep his time, distance of A in this new frame from the position he was coincident where he switched the frame is
ravels 0.5 unit of his proper time so the distance of A in his frame would be 0.5x0.866=0.433. Now A’ switches into the frame of A and makes that frame his new reference frame. Though, he can keep his time, distance of A in this new frame from the position he was coincident where he switched the frame is 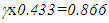 according to SR. This shows that A’ has to recalculate his trip data every time he switches the frame as implied by his velocity change.Many published papers dealing with KSR theory are for a uniformly accelerated observer that is described with a hyperbolic trajectory as shown in [1]. More general KSR theory that includes acceleration and rotation is described in [2] and the majority of subsequent publications use results obtained therein when dealing with non-inertial frames. All those theories have in common the TTR as
according to SR. This shows that A’ has to recalculate his trip data every time he switches the frame as implied by his velocity change.Many published papers dealing with KSR theory are for a uniformly accelerated observer that is described with a hyperbolic trajectory as shown in [1]. More general KSR theory that includes acceleration and rotation is described in [2] and the majority of subsequent publications use results obtained therein when dealing with non-inertial frames. All those theories have in common the TTR as 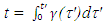 at
at 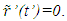 As the traveller changes velocity after the first value, his position in the new frame is not at
As the traveller changes velocity after the first value, his position in the new frame is not at 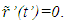 The proper time and distance of the stationary observer in relation to the space-time coordinate of the traveller are not the same as that for a coincident observer’s space-time coordinates in the new reference frame where the traveller will be positioned as he switches frame. This means
The proper time and distance of the stationary observer in relation to the space-time coordinate of the traveller are not the same as that for a coincident observer’s space-time coordinates in the new reference frame where the traveller will be positioned as he switches frame. This means 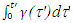 is in error because at each incremental frame switching some STR correction is required. SILT, FC and earlier theories fail to include such corrections. Even with inclusion of corrections earlier theories cannot be remedied because simultaneity and the information propagation time are not considered in their development. In cases where simultaneity is obvious such as in the twin paradox when twins meet, inclusion of the correction would produce valid results but that may not be the case in general.If the trajectory is specified in a stationary observer’s proper time making his frame as the reference,
is in error because at each incremental frame switching some STR correction is required. SILT, FC and earlier theories fail to include such corrections. Even with inclusion of corrections earlier theories cannot be remedied because simultaneity and the information propagation time are not considered in their development. In cases where simultaneity is obvious such as in the twin paradox when twins meet, inclusion of the correction would produce valid results but that may not be the case in general.If the trajectory is specified in a stationary observer’s proper time making his frame as the reference, 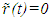 is true for any arbitrary motion of the traveller and no frame switching is required. LT provides,
is true for any arbitrary motion of the traveller and no frame switching is required. LT provides, 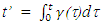 at the stationary observer’s position
at the stationary observer’s position 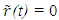 in this case.Obtaining the time difference between the event and its observation at a distance is obvious in a stationary frame. The same is difficult in a non-inertial frame because the information propagation length between two points is not the same as the distance between them. Information propagation direction changes with a change in velocity as revealed by stellar aberration. For that reason it is difficult to develop KSR theory with a trajectory in the traveller’s proper time. So KSR theory is developed using trajectory in the stationary observer’s proper time in this paper.
in this case.Obtaining the time difference between the event and its observation at a distance is obvious in a stationary frame. The same is difficult in a non-inertial frame because the information propagation length between two points is not the same as the distance between them. Information propagation direction changes with a change in velocity as revealed by stellar aberration. For that reason it is difficult to develop KSR theory with a trajectory in the traveller’s proper time. So KSR theory is developed using trajectory in the stationary observer’s proper time in this paper.3. Inconsistent Results with Existing KSR Theories
- Examples of inconsistent data resulting from earlier theories are provided to show the need for the use of correction and simultaneity. An easily understandable example is the “Twin Paradox.” Due to the coincident position of observers, simultaneity and information propagation consideration is not needed. To show this inconsistency, consider two twins A’ and B’ making non-inertial journeys for 1 unit forward and 1 unit return time round trip in opposite directions as described in [4]. A’ and B’ both have equal trajectory data in their own proper time and achieve nearly instantaneous velocity changes to produce
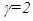 corresponding to velocity, v~0.866 in relation to a stationary frame F. A triplet C to the travelling twin is situated at the origin of F. The conclusion drawn in [4] is that the travelling twin as younger or older has no basis and the paradox cannot be resolved with earlier theories, but the author in [4] offers no solution to resolve it.Several issues arise if earlier theories are used to describe the Twin paradox. Postulate of locality means A’ and B’ have no way of judging their own velocity except from acceleration data or radar ranging with C. With acceleration data, A’ and B’ can know their own velocity in relation to C but not of each other’s. With radar ranging each can find the other’s trajectory data but there is a time delay involved so the observed STR may not be correct if the other changed velocity during the ranging time interval. When A’ and B’ use their frame as the reference they will have universal or global time over all positions, so connecting STR is only possible with a comparison to the inertial observer’s frame C. At the instant of velocity change by A’ (or B’) his frame’s designation as the reference frame is no longer valid.Consider how at the return position, A’ and a coincident observer in the frame of B’ would observe a clock in the frame of C if both A’ and B’ consider their own frame as the reference frame. Up to 1 unit return time all frames are inertial and we can use SR and LT to show that A’ would observe 2 units of time in the frame of C at a position X in his (A’) frame that corresponds to 2x0.866=1.732 from C in the stationary frame of C. Since B’ also uses his frame as the reference and travels 1 unit of time according his clock, C will be at 0.866 distance from him in his frame and the position X observed by A’ in the frame of C would be at a further
corresponding to velocity, v~0.866 in relation to a stationary frame F. A triplet C to the travelling twin is situated at the origin of F. The conclusion drawn in [4] is that the travelling twin as younger or older has no basis and the paradox cannot be resolved with earlier theories, but the author in [4] offers no solution to resolve it.Several issues arise if earlier theories are used to describe the Twin paradox. Postulate of locality means A’ and B’ have no way of judging their own velocity except from acceleration data or radar ranging with C. With acceleration data, A’ and B’ can know their own velocity in relation to C but not of each other’s. With radar ranging each can find the other’s trajectory data but there is a time delay involved so the observed STR may not be correct if the other changed velocity during the ranging time interval. When A’ and B’ use their frame as the reference they will have universal or global time over all positions, so connecting STR is only possible with a comparison to the inertial observer’s frame C. At the instant of velocity change by A’ (or B’) his frame’s designation as the reference frame is no longer valid.Consider how at the return position, A’ and a coincident observer in the frame of B’ would observe a clock in the frame of C if both A’ and B’ consider their own frame as the reference frame. Up to 1 unit return time all frames are inertial and we can use SR and LT to show that A’ would observe 2 units of time in the frame of C at a position X in his (A’) frame that corresponds to 2x0.866=1.732 from C in the stationary frame of C. Since B’ also uses his frame as the reference and travels 1 unit of time according his clock, C will be at 0.866 distance from him in his frame and the position X observed by A’ in the frame of C would be at a further 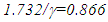 distance away from C making the distance between C and X as seen in the frame of B’ equal to 1.732 units. Using LT
distance away from C making the distance between C and X as seen in the frame of B’ equal to 1.732 units. Using LT 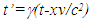 we find the time at the said position in the frame of C as 2x(1-1.732x0.866)=-1. Thus, at the coincident point at the position of A’ an observer in the frame of A’ sees clock time in the frame of C which is different from what an observer in the frame of B’ sees. This contradiction exists because both A’ and B’ are using their own proper time in the computation making their own frame as the reference frame. The inconsistency is removed if only one frame is used as the reference frame. In SILT and FC traveller uses his clock to define his travel making his frame as the reference frame. As the traveller changes the velocity his frame is switched and the switched frame becomes the new reference frame. This shifts the STR as velocity is changed. Earlier theories didn’t consider the implication of such frame switching resulting in an inconsistent outcome.The above mentioned inconsistency demonstrates that all SR data must be computed with one reference frame. If the frame of C is designated as the reference, then the time in the frame of C will be 2 units everywhere for the numerical illustration used. In this case, for 1 unit of proper time of A’, the time in frame of B’ at the position of A’ will be 7 units and A’ will observe the same. That is true even with any one frame as the reference because all frames are inertial up to this point as no velocity change has occurred.Another inconsistency is obvious when A’ and B’ meet again. Due to the perfect symmetry between A’ and B’, each should have the identical time when they meet. However, they have relative velocity corresponding to
we find the time at the said position in the frame of C as 2x(1-1.732x0.866)=-1. Thus, at the coincident point at the position of A’ an observer in the frame of A’ sees clock time in the frame of C which is different from what an observer in the frame of B’ sees. This contradiction exists because both A’ and B’ are using their own proper time in the computation making their own frame as the reference frame. The inconsistency is removed if only one frame is used as the reference frame. In SILT and FC traveller uses his clock to define his travel making his frame as the reference frame. As the traveller changes the velocity his frame is switched and the switched frame becomes the new reference frame. This shifts the STR as velocity is changed. Earlier theories didn’t consider the implication of such frame switching resulting in an inconsistent outcome.The above mentioned inconsistency demonstrates that all SR data must be computed with one reference frame. If the frame of C is designated as the reference, then the time in the frame of C will be 2 units everywhere for the numerical illustration used. In this case, for 1 unit of proper time of A’, the time in frame of B’ at the position of A’ will be 7 units and A’ will observe the same. That is true even with any one frame as the reference because all frames are inertial up to this point as no velocity change has occurred.Another inconsistency is obvious when A’ and B’ meet again. Due to the perfect symmetry between A’ and B’, each should have the identical time when they meet. However, they have relative velocity corresponding to 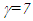 at all times due to the opposite direction of their journey. If A’ and B’ aged equally even with their constant relative motion then it violates SR theory or at least contradicts the accepted twin paradox outcome at present.An additional inconsistency occurs when one considers the simultaneity between A’ and C just after A’ reverses his journey. For this assume A’ travels 1 unit of his proper time in the forward direction. Now consider an event that takes place at the origin of F and is observed by A’ and an observer at the corresponding position X in F at the proper time of A’ equal to 1.1 units. According to the earlier theories the corresponding time at X would be 2.2 units. The distance in F between C and X, the position where the event is observed can be calculated using SR as
at all times due to the opposite direction of their journey. If A’ and B’ aged equally even with their constant relative motion then it violates SR theory or at least contradicts the accepted twin paradox outcome at present.An additional inconsistency occurs when one considers the simultaneity between A’ and C just after A’ reverses his journey. For this assume A’ travels 1 unit of his proper time in the forward direction. Now consider an event that takes place at the origin of F and is observed by A’ and an observer at the corresponding position X in F at the proper time of A’ equal to 1.1 units. According to the earlier theories the corresponding time at X would be 2.2 units. The distance in F between C and X, the position where the event is observed can be calculated using SR as 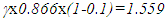 units. Since F is a stationary frame the event must have occurred at C at the time equal to 2.2-1.559/c=0.641 unit of time. The time observed by C in the frame of A’ at the time of event must be
units. Since F is a stationary frame the event must have occurred at C at the time equal to 2.2-1.559/c=0.641 unit of time. The time observed by C in the frame of A’ at the time of event must be 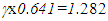 units according to SR calculated using
units according to SR calculated using 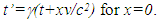 This means the event is observed by A’ at the time 1.1 unit while it occurred in his frame F’ at the time 1.282 units. This means A’ observed the event before it occurred at a distance in his frame.If the KSR theory as presented in this paper is used, which assumes the stationary frame as the reference, resolution of the Twin paradox occurs with the traveling twin as older according to recently reported in [5] that uses another concept. The traveling twin as older is contrary to the historical acceptance that he will be younger. Further discussion on this issue will be presented later. Publications also show that the stationary observer’s data must be used for obtaining STR of two non-inertial frames but without developing any theory for the non-inertial case [6-7].Inclusion of the STR correction as mentioned before for a velocity change in SILT and FC produces consistent results with the KSR theory described in this paper for the twin paradox because of their coincident position. At the velocity reversal position for proper travel time of 1 unit for A’ the time at the coincident point in the frame of B’ will be 7 units and the proper time of C would be 0.5 unit according to LT. As the frame switch occurs the proper distances change with the same ratio as the changes in time at the same position. This means in the frame of B’ the stationary observer C will appear to A’ at a distance 7 times the distance that was in the frame of A’ before A’ switched the frame. SILT, FC and earlier theories fail to realize this change in proper distance with frame switching. As A’ travels in the frame of B’ after frame switching A’ cannot reach C in 1 unit of his proper time but would require 7 units of his proper time. So, when A’ coincides with C his proper time will be 8 units and that of C will be
This means the event is observed by A’ at the time 1.1 unit while it occurred in his frame F’ at the time 1.282 units. This means A’ observed the event before it occurred at a distance in his frame.If the KSR theory as presented in this paper is used, which assumes the stationary frame as the reference, resolution of the Twin paradox occurs with the traveling twin as older according to recently reported in [5] that uses another concept. The traveling twin as older is contrary to the historical acceptance that he will be younger. Further discussion on this issue will be presented later. Publications also show that the stationary observer’s data must be used for obtaining STR of two non-inertial frames but without developing any theory for the non-inertial case [6-7].Inclusion of the STR correction as mentioned before for a velocity change in SILT and FC produces consistent results with the KSR theory described in this paper for the twin paradox because of their coincident position. At the velocity reversal position for proper travel time of 1 unit for A’ the time at the coincident point in the frame of B’ will be 7 units and the proper time of C would be 0.5 unit according to LT. As the frame switch occurs the proper distances change with the same ratio as the changes in time at the same position. This means in the frame of B’ the stationary observer C will appear to A’ at a distance 7 times the distance that was in the frame of A’ before A’ switched the frame. SILT, FC and earlier theories fail to realize this change in proper distance with frame switching. As A’ travels in the frame of B’ after frame switching A’ cannot reach C in 1 unit of his proper time but would require 7 units of his proper time. So, when A’ coincides with C his proper time will be 8 units and that of C will be 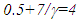 units. This is the same as predicted by KSR theory here and in recently published paper [5]. Correct data are obtained by selecting the stationary frame as the reference frame. Simultaneity is assured due to coincident observers while LT provides
units. This is the same as predicted by KSR theory here and in recently published paper [5]. Correct data are obtained by selecting the stationary frame as the reference frame. Simultaneity is assured due to coincident observers while LT provides 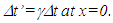 No frame switching and STR corrections are required in this case.
No frame switching and STR corrections are required in this case.4. Information Propagation Path Length Relation and STR Consideration between 2 Frames
- Clock synchronization in non-inertial frames has been studied in reference to GPS as described in [8] and provides guidance for developing KSR theory. In SR, velocity is constant therefore the traveller’s velocity data can be used to obtain the incremental
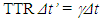 at
at 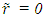 or
or 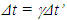 at
at 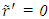 but as explained earlier, in KSR
but as explained earlier, in KSR 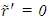 is true only for the initial velocity period. The trajectory of A’ in F is thus described by the incremental path
is true only for the initial velocity period. The trajectory of A’ in F is thus described by the incremental path 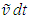 but the position of A, meaning the trajectory of A in F’ cannot be described in such a simple form. The spatial part, the position of A’ in F at any instant t can be found by integrating the incremental trajectory as,
but the position of A, meaning the trajectory of A in F’ cannot be described in such a simple form. The spatial part, the position of A’ in F at any instant t can be found by integrating the incremental trajectory as,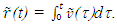 | (1) |
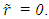 The proper time t’0 in F’ at the position of A with the proper time t0 of A in F is thus the integration,
The proper time t’0 in F’ at the position of A with the proper time t0 of A in F is thus the integration,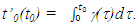 | (2) |
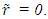 In order to obtain the TTR at the position of the traveller A’ the propagation of light needs to be considered. The light pulse propagation distance relation between stationary and non-inertial frames is required for KSR theory to ascertain the time relation for information propagation of an event in two frames. LT can be used to find the relationship between light pulse propagation distance
In order to obtain the TTR at the position of the traveller A’ the propagation of light needs to be considered. The light pulse propagation distance relation between stationary and non-inertial frames is required for KSR theory to ascertain the time relation for information propagation of an event in two frames. LT can be used to find the relationship between light pulse propagation distance 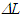 in F for the corresponding length
in F for the corresponding length 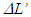 in F’ having a velocity
in F’ having a velocity 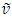 at an angle
at an angle 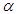 to the direction of light propagation in F. The propagation length parallel to
to the direction of light propagation in F. The propagation length parallel to 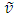 is
is 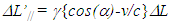 and the perpendicular component is
and the perpendicular component is 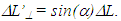 Thus, as a light pulse travels distance
Thus, as a light pulse travels distance 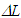 in F it will travel
in F it will travel 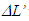 in F’ at a different angle from
in F’ at a different angle from 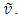 Addition of these two components provides,
Addition of these two components provides, 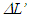 as,
as,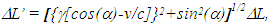 | (3) |
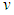 in Eq. (3) and in
in Eq. (3) and in 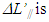 the signed magnitude of
the signed magnitude of 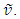 If the component of
If the component of 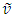 is along the light propagation direction then
is along the light propagation direction then 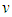 is positive otherwise it is negative.
is positive otherwise it is negative.5. Development of Kinematic Special Relativity (KSR) Theory
- KSR theory is used to relate space-time data of an inertial frame to space-time data of a non-inertial frame with a non-constant velocity trajectory. Basically, that entails finding the simultaneity time relation between two observers involved in an event and its simultaneous observation in both frames at a distance from the event position. The parameters involved in this case are event time t0 and t’0, observation time t and t’, distance between the event and the observation point
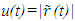 and u’, information propagation track length L and L’ and event to observer’s point propagation time tp and t’p in stationary and travelling frame F and F’, respectively. If the trajectory is specified as
and u’, information propagation track length L and L’ and event to observer’s point propagation time tp and t’p in stationary and travelling frame F and F’, respectively. If the trajectory is specified as 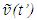 then t’, u, and u’ become known after the distance correction as discussed earlier is included. The event time is t’0 = t’-t’p can be found if t’p is known which is t’p =L’/c but for that L’ must be known. Finding L’ using the traveller’s trajectory becomes difficult because the relationship between distance and c is not straight forward. On the other hand, if the trajectory is specified as
then t’, u, and u’ become known after the distance correction as discussed earlier is included. The event time is t’0 = t’-t’p can be found if t’p is known which is t’p =L’/c but for that L’ must be known. Finding L’ using the traveller’s trajectory becomes difficult because the relationship between distance and c is not straight forward. On the other hand, if the trajectory is specified as 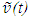 then t, t0, t’0, u, L and tp become known. Computation of t’ involves finding L’, so t’p = L’/c can be added to t’0 to obtain t’. As information of the event that occurs at time t0 at
then t, t0, t’0, u, L and tp become known. Computation of t’ involves finding L’, so t’p = L’/c can be added to t’0 to obtain t’. As information of the event that occurs at time t0 at 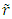 = 0 travels distance L=u to the position of A’ in F in time tp, the same information travels distance L’ from the location of the event at position of A to A’ in time t’P in F’.A narrative is presented for developing KSR theory with consideration of simultaneity and the fact that in a stationary frame the distance between two points divided by c provides the proper time interval while that is not the case in non-inertial frames. Only the temporal part of KSR is elaborated here. The spatial part of KSR doesn’t require considerations of simultaneity so Eq. (1) can be used to obtain the correct spatial relation between two frames at
= 0 travels distance L=u to the position of A’ in F in time tp, the same information travels distance L’ from the location of the event at position of A to A’ in time t’P in F’.A narrative is presented for developing KSR theory with consideration of simultaneity and the fact that in a stationary frame the distance between two points divided by c provides the proper time interval while that is not the case in non-inertial frames. Only the temporal part of KSR is elaborated here. The spatial part of KSR doesn’t require considerations of simultaneity so Eq. (1) can be used to obtain the correct spatial relation between two frames at 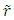 = 0. The spatial relation between two frames for any arbitrary point will be obtained in the later part. A’ would move from the origin of F to a position
= 0. The spatial relation between two frames for any arbitrary point will be obtained in the later part. A’ would move from the origin of F to a position 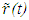 at time t according to Eq. (1) that corresponds to distance,
at time t according to Eq. (1) that corresponds to distance, 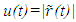 in F. An event that occurs at the position of A and is simultaneously observed by A’ at time t’ and an observer at his coincident position in F at time t must have occurred at A at time,
in F. An event that occurs at the position of A and is simultaneously observed by A’ at time t’ and an observer at his coincident position in F at time t must have occurred at A at time, 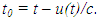 The relation between t’0 and t0 is provided by Eq. (2). The reciprocal relation to Eq. (2), to in terms of t’0 is not true at
The relation between t’0 and t0 is provided by Eq. (2). The reciprocal relation to Eq. (2), to in terms of t’0 is not true at 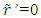 as concluded before. One can refer t’0 as the “base” time, t’B for frame F’.The event that occurred at t’0 in F’ is detected by A’ after the information propagation time or “relay” time, t’R. The distance between the position of the event and the traveller, designated as the relay distance
as concluded before. One can refer t’0 as the “base” time, t’B for frame F’.The event that occurred at t’0 in F’ is detected by A’ after the information propagation time or “relay” time, t’R. The distance between the position of the event and the traveller, designated as the relay distance 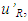 in the traveller’s frame F’ at the time t’0 of the event is
in the traveller’s frame F’ at the time t’0 of the event is 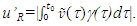 The proper time of the traveller when he observes the event would be equal to the event time t’0 plus the relay time
The proper time of the traveller when he observes the event would be equal to the event time t’0 plus the relay time 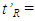
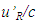 provided the traveller’s velocity is constant during the information propagation time. The non-inertial traveller may not have a constant velocity so the relay time, t’R needs to be found from the light pulse travel distance relation in two frames F and F’ as given in Eq. (3). As light pulse travels relay distance
provided the traveller’s velocity is constant during the information propagation time. The non-inertial traveller may not have a constant velocity so the relay time, t’R needs to be found from the light pulse travel distance relation in two frames F and F’ as given in Eq. (3). As light pulse travels relay distance 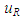 in F it travels the relay distance
in F it travels the relay distance 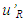 in F’. With the velocity of light being invariant, the relay time relation for two frames is obtained by dividing the relay distance relation by c. Eq. (3) provides this relation as,
in F’. With the velocity of light being invariant, the relay time relation for two frames is obtained by dividing the relay distance relation by c. Eq. (3) provides this relation as,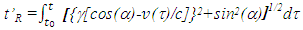 | (4) |
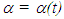 and
and 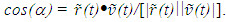 In Eq. (4)
In Eq. (4) 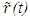 is used for the light propagation direction because light from the event has to reach A’ at its position at t. The sum of t’B and t’R is the proper time of A’ as,
is used for the light propagation direction because light from the event has to reach A’ at its position at t. The sum of t’B and t’R is the proper time of A’ as, 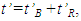
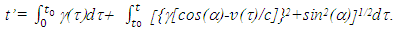 | (5) |
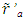 in F’ can be transformed in F with the LB matrix. The spatial coordinates of A’a in F at time t will be,
in F’ can be transformed in F with the LB matrix. The spatial coordinates of A’a in F at time t will be,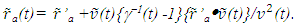 | (6) |
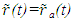
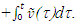 Using this new value of
Using this new value of 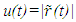 in
in 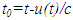 and in Eq. (5) the proper time t’ of A’a can be found. Those results provide the STR between A’a and F at time t. If the initial position of A’a is given in F as
and in Eq. (5) the proper time t’ of A’a can be found. Those results provide the STR between A’a and F at time t. If the initial position of A’a is given in F as 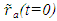 then
then 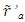 can be obtained with inverse relation using Eq. (6) with t=0.If the STR are required for an arbitrary observer Aa in F with the spatial coordinate
can be obtained with inverse relation using Eq. (6) with t=0.If the STR are required for an arbitrary observer Aa in F with the spatial coordinate 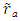 then again time independent
then again time independent 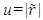 is used for t0 and in Eq. (5) for the TTR. The initial STR at the position of Aa are obtained with the LB matrix for the initial velocity
is used for t0 and in Eq. (5) for the TTR. The initial STR at the position of Aa are obtained with the LB matrix for the initial velocity 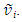 The origin of F’ in F at time t will be at
The origin of F’ in F at time t will be at 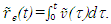 The vector
The vector 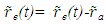 represents the position of the origin F’ in frame F from the location of Aa or
represents the position of the origin F’ in frame F from the location of Aa or 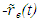 is the transformed spatial coordinate of Aa of the frame F’ at time t and velocity
is the transformed spatial coordinate of Aa of the frame F’ at time t and velocity 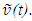 This spatial coordinate
This spatial coordinate 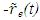 in F can be transformed to
in F can be transformed to 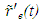 in F’ with the LB matrix or with inverse relation using Eq. (5).Eq. (5) and subsequent paragraphs that explain how to handle any arbitrary position of observers provide the STR between F and F’ at any time and position. That is essentially the KSR theory. The STR obtained with the KSR theory presented in this paper follows LT and satisfies the simultaneity condition. It provides consistent results for travel of A’ such as at constant velocity, sudden start and stop, with velocity step and round trip as described in [5].Computed plots of t’ are shown in Fig. 1 for cases: (i) round trip travel as in twin paradox (ii) velocity step, (iii) hyperbolic travel with acceleration g as described in [1] which provides
in F’ with the LB matrix or with inverse relation using Eq. (5).Eq. (5) and subsequent paragraphs that explain how to handle any arbitrary position of observers provide the STR between F and F’ at any time and position. That is essentially the KSR theory. The STR obtained with the KSR theory presented in this paper follows LT and satisfies the simultaneity condition. It provides consistent results for travel of A’ such as at constant velocity, sudden start and stop, with velocity step and round trip as described in [5].Computed plots of t’ are shown in Fig. 1 for cases: (i) round trip travel as in twin paradox (ii) velocity step, (iii) hyperbolic travel with acceleration g as described in [1] which provides 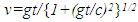 and
and 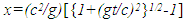 and (iv) travel with stop. Eq. (5) was used to compute the data for the plots.
and (iv) travel with stop. Eq. (5) was used to compute the data for the plots.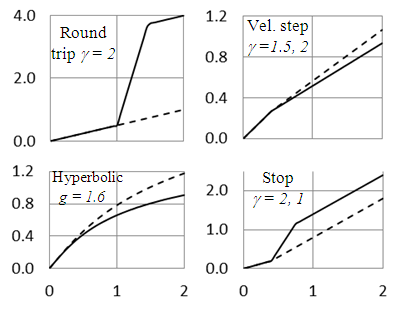 | Figure 1. Computed t’ vs. t for trajectories: round trip; velocity step; hyperbolic travel and stop after travel. Solid lines are using theory of this paper, dashed lines using earlier theories |
6. Historical Experimental Results
- Several publications dealing with experimental measurement of TTR with a high velocity round trip travel type arrangement show agreement with earlier theories [9-11]. In all those experiments, unlike in the twin paradox, a traveling observer is influenced by acceleration during most of the time. Data of those experiments are compared to data predicted by earlier KSR theories which neglect the effect of acceleration (and its associated gravity and general relativity effect). Earlier theories predict the result
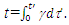 Due to prolonged acceleration in those experiments general relativity should play a significant role. A significant amount of time dilation should add into the time dilation predicted by earlier theories because of the gravitational equivalent of acceleration. Hence the measured time dilation should be much larger than reported. The KSR theory presented here predicts time contraction for round trip trajectory. This is opposite to the time dilation that would arise from the general relativity theory as the equivalent gravitational effect of acceleration. The observed data would agree with the present theory if the time dilation due to prolonged acceleration was larger in magnitude (and possibly twice) than the time contraction. Wang in [4] and Millette in [12] separately elaborate on those experimental results and express doubt on their accuracy. In the case of muon which is trapped in a circular orbit [10], can muon be considered as inertial traveller like the weightlessness of a circling astronaut while the CERN setup considered non-inertial? In that case the observed result would agree with the KSR theory presented here. In any event, if the experimental data and earlier theories are correct then the anomalies pointed out in this paper need to be resolved.
Due to prolonged acceleration in those experiments general relativity should play a significant role. A significant amount of time dilation should add into the time dilation predicted by earlier theories because of the gravitational equivalent of acceleration. Hence the measured time dilation should be much larger than reported. The KSR theory presented here predicts time contraction for round trip trajectory. This is opposite to the time dilation that would arise from the general relativity theory as the equivalent gravitational effect of acceleration. The observed data would agree with the present theory if the time dilation due to prolonged acceleration was larger in magnitude (and possibly twice) than the time contraction. Wang in [4] and Millette in [12] separately elaborate on those experimental results and express doubt on their accuracy. In the case of muon which is trapped in a circular orbit [10], can muon be considered as inertial traveller like the weightlessness of a circling astronaut while the CERN setup considered non-inertial? In that case the observed result would agree with the KSR theory presented here. In any event, if the experimental data and earlier theories are correct then the anomalies pointed out in this paper need to be resolved.7. Conclusions
- An appropriate KSR theory involving non-inertial frames requires stationary frames as the reference frame with consideration of the information propagation time and its relation between two frames and simultaneity. The KSR theory developed here provides consistent results for a variety of trajectories and is like generalized LT for inertial as well as non-inertial frames.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML