Witold Nawrot
NW TECH LTD, Łódź 91-155, Aleksandrowska, Poland
Correspondence to: Witold Nawrot, NW TECH LTD, Łódź 91-155, Aleksandrowska, Poland.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
According to the thesis presented here, the correct model of reality should be based on two major discoveries of the 20th century: Einstein's discovery that reality is four-dimensional (1905) and de Broglie's wave structure of matter (1924). In 1905, Einstein did not have all the information necessary to construct the proper model of relativity; therefore, by publishing the Theory of Relativity without knowledge of the wave structure of matter, he made a kind of a false start, which resulted in the excessive complexity and unintuitive nature of the Theory of Relativity. Including the wave nature of matter in the basic assumptions of the model of reality allows to greatly simplify the model, expand its capabilities compared to the model currently in force, and remove many problems specific to the Theory of Relativity. In this work, using the trivial example of waves on the surface of water, I derive relativistic relationships and give an unambiguous and precise interpretation of basic concepts like time, space, relativity of motion, and simultaneity of events. The new definition of time- and space dimensions also allows to define the proper time of particles directly as the number of de Broglie’s wave periods for both relativistic physics and Quantum Mechanics.
Keywords:
Euclidean reality, Absolute reference system, Relative and absolute motion, Time- and space dimensions, Absolute time, Proper time
Cite this paper: Witold Nawrot, Theory of Relativity – Biggest Mistake of the 20th Century?, International Journal of Theoretical and Mathematical Physics, Vol. 11 No. 1, 2021, pp. 1-14. doi: 10.5923/j.ijtmp.20211101.01.
1. Introduction – A Bit of History
Any attempt to challenge Einstein's Theory of Relativity is practically a scientific suicide. It entails criticizing a theory put forth by an undisputed authority, a theory which has repeatedly been tested experimentally, which has been the basis of numerous inventions, from nuclear reactors to the GPS systems; the theory that predicted the existence of black holes, explained the phenomenon of gravity, and achieved many other spectacular successes. To put it bluntly, is it even possible to find any fault there?I wanted to demonstrate that, despite its unquestionable success, the Theory of Relativity may have, in its underlying structure, errors typical of new theories built with the assumption that it is sufficient to classify observed physical phenomena and then describe them mathematically. This approach usually works well, but sometimes you need to look at phenomena from a greater distance and with more imagination. It turns out that in some cases the description should be supplemented by a model of a new structure of reality, in which processes take place, which we are not able to observe and which indirectly manifest themselves in our reality in the form of observable physical phenomena. In my opinion, this is precisely the case with the Theory of Relativity. The phenomena described by TR may be the result of other, simpler phenomena, which in turn result from a different structure of reality than the one we observe and imagine from our direct observations.To justify the above thesis, let us go back to the times immediately preceding the emergence of the Theory of Relativity. It all started in the middle of the 19th century, when J.C.Maxwell formulated his equations which, in fact, turned out to be the first relativistic equations. The equations showed that electromagnetic waves move in space at a constant speed, independent of the speed of the observer’s system. At that time, the space thought to be filled with Ether, where electromagnetic waves propagated. At the end of the 19th century, in order to link the motion of waves and bodies in the medium with the observed constant speed of EM waves, G.F. Fitzgerald brought up the concept of the length contraction of objects in motion relative to Ether, which H.A.Lorentz then expanded by proposing the rules for the transformation of coordinate systems in motion relative to the Ether, known as the Lorentz transformation. At the same time, it turned out that under certain conditions, electromagnetic waves behave like particles that can be thought of as quanta of energy. The introduction of the concept of quantum allowed to treat both electromagnetic waves and particles in the same way. In 1905, Einstein rejected the hypothesis of the motion relative to Ether - because particles do not require any such medium for their existence - and consequently introduced the principle of relativity of motion. Particles would therefore move in empty space, and the motion of these particles, due to the absence of a medium, could only be considered as relative motion. To justify the constant velocity of some particles - quanta - relative to the others, Einstein adopted in Relativity the Lorentz transformation in its 19th-century form, developed with the existence of Ether in mind. The Theory of Relativity was subsequently supplemented by Minkowski with the concept of Minkowski's spacetime, which has since become the model of physical reality. The creation of TR turned out to be a great successes, and when in the mid-1920s de Broglie introduced the concept of the wave structure of matter, complementing Einstein’s concept (concerning the relative motion of particles) with the wave properties of particles seemed only natural.
2. First Doubts
This is where problems begin. The concept of particles and their motion does not require the existence of any medium and the motion of all bodies can exclusively be considered a relative motion. Meanwhile, waves require such a medium. Reconciling these two conflicting concepts with Quantum Mechanics required various mathematical tricks, which further muddled the already complicated and unintuitive theory of the structure of reality. However, at the time of de Broglie's publication of the concept of the wave structure of matter, the concept of reality as space filled with particles which were moving with relative motion was so ubiquitous that the idea of revising the concept of motion, to describe motion not as motion of particles with abstract wave properties but directly as motion of waves, likely did not enter anyone's head. Meanwhile, descriptions of these two motions are completely different and this, in turn, has important consequences for the description of physical phenomena. In my opinion, the correct theory of the construction of the Universe should be based on two discoveries of the 20th century: Einstein's discovery that reality is four-dimensional, and de Broglie's discovery of the wave nature of matter. Einstein, however, built the Theory of Relativity, without the knowledge of de Broglie's discovery, treating bodies as points that do not require any medium to exist. Treating bodies as waves, which became possible around 20 years after the publication of TR, allows us to combine the relativity of motion with the existence of a medium that is the carrier of these waves – which was impossible in the Theory of Relativity, describing bodies as projectiles moving in the empty space. I believe that Einstein, by adopting a definition of motion specific to discrete bodies that do not have wave properties and announcing the principle of the relativity of motion, made a kind of false start – an error that led to the excessive complexity of the model of reality and limited its capabilities. If Einstein had waited with the formulation of his theory until de Broglie’s discovery, he could have derived the principle of the relativity of motion directly from the analysis of the wave motion, while keeping the absolute medium in which these waves propagate. However, the premature publication of the principle of the relativity of motion and its high popularity have led to almost 100 years of attempts to reconcile Einstein's philosophy of discrete bodies with the wave properties of bodies. Meanwhile, after de Broglie's discovery, the description of reality should have been reworked based on both Einstein's discovery that reality is four-dimensional and on the concept of bodies as waves in this four-dimensional reality. And in this paper, I propose to finally do what, in my opinion, should have been done a hundred years ago – as soon as the wave structure of matter was discovered.
3. Motion from the Point of View of the Wave
Let us consider what reality looks like from the point of view of a particle treated as a wave, i.e. a disturbance of the medium. Let me start with an example: the motion of waves on the water. The example is trivial, however, due to the need to redefine basic and intuitive ideas such as time or space it should present the new approach in the simple, unambiguous and comprehensible way.To consider the motion of waves on water, let us imagine a water plane described by two space dimensions and time T, which in this case is not a dimension but a parameter in relation to which a sequence of events is determined. We will assume that all waves move at the same speed V relative to water, which constitutes here an absolute reference system (the absolute reference system in this case can be defined, for example, as a system in which the average velocity of water molecules is zero). In addition, let us imagine that on their way, the waves come across two poles set at a distance equal to "D" from one another. This situation is shown in Figure 1. Because, as we will see, the dimensions interpreted by the waves as the dimensions of time and space (here: x,t) will depend on the manner in which the waves observe their environment, the dimensions determining the surface of the water are going to be marked as a1 and a2 (Fig. 1). In addition, if we assume that the wave constitutes a model of a particle, we should also assume that the amplitude of the wave in the middle of this wave is the largest and then decreases as a function of distance from the center.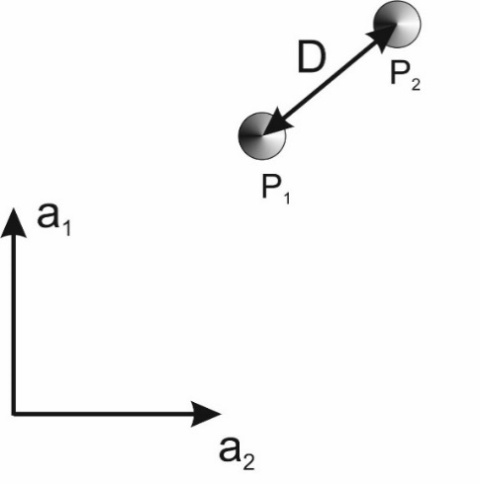 | Figure 1. The surface of the water is described by coordinate system a1,a2. In the water there are two poles P1 and P2 at a distance D from one another. Time T is not an additional dimension here but is a parameter against which a sequence of events is determined |
To begin with, consider a wave moving at a constant speed relative to the medium described by the coordinate system "ai" along the line connecting the two poles. In this case, the wave will hit the first pole P1 in time T1 and then on the second pole P2 in time T2 (Fig. 2). The wave will register both strikes in the same place relative to the center of the wave, but at different times. Since the wave moves at a constant speed, it can be assumed that for the wave the measure of time is going to be the length of the path traveled along the direction in which the wave propagates. Thus, the hitting of poles occurs in the wave's reference system at a time equal to the distance between the poles, i.e. D, where D is associated with the "real" time T by the dependency: D=V(T2-T1). 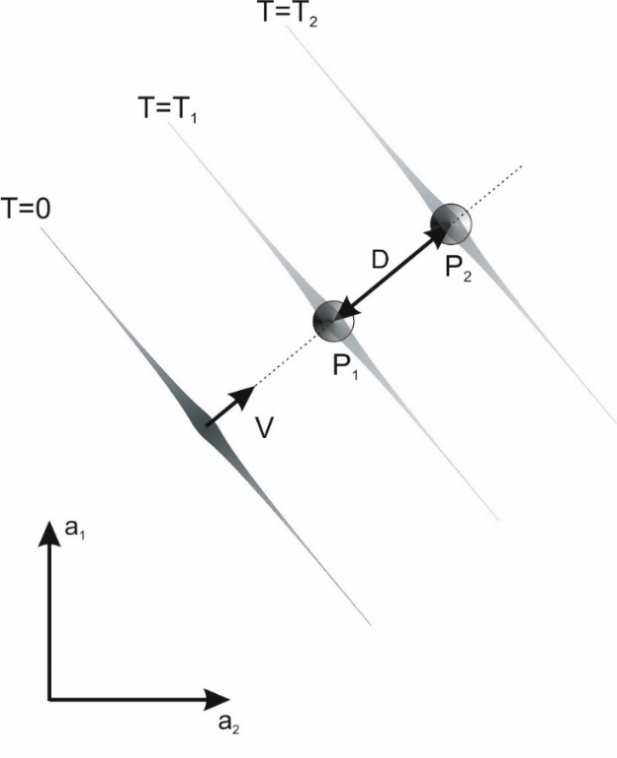 | Figure 2. The wave moves along the direction of the line connecting the two poles. The wave records the pole impacts in the same place but at different times. The distance between the poles is interpreted by the wave as the time distance Δt=D=V(T2-T1) |
The direction along which the wave propagates is interpreted by this wave as the time dimension "t" and is associated with the time T as follows: t=VT. As a result, the wave interprets the distance D between the poles as the time distance Δt=D. Now let's take a wave moving in a direction perpendicular to the line connecting the two poles (Fig. 3).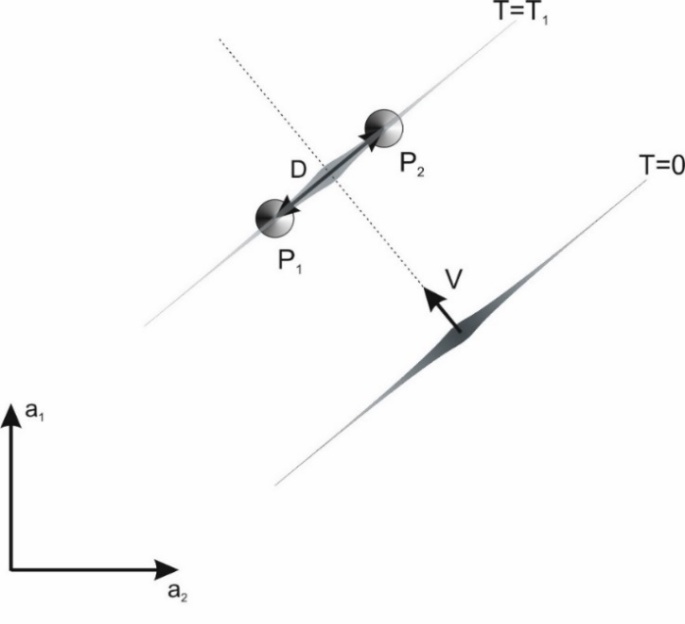 | Figure 3. The wave moves in a direction perpendicular to the direction of the line joining the two poles P1 and P2 and strikes both poles at the same time. In this case, the distance between the poles, from the point of view of the wave, is the space distance measured along the ridge of the wave: Δx=D |
In this case, the wave hits both poles at the same time equal to T1, but it detects the two impacts in different places along its ridge. From the point of view of the wave, both strikes are simultaneous. In this case, events – i.e. wave impacts on poles – now correspond to space distance Δx=D. According to these examples, a propagating wave, encountering various obstacles, interprets the distances between events along the direction of the wave's propagation as time distances, and distances along the ridge of the wave as space distances. Thus, the wave interprets the water surface described by coordinates a1,a2 as a two-dimensional spacetime x,t where dimension x is the direction measured along the ridge of the wave, while the time dimension is measured along the direction of the wave’s propagation. Thus, the coordinates of events such as the wave hitting the poles, in the wave's reference system, have the spacetime coordinates dependent on the direction of wave propagation on the water surface. Since the time- and space dimensions in the wave's reference system are in practice different directions on a plane made up of dimensions a1 and a2 whose properties are identical, then in practice the dimensions x,t must have similar properties from the point of view of the wave.Thus, it can be seen that depending on the direction of motion, the wave interprets the same distance on the water surface – here the distance between the poles equal to D – either as a time distance or as a space distance.Because the time measured by the wave in its reference system is equal to the distance that the wave travels along its direction of motion, the speed of the wave’s motion in the water in the wave's reference system should be equal to one. However, if time and distance are measured in different units in the wave’s system, the wave will record a speed not equal to one but to a factor determining the scale of these units relative to each other. In this case, the speed will be indicated as "c" but, rather than the actual speed of the wave, it is only the scale factor between the time- and space dimension in the coordinate system associated with the wave. In conclusion: The wave perceives the surface of the water as a two-dimensional spacetime. This means that from the point of view of the wave, the surface of the water is one-dimensional, while the condition of the motion of the wave with a constant speed along the direction of its propagation leads to the second direction on the surface of the water being perceived by the wave as a dimension of time (Fig. 4). Fig. 4 shows what the space and time distances between the wave’s impacts on the poles will look like from the point of view of the wave, for the wave propagating in any direction.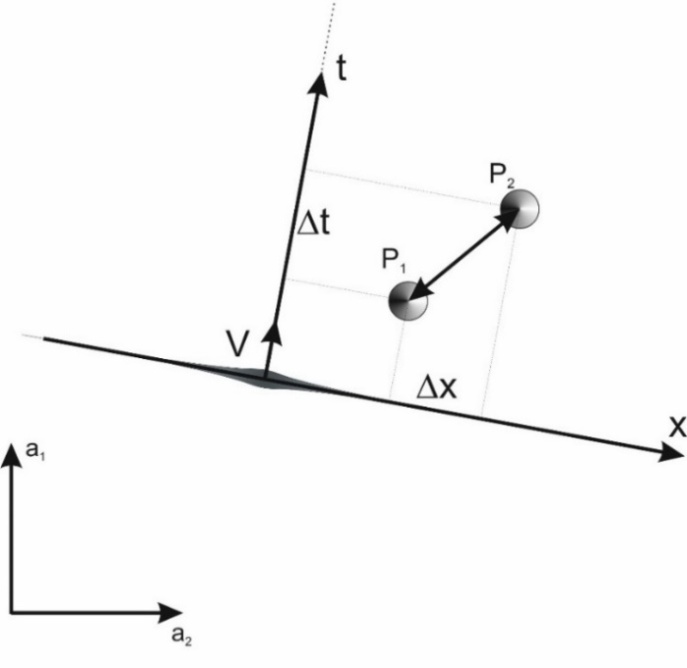 | Figure 4. The wave treats the distances between the poles measured along the direction of its propagation as the time distances "Δt" and the distances measured along its ridge as space distances "Δx". Thus, the wave perceives the two-dimensional surface of the water as a two-dimensional spacetime consisting of one time dimension "t" and one space dimension "x" |
The wave knows nothing about the surrounding reality. All information comes from interactions with ambient elements and waves.As shown above, the direct interaction of waves with fixed elements on the surface of the water causes the wave to perceive its direction of motion as a dimension of time and the direction along its ridge as a space dimension. The existence of the surrounding reality is perceived by the wave through interaction with the surrounding objects. The above example of interactions, although seemingly obvious, is purely theoretical, as it does not include interactions with other waves. Meanwhile, in the real world, it is the interactions with the bodies/waves around us that give us an idea of distances, motion, or the flow of time. Thus, the way in which information is exchanged will have a significant impact on our perception of reality.
4. Interaction between Waves
Since the path travelled by the wave on the surface of water is the measure of the flow of time in the wave’s reference system, for further consideration we will assume that the wave’s speed relative to the medium measured in the wave reference system is equal to one. We assume that waves transmit interactions along their ridges, and these interactions spread along the ridges of the waves also at a speed equal to 1 (Fig. 5).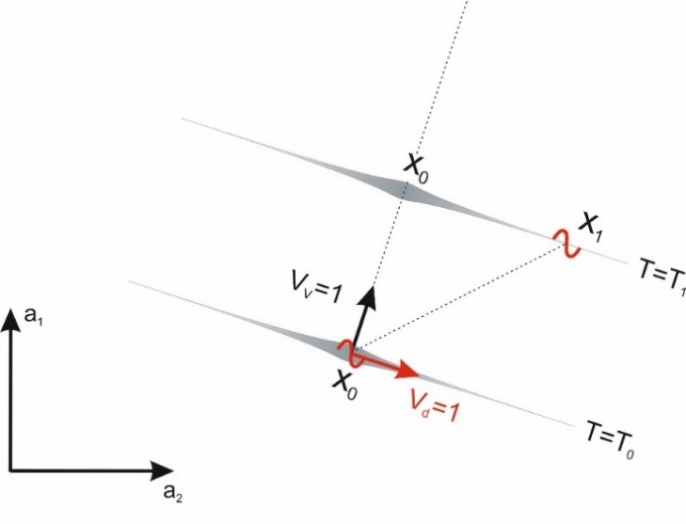 | Figure 5. The wave moves along its direction of propagation at a velocity Vv=1. At the same time, the disturbance moves along the ridge of the wave at the velocity Vd=1. Thus, in time Δt=T1-T0 the disturbance travels along the ridge of the wave the path Δx= x1-x2 equal to the difference in time distance Δt |
The exchange of information between the waves relies on transmitting the disturbance from the ridge of the signal-sending wave, marked here as the S-wave, to the ridge of the receiving wave, marked as the R wave. Because disturbances move along the ridges of waves at the same speed as the waves moving relative to the medium, the path traveled by the disturbance along the direction of propagation of the wave (interpreted as time dimension) is equal to the path of the disturbance along the ridge of the waves (interpreted as a space dimension). This occurs both for the sending wave and for the receiving wave, so that the sum of the distances traveled by disturbances along the direction of motion of both waves interpreted as the time flow, is always equal to the path traveled by the disturbance along the ridges of the waves, interpreted by these waves as space dimensions (Fig. 6). Regardless of the angle at which the two waves move relative to each other, and regardless of the point at which the disturbance passes from the ridge of the first wave to the ridge of the second wave, both of these distances are identical. Thus, from the point of view of waves, the propagation velocity of the interactions described in Figure 6 is always constant and is equal to one – this is shown in Figure 6.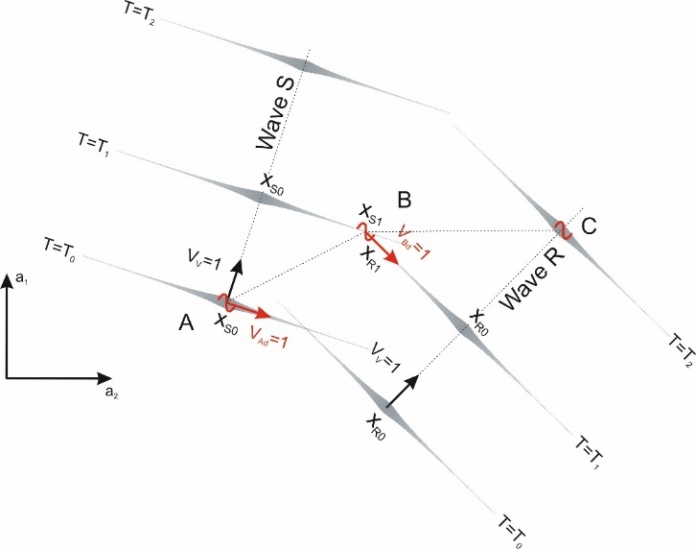 | Figure 6. Principle of transmitting interactions between waves. Wave S sends a signal from point A. The signal propagates along the direction of motion of wave S at velocity Vv=1 and at the same time along the ridge of wave S also at velocity Vad=1. At point B the signal is transmitted to the wave R receiving the signal. Now the signal travels along the ridge of wave R at velocity Vbd=1 and along the direction of motion of wave R at velocity Vv=1. The signal reaches the center of the R wave at point C. The signal travels the distance T1-T0 along the direction of propagation of wave S and then the distance T2-T1 along the propagation direction of the wave R; this distance is interpreted by the waves as a measure of time. At the same time, the signal travels the route xS1- xS0 along the ridge of the wave S and then xR0-xR1 along the ridge of the wave R; this path is interpreted by the waves as a path along space directions. Both of these paths are equal, so the velocity of transmission of interactions defined as 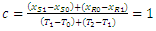 is always constant and equal to one is always constant and equal to one |
When transmitting information in the manner described above, each wave that sends and receives a signal interprets its own direction of motion as a time dimension and the direction along its ridge as a space dimension. These directions are different for different waves, so when transmitting the signal, each wave (sender and receiver) interprets different directions on the surface of the water as space dimensions and as time dimensions. So which direction on the surface of the water will the wave receiving the signal ultimately interpret as the time dimension and what direction as a space dimension during such observation?The observer is unable to observe the trajectory of the signal - they only know the point of sending the signal A (Fig. 6,7), the point of reception of the signal C, they interpret their direction of motion as a time axis "t", and know that the speed of propagation of the signal is constant and is equal to 1. Point B, where the signal passes from the ridge of one wave to the ridge of the other, is unavailable to the observer. Thus, the direction interpreted by the observer (the wave R) as a space axis must be so chosen that the signal propagation speed measured by the observer is also equal to 1; that is, that the space distance measured at the time of sending the signal, equal to Δx, is equal to the time distance between sending the signal and its reception - Δt (Fig. 7).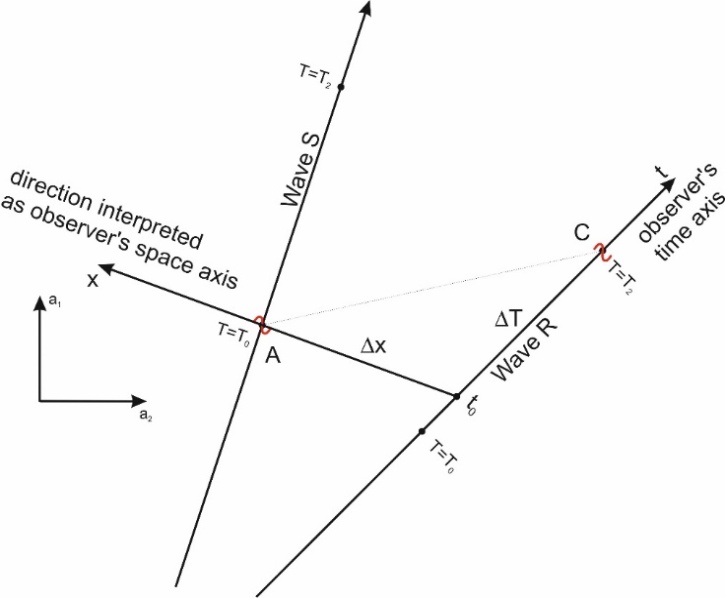 | Figure 7. The observer, body/wave S, knows only the place of signal emission (point A), the place of reception of the signal (point C), and knows that the propagation speed of the signal is equal to one. However, the observer is unable to determine the signal’s trajectory. Thus, the direction interpreted by the observer as a space dimension when observing the body/wave S must be chosen in such a way that the following condition is met: 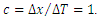 In the coordinate system bound with the surface of water, the emission of signal took place in time T=T0, like in Fig 6; however, the observer is convinced that the emission took place at time t0 on its time axis In the coordinate system bound with the surface of water, the emission of signal took place in time T=T0, like in Fig 6; however, the observer is convinced that the emission took place at time t0 on its time axis |
As we can see, in general, the direction interpreted as a space coordinate does not have to coincide with the ridge of any of the waves.Knowing that wave trajectory lengths correspond to the elapsed times in their reference systems, and knowing the direction interpreted as a space dimension, we should immediately obtain the relationship between these values from the simple geometric relationships between these coordinates shown in Figure 8. These relationships should be obtainable directly from the relationship between the sides of the triangle formed by the time axes of both waves and the direction interpreted by the observer as a space dimension – triangle ABC in Figure 8. However, it turns out that due to the different values of the angles between the axes of the coordinate systems of both waves (angles α, β, γ - Fig. 8), resulting from the freedom to choose the directions of wave propagation and from the various possible locations of point B where the disturbance passes from the ridge of the wave sending the signal to the ridge of the receiving wave, these relationships are quite complex and do not resemble any known relationships.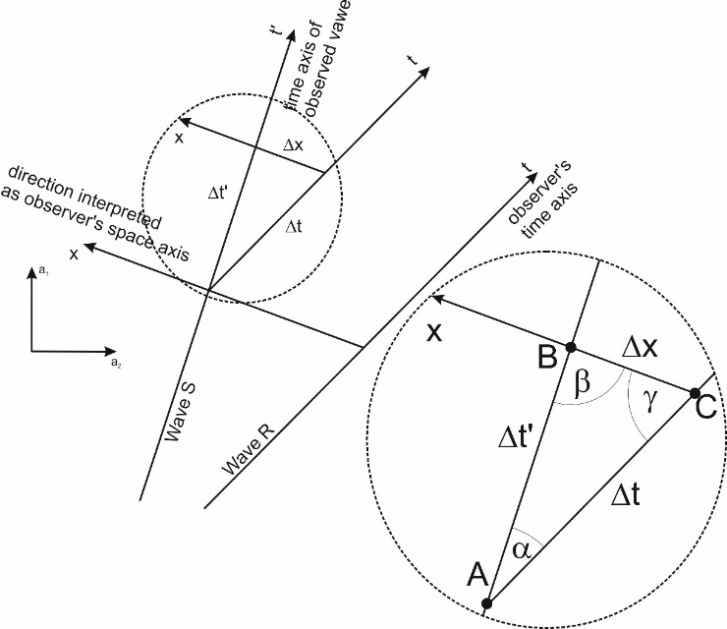 | Figure 8. The ABC triangle, formed by the values of the elapsed times in the systems of the observer body/wave and the observed body/wave, as well as the distance ∆x, observed by the observer wave/particle, determines the relationship between the time elapsing in the systems of both bodies/waves as a function of velocity defined by the relationship 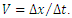 Due to the variability of the angles of this triangle (resulting from the angle between directions of propagation of the waves and/or the location of the point of transmission of the signal from the ridge of the sender wave to the ridge of the receiver wave– point B in Fig. 6), it is not possible to determine an unambiguous relationship between the times Due to the variability of the angles of this triangle (resulting from the angle between directions of propagation of the waves and/or the location of the point of transmission of the signal from the ridge of the sender wave to the ridge of the receiver wave– point B in Fig. 6), it is not possible to determine an unambiguous relationship between the times 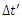 and and 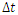 , and the relative velocity V , and the relative velocity V |
However, the ABC triangle on Figure 8 has one interesting feature. In one specific case, when the angle β = 90°, we see the following dependencies:The relative velocity of the waves is 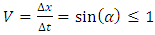 | (1) |
While the relationship between the paths traveled by the waves – which, in the coordinate systems of these waves, are the measure of their proper times – is as follows: 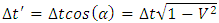 | (2) |
As you can see, these dependencies are identical to relativistic dependencies describing the time dilation in the system in motion, for the value of light speed c=1. In addition, let us note that in the definition of relative wave speed there is a built-in speed limit to a value equal to 1, i.e., in this case, to the speed of light. Thus, for angle β with the value of 90°, the described waves on the water observing each other by interactions transmitted along their ridges at a speed equal to 1 record the relativistic effects described by the Theory of Relativity. To sum up, for this case, we get:1. Effects described by the Theory of Relativitya. Constancy of the speed of the propagation of interactions, here equal to c=1 (Fig. 7).b. The relativity of motion resulting from defining relative speed as the sine of the angle between the directions of propagation of waves (1). Due to the lack of distinguished direction on the surface of the water, the relative velocity of the waves can only be determined relative to the direction of another wave.c. Relative speed limit V<=1 resulting from the definition of speed (1). This is only a limitation due to the manner of performing observation and does not exclude the motion of waves in all directions at angles of 0-360°.d. Observed time dilation in the wave system which moves in relation to the observer wave (2). 2. Effects not described by the Theory of Relativity a. Absolute reference system bound with medium (here – water).b. The motion of waves with absolute and constant speed relative to the absolute reference system (here – water).Using the example of waves propagating on water, we obtained relativistic relationships identical to those described in the Theory of Relativity. However, obtaining these dependencies requires that the angle condition β = 90° in triangle ABC in Figure 8 be met. What does this condition mean in practice?It appears that, in the case of the two-dimensional surface of the water, this condition is met for waves whose directions had a common origin and the waves at that point met or were simultaneously generated at the time T0 (Fig. 9). The analytical proof for this is presented in point 9 of the Appendix.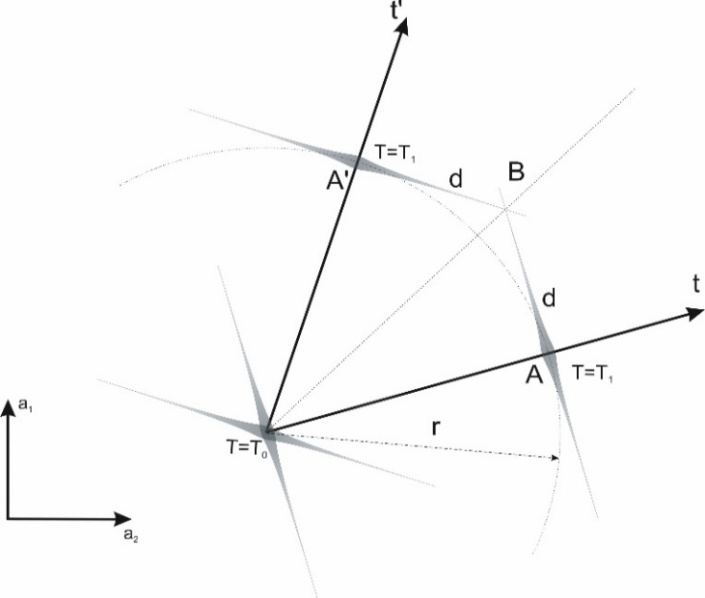 | Figure 9. Two waves that meet at one point (a10,a20) at the same time T0 are simultaneous waves. During the motion, simultaneous waves are at the same distance from the meeting point – on the circle with the radius r with the center at the meeting point/generation point of both waves. The distances “d” between the center of waves and the point of intersection of the ridges of waves ( B), measured along the ridges, are in this case identical even in a space with more than two dimensions |
Such waves can be called simultaneous waves. Note that the feature of such simultaneous waves shown in Figure 9 is that both waves maintain the same distance from the meeting point/wave generation throughout their motion. For spaces with more dimensions, you may not be able to find such a point. In this case, the condition for simultaneity will be the existence of an intersection line of the ridges of waves, at which the distances from the point of intersection of the ridges - B - to the center of the wave (marked in the figure with the letter d), measured along the ridge of the wave, are identical for both of these waves throughout their motion.An example of non-simultaneous waves is shown in Figure 6. In this case, the distances from the intersection of the ridges of the waves to their trajectories measured along the ridges of those waves are different, which corresponds to the fact that both waves appeared at the intersection of the trajectory at different times T. In the case of simultaneous waves, the direction interpreted as a space dimension during the observation of a wave coincides with the ridge of the observed wave (Fig. 10).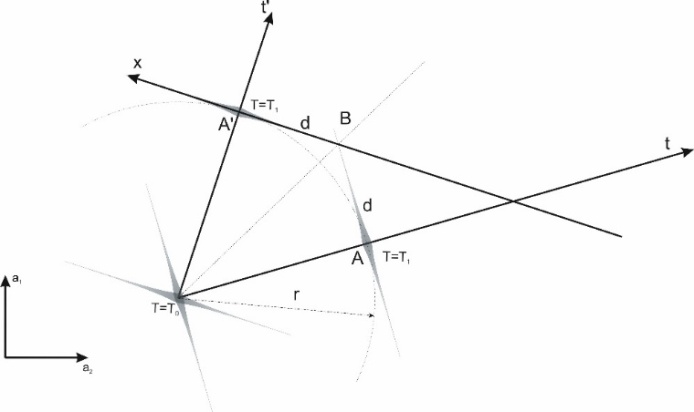 | Figure 10. In the case of simultaneous waves on a plane, the concept of simultaneity refers to the waves in the circle with the center at the intersection of the lines determining the direction of motions of the midpoints of those waves. For waves in the figure, these are points A, A'. Such simultaneity will be called absolute simultaneity. Meanwhile, an observer/wave moving along the trajectory "t" during the observation of a body/wave moving along a trajectory t' interprets the events lying on its space axis "x" as simultaneous events. This simultaneity will be called relative simultaneity |
Note that from the point of view of the observer wave, simultaneous events are events lying on the x-axis of the coordinate system, while from the point of view of the absolute coordinate system, simultaneous events correspond to points A and A' on the trajectories of motion of both waves. This difference in the interpretation of simultaneity – one interpretation for the absolute coordinate system “ai”, and another from the point of view of the wave/observer – is precisely the source of the observed time dilation in the reference system of the observed wave, even though in the case of both waves, the lengths of their trajectories are in practice a measure of the absolute time T, identical for both waves. To distinguish the concept of simultaneity that we are used to from the one described here, we will call the simultaneity of waves the absolute simultaneity.Is the condition of absolute simultaneity met in the case of our four-dimensional spacetime? According to the Big Bang hypothesis, all existing particles in the Universe move along trajectories with a common origin, which is the location of the Big Bang. Thus, in the initial period, all of the resulting particles were absolutely simultaneous. Of course, over time, during the formation of particles and relative motions, the condition of absolute simultaneity may have been disrupted. This should manifest itself as the appearance of deviations from the relativistic relationships we know. However, the observed relativistic relationships suggest that in the vast majority of cases, the principle of absolute simultaneity is maintained. If this is the case, it can be also said that the very existence of relativistic dependencies in their current form constitutes proof for the Big Bang hypothesis.As I wrote earlier and as shown by the definition of speed (1), observation with the help of quanta can only be carried out for particles/waves moving along trajectories inclined to the observer's trajectory at an angle of less than 90°.At an angle of 90°, the direction of propagation of the disturbance along the ridge of the signal-sending wave is parallel to the direction of motion of the wave which could receive that signal. However, because both of these speeds are identical and the directions are parallel, it is not possible to transmit the signal from one wave to another. The signal simply cannot catch up with this running away wave. In addition, it is easy to notice that for angles larger than 90°, this effect increases. Thus, although waves can propagate in any direction, waves are only able to observe those waves that move relative to them at an angle of less than 90° (Fig. 11).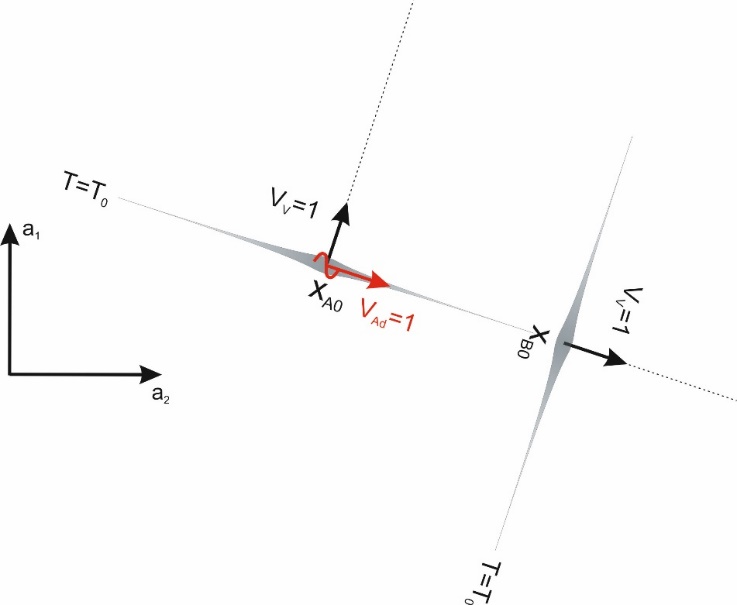 | Figure 11. A wave at point xA0 moving along its direction at velocity Vv=1 sends a signal which moves perpendicularly to its direction of motion – along the ridge of the wave – at velocity VAd=1. The wave at point xB0 moves along a trajectory perpendicular to the signal-sending wave also at velocity Vv=1. The velocity of the wave which is to receive the signal and the velocity of the signal are pointed in the same direction and are equal to each other, so the signal will never catch up with the wave that should receive this signal |
The example of waves on the water shows how waves interpret the environment and how they exchange interactions. If the two-dimensional spacetime described in the example above is the result of existence of a two-dimensional Euclidean plane and a time T treated as a parameter, the four-dimensional spacetime will be the result of existence of the four-dimensional Euclidean space and the time T also treated as a parameter. The ridge of the wave, which in our examples was a straight line, will be a three-dimensional hyperplane moving at a constant speed equal to one - V=1 - along the fourth direction perpendicular to this hyperplane. A description of such a structure of reality, which can be the basis for further development of the problems of Special and Genaral Relativity, is presented in the Appendix, while other conclusions, formulas, etc. in the field of Relativity and Quantum Mechanics have been published in [1].
5. Summary
To sum up the considerations so far, we can conclude that when observing reality from the point of view of waves, the directions interpreted by waves as time- and space directions are not constant, but depend on two factors – on the currently observed wave and on how the interactions are exchanged.Regardless of how you observe it, the wave/observer interprets its trajectory in E4 as the time axis of its coordinate system.Directions that the observer interprets as space dimensions can be divided into three groups:1. Observation via exchange of interactions for absolutely simultaneous eventsIn everyday observations, i.e. when observing reality by quantum exchange and for absolutely simultaneous waves, the observer interprets three directions perpendicular to the direction of the trajectory of the observed wave as space dimensions. For each observed wave, these are theoretically different directions. We compose the image of reality of observing individual waves along directions interpreted as space dimensions, just as we compose an image on a computer monitor of individual pixel flashes on the screen. In most cases, in our non-relativistic environment, all such directions of non-relativistic bodies practically overlap. However, the observer observes relativistic objects along different directions (interpreted as space dimensions) than the other, non-relativistic bodies. The observer is not able to directly record the fact that waves/relativistic bodies are observed along other directions in E4. This unobservable difference in directions interpreted as space dimensions is revealed to the observer in the form of relativistic effects (Fig. 12).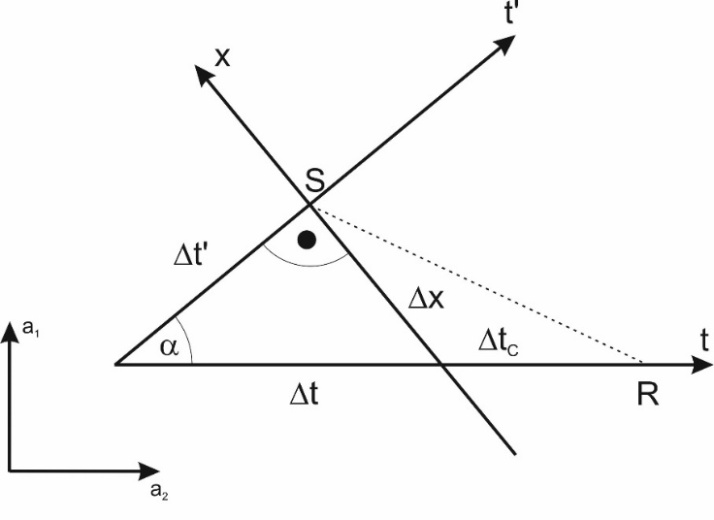 | Figure 12. Interpretation of directions in the Euclidean plane E2 as spacetime dimensions for absolutely simultaneous waves. The directions interpreted by both waves as time dimensions are the directions of their motion on plane E2, while the direction interpreted by the observer wave as a space dimension is perpendicular to the direction of propagation of the currently observed wave. The following dependencies are maintained here: a. Constancy of light speed equal to 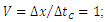 b. The values Δt' and Δt meet the relativistic dependencies that are a function of speed b. The values Δt' and Δt meet the relativistic dependencies that are a function of speed 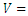 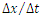 |
2. Observation via exchange of interactions for absolutely non-simultaneous eventsSuch observation works similarly to the observation described in the previous point, except that the directions interpreted as space dimensions are not perpendicular to the trajectory of the observed bodies. In this case, the observer should record other relativistic dependencies than those resulting from observations for absolutely simultaneous phenomena. With relatively small deviations from the principle of the absolute simultaneity, this effect is likely to be imperceptible; however, if such discrepancies exist, they should most likely be detectable during astronomical observations. An example of observations for absolutely non-simultaneous bodies/waves (Figure 13) was previously shown in Figure 6, 7, 8.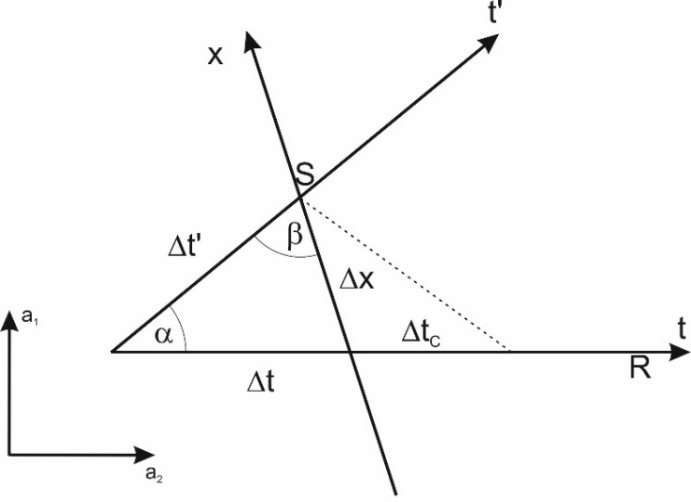 | Figure 13. Interpretation of directions in the Euclidean plane E2 interpreted as spacetime dimensions for the case of absolutely non-simultaneous waves. The directions interpreted by both waves as time dimensions are still the directions of their motion on the E2 plane, while the direction interpreted by the observer-wave as a space dimension is no longer perpendicular to the direction of propagation of the observed wave. In this case: a. The constancy of light speed is maintained and equal to 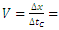 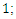 b. Due to the absence of perpendicularity of the direction interpreted as a space dimension to the direction of propagation of the observed wave, the values Δt' and Δt no longer meet relativistic dependencies, consistent with the Theory of Relativity, which are a function of speed b. Due to the absence of perpendicularity of the direction interpreted as a space dimension to the direction of propagation of the observed wave, the values Δt' and Δt no longer meet relativistic dependencies, consistent with the Theory of Relativity, which are a function of speed 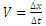 |
3. Observation by direct interaction (interference)This is the case described in the analysis of wave impacts on poles standing in the water. In practice, these are particle interactions in which information is not transmitted using quanta. This applies in the cases described by Quantum Mechanics and in cases of interactions with waves that move along trajectories for which observation is not possible, i.e. those inclined at an angle of >=90° to the observer's trajectory. In such cases, three directions perpendicular to the observer's trajectory are interpreted as space dimensions (Fig. 14).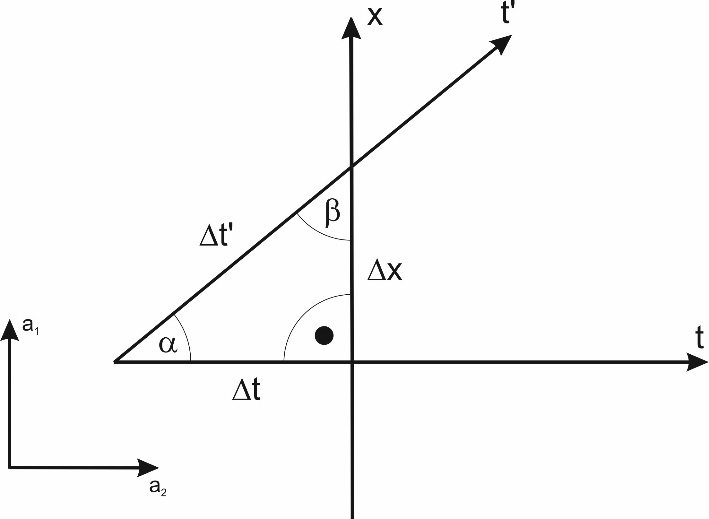 | Figure 14. Direct interaction (interference) of particles/waves (without signal exchange). In this case, the direction interpreted as a space dimension is perpendicular to the direction of propagation of the wave-observer – it is an inverse phenomenon to the case of observations via signal exchange. The relationship between the times is also the inverse of the relationship between the times for observations by means of signal exchange presented in Fig.12. Here, the time elapsing in the reference frame of the wave in motion is longer than the time in the observer wave’s system. In this case, when defining the particle's proper time as the number of de Broglie’s wave periods [1], we will observe an increase in the frequency of the wave/particle in motion which corresponds to the increase in the energy of the particle defined as 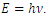 A detailed description of this situation is given in [1] A detailed description of this situation is given in [1] |
As we can see, there is a fundamental difference between the assumptions of the Theory of Relativity and the model presented here. In the Theory of Relativity, time and space were the dimensions that make up reality. Regardless of the type of interaction – whether it was interactions at the macroscopic level via quanta exchange or at the microscopic level described by Quantum Mechanics, time- and space dimensions have always been subject to the same rules.According to the new approach, the dimensions of time and space that we observe are not dimensions that create reality, but only directions interpreted by us as time- and space dimensions. However, these directions are not constant, but depend on two different factors: on the body currently being observed and on the manner of performing observation. Different interpretations of space dimensions for two different approaches to observation in Quantum Mechanics and macroscopic physics allow you to define the particle's proper time directly as the number of de Broglie wave periods of a particular particle while maintaining both relativistic dependencies for macroscopic physics and the ability to describe particle energy by the formula 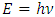 [1]. As a result, both relativistic and quantum phenomena now belong to the same model of reality, which is described in detail in [1]. In turn, the wave equation in E4, when transformed to a Minkowski spacetime coordinate system, takes the form of a wave function which is the solution to the Schrodinger equation. Thanks to the new approach, many other issues of Quantum Mechanics also become simple and understandable and easy to derive, such as the Heisenberg's principle of uncertainty or the reason for the probability of a specific reaction, which is no longer some mysterious property of particles but a simple consequence of the structure of a wave observed by us as a particle [1].Another difference between the Theory of Relativity and the approach proposed here is the definition of motion. According to the Theory of Relativity, the motion of all bodies can only be determined relative to other bodies, and this applies to inertial and non-inertial motions. This was a source of problems, for example, with the Mach principle. In the approach proposed here, the motion of waves relative to the medium is an absolute motion, while the motion of waves relative to each other is the result of the propagation of waves in this medium at different angles. Thus, the relative speed of the waves has nothing to do with the speed of the waves relative to the medium, because the relative speed is only a function of the angle between the wave propagation directions. The absence of a distinguished direction in E4 means that the angle of the trajectory of the selected wave (i.e. speed) can only be determined relative to the trajectory of another wave, that is, in this sense, the motion of the waves is a relative motion. However, while the angle of the trajectory is a relative value, for curvilinear trajectories corresponding to non-inertial movements, the curvature of the trajectory along which the wave propagates no longer depends on the angle at which the wave moves relative to the observer. In this sense, the curvature of the trajectory and, therefore, the acceleration as a measure of that curvature, does not depend on the angle of inclination of the observer's trajectory, i.e., they do not depend on the choice of the observer. Thus, while the trajectory angle, i.e. the observed speed, is locally a relative value, the derivative of that angle, i.e. the curvature corresponding to the acceleration, does not depend on the angle of inclination of the observer's trajectory, and in this sense is an absolute value associated with the absolute reference system. Thus, when bodies are treated as waves and not as projectiles, the relativity of motion in the sense presented by the Theory of Relativity is limited only to inertial motions, i.e. along straight-line trajectories. At the same time, this solves the problems with the Mach principle.
[1]. As a result, both relativistic and quantum phenomena now belong to the same model of reality, which is described in detail in [1]. In turn, the wave equation in E4, when transformed to a Minkowski spacetime coordinate system, takes the form of a wave function which is the solution to the Schrodinger equation. Thanks to the new approach, many other issues of Quantum Mechanics also become simple and understandable and easy to derive, such as the Heisenberg's principle of uncertainty or the reason for the probability of a specific reaction, which is no longer some mysterious property of particles but a simple consequence of the structure of a wave observed by us as a particle [1].Another difference between the Theory of Relativity and the approach proposed here is the definition of motion. According to the Theory of Relativity, the motion of all bodies can only be determined relative to other bodies, and this applies to inertial and non-inertial motions. This was a source of problems, for example, with the Mach principle. In the approach proposed here, the motion of waves relative to the medium is an absolute motion, while the motion of waves relative to each other is the result of the propagation of waves in this medium at different angles. Thus, the relative speed of the waves has nothing to do with the speed of the waves relative to the medium, because the relative speed is only a function of the angle between the wave propagation directions. The absence of a distinguished direction in E4 means that the angle of the trajectory of the selected wave (i.e. speed) can only be determined relative to the trajectory of another wave, that is, in this sense, the motion of the waves is a relative motion. However, while the angle of the trajectory is a relative value, for curvilinear trajectories corresponding to non-inertial movements, the curvature of the trajectory along which the wave propagates no longer depends on the angle at which the wave moves relative to the observer. In this sense, the curvature of the trajectory and, therefore, the acceleration as a measure of that curvature, does not depend on the angle of inclination of the observer's trajectory, i.e., they do not depend on the choice of the observer. Thus, while the trajectory angle, i.e. the observed speed, is locally a relative value, the derivative of that angle, i.e. the curvature corresponding to the acceleration, does not depend on the angle of inclination of the observer's trajectory, and in this sense is an absolute value associated with the absolute reference system. Thus, when bodies are treated as waves and not as projectiles, the relativity of motion in the sense presented by the Theory of Relativity is limited only to inertial motions, i.e. along straight-line trajectories. At the same time, this solves the problems with the Mach principle.
6. Conclusions
In announcing the Theory of Relativity in 1905, Einstein made a major breakthrough in contemporary physics by proposing four-dimensional reality and the relativity of motion. These were fundamental changes at the time, and Einstein’s new vision of reality seemed to be complete and did not require further changes. Two years later, Minkowski proposed a model of the structure of reality, and in this form the Theory of Relativity was recognized by the scientific world. The vast majority of the predictions of the Theory of Relativity in Einstein and Minkowski's version was experimentally confirmed, and Einstein himself became an undisputed authority, while his theory, although little understood and repeatedly misinterpreted [2,3] became the most important theory of the 20th century.Thus, when de Broglie announced the existence of the wave structure of matter twenty years later, Einstein's model seemed so obvious that all the efforts of scientists focused on incorporating wave theory of matter into the model of reality proposed in the Theory of Relativity, depicting reality as an empty space filled with discrete particles moving relative to each other. To combine the two ideas, Quantum Mechanics was created – a highly unintuitive theory, complicated, but correctly describing the vast majority of phenomena.Meanwhile, in my opinion, de Broglie's discovery was of much more importance than modern science attributed to it. The laws governing the motion of waves are completely different from the laws governing the motion of bodies in the empty space, so after the discovery of de Broglie, research should have been conducted on the possibility of describing bodies not as discrete particles with enigmatic wave properties, but directly as waves. The fact that we perceive bodies as particles and not as waves cannot determine their nature, because our perception of reality is very limited by our cognitive abilities and we cannot figure out the shape of reality solely on the basis of our - often mistaken (vide Ptolemy’s geocentric theory) – perceptions of its shape. De Broglie's discovery should have resulted in a revision of the accepted shape of reality in a way that describes bodies directly as waves, which, as I have shown in this article, is possible, and drastically simplifies the description of reality. The description of phenomena, which in the Theory of Relativity required advanced mathematics, becomes trivially simple after applying the model of particles as waves, although such great simplicity of description carries the risk of being dismissed as a manifestation of ignorance and lack of knowledge of the formalism of the Theory of Relativity, rather than treated as an advantage of the model. Taking my body of work, which greatly simplifies the description of reality, as the basis of these considerations, I believe that, in contrast to the approach proposed in this article, treating reality as a space filled with waves propagating in the medium, the Theory of Relativity contains two important errors:1. It describes reality by means of the wrong coordinate system – made up of spacetime dimensions that are not the actual dimensions that make up this reality, but only the directions in this reality misinterpreted by us as its dimensions. These directions are not constant, but change depending on the type of interactions between the particles and on the currently observed body.2. It accepts too broad an interpretation of the relativity of the motions, including also non-inertial motions.These errors caused the mathematical description of physical reality to become too complex and resulted in limitations such as singularities. These errors are the source of problems, for example, with the Mach principle, or with the proof of Lorentz's transformation where, with clear evidence of the time dilation in the systems in motion, no equally convincing evidence of the relativistic length contraction was obtained.However, the adoption by the Theory of Relativity of a four-dimensional model of reality and transformational rules (admittedly not quite correct [1,4], but leading to conclusions, the majority of which were repeatedly tested experimentally), as well as the adoption of the principle of the relativity of motion (although in a slightly erroneous, overly extended form), was a significant change in the right direction and had a major impact on the development of science in the early 20th century. These errors, despite the resulting excessive complexity of the mathematical description and certain interpretation issues, did not have a significant impact on the correctness of most of the conclusions resulting from the Theory of Relativity, but they are a source of unnecessary complexity of the mathematical description of phenomena and pose significant limitations on the development of science, which under the model proposed by Einstein and Minkowski cannot be overcome and additionally represent the false shape of physical reality.The proposed approach of applying a wave model to describe the motion of bodies and the resulting new interpretation of the notions of time, space, relativity of motion, etc., was not possible when Einstein was publishing the Theory of Relativity, because the wave structure of matter was not proposed by de Broglie until 20 years later. It can be contemplated whether, if Einstein had waited with the formulation of the Theory of Relativity to discover de Broglie, science would have made more progress and whether the publication of Relativity in its premature form actually accelerated or delayed the development of science. However, I believe that at the moment, knowing the wave structure of matter, and the above described effect on the concept of the perceived time and space, it is necessary to organize the Theory of Relativity and rewrite it in the new form. This would significantly simplify the descriptions of both relativistic phenomena and Quantum Mechanics, and the hitherto incomprehensible assumptions and requirements introduced into science on a "because!" basis would become understandable and justified. Moreover, this would allow to extend the description of reality to the areas of phenomena which the Theory of Relativity has not been able to describe, such as areas of singularities or new classes of motions unknown in the Theory of Relativity.It is, therefore, difficult to give a clear answer to the question of whether the Theory of Relativity was the biggest mistake of the 20th century. Certainly, the premature publication of the Theory of Relativity, based on Einstein's misconception of the lack of an absolute reference system and the discrete nature of bodies, was a mistake and introduced a skewed image of the reality in which we live. However, since in most cases it is possible to transform the description of events from E4 space to Minkowski spacetime, it appears that even in this erroneous form, the Theory of Relativity correctly predicted many new phenomena in physics that generated many spectacular successes. On the other hand, the problems arising from the erroneous model of reality and the resulting difficulties of interpretation have led to skepticism in parts of the scientific community, as probably evidenced by the lack of Nobel prize for Einstein for the theory that became the most famous theory in the history of the 20th century.I believe that Einstein's description should now be improved by building into the model the philosophy described above, resulting from the wave structure of matter. This should allow science to progress further by bringing better understanding the nature of reality and by removing the barriers existing in its description to date. The new interpretation of a particle and field as two different areas of the same wave [1] and an analysis of the interactions of such waves should be considered as a route alternative to the existing form of TR and QM, which should lead to the unification of electromagnetic and gravitational interactions without the need to multiply spacetime dimensions. However, at this time, it is the problems of particle/waveform, wave interactions, and mathematical formalism resulting from the new model of reality that should be regarded seriously as topics of interest and as a way of developing our knowledge of the world around us.In the Appendix, I am presenting the basic concept of the new model of reality, based on the reasoning described here. I had previously included the conclusions offered in this paper in another paper published in 2017 [1], as assumptions. At the time, I needed the assumptions, but did not yet know the physics of the phenomena (described here) responsible for the need for these assumptions. Now, the physics described above and the basics of the new model of reality resulting from the above approach, included in the Appendix, complement my work presented in 2017 [1].
Appendix
7. New Definition of the Reality7.1. Absolute Coordinate SystemAssumption 1: The reality is a structure consisting of four-dimensional Euclidean reality and an absolute time: (E4, T). Let us denote coordinates of the E4 with symbols ai (i=1,2,3,4). The coordinates of an event are defined by five values: four coordinates and an absolute time: 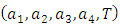 | (3) |
E4 is the Euclidean space with all its properties. The absolute time T is a value, which does not carry the meaning of a fifth dimension of the Euclidean space. It means, for example, that if in Minkowski space-time two events have four identical space-time coordinates, then they take place in an identical time and location, while in E4 the four identical coordinates of two events, „ai” do not automatically mean the simultaneity of these events, although in the next points I will show the dependence between coordinates E4 and the corresponding Minkowski space-time coordinates. 7.2. Absolute MotionAssumption 2: Absolute motion means a change of location of a body in E4 as a function of the absolute time T. In this absolute reality there exist waves perceived by us as bodies moving along certain trajectories in relation to the absolute coordinate system. In case of rectilinear trajectories, it is motion with constant absolute velocity equal to 1. In E4 there are no distinguished trajectories – trajectories of all waves/bodies are equivalent. In other words – none of the directions in E4 can be distinguished in any way. The equation of trajectory of a body in E4 is shown below: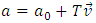 | (4) |
Where: T is the scalar value describing the absolute time, 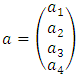 | (5) |
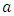 is the current point in E4 of a body on its trajectory at the absolute time T
is the current point in E4 of a body on its trajectory at the absolute time T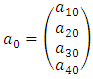 | (6) |
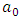 is the starting point of the body on its trajectory at the absolute time
is the starting point of the body on its trajectory at the absolute time 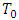
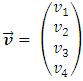 | (7) |
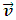 is the direction vector of the observed body’s trajectory,
is the direction vector of the observed body’s trajectory, 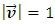 .7.3. The Proper Time of a BodyThe proper time of a body is the time flowing in the observed body’s reference frame. It will be marked with t’.If waves/bodies move along rectilinear trajectories with constant velocity equal to one, then we can conclude that for any wave/body, the measure of time indicated by its clock is equal to the length of path traveled by this body along its trajectory in E4. According to the model presented here, the proper time of a wave/body, for rectilinear trajectory, is equal to the absolute time T (in case of curvilinear trajectories, not discussed in this paper, the proper time will flow slower than the absolute time). A more detailed description of the proper time, its sense and relationship with the wave structure of matter, origin of the time dilation phenomenon, and time slowing for non-inertial motions, are presented in [1].The coordinates of the observed body in E4 at the time equal to Ti can be found with the formula:
.7.3. The Proper Time of a BodyThe proper time of a body is the time flowing in the observed body’s reference frame. It will be marked with t’.If waves/bodies move along rectilinear trajectories with constant velocity equal to one, then we can conclude that for any wave/body, the measure of time indicated by its clock is equal to the length of path traveled by this body along its trajectory in E4. According to the model presented here, the proper time of a wave/body, for rectilinear trajectory, is equal to the absolute time T (in case of curvilinear trajectories, not discussed in this paper, the proper time will flow slower than the absolute time). A more detailed description of the proper time, its sense and relationship with the wave structure of matter, origin of the time dilation phenomenon, and time slowing for non-inertial motions, are presented in [1].The coordinates of the observed body in E4 at the time equal to Ti can be found with the formula: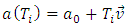 | (8) |
The distance traveled by the observed body along its trajectory from time T1 to T2 equal to the indications of a of this body’s clock, i.e. the proper time, is equal to: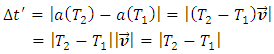 | (9) |
7.4. Space DimensionsIn E4 there is no notion of space dimensions assigned in advance. We learn about the existence of space by observing motions of the surrounding waves/bodies. We perform observations by exchanging interactions or by interference with the surrounding waves/bodies.In the case of direct interactions – interferences of waves (bodies) – the directions in E4 interpreted as the space dimensions are perpendicular to the trajectory of an observer. In the case when we are exchanging information via quanta, we measure/observe all motions of these waves/bodies along the directions of propagation of these quanta, i.e. interactions in E4. Therefore, we interpret the directions of propagation of interaction in E4 as our space dimensions. According to the approach proposed in this paper, the space dimensions are the property of observation and they are not an integral property of the reality as it is currently assumed. Let us consider observation via quanta of the body described in the previous point (7.3). We will assume that at the time T0, the starting point of the trajectory of the observed body was the origin of the coordinate sytem of E4: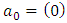 | (10) |
Therefore, the equation of the trajectory of the observed body (8) takes the following form: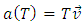 | (11) |
In the case of observation, with the help of quanta, of absolutely simultaneous waves/bodies, here moving along trajectories with a common origin, we interpret the three-dimensional hyperplane perpendicular to the trajectory of the currently observed body as our space (built of the three space dimensions). Hence the equation describing this hyperplane takes the following form: 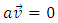 | (12) |
While the observed body is moving along the trajectory (11), each point of the hyperplane (12) must also be translated by the vector 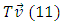 :
: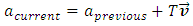 | (13) |
Therefore, the equation of the hyperplane perpendicular to the currently observed body can be formulated as follows: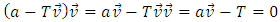 | (14) |
or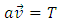 | (15) |
During observation of a specific body, the three-dimensional hyperplane (15) is interpreted by us as the three-dimensional space xyz. If we are observing several objects moving along several trajectories described with the direction vectors 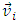 , then for each observation we will interpret a different hyperplane perpendicular to the trajectoryof the observed body as the space xyz:
, then for each observation we will interpret a different hyperplane perpendicular to the trajectoryof the observed body as the space xyz: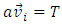 | (16) |
The difference between the hyperplanes,, which we interpret as the xyz space for observation of different bodies, will be perceived by us as relativistic effects. Note that each hyperplane, interpreted by us as three-dimensional space, is moving at absolute speed equal to 1 in absolute space E4.7.5. The Time Dimension Waves/bodies move in E4 along various trajectories – in this paper, rectilinear. Since, from the point of view of an observer moving along a chosen trajectory, the measure of their proper time is the length of traveled trajectory in E4, then each observer interprets their trajectory in E4 as the time axis of their coordinate system, where the order of the axis of time is defined by direction of the body’s motion along the trajectory. However, the order of the time axis only shows the direction of motion of bodies in E4 – not the direction of time flow. The true time flow is described with the absolute time T, while we only perceive the path travelled in E4 in any direction as the time flow (growth of the path travelled in E4 is equivalent to the growth of time in the coordinate system of a body). Therefore, in E4, there is no single time axis common for all of observers. The axis of time is an individual notion bound with a specific observer and their trajectory. Each observer interprets a different direction in E4 as the dimension of time. The trajectory of an observer can be written as: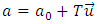 | (17) |
Where 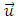 is the direction vector of the observer’s trajectory,
is the direction vector of the observer’s trajectory, 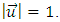 During observation performed via quanta, the lengths of axes of time of the observed body and of the observer are the measure of time indicated by their clocks. However, the axis of time of the observed body (describing the “proper time”) is pependicular to the directions interpreted by the observer as the space dimensions, while the time dimension (i.e. the axis of time of the observer) is inclined to this “space dimensions” at an angle which is the measure of relative velocity of these two bodies. That is why the value of time differs from the value of the proper time – see also Fig. 12 (and Fig. 6 for - the manner of performing observation via quanta ). In general the dependence (2) between the time
During observation performed via quanta, the lengths of axes of time of the observed body and of the observer are the measure of time indicated by their clocks. However, the axis of time of the observed body (describing the “proper time”) is pependicular to the directions interpreted by the observer as the space dimensions, while the time dimension (i.e. the axis of time of the observer) is inclined to this “space dimensions” at an angle which is the measure of relative velocity of these two bodies. That is why the value of time differs from the value of the proper time – see also Fig. 12 (and Fig. 6 for - the manner of performing observation via quanta ). In general the dependence (2) between the time 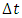 and the proper time
and the proper time 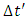 can be written in E4 as follows:
can be written in E4 as follows: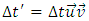 | (18) |
7.6. The Relative Motion Above it was shown that in case of rectilinear motions, all bodies/waves and three-dimensional hyperplanes of E4 are moving in absolute space E4 with absolute speed equal to 1. The relative motion is a function of an angle between trajectories the waves/bodies are traveling along. Such defined relative motion has nothing to do with the absolute motion described in the point 7.2 For two absolutly simultaneous bodies/waves moving along trajectories with a common origin, the relative velocity was defined with the formula (1). We can generalize the definition of the velocity for any trajectories in E4 described with direction vectors 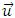 and
and 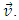 It can be written with the following formula:
It can be written with the following formula: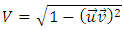 | (19) |
We must remember that though the mathematical form of the velocity (1) and (19) allows to define the velocity for any two trajectories, the velocity has a physical sense only for the trajectories inclined to each other at an angle lower than 90°. 8. Practical Tools: How to Determine the Directions Interpreted as the Space and Time Dimensions in E4For simplicity, this problem will be considered only for two trajectories lying in the same plane.We know the trajectories of an observer and observed body, the points of emission and reception of the signal on these trajectories, and we know that the directions interpreted as the time- and space axes of the observer have to be chosen in a way that ensures the value of the speed of light equal to 1. This problem is presented in the Fig. 15. 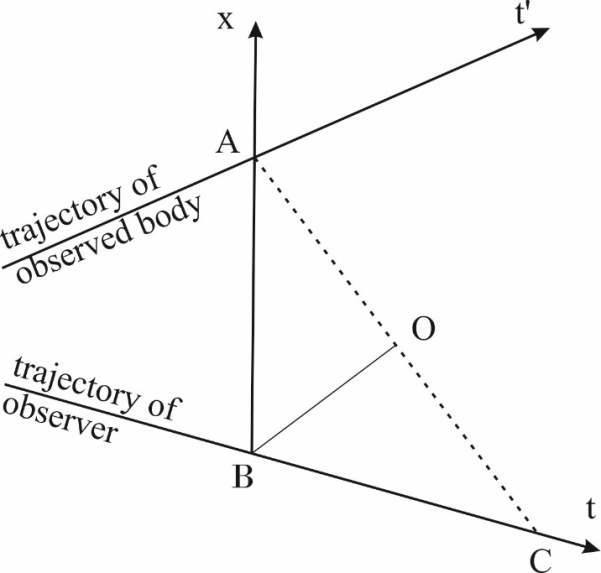 | Figure 15. An observed body moving along its trajectory (time axis) is sending a signal at point A. The observer receives the signal at point C on its trajectory (time axis). The segment AO is the trajectory of the signal as imagined by the observer. If the velocity of the signal is to be equal to one, then segments AB – the space distance between the sender and the receiver – must be equal to the segment BC – the time between the moment of sending and receiving the signal measured by the observer. Therefore, the triangle ABC must be an isosceles triangle |
From Fig. 15. we see that the triangle ABC is isosceles. The base of the triangle is the segment AC, an the second side of this triangle overlaps the trajectory of the observer. In order to find point B and, consequently, the direction interpreted by the observer as x-axis of its coordinate sytem during observation of this body, it is enough to draw the line perpendicular to the base of the triangle from the middle of the base. The line crosses the trajectory of the observer in point B and thus we find the segment AB belonging to the sought x-axis of the observer’s frame. Note that the x-axis in Fig. 15 is not perpendicular to any of the trajectories of bodies. It means that the bodies are absolutely non-simultaneous. In chapter 4 (Interaction between waves) it was stated that if the relativistic dependencies known from the Special Theory of Relativity are to be fulfilled, the direction interpreted by the observer as the space axis must be perpendicular to the trajectory of an observed body/wave and this, in turn, is true for absolutely simultaneous bodies/waves. The proof that it is true can be found below. 9. Proof that for Absolutely Simultaneous Bodies/Waves the Space Axis of the Observer’s Frame is Perpendicular to the Trajectory of an Observed BodyLet us consider two absolutely simultaneous bodies. One sends the signal, the second receives it. If it is true that for the absolutely simultaneous bodies the direction interpreted by the observer as its space axis is perpendicular to the trajectory, then for such case we should obtain the velocity of signal measured by the observer equal to 1. As we see from Fig. 16, we must prove that for the right angle between the x- axis of the observer’s frame and the trajectory of body sending the signal, and for absolutely simultaneous bodies/waves, the segments AB and BC must be equal to each other, which will give an observed speed of the signal equal to V=AB/BC=1.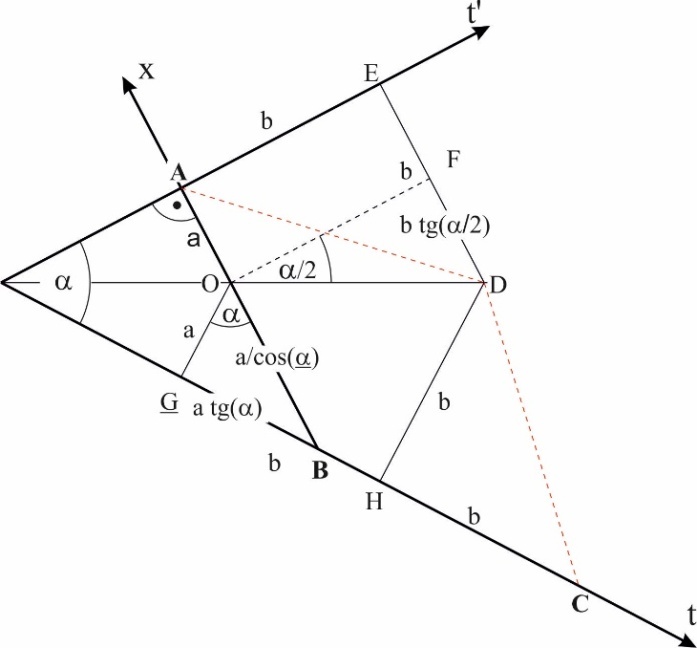 | Figure 16. Two absolutely simultaneous bodies/waves move along their trajectories – observer along t, observed body along t’. When both bodies are in points A and G on their trajectories, the observed body sends a signal. Because both bodies are absolutely simultaneous, the segments AO and GO are equal to each other and equal to a. When the signal passes the segment AD, both bodies will move along their trajectories for a segment equal to b (AE and GH). At the same time, the signal will pass the segment ED, equal to b, along direction perpendicular to the trajectory od the body sending the signal. In point D, the signal starts to propagate along the ridge of the wave of the body receiving the signal and travels along a segment equal to b (DH), while at the same time the body receiving the signal will pass the segment equal to b (HC) along its trajectory. Finally, the signal will catch up the receiver in point C |
For the right angle between t’ and x in Fig 16, we can see that: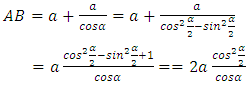 | (20) |
In turn: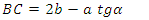 | (21) |
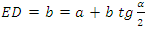 | (22) |
then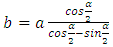 | (23) |
Using (23) tin (21) we get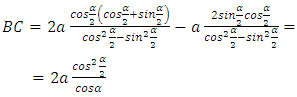 | (24) |
So we can see that AB=BC.
References
| [1] | W. Nawrot „Alternative Idea of Relativity” International Journal of Theoretical and Mathematical Physics 7(5) (2017) 95-112 http://article.sapub.org/10.5923.j.ijtmp.20170705.01.html. |
| [2] | W. Nawrot "The Hafele and Keating Paradox" Phys. Essays 17, 518 (2004). |
| [3] | W. Nawrot, "The Hafele-Keating paradox - Serious problems of the special theory of relativity (SRT)?" Phys. Essays 27, 4, pp. 598-600 (2014). |
| [4] | W. Nawrot "Is the Lorentz Transformation a physically correct solution of the spacetime interval equation?" - Galilean Electrodynamics Vol 20, Special Issue 2, 34-37 (2009)”. |
| [5] | W. Nawrot "Proposal of simpler description of SRT" - Galilean Electrodynamics 18, 43-48 (2007). |
| [6] | W. Nawrot, "New philosophy of Aether in Euclidean Reality model and interpretation of indications of Sagnac and MM interferometers" Proceedings of the 20 NPA Minneapolis, MN USA 2013. |
| [7] | Rob van Linden, “Dimensions in Special Relativity Theory”, Galilean Electrodynamics 18, 12-18 (2007). |
| [8] | W. Nawrot, "Proposal of experiment disproving the Theory of Relativity" Accepted for publication in the Galilean Electrodynamics Available at http://euclideanreality.com/pdf/DisproofOfSTR.pdf. |
| [9] | D. Brill, Ted Jacobson “Spacetime and Euclidean Geometry” Arxiv.org (2004) DOI: 10.1007/s10714-006-0254-9 https://arxiv.org/pdf/gr-qc/0407022.pdf (2004). |
| [10] | A. Gersten “Euclidean Special Relativity,” Foundation of Physics, 33 (2003) 1237-1251 DOI: https://doi.org/10.1023/A:1025631125442. |
| [11] | Hans Montanus “Special relativity in an absolute Euclidean Space-Time” (Physics Essays, vol. 4, nr 3, 1991). |
| [12] | Jose Almeida “An alternative to Minkowski space-time” (arXiv:gr-qc/0104029, 2001). |
| [13] | Giorgio Fontana “The Four Space-times Model of Reality” (arXiv.org, physics/0410054A). |
| [14] | W. Nawrot "The structure of time and the wave structure of the matter" - Galilean Electrodynamics 18, 49-53, (2007). |
| [15] | W. Nawrot "Four-Dimensional Euclidean Reality - The basic properties of the model" Proc. International Scientific Congress "Fundamental Problems of Natural Science and Engineering" Saint-Petersburg, Russia 2008. |
| [16] | W. Nawrot "Euclidean Reality Theory - Spectacular Conclusions and New Problems" - Proc. International Scientific Congress "Fundamental Problems of Natural Science and Engineering" Saint-Petersburg, Russia 2008. |
| [17] | W. Nawrot "Recession of galaxies, simpler explanation" - Galilean Electrodynamics Vol 20, Special Issue 2, 38-40 (2009). |
| [18] | W. Nawrot, "Euclidean model of the space-time - is the reality exactly as we can observe it?" - Mathematics, Physics and Philosophy in the Interpretations of Relativity Theory, Budapest, 4 - 6 September 2009. |
| [19] | W. Nawrot, "Explanation of twin paradox according to the Euclidean Reality Model" Proceedings of the 20 NPA Minneapolis, MN USA 2013. |


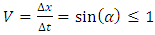
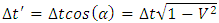
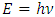 [1]. As a result, both relativistic and quantum phenomena now belong to the same model of reality, which is described in detail in [1]. In turn, the wave equation in E4, when transformed to a Minkowski spacetime coordinate system, takes the form of a wave function which is the solution to the Schrodinger equation. Thanks to the new approach, many other issues of Quantum Mechanics also become simple and understandable and easy to derive, such as the Heisenberg's principle of uncertainty or the reason for the probability of a specific reaction, which is no longer some mysterious property of particles but a simple consequence of the structure of a wave observed by us as a particle [1].Another difference between the Theory of Relativity and the approach proposed here is the definition of motion. According to the Theory of Relativity, the motion of all bodies can only be determined relative to other bodies, and this applies to inertial and non-inertial motions. This was a source of problems, for example, with the Mach principle. In the approach proposed here, the motion of waves relative to the medium is an absolute motion, while the motion of waves relative to each other is the result of the propagation of waves in this medium at different angles. Thus, the relative speed of the waves has nothing to do with the speed of the waves relative to the medium, because the relative speed is only a function of the angle between the wave propagation directions. The absence of a distinguished direction in E4 means that the angle of the trajectory of the selected wave (i.e. speed) can only be determined relative to the trajectory of another wave, that is, in this sense, the motion of the waves is a relative motion. However, while the angle of the trajectory is a relative value, for curvilinear trajectories corresponding to non-inertial movements, the curvature of the trajectory along which the wave propagates no longer depends on the angle at which the wave moves relative to the observer. In this sense, the curvature of the trajectory and, therefore, the acceleration as a measure of that curvature, does not depend on the angle of inclination of the observer's trajectory, i.e., they do not depend on the choice of the observer. Thus, while the trajectory angle, i.e. the observed speed, is locally a relative value, the derivative of that angle, i.e. the curvature corresponding to the acceleration, does not depend on the angle of inclination of the observer's trajectory, and in this sense is an absolute value associated with the absolute reference system. Thus, when bodies are treated as waves and not as projectiles, the relativity of motion in the sense presented by the Theory of Relativity is limited only to inertial motions, i.e. along straight-line trajectories. At the same time, this solves the problems with the Mach principle.
[1]. As a result, both relativistic and quantum phenomena now belong to the same model of reality, which is described in detail in [1]. In turn, the wave equation in E4, when transformed to a Minkowski spacetime coordinate system, takes the form of a wave function which is the solution to the Schrodinger equation. Thanks to the new approach, many other issues of Quantum Mechanics also become simple and understandable and easy to derive, such as the Heisenberg's principle of uncertainty or the reason for the probability of a specific reaction, which is no longer some mysterious property of particles but a simple consequence of the structure of a wave observed by us as a particle [1].Another difference between the Theory of Relativity and the approach proposed here is the definition of motion. According to the Theory of Relativity, the motion of all bodies can only be determined relative to other bodies, and this applies to inertial and non-inertial motions. This was a source of problems, for example, with the Mach principle. In the approach proposed here, the motion of waves relative to the medium is an absolute motion, while the motion of waves relative to each other is the result of the propagation of waves in this medium at different angles. Thus, the relative speed of the waves has nothing to do with the speed of the waves relative to the medium, because the relative speed is only a function of the angle between the wave propagation directions. The absence of a distinguished direction in E4 means that the angle of the trajectory of the selected wave (i.e. speed) can only be determined relative to the trajectory of another wave, that is, in this sense, the motion of the waves is a relative motion. However, while the angle of the trajectory is a relative value, for curvilinear trajectories corresponding to non-inertial movements, the curvature of the trajectory along which the wave propagates no longer depends on the angle at which the wave moves relative to the observer. In this sense, the curvature of the trajectory and, therefore, the acceleration as a measure of that curvature, does not depend on the angle of inclination of the observer's trajectory, i.e., they do not depend on the choice of the observer. Thus, while the trajectory angle, i.e. the observed speed, is locally a relative value, the derivative of that angle, i.e. the curvature corresponding to the acceleration, does not depend on the angle of inclination of the observer's trajectory, and in this sense is an absolute value associated with the absolute reference system. Thus, when bodies are treated as waves and not as projectiles, the relativity of motion in the sense presented by the Theory of Relativity is limited only to inertial motions, i.e. along straight-line trajectories. At the same time, this solves the problems with the Mach principle. 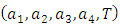
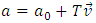
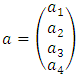
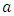 is the current point in E4 of a body on its trajectory at the absolute time T
is the current point in E4 of a body on its trajectory at the absolute time T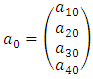
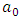 is the starting point of the body on its trajectory at the absolute time
is the starting point of the body on its trajectory at the absolute time 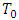
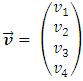
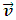 is the direction vector of the observed body’s trajectory,
is the direction vector of the observed body’s trajectory, 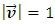 .7.3. The Proper Time of a BodyThe proper time of a body is the time flowing in the observed body’s reference frame. It will be marked with t’.If waves/bodies move along rectilinear trajectories with constant velocity equal to one, then we can conclude that for any wave/body, the measure of time indicated by its clock is equal to the length of path traveled by this body along its trajectory in E4. According to the model presented here, the proper time of a wave/body, for rectilinear trajectory, is equal to the absolute time T (in case of curvilinear trajectories, not discussed in this paper, the proper time will flow slower than the absolute time). A more detailed description of the proper time, its sense and relationship with the wave structure of matter, origin of the time dilation phenomenon, and time slowing for non-inertial motions, are presented in [1].The coordinates of the observed body in E4 at the time equal to Ti can be found with the formula:
.7.3. The Proper Time of a BodyThe proper time of a body is the time flowing in the observed body’s reference frame. It will be marked with t’.If waves/bodies move along rectilinear trajectories with constant velocity equal to one, then we can conclude that for any wave/body, the measure of time indicated by its clock is equal to the length of path traveled by this body along its trajectory in E4. According to the model presented here, the proper time of a wave/body, for rectilinear trajectory, is equal to the absolute time T (in case of curvilinear trajectories, not discussed in this paper, the proper time will flow slower than the absolute time). A more detailed description of the proper time, its sense and relationship with the wave structure of matter, origin of the time dilation phenomenon, and time slowing for non-inertial motions, are presented in [1].The coordinates of the observed body in E4 at the time equal to Ti can be found with the formula: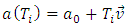
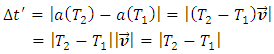
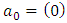
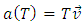
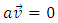
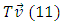 :
:
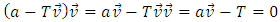
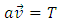
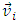 , then for each observation we will interpret a different hyperplane perpendicular to the trajectoryof the observed body as the space xyz:
, then for each observation we will interpret a different hyperplane perpendicular to the trajectoryof the observed body as the space xyz: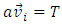
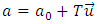
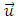 is the direction vector of the observer’s trajectory,
is the direction vector of the observer’s trajectory, 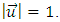 During observation performed via quanta, the lengths of axes of time of the observed body and of the observer are the measure of time indicated by their clocks. However, the axis of time of the observed body (describing the “proper time”) is pependicular to the directions interpreted by the observer as the space dimensions, while the time dimension (i.e. the axis of time of the observer) is inclined to this “space dimensions” at an angle which is the measure of relative velocity of these two bodies. That is why the value of time differs from the value of the proper time – see also Fig. 12 (and Fig. 6 for - the manner of performing observation via quanta ). In general the dependence (2) between the time
During observation performed via quanta, the lengths of axes of time of the observed body and of the observer are the measure of time indicated by their clocks. However, the axis of time of the observed body (describing the “proper time”) is pependicular to the directions interpreted by the observer as the space dimensions, while the time dimension (i.e. the axis of time of the observer) is inclined to this “space dimensions” at an angle which is the measure of relative velocity of these two bodies. That is why the value of time differs from the value of the proper time – see also Fig. 12 (and Fig. 6 for - the manner of performing observation via quanta ). In general the dependence (2) between the time 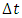 and the proper time
and the proper time 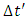 can be written in E4 as follows:
can be written in E4 as follows: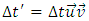
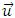 and
and 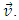 It can be written with the following formula:
It can be written with the following formula: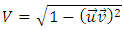
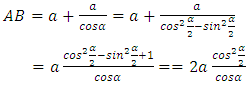
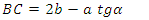
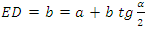
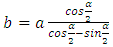
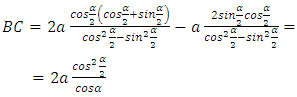
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





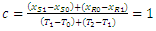 is always constant and equal to one
is always constant and equal to one
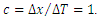 In the coordinate system bound with the surface of water, the emission of signal took place in time T=T0, like in Fig 6; however, the observer is convinced that the emission took place at time t0 on its time axis
In the coordinate system bound with the surface of water, the emission of signal took place in time T=T0, like in Fig 6; however, the observer is convinced that the emission took place at time t0 on its time axis
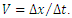 Due to the variability of the angles of this triangle (resulting from the angle between directions of propagation of the waves and/or the location of the point of transmission of the signal from the ridge of the sender wave to the ridge of the receiver wave– point B in Fig. 6), it is not possible to determine an unambiguous relationship between the times
Due to the variability of the angles of this triangle (resulting from the angle between directions of propagation of the waves and/or the location of the point of transmission of the signal from the ridge of the sender wave to the ridge of the receiver wave– point B in Fig. 6), it is not possible to determine an unambiguous relationship between the times 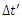 and
and 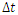 , and the relative velocity V
, and the relative velocity V



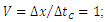 b. The values Δt' and Δt meet the relativistic dependencies that are a function of speed
b. The values Δt' and Δt meet the relativistic dependencies that are a function of speed 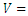
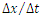

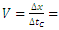
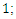 b. Due to the absence of perpendicularity of the direction interpreted as a space dimension to the direction of propagation of the observed wave, the values Δt' and Δt no longer meet relativistic dependencies, consistent with the Theory of Relativity, which are a function of speed
b. Due to the absence of perpendicularity of the direction interpreted as a space dimension to the direction of propagation of the observed wave, the values Δt' and Δt no longer meet relativistic dependencies, consistent with the Theory of Relativity, which are a function of speed 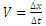

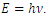 A detailed description of this situation is given in [1]
A detailed description of this situation is given in [1]
