-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2020; 10(6): 135-142
doi:10.5923/j.ijtmp.20201006.04
Received: Dec. 15, 2020; Accepted: Dec. 29, 2020; Published: Dec. 31, 2020

A New Approach to Duality of Electron
Sultan Muhammad, Miss Omama
Qurtuba University Phase 3 Hayatabad Peshawar, Pakistan
Correspondence to: Sultan Muhammad, Qurtuba University Phase 3 Hayatabad Peshawar, Pakistan.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

I decipher quantum duality of electron in Young’s Double-Slit experiment. Hypothesis intends to decode interaction of knocked-electrons with observer, and perturbative disappearance of interference pattern. Hypothesis is based on Bohr’s Atomic Model, and the theoretical concepts of Quantization of electron. The hypothesis proposes a universal field, similar to Higg’s field, that conserves the potential energy of electron through interaction with knocked-electrons, utilizing phenomena of pair-production. The hypothesis provides comprehensive theoretical and mathematical solutions to possibly elaborate, in a broader context, why electrons exhibit duality and the role of observer in Young’s Double-Slit experiment through introduction of universal field (SM Field). The interactions between photon and knocked-electrons have been discussed. Through using Schrodinger wave equation (SWE), a mathematical model has been derived, that is used to explain role of the observer, and duality of electron by using SM field as a supplement.
Keywords: Electron, Wave-Particle Duality, Quantum
Cite this paper: Sultan Muhammad, Miss Omama, A New Approach to Duality of Electron, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 6, 2020, pp. 135-142. doi: 10.5923/j.ijtmp.20201006.04.
Article Outline
1. Introduction
- The postulation and understanding of wave-particle dual nature was a controversial topic to begin with. It is closely entangled with the origin of the Quantum theory. Many questions are associated with it. Why are electrons dual in nature? Why does the electron deter from presumed particle nature, and exhibit wave nature? What is the role of the observer in the change in behaviour of electron? Why does it behave differently when in external environment, i.e outside the nucleus? The solutions to these quantum mechanical problems were developed with assistance of currently existing theories, such as thermionic emission, De Broglie relation, Schrodinger wave equation.The double slit experiment is the heart of Quantum mechanics (Feynman) [1] following the experiment:If the beam of electrons passes through two slits, we result with diffraction pattern, instead of envisioned single line. [5] [6]. The dual nature of electron is observed. But an intriguing event occurs when a detector is positioned in order to observe the electron going through slit ’A’ or ‘B’. The wave pattern disappears [7] [8]. What ramificates the electron? What role does the detector play? How to elucidate this phenomena?We know that electron gun produces knocked electron in the experiment. [10] Most quotidian method is thermionic emission. [11,12,13] The electrons are ejected from the surface of the metal with the virtue of temperature. But one thing to be discerned, is that enough energy is to be supplied to overcome the wave function, in order to liberate the electrons, or, to over come the electrostatic force. That minimum energy can be stated as “Ionization Potential Energy”. [14,15,16]The electron has a distinctive property to have “n” numbers of energies when attainable [2,3]. This implies that it can occupy energy state, and expel it through the process of absorption and emission, respectively. It is understood that, from Bohr’s model, when electron is confined to the nucleus, the electron jumps to higher energy-level or principle Quantum number when it absorbs the energy, and jumps back when emission occurs. [4](see appendix “A”)Likewise, unless the electron emits the energy, it persists in that upper energy-level. If no higher energy-level exists, then the electron is liberated from the atom, and henceforth, is known as ‘knocked electron’.For Hydrogen, the ionization-energy can be written as(See appendix “B”)
2. Problem
- As it is discussed that the electron is dual in nature, and it is also verified in the context of double slit experiment; The question arises, what is the explanation? Why does the electron, being matter, behave as a wave? Where does this dual nature stem from? Perhaps, it is just like De Broglie suggested in his hypothesis, that the motion is the agent to the wave nature of electron. But then, this would raise a serious objection.If the wave nature of electron is dependent on the relative motion of electron, then we can establish a statement. “When a detector is positioned to measure the position of electron, the wave function is collapsed”. Therefore, from the above statement, we could postulate that “Either the electron has became stationary, or the wave length has approached infinity (as the relation suggests)”.

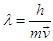
 (a)Anomaly: Theoretically, if the wave function collapses, then we can assume the electrons are stationary, but, in the experiment the electrons are observed (detected) on the screen. figure (1) & (2) shows the results of double-slit experiment:Diffraction pattern of electrons using two slits
(a)Anomaly: Theoretically, if the wave function collapses, then we can assume the electrons are stationary, but, in the experiment the electrons are observed (detected) on the screen. figure (1) & (2) shows the results of double-slit experiment:Diffraction pattern of electrons using two slits  | Figure 1 |
 | Figure 2 |
3. A Field Model to Explain the Potential Energy of Knocked Electron
- A theoretical field is proposed to explain the nature of electron.We can characterize the electrons on the basics of Quantization of the properties of electron, such as:1) Mass2) Charge3) EnergySo, to interact with the “Knocked- electron”, we need a “field” or “condensate” with any of above mentioned quantized property.A field of neutral Boson [18] is proposed with quantized energy, with capability to trigger Pair-production when the knocked electron enters the field. Thus, the potential energy of the electron is retained, and the knocked electrons are no longer considered with “ZERO POTENTIAL”. The potential energy outside the Principle Quantum Number is due to the field.Interaction of field with ElectronWhen the electrons are knocked out of the Principle- Shell, the electrons are subjected to uniform non- changing field, just like Higgs field. The field is neutral, but has a minimum function of energy, and interacts with the Ionization Potential-energy of the electron, subsequently triggering pair-production [19] at any instance. The produced pair of electron and positron interacts with the knocked electron. The interaction is repulsive in nature, as most knocked electron and produced electron have with each other. This pair-production phenomena occurs at the “Amplitude of the wave of knocked electron”.As soon as the knocked electron (not bounded to the nucleus) descends from amplitude peak, the produced pair annihilate each other, and the energy is returned to the field and electron:
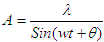 | (1.1) |
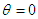 , “w” is frequency, and it depends on Potential energy of the electron
, “w” is frequency, and it depends on Potential energy of the electron 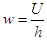 and “t” is the time period that is taken to form single wave length. It depends on the kinetic energy of the electron:
and “t” is the time period that is taken to form single wave length. It depends on the kinetic energy of the electron: 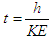 .
. 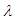 is the wave length from DeBroglie hypothesis [20].By putting the values in equation (1.1):
is the wave length from DeBroglie hypothesis [20].By putting the values in equation (1.1):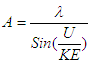 | (1.2) |
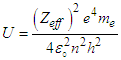 Where “KE” is the kinetic energy of the knocked electron, as we use the electron gun to accelerate the electron. Thus,
Where “KE” is the kinetic energy of the knocked electron, as we use the electron gun to accelerate the electron. Thus, 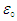 is vacuum permittivity [23,24], “h” is plank’s constant [25], “e” is elementary charge [26,27,28], “me” is the mass of electron [29,30,31], “Zeff” is effective nuclear charge [32,33,34]KE becomes:
is vacuum permittivity [23,24], “h” is plank’s constant [25], “e” is elementary charge [26,27,28], “me” is the mass of electron [29,30,31], “Zeff” is effective nuclear charge [32,33,34]KE becomes: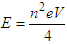 (“V” is the voltage applied)Putting the values of “U” & “KE” in equation (1.2):
(“V” is the voltage applied)Putting the values of “U” & “KE” in equation (1.2):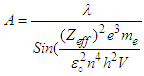 | (1.3) |
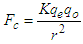 | (1.4) |
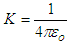 , “qe” is the charge of electron and “qo” is the charge of the pair produced electron.We know that:
, “qe” is the charge of electron and “qo” is the charge of the pair produced electron.We know that: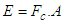 | (1.5) |
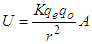 | (1.6) |
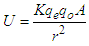 | (1.6a) |
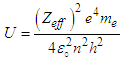 | (1.7) |
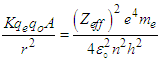 | (1.8) |
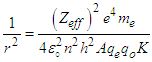 | (1.8a) |
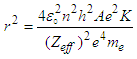 | (1.9) |
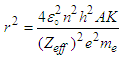 | (2.0) |
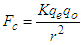 | (1.4) |
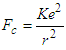 | (1.4a) |
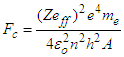 | (2.1) |
4. Hypothesis
- To answer the question, we initially try to describe the motion of electron, which is a general wave motion, but, a wave motion can be described by two parameters in our case:1) Wave length2) Amplitude / FrequencyThe wave-motion may be evaluated as the amalgamation of two fully contrasting motions. Straight-line motion or “translatory” motion of electron along x-axis, and a vibratory motion along y-axis. The vibratory motion is due to the SM field, and its interaction with knocked electron. The two motions of the particle are additive.Let us suppose two particles “A” & “B”.The particle A has some kinetic energy. It progresses along x-axis in a straight line. Consequently, this motion can be termed as translatory motion.Now, consider Particle “B”.The particle B has some energy (may or may not be kinetic), and it vibrates along y-axis only. Accordingly, this motion can be termed as vibratory motion.We can say both particles A & B have some motion, but none of them have wave motion (Sine-wave). But, what if we have another particle “C” that is allowed to have both motions simultaneously. Or, we can say, particle “C” is in articulate motion, that is additive of Translatory and Vibratory motion. Such motions result in the “wave motion”. Figure (3) demonstrates the analogy:
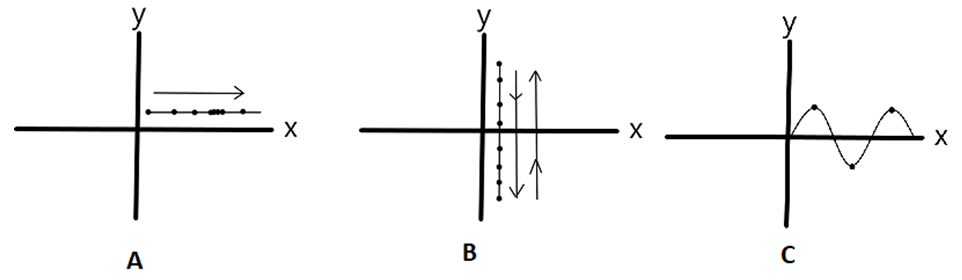 | Figure 3 |
5. Equations and Derivations
- To solve the stated problems, we use Schrodinger wave equation, The developed mathematics is similar to the prevalent problem of physics “Particle in box 1D”.
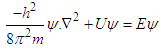 | (3) |
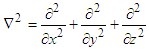 As the electron maneuvers in straight line, we consider that electron is moving along x-axis only. Thus, the Laplace operator reduces to:
As the electron maneuvers in straight line, we consider that electron is moving along x-axis only. Thus, the Laplace operator reduces to: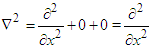 We can rewrite the equation (3):
We can rewrite the equation (3):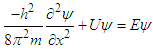 | (3.1) |
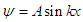 Where:
Where: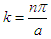 | (3.2) |
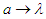 Unlike particle in one dimension we make some modifications:1) Electron has some potential energy. The non-zero potential energy is due to the fact that “Electron acts as energy carrier”, and there is a field external to the atom. Thus, the potential energy is nothing but the ionization potential-energy, or, the work-function of the metal used as source in the electron gun.2) The parameter “a” in equation (3.2) is to be replaced with wavelength of the moving electron, as the electron is fired from electron gun, we consider the wave length as a discrete box, where it interacts with the external field, where the electron exists for a period of time and then moves to second one, i.e “from one wave length to another”. To find wavelength, we use De-Broglie relation [9]:
Unlike particle in one dimension we make some modifications:1) Electron has some potential energy. The non-zero potential energy is due to the fact that “Electron acts as energy carrier”, and there is a field external to the atom. Thus, the potential energy is nothing but the ionization potential-energy, or, the work-function of the metal used as source in the electron gun.2) The parameter “a” in equation (3.2) is to be replaced with wavelength of the moving electron, as the electron is fired from electron gun, we consider the wave length as a discrete box, where it interacts with the external field, where the electron exists for a period of time and then moves to second one, i.e “from one wave length to another”. To find wavelength, we use De-Broglie relation [9]: | (3.3) |
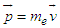 | (3.3a) |
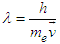 | (3.4) |
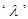 into equation (3.2):
into equation (3.2):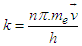 | (3.5) |
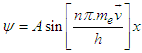 | (3.6) |
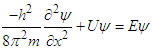 | (3.1) |
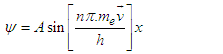 | (3.6) |
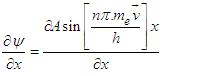 | (3.7) |
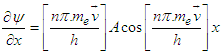 | (3.8) |
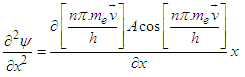 | (3.9) |
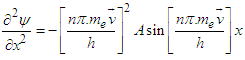 | (4.0) |
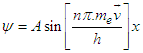 Subsisting the value from equation (3.6) into equation (4.0):
Subsisting the value from equation (3.6) into equation (4.0):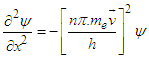 | (4.1) |
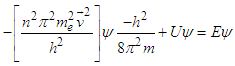 | (4.2) |
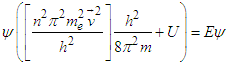 | (4.2a) |
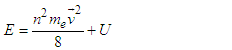 | (4.3) |
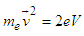 | (4.4) |
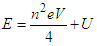 | (4.5) |
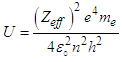 | (4.6) |
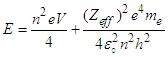 | (4.7) |
6. Solution to Double Slit Experiment
- Thought experiment:The kinetic part of the equation is the force that accelerates the electron. The acceleration is linear, a straight line. Let us suppose that we have a tiny piece of matter, and we provide some force, so that the tiny piece starts to move. We always get a straight line motion.The electron always had some potential energy while being in orbits of the atom. That potential-energy function was being neutralized by working against electrostatic force between electron and proton (Hydrogen).In this case, the knocked electrons are not bounded by the nucleus, thus, the potential function is not being neutralized. In case of knocked electrons, the potential function is used to produce oscillations of electrons through interaction with the field.Now, suppose a tiny oscillating piece of matter, and we provide some force, so that it accelerates and gains momentum. But this time, the particle is oscillating. We know that oscillating particle will produce wave pattern when it moves in a straight line.From the above supposition, we can assume that the wave nature partially depends on both kinetic and potential energy of the knocked electrons.The famous double slit experiment is indeed a simple, yet complex procedure, that unlocked many mysteries in quantum mechanics. Yet, a certain case remains unresolved till now. “The role of the detector/Observer”. Why does the diffraction pattern disappear when we try to measure the position or path of electron?From the equation (4.7), it is clear that the total energy of the knocked electron comes in two parts, i.e “kinetic-function” and “Potential-function”, and the Potential-function is well quantized. Thus, the quantum nature of the Potential function may interact with other quantum entities around it. Thus, it interacts with the detector’s photons, which may be the cause of the potential function to collapse. No observer:
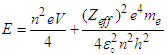 | (5) |
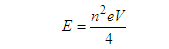 | (5.1) |
7. Interaction of Detector’s Photon with Pair-Production
- When ever knocked- electron approaches Amplitude of the wave in the SM field, Pair-production occurs due to the potential energy of the knocked electron.The interaction is demonstrated through Feynman diagram: (Figure: 4)
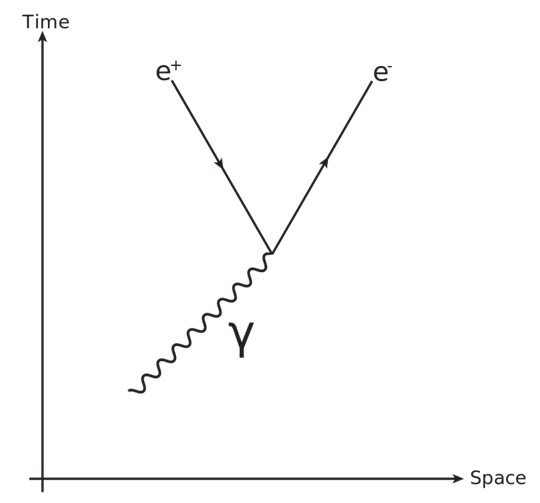 | Figure 4 |
8. Conclusions
- The hypothesis successfully explains the role of observer in double-slit experiment and accurately predicts interaction of the detector’s photons with the Knocked-electron. It becomes clear that knocked-electron fired from electron gun has total energy, that is the sum of two different energy functions, such as kinetic-function and potential-function due to presence of the SM field (Theoretical), instead of only kinetic, as previously thought which explains the duality of electron.The hypothesis is strongly supported by the double-slit experiments, and, successfully predicts the behaviour of the knocked-electron when detector is on/off.The SM field is yet to be proved experimentally, but theoretically, it is the hidden parameter to solve the problem of duality of electron (17).
ACKNOWLEDGEMENTS
- I offer concise but sincere acknowledgements to Prof Dr. Fazal-ur-Rehman Sethi (supervisor), Syeda Aiman Jamshaid (Contributor), Zainab, Maham Tariq (Major contributor) and all those who offered their wisdom and time in my research.
Appendix
- A) The equation shows the transition of electron from ground Principle Quantum number to higher Quantum number.
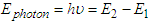
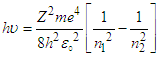 B) It shows the basics wave function of ionization for hydrogen:
B) It shows the basics wave function of ionization for hydrogen: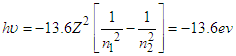
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML