Doron Kwiat
Israel
Correspondence to: Doron Kwiat, Israel.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Ven diagram description of sets logic cannot describe correctly a 3-phased sequential experiment of true-false filters. In a 3 filters experiment with sequence of filters A B and C, a particle can never arrive at C without passing first through B. Thus, when excluding particles from C, one should also consider those which never got into C in the first place. Hence, Bell's inequality is never violated, not even in the case of quantum pairs. Entanglement is due to hidden variables – time oscillations.
Keywords:
Bell's inequality, Entanglement, Hidden variables
Cite this paper: Doron Kwiat, No Violation of Bell's Inequality, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 6, 2020, pp. 130-134. doi: 10.5923/j.ijtmp.20201006.03.
1. Introduction
There are two issues in the attempts to explain the source of debate around the EPR paradox, that need to be explained.A thought experiment is always brought where a pair of electron positron is created with opposite momentum and spin, so that their initial total momentum and spin is null.This leads to a claimed contradiction of Heisenberg's uncertainty principle. Measurement of the spin of one particle in one direction (say z), leads to non-local knowledge of the spin of the second particle in same direction. Thereof, the second particle may have its spin in the conjugate direction (say x) measured as well.The claim is that this contradicts Heisenberg's uncertainty principle which forbids the measurement of two conjugate observables (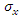 and
and 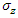 in the case of the second particle), simultaneously.As Heisenberg claims, no experiments that allow a simultaneous precise measurement of two conjugate quantities, then these quantities are also not simultaneously well-defined.The first mathematically exact formulation of the uncertainty relations is due to Robertson [1] who proved the theorem that for all normalized state vectors |ψ⟩ and for all observables (self-adjoint operators) A and B, the following inequality holds:
in the case of the second particle), simultaneously.As Heisenberg claims, no experiments that allow a simultaneous precise measurement of two conjugate quantities, then these quantities are also not simultaneously well-defined.The first mathematically exact formulation of the uncertainty relations is due to Robertson [1] who proved the theorem that for all normalized state vectors |ψ⟩ and for all observables (self-adjoint operators) A and B, the following inequality holds: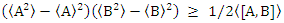 | (1) |
where 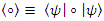 denotes the expectation value in state
denotes the expectation value in state 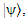 and where
and where 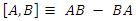 is the commutation operation.In quantum mechanics a system is supposed to be described by its wave function, also called its quantum state or state vector. Given the state vector |ψ⟩, one can derive probability distributions for all the physical quantities pertaining to the system, usually called its observables, such as its position, momentum, angular momentum, spin, energy, etc. The operational meaning of these probability distributions is that they correspond to the distribution of the values obtained for these quantities in a long series of repetitions of the measurement. More precisely, one imagines a great number of copies of the system under consideration, all prepared in the same way. On each copy the observable, is measured. Generally, the outcomes of these measurements differ and a distribution of outcomes is obtained. The theoretical observable distribution derived from the quantum state is supposed to coincide with the hypothetical distribution of outcomes obtained in an infinite series of repetitions of the observable measurement. The same holds, mutatis mutandis, for all the physical quantities pertaining to the system. Note that no simultaneous measurements of two or more quantities are required in defining the operational meaning of the probability distributions.The uncertainty relations discussed above can be considered as statements about the spreads of the probability distributions of the several physical quantities arising from the same state. The uncertainty relation between the position and momentum of a system may be understood as the statement that the position and momentum distributions cannot both be arbitrarily narrow—No two separate observables of a system may be measured simultaneously.Notice that the uncertainty principle always refers to measurements and not to knowledge (information).As for Bell's inequality. It was this inequality that was used, in a thought experiment, to show that hidden variables cannot be used in order to explain the so-called entanglement. Namely, in a triple slit Stern-Gerlach experiment, the fact that the spin of the outgoing electron is somehow aware of the spin of the incoming electron. In other words, if hidden variables existed, then one could explain this "spooky" connection between the electron states. But if hidden variables is negated, then one cannot explain this connection and one is led to weird conclusions about our understanding of quantum mechanics fundumantals.
is the commutation operation.In quantum mechanics a system is supposed to be described by its wave function, also called its quantum state or state vector. Given the state vector |ψ⟩, one can derive probability distributions for all the physical quantities pertaining to the system, usually called its observables, such as its position, momentum, angular momentum, spin, energy, etc. The operational meaning of these probability distributions is that they correspond to the distribution of the values obtained for these quantities in a long series of repetitions of the measurement. More precisely, one imagines a great number of copies of the system under consideration, all prepared in the same way. On each copy the observable, is measured. Generally, the outcomes of these measurements differ and a distribution of outcomes is obtained. The theoretical observable distribution derived from the quantum state is supposed to coincide with the hypothetical distribution of outcomes obtained in an infinite series of repetitions of the observable measurement. The same holds, mutatis mutandis, for all the physical quantities pertaining to the system. Note that no simultaneous measurements of two or more quantities are required in defining the operational meaning of the probability distributions.The uncertainty relations discussed above can be considered as statements about the spreads of the probability distributions of the several physical quantities arising from the same state. The uncertainty relation between the position and momentum of a system may be understood as the statement that the position and momentum distributions cannot both be arbitrarily narrow—No two separate observables of a system may be measured simultaneously.Notice that the uncertainty principle always refers to measurements and not to knowledge (information).As for Bell's inequality. It was this inequality that was used, in a thought experiment, to show that hidden variables cannot be used in order to explain the so-called entanglement. Namely, in a triple slit Stern-Gerlach experiment, the fact that the spin of the outgoing electron is somehow aware of the spin of the incoming electron. In other words, if hidden variables existed, then one could explain this "spooky" connection between the electron states. But if hidden variables is negated, then one cannot explain this connection and one is led to weird conclusions about our understanding of quantum mechanics fundumantals.
2. Information vs. Measurement
The quantum measurement problem has been discussed extensively [3]. Many dynamical models were proposed over the years for elucidating quantum measurements. The approaches range from standard quantum theory, relying for instance on quantum statistical mechanics or on decoherence, to quantum-classical methods, to consistent histories and to modifications of the theory. When we say that we know a certain parameter to have a given value, it means that we have accepted a given value which was delivered to us from some source (information). This is an information transfer. Information can only be verified by measurement. But if the information is deduced by us based on a given source, where we did not actually measure it, this means we have information without direct measurement.For example, suppose we are given an empty box. How do we know that the box is empty?By one of two options. Either we open the box and see in our own eyes (measure), or we are given (from a reliable source) the information about the box being empty. This information was obtained earlier, by another spectator, via measurement. For instance, the one who closed thr box earlier.So, in the case of the empty box, we can tell its discrete state at a given instance of time and a given position in space, without performing any measurement.There is no such thing as an expectation value for a given parameter, which value was obtained via a clean information transfer. If there is no noise involved, the information will be delivered clean and uninterrupted.When two observables are represented by two non-commuting operators, the two observables cannot be measured simultaneously. However, measurement is not equivalent to knowledge.We may know simultaneously the values of two non-commuting observables, but we cannot measure then simultaneously.Heisenberg uncertainty principle is valid as long as one refers to measurements, not for information.An example:Suppose Alice and Bob have a single coin to hold. Only one of them can have it. This means that if for instance Alice holds the coin, she knows by measurement (i.e. by way of looking or feeling), that she has it and knows without measurement, that Bob does not have it.Likewise, Bob knows by measurement that he does not have the coin, and by deduction without measurement, that Alice got it.Let |A> represent the state of Alice hand and |B> represent the state of Bob's hand. Clearly σz is the operator which reveals the coin's position.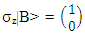 if Alice has the coin, and
if Alice has the coin, and 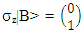 if she doesn't have it.In this case we are bluffing the reality. Instead of saying that Alice is certain about the fact of having the coin at her hand, we are allowing a false probabilistic description of the situation.We are saying that Alice has a probability of 100% of having the coin at her hand. This means that according to quantum probabilistic description of reality, instead of using a False-True logic, we are using a probabilistic description of discrete logic.This is what we call "Schrodinger's Cat" gedanken experiment.One cannot allocate quantum description to discrete logic. Otherwise one gets impossible results.Therefore, in the case of the pair production, there is no violation of Heisenberg's uncertainty principle. Knowledge of the spin state is not equivalent to an act of measuring it.This is the difference between measurement and information.
if she doesn't have it.In this case we are bluffing the reality. Instead of saying that Alice is certain about the fact of having the coin at her hand, we are allowing a false probabilistic description of the situation.We are saying that Alice has a probability of 100% of having the coin at her hand. This means that according to quantum probabilistic description of reality, instead of using a False-True logic, we are using a probabilistic description of discrete logic.This is what we call "Schrodinger's Cat" gedanken experiment.One cannot allocate quantum description to discrete logic. Otherwise one gets impossible results.Therefore, in the case of the pair production, there is no violation of Heisenberg's uncertainty principle. Knowledge of the spin state is not equivalent to an act of measuring it.This is the difference between measurement and information.
3. Bell's Arguments
The paradox of Einstein, Podolsky and Rosen was advanced as an argument that quantum mechanics could not be a complete theory but should be supplemented by additional variables. These additional variables were to restore to the theory causality and locality. In his work [2], Bell claimed that the additional variables idea is incompatible with the statistical predictions of quantum mechanics. It is the requirement of locality, or more precisely that the result of a measurement on one system be unaffected by operations on a distant system with which it has interacted in the past, that creates the essential difficulty. Consider a pair of spin one-half particles formed somehow in the singlet spin state and moving freely in opposite directions. Measurements can be made, say by Stern-Gerlach magnets, on selected components of the spins 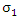 and
and 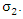 If measurement of the component
If measurement of the component 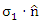 , where
, where 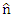 is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of
is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of 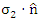 must yield the value -1 and vice versa.Now, when stating the above statement about the actual results of measuring spins, one should remember that the results are always statistical. It is only by repetition of the measurements over a large number of times, that one gets the expectation values +1 or -1. One cannot tell the outcome of a single measurement unless it is repeated many times.Thus, measuring the spin of the first particle of the pair in a direction
must yield the value -1 and vice versa.Now, when stating the above statement about the actual results of measuring spins, one should remember that the results are always statistical. It is only by repetition of the measurements over a large number of times, that one gets the expectation values +1 or -1. One cannot tell the outcome of a single measurement unless it is repeated many times.Thus, measuring the spin of the first particle of the pair in a direction 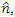 and the spin of the second particle in direction
and the spin of the second particle in direction 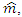 the quantum mechanical description of the probability of finding the spin of the second particle in the
the quantum mechanical description of the probability of finding the spin of the second particle in the 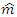 direction, provided that spin of the first spin was in the
direction, provided that spin of the first spin was in the 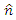 direction.Thus, the expectation value for such a result will depend on the actual number of experiment n and the probability
direction.Thus, the expectation value for such a result will depend on the actual number of experiment n and the probability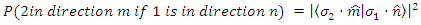 In other words, N(1 in direction n, 2 in direction m) will be
In other words, N(1 in direction n, 2 in direction m) will be 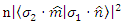 If one selects direction
If one selects direction 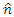 to be up in the +Z direction, then one may phrase the above as follows.What is the expected number of spins with an up (+Z) spins for the first particle and spin up in for the second particle, if the second particle is measured in the m direction, tilted by an angle at
to be up in the +Z direction, then one may phrase the above as follows.What is the expected number of spins with an up (+Z) spins for the first particle and spin up in for the second particle, if the second particle is measured in the m direction, tilted by an angle at 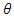 degrees with respect to the +Z direction.The answer is
degrees with respect to the +Z direction.The answer is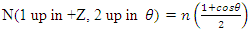 | (2) |
As a matter of fact, no single spin can be tilted in any direction 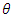 . It is rather the average outcome of spins up and down that results in a component in the
. It is rather the average outcome of spins up and down that results in a component in the 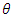 direction.In the most general form, if the spin of the entering particle is tilted at an angle
direction.In the most general form, if the spin of the entering particle is tilted at an angle 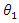 with respect to the +Z axis, then the probability of the outgoing spin to be tilted at an angle
with respect to the +Z axis, then the probability of the outgoing spin to be tilted at an angle 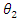 with respect to the +Z axis, is given by
with respect to the +Z axis, is given by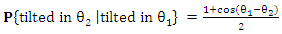 | (3) |
4. Bell's Inequality Application is False
John Bell [2] is generally credited to have accomplished the remarkable “proof” that any theory of physics, which is both Einstein local and “realistic” (counterfactually definite), results in a strong upper bound to the correlations that are measured in space and time. He thus predicts that Einstein-Podolsky-Rosen experiments cannot violate Bell- type inequalities. counterexamples to this claim, based on discrete-event computer simulations. Our model-results fully agree with the predictions of quantum theory for Einstein-Podolsky-Rosen-Bohm experiments and are free of the detection- or a coincidence-loophole. The problem with the "proof" of the violation of Bell's inequality, lies in its application [5,6].Bell's inequality states that for any partly overlapping sets A, B and C, the number of member elements of the sets: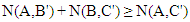 | (4) |
where primes indicate the logical NOT.Bell's inequality is correct for sets that represent a state of elements that do not represent their positions in a chain of experiments.For instance, for a setup with two filters A and B, the common set 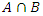 is the same in the Venn diagram for both experiment setups, but the experiments will yield different results for
is the same in the Venn diagram for both experiment setups, but the experiments will yield different results for 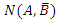 and
and 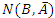 .
. For example, if A transfers 70% and B transfers 10%, then for every 1000, incoming particles,
For example, if A transfers 70% and B transfers 10%, then for every 1000, incoming particles, 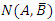 = 630 while
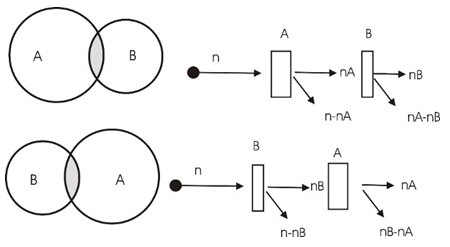
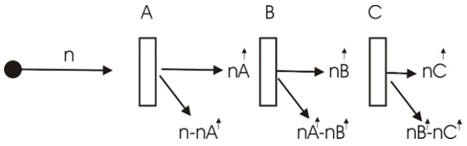
= 630 while 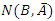 = 30.One cannot describe a quantum mechanical system classically. But since the outcome of an experiment must have a definite value each time the experiment is performed, though one can never tell the exact result of each individual experiment, one may assign a certain unknown outcome each time and repeat it with random outcome. It will be the statistical expectation value, that connect the quantum mechanical values with the real classical results.Let us look at the following example.Create a table of possible outcomes in a 3-filters experiment.Filter A: pass or failFilter B: pass or failFilter C: pass or failThe three filters are placed one after the other, so that the entering particle, if successful, has to go through all three filters.Notice however, that the events in this scenario do not occur simultaneously. Therefore, one must be careful in counting the sets of events to be included in the totality of elements in the set.
= 30.One cannot describe a quantum mechanical system classically. But since the outcome of an experiment must have a definite value each time the experiment is performed, though one can never tell the exact result of each individual experiment, one may assign a certain unknown outcome each time and repeat it with random outcome. It will be the statistical expectation value, that connect the quantum mechanical values with the real classical results.Let us look at the following example.Create a table of possible outcomes in a 3-filters experiment.Filter A: pass or failFilter B: pass or failFilter C: pass or failThe three filters are placed one after the other, so that the entering particle, if successful, has to go through all three filters.Notice however, that the events in this scenario do not occur simultaneously. Therefore, one must be careful in counting the sets of events to be included in the totality of elements in the set.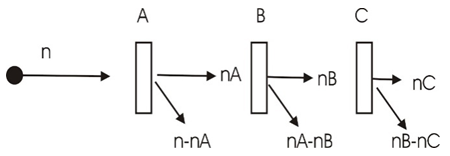 There are n particles entering from the left. There are nA particles passing filter A and n-nA particles blocked. There are nA particles entering filter B, and nB passing filter B while nA-nB blocked.Finally, there are nB particles entering filter C, and nC passing filter C while nB-nC blocked.In the following, N(A,B') stands for the number of occurrences of A but not B. N(B,C') stands for the number of occurrences of B but not C. N(A,C') stands for the number of occurrences of A but not C.By looking at the drawing it is clear that
There are n particles entering from the left. There are nA particles passing filter A and n-nA particles blocked. There are nA particles entering filter B, and nB passing filter B while nA-nB blocked.Finally, there are nB particles entering filter C, and nC passing filter C while nB-nC blocked.In the following, N(A,B') stands for the number of occurrences of A but not B. N(B,C') stands for the number of occurrences of B but not C. N(A,C') stands for the number of occurrences of A but not C.By looking at the drawing it is clear that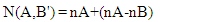 | (5) |
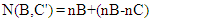 | (6) |
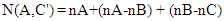 | (7) |
Notice that in this case one has to count both particles that failed B and those that failed C. This is a consequence of the fact that the counting of elements in the set depends on their order in the chain of events. Otherwise, some members of the set will be excluded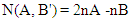 | (8) |
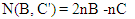 | (9) |
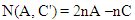 | (10) |
Hence,N(A, B') + N(B, C') = 2nA – nB + 2nB - nC = 2nA+ nB -nC, and since 2nA+ nB -nC ≥ 2nA -nC (withe equality only if nB=0). Therefore. Irrespective of the ratios, it is always true that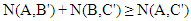 | (11) |
This is in accordance with Bell's inequality. No violation of the inequality occurs. Not even if we repeat the above experiment a large number of times. In this case, the numbers nA, nB and nC may vary according to the probabilistic distribution function of the experiment at each filter, but the inequality will still hold provide we replace nA, nB and nC with their expectation values <nA>, <nB> and <nC> respectively.In all theoretical explanations of spins or polarization, one must be careful in the calculation of the N(A, C') term. It must include those elements of N(B,C') as well.As mentioned, the order of the filters in the chain is important for the end result. For instance, an experiment setup as described in the following figure: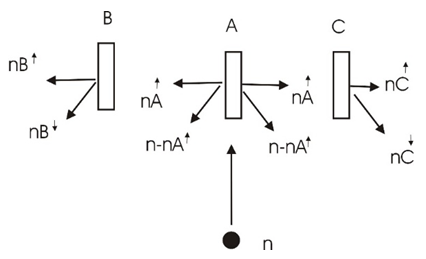 Has a completely different logic if one tries to conclude anything about the expected numbers of particles in a given state. In this setup, the filters B and C are disconnected logically. Particles leaving A with spin-up in the direction of B, will never arrive filter C, and likewise, particles leaving A with spin-up in the direction of C, will never arrive filter B. Therefore, the meaning of
Has a completely different logic if one tries to conclude anything about the expected numbers of particles in a given state. In this setup, the filters B and C are disconnected logically. Particles leaving A with spin-up in the direction of B, will never arrive filter C, and likewise, particles leaving A with spin-up in the direction of C, will never arrive filter B. Therefore, the meaning of 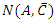 has a different meaning than in the previous sequential experimntal setup.At every filter, there is a certain probability for the outcome. This probability depends on the angle between the two filters and maybe some other qualities of the filter.If for a given filter, the probability of transfer is designated by p, then for the three filters A, B, and C we have the transfer probabilities given by PA PB and PC respectively.Therefore:
has a different meaning than in the previous sequential experimntal setup.At every filter, there is a certain probability for the outcome. This probability depends on the angle between the two filters and maybe some other qualities of the filter.If for a given filter, the probability of transfer is designated by p, then for the three filters A, B, and C we have the transfer probabilities given by PA PB and PC respectively.Therefore: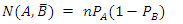 | (12) |
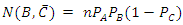 | (13) |
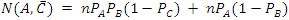 | (14) |
The third equation includes those particles that have passed A but have not passed B, as part of the number of particles that pass A but do not pass C.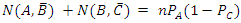 | (15) |
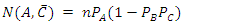 | (16) |
Thus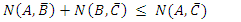 | (17) |
And Bell's inequality is violated.The entering particle is a spin half particle. It enters a magnetic field directed in the +Z direction. The outcoming particles from an experiment over n incoming particles (or of n repetitive experiments with a single particle) has a 50% chance of coming out as a spin up particle. This is not a deterministic outcome but rather statistical. So, we denote the number of spin-up outcome by 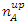 and the number of spin-down outcome, by
and the number of spin-down outcome, by 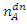 .The beam of
.The beam of 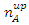 enters a second filter B, of magnetic field tilted by
enters a second filter B, of magnetic field tilted by 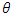 degrees to the +Z direction. By quantum mechanics, we know the probability of outcome in an up state as given by
degrees to the +Z direction. By quantum mechanics, we know the probability of outcome in an up state as given by 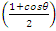 , but we do not calculate it. Let us assume that the number of outcoming spin-up particles will be
, but we do not calculate it. Let us assume that the number of outcoming spin-up particles will be 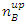 and the number of spin-down particles will be
and the number of spin-down particles will be 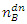 . Obviously,
. Obviously, 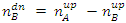 .Finally, the number of outcoming spin-up particles from the third filter C, tilted by an angle
.Finally, the number of outcoming spin-up particles from the third filter C, tilted by an angle 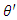 degrees to the +Z is dictated by the probability
degrees to the +Z is dictated by the probability 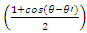 . We assume the number of outcoming particles with spin-up to be
. We assume the number of outcoming particles with spin-up to be 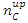 . Obviously,
. Obviously, 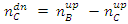 .
. It will now be assigned a value TRUE for particles passing a filter in the up state and a value of FALSE to particles passing a filter in a spin down state.Therefore,
It will now be assigned a value TRUE for particles passing a filter in the up state and a value of FALSE to particles passing a filter in a spin down state.Therefore, 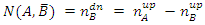 . Likewise,
. Likewise, 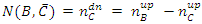 .Lastly,
.Lastly, 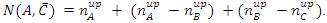
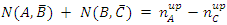 Whereas
Whereas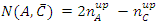 Therefore
Therefore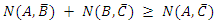 | (18) |
With equality only when 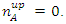 The above is true for a single particle experiment, repeated n times, as well as for a single experiment with a multitude of n particles.The numbers
The above is true for a single particle experiment, repeated n times, as well as for a single experiment with a multitude of n particles.The numbers 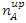 ,
, 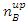 and
and 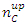 may vary from experiment to experiment but the resulting expectation values will always be true.In the case where a direct arrival to C is possible (not through B)
may vary from experiment to experiment but the resulting expectation values will always be true.In the case where a direct arrival to C is possible (not through B)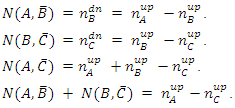 Whereas
Whereas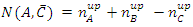 Therefore
Therefore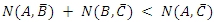 | (19) |
So, only under this "direct" case, Bell's inequality is violated.It can be seen, that the Bell inequality is violated, but not because of quantum mechanical reasons. Rather, it is because of a fundamental mistake caused by the omission from the calculation, of particles failing to pass B (and evidently fail to pass C).
5. Conclusions
Bell's inequality is not violated by quantum arguments and the validity of hidden variables should not be ruled out.The fact that two independent electron positron pair retain the so-called entanglement is nothing but a result of their simultaneous creation instance.An electron positron pair that is not a result of a simultaneous creation incident will not have any entanglement.Yet, the option of a simultaneous pair production is the subject of experimental tests [8], and its application to cyphering has been suggested [9].There must be some time mechanism (oscillation) which keeps track of the state of each particle in the pair. As long as there is no external interference, the two particles will keep their original state at the mutual creation moment.The case of a pair that eventually decayed into a common singlet state is ruled out, since if the pair are together long enough for a mutual exchange to occur and bring them into the singlet state, they must remain together and will not part away without an external intervention.
References
| [1] | Robertson, H.P., "The uncertainty principle", Physical Review, 34: 573–574; (1929). |
| [2] | Bell, J. S. "On the Einstein Podolsky Rosen Paradox", Physics Vol. 1, No. 3, pp. 195—200, (1964). |
| [3] | Allahverdyan, A. E, Balian, R, & Nieuwenhuizen, T. M. "Understanding quantum measurement from the solution of dynamical models". Phys. Reports, 525, 1 – 166. arXiv:1107.2138v4 (2013). |
| [4] | Clauser J.f. and Shimony A., "Bell’s theorem: experimental tests and implications", Reports on Progress in Physics, 41, 1881, (1978). |
| [5] | Brans, C. "Bell's theorem does not eliminate fully causal hidden variables". Int J Theor Phys 27, 219–226 (1988). |
| [6] | Nieuwenhuizen, T. M." Is the contextuality loophole fatal for the derivation of Bell inequalities?" Found. Phys. 41, 580 – 591, (2011). |
| [7] | De Raedt, H, Michielsen, K, and Hess, K. "Irrelevance of Bell’s Theorem for experiments involving correlations in space and time: a specific loophole-free computer-example", arXiv:1605.05237v1 [physics.gen-ph] (2016). |
| [8] | Dirkse B., Pompili M., Hanson R., Walter M. and Wehner S., "Witnessing entanglement in experiments with correlated noise". Quantum Sci. Technol. 5 (2020). |
| [9] | Ekert A.K., Quantum Cryptography based on Bell's Theorem. Phys. Rev. Letters, 67, 6, (1991). |



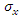 and
and 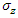 in the case of the second particle), simultaneously.As Heisenberg claims, no experiments that allow a simultaneous precise measurement of two conjugate quantities, then these quantities are also not simultaneously well-defined.The first mathematically exact formulation of the uncertainty relations is due to Robertson [1] who proved the theorem that for all normalized state vectors |ψ⟩ and for all observables (self-adjoint operators) A and B, the following inequality holds:
in the case of the second particle), simultaneously.As Heisenberg claims, no experiments that allow a simultaneous precise measurement of two conjugate quantities, then these quantities are also not simultaneously well-defined.The first mathematically exact formulation of the uncertainty relations is due to Robertson [1] who proved the theorem that for all normalized state vectors |ψ⟩ and for all observables (self-adjoint operators) A and B, the following inequality holds: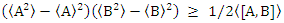
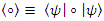 denotes the expectation value in state
denotes the expectation value in state 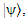 and where
and where 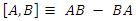 is the commutation operation.In quantum mechanics a system is supposed to be described by its wave function, also called its quantum state or state vector. Given the state vector |ψ⟩, one can derive probability distributions for all the physical quantities pertaining to the system, usually called its observables, such as its position, momentum, angular momentum, spin, energy, etc. The operational meaning of these probability distributions is that they correspond to the distribution of the values obtained for these quantities in a long series of repetitions of the measurement. More precisely, one imagines a great number of copies of the system under consideration, all prepared in the same way. On each copy the observable, is measured. Generally, the outcomes of these measurements differ and a distribution of outcomes is obtained. The theoretical observable distribution derived from the quantum state is supposed to coincide with the hypothetical distribution of outcomes obtained in an infinite series of repetitions of the observable measurement. The same holds, mutatis mutandis, for all the physical quantities pertaining to the system. Note that no simultaneous measurements of two or more quantities are required in defining the operational meaning of the probability distributions.The uncertainty relations discussed above can be considered as statements about the spreads of the probability distributions of the several physical quantities arising from the same state. The uncertainty relation between the position and momentum of a system may be understood as the statement that the position and momentum distributions cannot both be arbitrarily narrow—No two separate observables of a system may be measured simultaneously.Notice that the uncertainty principle always refers to measurements and not to knowledge (information).As for Bell's inequality. It was this inequality that was used, in a thought experiment, to show that hidden variables cannot be used in order to explain the so-called entanglement. Namely, in a triple slit Stern-Gerlach experiment, the fact that the spin of the outgoing electron is somehow aware of the spin of the incoming electron. In other words, if hidden variables existed, then one could explain this "spooky" connection between the electron states. But if hidden variables is negated, then one cannot explain this connection and one is led to weird conclusions about our understanding of quantum mechanics fundumantals.
is the commutation operation.In quantum mechanics a system is supposed to be described by its wave function, also called its quantum state or state vector. Given the state vector |ψ⟩, one can derive probability distributions for all the physical quantities pertaining to the system, usually called its observables, such as its position, momentum, angular momentum, spin, energy, etc. The operational meaning of these probability distributions is that they correspond to the distribution of the values obtained for these quantities in a long series of repetitions of the measurement. More precisely, one imagines a great number of copies of the system under consideration, all prepared in the same way. On each copy the observable, is measured. Generally, the outcomes of these measurements differ and a distribution of outcomes is obtained. The theoretical observable distribution derived from the quantum state is supposed to coincide with the hypothetical distribution of outcomes obtained in an infinite series of repetitions of the observable measurement. The same holds, mutatis mutandis, for all the physical quantities pertaining to the system. Note that no simultaneous measurements of two or more quantities are required in defining the operational meaning of the probability distributions.The uncertainty relations discussed above can be considered as statements about the spreads of the probability distributions of the several physical quantities arising from the same state. The uncertainty relation between the position and momentum of a system may be understood as the statement that the position and momentum distributions cannot both be arbitrarily narrow—No two separate observables of a system may be measured simultaneously.Notice that the uncertainty principle always refers to measurements and not to knowledge (information).As for Bell's inequality. It was this inequality that was used, in a thought experiment, to show that hidden variables cannot be used in order to explain the so-called entanglement. Namely, in a triple slit Stern-Gerlach experiment, the fact that the spin of the outgoing electron is somehow aware of the spin of the incoming electron. In other words, if hidden variables existed, then one could explain this "spooky" connection between the electron states. But if hidden variables is negated, then one cannot explain this connection and one is led to weird conclusions about our understanding of quantum mechanics fundumantals.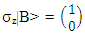 if Alice has the coin, and
if Alice has the coin, and 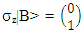 if she doesn't have it.In this case we are bluffing the reality. Instead of saying that Alice is certain about the fact of having the coin at her hand, we are allowing a false probabilistic description of the situation.We are saying that Alice has a probability of 100% of having the coin at her hand. This means that according to quantum probabilistic description of reality, instead of using a False-True logic, we are using a probabilistic description of discrete logic.This is what we call "Schrodinger's Cat" gedanken experiment.One cannot allocate quantum description to discrete logic. Otherwise one gets impossible results.Therefore, in the case of the pair production, there is no violation of Heisenberg's uncertainty principle. Knowledge of the spin state is not equivalent to an act of measuring it.This is the difference between measurement and information.
if she doesn't have it.In this case we are bluffing the reality. Instead of saying that Alice is certain about the fact of having the coin at her hand, we are allowing a false probabilistic description of the situation.We are saying that Alice has a probability of 100% of having the coin at her hand. This means that according to quantum probabilistic description of reality, instead of using a False-True logic, we are using a probabilistic description of discrete logic.This is what we call "Schrodinger's Cat" gedanken experiment.One cannot allocate quantum description to discrete logic. Otherwise one gets impossible results.Therefore, in the case of the pair production, there is no violation of Heisenberg's uncertainty principle. Knowledge of the spin state is not equivalent to an act of measuring it.This is the difference between measurement and information.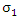 and
and 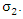 If measurement of the component
If measurement of the component 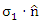 , where
, where 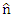 is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of
is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of 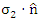 must yield the value -1 and vice versa.Now, when stating the above statement about the actual results of measuring spins, one should remember that the results are always statistical. It is only by repetition of the measurements over a large number of times, that one gets the expectation values +1 or -1. One cannot tell the outcome of a single measurement unless it is repeated many times.Thus, measuring the spin of the first particle of the pair in a direction
must yield the value -1 and vice versa.Now, when stating the above statement about the actual results of measuring spins, one should remember that the results are always statistical. It is only by repetition of the measurements over a large number of times, that one gets the expectation values +1 or -1. One cannot tell the outcome of a single measurement unless it is repeated many times.Thus, measuring the spin of the first particle of the pair in a direction 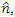 and the spin of the second particle in direction
and the spin of the second particle in direction 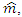 the quantum mechanical description of the probability of finding the spin of the second particle in the
the quantum mechanical description of the probability of finding the spin of the second particle in the 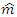 direction, provided that spin of the first spin was in the
direction, provided that spin of the first spin was in the 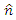 direction.Thus, the expectation value for such a result will depend on the actual number of experiment n and the probability
direction.Thus, the expectation value for such a result will depend on the actual number of experiment n and the probability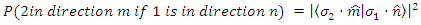 In other words, N(1 in direction n, 2 in direction m) will be
In other words, N(1 in direction n, 2 in direction m) will be 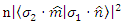 If one selects direction
If one selects direction 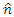 to be up in the +Z direction, then one may phrase the above as follows.What is the expected number of spins with an up (+Z) spins for the first particle and spin up in for the second particle, if the second particle is measured in the m direction, tilted by an angle at
to be up in the +Z direction, then one may phrase the above as follows.What is the expected number of spins with an up (+Z) spins for the first particle and spin up in for the second particle, if the second particle is measured in the m direction, tilted by an angle at 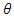 degrees with respect to the +Z direction.The answer is
degrees with respect to the +Z direction.The answer is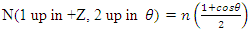
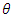 . It is rather the average outcome of spins up and down that results in a component in the
. It is rather the average outcome of spins up and down that results in a component in the 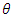 direction.In the most general form, if the spin of the entering particle is tilted at an angle
direction.In the most general form, if the spin of the entering particle is tilted at an angle 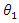 with respect to the +Z axis, then the probability of the outgoing spin to be tilted at an angle
with respect to the +Z axis, then the probability of the outgoing spin to be tilted at an angle 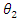 with respect to the +Z axis, is given by
with respect to the +Z axis, is given by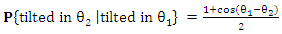
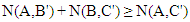
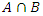 is the same in the Venn diagram for both experiment setups, but the experiments will yield different results for
is the same in the Venn diagram for both experiment setups, but the experiments will yield different results for 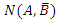 and
and 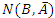 .
. For example, if A transfers 70% and B transfers 10%, then for every 1000, incoming particles,
For example, if A transfers 70% and B transfers 10%, then for every 1000, incoming particles, 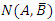 = 630 while
= 630 while 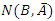 = 30.One cannot describe a quantum mechanical system classically. But since the outcome of an experiment must have a definite value each time the experiment is performed, though one can never tell the exact result of each individual experiment, one may assign a certain unknown outcome each time and repeat it with random outcome. It will be the statistical expectation value, that connect the quantum mechanical values with the real classical results.Let us look at the following example.Create a table of possible outcomes in a 3-filters experiment.Filter A: pass or failFilter B: pass or failFilter C: pass or failThe three filters are placed one after the other, so that the entering particle, if successful, has to go through all three filters.Notice however, that the events in this scenario do not occur simultaneously. Therefore, one must be careful in counting the sets of events to be included in the totality of elements in the set.
= 30.One cannot describe a quantum mechanical system classically. But since the outcome of an experiment must have a definite value each time the experiment is performed, though one can never tell the exact result of each individual experiment, one may assign a certain unknown outcome each time and repeat it with random outcome. It will be the statistical expectation value, that connect the quantum mechanical values with the real classical results.Let us look at the following example.Create a table of possible outcomes in a 3-filters experiment.Filter A: pass or failFilter B: pass or failFilter C: pass or failThe three filters are placed one after the other, so that the entering particle, if successful, has to go through all three filters.Notice however, that the events in this scenario do not occur simultaneously. Therefore, one must be careful in counting the sets of events to be included in the totality of elements in the set. There are n particles entering from the left. There are nA particles passing filter A and n-nA particles blocked. There are nA particles entering filter B, and nB passing filter B while nA-nB blocked.Finally, there are nB particles entering filter C, and nC passing filter C while nB-nC blocked.In the following, N(A,B') stands for the number of occurrences of A but not B. N(B,C') stands for the number of occurrences of B but not C. N(A,C') stands for the number of occurrences of A but not C.By looking at the drawing it is clear that
There are n particles entering from the left. There are nA particles passing filter A and n-nA particles blocked. There are nA particles entering filter B, and nB passing filter B while nA-nB blocked.Finally, there are nB particles entering filter C, and nC passing filter C while nB-nC blocked.In the following, N(A,B') stands for the number of occurrences of A but not B. N(B,C') stands for the number of occurrences of B but not C. N(A,C') stands for the number of occurrences of A but not C.By looking at the drawing it is clear that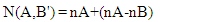
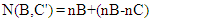
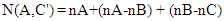
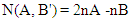
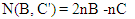
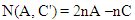
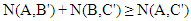
 Has a completely different logic if one tries to conclude anything about the expected numbers of particles in a given state. In this setup, the filters B and C are disconnected logically. Particles leaving A with spin-up in the direction of B, will never arrive filter C, and likewise, particles leaving A with spin-up in the direction of C, will never arrive filter B. Therefore, the meaning of
Has a completely different logic if one tries to conclude anything about the expected numbers of particles in a given state. In this setup, the filters B and C are disconnected logically. Particles leaving A with spin-up in the direction of B, will never arrive filter C, and likewise, particles leaving A with spin-up in the direction of C, will never arrive filter B. Therefore, the meaning of 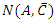 has a different meaning than in the previous sequential experimntal setup.At every filter, there is a certain probability for the outcome. This probability depends on the angle between the two filters and maybe some other qualities of the filter.If for a given filter, the probability of transfer is designated by p, then for the three filters A, B, and C we have the transfer probabilities given by PA PB and PC respectively.Therefore:
has a different meaning than in the previous sequential experimntal setup.At every filter, there is a certain probability for the outcome. This probability depends on the angle between the two filters and maybe some other qualities of the filter.If for a given filter, the probability of transfer is designated by p, then for the three filters A, B, and C we have the transfer probabilities given by PA PB and PC respectively.Therefore: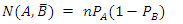
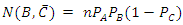
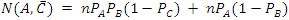
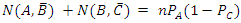
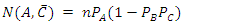
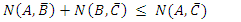
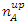 and the number of spin-down outcome, by
and the number of spin-down outcome, by 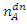 .The beam of
.The beam of 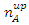 enters a second filter B, of magnetic field tilted by
enters a second filter B, of magnetic field tilted by 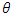 degrees to the +Z direction. By quantum mechanics, we know the probability of outcome in an up state as given by
degrees to the +Z direction. By quantum mechanics, we know the probability of outcome in an up state as given by 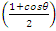 , but we do not calculate it. Let us assume that the number of outcoming spin-up particles will be
, but we do not calculate it. Let us assume that the number of outcoming spin-up particles will be 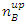 and the number of spin-down particles will be
and the number of spin-down particles will be 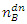 . Obviously,
. Obviously, 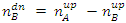 .Finally, the number of outcoming spin-up particles from the third filter C, tilted by an angle
.Finally, the number of outcoming spin-up particles from the third filter C, tilted by an angle 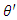 degrees to the +Z is dictated by the probability
degrees to the +Z is dictated by the probability 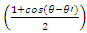 . We assume the number of outcoming particles with spin-up to be
. We assume the number of outcoming particles with spin-up to be 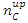 . Obviously,
. Obviously, 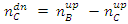 .
. It will now be assigned a value TRUE for particles passing a filter in the up state and a value of FALSE to particles passing a filter in a spin down state.Therefore,
It will now be assigned a value TRUE for particles passing a filter in the up state and a value of FALSE to particles passing a filter in a spin down state.Therefore, 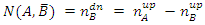 . Likewise,
. Likewise, 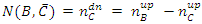 .Lastly,
.Lastly, 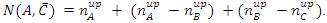
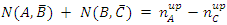 Whereas
Whereas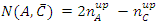 Therefore
Therefore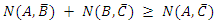
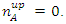 The above is true for a single particle experiment, repeated n times, as well as for a single experiment with a multitude of n particles.The numbers
The above is true for a single particle experiment, repeated n times, as well as for a single experiment with a multitude of n particles.The numbers 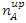 ,
, 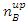 and
and 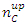 may vary from experiment to experiment but the resulting expectation values will always be true.In the case where a direct arrival to C is possible (not through B)
may vary from experiment to experiment but the resulting expectation values will always be true.In the case where a direct arrival to C is possible (not through B)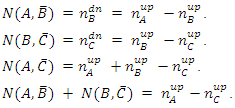 Whereas
Whereas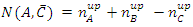 Therefore
Therefore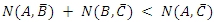
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML