Doron Kwiat
Israel
Correspondence to: Doron Kwiat, Israel.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The existence of black holes is based on singularity in the Schwarzschild metric at the Schwarzschild radius. Another singularity is at r = 0. These singularities of a spherically symmetric non-rotating, uncharged mass of radius R, are considered here.Considering Newton's shell theorem, the gravitational potential falls off linearly with r for 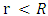 . The point r = 0 is an infinitesimally small location in space. No mass can be indefinitely condensed to this point. Thus, when investigating the concept of a mass, one has to consider its finite radius. By including the shell theorem for
. The point r = 0 is an infinitesimally small location in space. No mass can be indefinitely condensed to this point. Thus, when investigating the concept of a mass, one has to consider its finite radius. By including the shell theorem for 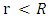 , the singularity at
, the singularity at 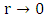 is removed. It is also shown, that a situation where rs < R but
is removed. It is also shown, that a situation where rs < R but 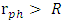 is possible. Therefore, the existence of a photon sphere light ring does not necessarily indicate a black hole.It is shown, that the condition for a gravitational collapse is
is possible. Therefore, the existence of a photon sphere light ring does not necessarily indicate a black hole.It is shown, that the condition for a gravitational collapse is 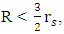 and not
and not 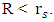 Further in this work, the question of maximal density is considered and compared to the quantum limit of mass density put by Planck's units as dictated from dimensional analysis.There are two main claims here:1. Black holes (if exist) will result only if the Schwarzschild radius is larger than 2/3R.2. General relativity leads to quantization of gravity.
Further in this work, the question of maximal density is considered and compared to the quantum limit of mass density put by Planck's units as dictated from dimensional analysis.There are two main claims here:1. Black holes (if exist) will result only if the Schwarzschild radius is larger than 2/3R.2. General relativity leads to quantization of gravity.
Keywords:
Newton's Shell theorem, Schwarzschild singularities, Photon sphere, Planck's units, Quantization of Gravity
Cite this paper: Doron Kwiat, About the Existence of Black Holes, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 6, 2020, pp. 120-129. doi: 10.5923/j.ijtmp.20201006.02.
1. Introduction
The Schwarzschild solution appears to have singularities at r = 0 and 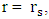 with
with 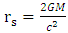 which cause the metric to diverge at these radii. There is no problem as long as
which cause the metric to diverge at these radii. There is no problem as long as 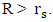 The singularity at
The singularity at 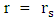 divides the Schwarzschild coordinates in two disconnected regions. The exterior Schwarzschild solution with
divides the Schwarzschild coordinates in two disconnected regions. The exterior Schwarzschild solution with 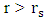 is the one that is related to the gravitational fields of stars and planets. The interior Schwarzschild solution with
is the one that is related to the gravitational fields of stars and planets. The interior Schwarzschild solution with 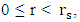 which contains the singularity at r = 0, is completely separated from the outer region by the so-called singularity at r =
which contains the singularity at r = 0, is completely separated from the outer region by the so-called singularity at r = 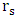 . The Schwarzschild coordinates therefore give no physical connection between these two regions.The singularity at r =
. The Schwarzschild coordinates therefore give no physical connection between these two regions.The singularity at r = 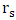 is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions. When changing to a different coordinate system, the metric becomes regular at r =
is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions. When changing to a different coordinate system, the metric becomes regular at r = 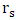 and can extend the external region to values of r smaller than
and can extend the external region to values of r smaller than 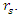 Using a different coordinate transformation one can then relate the extended external region to the inner region. As will be shown later on, this so-called singularity is completely removed even for the Schwarzschild coordinates.The case r = 0 is different, however. If one asks that the solution be valid for all r, one runs into a true physical singularity, or gravitational singularity, at the origin. To see whether this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant [19], which is given by
Using a different coordinate transformation one can then relate the extended external region to the inner region. As will be shown later on, this so-called singularity is completely removed even for the Schwarzschild coordinates.The case r = 0 is different, however. If one asks that the solution be valid for all r, one runs into a true physical singularity, or gravitational singularity, at the origin. To see whether this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant [19], which is given by 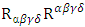 For a Schwarzschild black hole of mass M and radius R, the Kretschmann invariant is
For a Schwarzschild black hole of mass M and radius R, the Kretschmann invariant is 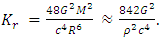 Obviously it is independent of the radius R, and is always greater than 0 (provided we accept the physical requirement that the density
Obviously it is independent of the radius R, and is always greater than 0 (provided we accept the physical requirement that the density 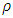 is never infinite).At r = 0 the curvature can become infinite, if and only if, it represents a point particle of zero mass. One cannot compress a finite mass into an infinitesimal point (of radius R = 0). Any finite mass should have a finite radius R > 0. Therefore, when looking into the point r = 0, one needs to consider the effects of the outer shells of matter which surround the r = 0 point.General relativity predicts that any object collapsing beyond a certain point (for stars this is the Schwarzschild radius) would form a black hole, inside which a singularity (covered by an event horizon) would be formed. As will be shown in the following, no such singularities exist.
is never infinite).At r = 0 the curvature can become infinite, if and only if, it represents a point particle of zero mass. One cannot compress a finite mass into an infinitesimal point (of radius R = 0). Any finite mass should have a finite radius R > 0. Therefore, when looking into the point r = 0, one needs to consider the effects of the outer shells of matter which surround the r = 0 point.General relativity predicts that any object collapsing beyond a certain point (for stars this is the Schwarzschild radius) would form a black hole, inside which a singularity (covered by an event horizon) would be formed. As will be shown in the following, no such singularities exist.
2. Spherically Symmetric, Non-rotating, Uncharged Spherical Body
Consider a spherically symmetric, non-rotating, uncharged mass (a stellar object or an elementary particle).Under spherical symmetry, and at a remote distance in empty space outside the object, the Schwarzschild metric [1,2,3] is given by: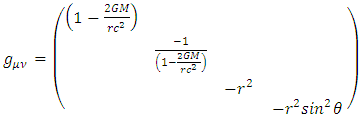 | (1) |
This metric describes very well the gravitational effects of that mass on gravitational field curvature, and dynamics of moving particles, in the empty regions outside the object.However, it suffers of two problems:1. At the Schwarzschild radius 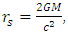 the metric has a singularity.2. At r à 0, the metric diverges.The first singularity is not a real one, as it can be removed by appropriate coordinate transformations [5-13]. The second singularity cannot be removed by coordinate transformation. It is an inherent singularity at
the metric has a singularity.2. At r à 0, the metric diverges.The first singularity is not a real one, as it can be removed by appropriate coordinate transformations [5-13]. The second singularity cannot be removed by coordinate transformation. It is an inherent singularity at 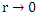 in any inverse square law central force problem of gravitational field). One so far have not been able to relate to the divergency problem of force which is inversely proportional to the square of the distance r from center of the field source.To solve this problem, we must investigate the behavior of the field inside the mass.If any mass source is finite in size, the solution to the potential as a function of distance must be modified, so that it includes the region where r < R, the radius of the mass.In addition, the Einstein field equation should be related to in non-empty space. But to a very good approximation, the Einstein equation in the inside of even the heaviest stellar objects can be considered same as empty space.This assumption will only be valid for a perfect fluid solution, where of the
in any inverse square law central force problem of gravitational field). One so far have not been able to relate to the divergency problem of force which is inversely proportional to the square of the distance r from center of the field source.To solve this problem, we must investigate the behavior of the field inside the mass.If any mass source is finite in size, the solution to the potential as a function of distance must be modified, so that it includes the region where r < R, the radius of the mass.In addition, the Einstein field equation should be related to in non-empty space. But to a very good approximation, the Einstein equation in the inside of even the heaviest stellar objects can be considered same as empty space.This assumption will only be valid for a perfect fluid solution, where of the 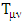 tensor, only energy density is considered, while momentum density, shear stress, momentum flux and pressure are either null or irrelevant.
tensor, only energy density is considered, while momentum density, shear stress, momentum flux and pressure are either null or irrelevant.
3. Shell Theorem
Let R be the radius of an uncharged non-rotating spherically symmetric mass, of given density 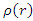 , with r being the radial distance from center (at r = 0).Assuming this object has a volume
, with r being the radial distance from center (at r = 0).Assuming this object has a volume 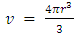 and radius R, its average density will be
and radius R, its average density will be 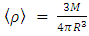 and since
and since 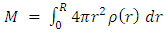 it is straightforward to see that
it is straightforward to see that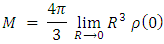 This means that unless the density at the center
This means that unless the density at the center 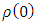 is infinite, the mass must vanish (M = 0).The only case of M > 0 is possible if and only if
is infinite, the mass must vanish (M = 0).The only case of M > 0 is possible if and only if 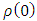 is infinite. And if we assume physical continuity, then we may write
is infinite. And if we assume physical continuity, then we may write 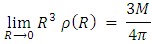 In other words
In other words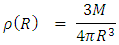 And for any finite mass M
And for any finite mass M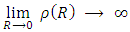 However, as will be shown later, the density of any object must have an upper limit and it cannot become infinitely large. To resolve this contradiction, one must accept, that no mass can be condensed to a singular point r = 0. A mass will always have some finite density and a finite radius (volume).Therefore, when considering gravitation at r = 0, one must consider the effects of surrounding mass. Condensed as it might be, but still of finite density and surrounding r = 0.In classical mechanics, the shell theorem, proven already by Isaac Newton [14] states that:A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center.If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object's location within the shell.A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass.Due to the shell theorem, the gravitational potential of a spherically symmetric object of mass M and radius R, as a function of distance r, from the object's center is given by:
However, as will be shown later, the density of any object must have an upper limit and it cannot become infinitely large. To resolve this contradiction, one must accept, that no mass can be condensed to a singular point r = 0. A mass will always have some finite density and a finite radius (volume).Therefore, when considering gravitation at r = 0, one must consider the effects of surrounding mass. Condensed as it might be, but still of finite density and surrounding r = 0.In classical mechanics, the shell theorem, proven already by Isaac Newton [14] states that:A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center.If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object's location within the shell.A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass.Due to the shell theorem, the gravitational potential of a spherically symmetric object of mass M and radius R, as a function of distance r, from the object's center is given by: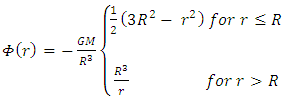 | (2) |
The result for r < R is obtained by summation of the potential at some point p inside the mass from its spherical shell between R and r, and the remaining mass inside sphere of radius r.The potential at point p due to the shell is given by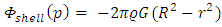 | (3) |
The potential at same point p due to the remaining inner sphere is given by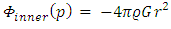 | (4) |
The total potential at point p inside the sphere is a superposition of both 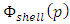 , and
, and 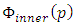 . Thus, (for r < R):
. Thus, (for r < R):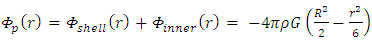 | (5) |
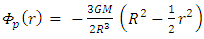 | (6) |
4. The Identification of Φ(r) as the Gravitational Potential
In the Schwarzschild metric, the 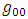 term is a function of the distance r and one may write:
term is a function of the distance r and one may write: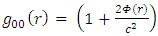 | (7) |
First argument – dimensions is a function of distance r, and must have the dimensions of
is a function of distance r, and must have the dimensions of  . It must obey the constraint of
. It must obey the constraint of 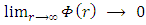 as should be the case at infinite distance in empty flat space.Its units should be [G][Kg]/[m] in order to make
as should be the case at infinite distance in empty flat space.Its units should be [G][Kg]/[m] in order to make 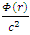 dimensionless.We therefore have a good reason to assume that
dimensionless.We therefore have a good reason to assume that 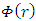 is the gravitational potential due to a spherically symmetric object, independent of the size and of the density of that object. Exactly as described by eq. 2.Second argument- Einstein equation under spherical symmetryFor a curved spacetime, based on the Riemann tensor, it can be shown that
is the gravitational potential due to a spherically symmetric object, independent of the size and of the density of that object. Exactly as described by eq. 2.Second argument- Einstein equation under spherical symmetryFor a curved spacetime, based on the Riemann tensor, it can be shown that 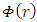 must have the form of a gravitational potential (see Appendix 1).Following these arguments, it is justified to identify
must have the form of a gravitational potential (see Appendix 1).Following these arguments, it is justified to identify 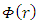 , as the gravitational potential of the field created by a spherically symmetric non-rotating uncharged mass.
, as the gravitational potential of the field created by a spherically symmetric non-rotating uncharged mass.
5. Inside the Sphere (r < R)
In the case where r < R (inside the mass), 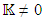 where
where 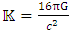
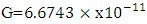 and so
and so 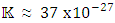 , so unless the internal density
, so unless the internal density 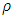 is of the order of
is of the order of 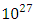 Kg/m3, the equation can be solved with the assumption of
Kg/m3, the equation can be solved with the assumption of 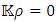 .Even the heaviest neutron stars have overall densities of the order of
.Even the heaviest neutron stars have overall densities of the order of 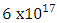 Kg/m3. For elementary particles, the neutron for instance, has density of approximately
Kg/m3. For elementary particles, the neutron for instance, has density of approximately 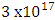 Kg/m3. So, for all practical calculations one may assume
Kg/m3. So, for all practical calculations one may assume 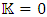 inside any mass (that is, for r < R).For the internal pressure p, as long as the internal pressure is much less than
inside any mass (that is, for r < R).For the internal pressure p, as long as the internal pressure is much less than 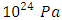 ,
, 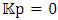 . For the Sun for instance, the internal core pressure is
. For the Sun for instance, the internal core pressure is 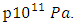 Finding the solution of the homogeneous differential equation with
Finding the solution of the homogeneous differential equation with 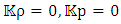 , will lead to the non-homogeneous solution with
, will lead to the non-homogeneous solution with 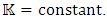 But we will concentrate on the homogeneous solution, since
But we will concentrate on the homogeneous solution, since 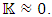 In case of a constant
In case of a constant 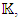 the non-homogeneous solution can be found.This is the case for a perfect fluid.Under the assumption of
the non-homogeneous solution can be found.This is the case for a perfect fluid.Under the assumption of 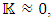 for the interior of the sphere, the time separation inside the sphere is given by
for the interior of the sphere, the time separation inside the sphere is given by 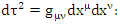
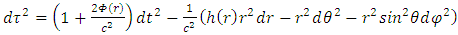 | (8) |
6. Modified Schwarzschild Metric
Inserting the expression for 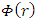 :
: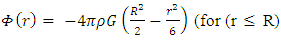
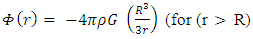 The Schwarzschild metric inside the sphere (r ≤ R) becomes
The Schwarzschild metric inside the sphere (r ≤ R) becomes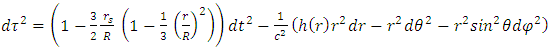 | (9) |
while outside the sphere (r > R) it becomes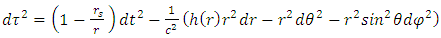 | (10) |
There are now three different possibilities, depicted in the following:A a situation where both 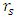 and
and 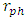 are inside the objects radius R.
are inside the objects radius R. 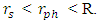 This is a standard object.B - a situation where
This is a standard object.B - a situation where 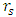 is inside the object's radius R (a standard object) while
is inside the object's radius R (a standard object) while 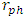 is outside the object.
is outside the object. 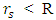
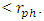 C - a situation of a black hole, where both
C - a situation of a black hole, where both 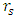 and
and 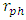 are outside R.
are outside R. 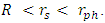 Therefore, B represents a possible situation where a photon sphere light ring exists around a standard (not a black hole) body.For said cases, the photon sphere radius
Therefore, B represents a possible situation where a photon sphere light ring exists around a standard (not a black hole) body.For said cases, the photon sphere radius 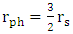 may fall inside or outside R.
may fall inside or outside R. Case A is a standard object, with both
Case A is a standard object, with both 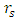 , and
, and 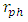 falling inside R.Case B is a white object, with
falling inside R.Case B is a white object, with 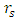 falling inside R but
falling inside R but 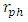 falling outside R. Light is trapped in the photon sphere, causing the object to have a white glowing ring around it. There is no gravitational collapse.Case C is a true black body, with both
falling outside R. Light is trapped in the photon sphere, causing the object to have a white glowing ring around it. There is no gravitational collapse.Case C is a true black body, with both 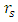 and
and 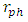 falling outside R.Case A, both
falling outside R.Case A, both 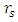 and
and 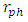 are inside R (holds for most stellar objects – but not for black holes). One obtains:
are inside R (holds for most stellar objects – but not for black holes). One obtains: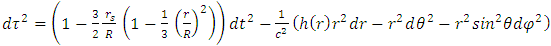 | (11) |
Picking the coordinate system so that the radius r is along the x axis, the 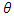 and
and 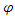 terms are zeroIn other words, for r > R
terms are zeroIn other words, for r > R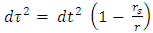 | (12) |
while for 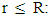
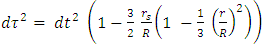 | (13) |
Obviously, for 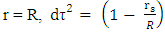 , for both.Investigating the condition
, for both.Investigating the condition 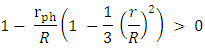 we see that in Case B, for all
we see that in Case B, for all 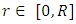 and as long as
and as long as 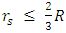 there is no singularity in the Schwarzschild metric.At
there is no singularity in the Schwarzschild metric.At 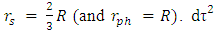 becomes zero, and the object evaporates into photons
becomes zero, and the object evaporates into photons 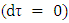 . Thus,
. Thus, 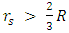 is the condition for a gravitational collapse. As long as
is the condition for a gravitational collapse. As long as 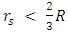 the object is a standard object and does not undergo any gravitational collapse. This, in contrast to the current assertion (for r > R), is based on Eq. 37, which states that
the object is a standard object and does not undergo any gravitational collapse. This, in contrast to the current assertion (for r > R), is based on Eq. 37, which states that 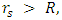 is the condition for a gravitational collapse.We see that as long as the photon sphere is inside the object (
is the condition for a gravitational collapse.We see that as long as the photon sphere is inside the object (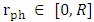 , the Schwarzschild radius
, the Schwarzschild radius 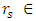
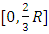 . In other words, as long as the photon sphere does not show, the object is stable and does not suffer gravitational collapse. Once the photon sphere shows up
. In other words, as long as the photon sphere does not show, the object is stable and does not suffer gravitational collapse. Once the photon sphere shows up 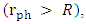 the object undergoes gravitational collapse.Anywhere in the region where
the object undergoes gravitational collapse.Anywhere in the region where 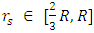 the object undergoes gravitational collapse, and since
the object undergoes gravitational collapse, and since 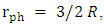 the photon sphere is outside the object, creating a bright light ring outside R, at
the photon sphere is outside the object, creating a bright light ring outside R, at 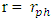 .Near the sphere's center, where
.Near the sphere's center, where 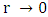 and r < R, one has
and r < R, one has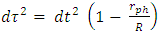 | (14) |
And, as long as, 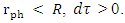 It may be re-written as:
It may be re-written as: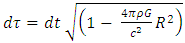 | (15) |
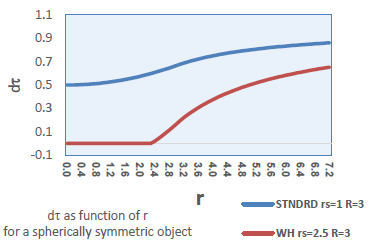 | Figure 1. For an object of radius R=3(*). The lines represent the behavior of d, for the cases where 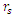 < R (A-STNDRD) and < R (A-STNDRD) and 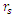 > 2/3R (B-WH). As can be seen, in case B, the inner part of the object is below the horizon > 2/3R (B-WH). As can be seen, in case B, the inner part of the object is below the horizon 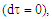 but some of the the external part is not. This case allows for the photon sphere to be visible outside the body and yet the object is not a black hole yet. In this figure, but some of the the external part is not. This case allows for the photon sphere to be visible outside the body and yet the object is not a black hole yet. In this figure, 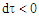 is set to is set to 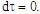 *(The dimensions are relative only) *(The dimensions are relative only) |
In the case of infinitesimally small r, we see that the time component becomes independent of the distance r from the origin. In any case, the divergence at 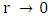 is removed.The proper time
is removed.The proper time 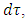 must remain well defined. Therefore, an upper limit on the density must exist for a given radius R, otherwise the expression for
must remain well defined. Therefore, an upper limit on the density must exist for a given radius R, otherwise the expression for 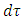 becomes undefined.Notice that this assertion leads to the constraint
becomes undefined.Notice that this assertion leads to the constraint 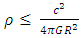 | (16) |
In other words, there is an upper limit on the density 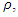 of any object with radius R. When
of any object with radius R. When 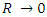 , the density may increase indefinitely, but as will be shown next, there is an upper limit on the density.
, the density may increase indefinitely, but as will be shown next, there is an upper limit on the density.
7. Density must have an Upper Limit
Simple dimensional arguments show that the physical phenomena where quantum gravitational effects become relevant are those characterized by the Planck length 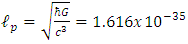 m. Here
m. Here 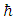 is the Planck constant that governs the scale of the quantum effects, G is the Newton constant that governs the strength of the gravitational force, and c is the speed of light, that governs the scale of the relativistic effects. The Planck length is many times smaller than what current technology is capable of observing. physical effects at scales that are so small. Because of this, we have no direct experimental guidance for building a quantum theory of gravity [16]. Suppose there exists a quantum minimum for distance. We call it the Planck length and denote it by
is the Planck constant that governs the scale of the quantum effects, G is the Newton constant that governs the strength of the gravitational force, and c is the speed of light, that governs the scale of the relativistic effects. The Planck length is many times smaller than what current technology is capable of observing. physical effects at scales that are so small. Because of this, we have no direct experimental guidance for building a quantum theory of gravity [16]. Suppose there exists a quantum minimum for distance. We call it the Planck length and denote it by 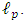 It is given by
It is given by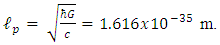 Define in addition the Planck massPlanck's mass
Define in addition the Planck massPlanck's mass 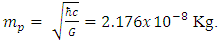 If this assumption is true, then the minimal spherical volume possible is
If this assumption is true, then the minimal spherical volume possible is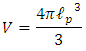 Let
Let 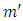 denote the mass of this volume, so its density will be given by
denote the mass of this volume, so its density will be given by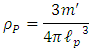 Since by assumption
Since by assumption 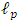 is the minimal length possible in nature, then for any mass m' the density
is the minimal length possible in nature, then for any mass m' the density 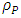 is the maximum possible.It can be showed, that for a classical spherically symmetric object of mass m' and radius R, the general relativistic limit gives
is the maximum possible.It can be showed, that for a classical spherically symmetric object of mass m' and radius R, the general relativistic limit gives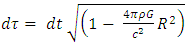 | (17) |
Since the expression in brackets must be real, we arrive at the restriction: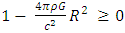 | (18) |
And therefore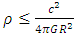 | (19) |
For an object of any given mass m' and radius R we have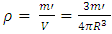 | (20) |
Since for any mass m' of radius R one must have, by Eq. 16 above, 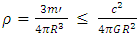 | (21) |
The result is that for any mass m'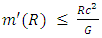 | (22) |
Obviously, the smaller the radius R, the smaller the allowed mass m'.For the minimal possible length (according to Planck) 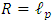 one obtains:
one obtains: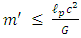 | (23) |
Recall now, by Planck's dimensionality analysis) that 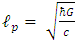 and
and 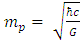 so
so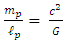 | (24) |
Therefore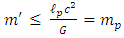 | (25) |
Therefore, for any mass m' (with radius 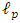 )
)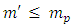 | (26) |
And since 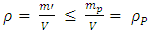 | (27) |
We have the result that 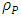 is the maximal possible density, namely Planck density.In other words, for any given radius R, the mass m'(R) becomes smaller and smaller with R, but when one reaches the smallest possible radius
is the maximal possible density, namely Planck density.In other words, for any given radius R, the mass m'(R) becomes smaller and smaller with R, but when one reaches the smallest possible radius 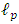 , the mass must be smaller than the Planck mass
, the mass must be smaller than the Planck mass 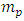 , and so, the density will always be smaller than the Planck density
, and so, the density will always be smaller than the Planck density 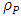 . One can reduce the radius R, but the density will never exceed the Planck density.
. One can reduce the radius R, but the density will never exceed the Planck density.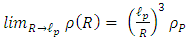 | (28) |
Assume next, that the sphere has density 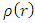 , which varies with distance r from its center.Assume the sphere is of minimal possible radius
, which varies with distance r from its center.Assume the sphere is of minimal possible radius 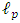 .We need to calculate the radius R of a quantized particle by its average normalized density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to a volume, with constant density
.We need to calculate the radius R of a quantized particle by its average normalized density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to a volume, with constant density 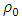 one obtains:
one obtains: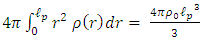 | (29) |
By definition, the average classical distance 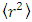 is given by the integral over the normalized density:
is given by the integral over the normalized density: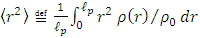 | (30) |
Thus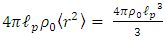 | (31) |
and so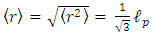 | (32) |
Hence, the actual measured classical radius R is given by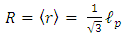 | (33) |
The above result shows how the lower limit of the classical gravitation theory by Einstein, is related to the Planck length, which is a quantum phenomenon posed by dimensional analysis of the universe constants.Therefore, classical relativity and the relationship between the universal constants leads to quantization of space.
8. Quantization by Planck's Units and Maximal Density Limit
In the limit where 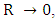 one needs to consider quantum limits and the uncertainty principle.Planck's mass
one needs to consider quantum limits and the uncertainty principle.Planck's mass 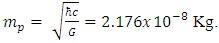 Planck's length
Planck's length 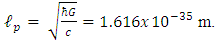 However, dimensional analysis can only determine the Planck's units up to a dimensionless multiplicative factor. For instance, use h instead of
However, dimensional analysis can only determine the Planck's units up to a dimensionless multiplicative factor. For instance, use h instead of 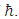 Based on Planck's units one obtains Planck's maximal density
Based on Planck's units one obtains Planck's maximal density 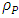 as Planck's mass/Planck's volume (assuming
as Planck's mass/Planck's volume (assuming 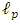 is the lowest possible physical distance, leads to the maximal possible physical density assumption).
is the lowest possible physical distance, leads to the maximal possible physical density assumption).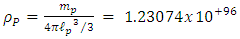 | (34) |
(If one uses the Planck constant instead of the reduced Planck's constant, the Planck density will be modified by a factor of 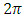 ).Since one must assume that Planck's density is the maximum possible density allowed, we now ask, what should the minimum classical radius R be, in order for
).Since one must assume that Planck's density is the maximum possible density allowed, we now ask, what should the minimum classical radius R be, in order for 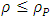 . (any classical density cannot exceed the Planck density).Therefore:
. (any classical density cannot exceed the Planck density).Therefore: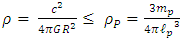 | (35) |
Doing the calculation, we find that one must have 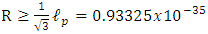 m.Compared to Planck's length
m.Compared to Planck's length 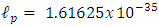 m, the classically derived radius R is smaller than the allowed Planck's length
m, the classically derived radius R is smaller than the allowed Planck's length 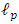 , by an unexplained factor of 0.5774.These calculations were based on the assumptions of negligible
, by an unexplained factor of 0.5774.These calculations were based on the assumptions of negligible 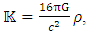 and
and 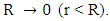 It seems now, that the classical solution to the metric of a spherically symmetric object, puts a lower limit on the radius R of an object. It looks like there is a sort of quantization limit to small scale objects in spacetime.Instead of having
It seems now, that the classical solution to the metric of a spherically symmetric object, puts a lower limit on the radius R of an object. It looks like there is a sort of quantization limit to small scale objects in spacetime.Instead of having  we find
we find 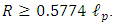 The reason for this 0.5774 factor is due to the fact that we have assumed a constant density inside the sphere. If instead we assume variation in density with radius (highest density at
The reason for this 0.5774 factor is due to the fact that we have assumed a constant density inside the sphere. If instead we assume variation in density with radius (highest density at  and then it falls off to zero at
and then it falls off to zero at  ). We need to calculate the radius R of a quantized particle by its average density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to the same volume, but with a constant average density
). We need to calculate the radius R of a quantized particle by its average density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to the same volume, but with a constant average density 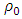 one obtains (see paragraph VI on density upper limit)):
one obtains (see paragraph VI on density upper limit)):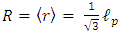 | (36) |
Since 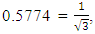 it is now clear where the reduction factor came from.The above result shows how the lower limit of the classical gravitation theory by Einstein, (Schwarzschild radius), and the dimensional constraints between the constants of the universe, result in a quantized material space.
it is now clear where the reduction factor came from.The above result shows how the lower limit of the classical gravitation theory by Einstein, (Schwarzschild radius), and the dimensional constraints between the constants of the universe, result in a quantized material space.
9. A Tunneled Sphere "Thought Experiment"
Consider a sphere with a thin penetrating tunnel through center of sphere between opposite surfaces.The sphere of radius R and of mass M will exert a gravitational attractive force on a remote particle. The force will be directed towards the center of the sphere, as if all of its mass is concentrated at its center (where r = 0).The attracted particle will be accelerated until it reaches the surface, but then will continue its path through the hole. It will continue with no acceleration inside the shell and then come out through the opposite hole.On its journey, the particle will pass twice the Schwarzschild radius 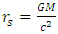 on its way towards the center and on its way out.The metric of this shell will be similar to that of a spherical mass. Only that this time, even though
on its way towards the center and on its way out.The metric of this shell will be similar to that of a spherical mass. Only that this time, even though 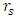 is inside the body, one can reach the Schwarzschild radius independently of whether it is a black hole or a standard mass.One way of doing the experiment would be to send a photon through the hole in the mass and compare its time of arrival with a simultaneously emitted photon traveling outside the mass. One would then be able to compare differences in the time of arrival for the two photons.This gedanken experiment can reveal whether the approach to
is inside the body, one can reach the Schwarzschild radius independently of whether it is a black hole or a standard mass.One way of doing the experiment would be to send a photon through the hole in the mass and compare its time of arrival with a simultaneously emitted photon traveling outside the mass. One would then be able to compare differences in the time of arrival for the two photons.This gedanken experiment can reveal whether the approach to 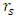 will last forever in the eyes of the external observer. If it does, then the particle will never be able to come out through the opposite hole.
will last forever in the eyes of the external observer. If it does, then the particle will never be able to come out through the opposite hole.
10. Dynamics Near Center
It is interesting to see what are the equations of motion near center (where r<< R).Assuming spherical symmetry [21,22], it is allowed to investigate it along the radial distance r, and assume it is the x axis.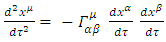 | (37) |
where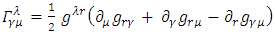 | (38) |
The total time of flight in the classical case will be given by (see Appendix 2):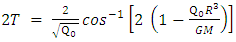 Whereas in the general relativistic case it will be:
Whereas in the general relativistic case it will be: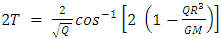 Comparing the two results,
Comparing the two results, 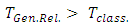 As an example, for the Sun, with
As an example, for the Sun, with 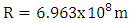 and Sun density
and Sun density 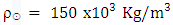 the predicted general relativistic cross time will be 6.6 mSec longer than the classical calculated cross time. This result is based on average Q over r from 0 to R.For an average Neutron star of radius R=11,000 m and density
the predicted general relativistic cross time will be 6.6 mSec longer than the classical calculated cross time. This result is based on average Q over r from 0 to R.For an average Neutron star of radius R=11,000 m and density 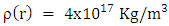 , the passage time under general relativity prediction, will last 0.13 mSec longer than under classical calculation.
, the passage time under general relativity prediction, will last 0.13 mSec longer than under classical calculation.
11. Conclusions
Using Newton's classical shell theorem, the Schwarzschild metric was modified. This removed the singularity at r = 0 for a standard object (not a black hole). For all practical matters, r < R can be treated as an empty space even for the densest known stellar objects (neutron stars) and also for elementary particles (neutrons for instance).It was demonstrated how general relativity evidently leads to quantization of space-time. Both classical and quantum mechanical limits on density give the same result.
Appendix 1
For a curved spacetime we define the Riemann tensor: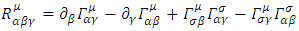 [1]Where
[1]Where 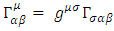 are the Christoffel symbols:
are the Christoffel symbols: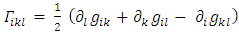 | (39) |
The Ricci tensor 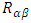 is defined by:
is defined by: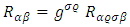 | (40) |
And the curvature scalar R is defined by: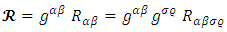 | (41) |
For the Einstein equation one has: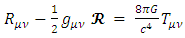 | (42) |
In empty space 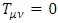 everywhere and therefore
everywhere and therefore 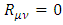 everywhere. Due to spherical symmetry, the metric must be of the form
everywhere. Due to spherical symmetry, the metric must be of the form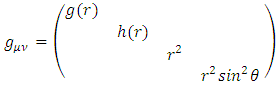 | (43) |
Where g(r) and h(r) are functions of the distance r from the coordinate center (located at the center of the mass.So, the infinitesimal proper time interval 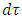 between two events along a time-like path is given by
between two events along a time-like path is given by 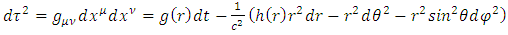 | (44) |
With the flat space metric 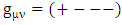 .In order to solve Einstein's equation everywhere, one can no longer assume that the curvature
.In order to solve Einstein's equation everywhere, one can no longer assume that the curvature 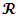 is null anywhere. This is true only outside the mass and so
is null anywhere. This is true only outside the mass and so 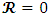 only for r > R.Assuming the mass density of the object being homogeneous and at total freeze of motion,
only for r > R.Assuming the mass density of the object being homogeneous and at total freeze of motion, 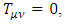 except for
except for 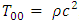 , with
, with 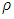 being the mass density.
being the mass density.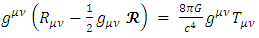 | (45) |
Under perfect fluid conditions, 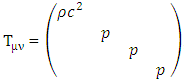 , where p is the pressure.Define
, where p is the pressure.Define 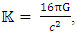 and so,
and so,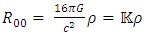 | (46) |
For all other terms, 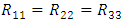 :
: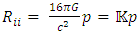 | (47) |
From the definitions of the Riemann tensor and the Ricci tensor we obtain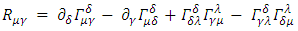 | (48) |
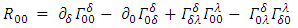 | (49) |
Following some tedious mathematical work, one arrives at [4]: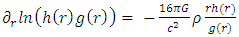 | (50) |
And so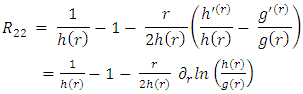 | (51) |
We have then two equations: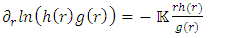 | (52) |
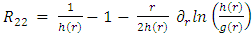 | (53) |
Outside the mass (r>R)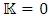 and so:
and so: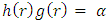 (some constant).Substitute in eq. 2 to obtain:
(some constant).Substitute in eq. 2 to obtain: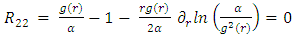 | (54) |
And after few steps: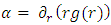 | (55) |
So finally: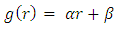 | (56) |
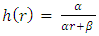 | (57) |
The metric becomes: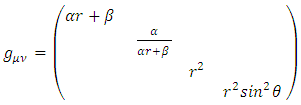 | (58) |
Comparing this metric with the asymptotic weak-field metric 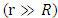 :
: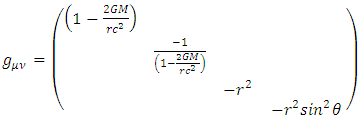 | (59) |
It is suggested that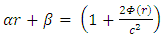 | (60) |
Therefore, 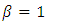 | (61) |
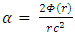 | (62) |
This shows us that the structure of the Schwarzschild metric in Eq. 7, is not only a result of dimensional considerations discussed above, but also a result of spherical symmetry considerations of the Einstein Equation, Eq. 17.This result was obtained based on symmetry arguments only, and it is independent of the weak-field approximation.Inside the mass (r < R)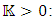 The only approximation made was the assumption on empty space solution. For non-empty space, it will be valid for a perfect fluid of zero pressure.However, one may use a model where the pressure p is proportional o the density [18], and so
The only approximation made was the assumption on empty space solution. For non-empty space, it will be valid for a perfect fluid of zero pressure.However, one may use a model where the pressure p is proportional o the density [18], and so 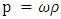 where
where 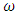 is a proportionality factor.
is a proportionality factor.
Appendix 2
Since by coordinates choice and symmetry, only 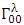 and
and 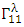 are non-zero (assuming constant gravitational field
are non-zero (assuming constant gravitational field 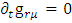 ).
).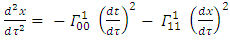 | (63) |
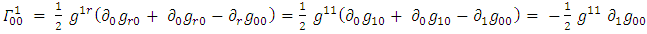 | (64) |
and likewise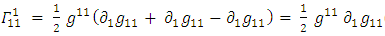 | (65) |
The equation of motion in the x direction becomes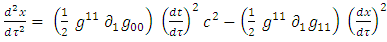 | (66) |
Since the choice of coordinates is such that x is represented by r, one can write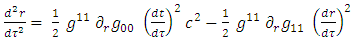 | (67) |
From the proper-time result (which holds inside the sphere, where r < R)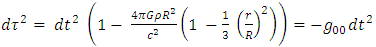 | (68) |
Define for convenience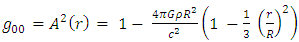 | (69) |
And so 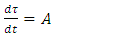 | (70) |
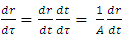 | (71) |
And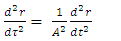 | (72) |
From the metric definition: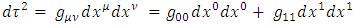 | (73) |
and since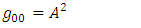 | (74) |
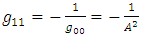 | (75) |
One obtains: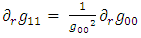 | (76) |
Inserting into Eq. [49] one obtains: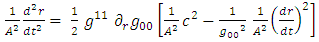 | (77) |
And so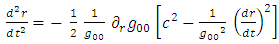 | (78) |
For 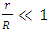
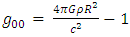 | (79) |
And so 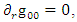 which means that
which means that 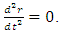 The acceleration near the center is zero.However, if one moves away from the center:
The acceleration near the center is zero.However, if one moves away from the center: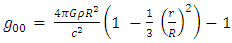 | (80) |
And so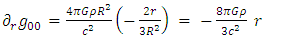 | (81) |
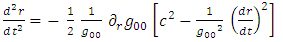 | (82) |
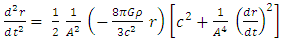 | (83) |
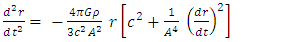 | (84) |
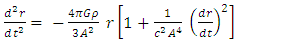 | (85) |
Near center (where r à 0), 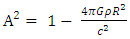 depends on r only through the density
depends on r only through the density 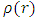 .We may write
.We may write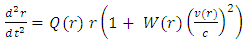 | (86) |
Here, 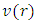 is the approach velocity. Q and W depend on r and are defined by:
is the approach velocity. Q and W depend on r and are defined by: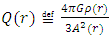 | (87) |
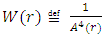 | (88) |
The result shows how on approach to center (r à 0), where 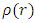 is assumed constant, the acceleration decreases in proportion with r on one hand, but depends also on the square of the approach velocity.For small approach-to-center velocity
is assumed constant, the acceleration decreases in proportion with r on one hand, but depends also on the square of the approach velocity.For small approach-to-center velocity 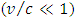
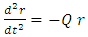 | (89) |
One may approximate though for a slow approach velocity 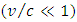 :
: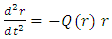 | (90) |
where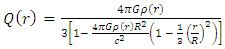 | (91) |
(Recall that by the assumption on the maximal density (Eq. 38), 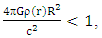 and so,
and so, 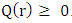 . Also, note that
. Also, note that 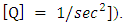 One may solve this under certain approximation:
One may solve this under certain approximation: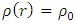 constant density inside r < R.In this case
constant density inside r < R.In this case 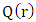 is nearly a constant independent of r, and the equation becomes
is nearly a constant independent of r, and the equation becomes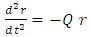 | (92) |
Which general solution is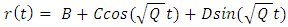 | (93) |
Even though 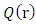 is not constant, the term
is not constant, the term 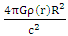 in the denominator of
in the denominator of 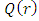 is of the order of, or less than,
is of the order of, or less than, 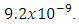 Q(r) may be approximated as:
Q(r) may be approximated as: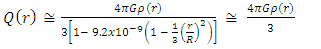 | (94) |
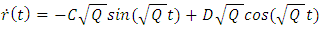 | (95) |
Assuming zero start velocity, 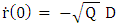 one must have D = 0.Hence
one must have D = 0.Hence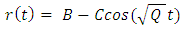 | (96) |
Also, 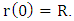 Therefore
Therefore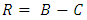 | (97) |
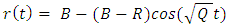 | (98) |
Assume the acceleration 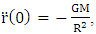
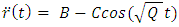 | (99) |
Using these assumptions, one obtains: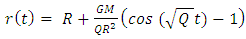 | (100) |
Furthermore, if the object arrives at the center (r = 0) at some later time T, one has: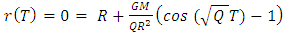 | (101) |
The time to cross the diameter 2R (from surface to surface through the center) is thus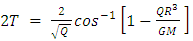 | (102) |
Where 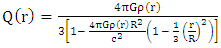 In this case
In this case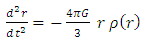 | (103) |
Classically, a falling object of mass m, starting at r < R, will be accelerated towards center according to the potential: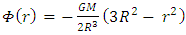 | (104) |
And the acceleration will be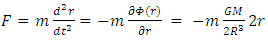 | (105) |
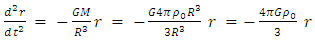 | (106) |
Classically, the acceleration will be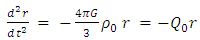 | (107) |
with 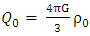 This, in comparison to the general relativistic solution:
This, in comparison to the general relativistic solution: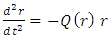 | (108) |
References
| [1] | Kevin Brown, Reflections on Relativity, ISBN-12: 9781257033027 Lulu.com. 2010. |
| [2] | Landau, L. D.; Lifshitz, E. M.. The Classical Theory of Fields. Course of Theoretical Physics. 2 (4th Revised English ed.). Pergamon Press. (1950). |
| [3] | Buchdahl H. A., Isotropic Coordinates and Schwarzschild Metric, International Journal of Theoretical Physics, Volume 24, Issue 7, pp.731-739, (1985). |
| [4] | Davie R, Schwarzschild metric 1-3, https://www.youtube.com/watch?v=D1mmLjR-szY. |
| [5] | José P. S. Lemos, Diogo L. F. G. Silva. "Maximal extension of the Schwarzschild metric: From Painlevé-Gullstrand to Kruskal-Szekeres", arXiv:2005.14211. (2020). |
| [6] | P. Painlevé, “La mécanique classique et la théorie de la relativité”, Comptes Rendus de l’Académie des Sciences 173, 677 (1921). |
| [7] | A. Gullstrand, “Allgemeine Lösung des statischen Einkörperproblems in der Einsteinschen Gravitationstheorie”, Arkiv för Matematik, Astronomi och Fysik 16, 1 (1922). |
| [8] | A. S. Eddington, “A comparison of Whitehead’s and Einstein’s formula”, Nature 113, 192 (1924). |
| [9] | D. Finkelstein, “Past-future asymmetry of the gravitational field of a point particle”, Phys. Rev. 110, 965 (1958). |
| [10] | G. Lemaître, “L’Univers en expansion”, Annales de la Société Scientifique de Bruxelles 53A, 51 (1933). |
| [11] | J. Synge, “The gravitational field of a particle”, Proceedings of the Royal Irish Academy, Section A: Mathematical and Physical Sciences 53, 83 (1950). |
| [12] | M. Kruskal, “Maximal extension of Schwarzschild metric”, Phys. Rev. 119, 1743 (1959). |
| [13] | G. Szekeres, “On the singularities of a Riemannian manifold”, Publicationes Mathematicae Debrecen 7, 285 (1959). |
| [14] | I. Newton, Philosophiae Naturalis Principia Mathematica. London. pp. Theorem XXXI. (1687). |
| [15] | R. Arens, "Newton\'s observations about the field of a uniform thin spherical shell".Note di Matematica, Vol. x, Suppl. n. 1, 39-45. (1990). |
| [16] | Carlo Rovelli, Scholarpedia, 3(5): 7117. doi.org/10.4249/scholarpedia.7117 (2008). |
| [17] | I. Gkigkitzis, I. Haranas, O. Ragos, "Kretschmann Invariant and Relations between Spacetime Singularities, Entropy and Information". arXiv preprint arXiv:1406.1581, (2014). |
| [18] | R. Moradi, J. T. Firouzjaee, R. Mansouri. "Cosmological black holes: the spherical perfect fluid collapse with pressure in a FRW background", Classical and Quantum Gravity. 32, 21 (2015). |
| [19] | Richard C. Henry (2000). "Kretschmann Scalar for a Kerr-Newman Black Hole". The Astrophysical Journal. The American Astronomical Society. 535 (1): 350–353. |
| [20] | A. Zee, "Einstein Gravity in a Nutshell",Princeton University Press, 2013. |
| [21] | Ray D'Inverno, ""Introducing Einstein's Relativity", Oxford University Press, 1992. |
| [22] | Misner, K. Thorne and A. Wheeler, "Gravitation", Freeman and Co. 1975. |



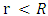 . The point r = 0 is an infinitesimally small location in space. No mass can be indefinitely condensed to this point. Thus, when investigating the concept of a mass, one has to consider its finite radius. By including the shell theorem for
. The point r = 0 is an infinitesimally small location in space. No mass can be indefinitely condensed to this point. Thus, when investigating the concept of a mass, one has to consider its finite radius. By including the shell theorem for 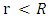 , the singularity at
, the singularity at 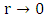 is removed. It is also shown, that a situation where rs < R but
is removed. It is also shown, that a situation where rs < R but 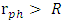 is possible. Therefore, the existence of a photon sphere light ring does not necessarily indicate a black hole.It is shown, that the condition for a gravitational collapse is
is possible. Therefore, the existence of a photon sphere light ring does not necessarily indicate a black hole.It is shown, that the condition for a gravitational collapse is 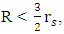 and not
and not 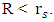 Further in this work, the question of maximal density is considered and compared to the quantum limit of mass density put by Planck's units as dictated from dimensional analysis.There are two main claims here:1. Black holes (if exist) will result only if the Schwarzschild radius is larger than 2/3R.2. General relativity leads to quantization of gravity.
Further in this work, the question of maximal density is considered and compared to the quantum limit of mass density put by Planck's units as dictated from dimensional analysis.There are two main claims here:1. Black holes (if exist) will result only if the Schwarzschild radius is larger than 2/3R.2. General relativity leads to quantization of gravity.
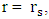 with
with 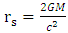 which cause the metric to diverge at these radii. There is no problem as long as
which cause the metric to diverge at these radii. There is no problem as long as 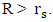 The singularity at
The singularity at 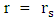 divides the Schwarzschild coordinates in two disconnected regions. The exterior Schwarzschild solution with
divides the Schwarzschild coordinates in two disconnected regions. The exterior Schwarzschild solution with 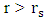 is the one that is related to the gravitational fields of stars and planets. The interior Schwarzschild solution with
is the one that is related to the gravitational fields of stars and planets. The interior Schwarzschild solution with 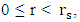 which contains the singularity at r = 0, is completely separated from the outer region by the so-called singularity at r =
which contains the singularity at r = 0, is completely separated from the outer region by the so-called singularity at r = 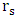 . The Schwarzschild coordinates therefore give no physical connection between these two regions.The singularity at r =
. The Schwarzschild coordinates therefore give no physical connection between these two regions.The singularity at r = 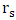 is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions. When changing to a different coordinate system, the metric becomes regular at r =
is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions. When changing to a different coordinate system, the metric becomes regular at r = 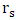 and can extend the external region to values of r smaller than
and can extend the external region to values of r smaller than 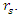 Using a different coordinate transformation one can then relate the extended external region to the inner region. As will be shown later on, this so-called singularity is completely removed even for the Schwarzschild coordinates.The case r = 0 is different, however. If one asks that the solution be valid for all r, one runs into a true physical singularity, or gravitational singularity, at the origin. To see whether this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant [19], which is given by
Using a different coordinate transformation one can then relate the extended external region to the inner region. As will be shown later on, this so-called singularity is completely removed even for the Schwarzschild coordinates.The case r = 0 is different, however. If one asks that the solution be valid for all r, one runs into a true physical singularity, or gravitational singularity, at the origin. To see whether this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant [19], which is given by 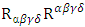 For a Schwarzschild black hole of mass M and radius R, the Kretschmann invariant is
For a Schwarzschild black hole of mass M and radius R, the Kretschmann invariant is 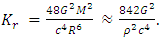 Obviously it is independent of the radius R, and is always greater than 0 (provided we accept the physical requirement that the density
Obviously it is independent of the radius R, and is always greater than 0 (provided we accept the physical requirement that the density 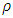 is never infinite).At r = 0 the curvature can become infinite, if and only if, it represents a point particle of zero mass. One cannot compress a finite mass into an infinitesimal point (of radius R = 0). Any finite mass should have a finite radius R > 0. Therefore, when looking into the point r = 0, one needs to consider the effects of the outer shells of matter which surround the r = 0 point.General relativity predicts that any object collapsing beyond a certain point (for stars this is the Schwarzschild radius) would form a black hole, inside which a singularity (covered by an event horizon) would be formed. As will be shown in the following, no such singularities exist.
is never infinite).At r = 0 the curvature can become infinite, if and only if, it represents a point particle of zero mass. One cannot compress a finite mass into an infinitesimal point (of radius R = 0). Any finite mass should have a finite radius R > 0. Therefore, when looking into the point r = 0, one needs to consider the effects of the outer shells of matter which surround the r = 0 point.General relativity predicts that any object collapsing beyond a certain point (for stars this is the Schwarzschild radius) would form a black hole, inside which a singularity (covered by an event horizon) would be formed. As will be shown in the following, no such singularities exist.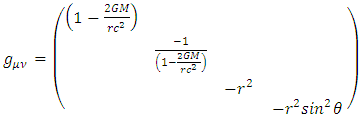
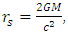 the metric has a singularity.2. At r à 0, the metric diverges.The first singularity is not a real one, as it can be removed by appropriate coordinate transformations [5-13]. The second singularity cannot be removed by coordinate transformation. It is an inherent singularity at
the metric has a singularity.2. At r à 0, the metric diverges.The first singularity is not a real one, as it can be removed by appropriate coordinate transformations [5-13]. The second singularity cannot be removed by coordinate transformation. It is an inherent singularity at 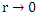 in any inverse square law central force problem of gravitational field). One so far have not been able to relate to the divergency problem of force which is inversely proportional to the square of the distance r from center of the field source.To solve this problem, we must investigate the behavior of the field inside the mass.If any mass source is finite in size, the solution to the potential as a function of distance must be modified, so that it includes the region where r < R, the radius of the mass.In addition, the Einstein field equation should be related to in non-empty space. But to a very good approximation, the Einstein equation in the inside of even the heaviest stellar objects can be considered same as empty space.This assumption will only be valid for a perfect fluid solution, where of the
in any inverse square law central force problem of gravitational field). One so far have not been able to relate to the divergency problem of force which is inversely proportional to the square of the distance r from center of the field source.To solve this problem, we must investigate the behavior of the field inside the mass.If any mass source is finite in size, the solution to the potential as a function of distance must be modified, so that it includes the region where r < R, the radius of the mass.In addition, the Einstein field equation should be related to in non-empty space. But to a very good approximation, the Einstein equation in the inside of even the heaviest stellar objects can be considered same as empty space.This assumption will only be valid for a perfect fluid solution, where of the 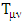 tensor, only energy density is considered, while momentum density, shear stress, momentum flux and pressure are either null or irrelevant.
tensor, only energy density is considered, while momentum density, shear stress, momentum flux and pressure are either null or irrelevant.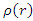 , with r being the radial distance from center (at r = 0).Assuming this object has a volume
, with r being the radial distance from center (at r = 0).Assuming this object has a volume 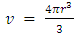 and radius R, its average density will be
and radius R, its average density will be 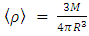 and since
and since 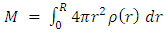 it is straightforward to see that
it is straightforward to see that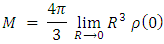 This means that unless the density at the center
This means that unless the density at the center 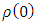 is infinite, the mass must vanish (M = 0).The only case of M > 0 is possible if and only if
is infinite, the mass must vanish (M = 0).The only case of M > 0 is possible if and only if 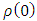 is infinite. And if we assume physical continuity, then we may write
is infinite. And if we assume physical continuity, then we may write 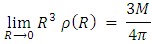 In other words
In other words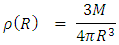 And for any finite mass M
And for any finite mass M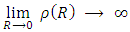 However, as will be shown later, the density of any object must have an upper limit and it cannot become infinitely large. To resolve this contradiction, one must accept, that no mass can be condensed to a singular point r = 0. A mass will always have some finite density and a finite radius (volume).Therefore, when considering gravitation at r = 0, one must consider the effects of surrounding mass. Condensed as it might be, but still of finite density and surrounding r = 0.In classical mechanics, the shell theorem, proven already by Isaac Newton [14] states that:A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center.If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object's location within the shell.A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass.Due to the shell theorem, the gravitational potential of a spherically symmetric object of mass M and radius R, as a function of distance r, from the object's center is given by:
However, as will be shown later, the density of any object must have an upper limit and it cannot become infinitely large. To resolve this contradiction, one must accept, that no mass can be condensed to a singular point r = 0. A mass will always have some finite density and a finite radius (volume).Therefore, when considering gravitation at r = 0, one must consider the effects of surrounding mass. Condensed as it might be, but still of finite density and surrounding r = 0.In classical mechanics, the shell theorem, proven already by Isaac Newton [14] states that:A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center.If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object's location within the shell.A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass.Due to the shell theorem, the gravitational potential of a spherically symmetric object of mass M and radius R, as a function of distance r, from the object's center is given by: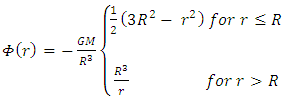
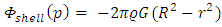
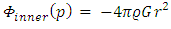
 , and
, and 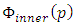 . Thus, (for r < R):
. Thus, (for r < R):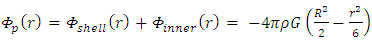
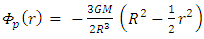
 term is a function of the distance r and one may write:
term is a function of the distance r and one may write: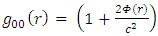
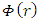 is a function of distance r, and must have the dimensions of
is a function of distance r, and must have the dimensions of 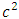 . It must obey the constraint of
. It must obey the constraint of 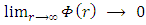 as should be the case at infinite distance in empty flat space.Its units should be [G][Kg]/[m] in order to make
as should be the case at infinite distance in empty flat space.Its units should be [G][Kg]/[m] in order to make 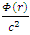 dimensionless.We therefore have a good reason to assume that
dimensionless.We therefore have a good reason to assume that 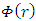 is the gravitational potential due to a spherically symmetric object, independent of the size and of the density of that object. Exactly as described by eq. 2.Second argument- Einstein equation under spherical symmetryFor a curved spacetime, based on the Riemann tensor, it can be shown that
is the gravitational potential due to a spherically symmetric object, independent of the size and of the density of that object. Exactly as described by eq. 2.Second argument- Einstein equation under spherical symmetryFor a curved spacetime, based on the Riemann tensor, it can be shown that 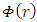 must have the form of a gravitational potential (see Appendix 1).Following these arguments, it is justified to identify
must have the form of a gravitational potential (see Appendix 1).Following these arguments, it is justified to identify 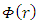 , as the gravitational potential of the field created by a spherically symmetric non-rotating uncharged mass.
, as the gravitational potential of the field created by a spherically symmetric non-rotating uncharged mass.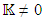 where
where 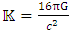
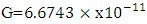 and so
and so 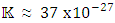 , so unless the internal density
, so unless the internal density 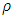 is of the order of
is of the order of 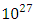 Kg/m3, the equation can be solved with the assumption of
Kg/m3, the equation can be solved with the assumption of 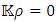 .Even the heaviest neutron stars have overall densities of the order of
.Even the heaviest neutron stars have overall densities of the order of 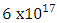 Kg/m3. For elementary particles, the neutron for instance, has density of approximately
Kg/m3. For elementary particles, the neutron for instance, has density of approximately 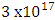 Kg/m3. So, for all practical calculations one may assume
Kg/m3. So, for all practical calculations one may assume 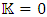 inside any mass (that is, for r < R).For the internal pressure p, as long as the internal pressure is much less than
inside any mass (that is, for r < R).For the internal pressure p, as long as the internal pressure is much less than 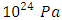 ,
, 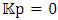 . For the Sun for instance, the internal core pressure is
. For the Sun for instance, the internal core pressure is 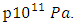 Finding the solution of the homogeneous differential equation with
Finding the solution of the homogeneous differential equation with 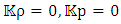 , will lead to the non-homogeneous solution with
, will lead to the non-homogeneous solution with 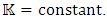 But we will concentrate on the homogeneous solution, since
But we will concentrate on the homogeneous solution, since 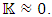 In case of a constant
In case of a constant 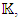 the non-homogeneous solution can be found.This is the case for a perfect fluid.Under the assumption of
the non-homogeneous solution can be found.This is the case for a perfect fluid.Under the assumption of 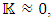 for the interior of the sphere, the time separation inside the sphere is given by
for the interior of the sphere, the time separation inside the sphere is given by 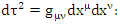
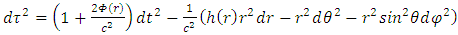
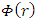 :
: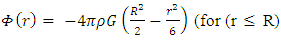
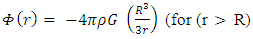 The Schwarzschild metric inside the sphere (r ≤ R) becomes
The Schwarzschild metric inside the sphere (r ≤ R) becomes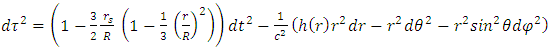
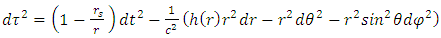
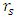 and
and 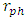 are inside the objects radius R.
are inside the objects radius R. 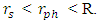 This is a standard object.B - a situation where
This is a standard object.B - a situation where 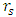 is inside the object's radius R (a standard object) while
is inside the object's radius R (a standard object) while 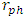 is outside the object.
is outside the object. 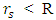
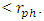 C - a situation of a black hole, where both
C - a situation of a black hole, where both 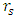 and
and 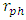 are outside R.
are outside R. 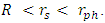 Therefore, B represents a possible situation where a photon sphere light ring exists around a standard (not a black hole) body.For said cases, the photon sphere radius
Therefore, B represents a possible situation where a photon sphere light ring exists around a standard (not a black hole) body.For said cases, the photon sphere radius 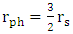 may fall inside or outside R.
may fall inside or outside R. Case A is a standard object, with both
Case A is a standard object, with both 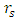 , and
, and 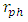 falling inside R.Case B is a white object, with
falling inside R.Case B is a white object, with 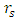 falling inside R but
falling inside R but 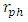 falling outside R. Light is trapped in the photon sphere, causing the object to have a white glowing ring around it. There is no gravitational collapse.Case C is a true black body, with both
falling outside R. Light is trapped in the photon sphere, causing the object to have a white glowing ring around it. There is no gravitational collapse.Case C is a true black body, with both 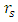 and
and 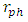 falling outside R.Case A, both
falling outside R.Case A, both 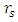 and
and 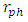 are inside R (holds for most stellar objects – but not for black holes). One obtains:
are inside R (holds for most stellar objects – but not for black holes). One obtains: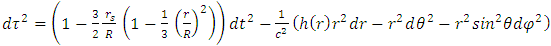
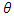 and
and 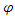 terms are zeroIn other words, for r > R
terms are zeroIn other words, for r > R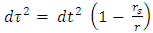
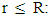
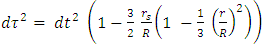
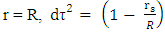 , for both.Investigating the condition
, for both.Investigating the condition 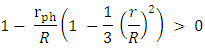 we see that in Case B, for all
we see that in Case B, for all 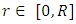 and as long as
and as long as 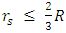 there is no singularity in the Schwarzschild metric.At
there is no singularity in the Schwarzschild metric.At 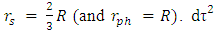 becomes zero, and the object evaporates into photons
becomes zero, and the object evaporates into photons 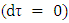 . Thus,
. Thus, 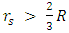 is the condition for a gravitational collapse. As long as
is the condition for a gravitational collapse. As long as 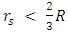 the object is a standard object and does not undergo any gravitational collapse. This, in contrast to the current assertion (for r > R), is based on Eq. 37, which states that
the object is a standard object and does not undergo any gravitational collapse. This, in contrast to the current assertion (for r > R), is based on Eq. 37, which states that 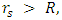 is the condition for a gravitational collapse.We see that as long as the photon sphere is inside the object (
is the condition for a gravitational collapse.We see that as long as the photon sphere is inside the object (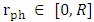 , the Schwarzschild radius
, the Schwarzschild radius 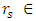
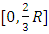 . In other words, as long as the photon sphere does not show, the object is stable and does not suffer gravitational collapse. Once the photon sphere shows up
. In other words, as long as the photon sphere does not show, the object is stable and does not suffer gravitational collapse. Once the photon sphere shows up 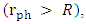 the object undergoes gravitational collapse.Anywhere in the region where
the object undergoes gravitational collapse.Anywhere in the region where 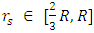 the object undergoes gravitational collapse, and since
the object undergoes gravitational collapse, and since 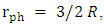 the photon sphere is outside the object, creating a bright light ring outside R, at
the photon sphere is outside the object, creating a bright light ring outside R, at 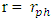 .Near the sphere's center, where
.Near the sphere's center, where 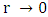 and r < R, one has
and r < R, one has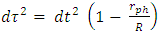
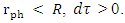 It may be re-written as:
It may be re-written as: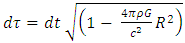
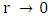 is removed.The proper time
is removed.The proper time 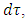 must remain well defined. Therefore, an upper limit on the density must exist for a given radius R, otherwise the expression for
must remain well defined. Therefore, an upper limit on the density must exist for a given radius R, otherwise the expression for 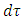 becomes undefined.Notice that this assertion leads to the constraint
becomes undefined.Notice that this assertion leads to the constraint 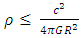
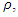 of any object with radius R. When
of any object with radius R. When 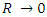 , the density may increase indefinitely, but as will be shown next, there is an upper limit on the density.
, the density may increase indefinitely, but as will be shown next, there is an upper limit on the density.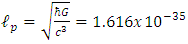 m. Here
m. Here 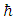 is the Planck constant that governs the scale of the quantum effects, G is the Newton constant that governs the strength of the gravitational force, and c is the speed of light, that governs the scale of the relativistic effects. The Planck length is many times smaller than what current technology is capable of observing. physical effects at scales that are so small. Because of this, we have no direct experimental guidance for building a quantum theory of gravity [16]. Suppose there exists a quantum minimum for distance. We call it the Planck length and denote it by
is the Planck constant that governs the scale of the quantum effects, G is the Newton constant that governs the strength of the gravitational force, and c is the speed of light, that governs the scale of the relativistic effects. The Planck length is many times smaller than what current technology is capable of observing. physical effects at scales that are so small. Because of this, we have no direct experimental guidance for building a quantum theory of gravity [16]. Suppose there exists a quantum minimum for distance. We call it the Planck length and denote it by 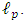 It is given by
It is given by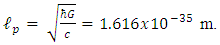 Define in addition the Planck massPlanck's mass
Define in addition the Planck massPlanck's mass 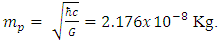 If this assumption is true, then the minimal spherical volume possible is
If this assumption is true, then the minimal spherical volume possible is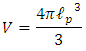 Let
Let 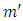 denote the mass of this volume, so its density will be given by
denote the mass of this volume, so its density will be given by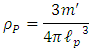 Since by assumption
Since by assumption 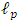 is the minimal length possible in nature, then for any mass m' the density
is the minimal length possible in nature, then for any mass m' the density 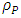 is the maximum possible.It can be showed, that for a classical spherically symmetric object of mass m' and radius R, the general relativistic limit gives
is the maximum possible.It can be showed, that for a classical spherically symmetric object of mass m' and radius R, the general relativistic limit gives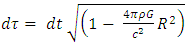
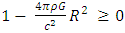
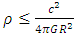
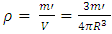
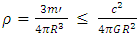
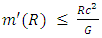
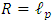 one obtains:
one obtains: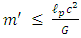
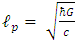 and
and 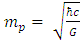 so
so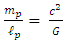
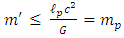
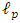 )
)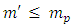
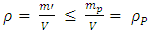
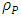 is the maximal possible density, namely Planck density.In other words, for any given radius R, the mass m'(R) becomes smaller and smaller with R, but when one reaches the smallest possible radius
is the maximal possible density, namely Planck density.In other words, for any given radius R, the mass m'(R) becomes smaller and smaller with R, but when one reaches the smallest possible radius 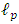 , the mass must be smaller than the Planck mass
, the mass must be smaller than the Planck mass 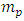 , and so, the density will always be smaller than the Planck density
, and so, the density will always be smaller than the Planck density 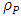 . One can reduce the radius R, but the density will never exceed the Planck density.
. One can reduce the radius R, but the density will never exceed the Planck density.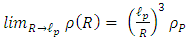
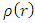 , which varies with distance r from its center.Assume the sphere is of minimal possible radius
, which varies with distance r from its center.Assume the sphere is of minimal possible radius 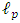 .We need to calculate the radius R of a quantized particle by its average normalized density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to a volume, with constant density
.We need to calculate the radius R of a quantized particle by its average normalized density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to a volume, with constant density 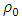 one obtains:
one obtains: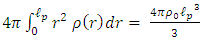
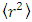 is given by the integral over the normalized density:
is given by the integral over the normalized density: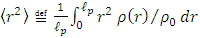
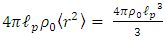
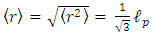
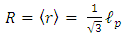
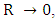 one needs to consider quantum limits and the uncertainty principle.Planck's mass
one needs to consider quantum limits and the uncertainty principle.Planck's mass 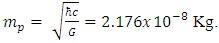 Planck's length
Planck's length 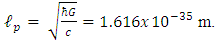 However, dimensional analysis can only determine the Planck's units up to a dimensionless multiplicative factor. For instance, use h instead of
However, dimensional analysis can only determine the Planck's units up to a dimensionless multiplicative factor. For instance, use h instead of 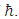 Based on Planck's units one obtains Planck's maximal density
Based on Planck's units one obtains Planck's maximal density 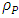 as Planck's mass/Planck's volume (assuming
as Planck's mass/Planck's volume (assuming 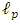 is the lowest possible physical distance, leads to the maximal possible physical density assumption).
is the lowest possible physical distance, leads to the maximal possible physical density assumption).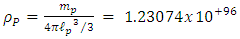
 ).Since one must assume that Planck's density is the maximum possible density allowed, we now ask, what should the minimum classical radius R be, in order for
).Since one must assume that Planck's density is the maximum possible density allowed, we now ask, what should the minimum classical radius R be, in order for 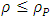 . (any classical density cannot exceed the Planck density).Therefore:
. (any classical density cannot exceed the Planck density).Therefore: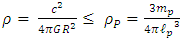
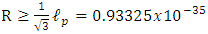 m.Compared to Planck's length
m.Compared to Planck's length 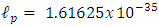 m, the classically derived radius R is smaller than the allowed Planck's length
m, the classically derived radius R is smaller than the allowed Planck's length 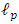 , by an unexplained factor of 0.5774.These calculations were based on the assumptions of negligible
, by an unexplained factor of 0.5774.These calculations were based on the assumptions of negligible 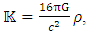 and
and 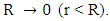 It seems now, that the classical solution to the metric of a spherically symmetric object, puts a lower limit on the radius R of an object. It looks like there is a sort of quantization limit to small scale objects in spacetime.Instead of having
It seems now, that the classical solution to the metric of a spherically symmetric object, puts a lower limit on the radius R of an object. It looks like there is a sort of quantization limit to small scale objects in spacetime.Instead of having  we find
we find 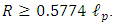 The reason for this 0.5774 factor is due to the fact that we have assumed a constant density inside the sphere. If instead we assume variation in density with radius (highest density at
The reason for this 0.5774 factor is due to the fact that we have assumed a constant density inside the sphere. If instead we assume variation in density with radius (highest density at 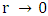 and then it falls off to zero at
and then it falls off to zero at 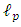 ). We need to calculate the radius R of a quantized particle by its average density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to the same volume, but with a constant average density
). We need to calculate the radius R of a quantized particle by its average density so that we obtain a reduced average radius.By comparing the integrated variable density over the Planck radius, to the same volume, but with a constant average density 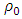 one obtains (see paragraph VI on density upper limit)):
one obtains (see paragraph VI on density upper limit)):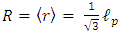
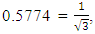 it is now clear where the reduction factor came from.The above result shows how the lower limit of the classical gravitation theory by Einstein, (Schwarzschild radius), and the dimensional constraints between the constants of the universe, result in a quantized material space.
it is now clear where the reduction factor came from.The above result shows how the lower limit of the classical gravitation theory by Einstein, (Schwarzschild radius), and the dimensional constraints between the constants of the universe, result in a quantized material space.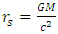 on its way towards the center and on its way out.The metric of this shell will be similar to that of a spherical mass. Only that this time, even though
on its way towards the center and on its way out.The metric of this shell will be similar to that of a spherical mass. Only that this time, even though 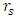 is inside the body, one can reach the Schwarzschild radius independently of whether it is a black hole or a standard mass.One way of doing the experiment would be to send a photon through the hole in the mass and compare its time of arrival with a simultaneously emitted photon traveling outside the mass. One would then be able to compare differences in the time of arrival for the two photons.This gedanken experiment can reveal whether the approach to
is inside the body, one can reach the Schwarzschild radius independently of whether it is a black hole or a standard mass.One way of doing the experiment would be to send a photon through the hole in the mass and compare its time of arrival with a simultaneously emitted photon traveling outside the mass. One would then be able to compare differences in the time of arrival for the two photons.This gedanken experiment can reveal whether the approach to 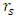 will last forever in the eyes of the external observer. If it does, then the particle will never be able to come out through the opposite hole.
will last forever in the eyes of the external observer. If it does, then the particle will never be able to come out through the opposite hole.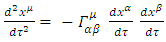
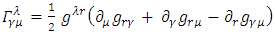
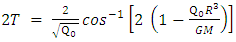 Whereas in the general relativistic case it will be:
Whereas in the general relativistic case it will be: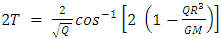 Comparing the two results,
Comparing the two results, 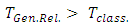 As an example, for the Sun, with
As an example, for the Sun, with 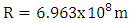 and Sun density
and Sun density 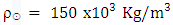 the predicted general relativistic cross time will be 6.6 mSec longer than the classical calculated cross time. This result is based on average Q over r from 0 to R.For an average Neutron star of radius R=11,000 m and density
the predicted general relativistic cross time will be 6.6 mSec longer than the classical calculated cross time. This result is based on average Q over r from 0 to R.For an average Neutron star of radius R=11,000 m and density 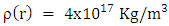 , the passage time under general relativity prediction, will last 0.13 mSec longer than under classical calculation.
, the passage time under general relativity prediction, will last 0.13 mSec longer than under classical calculation.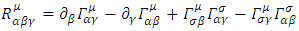 [1]Where
[1]Where 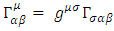 are the Christoffel symbols:
are the Christoffel symbols: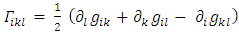
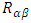 is defined by:
is defined by: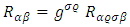
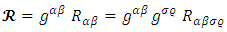
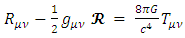
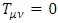 everywhere and therefore
everywhere and therefore 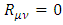 everywhere. Due to spherical symmetry, the metric must be of the form
everywhere. Due to spherical symmetry, the metric must be of the form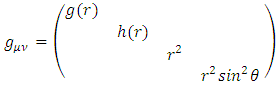
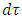 between two events along a time-like path is given by
between two events along a time-like path is given by 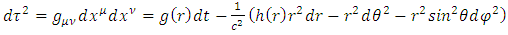
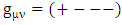 .In order to solve Einstein's equation everywhere, one can no longer assume that the curvature
.In order to solve Einstein's equation everywhere, one can no longer assume that the curvature 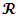 is null anywhere. This is true only outside the mass and so
is null anywhere. This is true only outside the mass and so 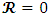 only for r > R.Assuming the mass density of the object being homogeneous and at total freeze of motion,
only for r > R.Assuming the mass density of the object being homogeneous and at total freeze of motion, 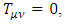 except for
except for 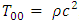 , with
, with 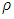 being the mass density.
being the mass density.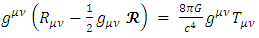
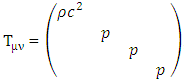 , where p is the pressure.Define
, where p is the pressure.Define 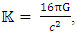 and so,
and so,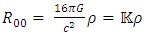
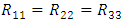 :
: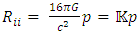
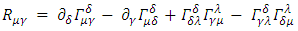
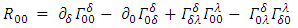
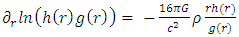
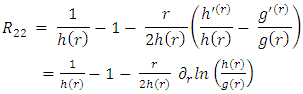
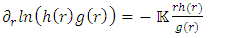
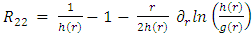
 and so:
and so: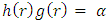 (some constant).Substitute in eq. 2 to obtain:
(some constant).Substitute in eq. 2 to obtain: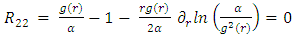
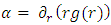
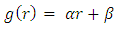
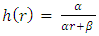
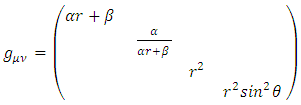
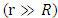 :
: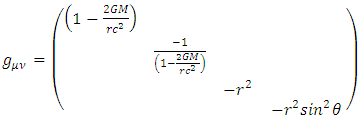
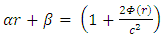
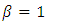
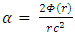
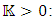 The only approximation made was the assumption on empty space solution. For non-empty space, it will be valid for a perfect fluid of zero pressure.However, one may use a model where the pressure p is proportional o the density [18], and so
The only approximation made was the assumption on empty space solution. For non-empty space, it will be valid for a perfect fluid of zero pressure.However, one may use a model where the pressure p is proportional o the density [18], and so 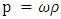 where
where  is a proportionality factor.
is a proportionality factor. 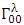 and
and 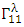 are non-zero (assuming constant gravitational field
are non-zero (assuming constant gravitational field 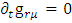 ).
).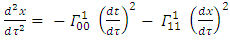
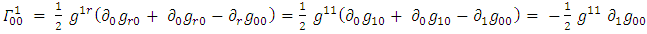
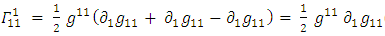
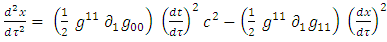
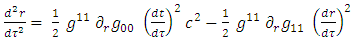
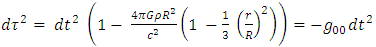
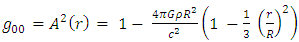
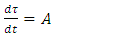
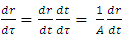
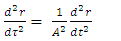
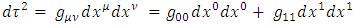
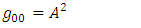
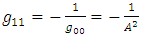
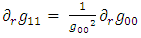
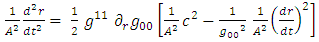
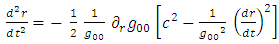
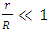
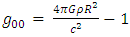
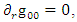 which means that
which means that 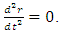 The acceleration near the center is zero.However, if one moves away from the center:
The acceleration near the center is zero.However, if one moves away from the center: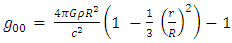
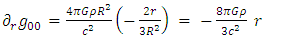
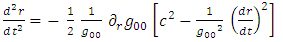
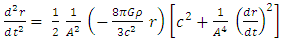
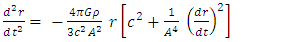
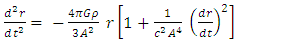
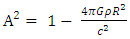 depends on r only through the density
depends on r only through the density  .We may write
.We may write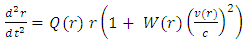
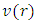 is the approach velocity. Q and W depend on r and are defined by:
is the approach velocity. Q and W depend on r and are defined by: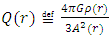
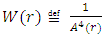
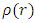 is assumed constant, the acceleration decreases in proportion with r on one hand, but depends also on the square of the approach velocity.For small approach-to-center velocity
is assumed constant, the acceleration decreases in proportion with r on one hand, but depends also on the square of the approach velocity.For small approach-to-center velocity 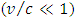
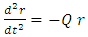
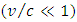 :
: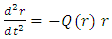
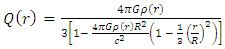
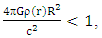 and so,
and so, 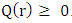 . Also, note that
. Also, note that 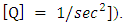 One may solve this under certain approximation:
One may solve this under certain approximation: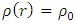 constant density inside r < R.In this case
constant density inside r < R.In this case 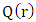 is nearly a constant independent of r, and the equation becomes
is nearly a constant independent of r, and the equation becomes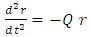
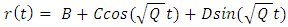
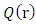 is not constant, the term
is not constant, the term 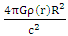 in the denominator of
in the denominator of 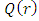 is of the order of, or less than,
is of the order of, or less than, 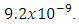 Q(r) may be approximated as:
Q(r) may be approximated as: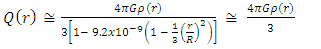
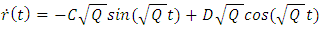
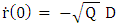 one must have D = 0.Hence
one must have D = 0.Hence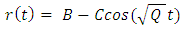
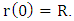 Therefore
Therefore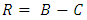
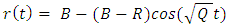
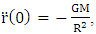
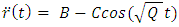
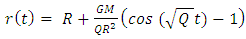
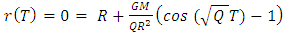
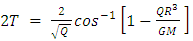
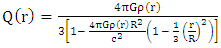 In this case
In this case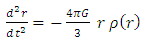
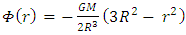
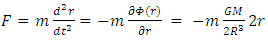
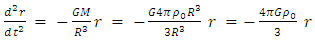
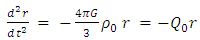
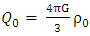 This, in comparison to the general relativistic solution:
This, in comparison to the general relativistic solution: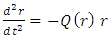
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
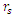 < R (A-STNDRD) and
< R (A-STNDRD) and 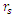 > 2/3R (B-WH). As can be seen, in case B, the inner part of the object is below the horizon
> 2/3R (B-WH). As can be seen, in case B, the inner part of the object is below the horizon 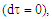 but some of the the external part is not. This case allows for the photon sphere to be visible outside the body and yet the object is not a black hole yet. In this figure,
but some of the the external part is not. This case allows for the photon sphere to be visible outside the body and yet the object is not a black hole yet. In this figure, 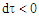 is set to
is set to 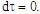 *(The dimensions are relative only)
*(The dimensions are relative only)