ZiQi Liu1, S. M. Feng2
1Jinan Foreign Language School International Center, P. R. China
2School of Physics and Astronomy, Shanghai Jiao Tong University, P. R. China
Correspondence to: S. M. Feng, School of Physics and Astronomy, Shanghai Jiao Tong University, P. R. China.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Different explication of some classical physics problems are very interesting for beginner. In this paper, according to the fact that the length-constant transformation is orthogonal transformation in the two reference frames, we simplified the four-dimensional space to two-dimensional space. Based on this, we described the derivation process of Lorentz transformation in detail. At the same time, it also proves that there is not the relativistic effect in two directions perpendicular to the direction of motion.
Keywords:
Lorentz transformation, Orthogonal matrix, Space-time interval
Cite this paper: ZiQi Liu, S. M. Feng, A Deduction Method of Lorentz Transformation in Special Theory of Relativity, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 5, 2020, pp. 108-111. doi: 10.5923/j.ijtmp.20201005.04.
1. Introduction
Special relativity is a very important content in modern physics. Based on this, people can discover many physical phenomena that do not appear in classical physics, which is very fascinating for people who like physics. The basis of special relativity is the Lorentz transformation. In most textbooks, many introductory courses on special relativity use thought experiments in order to demonstrate time dilation and length contraction from Einstein’s two postulates. Once these two effects are established, most authors return to the postulates to derive the Lorentz transformation. In fact, the Lorentz transformation can be derived by using the sole relativity principle and the invariance of the speed of light [1-6]. The derivation was limited to transformations between two reference frames, namely, one frame of reference moves along the x-direction of another reference frame. However, in addition to assuming the invariance of the speed of light, 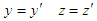 are also assumed to be used for derivation of Lorentz transformation, but this assumption often makes it difficult for beginners to understand. As known well, the length-invariant transformation is an orthogonal transformation, and can be represented by a matrix. Based on this orthogonal matrix, we prove that
are also assumed to be used for derivation of Lorentz transformation, but this assumption often makes it difficult for beginners to understand. As known well, the length-invariant transformation is an orthogonal transformation, and can be represented by a matrix. Based on this orthogonal matrix, we prove that 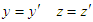 , and derive Lorentz transformation, which is very useful for deep understanding of special relativity theory.
, and derive Lorentz transformation, which is very useful for deep understanding of special relativity theory.
2. Theoretical Derivation
2.1. The Relationship between a Stationary Reference Frame and a Rotating Reference Frame
For the convenience of the following discussion, A simple two-dimensional analogy (seeing Fig.(1) to this invariant is given by considering two sets of axis, Oxy and Ox′ y′ having the same origin O, but there is an angle (θ) between the axis Ox′ and Ox, so one set of axes is the same as another set but rotated (seeing Fig.1). The point P with coordinates (x,y) has coordinates (x′,y′) measured on the Ox′ y′ axis. The square of the distance of the point P from the common origin O is x2+y2 and is also x′2+y′2, 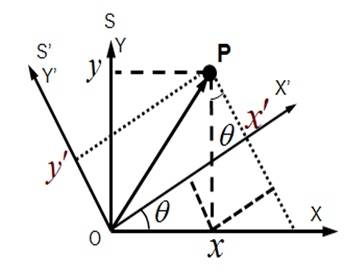 | Figure 1. Two reference frames |
So, for the transformation from coordinates (x,y) to (x′,y′), x2+y2 is an invariant. 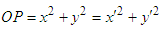 | (1) |
As can be seen from Fig. 1, we easily get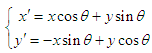 | (2) |
The equation (2) can be written in matrix form: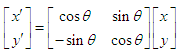 | (3) |
or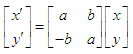 | (4) |
Here 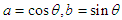 .
.
2.2. Lorentz Transformation
Let us consider two inertial reference frames S and S’. The reference frame S’ moves with velocity u relative to S along x-axis. The coordinates y and z are perpendicular to the velocity in both reference frames (seeing Fig.2). When t = t′= 0, the origins O point of reference frame S and S′ coincide with each other. At the same time, a light is emitted from the origin O and O’. The time for the light to reach the point P in two reference frames is defined as t and t’, respectively. 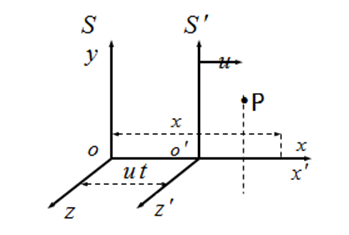 | Figure 2. A stationary reference frame and a moving reference frame |
In relativistic Minkowski space-time, the distance between two space-time points (events)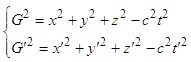 | (5) |
Here G and G’ are defined as Lorentz invariant, which are the physical parameter that unifies space and time. From equation (5), it is easily found that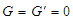 | (6) |
Equation (5) can also be changed into the following equation group containing imaginary numbers, namely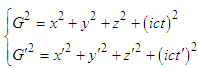 | (7) |
Let us therefore define 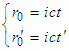 | (8) |
and 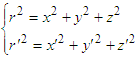 | (9) |
Equation (7) yields immediately 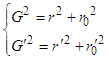 | (10) |
Based on equation (6) and (10), we can get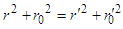 | (11) |
Equation (11) is very similar to equation (1), then, equation (11) can also be regarded as the spatial relationship between two reference frames, which is the stationary reference frame S(r, r0), and the rotating reference frame S'(r’, r0’) around the origin of reference frame, respectively. Thus, the equation (11) is also written in matrix 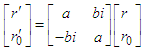 | (12) |
Here a, b is the elements in the matrix, respectively. Because r0’ contains an imaginary numbers, bi must be an imaginary numbers. Expansion of equation (12) produces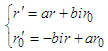 | (13) |
Substitution of equation (13) into (11) produces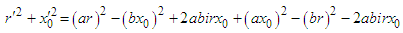 | (14) |
Equation (14) can be simplified to 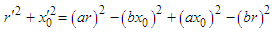 | (15) |
From equation (15), it is easy to find 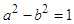 | (16) |
We naturally think another relationship in mathematics, namely,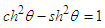 | (17) |
Comparison of equations (17) with (16) generates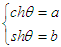 | (18) |
If we define 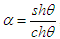 , one get from (17)
, one get from (17)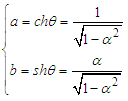 | (19) |
We bring equation (19) back to (13) and get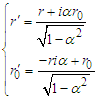 | (20) |
Substitution of equation (8) into (20) again generates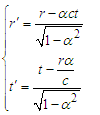 | (21) |
Using the above same way, we can also get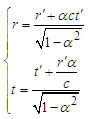 | (22) |
For a fixed point in S’ -reference frame, 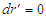 , the differentiate of equation (22) produces
, the differentiate of equation (22) produces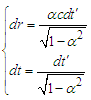 | (23) |
Dividing of one of equations by another equation in equation group (23) yields 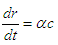 | (24) |
The derivative of equation (9) produces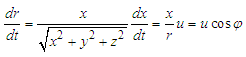 | (25) |
Here 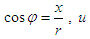 is the speed of the moving reference frame. Substitution of equation (25) into (24) produces
is the speed of the moving reference frame. Substitution of equation (25) into (24) produces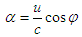 | (26) |
We put again equation (26) into (22) and to get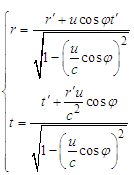 | (27) |
Using the above same method, we can also obtain another group of equation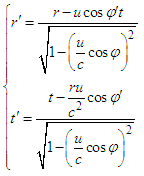 | (28) |
We again bring equation (9) into equation (27) and (28) to get, respectively, 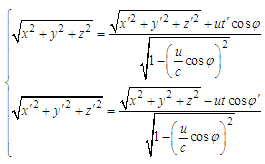 | (29) |
3. Discussion
For a fixed point on y-axis with coordinates 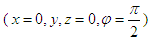 in S reference frame, We substitute them into equation (29) and get
in S reference frame, We substitute them into equation (29) and get 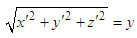 | (30) |
Similarly, for a fixed point with coordinates 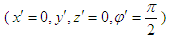 on y’-axis in S’ reference frame, we also substitute them into equation (29) and get
on y’-axis in S’ reference frame, we also substitute them into equation (29) and get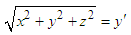 | (31) |
Equation (30) and (31) can also be written in the vector form. 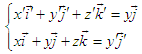 | (32) |
Obviously, to make the above two equations equal, there must be 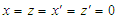 | (33) |
Comparison of equation (29) with (33), it is easy to find 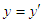 . Using the above same steps, we can also prove that
. Using the above same steps, we can also prove that 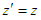 . The two conclusions means that there is not the relativistic effect in the direction perpendicular to the direction of movement.For a point on x-axis with coordinates
. The two conclusions means that there is not the relativistic effect in the direction perpendicular to the direction of movement.For a point on x-axis with coordinates 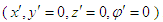 in S’ reference frame, based on that
in S’ reference frame, based on that 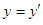 and
and 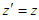 , we get from equation (29)
, we get from equation (29) 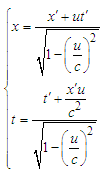 | (34) |
Thus, we obtain a equation group of Lorentz transformation 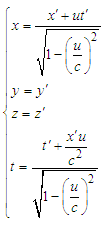 | (35) |
or 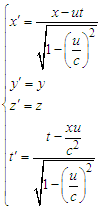 | (36) |
Equation (35) and (36) are called as Lorentz transformation equation group.In the special theory of relativity, the principle of constant speed of light is relatively easy to understand, but the related textbooks do not fully describe the reasons of 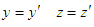 during the relevant derivation process. In this paper, we theoretically prove
during the relevant derivation process. In this paper, we theoretically prove 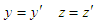 , which can better answer people’s confusion about relativity. This method does not have any assumptions, and directly derives the transformation, which allows beginners to better understand the special theory of relativity.
, which can better answer people’s confusion about relativity. This method does not have any assumptions, and directly derives the transformation, which allows beginners to better understand the special theory of relativity.
4. Conclusions
In this article, we give a method to derive Lorentz transformation. Compared with other derivation methods, the extension from the special four dimensional case to the 2-dimensional case is completely straightforward. Especially, the derivation method is not based on assumption of 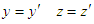 . In contrast,
. In contrast, 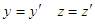 can be fully deduced through the theoretical derivation. This method can better reflect the space-time relationship in the two spaces.
can be fully deduced through the theoretical derivation. This method can better reflect the space-time relationship in the two spaces.
References
| [1] | S. Hajra, Classical Interpretations of Relativistic Phenomena, Journal of Modern Physics, Vol. 3, No. 2, 2012, 187-199. |
| [2] | V. Berzi, V. Gorini, Reciprocity Principle and the Lorentz Transformations, J. Math. Phys. 10(8), 1518-1524 (1969). |
| [3] | W. N. Mathews Jr. Relativistic velocity and acceleration transformations from thought experiments, Am. J. Phys. 73, 45-51 (2005). |
| [4] | Abraham A. Ungar, Formalism to deal with Reichenbach's special theory of relativity, Foundations of Physics, 21, 691–726 (1991). |
| [5] | Lakshya Malhotra, Robert Golub, Eva Kraegeloh, Nima Nouri & Bradley Plaster, Effect of Thomas Rotation on the Lorentz Transformation of Electromagnetic fields, Scientific Reports (2020) volume 10: 5522. |
| [6] | DanielCao Labora AntónioM. Lopes, J. A. Tenreiro, The Lorentz transformations and one observation in the perspective of fractional calculus, Communications in Nonlinear Science and Numerical Simulation, 78, 2019(11), 104855. |


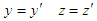 are also assumed to be used for derivation of Lorentz transformation, but this assumption often makes it difficult for beginners to understand. As known well, the length-invariant transformation is an orthogonal transformation, and can be represented by a matrix. Based on this orthogonal matrix, we prove that
are also assumed to be used for derivation of Lorentz transformation, but this assumption often makes it difficult for beginners to understand. As known well, the length-invariant transformation is an orthogonal transformation, and can be represented by a matrix. Based on this orthogonal matrix, we prove that 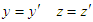 , and derive Lorentz transformation, which is very useful for deep understanding of special relativity theory.
, and derive Lorentz transformation, which is very useful for deep understanding of special relativity theory.
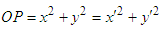
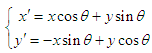
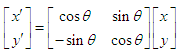
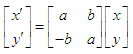
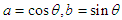 .
. 
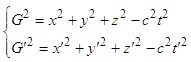
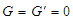
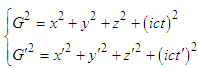
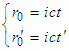
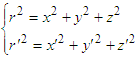
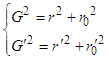
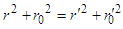
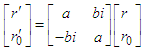
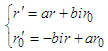
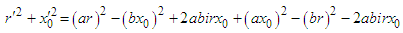
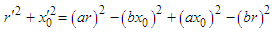
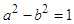
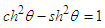
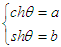
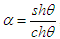 , one get from (17)
, one get from (17)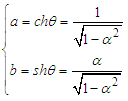
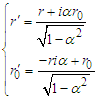
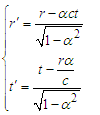
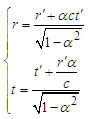
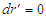 , the differentiate of equation (22) produces
, the differentiate of equation (22) produces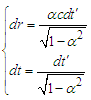
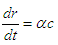
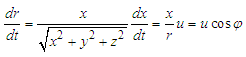
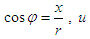 is the speed of the moving reference frame. Substitution of equation (25) into (24) produces
is the speed of the moving reference frame. Substitution of equation (25) into (24) produces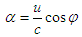
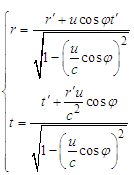
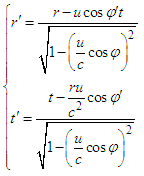
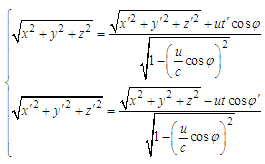
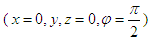 in S reference frame, We substitute them into equation (29) and get
in S reference frame, We substitute them into equation (29) and get 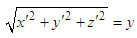
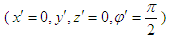 on y’-axis in S’ reference frame, we also substitute them into equation (29) and get
on y’-axis in S’ reference frame, we also substitute them into equation (29) and get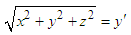
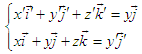
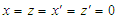
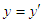 . Using the above same steps, we can also prove that
. Using the above same steps, we can also prove that 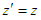 . The two conclusions means that there is not the relativistic effect in the direction perpendicular to the direction of movement.For a point on x-axis with coordinates
. The two conclusions means that there is not the relativistic effect in the direction perpendicular to the direction of movement.For a point on x-axis with coordinates 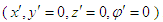 in S’ reference frame, based on that
in S’ reference frame, based on that 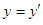 and
and 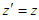 , we get from equation (29)
, we get from equation (29) 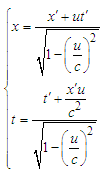
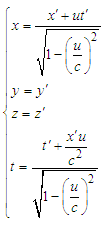
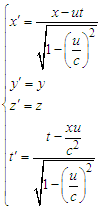
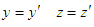 during the relevant derivation process. In this paper, we theoretically prove
during the relevant derivation process. In this paper, we theoretically prove 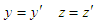 , which can better answer people’s confusion about relativity. This method does not have any assumptions, and directly derives the transformation, which allows beginners to better understand the special theory of relativity.
, which can better answer people’s confusion about relativity. This method does not have any assumptions, and directly derives the transformation, which allows beginners to better understand the special theory of relativity.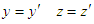 . In contrast,
. In contrast, 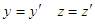 can be fully deduced through the theoretical derivation. This method can better reflect the space-time relationship in the two spaces.
can be fully deduced through the theoretical derivation. This method can better reflect the space-time relationship in the two spaces. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML