-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2020; 10(5): 100-107
doi:10.5923/j.ijtmp.20201005.03
Received: Sep. 22, 2020; Accepted: Oct. 6, 2020; Published: Oct. 15, 2020

A Dialectical Interpretation of Schrodinger Cat Paradox in Terms of Hidden "Variable Realties"
1Memorial Regional Hospital, Hollywood, Florida
2Department of Physics, Faculty of Science, University of Gujrat, Gujrat
Correspondence to: Tracy Klein, Memorial Regional Hospital, Hollywood, Florida.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Schrodinger's cat paradox is largely viewed as a defining cornerstone of the weirdness of Quantum mechanics. It examines the situation when a quantum object is coupled or entangled to a macroscopic object. At a point before any observation of the composite system has been made, the quantum object, atom particle etc., and thus additionally the cat, are in a superposition of states, i.e. the cat is dead and alive. This paradox highlights some questionable assumptions of the Copenhagen interpretation of Quantum Mechanics. In this article we address this question and develop a new assumption about Schrodinger cat experiment using mathematical interpretation of set theory. Through examining the paradox in light of dialectic reasoning and set theory, it is found that the state of the cat is largely dependent on the initial condition of the system. According to the initial conditions of system there is maximum probability that cat would be alive inside the box, represents by the overlapping or superposition of all common states or reality states of system.
Keywords: Schrodinger Cat, Set theory, Venn diagram, Quantum mechanics, Copenhagen
Cite this paper: Tracy Klein, M. B. Tahir, A Dialectical Interpretation of Schrodinger Cat Paradox in Terms of Hidden "Variable Realties", International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 5, 2020, pp. 100-107. doi: 10.5923/j.ijtmp.20201005.03.
1. Introduction
- One of the most famous paradoxes of quantum physics is that of Schrodinger’s cat in a box. this paradox is generally studied or correlated with so called “observer effect”, where an observation, typically through measurement, causes the collapse the wave function describing the quantum system. This interpretation raises some fundamental question regarding how we define an observer, as well as the relationship between the observer and the gross matter [1,2,3]. How do we resolve Schrodinger’s cat paradox? Is it a mere artifact of mathematics or is the cat truly in a superposition of states inside the box, and if so what is the probability to find it? In this paper we will show that Schrodinger’s cat paradox is a “self-emergent” phenomenon in any quantum system having two subsystems (cat +Maxwell’s demon) and (measuring device+ observer) in entangled state, hence the information transfer is by entanglement [4,5,6].The set-up of the thought experiment known as Schrodinger's Cat. In his 1935 paper, Schrodinger postulated a seemingly conceptual problem in quantum mechanics; he discusses and rejects the interpretation that a quantum system is physically somehow spread on different parts of a superposition... It described a cat apparently held in a superposition of alive and dead states, specifically, superposition of two coherent states with same amplitudes but opposite phases [7,8].. In the thought experiment a cat is confined to a steel chamber, alongside the accompanying gadget (which must be guarded against direct obstruction by the cat) comprising of a radioactive substance, that decays according to probabilistic quantum mechanical theory [9]. Here the decay of the radioactive substance, if it occurs, is responsible for the death of the cat by activating a counter cylinder which causes a hammer to break a little flask of poison [10]. The paradox is focused on the state of the cat after one has left this whole framework to itself for a period of time; do we really consider that the cat is in a superposition of states, or would one state that the cat despite everything lives in the interim? This thought experiment has raised many controversial arguments, [10,11]. Upon a closer investigation the Schrodinger dilemma can be seen to consist of different parts, often mixed carelessly:• What is the state of the cat in the box, is it really in a superposition?• Can quantum mechanics provide a full description of the entangled macroscopic system?• When does the state of the cat change? The so-called wave function collapse.• Can we have macroscopic system being in superposition of states? At what level does macroscopic realness exist? Each of the questions above should be regarded separately as they refer to different aspects of the problem, not necessarily on equal footing. We know (at least most of us believe) that the cat in the box is either dead, alive and not in a smeared-out state between those alternatives, so is something missing in order to have a valid quantum mechanical description of the system [12] [13]. Does quantum mechanics have the capacity to describe the macroscopic world as good as the microscopic world [14,15].Quantum mechanics is a hypothesis that gives an exact portrayal of frameworks containing the consistuents of matter and thus must be applicable to any physical real framework [15] As we known from our daily experience, classical mechanics works only for macroscopic and recognizable objects. We in this manner expect that when quantum mechanics is applied to such systems, it still correctly yields observed classical outcomes [16,17] This is that we refer to as the classical limit. Quantum mechanics, as indicated by its Schrodinger picture, is a non-relativistic hypothesis about the wave-like nature of matter and its dynamics [18]. There are two principle issues in the reasonable establishments of quantum mechanics. The first one concerns the physical importance of the wave function in the hypothesis. It has been generally contended that the likelihood translation isn't completely acceptable due to depending on the ambiguous idea of probability and uncertainty [19]. Then again, the importance of the wave function is likewise in question in the alternative interpretations of quantum mechanics, for example, the de Broglie-Bohm hypothesis and the many-universes translation [20] The subsequent issue concerns the advancement of the wave function. It incorporates two sections. One section concerns the direct Schrodinger advancement. For what reason does the non-relativistic development of the wave function fulfill the Schrodinger condition? It appears that a palatable deduction of the condition is yet missing [21]. The other part concerns the breakdown of the wave function during a measurement or observation. The breakdown hypothesizes or wave collapse model is still actively researched and doesn't disclose how a definite wave function collapses [22]. Although the alternative interpretations of quantum mechanics as of now give their separate answers for this issue, it has been a hot subject of discussion which interpretation is correct. In the final investigation, the wavefunction breakdown is still not known to be genuine or not. Regardless of whether the wave function falls under certain conditions, it stays muddled, why and how the wave function breakdown would occur [23]. The estimation issue has been universally recognized as one of the hardest and most significant issues in the establishments of quantum mechanics [24]. In this postulation, we will attempt to tackle these issues from an alternative focus, the dialectic nature of Quantum mechanics and how it is manifest in the Cat in the box paradox. The key is to understand that the deciphering the wave function collapse might be resolved when care is taken of the observation issue. Although the significance of the wave function ought to be positioned as the first interpretative issue of quantum mechanics, it has been treated as a negligible issue, particularly contrasted and the measurement issue [25].In order to deeper investigate the finer details of the paradox and present the dialectic nature of Quantum mechanics we rely in the mathematical backing of Set theory. Set theory, branch of mathematics that deals with the properties of well-defined collections of objects, such as numbers or functions. The theory is less valuable in direct application to ordinary experience than as a basis for precise and adaptable terminology for the definition of complex and sophisticated mathematical concepts [26]. In fact Set theory has already been identified as a suitable mathematical treatment of quantum systems [27], taking into account the indistinguishability of Quantum mechanical particles as well as an ontological extension to classical particles/elements required for macroscopic realness [28]. This concept of using set theory to evaluate the relationships between quantum sets has led to the recent development of quasi-set theory [29]. Such advancements in the use of Set theory are however not surprising from a dialectic point of view considering the essential elements of union, separation and intersection used to develop the axioms are all related to dialectic philosophy of synthesis of states. Having the logical framework all set, we can now develop axiomatic set theory as a specific first order theory. It might come as a surprise that requiring a single binary predicate symbol, usually written infix, suffices [30,31] The other set-theoretic symbols such as can all be defined within the theory, for instance
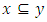 is an abbreviation for
is an abbreviation for 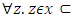
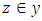 . Venn diagrams can be used to express the mathematical logical relationships between various sets, elements. Basically, Venn diagram depict us how different items or elements are relating with each other against an overall environment of system [32]. In this article, we will use Venn diagrams to illustrate various operations (union, intersection, difference) of various hierarchical aspects of quantum physics as well as relativity. This is done to evaluate how a dialectic interpretation [33] can lead to a better understanding of the Schrodinger cat paradox.
. Venn diagrams can be used to express the mathematical logical relationships between various sets, elements. Basically, Venn diagram depict us how different items or elements are relating with each other against an overall environment of system [32]. In this article, we will use Venn diagrams to illustrate various operations (union, intersection, difference) of various hierarchical aspects of quantum physics as well as relativity. This is done to evaluate how a dialectic interpretation [33] can lead to a better understanding of the Schrodinger cat paradox. 2. Methodology
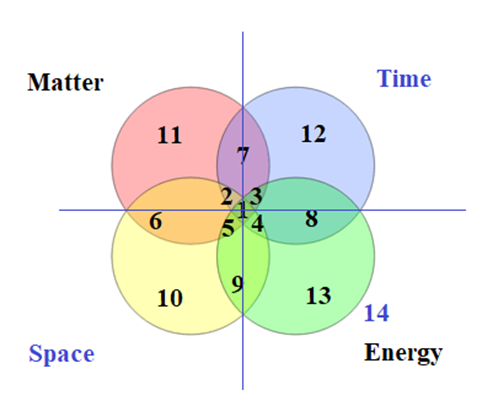
- As matter, energy, time and space intercept, quantum physics (M ∪ E) becomes a set that contains 11 elements (nine states that contain speed, one state that contains space and matter, and one state of matter). Relativity (T ∪ S) becomes a set that contains 11 elements (nine states that contain speed, one state that contains space and matter, and one state of space) shown in figure 1. Reconciling the states that contain the common trait of speed results in 10 possible states of reality coming together to form states 1, 2, 3, 4, 5, 7, 8, 9, 12 and 13. According to dialectical principles, reality is created through a union or synthesis of states that contain the common, interlocking trait of speed.
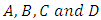 for convince to formulate the set theory. We can derive the corresponding inclusion-exclusion formula using the results for two events
for convince to formulate the set theory. We can derive the corresponding inclusion-exclusion formula using the results for two events 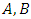 and three events
and three events 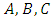 . Starting from benchmark formula of inclusion-exclusion we have;
. Starting from benchmark formula of inclusion-exclusion we have;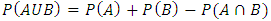 | (1) |
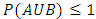 and so, Here the union of two or more sets is the set that contains all the elements of each of the sets; an element is in the union if it belongs to at least one of the sets. The symbol for union is
and so, Here the union of two or more sets is the set that contains all the elements of each of the sets; an element is in the union if it belongs to at least one of the sets. The symbol for union is  , and is associated with the word “or”, because
, and is associated with the word “or”, because  is the set of all elements that are in
is the set of all elements that are in 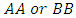 (or both). Similarly, the intersection of two or more sets is the set of elements that are common to each of the sets. An element is in the intersection if it belongs to all of the sets. The symbol for intersection is
(or both). Similarly, the intersection of two or more sets is the set of elements that are common to each of the sets. An element is in the intersection if it belongs to all of the sets. The symbol for intersection is 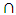 , and is associated with the word “and”, because
, and is associated with the word “and”, because 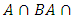
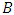 is the set of elements that are in
is the set of elements that are in 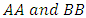 simultaneously
simultaneously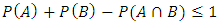 | (2) |
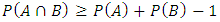 | (3) |
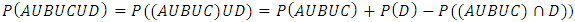 | (4) |
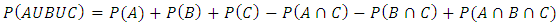 | (5) |
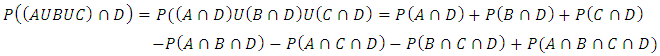 | (6) |
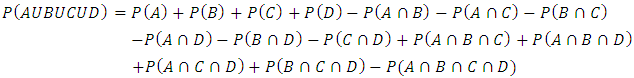 | (7) |
3. Results and Discussion
- In dialectical relationships, opposing states resolve the tension between them by means of a synthesis. This synthesis solves the conflict between two opposing forces by reconciling their common truths. Let’s assume the cat is alive in a closed box. There are seven (7) states where the cat can be alive: 1, 2, 3, 5, 6, 7 and 11. This includes: all possible states at once, objectively and subjectively alive, objectively alive and dead, subjectively alive and dead, subjectively alive, objectively alive, and alive. There are seven (7) states where the cat can be in a closed box: 1, 2, 3, 4, 7, 8 and 12. This includes: all possible states at once, objectively and subjectively alive, objectively alive and dead, objectively and subjectively dead, objectively alive, objectively dead, objectively. Common truths between the state of being alive and objectively being in the box are states 1, 2, 3 and 7: all possible states at once, objectively, and subjectively alive, objectively alive and dead, objectively alive. If we were to reconcile the common truths between these four states, the result would be that cat is objectively alive in the closed box. Let’s assume the cat is both subjectively and objectively alive. There are seven (7) states where the cat can be alive: 1, 2, 3, 5, 6, 7 and 11. This includes: all possible states at once, objectively and subjectively alive, objectively alive and dead, subjectively alive and dead, subjectively alive, objectively alive, and alive. There are seven (7) states where the cat may be observed subjectively from outside the box: 1, 2, 4, 5, 6, 9 and 10. This includes: all possible states at once, objectively and subjectively alive, objectively and subjectively dead, subjectively alive, subjectively alive and dead, and subjectively. There are (7) seven states where the cat can be in a closed box: 1, 2, 3, 4, 7, 8 and 12. This includes: all possible states at once, objectively and subjectively alive, objectively alive and dead, objectively and subjectively dead, objectively alive, objectively dead, objective. Common truths between the cat being alive, being observed subjectively from outside the box, and its objective state in the closed box include 1 and 2: all possible states at once, and objectively and subjectively alive. If we were to reconcile the common truths between these two states, the result would be that the cat is objectively and subjectively alive. This dialectical formula will hold true for any of the four possible states of reality for Schrodinger’s cat in a box. Actually, there are 3 separate, co-existing states of reality: objective, subjective, and the synthesis between the two; shown in figure 2. Reality is created through a union or synthesis of common, interlocking truths between dialectically opposing objective and subjective states of reality. For instance, if a tree falls in a forest (objective reality) and no one is around to hear it (subjective reality) then the synthesis of common, interlocking truths between objective and subjective states of reality is, “A tree falls in a forest, and no one is around to hear it.” As a quantum system and relativity come together, they create a distinct, third group that resolves the tension between them by means of a synthesis. This synthesis solves the conflict between two opposing states by reconciling their common truths. Speed is the one common trait or denominator that links quantum physics and relativity. In this way a dialectic hierarchical interpretation of the states of reality can be developed [30].
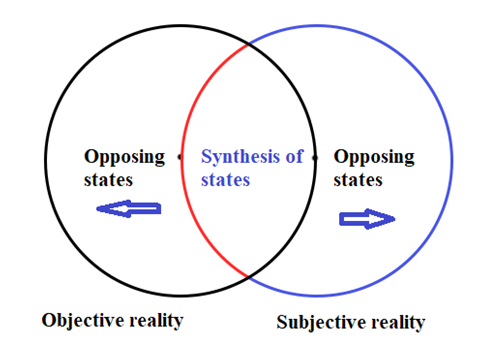 | Figure 2. Three distinct states of reality in space time with respect to subjective, objective realities in the presence of opposing forces |
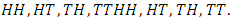 The sample space is thus
The sample space is thus 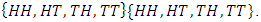 The event “at least one heads occurs” would be the set
The event “at least one heads occurs” would be the set 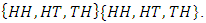 If the coin were a normal coin, we would assign the probability of
If the coin were a normal coin, we would assign the probability of 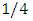 to each outcome. Similarly, starting from equation 7, we find out the common interest among four sets labeled as;
to each outcome. Similarly, starting from equation 7, we find out the common interest among four sets labeled as;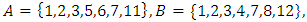
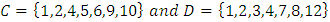 Left side of equation elucidate the probability of four sets, which one having more probability to appear depend on the elements of corresponding sets. First four term on right side of equation are
Left side of equation elucidate the probability of four sets, which one having more probability to appear depend on the elements of corresponding sets. First four term on right side of equation are 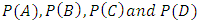 represents the probability of crossponding sets. In probability two events are mutually exclusive if they cannot occur at the same time. Another word that means mutually exclusive is disjoint. If two events are disjoint, then the probability of them both occurring at the same time is zero. While other terms in Eq.07 are represented by using Venn diagram for individual term, involving elements of
represents the probability of crossponding sets. In probability two events are mutually exclusive if they cannot occur at the same time. Another word that means mutually exclusive is disjoint. If two events are disjoint, then the probability of them both occurring at the same time is zero. While other terms in Eq.07 are represented by using Venn diagram for individual term, involving elements of 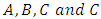 sets. Venn diagrams depict that
sets. Venn diagrams depict that 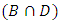 having maximum 100% probability to find the Schrodinger cat in Box, while
having maximum 100% probability to find the Schrodinger cat in Box, while 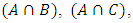 and
and 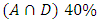 probability for having cat in Box. In three sets, probability of
probability for having cat in Box. In three sets, probability of 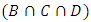 is maximum as compared to
is maximum as compared to 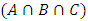 ,
, 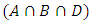 and
and 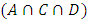 . Although, probability of Schrodinger cat within box in
. Although, probability of Schrodinger cat within box in 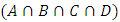 sets revealed by multi-dimensional Venn diagram. From the figure 3 we observed that every circle occupies maximum probability of alive cat within box. According to Heinsberg uncertainty principle, if we find out the position of cat then there exists certainty in the time span, we can find out alive cat within box. But there is a point when all of four sets Venn diagram are merged there is maximum probability of cat alive in Box. At the intersection of four sets there, four common states intersect from each set, and give a maximum point where all of states having maximum probability. We can assume, all of four sets are eventually subset of each other, because of one common state of reality. This point revealed whether subjectively or objectively there exist a point where all of common states give maximum probability to find out Schrodinger cat within box. Moreover, hypothetically there is possibility of cat until we will open the box to find the real state of system. Mathematical results are consistent with above stated dialectical formula. Because there exists one common state which prove the cat is alive within box.
sets revealed by multi-dimensional Venn diagram. From the figure 3 we observed that every circle occupies maximum probability of alive cat within box. According to Heinsberg uncertainty principle, if we find out the position of cat then there exists certainty in the time span, we can find out alive cat within box. But there is a point when all of four sets Venn diagram are merged there is maximum probability of cat alive in Box. At the intersection of four sets there, four common states intersect from each set, and give a maximum point where all of states having maximum probability. We can assume, all of four sets are eventually subset of each other, because of one common state of reality. This point revealed whether subjectively or objectively there exist a point where all of common states give maximum probability to find out Schrodinger cat within box. Moreover, hypothetically there is possibility of cat until we will open the box to find the real state of system. Mathematical results are consistent with above stated dialectical formula. Because there exists one common state which prove the cat is alive within box. | Figure 3. Schematic illustration of probability of finding alive Schrodinger cat inside the box with the superposition of common reality set elements |
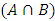 , in which there is probability forecasting about Schrodinger cat whether dead or alive in box is 30% and 40%, respectively.First of all we consider a classical mechanics because it will help us to calculate more accurately depending upon initial conditions. The fact is that these predictions are solely reflects the lack of knowledge of observer. Substantively, this prediction is deal with the subjective knowledge of observer instead of considering this prediction as a reality element. Moving towards quantum mechanics we may consider the prediction as a wave function subjectively (analogues to prediction knowing the knowledge of observer) or whether this predicted wave function as the reality element. According to second assumption, consider the reality, if we put any alive cat inside the box which mean it would possible to live inside the box (reality). The concept of whether the cat is alive or dead subjectively or objectively deals with predictions related to sets using mathematical set theory or position of wave function at specific time. Moreover, according to rational quantum mechanics, the probability of future aspects of any specific system depends on the past values or initial conditions of same system instead of past values of another system. According to this theory, in our case the initial condition of system is that we placed an alive cat inside the box, so there is maximum possibilities/probability that cat would be alive inside the box.
, in which there is probability forecasting about Schrodinger cat whether dead or alive in box is 30% and 40%, respectively.First of all we consider a classical mechanics because it will help us to calculate more accurately depending upon initial conditions. The fact is that these predictions are solely reflects the lack of knowledge of observer. Substantively, this prediction is deal with the subjective knowledge of observer instead of considering this prediction as a reality element. Moving towards quantum mechanics we may consider the prediction as a wave function subjectively (analogues to prediction knowing the knowledge of observer) or whether this predicted wave function as the reality element. According to second assumption, consider the reality, if we put any alive cat inside the box which mean it would possible to live inside the box (reality). The concept of whether the cat is alive or dead subjectively or objectively deals with predictions related to sets using mathematical set theory or position of wave function at specific time. Moreover, according to rational quantum mechanics, the probability of future aspects of any specific system depends on the past values or initial conditions of same system instead of past values of another system. According to this theory, in our case the initial condition of system is that we placed an alive cat inside the box, so there is maximum possibilities/probability that cat would be alive inside the box.4. Conclusions
- Schrödinger described a hypothetical apparatus, designed to illustrate, and even exaggerate some of the stranger consequences of the Copenhagen view of quantum theory. However, according to the Copenhagen interpretation, this is not merely a matter of our ignorance related to the prediction whether Schrodinger cat is alive or dead inside the box. We have applied set theory based on real/common truths/states of four different sets. According to mathematical theory there are appeared some common states using two different sets A and B. after the superposition of common truth or reality states from different sets give the maximum probability of finding the cat alive inside the box objectively or subjectively based on the knowledge of observer or initial conditions of system. When all of the possible states of the system are overlap or superimposed like withing specific time and space/position. Throughout time and space, the butterfly can exist as both a caterpillar and a butterfly. However, at any specific point in time and space, it can exist either as caterpillar or a butterfly, but not both. A collapse does not occur because a measurement takes place in analogy to a butterfly which exists throughout time and space and yet simultaneously exists at a specific point in time and space.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML