-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2020; 10(4): 73-80
doi:10.5923/j.ijtmp.20201004.01
Received: July 19, 2020; Accepted: August 3, 2020; Published: August 15, 2020

The Formulas of Relativity as a Consequence of Invariance of the Wave Equation in Inertial Frames
Khoroshavtsev Y. E.
Faculty of Automatic Control Systems, State University of Civil Aviation, St. Petersburg, Russia
Correspondence to: Khoroshavtsev Y. E. , Faculty of Automatic Control Systems, State University of Civil Aviation, St. Petersburg, Russia.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A hypothesis is put forward according to which the formulas of Relativity are a consequence of the laws of quantum physics and may be applied only to quantum objects. According to the wave - particle duality quantum bodies are simultaneously the waves and considered in the present research with a use of the wave equation and requirement of its Lorentz‘s invariance. The property of invariance with respect to the Lorentz’s transform is analysed in hyperbolic coordinates in an area of complex numbers. An examination showed that formulas of relativistic kinematics can be obtained based on the condition of equality of the amplitudes and phases of the wave, observed from different inertial frames. There is no need to introduce the concept of a unified entity of space-time, but the return to the idea of aether and matter waves de Broglie occurs. The physical model becomes borrowed partly from quantum field theory. It is assumed that the moving particle binds to a wave of the aether disturbance, and only this wave acts on the other particle like an electromagnetic field pushes an electrical charge. The model of colliding elastic balls becomes inapplicable, but equations of relativity mechanics remain the same, however, with a new interpretation. The mass of a particle in all coordinate systems is constant, in exchange the expressions of energy and momentum alter relative the classical case, include the property of aether – coefficient c of the wave equation, and acquire relativistic forms.
Keywords: Relativity, Invariance, Wave equation, Aether
Cite this paper: Khoroshavtsev Y. E. , The Formulas of Relativity as a Consequence of Invariance of the Wave Equation in Inertial Frames, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 4, 2020, pp. 73-80. doi: 10.5923/j.ijtmp.20201004.01.
Article Outline
1. Introduction
- One of fundamental tenets of classical mechanics is expressed by Galileo relativity principle: the laws of motion are the same in all inertial frames of reference, or – in the homogenous isotropic space there is not a specially favoured (unique) inertial coordinate system. But with the advent of Maxwell’s theory of electromagnetism and, in particular, when describing wave propagation, a possibility appeared, that was thought, to connect the basic universal frame to the motionless medium – aether, which served as a carrier of light waves. The major question was asked to measure an absolute velocity with respect to the luminiferous aether, and in 1887 Michelson and Morley performed the famous experiment to detect the aether wind [1]. But the wind was absent and none physical explanation to this fact was found. The hypothesis of aether collided with interne contradictions and was rejected. Besides, it was shown that in electromagnetic wave electric E and magnetic B components of field support each other and let a wave to propagate in a space without any aether. Finally, in order to explain the negative result of Michelson – Morley experiment and cope with the others, the Special Theory of Relativity was proposed. The history of its creation is well known [1-8].In accordance with Relativity in all inertial frames the length changes and time flows differently depending on relative velocities. Theory introduces the core concept of space-time as a unified entity of space and time - kinematics time dilation and length contraction. Moreover, in dynamics energy and mass are supposed to be equivalent and transmutable. These features are expressed mathematically by using Lorentz’s transform, and as a consequence – by equations of relativistic dynamics [1,2,7,8].From the beginning Relativity caused the criticism, reflected in many sources [9,12,15]. Generally, critical pertinent remarks can be divided on two groups. The first one contains the logical contradictions: paradoxes of twins, non addition of masses [13], divergence of relativistic addition of accelerations [14], impossibility to apply the relativity principle to de Broglie waves [17], etc. The second group contains the comments about carrying out experiments and errors of measurements. From the latest data it can be indicated a difference of corrections of clocks, positioned on the Earth and into satellites of GPS [15,16], i.e., a non equivalence of coordinate systems.However, the main problem, as it seems, is the other. Relativity ignores the fact, that a number of observed events in all frames is the same, including respectively the number of clock strokes. Instead of this number Relativity uses the notion of time span Δt between strokes, that varies, depending on relative velocities of frames. But if the number of strokes can be calculated, the span Δt does not. Any real clock measures elapsed time by discrete quantity of strokes and not by the dimension of span. This claim holds for any accuracy of clock, also when Δt → 0.The cornerstone of contemporaneous physics consists in the state, that only such values have a meaning, which could be experimentally measured. The idea that the moving clocks are measured to tick more slowly than an observer’s stationary clock is an abstraction unavailable of checking. Really, how to measure the slowness or Δt ? – By counting strokes of another clock ? But they are the same in all frames! The notion of Δt looses the sense until the method of its measurement would be elaborated. That obviously means the time stream is the same in all inertial frames. Then a multiplication of strokes number by speed of light yields the universal length unit unaltered in all inertial coordinate systems.And yet, how the criticism would be convincing, the tremendous experience, accumulated in atomic physics, gives an incontestable correctness proof of Relativity’s formulas, their predictions are verified by long standing practice and empirical discoveries.What is the matter? How to reconcile the mutually excluded strongest arguments from both sides? As it seems, the kernel consists of interpretation of formulas, their meaning is different from what to be thought. In order to understand that, it is necessary to look at quantum theory.The distinction between classical physics, based on determinism, and the quantum mechanics is the adoption of an uncertainty principle, the wave - like behaviour of matter and renunciation of the cause – effect relation. Quantum mechanics describes a picture of the world based on the idea of a wave particle - duality. Current scientific theory holds that all quantum entities exhibit a wave nature. The motion laws of elementary particles such an electron or photon cannot use the model of a point body, and vice versa, the results of experiments with quantum objects can’t be extrapolated to classical mechanics. But namely experiments with quantum - scale objects give the empirical basis to Relativity.Historically, Relativity appeared 20 years before the quantum theory and naturally, it was supposed, that macro and micro cosm differs only by the scale [4,5]. The modern physics proves that is not true. The quantum objects are the particle – waves, their interaction must not be considered as a collision of billiard – balls. However, from a similar model the relativity dynamics was built and the equivalency between energy and mass deduced.Theoretical construction of Relativity is built on interpretations of experiments, have been carried out with elementary particles. While in fact, quantum objects were used, obtained findings were applied to all physics.On the other hand, physics of elementary particles shows that the empty space even without electromagnetic and gravitational fields possesses energy, can create new particles [10]. Vacuum can excite [18,20], have a polarisation [21], be false [10,19]. In fact, the return to the hypothesis of aether with new name occurs. Physical vacuum (aether) as a medium permeating space, where processes of atomic and subatomic scale take place, is present in many newest theories [10,19,22].In the propositioned investigation it is supposed that relativistic formulas, expressed by Lorentz’s transform, issue from wave – particle origin of micro objects. Earlier, this hypothesis was mentioned in [23].It is admitted that the time and space are Euclidean and the same in all inertial frames, but the type of particle interaction changes. It is not a solid body which pushes another, as it passes in mechanics, but a wave, linked to one particle, acts on the second. An analogy to electromagnetism is seen here, when charges interact through fields and waves. The resemblance would be closer if in this model a photon would be associated somehow with E and B components of field. This approach is in concordance with quantum field theory (QFT), fields and particles are transmutable [10]. The obstacle to this way is that, the hypothesis does not explain the formulas of Lorentz transform – a foundation of contemporaneous relativity physics.
2. Wave Equation
2.1. Wave Equation in Hyperbolic Coordinates
- Let there is a homogenous wave equation
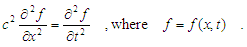 | (1) |
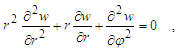 | (2) |
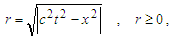 | (3) |
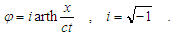 | (4) |
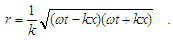 In that interpretation a solving of an equation (2) in a form of Dirichlet problem with the boundary condition, specified on a circle of radius r, becomes loosing a physical sense.To overcome this difficulty, the new problem is formulated with boundary setting
In that interpretation a solving of an equation (2) in a form of Dirichlet problem with the boundary condition, specified on a circle of radius r, becomes loosing a physical sense.To overcome this difficulty, the new problem is formulated with boundary setting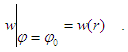 | (5) |
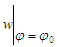 , which determines the boundary condition at
, which determines the boundary condition at 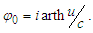 Physically boundary setting can be interpreted in two ways. Either to describe the wave by its snapshot, made from moving inertial frame, or by the waveform of time-unfolded oscillation of a point moving with speed u. This depends on how to represent a coordinate r in the boundary condition by admitting x/t = u:
Physically boundary setting can be interpreted in two ways. Either to describe the wave by its snapshot, made from moving inertial frame, or by the waveform of time-unfolded oscillation of a point moving with speed u. This depends on how to represent a coordinate r in the boundary condition by admitting x/t = u: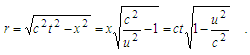 | (6) |
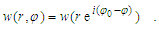 | (7) |
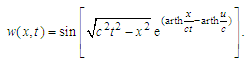 | (8) |
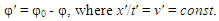 For this, velocities u, v, v′, must be interconnected according to the definition (4) and the solution (8), so as
For this, velocities u, v, v′, must be interconnected according to the definition (4) and the solution (8), so as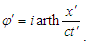 Hence,
Hence, 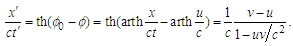 Thus,
Thus,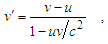 | (9) |
2.2. The Property of Invariance of the Wave Equation
- Let’s a wave, observing from two inertial frames with relative velocity u ( the inertiality’s requirement is stipulated for the boundary condition (6)). In the laboratory conventionally fixed frame 0x this wave is described by function w(r, φ), according to (7). In the uniform moving frame 0′x′ the solution of the wave equation (2) is the other, and expressed as w′(r′, φ′), where
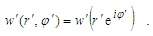 In order for the solutions of wave equation in both coordinate systems to be equal, i.e. w(r, φ) = w′(r′, φ′), obviously, two conditions must be met:
In order for the solutions of wave equation in both coordinate systems to be equal, i.e. w(r, φ) = w′(r′, φ′), obviously, two conditions must be met: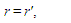 | (10) |
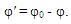 | (11) |
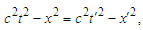 | (12) |
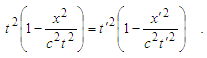 | (13) |
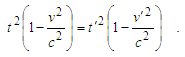 | (14) |
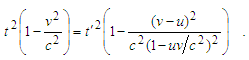 After some rearrangement, as it easy to show,
After some rearrangement, as it easy to show,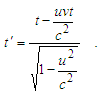 Because velocities are constant, then vt = x, and the final solution takes a view
Because velocities are constant, then vt = x, and the final solution takes a view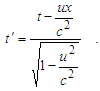 | (15) |
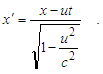 | (16) |
2.3. The Notion of 4–velocity
- An expression
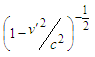 is taken. It may be rewritten by means of (9) in a form of an identity
is taken. It may be rewritten by means of (9) in a form of an identity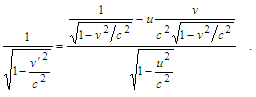 | (17) |
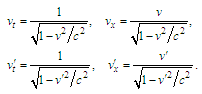 | (18) |
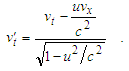 | (19) |
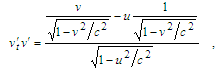 leads to
leads to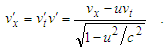 | (20) |
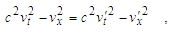 | (21) |
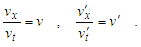 | (22) |
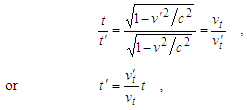 | (23) |
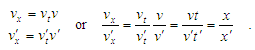 In accordance with this, x/vx = x′/v′x, that differs 4-velocities from ordinary ones, for which x′/v′ ≠ x/v, as it easy to show. Introducing denotations of time intervals τ = x/vx and τ′ = x′/v′x, finally a property follows τ=τ′.In other words v and v′ are such velocities, which during the equal time τ = τ′ will make such the displacements x and x′ of observers, from which the wave looks identical in the examined frames.Thus, it may be concluded, if in the frame 0x one observes a wave, in order that the requirement w = w′ holds in the system 0′x′ (in the area of complex numbers with imaginary time it), the velocities of observers must satisfy the setting (21), i.e.,
In accordance with this, x/vx = x′/v′x, that differs 4-velocities from ordinary ones, for which x′/v′ ≠ x/v, as it easy to show. Introducing denotations of time intervals τ = x/vx and τ′ = x′/v′x, finally a property follows τ=τ′.In other words v and v′ are such velocities, which during the equal time τ = τ′ will make such the displacements x and x′ of observers, from which the wave looks identical in the examined frames.Thus, it may be concluded, if in the frame 0x one observes a wave, in order that the requirement w = w′ holds in the system 0′x′ (in the area of complex numbers with imaginary time it), the velocities of observers must satisfy the setting (21), i.e.,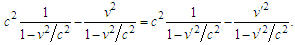 | (24) |
3. The Relationship between the Formulas of Relativity Physics and the Wave Equation
- Proceeding from the formulas (15), (16), the rule of relativistic addition of velocities (9) and an invariant (24) all the relativistic equations may be deduced purely mathematically. It is necessary to emphasize, that mentioned expressions are obtained without any use of the space-time transformation hypothesis, but exclusively analyzing the wave equation in the class of complex numbers by means of invariance property.Consequently, the basic postulates change: an investigation is applied only to the objects, having the wave – like nature. According to the wave-particle duality they are the quantum (elementary) particles. Their observation from the different coordinate systems should give the identical pattern.In order for the wave in both frames 0x and 0′x′ looks the same, the position coordinates and time instants of the compared wave points must fulfill the constraints (15) and (16). When observers of these points move with velocities v and v′, i.e. when the ratios x/t and x′/t′ are constant in (4), the velocities must obey demands (9) and (24).It is assumed, that in all inertial frames regardless of a relative motion, the time flows similarly, the length respectively does not contract, the mass of objects and density of electric charges are constant (and denoted m0 and ρ0, where the subscript is written according to the adopted agreement, while it is not needed). The multiplication of both sides in (24) by a constant m02c2 yields
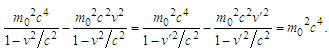 | (25) |
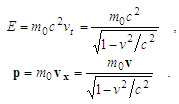 | (26) |
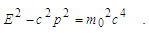 | (27) |
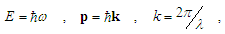 where ħ - reduced Planck’s constant, λ - wavelength de Broglie.In view of the known fact, that (ω, k) is the 4-vector (it can be checked either by using Lorentz formulas in the forms (15) and (16), or performing a scalar product of (t, x) and (ω, k)), its multiplication by Planck’s constant ħ gives the new 4-vector (ħω, ħk), that coincides with (E, p) for de Broglie wave.Analogically, 4-vector (ρ0, j) is derived from a multiplication of (24) by ρ0, where j - the vector of density of an electrical current. From here, referring to Maxwell’s equations, an invariant of electromagnetic field φe2-c2A2 is obtained [6].The scalar product of (ω, k) and (vt, vx) finally leads to
where ħ - reduced Planck’s constant, λ - wavelength de Broglie.In view of the known fact, that (ω, k) is the 4-vector (it can be checked either by using Lorentz formulas in the forms (15) and (16), or performing a scalar product of (t, x) and (ω, k)), its multiplication by Planck’s constant ħ gives the new 4-vector (ħω, ħk), that coincides with (E, p) for de Broglie wave.Analogically, 4-vector (ρ0, j) is derived from a multiplication of (24) by ρ0, where j - the vector of density of an electrical current. From here, referring to Maxwell’s equations, an invariant of electromagnetic field φe2-c2A2 is obtained [6].The scalar product of (ω, k) and (vt, vx) finally leads to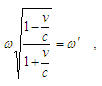 but, this is the expression of Doppler’s relativistic effect. By the way, this formula has been derived other as the solution of the wave equation in hyperbolic coordinates [24].So, it is demonstrated, that the relativistic formulas can be obtained by alternative method, excluding the space-time transformation. It remains to find out in which physical model they are embedded.
but, this is the expression of Doppler’s relativistic effect. By the way, this formula has been derived other as the solution of the wave equation in hyperbolic coordinates [24].So, it is demonstrated, that the relativistic formulas can be obtained by alternative method, excluding the space-time transformation. It remains to find out in which physical model they are embedded.4. The Wave Interpretation of Quantum Particles Interaction
- The wave – is the process of disturbance propagation (changes of states) in some mediums. According to the classical concept the waves are not connected with a transposition of matter, but transfer energy. To create wave energy is wasted; such waves are observed in experiments. For instance, an electromagnetic wave, defined by scalar φe and vector A potentials, can be measured by its effect on electrical charges.Waves need a transmission medium to exist, and are described by the wave equation (1), where the coefficient c is the parameter of the medium.However, there are the waves which are unobservable; their existence is postulated by indirect signs. The matter wave de Broglie serves as an example. According to the hypothesis all matter exhibits properties of both particles and waves, each object, having an energy E, and momentum p is associated with the de Broglie wave, so as E = ħω and p = ħk. In fact, the concept of de Broglie wave matches quantum bodies, although it is assumed that applies to all physics. De Broglie’s hypothesis explains well diffraction and interference of quantum – scale particles, but the wave cannot be measured because it does not transfer energy (energy is transferred by particle).There is another type of waves – waves of probability, described by the wave function ψ. Often, as a solution of quantum equations it takes a view
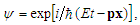 that is like outwardly a description of an ordinary wave. However, that is only a mathematical function, which does not clarify a mechanism of the propagation of such a wave, if generally, one can tell about a propagation of probability.Based on the above analysis the following generalized model is proposed. Moving at a speed v the quantum particle creates a bundle wave of the aether disturbance, propagating together with this particle, defined and located within the domain
that is like outwardly a description of an ordinary wave. However, that is only a mathematical function, which does not clarify a mechanism of the propagation of such a wave, if generally, one can tell about a propagation of probability.Based on the above analysis the following generalized model is proposed. Moving at a speed v the quantum particle creates a bundle wave of the aether disturbance, propagating together with this particle, defined and located within the domain 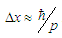 . The value vx, as it may be supposed, is the velocity of this propagation. So, there are two kinds of speed: the phase velocity c, and the group one of the bundle motion vx (plus, of course, the velocity of a particle v).When a collision with another particle occurs, it does not appear in the form of an elastic impact of two balls, but like an interaction between the wave of disturbed aether and the second particle according to the electromagnetic analogy. For the interaction will be invariant in all inertial frames, i. e. w = w′, the equalities (9), (15), (16), (24), (26) must be met.But this is the same thing, that an application of relativistic formulas. However, it is only a semblance, physical nature is fundamentally other: time, length, mass remain unchanged in all inertial systems. The character of the particle interaction changes from elastic collision to the wave – particle type. Mathematically it is expressed by use of 4-vector components vx or vx′ instead of v and v′.At difference from the de Broglie wave, the disturbance wave transfers energy and momentum (E, p), that are attributed either to the aether, or to field in QFT (the term does not matter).
. The value vx, as it may be supposed, is the velocity of this propagation. So, there are two kinds of speed: the phase velocity c, and the group one of the bundle motion vx (plus, of course, the velocity of a particle v).When a collision with another particle occurs, it does not appear in the form of an elastic impact of two balls, but like an interaction between the wave of disturbed aether and the second particle according to the electromagnetic analogy. For the interaction will be invariant in all inertial frames, i. e. w = w′, the equalities (9), (15), (16), (24), (26) must be met.But this is the same thing, that an application of relativistic formulas. However, it is only a semblance, physical nature is fundamentally other: time, length, mass remain unchanged in all inertial systems. The character of the particle interaction changes from elastic collision to the wave – particle type. Mathematically it is expressed by use of 4-vector components vx or vx′ instead of v and v′.At difference from the de Broglie wave, the disturbance wave transfers energy and momentum (E, p), that are attributed either to the aether, or to field in QFT (the term does not matter).5. Results and Discussion
- An alternative way of explaining the equations of the theory of relativity is obtained. A hypothesis is put forward according to which Relativity is the consequence of the quantum physics laws and the principle of wave-particle duality.Based on it, it is assumed that relativity phenomena should be described from the standpoint of the wave property of nature, and this description must give identical results in any inertial frame moving relative to one another.It is shown, that for invariability of the wave equation in two frames, i. e. w(r, φ)=w′(r′, φ′), the required conditions must be expressed by kinematics formulas (9), (15), (16).When coordinates of the wave adhere to constraints x/t = v and x′/t ′= v′, these formulas lead to the definition of 4-velocity, from which an energy – momentum invariant is derived, and 4-vector (m0c2vt, m0vx) equal to (E, p) is defined.The transition from corpuscular to the wave point of view does not change the expression E = mc2, but gives a different meaning. It is an energy of a wave disturbance of the aether
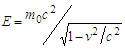 equal to energy of the matter wave de Broglie ħω. The wave and a particle are inseparable, that is why the coefficient c of the wave equation presents in all formulas. For electromagnetic interactions c - is the speed of light, defined by the properties of aether. The mass m0 in any frame remains the same and means ordinary mass (not the rest one).Consequently, 4-vector (E, p) is equivalent to 4-vector (ω, k) in the wave representation, they are the different projections of the same entity.According to this, the meaning of kinematics expressions (15) and (16) principally transforms. They determine not a change in time and lengths, but indicate the relation between coordinates of the wave points in two frames, in which complex amplitude and phase are equal.To explain the new content of the formulas, the QFT model, similar to the electromagnetic one, is proposed. The moving particle generates the wave of aether disturbance (de Broglie), and namely this wave acts to other particle. The feature of the wave is such, that the view of it from different inertial frames is the same and leads to the Relativity expressions.In this model not particles collide, but a wave and particle interact, or more precise, two particle-waves interfere.As for classical mechanics, the collision of billiard-balls, even accelerated to the speed of light, must obey Newton’s laws.The mathematical part in the present research is based on analysis of the classical wave equation, written into the domain of complex numbers with use of hyperbolic coordinates [24]. Analysis revealed an important property, that the solutions of the wave equation are Lorentz invariant for inertial reference frames. This means, that an impossibility of determining the absolute speed can be established not only on a basis of space-time transformation, but exclusively from applicability of the wave invariance feature.The transition from particle to wave interpretation fills relativistic formulas with different content. Instead of classical postulates the ideas of formalism of quantum mechanics should be recognized. The Michelson - Morley experiment, in which the light beams are employed (and so, photons - quantum entities), cannot be explained by the laws of Newton’s mechanics. In other words, Relativity should be examined as a part of quantum physics. To billiard-balls the relativistic equations are not applicable.The reject of the concept of space-time transformation leads to the adoption of new hypothesis about an existence of the aether disturbance as a modification of de Broglie waves. However, it is not a wave, associated with a particle, it is an ensemble of particle and aether, which could not exist separate Aether (physical vacuum) not only permeates a space, it constitutes also a part of elementary particles. This correlates with contemporaneous QFT that treats particles as excited states of their underlying fields, which are more fundamental than the particles themselves. Interactions between particles are described by means of LaGrangian, overwriting energy of corresponding fields. Accordingly, their mass, momentum and energy should be written by other formulas, then in classical mechanics, and include the property of aether – coefficient c from the wave equation. There is not a rest-mass, mass is the same in all frames, but that is the energy, that changes according (26).An interesting question is asked. What will it be, if the frames are not inertial? The answer is quite simple. In this case the ratio x/t cannot be presented as a constant speed, so the boundary condition (5) changes and the solution of (2) will distinguish from (7) and (8). Hence, all above made conclusions would not be applicable to exposed reasoning. Therefore, an extension of relativistic formulas to non uniform motion is not permitted, although there are several specific tasks [11,25].
equal to energy of the matter wave de Broglie ħω. The wave and a particle are inseparable, that is why the coefficient c of the wave equation presents in all formulas. For electromagnetic interactions c - is the speed of light, defined by the properties of aether. The mass m0 in any frame remains the same and means ordinary mass (not the rest one).Consequently, 4-vector (E, p) is equivalent to 4-vector (ω, k) in the wave representation, they are the different projections of the same entity.According to this, the meaning of kinematics expressions (15) and (16) principally transforms. They determine not a change in time and lengths, but indicate the relation between coordinates of the wave points in two frames, in which complex amplitude and phase are equal.To explain the new content of the formulas, the QFT model, similar to the electromagnetic one, is proposed. The moving particle generates the wave of aether disturbance (de Broglie), and namely this wave acts to other particle. The feature of the wave is such, that the view of it from different inertial frames is the same and leads to the Relativity expressions.In this model not particles collide, but a wave and particle interact, or more precise, two particle-waves interfere.As for classical mechanics, the collision of billiard-balls, even accelerated to the speed of light, must obey Newton’s laws.The mathematical part in the present research is based on analysis of the classical wave equation, written into the domain of complex numbers with use of hyperbolic coordinates [24]. Analysis revealed an important property, that the solutions of the wave equation are Lorentz invariant for inertial reference frames. This means, that an impossibility of determining the absolute speed can be established not only on a basis of space-time transformation, but exclusively from applicability of the wave invariance feature.The transition from particle to wave interpretation fills relativistic formulas with different content. Instead of classical postulates the ideas of formalism of quantum mechanics should be recognized. The Michelson - Morley experiment, in which the light beams are employed (and so, photons - quantum entities), cannot be explained by the laws of Newton’s mechanics. In other words, Relativity should be examined as a part of quantum physics. To billiard-balls the relativistic equations are not applicable.The reject of the concept of space-time transformation leads to the adoption of new hypothesis about an existence of the aether disturbance as a modification of de Broglie waves. However, it is not a wave, associated with a particle, it is an ensemble of particle and aether, which could not exist separate Aether (physical vacuum) not only permeates a space, it constitutes also a part of elementary particles. This correlates with contemporaneous QFT that treats particles as excited states of their underlying fields, which are more fundamental than the particles themselves. Interactions between particles are described by means of LaGrangian, overwriting energy of corresponding fields. Accordingly, their mass, momentum and energy should be written by other formulas, then in classical mechanics, and include the property of aether – coefficient c from the wave equation. There is not a rest-mass, mass is the same in all frames, but that is the energy, that changes according (26).An interesting question is asked. What will it be, if the frames are not inertial? The answer is quite simple. In this case the ratio x/t cannot be presented as a constant speed, so the boundary condition (5) changes and the solution of (2) will distinguish from (7) and (8). Hence, all above made conclusions would not be applicable to exposed reasoning. Therefore, an extension of relativistic formulas to non uniform motion is not permitted, although there are several specific tasks [11,25].6. Conclusions
- The new approach to explain the formulas of Relativity is proposed. It is based on exam of properties of the wave equation, which must be Lorentz invariant for the uniform motion. For this, physical objects must have the wave-like nature and their behavior must obey the quantum laws. There is no need to introduce the concept of space-time continuum, but the area of its applicability is limited by an atomic scale at which the particles and waves are interconnected.It is shown, in order that the wave equation would be Lorentz invariant into inertial frames, several conditions, defined by mentioned relativistic expressions, must be met. To prove this the domain of finding of solutions was extended to complex numbers, in which the time formally is an imaginary quantity it (so as in Schrödinger equation). Consequently, the propositioned approach should be regarded as a part of quantum mechanics, only without stochastic interpretation of obtained results.The particle interaction in the elaborated model differs from the generally accepted one [1-3]. Instead of elastic collision it is assumed that a particle gives rise to a wave of aether disturbance (excites it), and it is this wave that acts on other particle, as it occurs with electrical charges in electrodynamics. The difference is that an electromagnetic wave can propagate in an empty space, and in the given model the wave disturbs aether (field). That also differs it from matter wave de Broglie which is linked with the particle itself without any medium.The approach can be considered from the standpoint of QFT, when the particles and fields mutually turn.The mathematical model may be also examined as a singularity of the equation solution in hyperbolic coordinates, which is interpreted either like a shock wave, propagating at speed c, or an elementary particle (for example, photon moving at the same speed) [24].Because the wave equation is Lorentz invariant into inertial frames, then the description of quantum interactions does not depend on a choice of coordinate systems. In particular, this explains Michelson – Morley experiment.At the same time it follows, that formulas of Relativity do not extend to macro physics.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML