JP. C. Mbagwu1, Z. L. Abubakar2, J. O. Ozuomba1
1Department of Physics, Imo State University, Owerri, Nigeria
232 Artillery Brigade Owena Cantonment Akure, Ondo, Nigeria
Correspondence to: JP. C. Mbagwu, Department of Physics, Imo State University, Owerri, Nigeria.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The theory of relativity was initially conditioned by the unfinished electrodynamics theory. In the theory of relativity Albert Einstein kept some ideas in his mind which was important for the modification of Physics. The two basic principles of special relativity are: (1) the speed of light is a constant in a vacuum (Murkowski space), and (2) all the physical laws remain the same for local inertial frames. In Time Dilation and Length Contraction, Einstein established some notions with a range of anomalies. Time dilates and contracts because of the fluctuation of gravitational influence in numerous space-time. In the theory of equivalence, Einstein explained that gravitational and mass are identical. But this explanation of the principle of equivalence needs more elaboration. The body retains definite shape, size, and density, but it can only express mass with the help of gravitation. Beyond the force, the field body is unable to specific mass. This concept is not incorporated with the idea of the principle of equivalence.
Keywords:
Einstein Special theory of relativity, Reference frame, Time Dilation, Length Contraction
Cite this paper: JP. C. Mbagwu, Z. L. Abubakar, J. O. Ozuomba, A Review Article on Einstein Special Theory of Relativity, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 3, 2020, pp. 65-71. doi: 10.5923/j.ijtmp.20201003.03.
1. Introduction
Einstein’s concept could be a principle of time-space. It was proclaimed in his paper which was issued in 1905 based on a ‘’moving bodies of electrodynamics’’. The concept is generally acknowledged in physics also is experimentally established by physical ideas regarding the connection among time-space. Einstein’s principle is predicated on two hypothesizes which remain opposing in classical mechanics:i. Light travels at an endless speed in a vacuum.ii. Physical laws continue the same (invariant) in any indigenous inertial system. No inertial system is superior to others.Almost Einstein’s idea work in special relativity theory is made on the sooner work by Hendrik Lorentz. Einstein recommended the Special relativity principle initially in his first paper which was published on 26th September 1905 title, "On the Electrodynamics of Moving Bodies”. The discordancy of the procedure with Maxwell's equations of electromagnetism, and experimentally, the Michelson-Morley unpleasant result (and thus related trials) showed that frequently theorized aluminiferous aether didn't exist. Presently, the idea of Einstein’s relativity is recognized to be the main perfect ideal of motion at any speed, when gravitational effects are insignificant. Even so, the Newtonian ideal remains active as an easy and precise evaluation at low velocities (relative to the speed of light), for instance, the daily motions on Earth. Special relativity theory contains a wide selection of the significances. These are experimentally revealed and it includes length contraction, time dilation, mass, a universal ordinance, mass-energy equivalence, the speed of causality, and relativity of simultaneity. It has, for example, changed the outdated view of absolute time with the view of a time that's hooked in to synchronize system and three-dimensional position. Instead of an invariant measure between two events, there's an invariant space measure. Collective with other laws of physics, the second hypothesizes of special relativity notion predict the uniformity of mass and energy, as articulated within the mass-energy equivalence formula 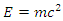 (m is mass and c is the speed of light in a very emptiness). A vital article of the special relativity theory is another of the Galilean transformations of mechanics with the Lorentz transformations. Time and space cannot be discrete individually from one another (as was previously thought to be the situation). Relatively, space and time are interwoven into one range called, " space-time”. Procedures that happen at an equal time for one observer can occur at dissimilar times for one more.
(m is mass and c is the speed of light in a very emptiness). A vital article of the special relativity theory is another of the Galilean transformations of mechanics with the Lorentz transformations. Time and space cannot be discrete individually from one another (as was previously thought to be the situation). Relatively, space and time are interwoven into one range called, " space-time”. Procedures that happen at an equal time for one observer can occur at dissimilar times for one more.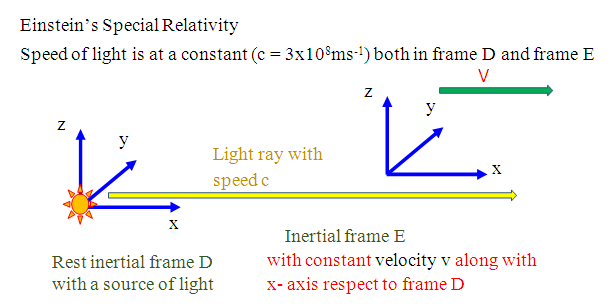 | Figure 1. Light (in a vacuum) moves at a constant speed 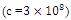 in any inertial frame. There is a source of light emitting at a rest frame D, the speed of light in frame D is in any inertial frame. There is a source of light emitting at a rest frame D, the speed of light in frame D is 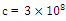 . The diagram shows that there is a frame E moving with a constant velocity v along with x-axis to frame D, and the velocity v also parallels to the direction of the light. Special relativity tells us that the speed of light observed in frame E is also at velocity . The diagram shows that there is a frame E moving with a constant velocity v along with x-axis to frame D, and the velocity v also parallels to the direction of the light. Special relativity tells us that the speed of light observed in frame E is also at velocity 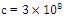 |
2. Time Dilation
The postulation of the individuality of the space and time have to be unrestricted. The dimension of space and time can only be determined by the observers, as contingency proclaims [11–13]. Assume an observer D is in static (in frame D), comparatively to another observer E (in frame E), which is in constant motion with constant velocity v. Observer D would notice that observer E is in sluggish motion, and find that the clock in frame E 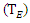 travels slower than the one stately in D
travels slower than the one stately in D 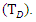 We call this weird occurrence a time dilation [1–3] (see Fig. 2). The relationship between
We call this weird occurrence a time dilation [1–3] (see Fig. 2). The relationship between 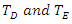 is given,
is given,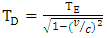 | (1) |
where 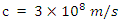 is the speed of light. Since the quantity
is the speed of light. Since the quantity 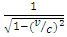 is always greater than 1 (you can check this for yourself), this means that, in your observation, your watch signals at a faster rate than the watch of someone on the train! This effect — that moving clocks run slow — is assumed of as time dilation. Note that, such as v approaches c, t approaches infinity! In other words, as a moving clock approaches the speed of light, the speed of its showing becomes slow and inactive (eventually infinitely slow) comparative to you, the observer at rest.For instance, super-train trips at 70 percent of the speed of light comparative to you on your seat. Due to the great ease of the seat, you inadvertently sleep off. Ultimately, you wake and determine that you just napped for 5 hours! How long would a proficient observer measure your nap to be? Well, using the time dilation formula, here we have
is always greater than 1 (you can check this for yourself), this means that, in your observation, your watch signals at a faster rate than the watch of someone on the train! This effect — that moving clocks run slow — is assumed of as time dilation. Note that, such as v approaches c, t approaches infinity! In other words, as a moving clock approaches the speed of light, the speed of its showing becomes slow and inactive (eventually infinitely slow) comparative to you, the observer at rest.For instance, super-train trips at 70 percent of the speed of light comparative to you on your seat. Due to the great ease of the seat, you inadvertently sleep off. Ultimately, you wake and determine that you just napped for 5 hours! How long would a proficient observer measure your nap to be? Well, using the time dilation formula, here we have 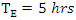 and v = 0.8c, so
and v = 0.8c, so 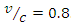 . Therefore, a trained observer measures your nap to last.
. Therefore, a trained observer measures your nap to last.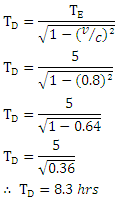
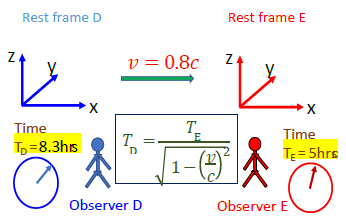 | Figure 2. Frame E is moving at a constant velocity v = 0.8c along with x-axis, to frame D. An observer in frame E finds that it experiences 5hrs, we call it as a proper time (TE). However, an observer in frame D may not agree with the result, and he finds that it experiences 8.3hrs in his measurement (frame D) correspondingly |
3. Length Contraction
The suitable length, 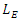 of an object is the length of an object that stately in the reference frame in which the body is at rest. It should be noted that in a reference frame in which the object is moving, the measured length is shorter than its proper length.Let us consider a rod at rest in frame
of an object is the length of an object that stately in the reference frame in which the body is at rest. It should be noted that in a reference frame in which the object is moving, the measured length is shorter than its proper length.Let us consider a rod at rest in frame 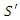 with ends of length at
with ends of length at 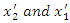 . The proper length n this frame is
. The proper length n this frame is 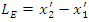 . Let us determine the length of the rod in frame S in which the rod is moving to the right with speed
. Let us determine the length of the rod in frame S in which the rod is moving to the right with speed 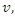 the speed of the frame S. The length in frame S is
the speed of the frame S. The length in frame S is 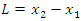 where
where 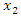 corresponds to the position of one end at time
corresponds to the position of one end at time 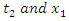 is the position of the other end at the same time
is the position of the other end at the same time 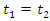 as measured in frame S.
as measured in frame S.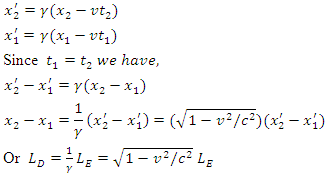 This is a contraction is known as Lorentz-Fitz-Gerald contraction. Tus a rod in motion appears to contract in length. Generally, the length of a rigid body moving with velocity
This is a contraction is known as Lorentz-Fitz-Gerald contraction. Tus a rod in motion appears to contract in length. Generally, the length of a rigid body moving with velocity 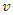 appears reduced by a factor
appears reduced by a factor 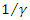 or
or 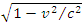 in the direction of motion.Similarly, an object of volume
in the direction of motion.Similarly, an object of volume 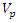 relative to an observer D at rest will have a volume V relative to observer E in uniform motion is given by:
relative to an observer D at rest will have a volume V relative to observer E in uniform motion is given by: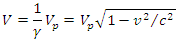
3.1. Basis in Relativity
First, it's a necessity to carefully consider the methods for measuring the lengths of resting and moving objects [5]. This idea, “object” solitary means a distance with endpoints that are always similarly at rest, i.e., that are at rest confidential at the identical frames of reference. If the absolute velocity between an observer (or his measuring instruments) and also the experimental object is zero, then the correct length of the object can simply be determined by directly superposing a measuring stick. However, if the relative velocity > 0, then one can proceed as follows: The observer installs a row of clocks that either is synchronized a) by exchanging light signals in step with the Poincare–Einstein synchronization, or e) by “slow clock transport”, that is, one clock is transported along the row of clocks within the limit of vanishing transport velocity. Now, when the synchronization process is finished, the article is moved along the clock row, and each clock stores the precise time when the left or the proper end of the article passes by. Subsequently, the observer solitary consumes to take a determined look at the location of a clock D that kept the time after the left end of the object was passing by, and a clock E at which the suitable end of the object was passing by at the same time. Distance DE is up to the length of the moving object [5]. Using this process, the description of simultaneity is vital for determining the moving length of an object. Another method is to use a clock indicating its proper time, which is traveling from one endpoint of the rod to the opposite in time as measured by the clocks within the rod's rest frame. The length of the rod may probably be determined by multiplying its time by its velocity, thus within the rod's rest frame or inside the clock's rest frame [6]. In Newtonian mechanics, simultaneity, and time duration are complete, and both techniques result in variation. Precisely, the theory is reliable at a light velocity all told about inertial frames that are the relativity of simultaneity and time dilation ends this equality. Hence, the basic technique is that an observer in one frame claims to have experimental the object's endpoints simultaneously, but the observers in all other inertial frames will claim that the object's endpoint wasn’t dignified simultaneously. Within the second method, times and aren't equal because of time dilation, leading to different lengths too. The irregularity between the measurements all told inertial frames is given by the approaches for Lorentz transformation, and time dilation. It appears that the exact length remains unchanged and frequently denotes the vital length of an object, and also the length of the identical object measured in another inertial system is shorter than the precise length. This contraction only happens along the path of motion and may be denoted by the relation.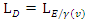 Where
Where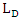 is the length observed by an observer in motion relative to the object
is the length observed by an observer in motion relative to the object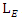 is the proper length (the length of the object in its rest frame)
is the proper length (the length of the object in its rest frame)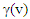 is the Lorentz factor, defined as
is the Lorentz factor, defined as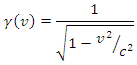 wherev is the relative velocity between the observer and the moving object.c is the speed of lightReplacing the Lorentz factor in the original formula leads to the relation
wherev is the relative velocity between the observer and the moving object.c is the speed of lightReplacing the Lorentz factor in the original formula leads to the relation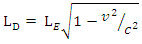 In this equation, both and LE are measured parallel to the object's line of movement. For instance, the observer in a relative measure measured the length of the object by subtracting the parallel distances measured at a mutually ends of the object. An observer at rest noticing an object traveling near to the speed of light would observe the length of the object in the direction of incidence as very close to zero.
In this equation, both and LE are measured parallel to the object's line of movement. For instance, the observer in a relative measure measured the length of the object by subtracting the parallel distances measured at a mutually ends of the object. An observer at rest noticing an object traveling near to the speed of light would observe the length of the object in the direction of incidence as very close to zero.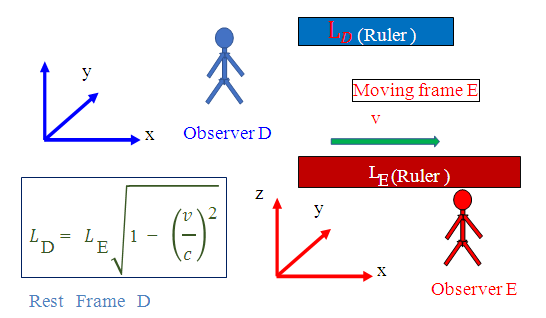 | Figure 3. The inertial frame E is again running at a constant velocity to a rest frame D. Suppose an observer E finds that the length of a rule in frame E is LE (called as proper length), and an observer D will find that the length of a rule is 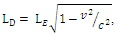 which is shorter than the one measured by the observer E, with a (Lorentz) factor which is shorter than the one measured by the observer E, with a (Lorentz) factor 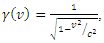 We call it as the Lorentz contraction. We call it as the Lorentz contraction. |
The observer D would mention that E moves slower when the typical velocity v of D increases [11–13]. As an example, as shown in Fig. 3, frame E is moving at a velocity v = 0.8c, constantly relation to frame D. An observer in frame E experiences 5 hrs. 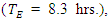 then observer D will obtain
then observer D will obtain 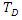 = 5 hrs. In his/her measurement (frame D) correspondingly. However, the observer E would insist that his/her clock is alright, as moving as normal as was common (the time
= 5 hrs. In his/her measurement (frame D) correspondingly. However, the observer E would insist that his/her clock is alright, as moving as normal as was common (the time 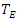 is named proper time). E would find that the punch in frame D runs slowly in E’s measurement otherwise. Who is correct? Einstein's theory of relativity asserts that both are correct, and also the measurement of your time only depends on the constant motion of observers [7–10].
is named proper time). E would find that the punch in frame D runs slowly in E’s measurement otherwise. Who is correct? Einstein's theory of relativity asserts that both are correct, and also the measurement of your time only depends on the constant motion of observers [7–10].
4. Lorentz Transformation
The Lorentz Transformation we may consider a coordinate transformation between two inertial frames as a dictionary by whose means observers residing on the two frames can make their meaning clear to every other. In ordinary experience we want the help of the Galilean transformation to reconcile the determination of velocities on two inertial frames. An observer on the bottom who measures the rate of an airplane concerning his/her frame will hit a completely different result than the pilot reading his airspeed indicator and his compass heading. If these observers communicate by radio, their results are completely contradictory until the conflict is resolved through the Galilean transformation. Consider the wants upon a group of transformation equations that can fulfill our needs. The transformation must be linear; that is, a single event in one inertial frame must transform into a single event in another frame, with a single set of coordinates. i. The transformation must approach the Galilean transformation in the limit of low speeds. Here low speeds mean low compared to c so that we wish to look at the transformation within the limit 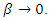 ii. The speed of light must have the same value, c, in every inertial frame. Just as the disturbance in a pond resulting from dropping a pebble into the water is a system of circular ripples, so a flash of light spreads out as a growing sphere. We may describe this sphere, whose radius grows at speed c, by the equation
ii. The speed of light must have the same value, c, in every inertial frame. Just as the disturbance in a pond resulting from dropping a pebble into the water is a system of circular ripples, so a flash of light spreads out as a growing sphere. We may describe this sphere, whose radius grows at speed c, by the equation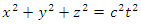 | (1) |
even as the spreading light flash forms a spreading sphere within the unprimed frame, so, it must also form a spreading sphere within the primed frame. Suppose the flash of light takes place at the moment when both t and t' are zero, and when the origins of the two frames coincide. Then the equation of the sphere of light within the primed frame must be: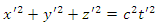 | (2) |
The coordinate transformation that satisfies these requirements is called the Lorentz transformation, after its discoverer, and forms the mathematical beginning of the special theory of relativity. Space and time coordinates of a happening recorded in two inertial frames whose axes are parallel, and whose origins coincide on time zero (in both frames), are related by the equations: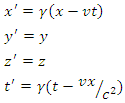 | (3) |
Inverting primed and unprimed coordinates (v → −v) gives: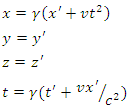 | (4) |
Note, that when  , or
, or 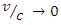 , then
, then 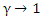 and
and 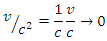 , and
, and 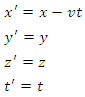 | (5) |
So Galilean transformations are a limiting case of the Lorentz transformations when 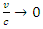 .
.
5. Galilean Transformation
Galilean transformation does not state that whether there's one or numerous inertial frames of reference, nor, if there is completed one, it tells us how we can relate the coordinates of a trendy as observed from an event to the coordinates of the identical event as observed in another. Informing the previous, we can express there is, after all, an infinite number of inertial reference frames. Furthermore, the transformation equivalences that we derive are then the scientific foundation on which it will be shown that Newton’s Laws are each the notion of relativity. To develop these transformation equations, consider an inertial frame of reference K and a second reference frame 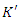 moving with a velocity
moving with a velocity 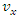 relative to S.
relative to S.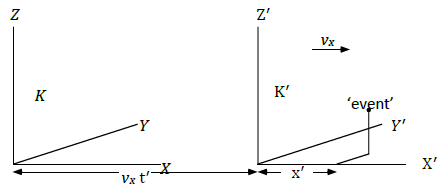 | Figure 4. A frame of reference 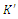 is moving with a velocity is moving with a velocity 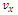 comparative to the inertial frame K. An incidence occurs with spatial coordinates (x, y, z) at time t in K and at comparative to the inertial frame K. An incidence occurs with spatial coordinates (x, y, z) at time t in K and at 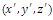 at time at time 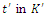 |
Let us assume that the clocks in K and 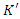 are established such that when the backgrounds of the two reference frames O and
are established such that when the backgrounds of the two reference frames O and 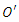 coincide, all the clocks in both frames of reference read zero i.e.
coincide, all the clocks in both frames of reference read zero i.e. 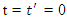 . According to ‘mutual sense’, if the clocks in K and
. According to ‘mutual sense’, if the clocks in K and 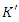 are coordinated at
are coordinated at 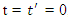 , then they will read the same, i.e.
, then they will read the same, i.e. 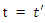 always. Once again, this concept is complete time. Assume now that an occurrence of approximately kind, e.g. an explosion, occurs at a point
always. Once again, this concept is complete time. Assume now that an occurrence of approximately kind, e.g. an explosion, occurs at a point 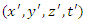 according to
according to 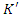 . Then, by examining Fig. (4), agreeing to K, it happens at the point
. Then, by examining Fig. (4), agreeing to K, it happens at the point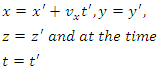 | (6) |
These equivalences together are known as the Galilean Transformation, and they express how the coordinates of an incident in one reference system K are connected with the coordinates of the same event as measured in a different frame 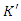 moving with an outstanding velocity virtual to K. Now assume that in reference frame K, a particle is acted on by no forces and later is moving along the line path known as:
moving with an outstanding velocity virtual to K. Now assume that in reference frame K, a particle is acted on by no forces and later is moving along the line path known as: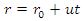 | (7) |
Here u is the velocity of the particle as measured in K. Then in 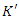 , a frame of reference moving with a velocity v =
, a frame of reference moving with a velocity v = 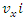 relative to K, the particle will be following a path
relative to K, the particle will be following a path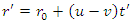 | (8) |
Where we've simply replaced for the components of 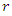 using equation (6) above. This last result also clearly represents the particle occupation a line path at a constant speed, and since the particle is being acted on by no forces,
using equation (6) above. This last result also clearly represents the particle occupation a line path at a constant speed, and since the particle is being acted on by no forces, 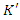 is furthermore a frame of reference, and since v is bigoted, there's usually an infinite number of such frames.Incidentally, if we take the derivative of Eq. (6) with respect to t, and use the fact that
is furthermore a frame of reference, and since v is bigoted, there's usually an infinite number of such frames.Incidentally, if we take the derivative of Eq. (6) with respect to t, and use the fact that 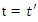 , we obtain
, we obtain 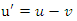 | (9) |
which is the acquainted addition law for relative velocities.It is a reliable exercise to work out how the inverse transformation may be calculated from the above equations. We will do that in two methods. A method is just to resolve this equation, so on precise the primed variables regarding the unprimed variable. An alternate method, one unprimed variable. An alternate method, one that's more revealing of the underlying symmetry of space, is to notice that if 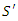 is moving with a velocity
is moving with a velocity 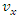 with relevancy S, then S is moving with velocity
with relevancy S, then S is moving with velocity 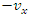 with relevancy
with relevancy 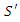 therefore the inverse transformation should be obtainable by simply exchanging the primed and unprimed variables, and replacing
therefore the inverse transformation should be obtainable by simply exchanging the primed and unprimed variables, and replacing 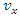 by
by 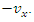 Either way, the result obtained is:
Either way, the result obtained is: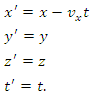 | (10) |
Equation (10) is known as the Galilean transformation equation.
6. Mass-Energy Equivalence
The famous Einstein mass-energy relationship, 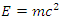 gives the equivalent of mass and energy. The disappearance of even a second mass results in the looks of the same amount of energy which may be very large indeed. Various processes have revealed that energy may be transformed from one form to a different, e.g. mechanical, chemical, heat, etc., but energy will always be conserved. In classical physics, we had two separate conservation principles--- conservation of mass as in chemical reactions, and therefore the conservation of energy. It's on this principle that a lot of nuclear reactions (including fission and fusion) function. This represents probably the foremost important results of special relativity theory and provides a deep physical desiring to the concept of the whole relativistic energy E. To calculate the significance of E during this concern, contemplate the collapse of a body of mass
gives the equivalent of mass and energy. The disappearance of even a second mass results in the looks of the same amount of energy which may be very large indeed. Various processes have revealed that energy may be transformed from one form to a different, e.g. mechanical, chemical, heat, etc., but energy will always be conserved. In classical physics, we had two separate conservation principles--- conservation of mass as in chemical reactions, and therefore the conservation of energy. It's on this principle that a lot of nuclear reactions (including fission and fusion) function. This represents probably the foremost important results of special relativity theory and provides a deep physical desiring to the concept of the whole relativistic energy E. To calculate the significance of E during this concern, contemplate the collapse of a body of mass 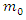 into two sections of rest masses
into two sections of rest masses 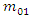 and
and 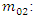
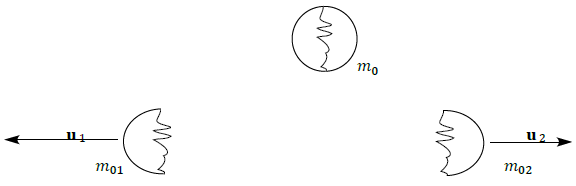 | Figure 5. Shows the disintegration of a body of rest mass m0 into two quantities of rest masses m01 and m02, moving with velocities u1 and u2 virtual to the rest frame of the exceptional object |
We could see from the figure (5) that the initial body could be a dangerous nucleus, or maybe simply two masses related to a twisted spring. For instance, the early body is static in nearly frame S, and also the rubble flies separately with velocities u1 and u2 relative to S at that moment, by the conservation of energy in S: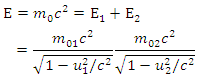 Thus,
Thus,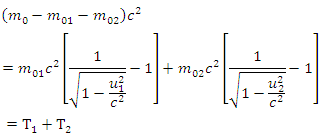 | (11) |
where 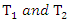 remain the relativistic kinetic energies of the two masses formed. Relatively,
remain the relativistic kinetic energies of the two masses formed. Relatively, 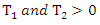 subsequently
subsequently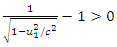 | (12) |
and equally for the other term and hence,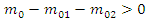 | (13) |
Or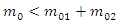 | (14) |
From equation (14), it means that the absolute rest mass of the two distinct masses is less than that of the original mass. The difference, ∆m say, is specified by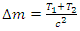 | (15) |
Hence, that quantity of the rest mass of the unique body has vanished, and an amount of kinetic energy known by 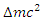 has appeared. The certain assumption is that approximately the rest mass of the original body has been transformed into the kinetic energy of the two masses formed. The interesting outcome is that not a bit of the masses involved needs to be traveling at speeds near to the speed of light. Eq. (15) can be written, for
has appeared. The certain assumption is that approximately the rest mass of the original body has been transformed into the kinetic energy of the two masses formed. The interesting outcome is that not a bit of the masses involved needs to be traveling at speeds near to the speed of light. Eq. (15) can be written, for 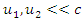 as
as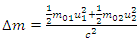 | (16) |
So that only classical Newtonian K.E. appears. To live the mass loss 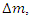 it wouldn’t be out of the problem to bring the masses to rest to regulate their rest masses. However, the truly extraordinary part of the above decisions is that its fundamental origin within the incontrovertible fact there exists a collective maximum possible speed, the speed of light which is made into the arrangement of space and time, and this structure eventually exerts an effect on the properties of matter occupying space and time, i.e., its mass and energy. The contrary can even occur i.e. matter will be created out of energy as in, for instance, an impact among particles having a number of their energy transformed into new particles as within the proton-proton collision,
it wouldn’t be out of the problem to bring the masses to rest to regulate their rest masses. However, the truly extraordinary part of the above decisions is that its fundamental origin within the incontrovertible fact there exists a collective maximum possible speed, the speed of light which is made into the arrangement of space and time, and this structure eventually exerts an effect on the properties of matter occupying space and time, i.e., its mass and energy. The contrary can even occur i.e. matter will be created out of energy as in, for instance, an impact among particles having a number of their energy transformed into new particles as within the proton-proton collision, 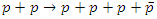 where an additional proton (p) and an antiproton
where an additional proton (p) and an antiproton 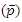 have been created. A more ordinary result of the above connection among energy and mass is that slightly than speaking about the rest mass of a particle, it is frequently more suitable to talk about its rest energy. A particle of rest mass
have been created. A more ordinary result of the above connection among energy and mass is that slightly than speaking about the rest mass of a particle, it is frequently more suitable to talk about its rest energy. A particle of rest mass 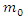 will, of course, have a rest energy
will, of course, have a rest energy  . Usually, the rest energy (or certainly any energy) arising in atomic, nuclear, or basic physics is given in units of electron volts. One electron volt (eV) is the energy added by an electron accelerated concluded a potential difference of 1 volt i.e.
. Usually, the rest energy (or certainly any energy) arising in atomic, nuclear, or basic physics is given in units of electron volts. One electron volt (eV) is the energy added by an electron accelerated concluded a potential difference of 1 volt i.e. 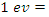
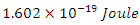 . For instance, the usual magnitudes of the rest energies of fundamental particles is that of the proton. With a rest mass of
. For instance, the usual magnitudes of the rest energies of fundamental particles is that of the proton. With a rest mass of 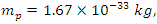 the proton has a rest energy of
the proton has a rest energy of 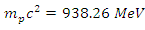 .
.
6.1. Mass-Energy Equivalence Derivation
Suppose a body is displaced by a force F, through a displacement, dx. Then by the work-energy theorem;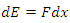 Where;
Where; 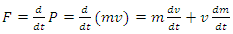 For this moment we consider m to be a variable.
For this moment we consider m to be a variable. 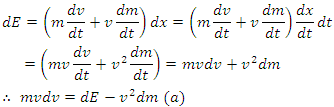 If we assume the relativistic mass transformation to be
If we assume the relativistic mass transformation to be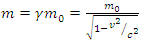 | (17) |
Squaring equation (17), we have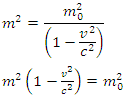 | (18) |
Differentiating both sides of equation (18) with respect to v we have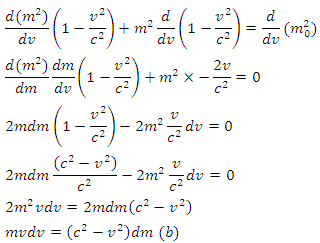 Equating equation (b) to the value of obtained in equation (a), we have;
Equating equation (b) to the value of obtained in equation (a), we have;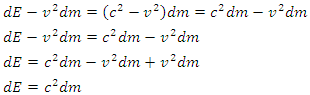 | (19) |
Integrating both sides of equation (19)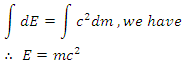 | (20) |
Equation (20) is Einstein’s famous mass-energy relation.
7. Conclusions
This research is a review of Einstein’s special theory of relativity. The fundamental's principle of Einstein’s theory of relativity is that light moves at a constant speed and every physical law is invariant for inertial frames. Time and space are certainly no longer complete. They depend upon the view of the observer’s D and E. Every frame describes the correct physics, and no reference system is before others. Besides, the frames are associated with one another by Lorentz’s transformation.
References
| [1] | Lu, Ed. "Expedition 7: Relativity". Ed's Musing from Space. NASA. Retrieved 2018-04-08. |
| [2] | Ashby, Neil (2003). "Relativity in the Global Positioning System" (PDF). Living Reviews in Relativity. 6 (1): 16. Bibcode: 2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638. |
| [3] | "Is time travel possible?". NASA Space Place. Retrieved 2018-08-03. |
| [4] | Dalarsson, Mirjana; Dalarsson, Nils (2015). Tensors, Relativity, and Cosmology (2nd ed.). Academic Press. p. 106–108. ISBN 978-0-12-803401-9. Extract of page 106. |
| [5] | Born, Max (1964), Einstein's Theory of Relativity, Dover Publications, ISBN 0-486-60769-0. |
| [6] | Edwin F. Taylor; John Archibald Wheeler (1992). Space time Physics: Introduction to Special Relativity. New York: W. H. Freeman. ISBN 0-7167-2327-1. |
| [7] | A. Einstein, Relativity: The Special and General Theory, Princeton University Press 1923. |
| [8] | A. Einstein, E. P. Adams, E. G. Straus, and S. Bargmann, The Meaning of Relativity, Princeton University Press 2014. |
| [9] | A. Einstein, Graviton Mass and inertial Mass, Ann Physik 1911, 35, 898. |
| [10] | A. Einstein, Zur Elektrodynamik bewegter Krper, Annalen der Physik 1905, 17, 891. |
| [11] | R. Harris, Modern Physics (2nd Edition), Pearson Addison Wesley 2008. |
| [12] | R. Gautreau and W. Savin, Modern Physics (2nd Edition), McGraw Hill 1999. |
| [13] | A. Z. Jones and D. Robbins, String Theory for Dummies, Wiley Publishing Inc. 2010. |
| [14] | P.N. Okeke, F.N. Okeke, and E.N. Mgbenu, special theory of relativity, Physics writers series creation. 2016. |
| [15] | Einstein, Albert (1905a) “Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?” Annalen der Physik, 18, pp. 639-641. (“Does the Inertia of a Body Depend upon its Energy Content?”) |
| [16] | Einstein, Albert (1917) Über die spezielle and die allgemeine Relativitäts theorie (Gemeinverständlich). Braunschweig: Friedr. Vieweg & Sohn; 15th expanded edition, trans. R. W. Lawson, Relativity: The Special and the General Theory. London: Methuen, 1954. |
| [17] | Einstein, Albert (1946) “An Elementary Derivation of the Equivalence of Mass and Energy”, pp. 116-19 in Out of my Later Years. New York: Bonanza, 1990. |
| [18] | Einstein, Albert (1905) “Zur Electrodynamik bewegter Körper,” Annalen der Physik, 17, pp. 891-921. (“On the Electrodynamics of Moving Bodies.”) |
| [19] | Janssen, Michel (2002) “Reconsidering a Scientific Revolution: The Case of Einstein versus Lorentz,” Physics in Perspective, 4, pp. 421–446. |
| [20] | Lorentz, Hendrik A. (1895) Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern. Leiden: E. J. Brill. (“Draft of a theory of electrical and optical phenomena in moving bodies.”) |
| [21] | Lorentz, Hendrik A. (1904) “Electromagnetic Phenomena in a System Moving with any Velocity less than that of Light,” Proceedings of the Academy of Sciences, Amsterdam, 6; reprinted pp. 11-34 H. A. Lorentz et al., The Principle of Relativity. Trans W. Perrett and G. B. Jeffrey. Methuen, 1923; Dover, 1952. |
| [22] | Miller, Arthur (1981) Albert Einstein’s Special Theory of Relativity. Reading, MA: Addison Wesley. |
| [23] | L.D. Landau, E.M. Lifshitz, Quantum Mechanics Nonrelativistic Theory: Course of Theoretical Physics Series (Volume 3), Butterworth-Heinemann 1981. |
| [24] | D. J. Griffiths, Introduction to Quantum Mechanics (2nd Edition), Pearson Education Limited 2014. |



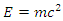 (m is mass and c is the speed of light in a very emptiness). A vital article of the special relativity theory is another of the Galilean transformations of mechanics with the Lorentz transformations. Time and space cannot be discrete individually from one another (as was previously thought to be the situation). Relatively, space and time are interwoven into one range called, " space-time”. Procedures that happen at an equal time for one observer can occur at dissimilar times for one more.
(m is mass and c is the speed of light in a very emptiness). A vital article of the special relativity theory is another of the Galilean transformations of mechanics with the Lorentz transformations. Time and space cannot be discrete individually from one another (as was previously thought to be the situation). Relatively, space and time are interwoven into one range called, " space-time”. Procedures that happen at an equal time for one observer can occur at dissimilar times for one more. travels slower than the one stately in D
travels slower than the one stately in D 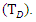 We call this weird occurrence a time dilation [1–3] (see Fig. 2). The relationship between
We call this weird occurrence a time dilation [1–3] (see Fig. 2). The relationship between 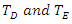 is given,
is given,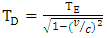
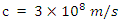 is the speed of light. Since the quantity
is the speed of light. Since the quantity 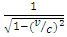 is always greater than 1 (you can check this for yourself), this means that, in your observation, your watch signals at a faster rate than the watch of someone on the train! This effect — that moving clocks run slow — is assumed of as time dilation. Note that, such as v approaches c, t approaches infinity! In other words, as a moving clock approaches the speed of light, the speed of its showing becomes slow and inactive (eventually infinitely slow) comparative to you, the observer at rest.For instance, super-train trips at 70 percent of the speed of light comparative to you on your seat. Due to the great ease of the seat, you inadvertently sleep off. Ultimately, you wake and determine that you just napped for 5 hours! How long would a proficient observer measure your nap to be? Well, using the time dilation formula, here we have
is always greater than 1 (you can check this for yourself), this means that, in your observation, your watch signals at a faster rate than the watch of someone on the train! This effect — that moving clocks run slow — is assumed of as time dilation. Note that, such as v approaches c, t approaches infinity! In other words, as a moving clock approaches the speed of light, the speed of its showing becomes slow and inactive (eventually infinitely slow) comparative to you, the observer at rest.For instance, super-train trips at 70 percent of the speed of light comparative to you on your seat. Due to the great ease of the seat, you inadvertently sleep off. Ultimately, you wake and determine that you just napped for 5 hours! How long would a proficient observer measure your nap to be? Well, using the time dilation formula, here we have 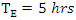 and v = 0.8c, so
and v = 0.8c, so 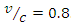 . Therefore, a trained observer measures your nap to last.
. Therefore, a trained observer measures your nap to last.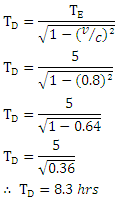
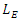 of an object is the length of an object that stately in the reference frame in which the body is at rest. It should be noted that in a reference frame in which the object is moving, the measured length is shorter than its proper length.Let us consider a rod at rest in frame
of an object is the length of an object that stately in the reference frame in which the body is at rest. It should be noted that in a reference frame in which the object is moving, the measured length is shorter than its proper length.Let us consider a rod at rest in frame 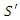 with ends of length at
with ends of length at 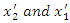 . The proper length n this frame is
. The proper length n this frame is 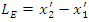 . Let us determine the length of the rod in frame S in which the rod is moving to the right with speed
. Let us determine the length of the rod in frame S in which the rod is moving to the right with speed 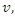 the speed of the frame S. The length in frame S is
the speed of the frame S. The length in frame S is 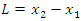 where
where 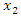 corresponds to the position of one end at time
corresponds to the position of one end at time 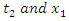 is the position of the other end at the same time
is the position of the other end at the same time 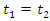 as measured in frame S.
as measured in frame S.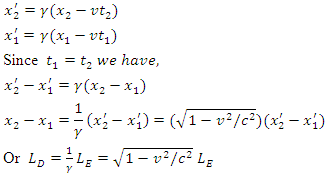 This is a contraction is known as Lorentz-Fitz-Gerald contraction. Tus a rod in motion appears to contract in length. Generally, the length of a rigid body moving with velocity
This is a contraction is known as Lorentz-Fitz-Gerald contraction. Tus a rod in motion appears to contract in length. Generally, the length of a rigid body moving with velocity 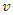 appears reduced by a factor
appears reduced by a factor 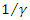 or
or 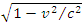 in the direction of motion.Similarly, an object of volume
in the direction of motion.Similarly, an object of volume 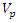 relative to an observer D at rest will have a volume V relative to observer E in uniform motion is given by:
relative to an observer D at rest will have a volume V relative to observer E in uniform motion is given by: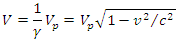
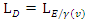 Where
Where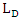 is the length observed by an observer in motion relative to the object
is the length observed by an observer in motion relative to the object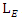 is the proper length (the length of the object in its rest frame)
is the proper length (the length of the object in its rest frame)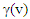 is the Lorentz factor, defined as
is the Lorentz factor, defined as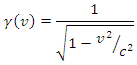 wherev is the relative velocity between the observer and the moving object.c is the speed of lightReplacing the Lorentz factor in the original formula leads to the relation
wherev is the relative velocity between the observer and the moving object.c is the speed of lightReplacing the Lorentz factor in the original formula leads to the relation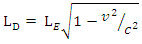 In this equation, both and LE are measured parallel to the object's line of movement. For instance, the observer in a relative measure measured the length of the object by subtracting the parallel distances measured at a mutually ends of the object. An observer at rest noticing an object traveling near to the speed of light would observe the length of the object in the direction of incidence as very close to zero.
In this equation, both and LE are measured parallel to the object's line of movement. For instance, the observer in a relative measure measured the length of the object by subtracting the parallel distances measured at a mutually ends of the object. An observer at rest noticing an object traveling near to the speed of light would observe the length of the object in the direction of incidence as very close to zero.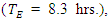 then observer D will obtain
then observer D will obtain 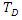 = 5 hrs. In his/her measurement (frame D) correspondingly. However, the observer E would insist that his/her clock is alright, as moving as normal as was common (the time
= 5 hrs. In his/her measurement (frame D) correspondingly. However, the observer E would insist that his/her clock is alright, as moving as normal as was common (the time 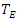 is named proper time). E would find that the punch in frame D runs slowly in E’s measurement otherwise. Who is correct? Einstein's theory of relativity asserts that both are correct, and also the measurement of your time only depends on the constant motion of observers [7–10].
is named proper time). E would find that the punch in frame D runs slowly in E’s measurement otherwise. Who is correct? Einstein's theory of relativity asserts that both are correct, and also the measurement of your time only depends on the constant motion of observers [7–10].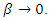 ii. The speed of light must have the same value, c, in every inertial frame. Just as the disturbance in a pond resulting from dropping a pebble into the water is a system of circular ripples, so a flash of light spreads out as a growing sphere. We may describe this sphere, whose radius grows at speed c, by the equation
ii. The speed of light must have the same value, c, in every inertial frame. Just as the disturbance in a pond resulting from dropping a pebble into the water is a system of circular ripples, so a flash of light spreads out as a growing sphere. We may describe this sphere, whose radius grows at speed c, by the equation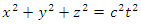
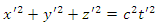
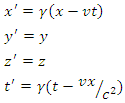
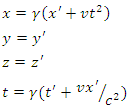
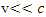 , or
, or 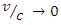 , then
, then 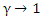 and
and 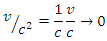 , and
, and 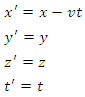
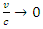 .
. moving with a velocity
moving with a velocity 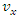 relative to S.
relative to S.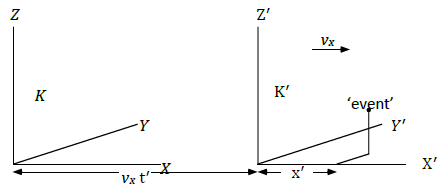
 is moving with a velocity
is moving with a velocity 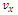 comparative to the inertial frame K. An incidence occurs with spatial coordinates (x, y, z) at time t in K and at
comparative to the inertial frame K. An incidence occurs with spatial coordinates (x, y, z) at time t in K and at 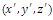 at time
at time 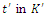
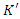 are established such that when the backgrounds of the two reference frames O and
are established such that when the backgrounds of the two reference frames O and 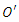 coincide, all the clocks in both frames of reference read zero i.e.
coincide, all the clocks in both frames of reference read zero i.e. 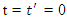 . According to ‘mutual sense’, if the clocks in K and
. According to ‘mutual sense’, if the clocks in K and 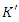 are coordinated at
are coordinated at 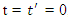 , then they will read the same, i.e.
, then they will read the same, i.e. 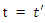 always. Once again, this concept is complete time. Assume now that an occurrence of approximately kind, e.g. an explosion, occurs at a point
always. Once again, this concept is complete time. Assume now that an occurrence of approximately kind, e.g. an explosion, occurs at a point 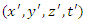 according to
according to 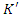 . Then, by examining Fig. (4), agreeing to K, it happens at the point
. Then, by examining Fig. (4), agreeing to K, it happens at the point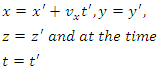
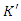 moving with an outstanding velocity virtual to K. Now assume that in reference frame K, a particle is acted on by no forces and later is moving along the line path known as:
moving with an outstanding velocity virtual to K. Now assume that in reference frame K, a particle is acted on by no forces and later is moving along the line path known as: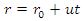
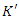 , a frame of reference moving with a velocity v =
, a frame of reference moving with a velocity v = 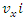 relative to K, the particle will be following a path
relative to K, the particle will be following a path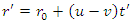
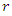 using equation (6) above. This last result also clearly represents the particle occupation a line path at a constant speed, and since the particle is being acted on by no forces,
using equation (6) above. This last result also clearly represents the particle occupation a line path at a constant speed, and since the particle is being acted on by no forces, 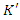 is furthermore a frame of reference, and since v is bigoted, there's usually an infinite number of such frames.Incidentally, if we take the derivative of Eq. (6) with respect to t, and use the fact that
is furthermore a frame of reference, and since v is bigoted, there's usually an infinite number of such frames.Incidentally, if we take the derivative of Eq. (6) with respect to t, and use the fact that 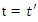 , we obtain
, we obtain 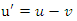
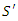 is moving with a velocity
is moving with a velocity 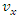 with relevancy S, then S is moving with velocity
with relevancy S, then S is moving with velocity 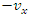 with relevancy
with relevancy 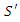 therefore the inverse transformation should be obtainable by simply exchanging the primed and unprimed variables, and replacing
therefore the inverse transformation should be obtainable by simply exchanging the primed and unprimed variables, and replacing 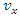 by
by 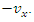 Either way, the result obtained is:
Either way, the result obtained is: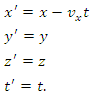
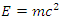 gives the equivalent of mass and energy. The disappearance of even a second mass results in the looks of the same amount of energy which may be very large indeed. Various processes have revealed that energy may be transformed from one form to a different, e.g. mechanical, chemical, heat, etc., but energy will always be conserved. In classical physics, we had two separate conservation principles--- conservation of mass as in chemical reactions, and therefore the conservation of energy. It's on this principle that a lot of nuclear reactions (including fission and fusion) function. This represents probably the foremost important results of special relativity theory and provides a deep physical desiring to the concept of the whole relativistic energy E. To calculate the significance of E during this concern, contemplate the collapse of a body of mass
gives the equivalent of mass and energy. The disappearance of even a second mass results in the looks of the same amount of energy which may be very large indeed. Various processes have revealed that energy may be transformed from one form to a different, e.g. mechanical, chemical, heat, etc., but energy will always be conserved. In classical physics, we had two separate conservation principles--- conservation of mass as in chemical reactions, and therefore the conservation of energy. It's on this principle that a lot of nuclear reactions (including fission and fusion) function. This represents probably the foremost important results of special relativity theory and provides a deep physical desiring to the concept of the whole relativistic energy E. To calculate the significance of E during this concern, contemplate the collapse of a body of mass 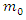 into two sections of rest masses
into two sections of rest masses 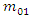 and
and 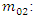

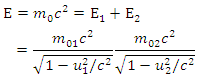 Thus,
Thus,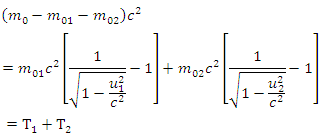
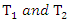 remain the relativistic kinetic energies of the two masses formed. Relatively,
remain the relativistic kinetic energies of the two masses formed. Relatively, 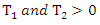 subsequently
subsequently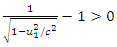
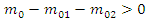
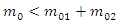
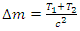
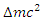 has appeared. The certain assumption is that approximately the rest mass of the original body has been transformed into the kinetic energy of the two masses formed. The interesting outcome is that not a bit of the masses involved needs to be traveling at speeds near to the speed of light. Eq. (15) can be written, for
has appeared. The certain assumption is that approximately the rest mass of the original body has been transformed into the kinetic energy of the two masses formed. The interesting outcome is that not a bit of the masses involved needs to be traveling at speeds near to the speed of light. Eq. (15) can be written, for 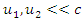 as
as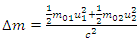
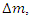 it wouldn’t be out of the problem to bring the masses to rest to regulate their rest masses. However, the truly extraordinary part of the above decisions is that its fundamental origin within the incontrovertible fact there exists a collective maximum possible speed, the speed of light which is made into the arrangement of space and time, and this structure eventually exerts an effect on the properties of matter occupying space and time, i.e., its mass and energy. The contrary can even occur i.e. matter will be created out of energy as in, for instance, an impact among particles having a number of their energy transformed into new particles as within the proton-proton collision,
it wouldn’t be out of the problem to bring the masses to rest to regulate their rest masses. However, the truly extraordinary part of the above decisions is that its fundamental origin within the incontrovertible fact there exists a collective maximum possible speed, the speed of light which is made into the arrangement of space and time, and this structure eventually exerts an effect on the properties of matter occupying space and time, i.e., its mass and energy. The contrary can even occur i.e. matter will be created out of energy as in, for instance, an impact among particles having a number of their energy transformed into new particles as within the proton-proton collision, 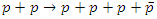 where an additional proton (p) and an antiproton
where an additional proton (p) and an antiproton 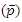 have been created. A more ordinary result of the above connection among energy and mass is that slightly than speaking about the rest mass of a particle, it is frequently more suitable to talk about its rest energy. A particle of rest mass
have been created. A more ordinary result of the above connection among energy and mass is that slightly than speaking about the rest mass of a particle, it is frequently more suitable to talk about its rest energy. A particle of rest mass 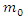 will, of course, have a rest energy
will, of course, have a rest energy 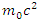 . Usually, the rest energy (or certainly any energy) arising in atomic, nuclear, or basic physics is given in units of electron volts. One electron volt (eV) is the energy added by an electron accelerated concluded a potential difference of 1 volt i.e.
. Usually, the rest energy (or certainly any energy) arising in atomic, nuclear, or basic physics is given in units of electron volts. One electron volt (eV) is the energy added by an electron accelerated concluded a potential difference of 1 volt i.e. 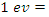
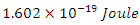 . For instance, the usual magnitudes of the rest energies of fundamental particles is that of the proton. With a rest mass of
. For instance, the usual magnitudes of the rest energies of fundamental particles is that of the proton. With a rest mass of 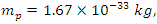 the proton has a rest energy of
the proton has a rest energy of 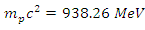 .
.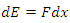 Where;
Where; 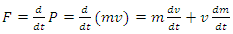 For this moment we consider m to be a variable.
For this moment we consider m to be a variable. 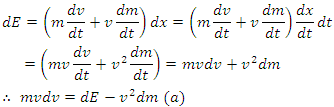 If we assume the relativistic mass transformation to be
If we assume the relativistic mass transformation to be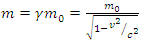
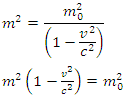
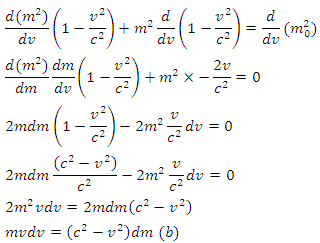 Equating equation (b) to the value of obtained in equation (a), we have;
Equating equation (b) to the value of obtained in equation (a), we have;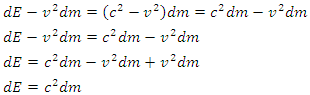
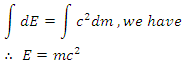
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
 in any inertial frame. There is a source of light emitting at a rest frame D, the speed of light in frame D is
in any inertial frame. There is a source of light emitting at a rest frame D, the speed of light in frame D is 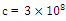 . The diagram shows that there is a frame E moving with a constant velocity v along with x-axis to frame D, and the velocity v also parallels to the direction of the light. Special relativity tells us that the speed of light observed in frame E is also at velocity
. The diagram shows that there is a frame E moving with a constant velocity v along with x-axis to frame D, and the velocity v also parallels to the direction of the light. Special relativity tells us that the speed of light observed in frame E is also at velocity 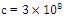


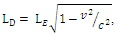 which is shorter than the one measured by the observer E, with a (Lorentz) factor
which is shorter than the one measured by the observer E, with a (Lorentz) factor 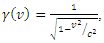 We call it as the Lorentz contraction.
We call it as the Lorentz contraction.