| [1] | W. Pics and A. Weiss, Crystal Structure of Inorganic Compounds: Keys Elements F, Cl, Br, I, 3rd ed., K.H. Hellwege, A.M. Hellwege, Landolt-B¨ornstein, Berlin, Germany: Springer, 1973, vol. 7. |
| [2] | L. Gerward, M. Malinowski, S. Asbrink and A. Waskowska, 1992, X‐ray diffraction investigateons of CaF2 at high pressure, J. Appl. Cryst. 25(5), 578-581. |
| [3] | R.M. Hazen and L.W. Finger, 1981, Calcium fluoride as an internal pressure standard in high-pressure crystallography, J. Appl. Cryst. 14(4), 234-236. |
| [4] | J.M. Leger, J. Haines, A. Atouf, O. Schulte and S. Hull, 1995, High-pressure x-ray and neutron-diffraction studies of BaF2: An example of a coordination number of 11 in AX2 compounds, Phys. Rev. B 52(18), 13247-13256. |
| [5] | G.A. Samara, 1976, Temperature and pressure dependences of the dielectric properties of PbF2 and the alkaline-earth fluorides, 1Phys. Rev. B 13(10), 4529-4544. |
| [6] | C. S´anchez and M. Cardona, 1972, Piezobirefringence in the vacuum ultraviolet: Alkali halides and alkaline‐earth fluorides, Phys. Status Solidi B 50(1), 293-304. |
| [7] | O.V. Shakin, M.F. Bryzhina and V.V. Lamanov, 1972, Photoelastic constants of Alkaline earth fluorides, Sov. Phys. solid State, 13(10-12), 3141-3142. |
| [8] | A.K. McCurdy, 1982, Phonon conduction in elastically anisotropic cubic cryst, Phys. Rev. B 26(12), 6971-69. |
| [9] | J. Barth, R.L. Johenson and M. Cardona, 1990, Dielectric function of CaF2 between 10 and 35eV, Phys. Rev. B 41(5), 3291-32. |
| [10] | S C Sabharwal, S N Jha and Sangeeta 2002, Optical and X-ray photoelectron spectroscopy of PbGeO3 and Pb5Ge3O11 single crystals, J. Cryst. Growth, 33(4), 395-400. |
| [11] | R.T. Poole, J. Szajman, R.C.G. Leckey, J.C. Jenkin and J. Liesegang, 1975, Electronic structure of the Alkaline earth fluorides studied by photoelectron spectroscopy, Phys. Rev. B 12(12), 5872-5877. |
| [12] | B. Li. and L. Wang, 2000, Lithography birefringence in fused silica and CaF2 for lithography, Solid State Technol. 43(1), 77-8. |
| [13] | J.H. Burnett, R. Gupta and U. Griesmann, 2002, Absolute refractive indices and thermal coefficients of CaF2, SrF2, BaF2 and LiF near 157nm, Appl. Opt. 41(13), 2508-2513. |
| [14] | W. Hayes, A.B. Kunz and E.E. Koch, 1971, Reflectance spectra of alkaline earth fluorides in the vacuum ultraviolet, J. Phys. C: Solid state Physics, 4(10), L200. |
| [15] | A. Feldman and R.M. Waxler, 1980, Strain induced splitting and Oscillator-Strength Anisotropy of the infrared transverse optic phonon in calcium fluoride, strontium fluoride and Barium fluoride, Phys. Rev. Lett. 45(2), 126-. |
| [16] | B. Ruprecht, M. Wilkening, S. Steuernagel and P. Heitjans, 2008, Anion difussivity in highly conductive nanocrystalline BaF2:CaF2 composites prepared by high energy ball milling, J. Mater. Chem. 18(44), 5412-5416. |
| [17] | B. Ruprecht, M. Wilkening, A. Feldhoff, S. Steuernagel, P. Heitjans, 2009, High ion conductivity in a ternary non equilibrium phase of BaF2 and CaF2 with mixed cations, Phys. Chem. Chem. Phys. 11(17), 3071-3081. |
| [18] | A. Düvel, B. Ruprecht, P. Heitjans, M. Wilkening, 2011, Mixed alkaline-earth effect in the metastable anion conductor Ba1-xCaxF2 (0 ≤ x ≤ 1): correlating long-range ion transport with local structures revealed by ultrafast 19F MAS-NMR, J. Phys. Chem. C 115(48), 23784-23789. |
| [19] | B. Ruprecht, M. Wilkening, S. Steuernagel, P. Heitjans, 2008, Anion diffusivity in highly conductive nano crystalline BaF2:CaF2 composites prepared by high-energy ball milling, J. Mater. Chem. 18(44), 5412-5416. |
| [20] | F. Preishuber-Pflügl, V. Epp1, S. Nakhal, M. Lerch and M. Wilkening, 2015, Defect-enhanced F-ion conductivity in layer-structured nanocrystalline BaSnF4 prepared by high-energy ball milling combined with soft annealing, Phys. Status Solidi C 12(1-2), 10–14. |
| [21] | A.V. Chadwick, A. Düvel, P. Heitjans, D.M. Pickup, S. Ramos, D.C. Sayle and T.X.T. Sayle, 2005, X-Ray Absorption Spectroscopy and Computer Modelling Study of Nanocrystalline Binary Alkaline Earth Fluorides, Mat. Sci. and Eng. 80(1), 012005-0120. |
| [22] | N. Sata, K. Ebermann and K. Eberl and J. Maier, 2000, Mesoscopic fast ion conduction in nanometer scale planar heterostructures, Nature, 408(6815), 946-949. |
| [23] | M. Wilkening, A. Düvel, F. Preishuber-Pflügl, K. da Silva, S. Breuer, V. Šepelák and P. Heitjans, 2017, Structure and ion dynamics of mechanosynthesized oxides and fluorides, Z. Kristallogr. 232(1-3), 107–127. |
| [24] | A. Düvel, P. Heitjans, P. Fedorov, G. Scholz, G. Cibin, A. V. Chadwick, D. M. Pickup, S. Ramos, L.W.L. Sayle, E. K. Sayle, T. X.T. Sayle, D. C. Sayle, 2017, Is Geometric Frustration-Induced Disorder a Recipe for High Ionic Conductivity? J. Amer. Chem. Soc. 139(16), 5842-5848. |
| [25] | X. Mu, W. Sigle, A. Bach, D. Fischer, M. Jansen and P. A. van Aken, 2014, Influence of a second cation () on the phase evolution of BaxM1-XF2 starting from amorphous deposits, Zeitschrift anorganische und allgemeine Chemie, |
| [26] | D. Zahn, P. Heitjans and J. Maier, 2012, From composite to solid solutions: Modelling ionic conductivity in the CaF2-BaF2 System, Chem. Eur. J. 18(20), 6225-6229. |
| [27] | P. Hohenberg and W. Kohn, 1964, Inhomogenous electron gas, Phys. Rev. 136(3), B864-B871. |
| [28] | W. Kohn and L. J. Sham, 1965, Self-consistent equations including exchange and correlation effects, Phys. Rev. 140(4), A1133-1138. |
| [29] | P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G.L. Chiarotti, M. Cococcioni, I. Dabo, A.D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L, Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A.P. Seitsonen, A. Smogunov, P. Umari and R.M. Wentzcovitch, 2009, Quantum Espresso: a modular and opensource software project for quantum simulations of materials, J. Phys. 21(39), 395502-395520. |
| [30] | J. C. Furthmuller, P. Kachell and F. Bechstedt, 2000, Extreme softening of Vanderbilt pseudopotentials, Phys. Rev. B 61(7), 4576-4587. |
| [31] | H.J. Monkhorst and J.D. Pack, 1976, Special points for Brillouin-zone integrations, Phys. Rev. B 13(12), 5188-5192. |
| [32] | J. Perdew, K. Burke, and M. Ernzerhof, 1996, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77(18), 3865-3868. |
| [33] | F. D. Murnaghan, 1944, The Compressibility of Media under Extreme Pressures,. Proc. Natl Acad. Sci., 30(9), 244-247. |
| [34] | G. Onida, L. Reining, A. Rubio, 2002, Electronic excitations: density-functional versus many-body Greens-function approaches. Rev. Mod. Phys. 74(), 601-659. |
| [35] | Á. Morales-García, R. Valero and F. Illas, 2017, An empirical, yet practical way to predict the band gap in solids by using density functional band structure calculations, J. Phys. Chem. 121(134), 18862-18866. |
| [36] | P.J.L. Herve, and L.K.J. Vandamme, 1994, General relation between refractive index and energy gap in semiconductors, Infrared Physics and Technology, 35(4), 609-615. |
| [37] | A.R. West, 1999, Basic Solid State Chemistry, John Wiley and Sons, Chichester, England. pp126. |
| [38] | W.Y. Ching, F. Gan and M.Z. Huang, 1995, Band theory of linear and non linear susceptibilities of some ionic insulators, Phys. Rev. B 52(3), 1596-1611. |
| [39] | R.W.G. Wyckoff, Crystal structures, 2nd ed., Interscience Publisher, New York, 1982. |
| [40] | C. Wang and D. E. Schulle, 1968, Pressure and Temperature derivatives of the elastic constants of CaF2 and BaF2, J. Phys. Chem. Solids, 29(8), 1309-1330. |
| [41] | G.W. Rubloff, 1972, Far-Ultraviolet Reflectance Spectra and the Electronic structure of Ionic Crystals, Phys. Rev. B 5(2), 662-684. |
| [42] | N. Boukhris, H. Meradji, S. Ghemid, S. Drablia and F.E.H. Hassan, 2011, Ab initio study of the structural, electronic and thermodynamic properties of PbSe1-xSx, PbSe1−xTex and PbS1-xTex ternary Alloys, Physica Scripta, 83(6), 065701-065709. |


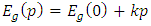
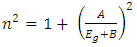
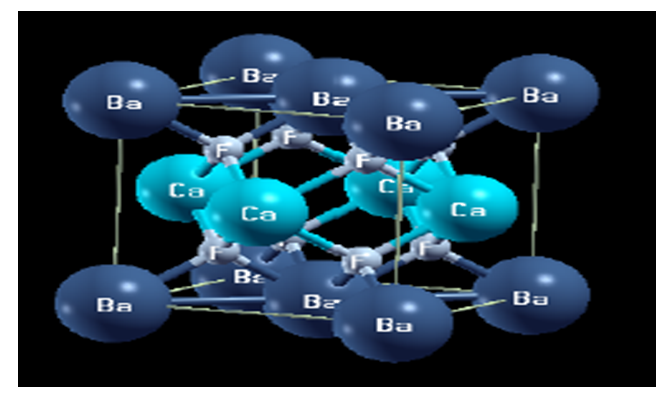
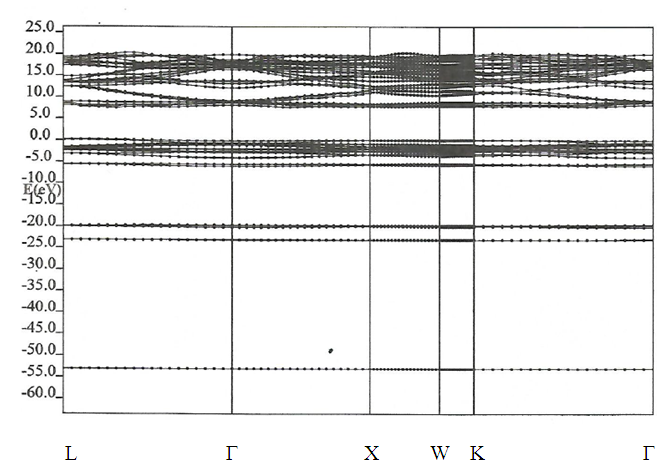
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML