Maciej Rybicki
Sas-Zubrzyckiego, Kraków, Poland
Correspondence to: Maciej Rybicki, Sas-Zubrzyckiego, Kraków, Poland.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Quantum extension of the Newton’s second law of motion in the relativistic form (referred to as Einstein’s second law) is proposed in order to adjust it to the realm of elementary particles subjected to extreme accelerations. An underlying idea is the quantization of proper time, set in a close connection with the concept of maximal proper acceleration. The relativistic concept of proper time 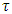 is identified with the quantum notion of evolution parameter. The postulated quantum of proper time
is identified with the quantum notion of evolution parameter. The postulated quantum of proper time 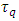 is thought to depend on the particle mass:
is thought to depend on the particle mass: 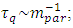 consequently relates to the Compton wavelength as
consequently relates to the Compton wavelength as 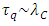 and to the Caianiello’s maximal proper acceleration as
and to the Caianiello’s maximal proper acceleration as 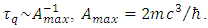 Quantization of proper time makes the relativistic increase of particle mass/energy discrete, which impacts on the general shape of Newton’s second law, now including both velocity and acceleration limits. Introducing the acceleration-dependent term results in a gradual neutralization of the mass increase as determined by the mass-velocity relation, together with the increasing proper acceleration. The new formula satisfies the correspondence principle with respect to the classical (Newtonian and relativistic) cases, and to the relevant formula connecting Planck units of force, mass and acceleration. The obtained results are juxtaposed with the quantization of spacetime proposed by the Causal Sets approach to quantum gravity.
Quantization of proper time makes the relativistic increase of particle mass/energy discrete, which impacts on the general shape of Newton’s second law, now including both velocity and acceleration limits. Introducing the acceleration-dependent term results in a gradual neutralization of the mass increase as determined by the mass-velocity relation, together with the increasing proper acceleration. The new formula satisfies the correspondence principle with respect to the classical (Newtonian and relativistic) cases, and to the relevant formula connecting Planck units of force, mass and acceleration. The obtained results are juxtaposed with the quantization of spacetime proposed by the Causal Sets approach to quantum gravity.
Keywords:
Quantization of time, Newton’s second law of motion, Maximal proper acceleration, Causal sets
Cite this paper: Maciej Rybicki, Relativistic Dynamics in the Quantum Limit of Maximal Proper Acceleration, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 3, 2020, pp. 51-59. doi: 10.5923/j.ijtmp.20201003.01.
1. Introduction
The idea of maximal acceleration has been the topic of lively debate during last decades. Different investigations have brought different results, all of them rooted in various quantum theories [1], [2], [3], [4]. The limits put on proper acceleration (defined as acceleration measured by an onboard accelerometer) appeared to depend on the mass of an accelerated point-like particle. A remarkable early example involving the concept of maximal proper acceleration refers to electron. Developing the earlier works by Sauter [5], Heisenberg and Euler [6] in the framework of Quantum Electrodynamics (QED), Schwinger derived the limit [7]: 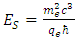 | (1) |
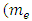 - electron mass,
- electron mass, 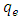 - elementary charge,
- elementary charge, 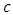 - speed of light,
- speed of light, 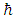 - reduced Planck constant,
- reduced Planck constant, 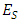 - Schwinger limit of the dimension
- Schwinger limit of the dimension 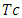 , where
, where  /Tesla/ is the magnetic induction). Beyond this limit electromagnetic field for the quantum vacuum becomes nonlinear making the photon-photon scattering inelastic, in consequence causing spontaneous creation of virtual electron-positron pairs. The resultant maximal limit for the proper acceleration of electron proves to be:
/Tesla/ is the magnetic induction). Beyond this limit electromagnetic field for the quantum vacuum becomes nonlinear making the photon-photon scattering inelastic, in consequence causing spontaneous creation of virtual electron-positron pairs. The resultant maximal limit for the proper acceleration of electron proves to be: 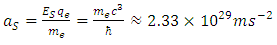 | (2) |
Another example is the Planck acceleration, defined as acceleration from zero speed to the speed of light within the Planck time. It is sometimes interpreted as the proper acceleration at the event horizon of a Planck black hole, i.e. black hole with the Schwarzschild radius equal to the Compton wavelength. Planck acceleration binds together the fundamental constants of physics, yielding an inconceivably great value: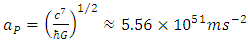 | (3) |
It is not clear whether Planck acceleration is a purely theoretical quantity, refers solely to the early universe, or is too present in definite quantum phenomena currently observed. Special Theory of Relativity (STR) does not allow massive body to achieve the speed of light; however, it does not basically prevent from changing mass for pure energy, i.e. from replacing massive particle by the massless photon. Like any other acceleration, Planck acceleration is expressible by different combinations of kinematical units, here specified as Planck length, Planck time and speed of light: 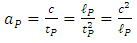 | (4) |
All the basic Planck units consist of fundamental constants: 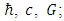 hence, the due conversion of any from the above expressions gives the Planck acceleration related to Planck mass:
hence, the due conversion of any from the above expressions gives the Planck acceleration related to Planck mass: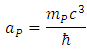 | (5) |
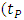 - Planck time,
- Planck time, 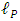 - Planck length,
- Planck length, 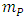 - Planck mass). Both Schwinger and Planck accelerations, regardless of possible difference in their physical meaning have identical structure. Therefore, they both can be considered as specific manifestations of the general concept known as Caianiello’s maximal proper acceleration, derived from quantum mechanics (QM), in particular from the Heisenberg uncertainty principle [8], [9], [10], [11]:
- Planck mass). Both Schwinger and Planck accelerations, regardless of possible difference in their physical meaning have identical structure. Therefore, they both can be considered as specific manifestations of the general concept known as Caianiello’s maximal proper acceleration, derived from quantum mechanics (QM), in particular from the Heisenberg uncertainty principle [8], [9], [10], [11]: 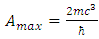 | (6) |
It is clearly evident from Eqns. (2), (5) and (6) that maximal proper acceleration is basically a quantum phenomenon. Special relativity does not apply itself a limit on acceleration, which results in the absence of respective term in the relativistic formula for the Newton’s second law of motion, hereinafter called the Einstein’s second law of motion. Meanwhile, it is reasonable to expect that the mass-dependent limit of the proper acceleration, assuming it really exist, should affect an ultimate shape of the second law. Using simple methods, we shall try to fulfil this expectation. Our goal is to implement the Caianiello’s limit into the Einstein’s second law of motion, so as to make it applicable to the extreme accelerations likely present in the quantum realm of elementary particles. This may provide us with a deeper insight into the atomic physics of “quantum jump”, usually interpreted as an abrupt (basically timeless) transition from one quantum state to another, e.g. in the pair production/annihilation or photon emission/absorption. These questions are the subject matter of Secs. 2 and 3. Instead, in Sec. 4 the obtained results are briefly compared with the idea of quantization of spacetime proposed by the Causal Sets Theory.
2. Dynamics Including Maximal Proper Acceleration. Quantization of Proper Time
STR applies a universal limit on velocity identified with the speed of light. Together with the principle of relativity, this determines both relativistic kinematics and dynamics, thereby redefines the Newtonian concepts of force, momentum, energy and mass. Mass, an invariant in the Newton’s second law: 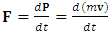 | (7) |
is subject in STR to the mass-velocity relation. The momentum is defined as 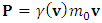 , where
, where 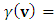
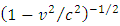 is the Lorentz factor. Differentiating gives the force formula:
is the Lorentz factor. Differentiating gives the force formula: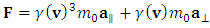 | (8) |
where 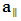 and
and 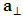 are the parallel and perpendicular components of acceleration, respectively. Hence, in the case of net force acting upon an object in the direction parallel to the instantaneous velocity vector (actually considered), the Einstein’s second law of motion is:
are the parallel and perpendicular components of acceleration, respectively. Hence, in the case of net force acting upon an object in the direction parallel to the instantaneous velocity vector (actually considered), the Einstein’s second law of motion is: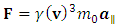 | (9) |
(hereinafter, we shall denote invariant/rest mass simply by 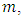 referred to as “mass”). In practice, energy and momentum of a particle are obtainable from the independent measurements, whereas mass becomes deduced from these measurements according to the relationship:
referred to as “mass”). In practice, energy and momentum of a particle are obtainable from the independent measurements, whereas mass becomes deduced from these measurements according to the relationship: 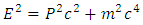 | (10) |
where 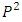 is the dot product of 3-momentum
is the dot product of 3-momentum 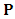 , i.e.
, i.e. 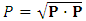 . This formula applies both to massive and massless particles. In the latter case (of photon) one has always:
. This formula applies both to massive and massless particles. In the latter case (of photon) one has always: 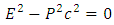 | (11) |
yielding zero mass. Time in QM is usually treated not as an observable (thus as a quantity defined by respective time-operator) but as the wave function parameter. This conforms with the classical dynamics and, in fact, with physics in general, considering the latter conceived as a description of how the inanimate objects behave in time. In accord with that, the wave function in the Schrodinger equation is basically time-dependent (except solutions with stationary waves/states). On the other hand, to comply with STR, time should be treated on equal footing with space. Hence, temporal and spatial coordinates (taken together) should be treated either as parameters or as operators. It is admittedly possible to treat both time and space as parameters (as it is in Quantum Field Theory). Consequently however, it should be also possible to treat all constituents of the position 4-vector as operators. Considering the correctness of this premise, another question arises: how the STR notions of coordinate time and proper time relate to the QM notions of time-as-parameter and time-as-operator? The answer here proposed is the following. Proper time is an observable (operator) and plays the role of evolution parameter. Instead, coordinate time is the function parameter. The reason for such distinction comes out from the fact that proper time is an invariant of Lorentz transformation; besides, in the context of acceleration, it refers to mass, specific for any (type of) elementary particle. This links the proper time with the concept of maximal proper acceleration, unique for each particle. Consequently, we postulate the proper time to be a discrete quantity. Expressed in terms of operators, energy and momentum are respectively: 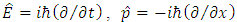 (along dimension). In connection with Eq. (10) this makes the starting point for any theory of relativistic quantum mechanics (RQM), i.e. QM formulated in the Poincare covariant form. However, RQM does not say what exactly happens in the time range during which the particles convert into one another, e.g. in the fermions-bosons exchange or in deep inelastic scattering. The same concerns the photon emission/absorption and the related quantum leap of electron from one orbital to another. The respective energy levels are connected with two separate probability functions; hence the change from one probability function to another means in fact the collapse of wave function. The problem is that, on one hand the respective “event” is treated as point-like (instantaneous), but on the other hand there is a certain time interval during which the probability to find electron in a given location must regard the superposition of both sequential wave functions. Hence, the question of duration of “quantum jump” is equivalent to the question of duration of respective superposition and the due probability to observe/detect given eigenstate. This problem is likely solvable if we assume that “quantum jump” is discrete with respect to the proper time of given particle, and is continuous, i.e. spreads over superposition, in the observer’s frame equipped with coordinate time. Only then this what is “instantaneous” according to the particle’s proper time may become “fuzzy” according to the inertial observer’s coordinate time. A direct consequence of setting the (proper) time-operator is the claim according to which superposition of two quantum states should be also comprehended as the superposition over time. The probability to find a system in a given eigenstate would then spread over time, exactly as it spreads over different eigenvalues of position, energy or momentum. In particular, the collapse of wave function connected with the act of measurement (always meaning interaction with observed object) would not be interpreted as instantaneous, hence would not be precisely fixed in the coordinate time.Let us return to the second law of motion. From Eq. (9) it follows that, unlike in the Newton’s second law (Eq. 7), acceleration does not depend linearly on force; by extension, for the constant force, velocity is no more a linear function of time. The mass component of momentum tends to infinity while the velocity component grows ever slower approaching the
(along dimension). In connection with Eq. (10) this makes the starting point for any theory of relativistic quantum mechanics (RQM), i.e. QM formulated in the Poincare covariant form. However, RQM does not say what exactly happens in the time range during which the particles convert into one another, e.g. in the fermions-bosons exchange or in deep inelastic scattering. The same concerns the photon emission/absorption and the related quantum leap of electron from one orbital to another. The respective energy levels are connected with two separate probability functions; hence the change from one probability function to another means in fact the collapse of wave function. The problem is that, on one hand the respective “event” is treated as point-like (instantaneous), but on the other hand there is a certain time interval during which the probability to find electron in a given location must regard the superposition of both sequential wave functions. Hence, the question of duration of “quantum jump” is equivalent to the question of duration of respective superposition and the due probability to observe/detect given eigenstate. This problem is likely solvable if we assume that “quantum jump” is discrete with respect to the proper time of given particle, and is continuous, i.e. spreads over superposition, in the observer’s frame equipped with coordinate time. Only then this what is “instantaneous” according to the particle’s proper time may become “fuzzy” according to the inertial observer’s coordinate time. A direct consequence of setting the (proper) time-operator is the claim according to which superposition of two quantum states should be also comprehended as the superposition over time. The probability to find a system in a given eigenstate would then spread over time, exactly as it spreads over different eigenvalues of position, energy or momentum. In particular, the collapse of wave function connected with the act of measurement (always meaning interaction with observed object) would not be interpreted as instantaneous, hence would not be precisely fixed in the coordinate time.Let us return to the second law of motion. From Eq. (9) it follows that, unlike in the Newton’s second law (Eq. 7), acceleration does not depend linearly on force; by extension, for the constant force, velocity is no more a linear function of time. The mass component of momentum tends to infinity while the velocity component grows ever slower approaching the 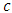 -limit. Hence, Newton’s second law
-limit. Hence, Newton’s second law 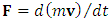 appears to be a good approximation for
appears to be a good approximation for 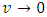 only. The question is whether these (relativistic) rules are universal; in particular, whether they also pertain to the relationship connecting the Planck units of force, mass and acceleration:
only. The question is whether these (relativistic) rules are universal; in particular, whether they also pertain to the relationship connecting the Planck units of force, mass and acceleration: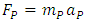 | (12) |
According to the STR phenomenology, the above equation constitutes no more than a purely static (purely formal) correlation between respective three quantities. From that viewpoint, the Planck relationship is by no means specific. Any (i.e. also bigger than Planck ones) two quantities from the above triad can be counterbalanced by the remaining one, in the image of the Newton’s second law. Since two of the quantities involved (force and acceleration) are, due to their immense values, definitely not “usual” in the Newtonian sense, so this equation cannot be treated as the “true” relativistic second law of motion in the Newtonian limit. On the contrary, what we deal here with is not the “low” (Newtonian) limit, but rather “high” limit (likely the extreme one), which means that Planck relationship demands new physical interpretation, different from Newtonian and relativistic ones. Dependently of the magnitude of relative velocity, the mass is assumed to include the velocity contribution determined by the Lorentz factor. Considering that 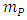 stands for the (rest) mass of a hypothetic Planck particle:
stands for the (rest) mass of a hypothetic Planck particle: 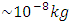 , and specifying:
, and specifying: 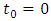 ,
, 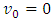 , one should consequently expect that in any infinitesimal time interval following
, one should consequently expect that in any infinitesimal time interval following 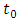 the mass would continuously increase in agreement with the Einstein’s second law. On the other hand, due to the physical reference of Planck units, it is likely that at the end of acceleration (i.e., after the time interval equal to Planck time:
the mass would continuously increase in agreement with the Einstein’s second law. On the other hand, due to the physical reference of Planck units, it is likely that at the end of acceleration (i.e., after the time interval equal to Planck time: 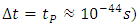 the velocity would somehow achieve the
the velocity would somehow achieve the 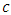 value. According to STR, this would imply an infinite value of mass, which makes this approach surely a wrong track. However, allowing for a certain departure from the relativistic orthodoxy, we may interpret Eq. (12) as revealing some hidden properties of nature, absent in the classical domain, but present in the quantum-mechanical regime. We shall namely consider scenario in which Planck mass subjected to Planck acceleration does not increase after
value. According to STR, this would imply an infinite value of mass, which makes this approach surely a wrong track. However, allowing for a certain departure from the relativistic orthodoxy, we may interpret Eq. (12) as revealing some hidden properties of nature, absent in the classical domain, but present in the quantum-mechanical regime. We shall namely consider scenario in which Planck mass subjected to Planck acceleration does not increase after 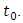 The reason for such conjecture is not simply that Planck force and Planck acceleration are so enormous
The reason for such conjecture is not simply that Planck force and Planck acceleration are so enormous 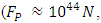
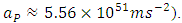 More important is that respective quantities, although dimensional, are nevertheless not arbitrary. With no doubt they are unique, regardless of whether they are normalized to unity or expressed in any of dimensional units. The supposition/premise according to which Planck time is the shortest physically sensible time interval implies the conclusion that acceleration cannot be sensed by the Planck particle within the time shorter than Planck time. We use the notion of “Planck particle”, instead of a wider notion “Planck-mass particle” since while identifying the particle size with the Compton wavelength, Planck mass can take the form of a particle only as Planck particle, i.e. Planck black hole. On the other hand, the Schwarzschild black hole as observed from distance does not differ from any other point mass. Let’s consider acceleration in the uniform field of a Planck particle equipped with an onboard accelerometer (which is tantamount with assumption as to the ability of Planck particle to “sense” acceleration). Say, at
More important is that respective quantities, although dimensional, are nevertheless not arbitrary. With no doubt they are unique, regardless of whether they are normalized to unity or expressed in any of dimensional units. The supposition/premise according to which Planck time is the shortest physically sensible time interval implies the conclusion that acceleration cannot be sensed by the Planck particle within the time shorter than Planck time. We use the notion of “Planck particle”, instead of a wider notion “Planck-mass particle” since while identifying the particle size with the Compton wavelength, Planck mass can take the form of a particle only as Planck particle, i.e. Planck black hole. On the other hand, the Schwarzschild black hole as observed from distance does not differ from any other point mass. Let’s consider acceleration in the uniform field of a Planck particle equipped with an onboard accelerometer (which is tantamount with assumption as to the ability of Planck particle to “sense” acceleration). Say, at 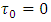 , this accelerator indicates Planck acceleration. Provided that proper time sensed by Planck particle is infinitely divisible, sequential indications of accelerometer after
, this accelerator indicates Planck acceleration. Provided that proper time sensed by Planck particle is infinitely divisible, sequential indications of accelerometer after 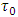 would exponentially decrease due to the mass increase in observer’s frame, so that at certain arbitrary
would exponentially decrease due to the mass increase in observer’s frame, so that at certain arbitrary 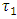 accelerometer would show certain definite nonzero value, in agreement with the Einstein’s second law. In this scenario, the speed of light would never be achieved.However, the assumed discreteness of proper time brings substantial change to the mass-velocity relation and the respective mass-acceleration dependence. If the time interval experienced by Planck particle cannot be shorter than
accelerometer would show certain definite nonzero value, in agreement with the Einstein’s second law. In this scenario, the speed of light would never be achieved.However, the assumed discreteness of proper time brings substantial change to the mass-velocity relation and the respective mass-acceleration dependence. If the time interval experienced by Planck particle cannot be shorter than 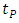 (which means that no change in acceleration is “sensed” during the time
(which means that no change in acceleration is “sensed” during the time 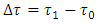 ), then Lorentz factor has no “occasion” to increase, hence to manifest itself in the observer’s frame. From the point of view of inertial observer equipped with standard clock measuring the coordinate time, this looks as if the quantum effect connected with the discreteness of proper time cancelled the time dilation and, consequently, the mass increase. Both the mass increase and respective extension of the coordinate time would not occur neither for particle nor for observer, with all three times equalized:
), then Lorentz factor has no “occasion” to increase, hence to manifest itself in the observer’s frame. From the point of view of inertial observer equipped with standard clock measuring the coordinate time, this looks as if the quantum effect connected with the discreteness of proper time cancelled the time dilation and, consequently, the mass increase. Both the mass increase and respective extension of the coordinate time would not occur neither for particle nor for observer, with all three times equalized: 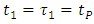 . Consequently, the respective phenomenon would be perceived as if obeyed the Newton’s second law. As a consequence, this means replacement of a scenario consistent with the Einstein’s second law by a different scenario obeying the new shape of the second law, appropriate for the quantum realm of elementary particles. By analogy to the Newtonian limit appropriate for
. Consequently, the respective phenomenon would be perceived as if obeyed the Newton’s second law. As a consequence, this means replacement of a scenario consistent with the Einstein’s second law by a different scenario obeying the new shape of the second law, appropriate for the quantum realm of elementary particles. By analogy to the Newtonian limit appropriate for 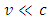 , we shall describe such scenario “quasi-Newtonian”.Eliminating the impact of Lorentz factor due to maximal proper acceleration, along with discreteness of proper time, opens doors to the possibility of achieving the speed of light by a massive particle. In the hypothetic case of Planck particle and Planck acceleration, the speed of light is obtainable according to the Planck relationship:
, we shall describe such scenario “quasi-Newtonian”.Eliminating the impact of Lorentz factor due to maximal proper acceleration, along with discreteness of proper time, opens doors to the possibility of achieving the speed of light by a massive particle. In the hypothetic case of Planck particle and Planck acceleration, the speed of light is obtainable according to the Planck relationship: 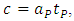 excluding the mass increase. Conversion of massive particle into photon (observed as a replacement of massive particle by photon) is the basically allowed and ubiquitous phenomenon under definite conditions, namely fulfilling the conservation laws, including the ones specific for QM like charge and lepton number. Hence, the postulated discreteness of proper time is a necessary but insufficient condition to “convert” massive particle into photon. In the Planck case, the hypothetic Planck photon would have the frequency:
excluding the mass increase. Conversion of massive particle into photon (observed as a replacement of massive particle by photon) is the basically allowed and ubiquitous phenomenon under definite conditions, namely fulfilling the conservation laws, including the ones specific for QM like charge and lepton number. Hence, the postulated discreteness of proper time is a necessary but insufficient condition to “convert” massive particle into photon. In the Planck case, the hypothetic Planck photon would have the frequency: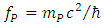 | (13) |
equal to the Planck angular frequency 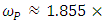
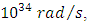 and to the inverse of Planck time
and to the inverse of Planck time 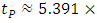
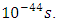 Based on above premises, let’s consider the case of electron-positron annihilation. Assuming that: (1) maximal proper acceleration is involved in this phenomenon; (2) on account of the discreteness of proper time the quasi-Newtonian equation
Based on above premises, let’s consider the case of electron-positron annihilation. Assuming that: (1) maximal proper acceleration is involved in this phenomenon; (2) on account of the discreteness of proper time the quasi-Newtonian equation 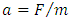 takes effect, we ask whether and how
takes effect, we ask whether and how 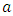 is identifiable with
is identifiable with 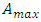 . First, to identify these quantities, we should assume that stands both for the coordinate and proper acceleration. This results from equality of proper and coordinate times; we shall additionally justify this assumption further below. In order to obtain the force acting between colliding particles we must divide the aggregated rest energy of electron and positron:
. First, to identify these quantities, we should assume that stands both for the coordinate and proper acceleration. This results from equality of proper and coordinate times; we shall additionally justify this assumption further below. In order to obtain the force acting between colliding particles we must divide the aggregated rest energy of electron and positron: 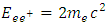 by the respective distance, assumed the latter to be the reduced Compton wavelength
by the respective distance, assumed the latter to be the reduced Compton wavelength 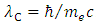 . Consequently, it follows:
. Consequently, it follows: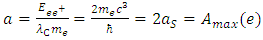 | (14) |
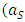 - Schwinger acceleration,
- Schwinger acceleration, 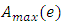 - maximal proper acceleration for electron)In the general case (including elastic collisions), the apparently smooth world line of an accelerated particle is supposed to reveal its discrete nature at a “quantum magnification”. In every quantum time-point (construed as iteration of given specific
- maximal proper acceleration for electron)In the general case (including elastic collisions), the apparently smooth world line of an accelerated particle is supposed to reveal its discrete nature at a “quantum magnification”. In every quantum time-point (construed as iteration of given specific 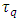 ) the particle’s “relativistic mass” changes discreetly adapting to the current relative velocity; then remains unchanged (as described in terms of coordinate time) until the next quantum time-point. In other words, the particle manifests itself in each comoving observer’s inertial frame in a discrete manner, each time with the mass corresponding to given relative velocity. Hence, despite discreteness, the Lorentz symmetry is preserved with the accuracy to the “lately” obtained mass value. The continuous increase of velocity becomes replaced by the sequence of discrete changes of velocity. Consequently, the continuous (smooth) mass-velocity function with mass tending to infinity becomes replaced by the “stepwise plot” (discrete function) that does not tend to infinity due to the “quantum ablation” of infinity.The above interpretation is, for sure, incompatible with the Einstein’s second law as it currently stands. Our goal is however to convert this law to a form suitable for quantum scale and extreme accelerations. Accordingly, we interpret Eq. (12) (let us call it the “Planck’s second law”) as it were “in opposition” to the purely relativistic approach, which means an expectation that Planck’s second law would emerge in natural way from the extended relativistic second law in the quantum realm of extreme accelerations. Let’s write some equations/definitions needful for the further reasoning. Coordinate acceleration is defined as:
) the particle’s “relativistic mass” changes discreetly adapting to the current relative velocity; then remains unchanged (as described in terms of coordinate time) until the next quantum time-point. In other words, the particle manifests itself in each comoving observer’s inertial frame in a discrete manner, each time with the mass corresponding to given relative velocity. Hence, despite discreteness, the Lorentz symmetry is preserved with the accuracy to the “lately” obtained mass value. The continuous increase of velocity becomes replaced by the sequence of discrete changes of velocity. Consequently, the continuous (smooth) mass-velocity function with mass tending to infinity becomes replaced by the “stepwise plot” (discrete function) that does not tend to infinity due to the “quantum ablation” of infinity.The above interpretation is, for sure, incompatible with the Einstein’s second law as it currently stands. Our goal is however to convert this law to a form suitable for quantum scale and extreme accelerations. Accordingly, we interpret Eq. (12) (let us call it the “Planck’s second law”) as it were “in opposition” to the purely relativistic approach, which means an expectation that Planck’s second law would emerge in natural way from the extended relativistic second law in the quantum realm of extreme accelerations. Let’s write some equations/definitions needful for the further reasoning. Coordinate acceleration is defined as: 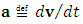 | (15) |
where 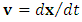 - (coordinate velocity) and
- (coordinate velocity) and 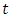 (coordinate time), both measured in the observer’s inertial frame. Instead, proper acceleration is defined as:
(coordinate time), both measured in the observer’s inertial frame. Instead, proper acceleration is defined as: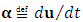 | (16) |
where 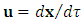 - the “proper velocity” is the quotient of coordinate distance by proper time. From that it follows that proper velocity is the product of coordinate velocity and Lorentz factor, the latter being
- the “proper velocity” is the quotient of coordinate distance by proper time. From that it follows that proper velocity is the product of coordinate velocity and Lorentz factor, the latter being 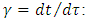
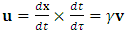 | (17) |
Hence, proper acceleration can be also written as: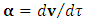 | (18) |
For the unidirectional motion with acceleration vector parallel to velocity vector, proper and coordinate accelerations relate to each other as: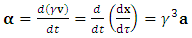 | (19) |
In order to validate the Planck’s second law, the coordinate acceleration should equal the proper acceleration implying 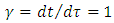 . For that to happen, coordinate time should equal the proper time, and both should equal the Planck time, as mentioned before. The question is how it can occur considering that proper and coordinate times tend to diverge (and not to converge) together with the increase of relative velocity; in particular, for
. For that to happen, coordinate time should equal the proper time, and both should equal the Planck time, as mentioned before. The question is how it can occur considering that proper and coordinate times tend to diverge (and not to converge) together with the increase of relative velocity; in particular, for 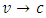 one has
one has 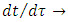
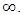 The latter is however true only if time is assumed to be infinitely divisible, hence differentiable variable. The condition
The latter is however true only if time is assumed to be infinitely divisible, hence differentiable variable. The condition 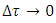 is vital for defining the Lorentz factor as
is vital for defining the Lorentz factor as 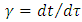 . In the classical mechanics change in velocity is axiomatically assumed to be continuous function of time so that differentiability is always secured; hence no departure from the Einstein’s second law of motion is possible. If, instead, proper time is discrete, then Lorentz factor defined as
. In the classical mechanics change in velocity is axiomatically assumed to be continuous function of time so that differentiability is always secured; hence no departure from the Einstein’s second law of motion is possible. If, instead, proper time is discrete, then Lorentz factor defined as 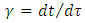 may serve as an approximation only, being only obtainable by the methods of numerical differentiation. Assuming the quantum (quanta) of proper time
may serve as an approximation only, being only obtainable by the methods of numerical differentiation. Assuming the quantum (quanta) of proper time 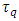 extremely small, the difference between discreteness and continuity (i.e., between
extremely small, the difference between discreteness and continuity (i.e., between 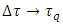 and
and 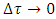 ) becomes meaningless in the usual macro scale. This means that, despite mathematical inadequacy, the derivative works “properly” for small
) becomes meaningless in the usual macro scale. This means that, despite mathematical inadequacy, the derivative works “properly” for small 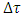 , yet big enough compared with
, yet big enough compared with 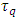 (
( ). However, in the range of coordinate time equivalent to the proper time such that
). However, in the range of coordinate time equivalent to the proper time such that 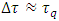 , the derivative becomes undefined; hence Lorentz factor defined as
, the derivative becomes undefined; hence Lorentz factor defined as 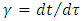 becomes inadequate. Consequently, Lorentz factor defined as
becomes inadequate. Consequently, Lorentz factor defined as 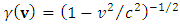 also becomes inadequate.Physically this means the absence (or limitation) of mass increase within the coordinate time corresponding to
also becomes inadequate.Physically this means the absence (or limitation) of mass increase within the coordinate time corresponding to 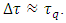 Quantization of proper time does not imply that physical properties of proper time are different from that of coordinate time. These are two faces of basically the same physical entity. The clock(s) measuring the coordinate time can, as well, utilize the reproducibility of quantum phenomena (as they directly do in atomic clocks). The property of continuity of the coordinate time are instead connected with fact that coordinate time is, first of all, a formal construct. This means that the assumed continuity of the coordinate time is taken by assumption. The only physical condition for a given clock to be appropriate tool in measuring the coordinate time is, apart from reproducibility, the demand of being at rest with respect to inertial observer. Instead, the discreteness of proper time pertains to the general property of time in the quantum scale. This property does not however refer to time itself, which here means the time considered in isolation of mass. It is instead (postulated to be) an intrinsic property of individual particles in relation to their mass, encoded in the observed quantum-mechanical phenomena. The postulate of quantization (discretization) of proper time and the concept of maximal proper acceleration are both connected with the Heisenberg uncertainty principle. Mathematically, the variables representing complementary quantities (such as position and momentum) do not commute, which physically means they cannot be measured at the same time with equal accuracy. This gave reason to suppose that, in the quantum (and Planck) scale, spacetime itself subjects to noncommutative, ergo “discrete” quantum geometry [12]. The particle’s maximal proper acceleration corresponds with the reduced Compton wavelength
Quantization of proper time does not imply that physical properties of proper time are different from that of coordinate time. These are two faces of basically the same physical entity. The clock(s) measuring the coordinate time can, as well, utilize the reproducibility of quantum phenomena (as they directly do in atomic clocks). The property of continuity of the coordinate time are instead connected with fact that coordinate time is, first of all, a formal construct. This means that the assumed continuity of the coordinate time is taken by assumption. The only physical condition for a given clock to be appropriate tool in measuring the coordinate time is, apart from reproducibility, the demand of being at rest with respect to inertial observer. Instead, the discreteness of proper time pertains to the general property of time in the quantum scale. This property does not however refer to time itself, which here means the time considered in isolation of mass. It is instead (postulated to be) an intrinsic property of individual particles in relation to their mass, encoded in the observed quantum-mechanical phenomena. The postulate of quantization (discretization) of proper time and the concept of maximal proper acceleration are both connected with the Heisenberg uncertainty principle. Mathematically, the variables representing complementary quantities (such as position and momentum) do not commute, which physically means they cannot be measured at the same time with equal accuracy. This gave reason to suppose that, in the quantum (and Planck) scale, spacetime itself subjects to noncommutative, ergo “discrete” quantum geometry [12]. The particle’s maximal proper acceleration corresponds with the reduced Compton wavelength 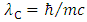 , namely for any given particle one has:
, namely for any given particle one has: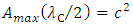 | (20) |
From the limit put on the measurement of particle position: 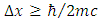 it follows that half of the reduced Compton wavelength is the minimal distance to determine the particle position:
it follows that half of the reduced Compton wavelength is the minimal distance to determine the particle position: 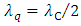 , where
, where 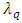 is the quantum of distance attached to given particle, provided its identity to be preserved. We interpret this property in terms of discretization of proper space in connection with respective discretization of proper time associated with a massive particle along its worldline, according to the Heisenberg uncertainty relation:
is the quantum of distance attached to given particle, provided its identity to be preserved. We interpret this property in terms of discretization of proper space in connection with respective discretization of proper time associated with a massive particle along its worldline, according to the Heisenberg uncertainty relation: 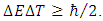 Hence, we postulate the proper time
Hence, we postulate the proper time 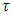 to be a discrete variable related to the Compton wavelength. The relevant quantum of proper time is the time that photon needs to cover the distance
to be a discrete variable related to the Compton wavelength. The relevant quantum of proper time is the time that photon needs to cover the distance 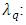
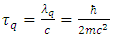 | (21) |
From 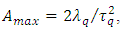 considering
considering 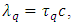 one has:
one has: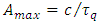 | (22) |
and, consequently: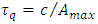 | (23) |
This allows formulating definition:Maximal proper acceleration is the acceleration causing discrete conversion of an elementary massive particle to photon, within the proper time equal to the respective single time quantum related to particle mass.The proper time interval in the classical view defined as: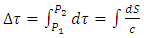 | (24) |
where 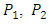 denote two sequential events on the particle’s world line, becomes redefined as:
denote two sequential events on the particle’s world line, becomes redefined as: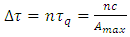 | (25) |
where 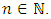
3. Derivation of the Extended Second Law of Motion
In result of assumed discreteness of proper time, reaching a given velocity succeeds without supplying energy in an amount exactly determined by the Lorentz factor. The resultant energy saving depends on the value of proper acceleration and thereby on the value of the force acting on given mass. In principle, this mechanism allows the massive particle to achieve the speed of light at the expense of finite energy, which should be interpreted as the change of entire energy connected with invariant mass for the pure energy of motion. As stated before, this takes the form of conversion of the mass particle to photon. The energy required to obtain 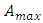 (and thus to reach the speed of light in a single “quantum jump”) is relatively small being just equal to the rest energy of an accelerated particle:
(and thus to reach the speed of light in a single “quantum jump”) is relatively small being just equal to the rest energy of an accelerated particle: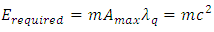 | (26) |
In the case of a particle with Planck mass, provided the formerly established relationships: 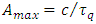 ;
; 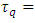
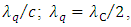 the required energy equals Planck energy:
the required energy equals Planck energy: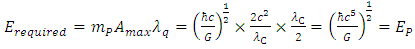 | (27) |
Planck energy 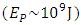 is immense, but only when considered in the scale of a single particle. The “difficulty” in achieving maximal proper acceleration lies therefore not in the amount of required energy but in focusing this energy on a single particle and expending it during extremely short time
is immense, but only when considered in the scale of a single particle. The “difficulty” in achieving maximal proper acceleration lies therefore not in the amount of required energy but in focusing this energy on a single particle and expending it during extremely short time 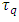 on the extremely short distance
on the extremely short distance 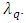 This is exactly postulated to happen in the “ideal” inelastic collisions. The mentioned above energy saving (maximal for
This is exactly postulated to happen in the “ideal” inelastic collisions. The mentioned above energy saving (maximal for 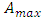 ) connected with quantization/discretization of proper time is the purely quantum effect connected with the Heisenberg uncertainty principle, which becomes evident considering that in the case of
) connected with quantization/discretization of proper time is the purely quantum effect connected with the Heisenberg uncertainty principle, which becomes evident considering that in the case of 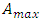 we have:
we have: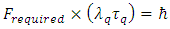 | (28) |
In the particular case of Planck acceleration, it is also: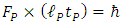 | (29) |
From our former consideration as to the consequences of quantization of proper time it follows that quantum extension of the second law of motion should consist in a due modification of the Lorentz factor, now supposed to depend both on velocity and acceleration. In analogy to velocity factor 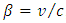 , let’s introduce an “acceleration factor”:
, let’s introduce an “acceleration factor”: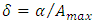 | (30) |
defined as the ratio of actual proper acceleration to the particle’s maximal proper acceleration. Mathematically, both 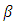 and
and 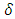 are just real numbers, such that
are just real numbers, such that 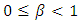 and
and 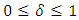 . Let’s insert the acceleration factor to the Lorentz factor:
. Let’s insert the acceleration factor to the Lorentz factor: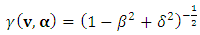 | (31) |
What is the reason or justification of such implementation of the factor 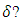 Let us notice first that it is not about the Lorentz factor present in the Lorentz transformation since the latter connects inertial frames, hence applies to uniform motions, for which it is always
Let us notice first that it is not about the Lorentz factor present in the Lorentz transformation since the latter connects inertial frames, hence applies to uniform motions, for which it is always 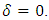 The same refers to other inertial transformations, in particular Tangherlini transformation (see “Additional remark” ending this paper). Admittedly, the above extension of the Lorentz factor including acceleration factor
The same refers to other inertial transformations, in particular Tangherlini transformation (see “Additional remark” ending this paper). Admittedly, the above extension of the Lorentz factor including acceleration factor 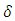 is rather “guessed” than formally derived. It is not however a rare practice in the physical research. Here, “derivation” consists in fact that this exact form fulfils expectations connected with the postulated consequences of the quantization of proper time, as implemented to the second law, each time determined by different assumptions as to velocity and acceleration. This is clearly visible in Eqns. (36 - 39). Besides, justification of Eq. (31) becomes more visible after rewriting respective quantities. Denoting maximal acceleration
is rather “guessed” than formally derived. It is not however a rare practice in the physical research. Here, “derivation” consists in fact that this exact form fulfils expectations connected with the postulated consequences of the quantization of proper time, as implemented to the second law, each time determined by different assumptions as to velocity and acceleration. This is clearly visible in Eqns. (36 - 39). Besides, justification of Eq. (31) becomes more visible after rewriting respective quantities. Denoting maximal acceleration 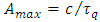 , and considering that proper acceleration
, and considering that proper acceleration 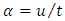 can also be expressed as
can also be expressed as 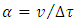 , we obtain the relationship:
, we obtain the relationship: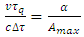 | (32) |
where 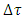 stands for the proper time in which given particle accelerates from zero coordinate velocity to the proper velocity
stands for the proper time in which given particle accelerates from zero coordinate velocity to the proper velocity 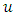 such that
such that 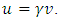 Hence, Eq. (31) rewrites to the form:
Hence, Eq. (31) rewrites to the form: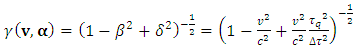 | (33) |
Ultimately then: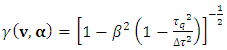 | (34) |
By definition 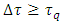 , which implies
, which implies 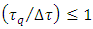 ; hence, it is always
; hence, it is always 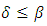 , which eliminates the otherwise absurd possibility, namely that acceleration process would be, by itself, the source of energy. Finally, the second law including the Caianiello’s limit takes the shape:
, which eliminates the otherwise absurd possibility, namely that acceleration process would be, by itself, the source of energy. Finally, the second law including the Caianiello’s limit takes the shape: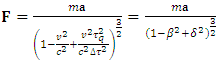 | (35) |
According to the principle of correspondence, dependently on different assumptions as to the velocity and acceleration, Eq. (35) reduces itself to the following four scenarios:1) Newton’s limit (Newton’s second law):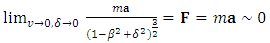 | (36) |
2) Einstein’s limit (Einstein’s second law):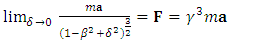 | (37) |
3) Quasi-Newtonian limit: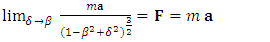 | (38) |
4) Quasi-Newtonian maximal limit: 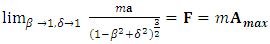 | (39) |
In accordance with above scenarios, the main properties of the “extended second law of motion” are the following: For small values of proper acceleration (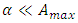 ), the Newton’s and/or Einstein’s second laws hold (Eqns. 36, 37); Provided acceleration keeps pace with the increasing velocity (
), the Newton’s and/or Einstein’s second laws hold (Eqns. 36, 37); Provided acceleration keeps pace with the increasing velocity (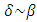 ), the quasi-Newtonian dynamics holds, regardless of the value of
), the quasi-Newtonian dynamics holds, regardless of the value of 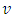 (Eq. 38). Unlike in the pure Einstein’s second law of motion, for
(Eq. 38). Unlike in the pure Einstein’s second law of motion, for 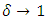 the condition
the condition 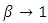 does not involve infinite energy. This may result in conversion of massive particle into photon at the finite expense of energy, hence the finite value of force (Eq. 39). In the particular (extreme) case, the “Planck’s second law”
does not involve infinite energy. This may result in conversion of massive particle into photon at the finite expense of energy, hence the finite value of force (Eq. 39). In the particular (extreme) case, the “Planck’s second law” 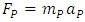 holds, assuming
holds, assuming 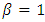 ,
, 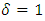 (implying
(implying 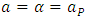 ) and
) and 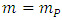 . This case is extreme in the twofold sense: as describing conversion of massive particle into photon due to
. This case is extreme in the twofold sense: as describing conversion of massive particle into photon due to 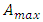 , and as determining maximum value for
, and as determining maximum value for 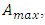 equal to Planck acceleration. In other words, the Planck particle of the otherwise “ordinary” mass is defined as the heaviest hypothetical particle subject to the maximal proper acceleration.There may arise an ambiguity while confronting the here-proposed extension of the second law of motion with the relativistic rules. The relevant questions are: What is the real energy of a particle in the uniform motion? Does it depend on its past acceleration (provided it occurred) and the respective amount of used energy? The general answer is: the particle’s energy does not depend on the past, but rather on future action applied to given particle. Any question concerning energy in the quantum context of acceleration should always refer to dynamics, no matter what state of motion (uniform or non-uniform) is considered. This in particular means that energy of a particle moving uniformly in a given inertial frame remains unspecified in the limits related to acceleration factor
equal to Planck acceleration. In other words, the Planck particle of the otherwise “ordinary” mass is defined as the heaviest hypothetical particle subject to the maximal proper acceleration.There may arise an ambiguity while confronting the here-proposed extension of the second law of motion with the relativistic rules. The relevant questions are: What is the real energy of a particle in the uniform motion? Does it depend on its past acceleration (provided it occurred) and the respective amount of used energy? The general answer is: the particle’s energy does not depend on the past, but rather on future action applied to given particle. Any question concerning energy in the quantum context of acceleration should always refer to dynamics, no matter what state of motion (uniform or non-uniform) is considered. This in particular means that energy of a particle moving uniformly in a given inertial frame remains unspecified in the limits related to acceleration factor 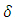 . The relativistic value of energy determined by the pure mass-velocity relation makes only the “reference point” corresponding with
. The relativistic value of energy determined by the pure mass-velocity relation makes only the “reference point” corresponding with 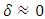 , and consequently with
, and consequently with 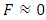 . Hence, energy (and momentum) remains unspecified until the actual “question is posed”, which in the quantum phenomenology means: until the measurement is executed. In this case, executing measurement of the particle mass/energy is tantamount with applying force, in the sense that exact result of this measurement depends on the value of applied force. Quantitively, the bigger force/acceleration is involved, the lesser energy is spent to obtain the same final effect, e.g. to stop the moving particle. Identifying the action made upon the particle with the measurement of its mass/energy is consistent with the classical modus operandi in measurements of total energy, according to the mass-velocity relation; it is too specifically consistent with the general demand of QM stating that relevant quantities remain unspecified until definite experiment is executed.
. Hence, energy (and momentum) remains unspecified until the actual “question is posed”, which in the quantum phenomenology means: until the measurement is executed. In this case, executing measurement of the particle mass/energy is tantamount with applying force, in the sense that exact result of this measurement depends on the value of applied force. Quantitively, the bigger force/acceleration is involved, the lesser energy is spent to obtain the same final effect, e.g. to stop the moving particle. Identifying the action made upon the particle with the measurement of its mass/energy is consistent with the classical modus operandi in measurements of total energy, according to the mass-velocity relation; it is too specifically consistent with the general demand of QM stating that relevant quantities remain unspecified until definite experiment is executed.
4. Mass-dependent Quantization of Spacetime vs. Causal Sets Theory
In the mid-nineteenth century Riemann considered a hypothesis of discrete manifold corresponding with quantized spacetime. A century later, Einstein returned to this idea within his attempts of unifying general relativity and quantum theory [13]. Currently, this idea has been undertaken by the theory (under construction) of Causal Sets (CST) [14], [15], [16], one of several attempts to formulate the complete theory of quantum gravity. The underlying idea, namely that spacetime is fundamentally discrete is not the sole property of CST within these attempts; e.g., the Quantum Loop Gravity also postulates discreteness of spacetime at the Planck scale. Specifically, CST replaces the classical causal structure of spacetime in relativity, i.e. the one determined on the smooth Lorentzian manifold by the “partial order” of spacetime events (called “elements”). Particular sets of the causally related “elements” form the “causal sets” (“causets”) or, considering the property of being “partially ordered”, “partially ordered sets” (“posets”), The partial order is defined as the binary relation satisfying the following conditions: (1) reflexivity, (2) transitivity, (3) anti-circularity and (4) finitarity (local finiteness). In particular, the condition of anti-circularity means exclusion of the closed causal curves (timelike loops), whereas local finiteness refers to the density of elements, i.e. secures their finite number, on the average proportional to the local “volume” of spacetime, defined according to GR. From the above four conditions, only (4) is specific for CST, while three others are basically appropriate for relativity. It should be noted however that non-circularity (3) is an external condition, arbitrarily applied to GR rather than intrinsic property resulting from this theory [17]. Anyway, causet is defined as the locally finite, partially ordered set. The mutual relations between the conditions (1-3), (4) and the resultant discrete geometry of spacetime are expressed by the rule (coined by Sorkin): Order + Number = Geometry. Deemed as important achievement of CST is the claim that, despite replacing the (smooth) manifold by discrete manifold reduced to elements, any causet defined according to the partial order retains the Lorentz invariance. This means that, despite the effects inherently connected with the Lorentz transformation (length contraction, time dilation, relativity of simultaneity), the causal partial order, i.e. cause-effect chain or (alternatively) causal disconnection is preserved for all inertial observers. In other words, causets are the Lorentz invariants. In consequence, the discrete geometry of spacetime postulated by CST can be consistently embedded in the smooth Lorentzian manifold. Another question refers to the scale of discretization. It is widely assumed that discreteness of spacetime refers to the extremely small sub-Planckian scales, which means that all spacetime quanta (elements) correspond to the Planck spacetime volume determined by Planck length and Planck time. The advantage connected with the uniformity of spacetime quanta is the conceptual simplicity of theory. Likewise, it seems reasonable to suppose that fundamental constituents of discrete spacetime are the smallest physically sensible quantities, actually the Planck ones. However, this, together with the questions related to general logic of this theory, brings us to the possible disadvantages of CST. Let us discuss them one by one.First, it is not true that, thanks to the partial order, the causets reconstruct the spacetime, as it is specifically defined in special and general relativity. It is rather true (but not as much unexpected) that any causet considered as embedded in the smooth Lorentzian manifold would satisfy these conditions. A possibility of reconstructing the relativity theory based on pure causal relations instead of known postulates (say, the known two of STR) would be fascinating. However, nothing like that takes place, neither in smooth nor discrete version. Hence, the concept of causets does not by itself reconstruct (but rather mimic) the relativity theory in the discrete form.Second, the assumed property of homogeneity of discrete spacetime (equality of spacetime quanta) is not consistent at least with the “spirit” of quantum theory. This claim is not obvious at first sight, hence demands justification. Let’s start from reminding the basic goal of CST, which is the pursuit of quantum gravity. In contrast to other (successful) attempts of unifying the fundamental interactions of nature (electromagnetic, week and strong), in the case of gravitation, spacetime is not a stage or a “background structure” [15] for interactions to occur, but is itself a part of unification. In other words, unlike in the case with other forces, unification including gravity means that we deal not only with quantum dynamics on spacetime structure, but also with quantum dynamics of spacetime structure [15]. This follows directly from the Einstein’s GR equation connecting energy-momentum tensor with the metric and curvature tensors/scalars (Riemannian metric on M). Any attempts of connecting GR with QM must take into account this basic fact. Considering that quantities denoted on the right side of Einstein’s equation undergo quantization, the terms on left-side describing metrical structure of Lorentzian manifold must do either. Consequently, according to the quantum point of view, the measurable properties of spacetime are the observables subject to the Heisenberg uncertainty principle, same as energy and momentum. As crazy as it may seem, considering spacetime in terms of observable, or quantum operator, should be taken seriously. Otherwise the equality sign connecting both sides of Einstein’s equation would be unjustified. This however points to a certain deficiency of CS approach. As far as the general assumption as to the discrete structure of spacetime is rational, its specific formulation within CST is not consistent with QM. This is because discretization of spacetime should not be determined in isolation of experiment, i.e. both homogeneity and the scale of discreteness should not be prespecified. The measurable properties of an observable not simply are but rather appear (manifest themselves) differently in different experiments.The third objection links to the previous one. It namely addresses the disproportion of hypothetic (homogenous) space-time quanta with the scale of observed constituents of physical reality (elementary particles and respective interactions). As a matter of fact, basic Planck units bind together fundamental constants of physics; nevertheless, Planck length and Planck time are many orders below the atomic scale, while Planck mass is many orders above. Say, for instance, we consider emission of photon, corresponding to the transition of atom from the excited to ground state. The subatomic distances between respective orbitals, although extremely small (and to some extent “fuzzy”, due to uncertainty principle), are however incomparably greater than Planck length 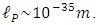 The same refers to the respective time intervals as compared with Planck time. Hence, if we intend to describe the said phenomenon as a discrete manifestation of different quantum states “before” and “after” (with no action in between), the CS approach seems to be an inadequate tool. In fact, using the Planck “bricks” for discretization of spacetime rather fixes than eliminates the continuous character of real phenomena in their “normal” quantum scale. This would be like describing the sandstorm in “quantum” terms, i.e. using the scale related to the granularity of sand.In contrast to that, connecting the postulated discreteness of spacetime with the (invariant) mass of elementary particles, and with related quantities/concepts, such as Compton wavelength and Caianiello’s maximal proper acceleration, seems to match better the demands of both relativity and quantum physics. This namely means fulfilling the general postulate of GR according to which spacetime and matter are inseparably connected, as well as the QM postulate stating that nature does not “exist” except of manifesting in experiments. The latter provides physical disambiguation to the prophetic Berkeley’s rule: esse = percipi.
The same refers to the respective time intervals as compared with Planck time. Hence, if we intend to describe the said phenomenon as a discrete manifestation of different quantum states “before” and “after” (with no action in between), the CS approach seems to be an inadequate tool. In fact, using the Planck “bricks” for discretization of spacetime rather fixes than eliminates the continuous character of real phenomena in their “normal” quantum scale. This would be like describing the sandstorm in “quantum” terms, i.e. using the scale related to the granularity of sand.In contrast to that, connecting the postulated discreteness of spacetime with the (invariant) mass of elementary particles, and with related quantities/concepts, such as Compton wavelength and Caianiello’s maximal proper acceleration, seems to match better the demands of both relativity and quantum physics. This namely means fulfilling the general postulate of GR according to which spacetime and matter are inseparably connected, as well as the QM postulate stating that nature does not “exist” except of manifesting in experiments. The latter provides physical disambiguation to the prophetic Berkeley’s rule: esse = percipi.
5. Conclusions
Based on the Caianiello’s idea of maximal proper acceleration, we have postulated the proper time sensed by individual elementary particles to be quantized in a direct relation to their mass. On that ground, we have derived the “extended second law of motion” including, apart from the relativistic velocity-dependent term (Lorentz factor), also the acceleration-dependent term, related to the Caianiello’s maximal acceleration. A limiting case of the so-defined extended second law of motion refers to the Planck time which is recognized not as a universal quantum of time (as it is proposed by the Causal Sets Theory) but as the smallest hypothetical quantum of proper time from the whole range of time quanta associated with different masses of elementary particles.The values of maximal proper acceleration are typically extremely high; even for the faint particles such as electron the respective corrections to the second law are in practice negligible compared with corrections caused by the relativistic increase of mass/energy. However, the proposed extension of the second law, verifiable in principle, is likely verifiable in the real specially aimed experiments, present or future.Assuming the Einstein’s equivalence principle, i.e. entire equivalence between effects caused by the uniform gravitational field and constant acceleration, the quantized proper time experienced by an accelerated massive particle should also be ascribed to a stationary particle subjected to gravitation. This observation may provide a clue in searching for the ultimate shape of quantum gravity.A particular prediction refers to the principle of the uniqueness of free fall. The particles of a smaller mass should, according to the smaller value of maximal proper acceleration, subject to a slightly greater acceleration than particles of bigger mass. However, the supposed effect (very small deviation from the universality of uniqueness of free fall) would be only noticeable in the presence of extremely strong gravitation, in which quantum effects likely dominate.Additional remark: This paper extends STR to the form including the quantum effects connected with acceleration. However, as shown in another my paper published in IJTMP [18], for the fundamental reasons of self-inconsistency STR demands to be replaced by the preferred frame theory (PFT), with the Tangherlini transformation replacing the Lorentz transformation. Hence, the quantum extension should indeed apply to PFT, not to STR. This is both possible and necessary; however, I did not find indicated to mix together two modifications in one paper.
References
| [1] | Parentani R, Potting R. (1989) Accelerating observer and the Hagedorn temperature, Phys. Rev. Lett., 63 (9), 945. |
| [2] | Rovelli C., Vidotto F. (2013) Evidence for maximal acceleration and singularity resolution in covariant Loop Quantum Gravity, Phys. Rev. Lett., 111, 091303. |
| [3] | Pati A.K. (1992) On the maximal acceleration and the maximal energy loss, Nuovo Cim. B107, 8, 895. |
| [4] | Feoli A. (2003) Maximal acceleration or maximal accelerations?, Int. J. Mod. Phys., D12, 271. |
| [5] | Sauter F. (1931) Uber das Verhalten eines Elektrons in homogenen elektrischen Feld nach der relativischen Theorie Diracs, Zeitschrift für Physik, 82, 742. |
| [6] | Heisenberg W., Euler H. (1931) Folgerungen aus der Diracschen Theorie des Positrons, Zeitschrift für Physik, 98, 714 English version: arXiv: physics/0605038v1. |
| [7] | Schwinger J. (1951) On gauge invariance and vacuum polarization, Phys. Rev. 82, 664. |
| [8] | Caianiello E.R. (1981) Is there a maximal acceleration, Lett. Nuovo Cim. 32, 65. |
| [9] | Caianiello E.R. (1984) Lett. Nuovo Cim. 41, 370. |
| [10] | Sharma C.S., Srirankanathan S. (1985) On Caianiello’s maximal acceleration, Lett. Nuovo Cim. 44, 275. |
| [11] | Papini G. (2003) Revisiting Caianiello’s maximal acceleration, Nuovo Cim. B117, 12. |
| [12] | Snyder H.S. (1947) Quantized space-time, Phys. Rev. 71, 38. |
| [13] | Einstein A. (1954) A letter to H.S. Joachim, cited in: Einstein and the Quantum: Fifty Years of Struggle, in “From quarks to quasars, philosophical problems of modern physics”, edited by R.G. Colodny, University Pittsburgh Press, 380 (1986). |
| [14] | Bombelli L., Lee J., Meyer D., Sorkin R.D. (1988) Space-time as Causal Set, Phys. Rev. Lett., 59, 521. |
| [15] | Reid D.D. (2001) Introduction to Causal Sets: An alternative view of spacetime structure, Canadian Journal of Physics, 79, 1-16. |
| [16] | Dowker F. (2005) Causal Sets and the deep structure of spacetime, arXiv:gr-qc/0508109. |
| [17] | Gödel K. (1949) An example of a new type of cosmological solution of Einstein’s field equations of gravitation, Rev. Mod. Phys., 21, 447. |
| [18] | Rybicki M. (2019) Failure of special relativity as a theory applied to more than one of spatial dimensions, Int. Journal of Theoretical and Mathematical Physics, 9 (3) 81-96. |


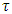 is identified with the quantum notion of evolution parameter. The postulated quantum of proper time
is identified with the quantum notion of evolution parameter. The postulated quantum of proper time 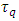 is thought to depend on the particle mass:
is thought to depend on the particle mass: 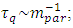 consequently relates to the Compton wavelength as
consequently relates to the Compton wavelength as 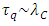 and to the Caianiello’s maximal proper acceleration as
and to the Caianiello’s maximal proper acceleration as 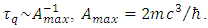 Quantization of proper time makes the relativistic increase of particle mass/energy discrete, which impacts on the general shape of Newton’s second law, now including both velocity and acceleration limits. Introducing the acceleration-dependent term results in a gradual neutralization of the mass increase as determined by the mass-velocity relation, together with the increasing proper acceleration. The new formula satisfies the correspondence principle with respect to the classical (Newtonian and relativistic) cases, and to the relevant formula connecting Planck units of force, mass and acceleration. The obtained results are juxtaposed with the quantization of spacetime proposed by the Causal Sets approach to quantum gravity.
Quantization of proper time makes the relativistic increase of particle mass/energy discrete, which impacts on the general shape of Newton’s second law, now including both velocity and acceleration limits. Introducing the acceleration-dependent term results in a gradual neutralization of the mass increase as determined by the mass-velocity relation, together with the increasing proper acceleration. The new formula satisfies the correspondence principle with respect to the classical (Newtonian and relativistic) cases, and to the relevant formula connecting Planck units of force, mass and acceleration. The obtained results are juxtaposed with the quantization of spacetime proposed by the Causal Sets approach to quantum gravity.
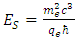
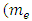 - electron mass,
- electron mass, 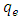 - elementary charge,
- elementary charge, 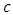 - speed of light,
- speed of light, 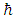 - reduced Planck constant,
- reduced Planck constant, 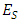 - Schwinger limit of the dimension
- Schwinger limit of the dimension 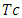 , where
, where 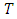 /Tesla/ is the magnetic induction). Beyond this limit electromagnetic field for the quantum vacuum becomes nonlinear making the photon-photon scattering inelastic, in consequence causing spontaneous creation of virtual electron-positron pairs. The resultant maximal limit for the proper acceleration of electron proves to be:
/Tesla/ is the magnetic induction). Beyond this limit electromagnetic field for the quantum vacuum becomes nonlinear making the photon-photon scattering inelastic, in consequence causing spontaneous creation of virtual electron-positron pairs. The resultant maximal limit for the proper acceleration of electron proves to be: 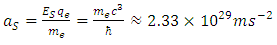
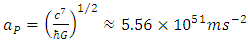
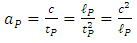
 hence, the due conversion of any from the above expressions gives the Planck acceleration related to Planck mass:
hence, the due conversion of any from the above expressions gives the Planck acceleration related to Planck mass: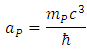
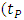 - Planck time,
- Planck time, 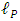 - Planck length,
- Planck length, 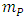 - Planck mass). Both Schwinger and Planck accelerations, regardless of possible difference in their physical meaning have identical structure. Therefore, they both can be considered as specific manifestations of the general concept known as Caianiello’s maximal proper acceleration, derived from quantum mechanics (QM), in particular from the Heisenberg uncertainty principle [8], [9], [10], [11]:
- Planck mass). Both Schwinger and Planck accelerations, regardless of possible difference in their physical meaning have identical structure. Therefore, they both can be considered as specific manifestations of the general concept known as Caianiello’s maximal proper acceleration, derived from quantum mechanics (QM), in particular from the Heisenberg uncertainty principle [8], [9], [10], [11]: 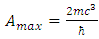
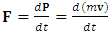
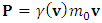 , where
, where 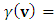
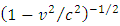 is the Lorentz factor. Differentiating gives the force formula:
is the Lorentz factor. Differentiating gives the force formula: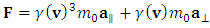
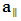 and
and 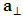 are the parallel and perpendicular components of acceleration, respectively. Hence, in the case of net force acting upon an object in the direction parallel to the instantaneous velocity vector (actually considered), the Einstein’s second law of motion is:
are the parallel and perpendicular components of acceleration, respectively. Hence, in the case of net force acting upon an object in the direction parallel to the instantaneous velocity vector (actually considered), the Einstein’s second law of motion is: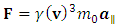
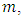 referred to as “mass”). In practice, energy and momentum of a particle are obtainable from the independent measurements, whereas mass becomes deduced from these measurements according to the relationship:
referred to as “mass”). In practice, energy and momentum of a particle are obtainable from the independent measurements, whereas mass becomes deduced from these measurements according to the relationship: 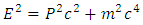
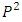 is the dot product of 3-momentum
is the dot product of 3-momentum 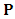 , i.e.
, i.e. 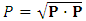 . This formula applies both to massive and massless particles. In the latter case (of photon) one has always:
. This formula applies both to massive and massless particles. In the latter case (of photon) one has always: 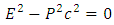
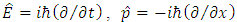 (along dimension). In connection with Eq. (10) this makes the starting point for any theory of relativistic quantum mechanics (RQM), i.e. QM formulated in the Poincare covariant form. However, RQM does not say what exactly happens in the time range during which the particles convert into one another, e.g. in the fermions-bosons exchange or in deep inelastic scattering. The same concerns the photon emission/absorption and the related quantum leap of electron from one orbital to another. The respective energy levels are connected with two separate probability functions; hence the change from one probability function to another means in fact the collapse of wave function. The problem is that, on one hand the respective “event” is treated as point-like (instantaneous), but on the other hand there is a certain time interval during which the probability to find electron in a given location must regard the superposition of both sequential wave functions. Hence, the question of duration of “quantum jump” is equivalent to the question of duration of respective superposition and the due probability to observe/detect given eigenstate. This problem is likely solvable if we assume that “quantum jump” is discrete with respect to the proper time of given particle, and is continuous, i.e. spreads over superposition, in the observer’s frame equipped with coordinate time. Only then this what is “instantaneous” according to the particle’s proper time may become “fuzzy” according to the inertial observer’s coordinate time. A direct consequence of setting the (proper) time-operator is the claim according to which superposition of two quantum states should be also comprehended as the superposition over time. The probability to find a system in a given eigenstate would then spread over time, exactly as it spreads over different eigenvalues of position, energy or momentum. In particular, the collapse of wave function connected with the act of measurement (always meaning interaction with observed object) would not be interpreted as instantaneous, hence would not be precisely fixed in the coordinate time.Let us return to the second law of motion. From Eq. (9) it follows that, unlike in the Newton’s second law (Eq. 7), acceleration does not depend linearly on force; by extension, for the constant force, velocity is no more a linear function of time. The mass component of momentum tends to infinity while the velocity component grows ever slower approaching the
(along dimension). In connection with Eq. (10) this makes the starting point for any theory of relativistic quantum mechanics (RQM), i.e. QM formulated in the Poincare covariant form. However, RQM does not say what exactly happens in the time range during which the particles convert into one another, e.g. in the fermions-bosons exchange or in deep inelastic scattering. The same concerns the photon emission/absorption and the related quantum leap of electron from one orbital to another. The respective energy levels are connected with two separate probability functions; hence the change from one probability function to another means in fact the collapse of wave function. The problem is that, on one hand the respective “event” is treated as point-like (instantaneous), but on the other hand there is a certain time interval during which the probability to find electron in a given location must regard the superposition of both sequential wave functions. Hence, the question of duration of “quantum jump” is equivalent to the question of duration of respective superposition and the due probability to observe/detect given eigenstate. This problem is likely solvable if we assume that “quantum jump” is discrete with respect to the proper time of given particle, and is continuous, i.e. spreads over superposition, in the observer’s frame equipped with coordinate time. Only then this what is “instantaneous” according to the particle’s proper time may become “fuzzy” according to the inertial observer’s coordinate time. A direct consequence of setting the (proper) time-operator is the claim according to which superposition of two quantum states should be also comprehended as the superposition over time. The probability to find a system in a given eigenstate would then spread over time, exactly as it spreads over different eigenvalues of position, energy or momentum. In particular, the collapse of wave function connected with the act of measurement (always meaning interaction with observed object) would not be interpreted as instantaneous, hence would not be precisely fixed in the coordinate time.Let us return to the second law of motion. From Eq. (9) it follows that, unlike in the Newton’s second law (Eq. 7), acceleration does not depend linearly on force; by extension, for the constant force, velocity is no more a linear function of time. The mass component of momentum tends to infinity while the velocity component grows ever slower approaching the 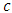 -limit. Hence, Newton’s second law
-limit. Hence, Newton’s second law 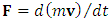 appears to be a good approximation for
appears to be a good approximation for 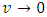 only. The question is whether these (relativistic) rules are universal; in particular, whether they also pertain to the relationship connecting the Planck units of force, mass and acceleration:
only. The question is whether these (relativistic) rules are universal; in particular, whether they also pertain to the relationship connecting the Planck units of force, mass and acceleration: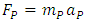
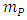 stands for the (rest) mass of a hypothetic Planck particle:
stands for the (rest) mass of a hypothetic Planck particle: 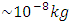 , and specifying:
, and specifying: 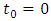 ,
, 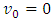 , one should consequently expect that in any infinitesimal time interval following
, one should consequently expect that in any infinitesimal time interval following 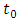 the mass would continuously increase in agreement with the Einstein’s second law. On the other hand, due to the physical reference of Planck units, it is likely that at the end of acceleration (i.e., after the time interval equal to Planck time:
the mass would continuously increase in agreement with the Einstein’s second law. On the other hand, due to the physical reference of Planck units, it is likely that at the end of acceleration (i.e., after the time interval equal to Planck time: 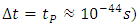 the velocity would somehow achieve the
the velocity would somehow achieve the 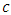 value. According to STR, this would imply an infinite value of mass, which makes this approach surely a wrong track. However, allowing for a certain departure from the relativistic orthodoxy, we may interpret Eq. (12) as revealing some hidden properties of nature, absent in the classical domain, but present in the quantum-mechanical regime. We shall namely consider scenario in which Planck mass subjected to Planck acceleration does not increase after
value. According to STR, this would imply an infinite value of mass, which makes this approach surely a wrong track. However, allowing for a certain departure from the relativistic orthodoxy, we may interpret Eq. (12) as revealing some hidden properties of nature, absent in the classical domain, but present in the quantum-mechanical regime. We shall namely consider scenario in which Planck mass subjected to Planck acceleration does not increase after 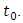 The reason for such conjecture is not simply that Planck force and Planck acceleration are so enormous
The reason for such conjecture is not simply that Planck force and Planck acceleration are so enormous 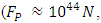
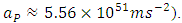 More important is that respective quantities, although dimensional, are nevertheless not arbitrary. With no doubt they are unique, regardless of whether they are normalized to unity or expressed in any of dimensional units. The supposition/premise according to which Planck time is the shortest physically sensible time interval implies the conclusion that acceleration cannot be sensed by the Planck particle within the time shorter than Planck time. We use the notion of “Planck particle”, instead of a wider notion “Planck-mass particle” since while identifying the particle size with the Compton wavelength, Planck mass can take the form of a particle only as Planck particle, i.e. Planck black hole. On the other hand, the Schwarzschild black hole as observed from distance does not differ from any other point mass. Let’s consider acceleration in the uniform field of a Planck particle equipped with an onboard accelerometer (which is tantamount with assumption as to the ability of Planck particle to “sense” acceleration). Say, at
More important is that respective quantities, although dimensional, are nevertheless not arbitrary. With no doubt they are unique, regardless of whether they are normalized to unity or expressed in any of dimensional units. The supposition/premise according to which Planck time is the shortest physically sensible time interval implies the conclusion that acceleration cannot be sensed by the Planck particle within the time shorter than Planck time. We use the notion of “Planck particle”, instead of a wider notion “Planck-mass particle” since while identifying the particle size with the Compton wavelength, Planck mass can take the form of a particle only as Planck particle, i.e. Planck black hole. On the other hand, the Schwarzschild black hole as observed from distance does not differ from any other point mass. Let’s consider acceleration in the uniform field of a Planck particle equipped with an onboard accelerometer (which is tantamount with assumption as to the ability of Planck particle to “sense” acceleration). Say, at 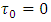 , this accelerator indicates Planck acceleration. Provided that proper time sensed by Planck particle is infinitely divisible, sequential indications of accelerometer after
, this accelerator indicates Planck acceleration. Provided that proper time sensed by Planck particle is infinitely divisible, sequential indications of accelerometer after 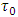 would exponentially decrease due to the mass increase in observer’s frame, so that at certain arbitrary
would exponentially decrease due to the mass increase in observer’s frame, so that at certain arbitrary 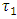 accelerometer would show certain definite nonzero value, in agreement with the Einstein’s second law. In this scenario, the speed of light would never be achieved.However, the assumed discreteness of proper time brings substantial change to the mass-velocity relation and the respective mass-acceleration dependence. If the time interval experienced by Planck particle cannot be shorter than
accelerometer would show certain definite nonzero value, in agreement with the Einstein’s second law. In this scenario, the speed of light would never be achieved.However, the assumed discreteness of proper time brings substantial change to the mass-velocity relation and the respective mass-acceleration dependence. If the time interval experienced by Planck particle cannot be shorter than 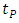 (which means that no change in acceleration is “sensed” during the time
(which means that no change in acceleration is “sensed” during the time 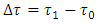 ), then Lorentz factor has no “occasion” to increase, hence to manifest itself in the observer’s frame. From the point of view of inertial observer equipped with standard clock measuring the coordinate time, this looks as if the quantum effect connected with the discreteness of proper time cancelled the time dilation and, consequently, the mass increase. Both the mass increase and respective extension of the coordinate time would not occur neither for particle nor for observer, with all three times equalized:
), then Lorentz factor has no “occasion” to increase, hence to manifest itself in the observer’s frame. From the point of view of inertial observer equipped with standard clock measuring the coordinate time, this looks as if the quantum effect connected with the discreteness of proper time cancelled the time dilation and, consequently, the mass increase. Both the mass increase and respective extension of the coordinate time would not occur neither for particle nor for observer, with all three times equalized: 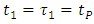 . Consequently, the respective phenomenon would be perceived as if obeyed the Newton’s second law. As a consequence, this means replacement of a scenario consistent with the Einstein’s second law by a different scenario obeying the new shape of the second law, appropriate for the quantum realm of elementary particles. By analogy to the Newtonian limit appropriate for
. Consequently, the respective phenomenon would be perceived as if obeyed the Newton’s second law. As a consequence, this means replacement of a scenario consistent with the Einstein’s second law by a different scenario obeying the new shape of the second law, appropriate for the quantum realm of elementary particles. By analogy to the Newtonian limit appropriate for 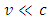 , we shall describe such scenario “quasi-Newtonian”.Eliminating the impact of Lorentz factor due to maximal proper acceleration, along with discreteness of proper time, opens doors to the possibility of achieving the speed of light by a massive particle. In the hypothetic case of Planck particle and Planck acceleration, the speed of light is obtainable according to the Planck relationship:
, we shall describe such scenario “quasi-Newtonian”.Eliminating the impact of Lorentz factor due to maximal proper acceleration, along with discreteness of proper time, opens doors to the possibility of achieving the speed of light by a massive particle. In the hypothetic case of Planck particle and Planck acceleration, the speed of light is obtainable according to the Planck relationship: 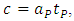 excluding the mass increase. Conversion of massive particle into photon (observed as a replacement of massive particle by photon) is the basically allowed and ubiquitous phenomenon under definite conditions, namely fulfilling the conservation laws, including the ones specific for QM like charge and lepton number. Hence, the postulated discreteness of proper time is a necessary but insufficient condition to “convert” massive particle into photon. In the Planck case, the hypothetic Planck photon would have the frequency:
excluding the mass increase. Conversion of massive particle into photon (observed as a replacement of massive particle by photon) is the basically allowed and ubiquitous phenomenon under definite conditions, namely fulfilling the conservation laws, including the ones specific for QM like charge and lepton number. Hence, the postulated discreteness of proper time is a necessary but insufficient condition to “convert” massive particle into photon. In the Planck case, the hypothetic Planck photon would have the frequency: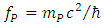
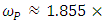
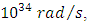 and to the inverse of Planck time
and to the inverse of Planck time 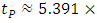
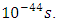 Based on above premises, let’s consider the case of electron-positron annihilation. Assuming that: (1) maximal proper acceleration is involved in this phenomenon; (2) on account of the discreteness of proper time the quasi-Newtonian equation
Based on above premises, let’s consider the case of electron-positron annihilation. Assuming that: (1) maximal proper acceleration is involved in this phenomenon; (2) on account of the discreteness of proper time the quasi-Newtonian equation 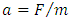 takes effect, we ask whether and how
takes effect, we ask whether and how  is identifiable with
is identifiable with  . First, to identify these quantities, we should assume that stands both for the coordinate and proper acceleration. This results from equality of proper and coordinate times; we shall additionally justify this assumption further below. In order to obtain the force acting between colliding particles we must divide the aggregated rest energy of electron and positron:
. First, to identify these quantities, we should assume that stands both for the coordinate and proper acceleration. This results from equality of proper and coordinate times; we shall additionally justify this assumption further below. In order to obtain the force acting between colliding particles we must divide the aggregated rest energy of electron and positron: 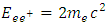 by the respective distance, assumed the latter to be the reduced Compton wavelength
by the respective distance, assumed the latter to be the reduced Compton wavelength 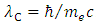 . Consequently, it follows:
. Consequently, it follows: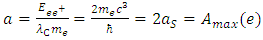
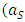 - Schwinger acceleration,
- Schwinger acceleration, 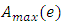 - maximal proper acceleration for electron)In the general case (including elastic collisions), the apparently smooth world line of an accelerated particle is supposed to reveal its discrete nature at a “quantum magnification”. In every quantum time-point (construed as iteration of given specific
- maximal proper acceleration for electron)In the general case (including elastic collisions), the apparently smooth world line of an accelerated particle is supposed to reveal its discrete nature at a “quantum magnification”. In every quantum time-point (construed as iteration of given specific 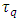 ) the particle’s “relativistic mass” changes discreetly adapting to the current relative velocity; then remains unchanged (as described in terms of coordinate time) until the next quantum time-point. In other words, the particle manifests itself in each comoving observer’s inertial frame in a discrete manner, each time with the mass corresponding to given relative velocity. Hence, despite discreteness, the Lorentz symmetry is preserved with the accuracy to the “lately” obtained mass value. The continuous increase of velocity becomes replaced by the sequence of discrete changes of velocity. Consequently, the continuous (smooth) mass-velocity function with mass tending to infinity becomes replaced by the “stepwise plot” (discrete function) that does not tend to infinity due to the “quantum ablation” of infinity.The above interpretation is, for sure, incompatible with the Einstein’s second law as it currently stands. Our goal is however to convert this law to a form suitable for quantum scale and extreme accelerations. Accordingly, we interpret Eq. (12) (let us call it the “Planck’s second law”) as it were “in opposition” to the purely relativistic approach, which means an expectation that Planck’s second law would emerge in natural way from the extended relativistic second law in the quantum realm of extreme accelerations. Let’s write some equations/definitions needful for the further reasoning. Coordinate acceleration is defined as:
) the particle’s “relativistic mass” changes discreetly adapting to the current relative velocity; then remains unchanged (as described in terms of coordinate time) until the next quantum time-point. In other words, the particle manifests itself in each comoving observer’s inertial frame in a discrete manner, each time with the mass corresponding to given relative velocity. Hence, despite discreteness, the Lorentz symmetry is preserved with the accuracy to the “lately” obtained mass value. The continuous increase of velocity becomes replaced by the sequence of discrete changes of velocity. Consequently, the continuous (smooth) mass-velocity function with mass tending to infinity becomes replaced by the “stepwise plot” (discrete function) that does not tend to infinity due to the “quantum ablation” of infinity.The above interpretation is, for sure, incompatible with the Einstein’s second law as it currently stands. Our goal is however to convert this law to a form suitable for quantum scale and extreme accelerations. Accordingly, we interpret Eq. (12) (let us call it the “Planck’s second law”) as it were “in opposition” to the purely relativistic approach, which means an expectation that Planck’s second law would emerge in natural way from the extended relativistic second law in the quantum realm of extreme accelerations. Let’s write some equations/definitions needful for the further reasoning. Coordinate acceleration is defined as: 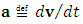
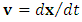 - (coordinate velocity) and
- (coordinate velocity) and 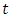 (coordinate time), both measured in the observer’s inertial frame. Instead, proper acceleration is defined as:
(coordinate time), both measured in the observer’s inertial frame. Instead, proper acceleration is defined as: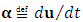
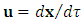 - the “proper velocity” is the quotient of coordinate distance by proper time. From that it follows that proper velocity is the product of coordinate velocity and Lorentz factor, the latter being
- the “proper velocity” is the quotient of coordinate distance by proper time. From that it follows that proper velocity is the product of coordinate velocity and Lorentz factor, the latter being 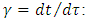
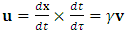
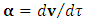
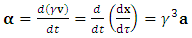
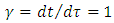 . For that to happen, coordinate time should equal the proper time, and both should equal the Planck time, as mentioned before. The question is how it can occur considering that proper and coordinate times tend to diverge (and not to converge) together with the increase of relative velocity; in particular, for
. For that to happen, coordinate time should equal the proper time, and both should equal the Planck time, as mentioned before. The question is how it can occur considering that proper and coordinate times tend to diverge (and not to converge) together with the increase of relative velocity; in particular, for 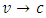 one has
one has 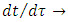
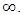 The latter is however true only if time is assumed to be infinitely divisible, hence differentiable variable. The condition
The latter is however true only if time is assumed to be infinitely divisible, hence differentiable variable. The condition 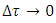 is vital for defining the Lorentz factor as
is vital for defining the Lorentz factor as 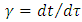 . In the classical mechanics change in velocity is axiomatically assumed to be continuous function of time so that differentiability is always secured; hence no departure from the Einstein’s second law of motion is possible. If, instead, proper time is discrete, then Lorentz factor defined as
. In the classical mechanics change in velocity is axiomatically assumed to be continuous function of time so that differentiability is always secured; hence no departure from the Einstein’s second law of motion is possible. If, instead, proper time is discrete, then Lorentz factor defined as 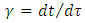 may serve as an approximation only, being only obtainable by the methods of numerical differentiation. Assuming the quantum (quanta) of proper time
may serve as an approximation only, being only obtainable by the methods of numerical differentiation. Assuming the quantum (quanta) of proper time 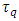 extremely small, the difference between discreteness and continuity (i.e., between
extremely small, the difference between discreteness and continuity (i.e., between 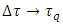 and
and 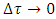 ) becomes meaningless in the usual macro scale. This means that, despite mathematical inadequacy, the derivative works “properly” for small
) becomes meaningless in the usual macro scale. This means that, despite mathematical inadequacy, the derivative works “properly” for small  , yet big enough compared with
, yet big enough compared with  (
( ). However, in the range of coordinate time equivalent to the proper time such that
). However, in the range of coordinate time equivalent to the proper time such that  , the derivative becomes undefined; hence Lorentz factor defined as
, the derivative becomes undefined; hence Lorentz factor defined as 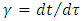 becomes inadequate. Consequently, Lorentz factor defined as
becomes inadequate. Consequently, Lorentz factor defined as 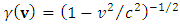 also becomes inadequate.Physically this means the absence (or limitation) of mass increase within the coordinate time corresponding to
also becomes inadequate.Physically this means the absence (or limitation) of mass increase within the coordinate time corresponding to 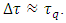 Quantization of proper time does not imply that physical properties of proper time are different from that of coordinate time. These are two faces of basically the same physical entity. The clock(s) measuring the coordinate time can, as well, utilize the reproducibility of quantum phenomena (as they directly do in atomic clocks). The property of continuity of the coordinate time are instead connected with fact that coordinate time is, first of all, a formal construct. This means that the assumed continuity of the coordinate time is taken by assumption. The only physical condition for a given clock to be appropriate tool in measuring the coordinate time is, apart from reproducibility, the demand of being at rest with respect to inertial observer. Instead, the discreteness of proper time pertains to the general property of time in the quantum scale. This property does not however refer to time itself, which here means the time considered in isolation of mass. It is instead (postulated to be) an intrinsic property of individual particles in relation to their mass, encoded in the observed quantum-mechanical phenomena. The postulate of quantization (discretization) of proper time and the concept of maximal proper acceleration are both connected with the Heisenberg uncertainty principle. Mathematically, the variables representing complementary quantities (such as position and momentum) do not commute, which physically means they cannot be measured at the same time with equal accuracy. This gave reason to suppose that, in the quantum (and Planck) scale, spacetime itself subjects to noncommutative, ergo “discrete” quantum geometry [12]. The particle’s maximal proper acceleration corresponds with the reduced Compton wavelength
Quantization of proper time does not imply that physical properties of proper time are different from that of coordinate time. These are two faces of basically the same physical entity. The clock(s) measuring the coordinate time can, as well, utilize the reproducibility of quantum phenomena (as they directly do in atomic clocks). The property of continuity of the coordinate time are instead connected with fact that coordinate time is, first of all, a formal construct. This means that the assumed continuity of the coordinate time is taken by assumption. The only physical condition for a given clock to be appropriate tool in measuring the coordinate time is, apart from reproducibility, the demand of being at rest with respect to inertial observer. Instead, the discreteness of proper time pertains to the general property of time in the quantum scale. This property does not however refer to time itself, which here means the time considered in isolation of mass. It is instead (postulated to be) an intrinsic property of individual particles in relation to their mass, encoded in the observed quantum-mechanical phenomena. The postulate of quantization (discretization) of proper time and the concept of maximal proper acceleration are both connected with the Heisenberg uncertainty principle. Mathematically, the variables representing complementary quantities (such as position and momentum) do not commute, which physically means they cannot be measured at the same time with equal accuracy. This gave reason to suppose that, in the quantum (and Planck) scale, spacetime itself subjects to noncommutative, ergo “discrete” quantum geometry [12]. The particle’s maximal proper acceleration corresponds with the reduced Compton wavelength 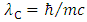 , namely for any given particle one has:
, namely for any given particle one has: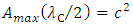
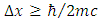 it follows that half of the reduced Compton wavelength is the minimal distance to determine the particle position:
it follows that half of the reduced Compton wavelength is the minimal distance to determine the particle position: 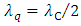 , where
, where  is the quantum of distance attached to given particle, provided its identity to be preserved. We interpret this property in terms of discretization of proper space in connection with respective discretization of proper time associated with a massive particle along its worldline, according to the Heisenberg uncertainty relation:
is the quantum of distance attached to given particle, provided its identity to be preserved. We interpret this property in terms of discretization of proper space in connection with respective discretization of proper time associated with a massive particle along its worldline, according to the Heisenberg uncertainty relation: 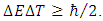 Hence, we postulate the proper time
Hence, we postulate the proper time 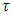 to be a discrete variable related to the Compton wavelength. The relevant quantum of proper time is the time that photon needs to cover the distance
to be a discrete variable related to the Compton wavelength. The relevant quantum of proper time is the time that photon needs to cover the distance 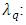
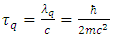
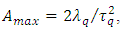 considering
considering 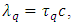 one has:
one has: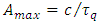
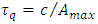
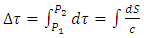
 denote two sequential events on the particle’s world line, becomes redefined as:
denote two sequential events on the particle’s world line, becomes redefined as: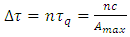
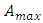 (and thus to reach the speed of light in a single “quantum jump”) is relatively small being just equal to the rest energy of an accelerated particle:
(and thus to reach the speed of light in a single “quantum jump”) is relatively small being just equal to the rest energy of an accelerated particle: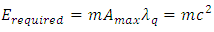
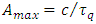 ;
; 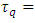
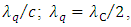 the required energy equals Planck energy:
the required energy equals Planck energy: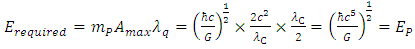
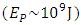 is immense, but only when considered in the scale of a single particle. The “difficulty” in achieving maximal proper acceleration lies therefore not in the amount of required energy but in focusing this energy on a single particle and expending it during extremely short time
is immense, but only when considered in the scale of a single particle. The “difficulty” in achieving maximal proper acceleration lies therefore not in the amount of required energy but in focusing this energy on a single particle and expending it during extremely short time 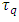 on the extremely short distance
on the extremely short distance 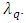 This is exactly postulated to happen in the “ideal” inelastic collisions. The mentioned above energy saving (maximal for
This is exactly postulated to happen in the “ideal” inelastic collisions. The mentioned above energy saving (maximal for 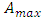 ) connected with quantization/discretization of proper time is the purely quantum effect connected with the Heisenberg uncertainty principle, which becomes evident considering that in the case of
) connected with quantization/discretization of proper time is the purely quantum effect connected with the Heisenberg uncertainty principle, which becomes evident considering that in the case of 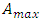 we have:
we have: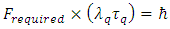
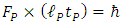
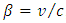 , let’s introduce an “acceleration factor”:
, let’s introduce an “acceleration factor”: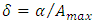
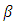 and
and 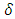 are just real numbers, such that
are just real numbers, such that 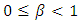 and
and 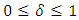 . Let’s insert the acceleration factor to the Lorentz factor:
. Let’s insert the acceleration factor to the Lorentz factor: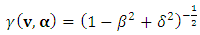
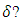 Let us notice first that it is not about the Lorentz factor present in the Lorentz transformation since the latter connects inertial frames, hence applies to uniform motions, for which it is always
Let us notice first that it is not about the Lorentz factor present in the Lorentz transformation since the latter connects inertial frames, hence applies to uniform motions, for which it is always 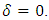 The same refers to other inertial transformations, in particular Tangherlini transformation (see “Additional remark” ending this paper). Admittedly, the above extension of the Lorentz factor including acceleration factor
The same refers to other inertial transformations, in particular Tangherlini transformation (see “Additional remark” ending this paper). Admittedly, the above extension of the Lorentz factor including acceleration factor 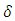 is rather “guessed” than formally derived. It is not however a rare practice in the physical research. Here, “derivation” consists in fact that this exact form fulfils expectations connected with the postulated consequences of the quantization of proper time, as implemented to the second law, each time determined by different assumptions as to velocity and acceleration. This is clearly visible in Eqns. (36 - 39). Besides, justification of Eq. (31) becomes more visible after rewriting respective quantities. Denoting maximal acceleration
is rather “guessed” than formally derived. It is not however a rare practice in the physical research. Here, “derivation” consists in fact that this exact form fulfils expectations connected with the postulated consequences of the quantization of proper time, as implemented to the second law, each time determined by different assumptions as to velocity and acceleration. This is clearly visible in Eqns. (36 - 39). Besides, justification of Eq. (31) becomes more visible after rewriting respective quantities. Denoting maximal acceleration 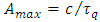 , and considering that proper acceleration
, and considering that proper acceleration 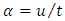 can also be expressed as
can also be expressed as 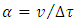 , we obtain the relationship:
, we obtain the relationship: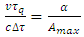
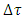 stands for the proper time in which given particle accelerates from zero coordinate velocity to the proper velocity
stands for the proper time in which given particle accelerates from zero coordinate velocity to the proper velocity 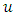 such that
such that 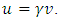 Hence, Eq. (31) rewrites to the form:
Hence, Eq. (31) rewrites to the form: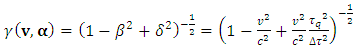
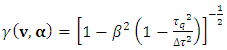
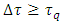 , which implies
, which implies 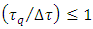 ; hence, it is always
; hence, it is always 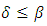 , which eliminates the otherwise absurd possibility, namely that acceleration process would be, by itself, the source of energy. Finally, the second law including the Caianiello’s limit takes the shape:
, which eliminates the otherwise absurd possibility, namely that acceleration process would be, by itself, the source of energy. Finally, the second law including the Caianiello’s limit takes the shape: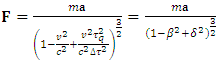
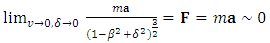
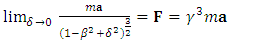
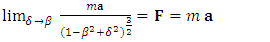
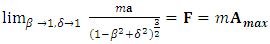
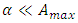 ), the Newton’s and/or Einstein’s second laws hold (Eqns. 36, 37); Provided acceleration keeps pace with the increasing velocity (
), the Newton’s and/or Einstein’s second laws hold (Eqns. 36, 37); Provided acceleration keeps pace with the increasing velocity (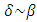 ), the quasi-Newtonian dynamics holds, regardless of the value of
), the quasi-Newtonian dynamics holds, regardless of the value of 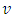 (Eq. 38). Unlike in the pure Einstein’s second law of motion, for
(Eq. 38). Unlike in the pure Einstein’s second law of motion, for 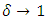 the condition
the condition 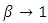 does not involve infinite energy. This may result in conversion of massive particle into photon at the finite expense of energy, hence the finite value of force (Eq. 39). In the particular (extreme) case, the “Planck’s second law”
does not involve infinite energy. This may result in conversion of massive particle into photon at the finite expense of energy, hence the finite value of force (Eq. 39). In the particular (extreme) case, the “Planck’s second law” 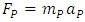 holds, assuming
holds, assuming 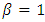 ,
, 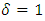 (implying
(implying 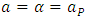 ) and
) and 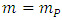 . This case is extreme in the twofold sense: as describing conversion of massive particle into photon due to
. This case is extreme in the twofold sense: as describing conversion of massive particle into photon due to 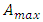 , and as determining maximum value for
, and as determining maximum value for 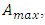 equal to Planck acceleration. In other words, the Planck particle of the otherwise “ordinary” mass is defined as the heaviest hypothetical particle subject to the maximal proper acceleration.There may arise an ambiguity while confronting the here-proposed extension of the second law of motion with the relativistic rules. The relevant questions are: What is the real energy of a particle in the uniform motion? Does it depend on its past acceleration (provided it occurred) and the respective amount of used energy? The general answer is: the particle’s energy does not depend on the past, but rather on future action applied to given particle. Any question concerning energy in the quantum context of acceleration should always refer to dynamics, no matter what state of motion (uniform or non-uniform) is considered. This in particular means that energy of a particle moving uniformly in a given inertial frame remains unspecified in the limits related to acceleration factor
equal to Planck acceleration. In other words, the Planck particle of the otherwise “ordinary” mass is defined as the heaviest hypothetical particle subject to the maximal proper acceleration.There may arise an ambiguity while confronting the here-proposed extension of the second law of motion with the relativistic rules. The relevant questions are: What is the real energy of a particle in the uniform motion? Does it depend on its past acceleration (provided it occurred) and the respective amount of used energy? The general answer is: the particle’s energy does not depend on the past, but rather on future action applied to given particle. Any question concerning energy in the quantum context of acceleration should always refer to dynamics, no matter what state of motion (uniform or non-uniform) is considered. This in particular means that energy of a particle moving uniformly in a given inertial frame remains unspecified in the limits related to acceleration factor 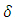 . The relativistic value of energy determined by the pure mass-velocity relation makes only the “reference point” corresponding with
. The relativistic value of energy determined by the pure mass-velocity relation makes only the “reference point” corresponding with 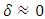 , and consequently with
, and consequently with 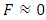 . Hence, energy (and momentum) remains unspecified until the actual “question is posed”, which in the quantum phenomenology means: until the measurement is executed. In this case, executing measurement of the particle mass/energy is tantamount with applying force, in the sense that exact result of this measurement depends on the value of applied force. Quantitively, the bigger force/acceleration is involved, the lesser energy is spent to obtain the same final effect, e.g. to stop the moving particle. Identifying the action made upon the particle with the measurement of its mass/energy is consistent with the classical modus operandi in measurements of total energy, according to the mass-velocity relation; it is too specifically consistent with the general demand of QM stating that relevant quantities remain unspecified until definite experiment is executed.
. Hence, energy (and momentum) remains unspecified until the actual “question is posed”, which in the quantum phenomenology means: until the measurement is executed. In this case, executing measurement of the particle mass/energy is tantamount with applying force, in the sense that exact result of this measurement depends on the value of applied force. Quantitively, the bigger force/acceleration is involved, the lesser energy is spent to obtain the same final effect, e.g. to stop the moving particle. Identifying the action made upon the particle with the measurement of its mass/energy is consistent with the classical modus operandi in measurements of total energy, according to the mass-velocity relation; it is too specifically consistent with the general demand of QM stating that relevant quantities remain unspecified until definite experiment is executed.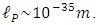 The same refers to the respective time intervals as compared with Planck time. Hence, if we intend to describe the said phenomenon as a discrete manifestation of different quantum states “before” and “after” (with no action in between), the CS approach seems to be an inadequate tool. In fact, using the Planck “bricks” for discretization of spacetime rather fixes than eliminates the continuous character of real phenomena in their “normal” quantum scale. This would be like describing the sandstorm in “quantum” terms, i.e. using the scale related to the granularity of sand.In contrast to that, connecting the postulated discreteness of spacetime with the (invariant) mass of elementary particles, and with related quantities/concepts, such as Compton wavelength and Caianiello’s maximal proper acceleration, seems to match better the demands of both relativity and quantum physics. This namely means fulfilling the general postulate of GR according to which spacetime and matter are inseparably connected, as well as the QM postulate stating that nature does not “exist” except of manifesting in experiments. The latter provides physical disambiguation to the prophetic Berkeley’s rule: esse = percipi.
The same refers to the respective time intervals as compared with Planck time. Hence, if we intend to describe the said phenomenon as a discrete manifestation of different quantum states “before” and “after” (with no action in between), the CS approach seems to be an inadequate tool. In fact, using the Planck “bricks” for discretization of spacetime rather fixes than eliminates the continuous character of real phenomena in their “normal” quantum scale. This would be like describing the sandstorm in “quantum” terms, i.e. using the scale related to the granularity of sand.In contrast to that, connecting the postulated discreteness of spacetime with the (invariant) mass of elementary particles, and with related quantities/concepts, such as Compton wavelength and Caianiello’s maximal proper acceleration, seems to match better the demands of both relativity and quantum physics. This namely means fulfilling the general postulate of GR according to which spacetime and matter are inseparably connected, as well as the QM postulate stating that nature does not “exist” except of manifesting in experiments. The latter provides physical disambiguation to the prophetic Berkeley’s rule: esse = percipi. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML