Doron Kwiat
Doctoral Degree, Self Employeed, Israel
Correspondence to: Doron Kwiat , Doctoral Degree, Self Employeed, Israel.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The existence of strings has not yet been proven, but it will be shown in the following, that if a classical fermion is considered as made up of two coupled strings, then the coupling between these two strings creates tension in the strings, and this tension is proportional to the coupling force via the Planck constant.
Keywords:
String coupling, Planck constant, Schroedinger equation
Cite this paper: Doron Kwiat , Derivation of Planck's Constant from Two Strings Coupling, International Journal of Theoretical and Mathematical Physics, Vol. 10 No. 2, 2020, pp. 46-49. doi: 10.5923/j.ijtmp.20201002.03.
1. Introduction
Classical quantum theory is the basis for our concept of modern physics elementary particles theory. Ever since its introduction in the early years of the 20th century. The birth of quantum mechanics is commonly attributed to the discovery of the Planck relation. In order to explain black-body radiation, Planck postulated that the radiation energy is transmitted in packages (“energy quanta”). Einstein later has found that light is absorbed by an electron in small “packets”, which, like Planck’s “energy quanta”, is proportional to the light frequency 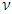 . This relation is now called the Planck relation or Planck–Einstein relation:
. This relation is now called the Planck relation or Planck–Einstein relation: 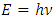 , where the constant “h” is “Planck’s constant”. Its value is
, where the constant “h” is “Planck’s constant”. Its value is 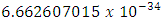 JSec and it is usually appears as
JSec and it is usually appears as 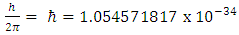 and is pronounced h bar.It has become one of the most important universal constants in physics. Yet, the exact physical meaning of Planck’s constant is unknown; it has not been derived based on first principles.Several approaches have been described recently (e.g. Lipovka [1,2], Brucholz [3] and Chang [4]), trying to derive h from basic principles.Lipovka [1,2] shows that the Planck constant is actually the adiabatic invariant of the electromagnetic field, characterized by scalar curvature of space of the Riemann – Cartan geometry. The main result of his work was to obtain the ratio between Riemannian scalar curvature of the Universe R, the Cosmological constant
and is pronounced h bar.It has become one of the most important universal constants in physics. Yet, the exact physical meaning of Planck’s constant is unknown; it has not been derived based on first principles.Several approaches have been described recently (e.g. Lipovka [1,2], Brucholz [3] and Chang [4]), trying to derive h from basic principles.Lipovka [1,2] shows that the Planck constant is actually the adiabatic invariant of the electromagnetic field, characterized by scalar curvature of space of the Riemann – Cartan geometry. The main result of his work was to obtain the ratio between Riemannian scalar curvature of the Universe R, the Cosmological constant 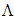 and Planck’s constant h.Brucholz [3] claims that since a photon must have a geometric boundary (which is why it behaves like a particle), the integration of its energy density (based on Maxwell equations) over a bounded volume must have
and Planck’s constant h.Brucholz [3] claims that since a photon must have a geometric boundary (which is why it behaves like a particle), the integration of its energy density (based on Maxwell equations) over a bounded volume must have 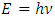 .Chang [4], by using the Maxwell theory, have, in a similar manner to Bruchholz, assumed a finite size photon. Thus, a relationship between the total electromagnetic energy of a single photon, its frequency, its width (Q factor) and the dielectric qualities of the vacuum. This provides a similar relation
.Chang [4], by using the Maxwell theory, have, in a similar manner to Bruchholz, assumed a finite size photon. Thus, a relationship between the total electromagnetic energy of a single photon, its frequency, its width (Q factor) and the dielectric qualities of the vacuum. This provides a similar relation 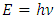 .In this work, a totally different approach to quantum mechanics was used. Referring to wave functions as a combination of real fields and observing of the differential equations as representing geometrical qualities of coupled classical strings. By assuming the coupled string like real wave functions, undergo some exchange interaction, leads us to the understanding that Planck constant h is the result of these exchange interactions between two coupled strings.Though this work uses the classical strings, it may be just as well extended to the concept of strings as the basic structure units of elementary particles [5-9].
.In this work, a totally different approach to quantum mechanics was used. Referring to wave functions as a combination of real fields and observing of the differential equations as representing geometrical qualities of coupled classical strings. By assuming the coupled string like real wave functions, undergo some exchange interaction, leads us to the understanding that Planck constant h is the result of these exchange interactions between two coupled strings.Though this work uses the classical strings, it may be just as well extended to the concept of strings as the basic structure units of elementary particles [5-9].
2. A Real Presentation of Schrödinger Equation
The basic equation of quantum mechanics is the one particle time-dependent Schrödinger equation: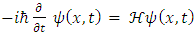 | (1) |
where 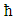 is the reduced Planck constant which is
is the reduced Planck constant which is 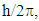
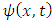 is the complex wave function of the quantum system, x is the position in a one-dimensional coordinate system, and t the time.
is the complex wave function of the quantum system, x is the position in a one-dimensional coordinate system, and t the time. 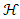 is the Hermitian Hamiltonian operator (which characterizes the total energy of the system under consideration).By decomposing the complex wave function into real and imaginary components
is the Hermitian Hamiltonian operator (which characterizes the total energy of the system under consideration).By decomposing the complex wave function into real and imaginary components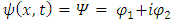 | (2) |
the Schrödinger equation may be written: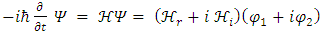 | (3) |
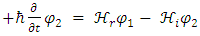 | (4) |
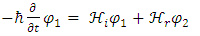 | (5) |
In other words, the traditional Schrödinger equation is in fact two coupled equations of real wave functions, with real operators on a real 3-dimensional space [1].The same procedure is also applicable to the relativistic Dirac equation, but this issue will not be discussed in here.For a time-independent classical Hamiltonian of a free particle, with mass m: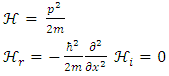 When separated into real and imaginary components, these are equivalent to:
When separated into real and imaginary components, these are equivalent to: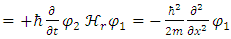 | (6) |
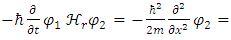 | (7) |
Which gives two coupled equations of the two real wave functions: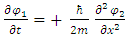 | (8) |
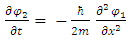 | (9) |
It does not worth any extra efforts to deal with the non-relativistic Schrödinger equation, because it will not render any new results as this is only a matter of representation change from complex to real. The results will be the same.However, it is interesting to see, that the real representation and solutions displays two real entities (wave functions) instead of a single, complex entity. And this can reveal an interesting new approach.It will be assumed herewith, that the quantum description and characteristics of a single particle are the result of a coupling interaction between two components (fields) which composes the single "particle".Based on this assumption, it will be described in the following, how can this real interpretation suggest an explanation to the non-relativistic Schrödinger equation through an interacting coupled two-strings classical model.
3. Tension in a Classical String
Let us start with a description of the forces in a classical one-dimensional, time independent, string.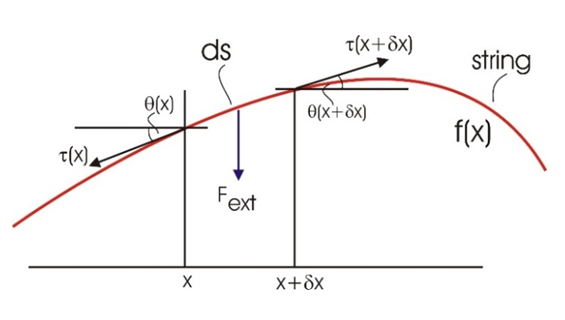 | Figure 1 |
Let the spatial distribution of a 1-dimensional string of mass density 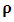 be described by the function f(x). Internal tension forces on the string are at two opposite directions. We will assume that the magnitude of the tension
be described by the function f(x). Internal tension forces on the string are at two opposite directions. We will assume that the magnitude of the tension 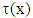 is the same along the string.Additionally, there is an external force Fext, y acting vertically on the infinitesimal element ds. This external force is due to some external interaction.The total horizontal component
is the same along the string.Additionally, there is an external force Fext, y acting vertically on the infinitesimal element ds. This external force is due to some external interaction.The total horizontal component 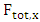 of the force on the elemental ds is given by
of the force on the elemental ds is given by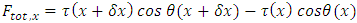 | (10) |
While the total vertical component 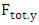 of the force on the elemental ds is given by
of the force on the elemental ds is given by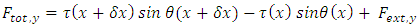 | (11) |
For infinitesimal small element ds, one may replace 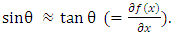 Hence
Hence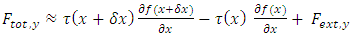 | (12) |
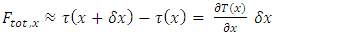 | (13) |
Thus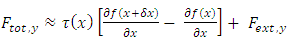 | (14) |
And so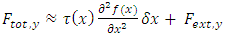 | (15) |
4. Interacting Strings
Consider next two strings 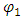 and
and 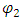 . Let
. Let 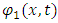 represent the amplitude of string 1 at time t and at position x. Let
represent the amplitude of string 1 at time t and at position x. Let 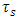 be some tension force in the string. As shown above, the net force exerted by this tension, on a small string element ds (see figure 2) is connected to the amplitude change along the x axis and is described by:
be some tension force in the string. As shown above, the net force exerted by this tension, on a small string element ds (see figure 2) is connected to the amplitude change along the x axis and is described by: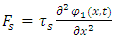 | (16) |
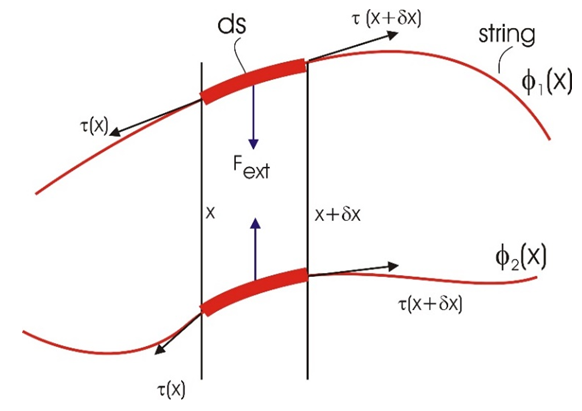 | Figure 2 |
Assume next, a second string is near the first one and is interacting with it by means of some coupling force, which couples the two strings together. Suppose now the second string, described by 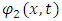 , undergoes some small temporal perturbation
, undergoes some small temporal perturbation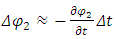 | (17) |
This perturbation induces a change in the coupling force 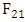 , exerted by string 2 on string 1. This force is proportional to
, exerted by string 2 on string 1. This force is proportional to 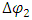 and attracts or repels string 1, in the opposite direction of
and attracts or repels string 1, in the opposite direction of 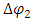 .We denote this proportionality coupling constant by
.We denote this proportionality coupling constant by 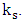 We will also assume, without loss of generality, that the coupling between the two strings is proportional to the mass of ds. This is a reasonable assumption as we may think that the more mass, the stronger the coupling.All in all here are the assumptions made:Assumption 1 (Hook's Law): The coupling force is proportional to displacement
We will also assume, without loss of generality, that the coupling between the two strings is proportional to the mass of ds. This is a reasonable assumption as we may think that the more mass, the stronger the coupling.All in all here are the assumptions made:Assumption 1 (Hook's Law): The coupling force is proportional to displacement 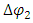 of string 2. We will denote this proportionality coupling constant by
of string 2. We will denote this proportionality coupling constant by 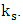 Assumption 2 (mass law): The coupling between the two strings is proportional to the mass of the elemental ds.Therefore, the disturbance in the force is described by:
Assumption 2 (mass law): The coupling between the two strings is proportional to the mass of the elemental ds.Therefore, the disturbance in the force is described by: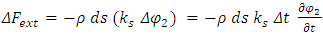 | (18) |
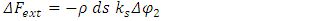 | (19) |
And from the projection of ds on x: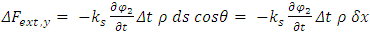 | (20) |
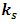 is the proportionality factor depending on the strength of the coupling interaction. Therefore, by Eq. 15:
is the proportionality factor depending on the strength of the coupling interaction. Therefore, by Eq. 15: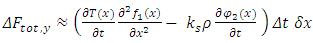 | (21) |
At equilibrium 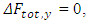 and so:
and so: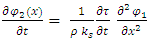 | (22) |
By symmetry reason, the action of disturbance string 1 on tension in string 2 will be described by (force in the opposite direction)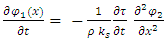 | (23) |
Equations 23 and 24 represent the coupling of two real strings.Looking at the term 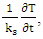 we see that it has units of angular momentum. We will thus assume:
we see that it has units of angular momentum. We will thus assume: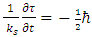 | (24) |
The above coupled equations now read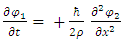 | (25) |
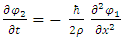 | (26) |
These equations are the coupled real presentation similar to Schrödinger equation.Equation [25] gives a physical meaning to the Planck constant, namely, independent of a particle's mass, the Planck constant 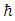 is derived from the internal quality of the real fields. It represents somehow the reaction of the tension of the string fields to perturbations. Up to a proportionality constant,
is derived from the internal quality of the real fields. It represents somehow the reaction of the tension of the string fields to perturbations. Up to a proportionality constant, 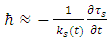 The left hand side of this equation is a constant. Therefore, one must have
The left hand side of this equation is a constant. Therefore, one must have 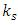 as a time-dependent variable (or else, both
as a time-dependent variable (or else, both 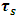 and
and 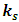 are constants).This leads to the conclusion:
are constants).This leads to the conclusion: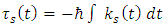 | (27) |
So, the tension in the strings is proportional to Planck constant 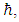 and to the coupling between the two strings.
and to the coupling between the two strings.
5. Exchange Interaction
From its defining equation 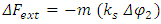 .The units of
.The units of 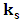 are:[N] =
are:[N] = 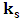 x [m/sec] x [sec] x [kg] =
x [m/sec] x [sec] x [kg] = 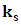 x [m] x [kg]
x [m] x [kg]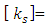 [N /(kgxm)] = [Kg x m/sec2 / (Kgxm)] = [1/sec2]The fact that
[N /(kgxm)] = [Kg x m/sec2 / (Kgxm)] = [1/sec2]The fact that 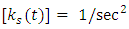 is indicative of the interaction type.It is like the shorter the exchange, the stronger is the interaction.This is characteristic of an exchange mechanism between the two strings. The higher the rate of exchange (particles/sec), the stronger the interaction.Indeed, if the exchange rate is designated by R [particles/sec], then the constant
is indicative of the interaction type.It is like the shorter the exchange, the stronger is the interaction.This is characteristic of an exchange mechanism between the two strings. The higher the rate of exchange (particles/sec), the stronger the interaction.Indeed, if the exchange rate is designated by R [particles/sec], then the constant 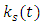 should be proportional with R2 (two strings interacting with eachother).Therefore,
should be proportional with R2 (two strings interacting with eachother).Therefore, 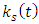 must have the units of 1/sec2.So, the tension in the strings is proportional to the Planck constant
must have the units of 1/sec2.So, the tension in the strings is proportional to the Planck constant 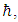 and to the coupling between the two strings (Figure 3).
and to the coupling between the two strings (Figure 3).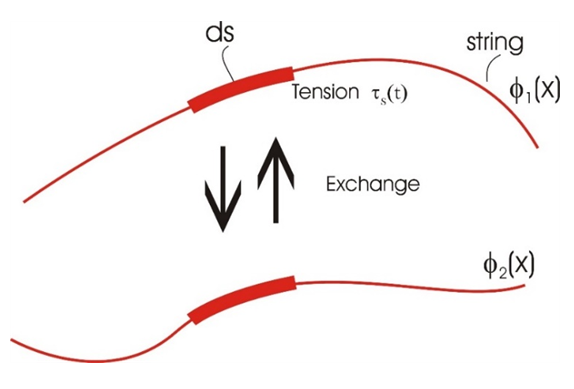 | Figure 3 |
The interaction caused be some sort of exchange mechanism between the two strings, results in tension in the strings, given by 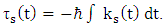 The proportionality between the exchange force and the tension is the Planck constant
The proportionality between the exchange force and the tension is the Planck constant 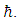
6. Conclusions
Based on the following assumptions:1. A Classical Fermion is made up of two interacting string-like entities.2. Tension in the strings is proportional to the coupling between the two strings.3. The coupling between the two strings is proportional to the amount of time the exchange lasts.One is lead to conclude, that Planck's constant 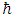 , is the proportionality constant, between the total exchange (of some sort) between the two strings, and the tension in these strings.
, is the proportionality constant, between the total exchange (of some sort) between the two strings, and the tension in these strings.
References
| [1] | Anton A. Lipovka, "Planck Constant as Adiabatic Invariant Characterized by Hubble’s and Cosmological Constants", Journal of Applied Mathematics and Physics, 2, 61-71, 2014. |
| [2] | Anton A. Lipovka, "Physics on the adiabatically changed Finslerian manifold and cosmology", Journal of Applied Mathematics and Physics, 5, 582-595. 2017. |
| [3] | Ulrich E. Bruchholz, "Derivation of Planck’s Constant from Maxwell’s Electrodynamics", 2009 Progress in Physics Volume 4. 2009. |
| [4] | Donald C. Chang, "Physical interpretation of the Planck’s constant based on the Maxwell theory". Chin. Phys. B Vol. 26, No. 4, 2017. |
| [5] | D Kwiat, "The Schrödinger Equation and Asymptotic Strings". International Journal of Theoretical and Mathematical Physics, Vol 8 (3) 2018. |
| [6] | Sunil Mukhi, "String theory: a perspective over the last 25 years", ArXiv: 1110.2569v3 [physics.pop-ph], Invited review, published in Classical and Quantum Gravity, 28, 2011. |
| [7] | Michael Dine, "Supersymmetry and string theory: beyond the standard model", 2nd edition, Cambridge university press. 2015. |
| [8] | J. Polchinski, "String theory". Cambridge university press. 2005. |
| [9] | Volodimir Simulik, "Relativistic quantum mechanics and field theory of arbitrary spin", Nova Science, New York, 341 pp. 2020. |



 . This relation is now called the Planck relation or Planck–Einstein relation:
. This relation is now called the Planck relation or Planck–Einstein relation: 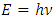 , where the constant “h” is “Planck’s constant”. Its value is
, where the constant “h” is “Planck’s constant”. Its value is 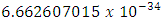 JSec and it is usually appears as
JSec and it is usually appears as 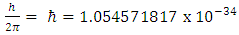 and is pronounced h bar.It has become one of the most important universal constants in physics. Yet, the exact physical meaning of Planck’s constant is unknown; it has not been derived based on first principles.Several approaches have been described recently (e.g. Lipovka [1,2], Brucholz [3] and Chang [4]), trying to derive h from basic principles.Lipovka [1,2] shows that the Planck constant is actually the adiabatic invariant of the electromagnetic field, characterized by scalar curvature of space of the Riemann – Cartan geometry. The main result of his work was to obtain the ratio between Riemannian scalar curvature of the Universe R, the Cosmological constant
and is pronounced h bar.It has become one of the most important universal constants in physics. Yet, the exact physical meaning of Planck’s constant is unknown; it has not been derived based on first principles.Several approaches have been described recently (e.g. Lipovka [1,2], Brucholz [3] and Chang [4]), trying to derive h from basic principles.Lipovka [1,2] shows that the Planck constant is actually the adiabatic invariant of the electromagnetic field, characterized by scalar curvature of space of the Riemann – Cartan geometry. The main result of his work was to obtain the ratio between Riemannian scalar curvature of the Universe R, the Cosmological constant 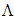 and Planck’s constant h.Brucholz [3] claims that since a photon must have a geometric boundary (which is why it behaves like a particle), the integration of its energy density (based on Maxwell equations) over a bounded volume must have
and Planck’s constant h.Brucholz [3] claims that since a photon must have a geometric boundary (which is why it behaves like a particle), the integration of its energy density (based on Maxwell equations) over a bounded volume must have 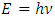 .Chang [4], by using the Maxwell theory, have, in a similar manner to Bruchholz, assumed a finite size photon. Thus, a relationship between the total electromagnetic energy of a single photon, its frequency, its width (Q factor) and the dielectric qualities of the vacuum. This provides a similar relation
.Chang [4], by using the Maxwell theory, have, in a similar manner to Bruchholz, assumed a finite size photon. Thus, a relationship between the total electromagnetic energy of a single photon, its frequency, its width (Q factor) and the dielectric qualities of the vacuum. This provides a similar relation 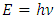 .In this work, a totally different approach to quantum mechanics was used. Referring to wave functions as a combination of real fields and observing of the differential equations as representing geometrical qualities of coupled classical strings. By assuming the coupled string like real wave functions, undergo some exchange interaction, leads us to the understanding that Planck constant h is the result of these exchange interactions between two coupled strings.Though this work uses the classical strings, it may be just as well extended to the concept of strings as the basic structure units of elementary particles [5-9].
.In this work, a totally different approach to quantum mechanics was used. Referring to wave functions as a combination of real fields and observing of the differential equations as representing geometrical qualities of coupled classical strings. By assuming the coupled string like real wave functions, undergo some exchange interaction, leads us to the understanding that Planck constant h is the result of these exchange interactions between two coupled strings.Though this work uses the classical strings, it may be just as well extended to the concept of strings as the basic structure units of elementary particles [5-9]. 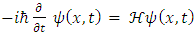
 is the reduced Planck constant which is
is the reduced Planck constant which is 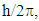
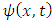 is the complex wave function of the quantum system, x is the position in a one-dimensional coordinate system, and t the time.
is the complex wave function of the quantum system, x is the position in a one-dimensional coordinate system, and t the time. 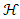 is the Hermitian Hamiltonian operator (which characterizes the total energy of the system under consideration).By decomposing the complex wave function into real and imaginary components
is the Hermitian Hamiltonian operator (which characterizes the total energy of the system under consideration).By decomposing the complex wave function into real and imaginary components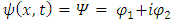
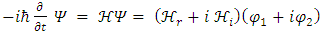
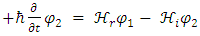
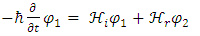
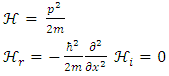 When separated into real and imaginary components, these are equivalent to:
When separated into real and imaginary components, these are equivalent to: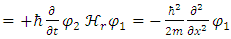
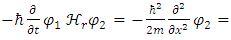
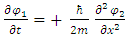
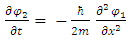

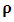 be described by the function f(x). Internal tension forces on the string are at two opposite directions. We will assume that the magnitude of the tension
be described by the function f(x). Internal tension forces on the string are at two opposite directions. We will assume that the magnitude of the tension 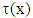 is the same along the string.Additionally, there is an external force Fext, y acting vertically on the infinitesimal element ds. This external force is due to some external interaction.The total horizontal component
is the same along the string.Additionally, there is an external force Fext, y acting vertically on the infinitesimal element ds. This external force is due to some external interaction.The total horizontal component 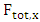 of the force on the elemental ds is given by
of the force on the elemental ds is given by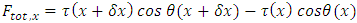
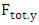 of the force on the elemental ds is given by
of the force on the elemental ds is given by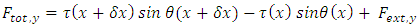
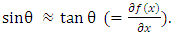 Hence
Hence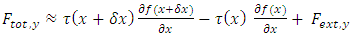
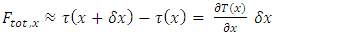
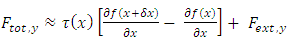
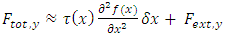
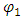 and
and 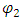 . Let
. Let 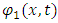 represent the amplitude of string 1 at time t and at position x. Let
represent the amplitude of string 1 at time t and at position x. Let 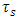 be some tension force in the string. As shown above, the net force exerted by this tension, on a small string element ds (see figure 2) is connected to the amplitude change along the x axis and is described by:
be some tension force in the string. As shown above, the net force exerted by this tension, on a small string element ds (see figure 2) is connected to the amplitude change along the x axis and is described by: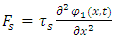

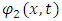 , undergoes some small temporal perturbation
, undergoes some small temporal perturbation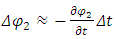
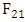 , exerted by string 2 on string 1. This force is proportional to
, exerted by string 2 on string 1. This force is proportional to 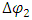 and attracts or repels string 1, in the opposite direction of
and attracts or repels string 1, in the opposite direction of 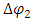 .We denote this proportionality coupling constant by
.We denote this proportionality coupling constant by 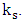 We will also assume, without loss of generality, that the coupling between the two strings is proportional to the mass of ds. This is a reasonable assumption as we may think that the more mass, the stronger the coupling.All in all here are the assumptions made:Assumption 1 (Hook's Law): The coupling force is proportional to displacement
We will also assume, without loss of generality, that the coupling between the two strings is proportional to the mass of ds. This is a reasonable assumption as we may think that the more mass, the stronger the coupling.All in all here are the assumptions made:Assumption 1 (Hook's Law): The coupling force is proportional to displacement 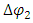 of string 2. We will denote this proportionality coupling constant by
of string 2. We will denote this proportionality coupling constant by 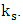 Assumption 2 (mass law): The coupling between the two strings is proportional to the mass of the elemental ds.Therefore, the disturbance in the force is described by:
Assumption 2 (mass law): The coupling between the two strings is proportional to the mass of the elemental ds.Therefore, the disturbance in the force is described by: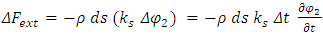
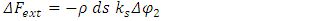
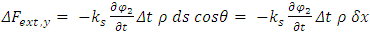
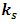 is the proportionality factor depending on the strength of the coupling interaction. Therefore, by Eq. 15:
is the proportionality factor depending on the strength of the coupling interaction. Therefore, by Eq. 15: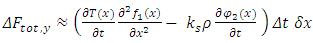
 and so:
and so: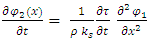
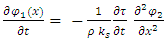
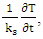 we see that it has units of angular momentum. We will thus assume:
we see that it has units of angular momentum. We will thus assume: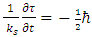
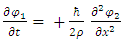
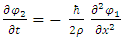
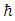 is derived from the internal quality of the real fields. It represents somehow the reaction of the tension of the string fields to perturbations. Up to a proportionality constant,
is derived from the internal quality of the real fields. It represents somehow the reaction of the tension of the string fields to perturbations. Up to a proportionality constant, 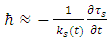 The left hand side of this equation is a constant. Therefore, one must have
The left hand side of this equation is a constant. Therefore, one must have 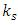 as a time-dependent variable (or else, both
as a time-dependent variable (or else, both 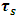 and
and 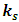 are constants).This leads to the conclusion:
are constants).This leads to the conclusion: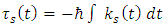
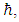 and to the coupling between the two strings.
and to the coupling between the two strings.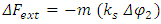 .The units of
.The units of 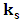 are:[N] =
are:[N] = 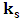 x [m/sec] x [sec] x [kg] =
x [m/sec] x [sec] x [kg] = 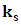 x [m] x [kg]
x [m] x [kg]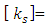 [N /(kgxm)] = [Kg x m/sec2 / (Kgxm)] = [1/sec2]The fact that
[N /(kgxm)] = [Kg x m/sec2 / (Kgxm)] = [1/sec2]The fact that 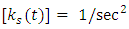 is indicative of the interaction type.It is like the shorter the exchange, the stronger is the interaction.This is characteristic of an exchange mechanism between the two strings. The higher the rate of exchange (particles/sec), the stronger the interaction.Indeed, if the exchange rate is designated by R [particles/sec], then the constant
is indicative of the interaction type.It is like the shorter the exchange, the stronger is the interaction.This is characteristic of an exchange mechanism between the two strings. The higher the rate of exchange (particles/sec), the stronger the interaction.Indeed, if the exchange rate is designated by R [particles/sec], then the constant 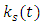 should be proportional with R2 (two strings interacting with eachother).Therefore,
should be proportional with R2 (two strings interacting with eachother).Therefore, 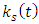 must have the units of 1/sec2.So, the tension in the strings is proportional to the Planck constant
must have the units of 1/sec2.So, the tension in the strings is proportional to the Planck constant 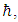 and to the coupling between the two strings (Figure 3).
and to the coupling between the two strings (Figure 3).
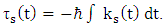 The proportionality between the exchange force and the tension is the Planck constant
The proportionality between the exchange force and the tension is the Planck constant 
 , is the proportionality constant, between the total exchange (of some sort) between the two strings, and the tension in these strings.
, is the proportionality constant, between the total exchange (of some sort) between the two strings, and the tension in these strings. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML