1. Introduction

In a previous paper [1] we have derived a general form of the Dirac radiation term [2], [3] based on his original physical assumptions (cf. [3]). In the relativistic case the usually accepted radiation term leads to the well-known Dirac (or Lorentz-Dirac) equations [3]

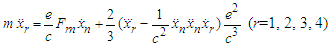(1)

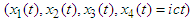where are the coordinates of the electron, e is its charge, m – its rest mass, c – the speed of the light, the dot is a differentiation with respect to the arc length, i.e.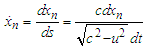, and the Einstein summation convention is valid. The second term in (1) is the Abraham four-vector of radiation reaction derived also by Dirac [3].

Here we replace the radiation term in (1) by the one obtained in [1]. We consider just first three equations because in [1] is proved that the fourth one is a consequence of the rest ones. We have applied a similar form of the radiation terms to two-body problem of classical electrodynamics [4]- [6]. Many results concerning radiation terms are contained in [7]-[32]. They are based on various methods. Here we use the fixed point method from [33].

The derivation of the new form of the radiation term is based on the relativistic form of the retarded and advanced Lienard-Wiechert potentials [8]-[10], [34], [35]. We stand on the theory of differential equations of neutral type with both retarded and advanced arguments caused by the finite propagation of the interaction – the basic assumption of the Einstein relativistic theory. So Dirac equations become second order neutral equations.

The main goal of the present paper is to prove an existence-uniqueness of a periodic solution for Dirac equations. We use an operator formulation of the periodic problem from [36]. In view of [37]-[39] we are able to apply the results obtained to betatron radiation.

The paper consists of six sections. In Section 2 we derive the Dirac equations using retarded and advanced potentials. In Section 3 we derive a new form of the radiation term. In Section 4 we formulate a periodic problem and give some preliminary assertions. In Section 5 we give an operator formulation of the periodic problem and by a suitable fixed point theorem prove an existence-uniqueness of periodic solution for Dirac equations. Section 6 contains a conclusion remark.

2. Derivation of Dirac Equations Using Retarded and Advanced Potentials

First we recall some basic notions and denotations following the Synge formalism [35] (cf. also [34]). Consider a charge e describing any curve L in the space-time. Let 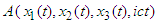be any event. The unit tangent vector to L at A is

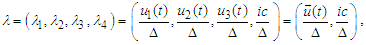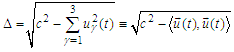where and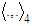

is the scalar product in 4-dimensional Minkowski space, while is the scalar product in 3-dimensional Euclidian subspace.

Let 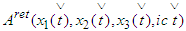be the intersection of L with the null-cone drawn into the past from A, and let 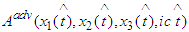be the intersection of L with the null-cone drawn into the future from A where and

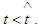Let 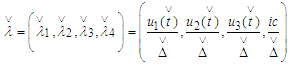be the unit tangent vector to the world line L at 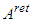, where 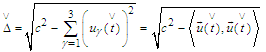and let 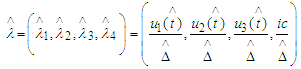be the unit tangent vector to L at 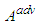, where

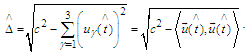Let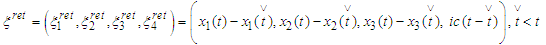

be the retarded isotropic vector 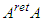and let

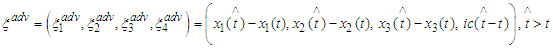be the advanced isotropic vector

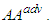In accordance with the Dirac assumptions [3] the radiation term is defined as a half of the difference between both retarded and advanced potentials, that is,

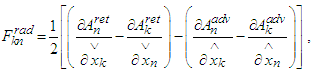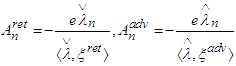where are the Lienard-Wiechert retarded and advanced potentials (cf. [8]-[10], [34], [35]).

So that the Dirac physical assumptions lead to the following form of the equations of motion:

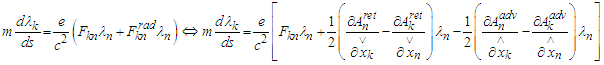or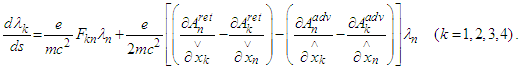

Further on we assume (cf. [1]) that

(AR):

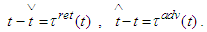In fact, postulating (AR) we extend the relation between the relativistic and Newton absolute time.

Since 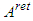and 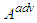lie on the trajectory L we obtain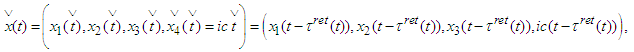

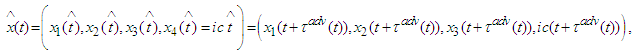and

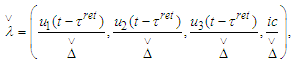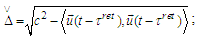
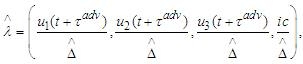where

where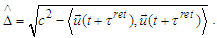

Therefore the isotropic vectors become

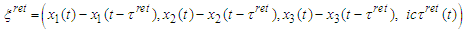and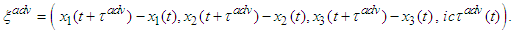

In general case the functions 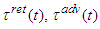can be obtained as solutions of the functional equations

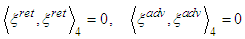or

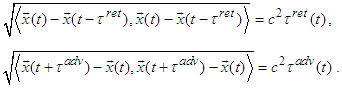In what follows we briefly repeat the calculations from [1]:

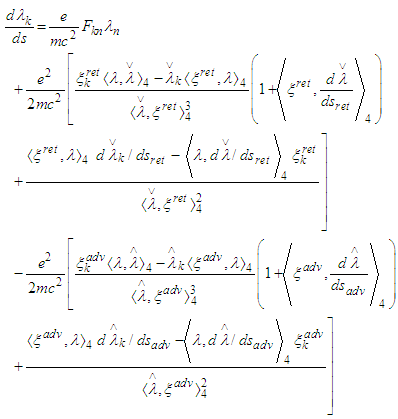(2)

(k=1,2,3,4),

where the elements of the electromagnetic tensor are:

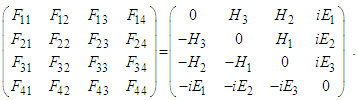Here 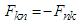and 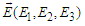is the electric field intensity vector, and 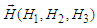− the magnetic field intensity vector.

3. Derivation of the Radiation Term

Following [1] we have to find the relations between the derivatives at past, present and future instants. The above system (2) can be split into “space-like” and “time-like” parts:

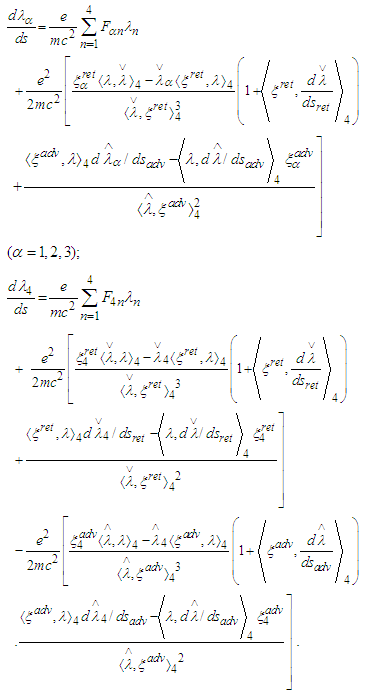Differentiating the relation

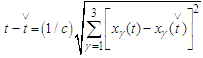with respect to 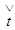, considering 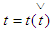we obtain

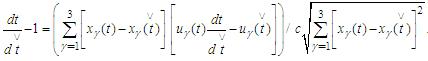In a similar way differentiating

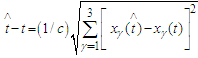with respect to 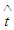(considering 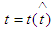) we obtain

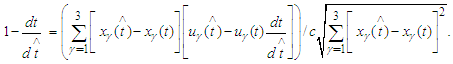We derive the radiation term under the Dirac assumptions (D):

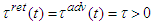where 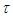is a small parameter.The Dirac assumption is justified by the fact that, for example, the electron radiation time is 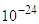sec.

Applying the Taylor theorem under assumption (D) we get

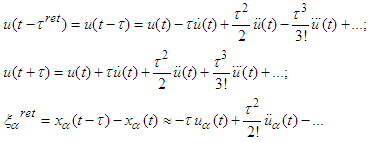It follows 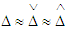. Consequently

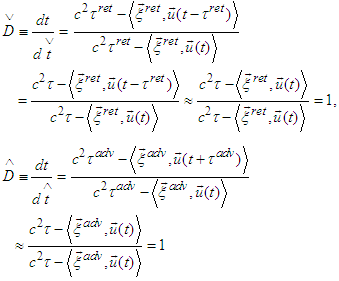and then

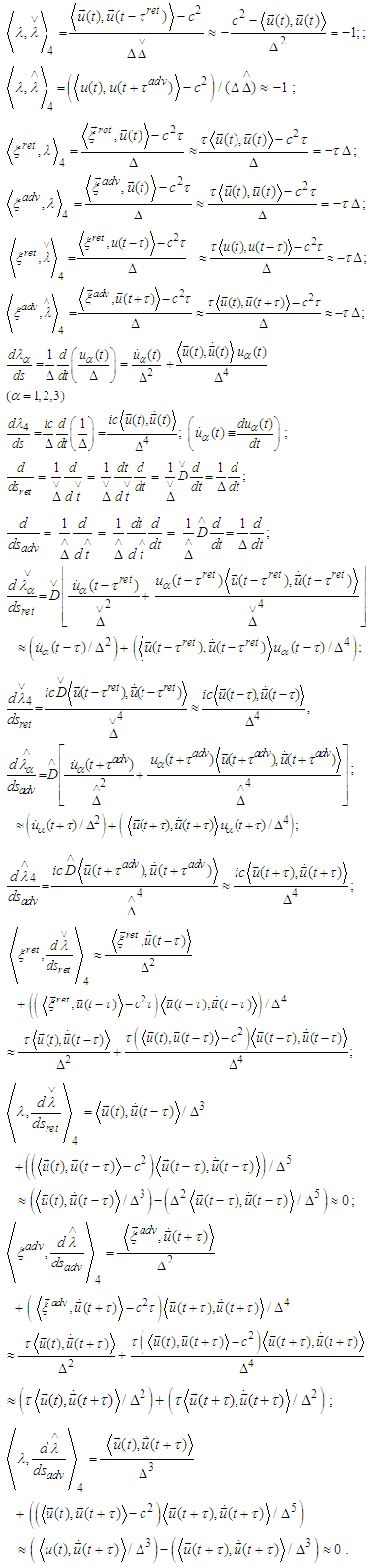Therefore the above system becomes

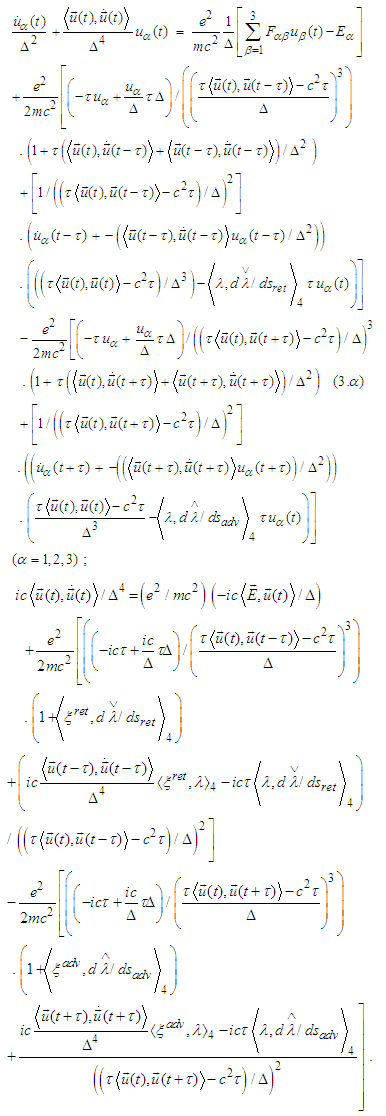(3)

The last equation should be divided by ic.

In [1] is proved that the 4-th equation (3) is a consequence of the first three ones (3.α).

Further on in view of

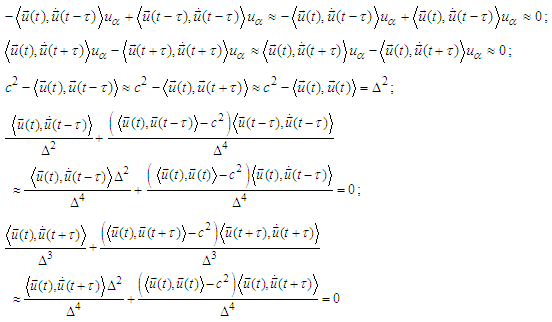we obtain

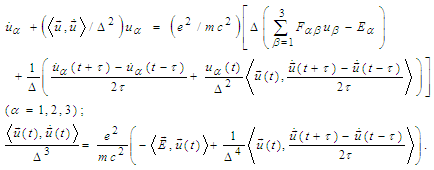Denoting by

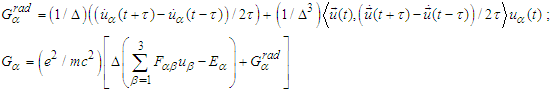we write the system in the form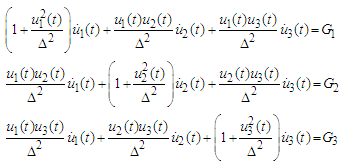

(4)

and we have to solve the last system with respect to .

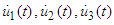Assumption (C): 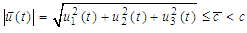for some constant .

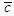Therefore 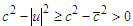and the determinant of the above system is obviously different from zero 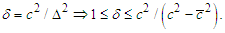Consequently, the uni- que solution of (4) is

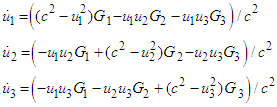(5)

where in view of

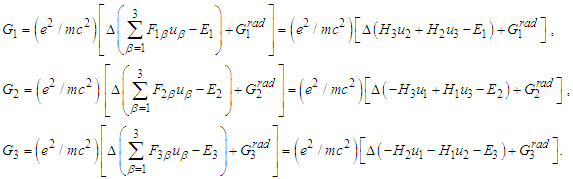we get

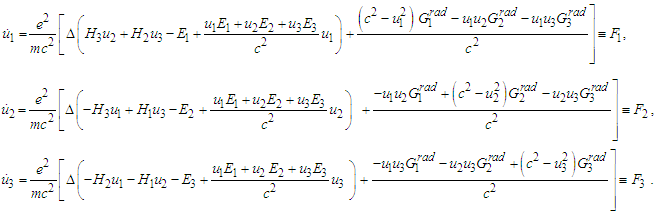(6)

4. An Operator Formulation of the Periodic Problem and Preliminary Assertions

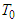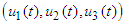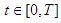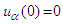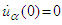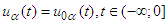
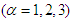We formulate the main periodic problem: to find a - periodic solution of the system (6) on the interval with initial conditions , and where 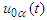are prescribed 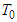-periodic initial functions.

Let 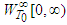be the set of all 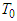-periodic functions from 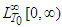whose derivatives of arbitrary order belong to 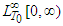. The functions from 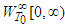are considered as all infinite differentiable functions on 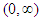having continuous extensions on 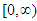. Introduce the function sets:

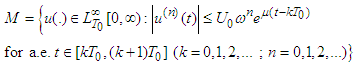where ,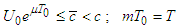

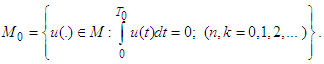Remark 1. It is easy to verify that substituting 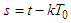we get

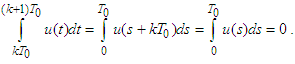We define the following family of pseudo-metrics

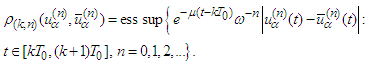Since for 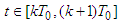we have

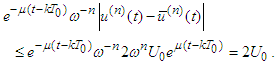It follows

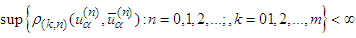and then we put

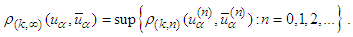Further on we set

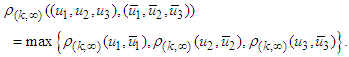Lemma 1. If 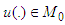then

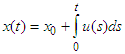is 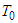-periodic function.

Proof: Let us set 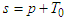and then we obtain

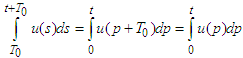. Therefore

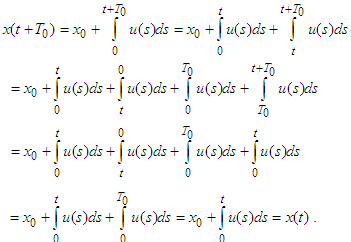Lemma 1 is thus proved.

Define the operator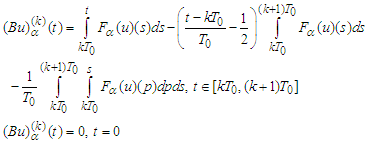

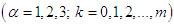where by assumption 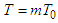and 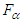are the right-hand sides of (6).

Lemma 2. ([36]) For every 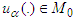it follows

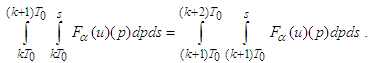Assumptions (H-E): The functions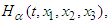

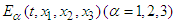are 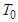-periodic and smooth in t and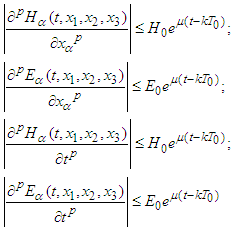

Lemma 3. (Main Lemma) The periodic problem (6) has a solution 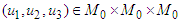iff the operator B has a fixed point belonging to 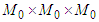, provided

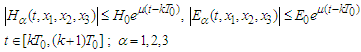where 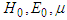are positive constants.

Proof: Let 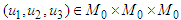be a 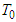-periodic solution of the system 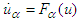. Then after integration in view of

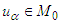(that is 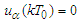and 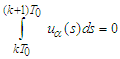) we obtain

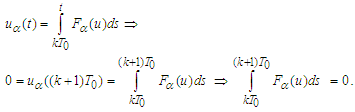(7)

Therefore

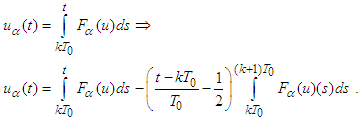Besides in view of (7) we have

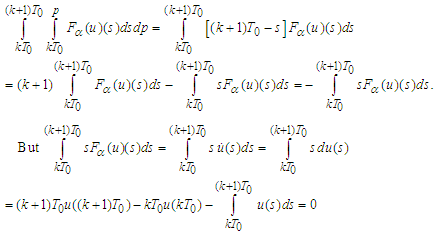that implies

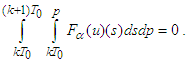Consequently,

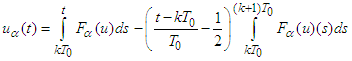can be written in the form

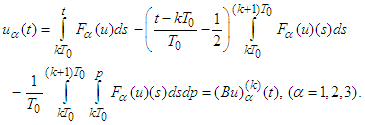The last equalities mean that B has a fixed point in .

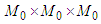Conversely, let 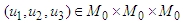be a fixed point of B. Then the last equalities are satisfied and substituting 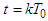we get

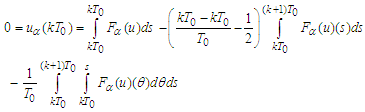that implies

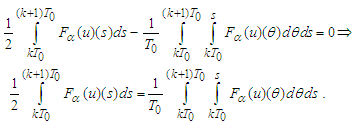We show that 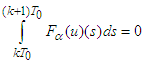. Indeed, Let us

suppose that 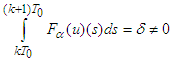. Then we obtain

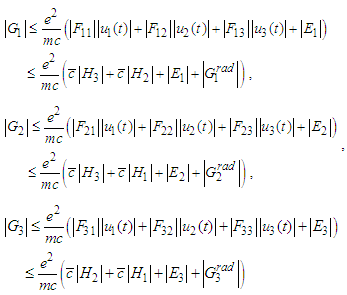which implies

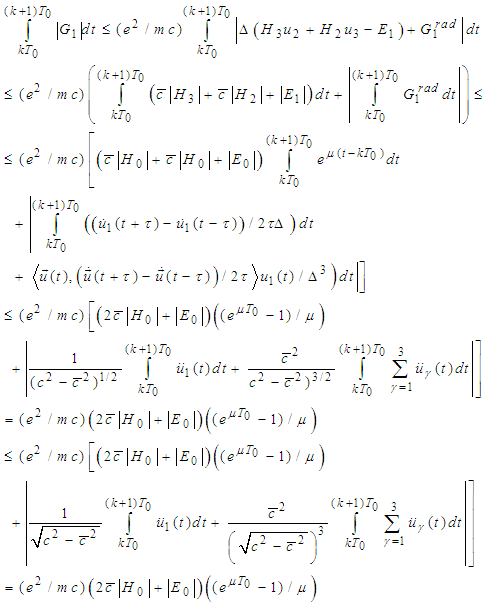since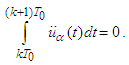

In a similar way we get

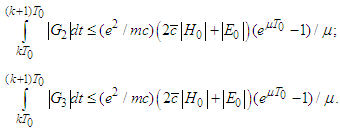Consequently

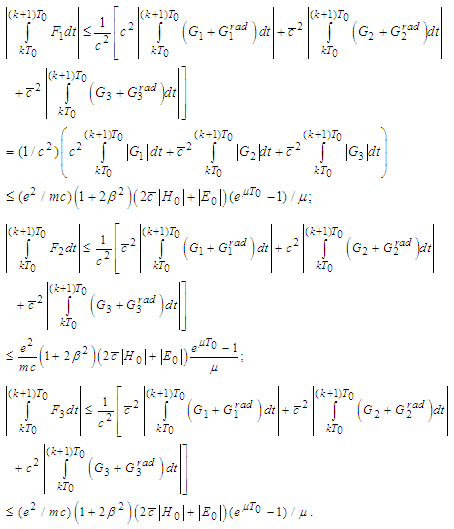Since 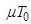= const for sufficiently large 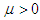and small 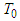we can obtain 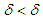. Therefore

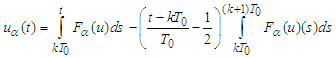becomes 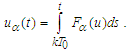Differentiating the last equality we obtain the required assertion.

Lemma 3 is thus proved.

5. Existence-Uniqueness of the Periodic Problem

Theorem 1 (Main result) Let the following conditions be fulfilled:

1. The initial functions 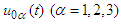are defined on 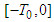and are such that their translations to the right on 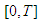coincide with some functions from 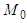and 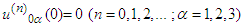, where 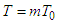for some positive integer m.

2. The components of intensity electric and magnetic vectors satisfy the assumptions (H-E);

3. The following inequalities are satisfied:

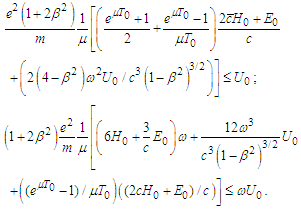Then there is a unique 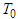-periodic solution of (6) .

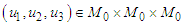Proof: In view of the Main Lemma 3 we have to prove that the operator B possesses a unique fixed point. This fixed point is a 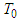-periodic solution of (6).

The set 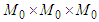turns out into a uniform space with a saturated family of pseudo-metrics for:

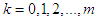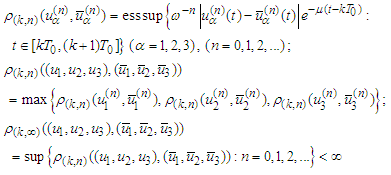since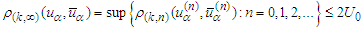

where the index set is

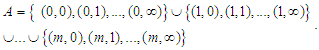Define the operator

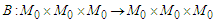by the formulas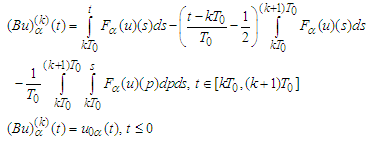

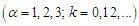, where 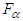are the right-hand sides of (6).

We show that B maps 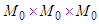into itself. Since

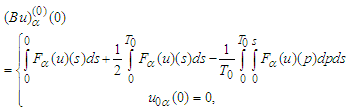we have shown in the Main Lemma 3 that

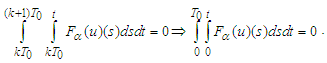Therefore

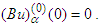First we check the following equality

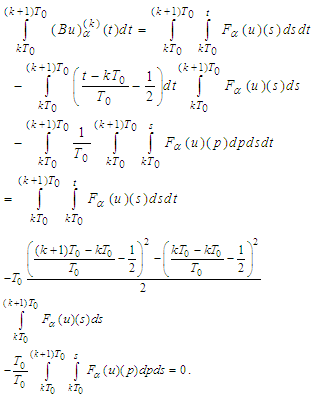Further on for 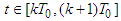we obtain

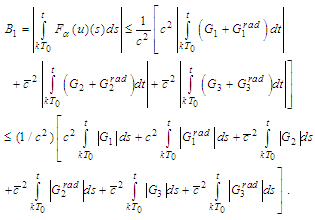We have

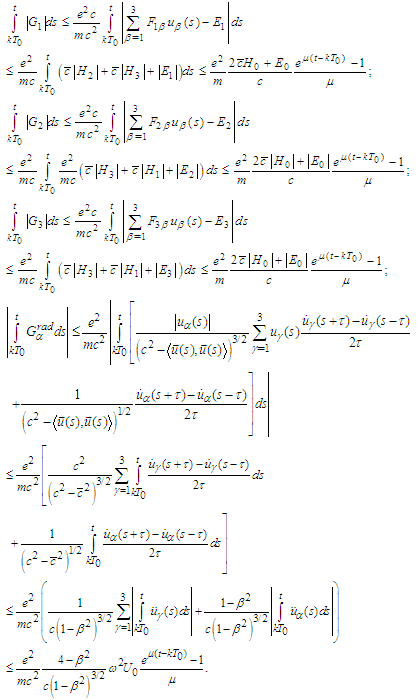Therefore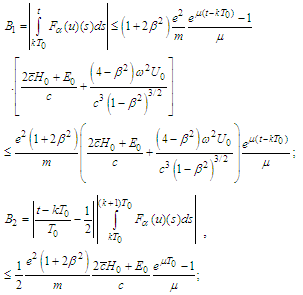

Finally we reach the estimate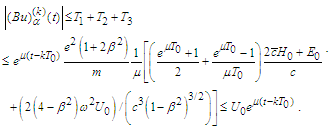

Let us estimate the derivatives

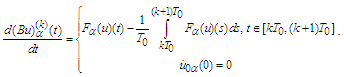Then in view of

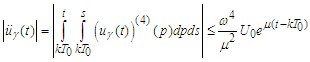we obtain

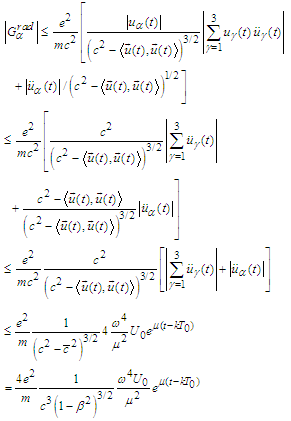we obtain

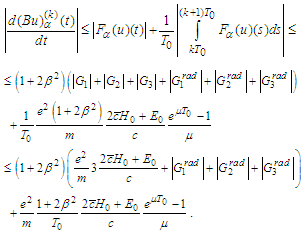But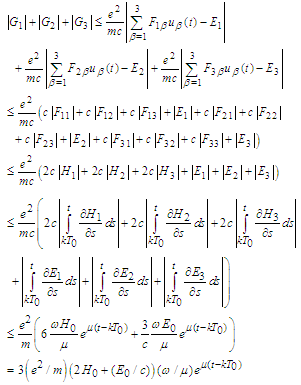

and consequently

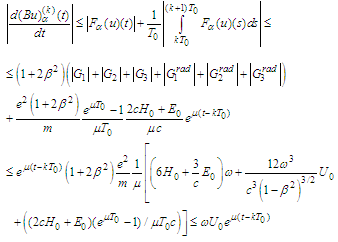and so on. Therefore .

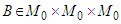Remark 2. In order to obtain suitable estimations for higher derivatives we use the chain of inequalities

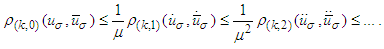In this way we compensate the degree of 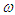in the nominator by the degree of 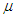in the denominator.

In what follows we show that B is contractive operator.

First we notice that the following Lipschitz estimate for the expression

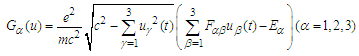is valid:

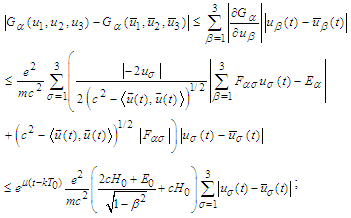and in a similar way from

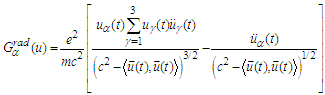we obtain

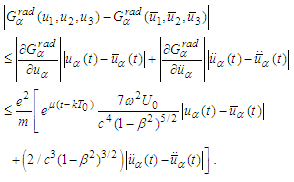Then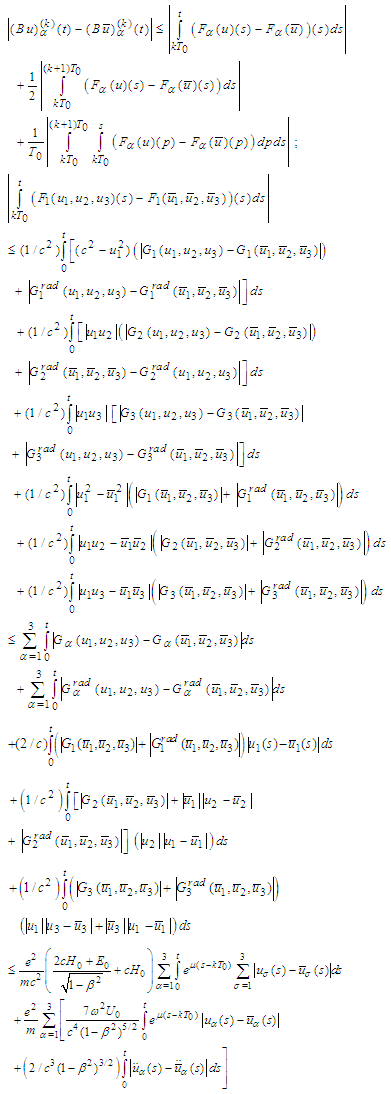

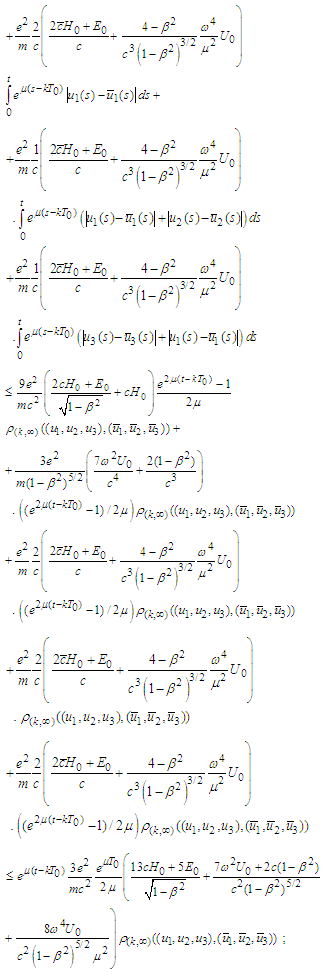
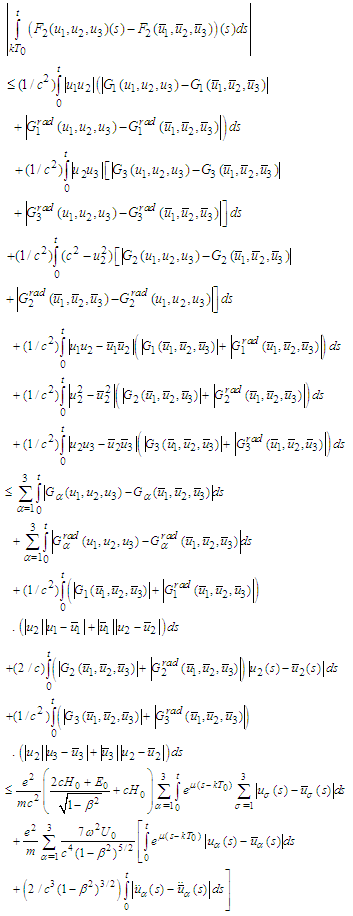
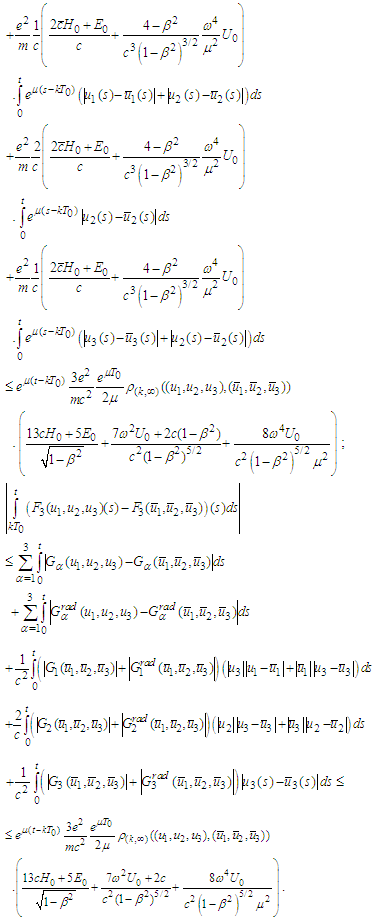For the second term we obtain

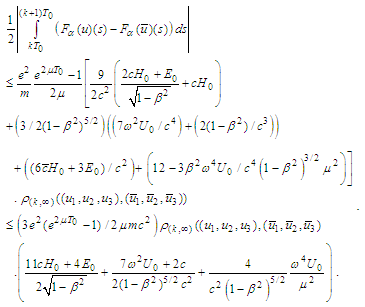For the third term we get

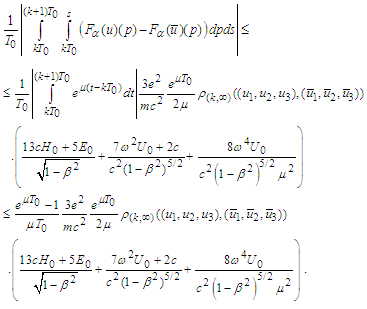Therefore

Consequently

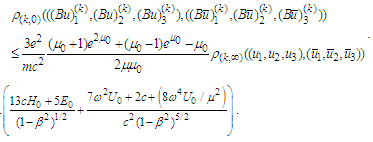In what follows we make the same estimates for the derivatives of the operator functions B (for higher derivatives we recall Remark1). Indeed,

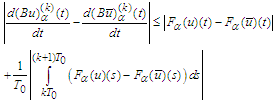and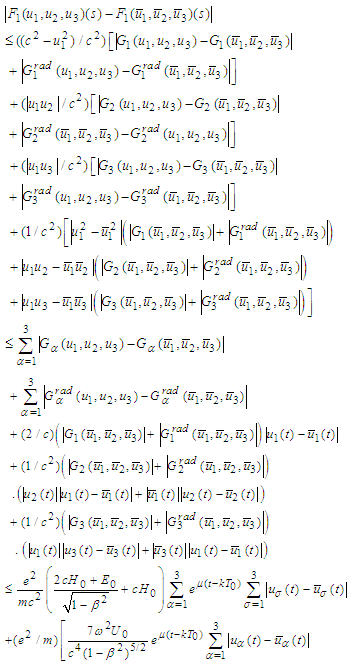

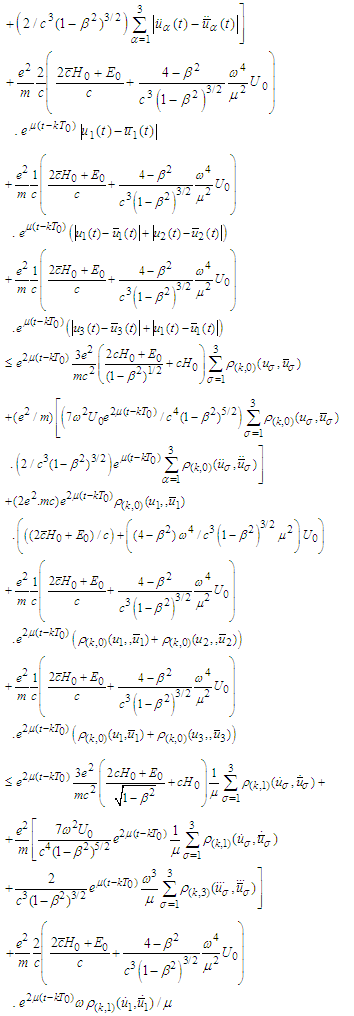
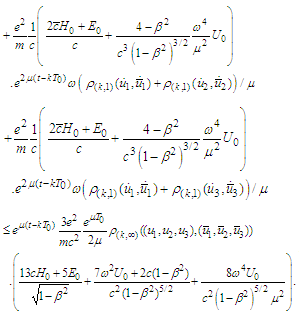Therefore the operator B is contractive in the sense of [35]. Its fixed point in view of the Main lemma is a 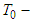periodic solution of (6).

Theorem 1 is thus proved.

6. Conclusions

As an immediate consequence we obtain an existence-uniqueness of periodic solution for betatron equation (cf. [14], [27], [38[-[41]). Specific applications we will give in next papers.