1. Introduction

In 1749, Benjamin Franklin first invented the electrical jack or electrostatic wheel. The electrical jack was, in fact, the first electrical motor in recorded history. The induction or Faraday disc would not follow until eighty years later. Franklin borrowed the word jack from the term smoke jack, a machine for turning a roasting-spit by means of a flywheel or wheels, set in motion by the current of ascending air in a chimney. The smoke jack was a labor-saving device and every housewife’s dream. With his discovery of electricity, Dr. Franklin set about inventing an improved electrical jack to a burgeoning domestic market in colonial America. Here is how Franklin described his electrical jack as follows:

“A small upright shaft of wood passes at right angles through a thin round board, of about twelve inches diameter, and turns on a sharp point of iron fixed in the lower end, while a strong wire in the upper-end passing thro' a small hole in a thin brass plate, keeps the shaft truly vertical. About thirty radii of equal length, made of sash glass cut in narrow strips, issue horizontally from the circumference of the board, the ends most distant from the center being about four inches apart. On the end of everyone, a brass thimble is fixed. If now the wire of a bottle electrified in the {29} common way, be brought near the circumference of this wheel, it will attract the nearest thimble, and so put the wheel in motion; that thimble, in passing by, receives a spark, and thereby being electrified is repelled and so driven forwards; while a second being attracted, approaches the wire, receives a spark, and is driven after the first, and so on till the wheel has gone once round, when the thimbles before electrified approaching the wire, instead of being attracted as they were at first, are repelled, and the motion presently ceases. — But if another bottle which had been charged through the coating be placed near the same wheel, its wire will attract the thimble repelled by the first, and thereby double the force that carries the wheel round; and not only taking out the fire that had been communicated to the thimbles by the first bottle, but even robbing them of their natural quantity, instead of being repelled when they come again towards the first bottle, they are more strongly attracted, so that the wheel mends its pace, till it goes with great rapidity twelve or fifteen rounds in a minute, and with such strength, as that the weight of one hundred Spanish dollars with which we once loaded it, did not seem in the least to retard its motion. — This is called an electrical jack; and if a large fowl were spitted on the upright shaft, it would be carried round before a fire with a motion fit for roasting.” [1]

Our solar system resembles Franklin’s “electrical jack”, but instead of the thimbles the Sun is one large self-excited dynamo. In place of cylindrical Leyden jars, we have spherical planets. Spherical stars and spherical planets are in fact like the Leyden jars of old. Using our imagination, by greatly increasing the size of the electrical jack to cosmic proportions, we can visualize rotating celestial bodies that are simply huge spherical capacitors, which momentarily store electricity. If I may borrow some of the many electrical terms Franklin coined; planets act as an electrical battery and store the positive and negative as an electrical charge. Our solar system acts like one large electrostatic motor transferring electrical fire (flux transfer events) from the Sun to the planets.

Figure 1. Solar System modelled as an Electrical Jack whereby Planets are treated as cylindrical Leyden jars

2. Wave Impedance

In my earlier work, it was put forth that time and space might be a function of wave impedance [2]. When a wave is propagated, it energizes the medium and the speed of the propagation is reduced or opposed by the impedance of the medium and by its ability to store energy. Both high inductance and high capacitance of the medium act to slow down the wave. It takes more energy and time to energize a medium with high impedance. The equation for the wave propagation speed in an ideal transmission line is 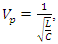where inductance and capacitance contribute proportionally to oppose or slow down the wave.

Impedance opposes the current or the magnetic field at a given level of voltage or electric field. This is expressed in a formula for the characteristic impedance of an ideal transmission line, Z0=√LC. Z0 does not depend on frequency. Inductance and capacitance are not contributing symmetrically: high capacitance encourages current flow, while high inductance impedes it.

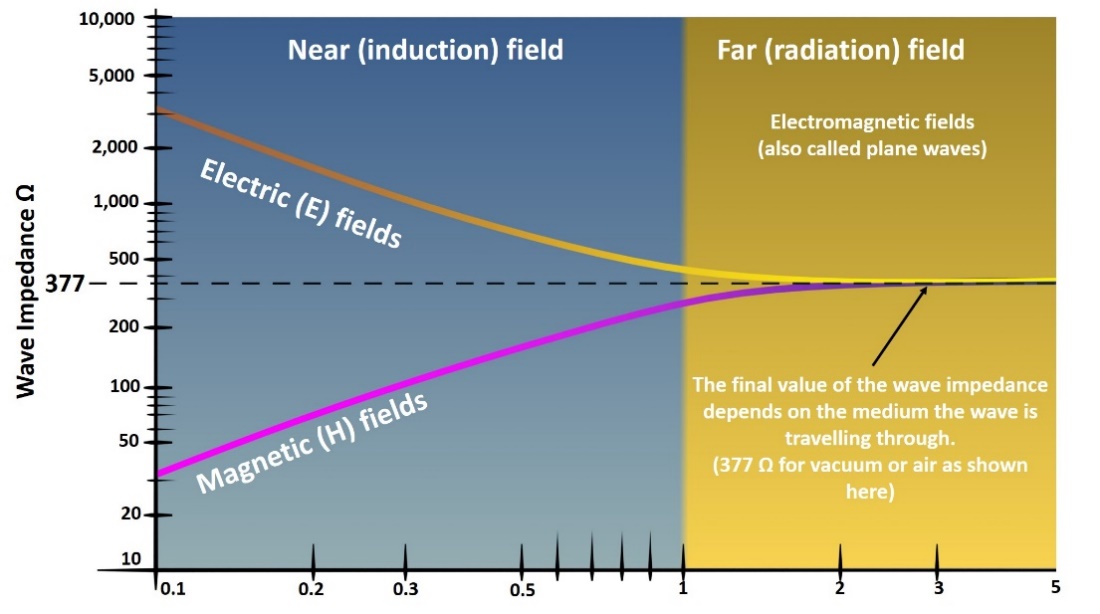Figure 2. Antenna Wave Impedance

The equation for the propagation of wave speed and impedance is V²=1/μϵ. The propagation is opposed or slowed down by both greater magnetic permeability (inductance) and electric permittivity (capacitance) of the medium. Conversely, the impedance increases with an increase in magnetic permeability and decreases with a decrease in electrical permittivity [3].

I wish to draw the readers’ attention to the left-hand portion of the chart closest to the emitter or planetary body. Near the induction field of the planetary antenna, at the distance of 0.159 λ the Wave Impedance in the Electric (E) field is 2370 Ω and 60 Ω in the Magnetic (H) field.

The work to be provide will center around a wavelength (λ) of 9 x 10⁹ meters, which coincides with a value near that of Coulombs constant. I will discuss more fully in the conclusion how the nature of this constant has been discovered.

3. Planetary RC Time Constant

The RC time constant, also called tau (τ- units in seconds), is equal to the product of the circuit resistance (in Ω) and the circuit capacitance (in farads- F), i.e.

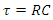(4)

It is the time required to charge the capacitor, through the resistor, from an initial charge voltage of zero to approximately 63.2% of the value of an applied DC voltage, or to discharge the capacitor through the same resistor to approximately 36.8% of its initial charge voltage. This value is derived from the mathematical constant e, also known at the Euler number. The number e is a mathematical constant that is the base of the natural logarithm: the unique number whose natural logarithm is equal to one. It is approximately equal to 2.71828 [1] and is the limit of (1 + 1/n)ⁿ as n approaches infinity. It is used in electrical engineering to derive voltage in a capacitor by the following:

Charging toward applied voltage

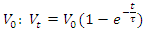Discharging from toward zero from initial voltage

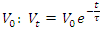All electrical circuits or systems have some form of “time-delay” between their inputs and outputs, when a signal or voltage, either continuous, (DC) or alternating (AC) is switched on or switched off. The electrical time delay is generally known as the Time Constant of the circuit. It is the time response of the circuit when a voltage is firstly applied. The resultant time constant of any electronic circuit or system will mainly depend upon the reactive components either inductive or capacitive connected to it and is a measurement of the response time with units of τ.

When an AC or DC voltage is applied to a discharged capacitor, the capacitor draws a charging current and “charges up”, and when the voltage is reduced, the capacitor discharges in the opposite direction. Because capacitors can store electrical energy they act like batteries and can store or release the energy as required. The charge on the plates of the capacitor is given as: Q = CV. This charging and discharging of a capacitor’s energy require a certain amount of time to occur. The time taken for the capacitor to charge or discharge to within a certain percentage of its maximum supply value being known as its Time Constant (τ). If a resistor is connected in series with the capacitor forming an RC circuit, the capacitor will charge up gradually through the resistor until the voltage across the capacitor reaches that of the supply voltage. The time also called the transient response, required for the capacitor to fully charge is equivalent to about 5-time constants or 5τ.

4. Cutoff Frequency

The time constant τ is related to the cutoff frequency f_c, an alternative parameter of the RC circuit, by

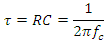Or, equivalently,

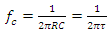(5)

where capacitance in F and resistance in Ω yields the time constant in seconds or the frequency in Hz. By convention, the bandwidth of an electrical power system is the frequency where |V_∞|² drops to half-value, or where ωτ = 1. This is the usual bandwidth convention, defined as the frequency range where power drops by less than half (at most −3 dB). As a voltage ratio this is a reduction to .707 of the passband voltage. Other useful equations are:

rise time (20% to 80%)

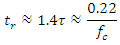rise time (10% to 90%)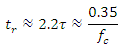

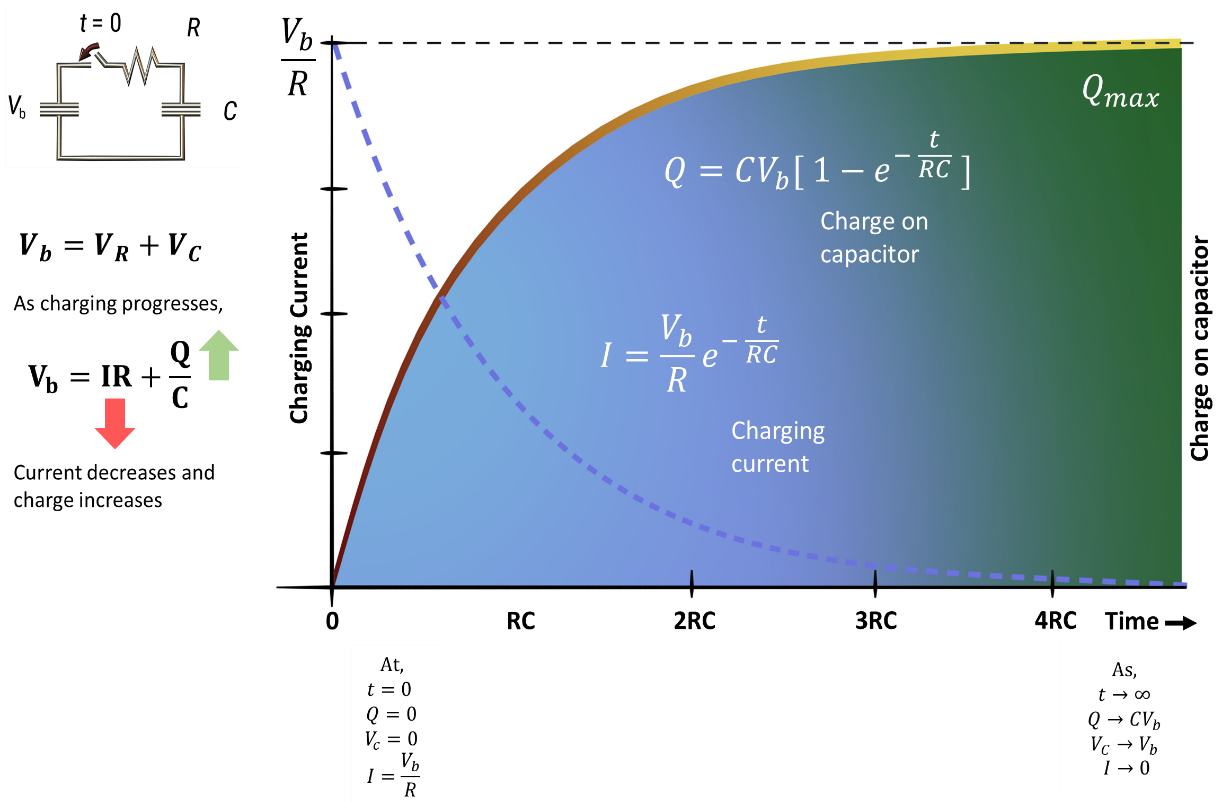Figure 3. Charging a Capacitor

5. Cosmic RC Charging Circuit

When a star or planet with a voltage is connected to space, the series resistor, inductor and capacitor, act as a load. The initial current is high as the Earth, for example, transports charge from one plate of the capacitor to the other. The charging current asymptotically approaches zero as the capacitor becomes charged up to the battery voltage. Charging the capacitor stores energy in the electric field between the capacitor plates. The rate of charging is typically described in terms of a time constant RC. Since more charge can be stored by forcing it with higher voltage, it makes sense to define capacitance as charge stored per unit voltage. When expressed in terms of maximum charge on a capacitor this becomes:

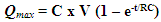
6. Calculate Radius of Earth Capacitive Sphere

To begin our exercise, I will pick a theoretical value for capacitance as 86,400 F. This decision may seem at first arbitrary, but we note that 86,400 seconds is equivalent to 1 day or 24 hours. To calculate the capacitance of a simple charged sphere based on the given values where, C = Capacitance of Sphere, a = Radius, ε_o = Permittivity of Free Space, ε_r = Relative Permittivity

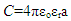Assuming the center of our earthly sphere, I calculate a radius of 7.77e14 meters, which is slightly shorter than 9.46e15 meters. If I were to use 9.46e15, commonly referred to as a lunar light year, I obtain a value slightly over 100,000 Farads.

To take our thought experiment one step further, I conceive of an inner and outer sphere surrounding the earth at great distances. I will use 7.1762e14 meters as my inner radius and 9.46e15 meters as my outer radius to calculate capacitance.

I then use the following double sphere equation:

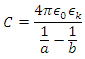where:

C is the capacitance measured in farads (symbol: F);

ε₀ is the vacuum permittivity;

ε_k is the relative permittivity. It is dimensionless;

a is the radius of the inner sphere;

b is the radius of the outer sphere.

Using the above values, I calculate the capacitance as 86,400 F.

7. Earth Far Field Calculation

The speed of light and gravity equation was derived in earlier work. [6]

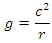Insert a lunar light year

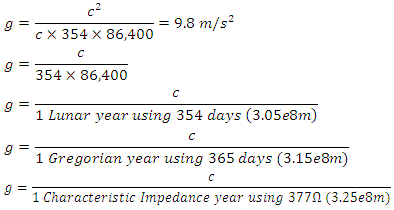I note that 3.15e8 falls midway between a lunar light year and a Characteristic Impedance light year.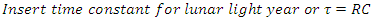

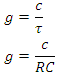Insert R equals impedance of space 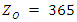and C is equal therefore equal to 86,400 Farads. There is an inner and outer spherical capacitor in the far field. The inner circle is 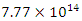meters and the outer circle is 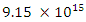. 86,400 is equivalent to the seconds in a day. τ is a time constant, thus a day and a year are relatively constant.

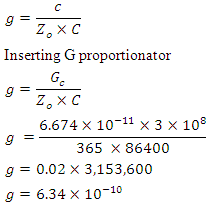This represents the value of gravity in the far field. Gravity is very weak in the far field.

8. Far Field Capacitor Charge Calculation

For the following circuit parameters:

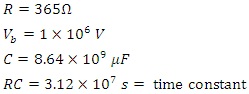This circuit will have a maximum current of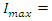 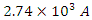just after the switch is closed.

The charge will approach a maximum value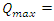

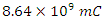At time

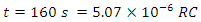The charging current is = 0.99

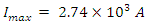and the charge on the capacitor is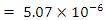

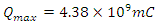I note the charging current is 1 A and that Earth Time is accurate to within 5 years due to the duration of charging time of the Earth’s far field capacitor. I note that voltage affects charging current but does not affect charge time. Time on Earth is a function of the characteristic impedance of free space and the capacitance of the far field. The characteristic impedance of free space is equal to the square root of the ratio of permeability of free space (in henrys per meter) to the permeability of free space (in farads per meter). Typically, it works out to about 377 Ω, and that is the characteristic impedance of the universe. The impedance of the Earth’s far field is closer to 365, which is the number of days in a year. The expression for the characteristic impedance of free space falls out of the plane wave solution to Maxwell’s equations.

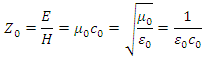Where,

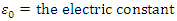
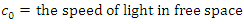
9. Earth Magnetoquasistatic Field Calculation (60Ω)

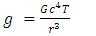(7)

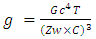(8)

Insert Impedance

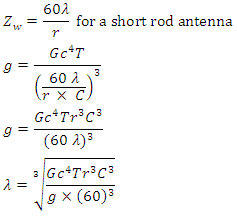
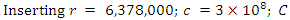
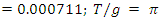
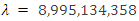I compare to Coulomb Constant of 8,987,551,787 and value is within 1%.

60 Ω is a standard antenna impedance based on 0.159 wavelength distance from an antenna. Using 8,996,654,770 as a radius results in C = 1 Farad.

10. Magnetoquasistatic Capacitor Charge Calculation (60Ω)

For the following circuit parameters:

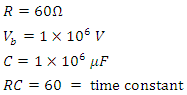This circuit will have a maximum current of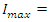 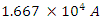just after the switch is closed.

The charge will approach a maximum value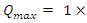

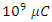At time

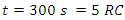The charging current is = 0.00674

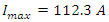and the charge on the capacitor is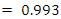

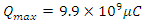
11. Earth Magnetoquasistatic Field Calculation (30Ω)

Moving closer to the Earth will increase the impedance resistance down to perhaps as low as 30 Ω at ground level. Inserting this value into our equation, we have the following:

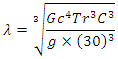
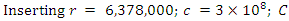
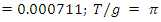
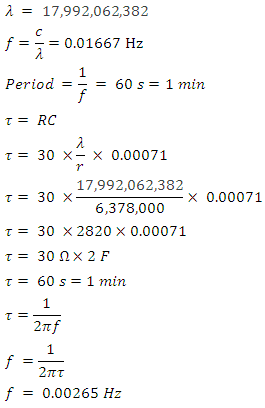
12. Magnetoquasistatic Capacitor Discharge Calculation (30Ω)

For the following circuit parameters:

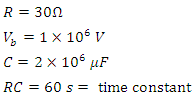This circuit will have a maximum current of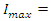 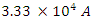just after the switch is closed.

The charge will approach a maximum value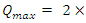

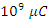At time

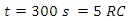The charging current is = 0.00674

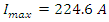and the charge on the capacitor is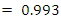

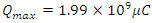Using 30 Ω and 1,000,000 V, I obtain a typical lightning strike of 33,333 A, which compares favorably with the known average of 20-25kA. At 60 Ω the value changes to 16,666 A, which confirms that our impedance and capacitance are realistic numbers. Lightning is a current driven phenomenon derived from the Magnetoquasistatic field. I also note that a time of 1 minute near the Earth is calibrated every 5 minutes based on a far field capacitor of 2 F.

13. Magnetoquasistatic Capacitor Discharge Calculation (5Ω) for Bolted Lightning Fault

In the following example, I will simulate a large bolt lightning fault of 200,000 Amps.

For the following circuit parameters:

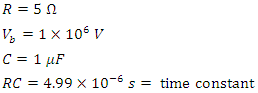This circuit will have a maximum current of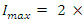 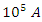just after the switch is closed.

The charge will approach a maximum value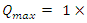

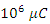At time

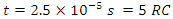The charging current is = 0.00674

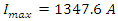and the charge on the capacitor is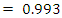

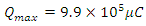A large 100,000 to 200,000 A lightning strike occurs when the Magnetoquasistatic atmospheric resistance breaks down and resistance plummets to 5 or 10 Ω. It results in a near short circuit condition of the field and a massive electrical fault occurs. A buildup of moisture in the atmosphere is the likely culprit as the Earth’s insulation system becomes conductive with more water.

14. Earth Near Field Calculation

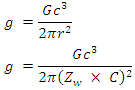Insert Near Field Impedance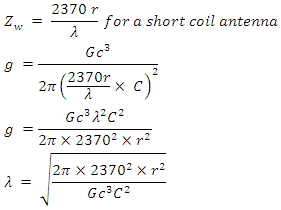

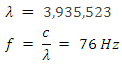Using a length of Coulomb’s constant,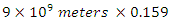 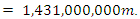. This radius results in a 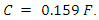I point out that the near field itself is further divided into the reactive near field and the radiative near field. The near-field designations are also a function of distance. The boundary regions are a fraction of one wavelength within the near field. The outer boundary of the reactive near-field region is commonly considered to be 1/2π times the wavelength (λ/2π or 0.159 × λ) from the antenna surface. The reactive near-field is also called the "inductive" near-field. The radiative near field (also called the "Fresnel region") covers the remainder of the near-field region, from λ/2π out to the Fraunhofer distance. [9]

15. Near Field Capacitor Charge Calculation (2370Ω)

For the following circuit parameters:

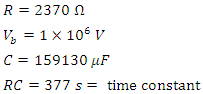This circuit will have a maximum current of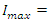 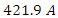just after the switch is closed.

The charge will approach a maximum value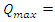

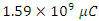At time

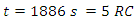The charging current is = 0.00673

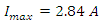and the charge on the capacitor is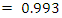

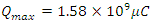Inserting this value with a standard Impedance point of an antenna at 0.159 results in a Time of 377 seconds.

16. Near Field Capacitor Charge Calculation (2263Ω)

For the following circuit parameters:

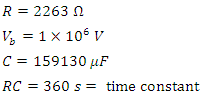This circuit will have a maximum current of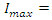 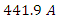just after the switch is closed.

The charge will approach a maximum value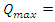

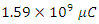At time

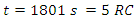The charging current is = 0.00673

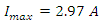and the charge on the capacitor is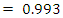

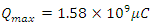By lowering R to 2263 Ω, I obtain RC = 360s or 6 min and 30 min is the calibration time at which the capacitor is fully charged.

17. Near Field Calculation (7700Ω)

The closer we get to the antenna or surface of the Earth the higher the impedance. Closer to the surface, Z_w approaches 7700 Ω, which changes the equations to:

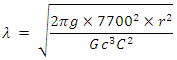
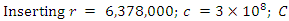
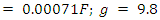
18. Near Field Calculation (23000Ω)

Approaching the surface even closer the impedance rises to Z_w =23000 ohms

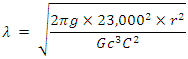
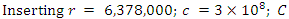
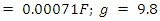
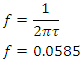
19. Near Field Capacitor Charge Calculation (22624Ω)

For the following circuit parameters:

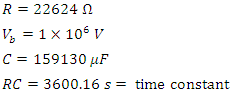This circuit will have a maximum current of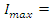 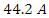just after the switch is closed.

The charge will approach a maximum value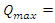

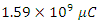At time

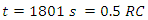The charging current is = 0.606

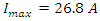and the charge on the capacitor is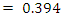

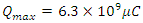Inserting a near field impedance of 22,624 Ω and a capacitance of 0.159, I calculate 3600 seconds, or 1 hour. This capacitor reaches full charge in roughly 5 hours. The charging current is 6 mA.

20. Calculate Voltage Discharge from Lightning

The three variables which affect how the initial voltage discharges is time, t, the resistance of the resistor, R, and the capacitance of the capacitor, C. Inserting the average duration of lightning at 0.2 s, C = 0.00071 F and an initial voltage of 1,000,000, I calculate outer the Earth resistance at 234 Ω for an atmospheric voltage of 300,000 V.

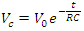If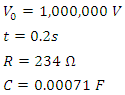

The voltage that the capacitor has discharged is 699,949 V

The voltage remaining across the capacitor is 300,050 V

21. Calculate RL and RC Time Constant of Inner Earth

When the L and C are placed in parallel or series, they have a resonant frequency. This resonant frequency is represented by the following equation:

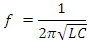Where: f is the resonant frequency in Hertz (Hz), L is the inductance in Henries (H), C is the capacitance in Farads (F), π is the constant (3.141592654…)

I note that the period of Flux Transfer Events shows,

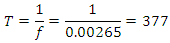It would seem the Flux Transfer Events is limited to the characteristic transmission line impedance of free space, and it is plausible that the inner core resistance is also limited to 377 Ω.

RL Time Constant is calculated using,

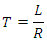If I use an estimated resistance value of 377 Ω and 22,800 H the Inductive Time Constant is 60 s. We can confirm using the RC Time Constant,

RC Time Constant Calculator

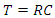Inserting the same value of 377 Ω and C = 0.159, I obtain 60 s.

These values are reflective to those I used in standard antenna equations.

22. Conclusions

An electrostatic motor has been used as an analogy of the solar system to provide answers and a pathway to one of the difficult questions of astrophysics—the origin of time itself. The electrical jack devised by Benjamin Franklin has been imagined representing spherical planets as capacitive Leyden jars with the Sun in the center hub. All celestial capacitive spheres have time constants based on voltage decay. Calculation of time constant and voltages have been made based on the radius of the capacitance. The capacitance, when multiplied with electromagnetic and electrostatic impedance values, generate interesting results. Some of the broad conclusions that may be asserted from this paper are as follows:

1. The Earth acts as a magnetic loop dipole and an electric short rod dipole. Together they produce the magnetic field which results in the near, far and magnetoquasistatic fields. The fields fall off according to 1/r, 1/r² and 1/r³ respectively. Gravity is the sum of the fields at any point P within the combined fields.

2. Stars, planets and the space between bodies is spherical in nature and thus represent capacitance, inductance and resistive losses. Charged spheres are commonly used in high voltage substation equipment to prevent the breakdown of voltage. These are typically manufactured in the shape of toroid’s and spheres. From my work in electrical modeling and electro relativity we know that planets electromagnetic radiation pattern is shaped in the form of spheres and toroid’s.

3. All celestial spheres have capacitance, which when multiplied with standard (60-ohm, 2370 Ω and 377 Ω) impedance values generate time constants that resemble time itself. Time, as we clock it, is the cross product of celestial capacitance and the respective antenna impedance of the near- and far-fields. Time is a derivative of time constants based on 0.707 maximum voltage at cutoff frequency. Earth’s clock is calibrated by its 5-year charge time. Time constants for all intended purposes, even those that are heavenly or divine, are absolute and since magnetic fields and voltages intermingle between stars and planets one can envision a cosmic metronome counting out seconds for the universe. Like power plant generators and motors on a utility grid, stars and planets are electrically synchronized to the same atomic time clock of the universe. This is not a redefinition of time and space; this is a more correct definition of time.

4. Time, as we experience, is a cosmic electronic clock that is localized to the Earth’s capacitance values. It is thought that since the Earth falls under the radius of spherical capacitance of the much larger Sun, that it is plausible that Earth’s time is synchronized to that of the Sun. And, the Sun in turn is synchronized to larger Sun’s and the galaxy. Like nested spheres our galaxy is synchronized to the universal clock. There may be a universal metronome or Universal τ that keeps time for all universes.

5. By international agreement, a standard second is "the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium atom." But in celestial terms, based on calculated time constants of the solar system, the Sun and the Earth, it is 1⁄60 of a minute, 1⁄3,600 an hour, 1⁄86,400 a day (IAU system of units), and 1⁄31,557,600 a Julian year.

6. Large spherical capacitors such as stars and planets store tremendous voltage charge that range from 300,000 volts to 10,000,000,000 volts. Dark energy throughout the universe may be derived from large celestial bodies that are voltage charging and discharging across great distance.

7. Space or dark matter can be modelled as capacitor impedance dependent upon capacitance, inductance, series resistance and frequency of space.

8. Energy flowing from the Sun to the planets is constant at 3.14e18 watts. The characteristic impedance of space is fixed at 377 Ω, which may be the limiting factor regarding the amount of energy to be transported through space.

9. Schumann Resonance is derived from the near field of the Earth. 7.85Hz is the calculated fundamental frequency using Z_w = 23,000 Ω. Impedance matching is the practice of designing the input impedance of an electrical load or the output impedance of its corresponding signal source to maximize the power transfer. In theory it is conceivable to transfer electrical power directly from the Earth to an electrical load via wireless transmission. In the case of complex source impedance Z_S and load impedance Z_L, maximum power transfer is when Z_S = Z_L.

10. The period of flux transfer events (7.1 to 8 minutes) from the Sun to the Earth may be traceable to the low atmospheric capacitance of the Earth. This would suggest that environmental changes of the impedance of the low atmosphere may affect the period of flux transfer events.

11. Planetary differences, such as opposite polarity, direction of rotation, can be reconciled using the electrical jack model as opposed to my earlier purely induction machine model. [10] Gaseous and magnetic planets can be modeled as Leyden jars; the most basic capacitor. Franklins Electrical Jack requires that Leyden jars be oppositely polarized. Jupiter’s polarity for example is the opposite of Earth. The model would suggest that other planets and dwarf planets may have opposite polarity, though the relative size of Jupiter (11X that of earth) may provide enough opposite charge to offset all the other planets combined.

12. The average lightning strike current of 20,000 A is created by the magnetoquasistatic field, whereby its atmospheric capacitor is discharged. Large electrical strikes of 100,000 to 200,000 A occur when moisture laden air lowers the resistance of the Earth’s insulation system. Adding more moisture to the atmosphere by way of global warming may lead to larger and more lethal lightning strikes.

13. The reduced atmospheric voltage of 300,000 V is maintained by repeated lightning strikes around the globe. The practice of installing lightning rods may have the effect of reducing near field atmospheric voltage.

14. The flux transfer frequency and our time of 60 s, or 1 min is determined by the resonant LC circuit within the inner core of the Earth.

15. Spacetime, is space and time, defined by the radial size and discharge time of a spherical or toroid capacitor. The speed of light (c²/r, c³/r², c⁴/r³) creates toroid and spherical shapes due to the bending of the photon brought about by the powerful electromagnetic (E & H) field. The toroid and sphere hold a charge (Q_max) which supports and maintains a high voltage. The voltage has a discharge associate which we call a time constant. Spacetime is thus a capacitor of dimension r that takes up space and has a time constant.

16. Time is experienced, and is relative, to the toroid(s) and sphere(s) within which we humans live. We all experience the same time from a different physical perspective, but it is the same solar system time constants or clock, that are continually being charges and discharged. The Sun charges the clock battery (capacitor) which discharges over time. As long as the Sun remains operational and the earth can store its charge, time will march on.

17. Electro relativity with its dipole foundation allows us to see Spacetime as an electrical phenomenon. Electro relativity can be solved for time (t) at any point P in space. Time is a function of E, H, I, c and r. Going backwards and forwards in time is possible by solving for time (t) and manipulating the other variables. A time machine is theoretically possible, and funds should be invested to research and develop.

ACKNOWLEDGEMENTS

The author wishes to acknowledge ASK Scientific (https://www.askscientific.com) for the formatting assistance and artwork. Special thanks to Michael Pollard retired field engineer from Industrial Tests for bringing Benjamin Franklin’s electrical jack invention to my attention. Benjamin Franklin as a scientist was a major figure in the American Enlightenment and the history of physics for his discoveries and theories regarding electricity. He invented the lightning rod, bifocals, and the Franklin stove, among other inventions. Franklin founded the University of Pennsylvania and published Poor Richards Almanac, still in print today.