1. Introduction

1.1. The Cosmological Lithium Problem

The predicted primordial abundance of 7Li predicted via the Big-Bang Nucleosynthesis (BBN) physics of the Standard model is higher by a factor of 3 compared to the observed abundance in the universe [1,2]. The predicted 7Li/H abundance is 5.1 * 10^-10 while the value inferred from old, metal-poor stars is 1.58 ± 0.31 * 10^-10 [2,3].

This problem has been troubling astrophysicists for decades since they have been unable to reconcile the predicted vs. observed 7Li abundance. The root cause of the status quo of the Lithium problem is that scientists have been mainly trying to solve it using the physics of the Standard Model. The BBN physics of the Standard Model predicts the abundance of the light elements based on the thermonuclear reactions, reaction rates, as well as on the free parameters baryon-to-photon ratio [4].

The abundance of 7Li is complicated due to several factors impacting it. 7Be (produced during the BBN) decays into 7Li prior to the formation of galaxies and stars due to electron capture [5]. Post BBN, 7Li can be depleted over the star’s lifetime. 7Li is destroyed in old star’s interiors (which produced the primordial 7Li abundance). It typically survives only on the surface dependent on the stellar temperature as well as in stars in their late giant evolution [1,5,6]. It is also produced in stellar interiors and is also synthesized by collisions of cosmic ray nuclei [5]. Thus, the overall trend is an increase in 7Li abundance over time.

Since the total matter content of the universe is much greater than the baryonic matter, it is hypothesized that the remaining fraction of the universe is made up of dark matter [5]. The 7Li discrepancy may have connections to dark matter and as such, to physics Beyond the Standard Model (BSM) [7].

1.2. Primordial Light Element Abundance

Other than 7Li, the light elements D, 3He, and 4He were produced as a result of BBN [3]. The abundance of the light elements predicted via Standard Model of Physics as well as the observed abundance of 7Li is provided in tables in Section 5.

1.3. The Standard and BSM Models

The Standard Model of Physics cannot explain and solve the discrepancy of 7Li abundance as it has its shortcomings. It cannot explain gravity, dark matter, dark energy, baryon asymmetry, and matter-antimatter symmetry [3,6].

Dark matter and dark energy are explained in Section 1.5. The Standard model cannot explain gravity and is incompatible with general relativity [8]. Per the Standard model, neutrinos are massless, but neutrino oscillations require neutrinos have a mass [8]. The Standard model predicts matter and antimatter to be created in equal amounts, but the universe is mostly made up of matter leading to the matter-antimatter symmetry problem [8,9]. Also, the Standard model inflation theory predicts baryon symmetry. But observations suggest that as the universe cooled down post inflation, excess quarks were left over after quarks-antiquarks annihilation which formed baryons. The Standard model does not account for this [9,10].

As such, we need to move to the BSM physics to explain the primordial 7Li discrepancy. BSM physics incorporates the shortcomings of the Standard model including dark matter, dark energy, matter-antimatter symmetry, gravity, compatibility with general relativity, baryon asymmetry, non-zero mass of neutrons, and an increase in the number of relativistic degrees of freedom.

1.4. The Friedmann Equation

The Friedmann equation is a dynamic equation which predicts an expanding universe as part of the Standard Model of Cosmology.

It allows us to examine the universe expansion time and temperature at the big bang time [11]:

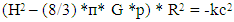(1)

where H is the Hubble parameter, G is the gravitational constant, R is the scaling parameter, k is the curvature parameter, _is the energy density of the universe.

BSM physics could allow us to have an expansion rate factor S which can arise from changes in the gravitational strength or from modifications in the Friedmann equation including the addition of dark energy density to the total energy density of the universe [4].

1.5. Dark Matter and Dark Energy

Dark matter is the matter in the universe which cannot be seen or observed. It is non-luminous, that is, it neither absorbs nor emits light. It is likely to be made up of some subatomic particles. The universe constitutes ~26-27% dark matter and ~68-69% dark energy (force that repels gravity) [5,9]. Thus, ~95% of the universe is dark material (mass and energy). Hence, only 4-5% of the universe is baryonic, that is, made up of ordinary matter [5,9,12-14].

But not all dark matter is non-baryonic. Baryonic matter means composed of protons and neutrons, i.e., consisting of normal atomic matter [15]. In the universe, baryonic matter includes planets, stars, comets, and asteroids. A small amount of dark matter is likely to be baryonic. More than 80% of the universe content is non-baryonic [15].

Dark matter plays a very important role in the fate of the universe. Its gravitational attraction is the glue that holds the galaxies and clusters of galaxies together [15]. The physics of dark matter and dark energy is now well established.

Dark Matter is invisible since it does not interact with electromagnetic radiation. It is discerned via a phenomena called gravitational lensing. The gravitational attraction of dark matter bends space as well as the background light [15].

1.6. Bosons and Fermions

Per the Standard Model of Physics, Bosons and Fermions are the two types of elementary particles present in the universe (see Figure 1). Fermions include quarks and leptons (electrons, muons) while bosons include gauge bosons and scalar bosons. The elementary particles have intrinsic spin angular momentum. The primary difference between bosons and fermions is their spin. Fermions have odd half-integer spin (1/2, 3/2, 5/2, . . . ) while bosons have integer spin (0, 1, 2, . . . ) [5,16,17].

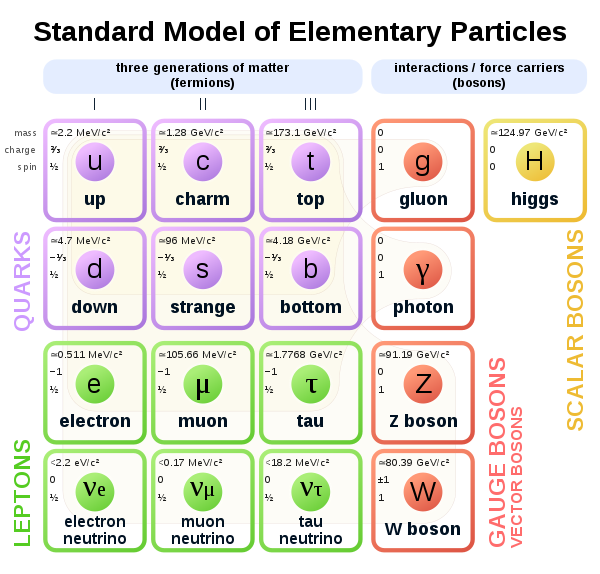Figure 1. Standard Model of Elementary Particles [19]

Secondly, fermions obey the Fermi-Dirac statistics and due to their odd half-integer spin and obey the Pauli exclusion principle while bosons obey Bose-Einstein statistics. The Pauli exclusion principle obeyed by fermions is very important as it implies that no fermions can occupy the same quantum state. This is the reason why atoms have different properties, elements have different physical and chemical properties, and huge variety of molecular configurations exist. Since bosons do not obey the Pauli exclusion principle, they can be put in the same quantum state leading to Bose-Einstein condensates [16-18].

Thirdly, fermions are represented by asymmetric wave function while bosons are represented by symmetric wave function. Photons are examples of bosons while electrons are examples of fermions [16,17].

1.7. Dark Matter Types

Dark matter may be cold or hot [20]. Cold Dark Matter (CDM) includes particles which are non-relativistic (travel slower than the speed of light) versus Hot Dark Matter (HDM) which consist of particles that are relativistic (travel near the speed of light) [21]. Neutrinos are the major HDM candidates. WIMPs and Massive Astrophysical Compact Halo Object (MACHOs) are the major CDM candidates [20]. CDM is said to account for most of the energy density or missing mass of the universe (see Section 1.7.1 for details).

1.7.1. Neutrinos

Neutrinos are HDM and move at relativistic velocities (near the speed of light). They are nearly massless, electrically neutral, and interact only with a weak force and gravity. They do not decay, are not deflected by magnetic fields, and can pass through baryonic matter (including thick lead plates and the Earth itself) without interacting or getting absorbed. As such, they are almost impossible to detect [5].

Majority of the neutrinos were created during the early stages of the Big Bang (when our universe was born). They are also continually being produced from stellar interiors, collapsing supernova, as well as from nuclear reactions in nuclear power plants and nuclear bombs [22,23]. They make up only about 0.5 to 1.5% of the dark matter mass in the universe. They cannot make up the rest of the dark matter because if that were the case, then all the hot dark matter would be moving at relativistic velocities and weak lensing signals rule this out. Hence, the remaining dark matter must be cold [21,24,39].

1.7.2. Number of Neutrinos

Per the Standard Model of Physics (see Figure 1), neutrinos are classified as leptons. The Standard Model predicts three types of neutrinos [25]. As can be noted from Figure 1, they are electron neutrino, muon neutrino, and tau neutrino. All three neutrino types are electrically neutral.

As such, in the Standard Model of Physics, the number of active neutrino species, Nv = 3. However, the three neutrino species were weakly coupled during the e+-e- annihilation in the photon-baryon plasma in the early universe so that a small amount of entropy gets shared with the neutrinos. Hence, the effective number of neutrinos in the Standard Model of Physics, Neff = 3.046 [26-28].

1.7.3. Energy Density of the Universe

The following equation gives the energy density of the universe [27-29]:

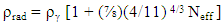(2)

where N_eff is the number of relativistic degrees of freedom defined in terms of the effective number of neutrinos in the standard physics model and is the energy density of the CMB photons background.

1.7.4. ΛCDM Model of Physics

CDM and the massless neutrinos are accounted in the ΛCDM physics model (which is a parameterization of the Standard Physics Model explained in Section 1.3). Λ represents the cosmological constant from Einstein’s field equations of general relativity. The model, as such, assumes a flat universe and does not account for new physics [31]. It would need to be extended to account for curved spacetime, dark radiation, neutrino oscillations, and non-zero neutrino masses [30].

1.7.5. Dark Radiation and the Need for Sterile Neutrinos

A recent analysis of cosmological data and new physics point to strong evidence of non-trivial amounts of non-standard energy density or Dark Radiation. This Dark radiation would likely be caused by decay of dark matter [32]. One possible cause of dark radiation are sterile neutrinos [26].

1.7.6. Extra Neutrino Species and the BSM Physics Model

The presence of Sterile neutrinos points to the need for extra neutrino species but it is not possible to account them in the ΛCDM Model of Physics [25]. Recent research, including the MiniBooNE experiment, points to the possibility of the existence of sterile neutrinos [33,34]. But their presence will be a deviation from the ΛCDM Model of Physics which constrains the number of neutrino species to 3 and the number of relativistic degrees of freedom (N_eff) to 3.046 [26,27]. As such, these point to a need to go to the Physics Beyond the Standard Model by requiring extensions to the ΛCDM Model of Physics [25,27,29,31]. The extra neutrino species will lead to an increase in Neff [26,35].

1.7.7. Impact of Sterile Neutrinos

The energy density of the sterile neutrinos would increase the cosmic expansion rate of the universe. This would have an impact on the BBN primordial light element abundance causing the abundance of D/H and Yp to increase [36].

The presence of sterile neutrinos would also point to a decrease in temperature since a lower temperature would cause an increase in the mixing angle leading to a higher production rate of sterile neutrinos. Thus, the model with sterile neutrinos would need a lower temperature compared to the standard model [36,37].

1.7.8. MACHOs

Massive Astrophysical Compact Halo Objects (MACHOs) are CDM candidates that include black holes, neutron stars, and dwarfs (red, white, and brown). Their bodies are composed of baryonic matter. Since they do not emit or radiate light, they are hard to detect, and their presence can only be inferred by gravitational lensing. Their presence is controversial but even if they exist, they can only account for 20% of the dark matter [12]. The remaining dark matter is not baryonic and so must be accounted for by WIMPs. Hence, WIMPs are the only viable candidates for dark matter and are discussed in the next section [5,38].

1.7.9. WIMPs

Weakly Interacting Massive Particles (or WIMPs) are the major CDM candidates. These are elementary particles and believed to be non-baryonic dark matter and interact very weakly with particles from the standard model. As such, they are difficult to detect. They are non-relativistic, heavy, and slow-moving. This allows them to clump together densely allowing galaxy formation [38,40]. Majorana Fermions, Dirac Fermions, Real Scalar Bosons, and Complex Scalar Bosons [5]. Details can be noted from Table 1 given below:

Table 1. Available WIMPs in AlterBBN model

The term self-conjugate means the particles are their own antiparticles. The chemical potential of WIMPs is the change in energy and entropy when a particle is added to the system.

1.8. Reheating

Post inflation of the universe, the delay of the inflation field transfers energy to the created particles which arrive at a thermal equilibrium at some temperature T called the reheating temperature [41]. The reheating process injects a lot of dark energy and entropy throughout the BBN epoch. This process increases the entropy density and dilutes the matter-antimatter symmetry [42].

1.9. BBN Thermonuclear Reaction Rates

Out of more than 88 BBN thermonuclear reactions, 12 are the most important as they impact the light element abundance of 4He, D, 3He, 7Li [43]. The 12 reactions are n-decay, p(n, γ)d, d(p, γ)3He, d(d,n)3He, d(d,p)t, 3He(n,p)t, t(d,n)4He, 3He(d,p)4He, 3He(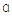, γ)7Be, t(, γ)7Li, 7Be(n,p)7Li, and 7Li(p, )4He. 7Li is fairly sensitive to rates of 8 major reactions and has low sensitivity to 4 reactions [3].

The nuclear reaction rates are essential inputs for modeling BBN and stellar evolution. Compared to BBN, different codes are involved in studying the stellar production of elements. The values of BBN thermonuclear reaction rate are entered as thermal rates [44].

7Li is more sensitive than the other light elements to several fundamental constants, baryon-photon ratio, and nuclear physics inputs [45]. Variation of the gravitational and cosmological constant during BBN can explain the low abundance of lithium compared to the standard model prediction [45]. This may help us understand the lithium discrepancy.

2. Idea

2.1. Problem

For decades, the cosmological lithium problem has stumped astrophysicists. Solving it is essential to understand the formation of our universe correctly, comprehend the physics of the BBN and better understand the impacts of Standard versus BSM Physics Models.

2.2. Possible Solution

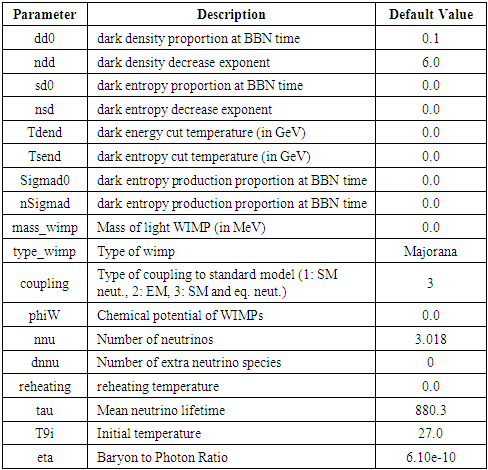
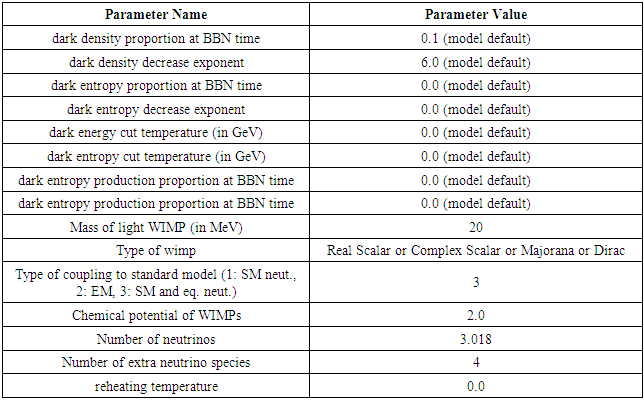
Since the problem cannot be solved just using the physics of the Standard Model, approaches from BSM physics need to be tried out. In this simulation, we try to vary a mix of standard and BSM physics approaches including variations in neutrino numbers, extra neutrino species, temperature, dark density, dark entropy, reheating, WIMP mass, and WIMP chemical potential.

We use a BBN simulation software called AlterBBN publicly available at https://alterbbn.hepforge.org/ [4,5,46]. AlterBBN is a C program which computes the abundances of the elements predicted by BBN. Different cosmological scenarios are implemented in AlterBBN, which can alter the BBN predictions. It includes the parameters shown in Table 2 [5]:

Table 2. Parameters available in AlterBBN model

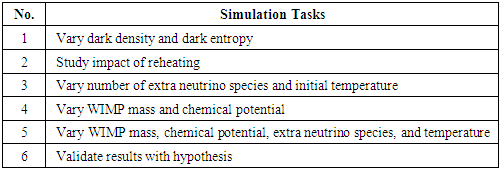
3. Research Goals

3.1. Prior Research Results

Reaction rate sensitivity analysis for BBN 7Li abundance was carried out in an earlier research project [47]. Simulations were performed using the BBN simulation software publicly available at http://www.bigbangonline.org/. Fractional change was observed in 2 of 11 major reactions, and greater impact (< factor 100) was observed in 9 of 11 major reactions.

3.2. Research Tasks

The research tasks are shown in Table 3.

Table 3. Research Tasks

4. Observations

4.1. Impact of Dark Energy and Dark Entropy

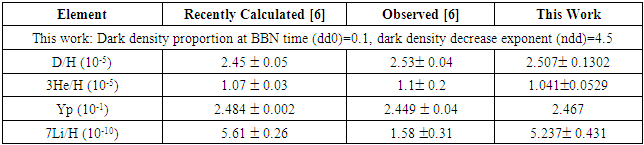
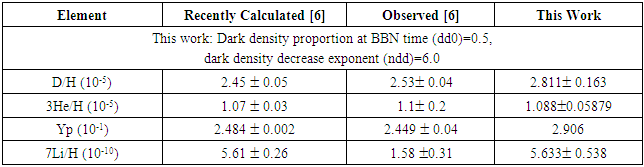
Increase of dark density proportion at BBN time (dd0) caused a minor increase in Yp (the primordial mass fraction of 4He) and a marginal increase in primordial abundance of D and 7Li.

An increase in dark density decrease exponent (ndd) led to a significant rise in the primordial abundance of Yp and D, both of which more than doubled with an increase of ndd from 4.5 to 7.0. It also led to a marginal increase in the abundance of 3He and had an insignificant impact on the primordial abundance of 7Li. Increase in dark entropy proportion at BBN time (sd0) had an insignificant effect on primordial abundance.

An increase in dark density proportion at BBN time (dd0) from 0.10 to 0.90 with dark density decrease exponent (ndd) = 7.0 led to a significant increase in abundance of Yp, a 2 to 3 times increase in primordial abundance of D, a 2 times increase in primordial abundance of 3He, and a marginal increase in 7Li. See Table 4 for details.

4.2. Impact of Reheating

Reheating resulted in a minor increase in Yp and primordial abundance of D and a marginal rise in the primordial abundance of 3He and 7Li. See Table 5 for details.

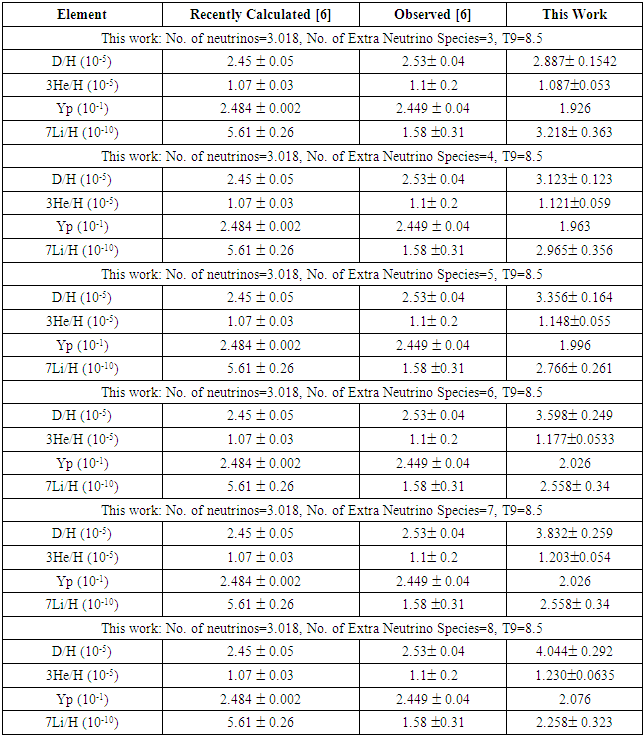
4.3. Impact of Neutrino Numbers and Extra Neutrino Species

4.3.1. Variation of Neutrino Numbers

Increase in the number of neutrinos resulted in a minor increase in the primordial abundance of Yp, D, and 3He, and a decrease in 7Li abundance.

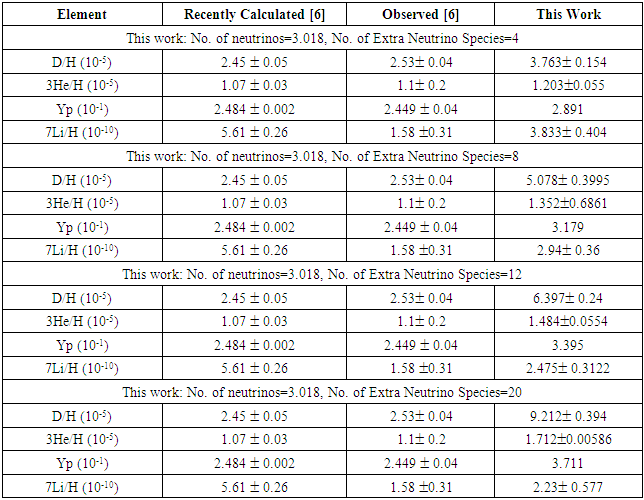
4.3.2. Variation of Extra Neutrino Species at the Model Default Initial Temperature

At the default model temperature, T9=27.0, an increase in extra neutrino species resulted in a significant increase in the abundance of Yp and D, a minor increase in the abundance of 3He, and a significant decrease in the abundance of 7Li.

From Table 6, it can be noted that at 4 extra neutrino species, the abundance of Yp was 3.763 ± 0.154 * 10^-5 (~1.49 times the observed value), abundance of 3He was 1.203 ± 0.055 * 10^-5 (~1.09 times the observed value), Yp abundance was 0.2891 (~1.18 times the observed value), and 7Li abundance was 3.833 ± 0.404 * 10^-10 (~2.43 times the observed value).

As the number of neutrinos increased, the abundance of D increased significantly and the gap between its value and the observed value widened. The abundance of Yp increased at a moderate pace and the gap between its value and the observed value also widened. The abundance of 3He increased slowly and the gap between its value and the observed value widened slowly. The abundance of 7Li decreased significantly and its value approached the observed value.

As such, it was found that Yp (4He) is moderately sensitive, D and 7Li are very sensitive, and 3He is less sensitive to variations in the number of extra neutrino species.

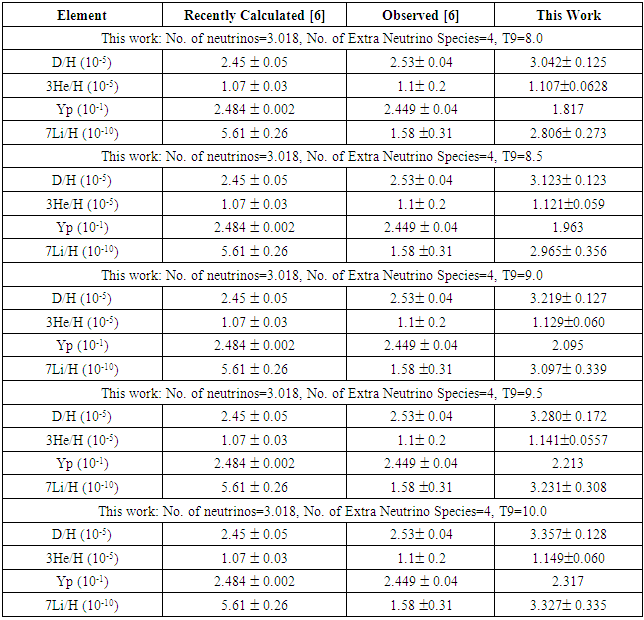
4.4. Variation of Initial Temperature and Extra Neutrino Species

As mentioned in Section 1.7.7, the presence of Extra Neutrino Species would have an impact of lowering the initial temperature.

Table 7 shows that simulations were carried out for T9 = 8.0, 8.5, 8.5, 9.0, and 10.0 with 4 extra neutrino species (see Figure 2). Primordial light element abundance values were much closer to the observed values compared at T9=27.0. At T9=8.5, D abundance was 3.123 ± 0.123*10^-5, which is 1.23 times the observed value. 3He abundance was 1.121 ± 0.059 * 10^-5, which is 1.02 times the observed value. Yp abundance was 0.1963 which is 0.80 times the observed value. 7Li abundance was 2.965 ± 0.356 * 10^-10, which is ~1.88 times the observed value.

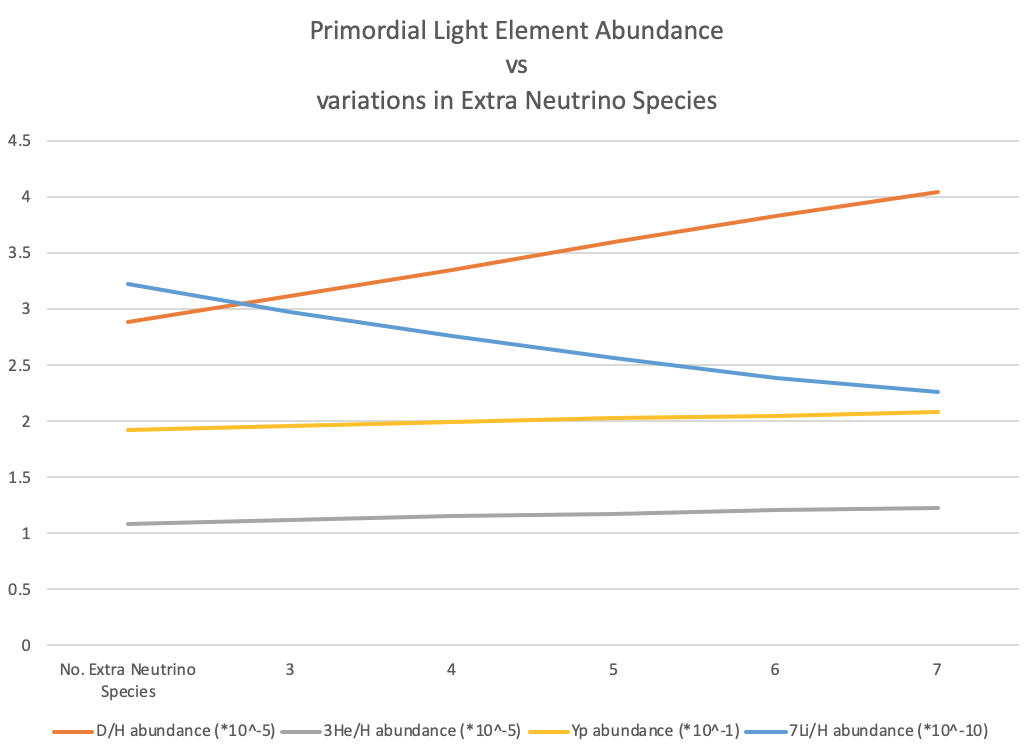Figure 2. Light element abundance with variation of initial temperature

Also, from Table 7, it can be noted that as the initial temperature increased, the primordial light element abundance of D, 3He, Yp, and 7Li also increased. Table 8 and Figure 3 shows the impact of variation of extra neutrino species at T9=8.50. As the number of extra neutrino species increased, the abundance of D, 3He, and Yp increased.

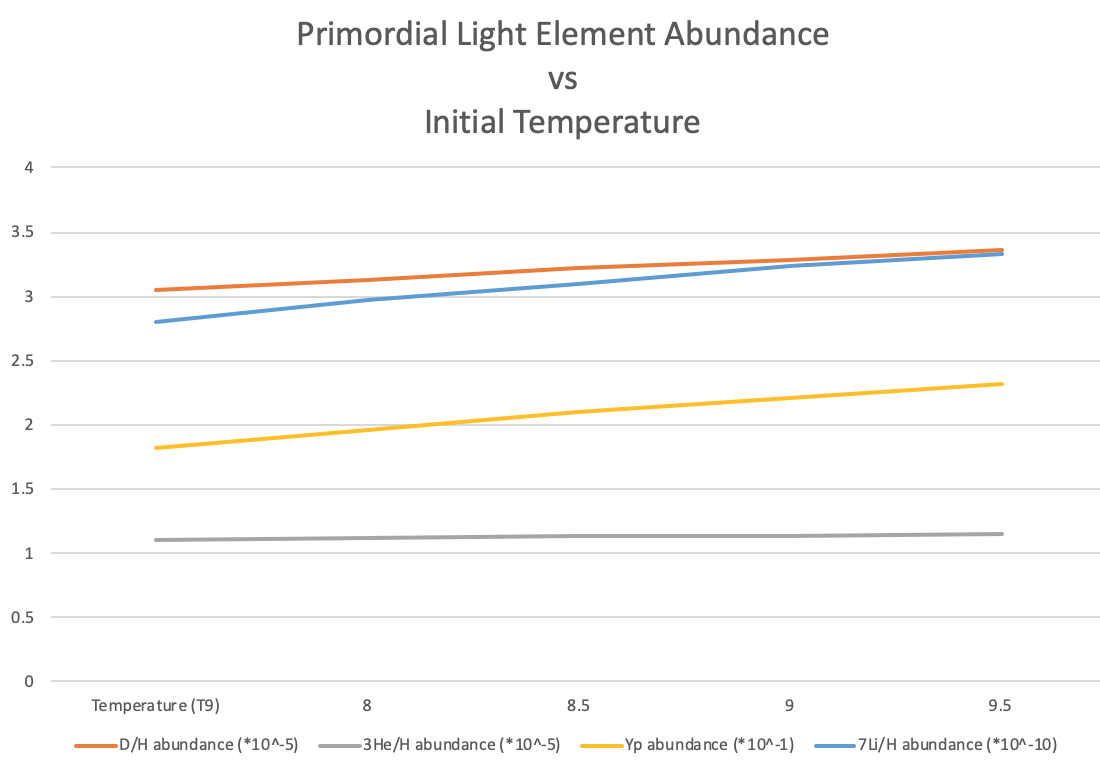Figure 3. Light element abundance with variation of extra neutrino species

But the abundance of 7Li decreased. Hence, although the abundance of D, 3He, and Yp is directly proportional to the number of extra neutrino species, the abundance of 7Li is inversely proportional to it.

4.5. Impact of WIMPs

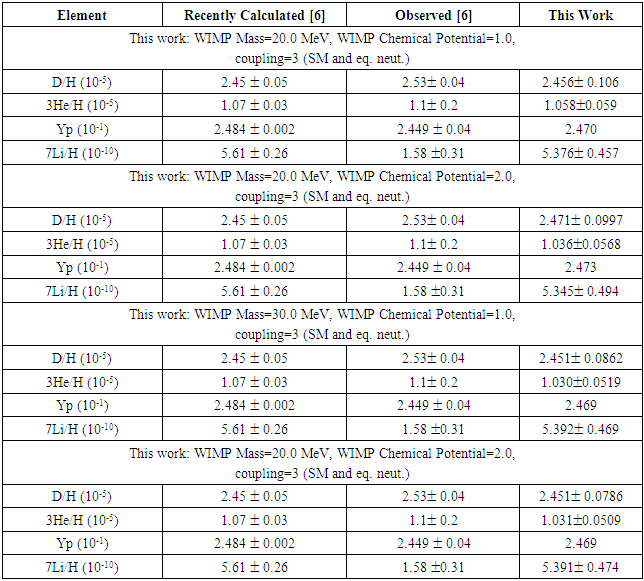
4.5.1. WIMP Mass and Chemical Potential

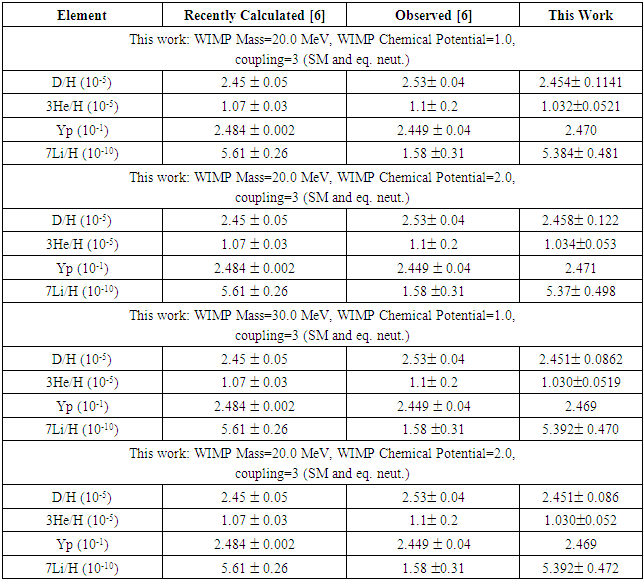
The combined impact of increasing mass and chemical potential of WIMPs had a minor impact on the light element abundance.

As can be noted from Table 9, with a mass of 20 MeV for Majorana Fermions, as the chemical potential increased from 1.0 to 2.0, there was a minor increase in the abundance of D and Yp, and a minor decrease in the abundance of 3He and 7Li. It can also be noted that for chemical potential = 2.0, as the mass increased from 20 MeV to 30 MeV, there was a minor decrease in abundance of D, 3He, and Yp, and a minor increase in the abundance of 7Li. At a mass of 20 MeV and 2.0 chemical potential, the 7Li abundance was 5.345 ± 0.494 * 10^-10 which is 3.38 times the observed value of 1.58 ± 0.31 * 10^-10.

A very similar trend can be noted for Real Scalar Bosons in Table 10.

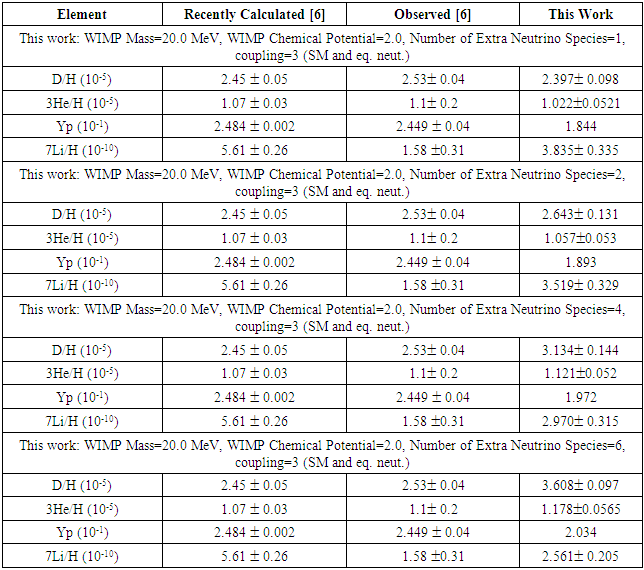
4.5.2. WIMPs, Temperature, and Extra Neutrino Species

From Tables 11, it can be noted that the combined impact of WIMPs and extra neutrino species had a significant impact on the abundance of D, Yp, and 7Li, and a minor impact on 3He abundance.

In the case of Majorana Fermions, at a WIMP Mass of 20 Mev, 2.0 chemical potential, 1 extra neutrino species, and T9=8.50, Yp abundance was 0.1844 and 7Li abundance was 3.835 ± 0.335 * 10^-10. With an increase in extra neutrino species from 1 to 4, the abundance of D increased to 3.134 ± 0.144 * 10-5 (1.279 times the observed value), Yp abundance was 0.1972 (~0.81 times the observed value), and 7Li abundance dropped to 2.970 ± 0.315  10^-10 (~1.88 times the observed value). Same values and trends were observed in the case of Real Scalar Bosons.

5. Table of Values

Table 4. Primordial Light Element Abundance - Impact of Dark Density

Table 5. Primordial Light Element Abundance - Impact of Reheating

Table 6. Primordial Light Element Abundance with Variation of Number of Neutrino Species at default temperature T9 = 27.0

Table 7. Primordial Light Element Abundance with Variation of Temperature and 4 Extra Neutrino Species

Table 8. Primordial Light Element Abundance with Variation of Extra Neutrino Species and T9=9.50

Table 9. Primordial Light Element Abundance by varying mass and chemical potential of Majorana WIMPs

Table 10. Primordial Light Element Abundance by varying mass and chemical potential of Real Scalar Bosons

Table 11. Primordial Light Element Abundance by varying mass, temperature, and number of extra neutrino species of Majorana Fermions

Table 12. BSM parameter combination discussed in this work

6. Conclusions

1. Increases in dark density proportion at BBN time (dd0) and dark density decrease exponent (ndd) led to a minor impact on 7Li.

2. Reheating produced minor changes in the abundance of 7Li.

3. Increase in neutrino numbers led to a minor decrease in the abundance of 7Li.

4. On the other hand, an increase in extra neutrino species coupled with a reduction in initial temperature resulted in light element abundance values that were much closer to the observed values compared to the model default temperature value of T9=27.0.

At T9=8.5, the 7Li abundance was 2.965 ± 0.356 * 10^-10 which is (~1.88 times the observed value of 1.58 ± 0.31*10^-10, Yp abundance was 0.80 times the observed value, 3He abundance was 1.02 times the observed value, and D abundance was 1.23 times the observed value.

5. Variation in WIMP mass and chemical potential had a minor impact on the primordial light element abundance.

6. At a lower initial temperature, an increase in extra neutrino species in the presence of WIMPs produced a significant decrease in the primordial abundance of 7Li, a significant increase in abundance of D, a moderate increase in abundance of Yp, and a minor increase in 3He abundance.

At T9=8.5, 4 extra neutrino species, 20 MeV WIMP mass, and 2.0 chemical potential, the abundance of D was 1.279 times the observed value, Yp abundance was 0.81 times the observed value, and 7Li abundance was

7. As such, using the BSM model, we were able to determine a possible solution of the Cosmological Lithium Problem, viz., at a lower initial temperature, an increase of extra neutrino species or the combined impact of WIMPs and extra neutrino species results in a significant decrease in 7Li abundance and brings its value within ~1.88 times the observed value of 1.58 ± 0.31 * 10^-10.

Abundance of other light elements including D, He, and Yp are also within reasonable limits of the observed values. Some other factors may need to be taken into account which will bring their abundance closer to the observed values.

8. As part of the BSM model, the following combination of parameters will reproduce the measured abundances of 7Li, D, 3He, and Yp discussed above in this work.

But this solution needs further investigation from a nuclear astrophysics perspective.

ACKNOWLEDGEMENTS

This work was done using the AlterBBN simulation software which is publicly available at https://alterbbn.hepforge.org/ [4,5,46].