1. Introduction

H₂ is found almost everywhere in the universe [1]. The bonds between hydrogen atoms form on the very cold surface of interstellar dust grains [2]. When a broad sample of more recent data from Cambridge is included in the average distance of the H₂ covalent bond measurement, it falls within 1% of Newton’s Constant. The source of Newton’s Constant may be hidden in an infinitely large H₂ gravitation field.

Gravity was a force between point masses according to Newton. Pierre-Simon Laplace attempted to model gravity as a radiation field or fluid [3]. The college curriculum of the 19th century taught gravity in terms of a field model, rather than a point attraction. In a field model, rather than two particles attracting each other, the particles distort spacetime via their mass, and this distortion is what is perceived and measured as a "force". In such a model one states that matter moves in certain ways in response to the curvature of spacetime, [4] and that there is either no gravitational force, [5] or that gravity is a fictitious force [6].

I seek to find a gravitation field which will readily explain Newton’s constant, satisfy Newtonian and General Relativity, and fit within the framework of my own Electro Relativity model. By modeling Newton’s constant as a wavelength, a search was made for similar wavelengths in the universe. Newton’s constant is a very short wavelength and few objects of significance are this small. The search has led to the Hydrogen Isotope H₂ as most closely resembling the wavelength of Newton’s constant when modeled as a micro antenna with a wavelength of 6.674 x 10^-11 meters. An explanation for a universal gravitation field is sought through Hydrogen Isotope H_2, the most common molecule in the cosmos.

2. Newton’s Constant

In the Principia, Newton considered the possibility of measuring gravity’s strength by measuring the deflection of a pendulum in the vicinity of a large hill but thought that the impact would be too small to be measurable. Nevertheless, he assessed the order of magnitude of the constant when he wrote that “the mean density of the Earth might be five or six times as great as the density of water”, which is comparable to the modern gravitational constant at 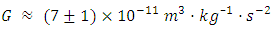[7]

The Schiehallion experiment, reported in 1778, was the first successful measurement of the mean density of the Earth, and suggested a density of 4.5 g/cm³ (4¹⁄₂ times the density of water), about 20% below the modern value. The outcome of this test produced a result equivalent to 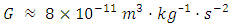[8].

Henry Cavendish performed the first direct measurement of gravitational attraction between two bodies in the laboratory in 1798. Using a torsion balance invented by the geologist Rev. John Michell (1753), he determined a value for G implicitly. Cavendish laboratory equipment used a horizontal torsion beam with lead balls whose inertia (in relation to the torsion constant) could be timed by the beam’s oscillation. Their very small attraction to other balls placed alongside the beam was detectable by measuring the slight deflection. Cavendish determined the average density of the Earth and Earth’s mass. His result, 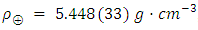, corresponds to value of 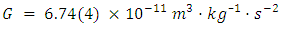. It is surprisingly accurate, about 1% above the modern value (comparable to the claimed standard uncertainty of 0.6%) [9].

3. Cosmic Abundance of H₂

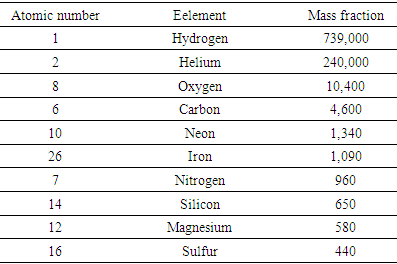
The abundance of chemical elements in the universe is dominated by the large amounts of hydrogen and helium which were produced in the Big Bang. The abundance of the lightest elements is well predicted by the standard cosmological model, since they were mostly produced within a few hundred seconds after the Big Bang, in a process known as Big Bang nucleosynthesis. Hydrogen and helium are estimated to make up roughly 74% and 24% of all baryonic matter in the universe respectively [10].

The remaining elements, making up only about 2% of the universe, were largely produced by supernovae and certain red giant stars. The elements from carbon to iron are common in the universe because of the ease of making them in supernova nucleosynthesis. Elements of higher atomic number than iron are rarer in the universe, because they increasingly absorb more energy in their production. Elements with even atomic numbers proliferate due favorable formative energy required.

The common elements in the Sun and planets is similar to that in the universe (Table 1).

The elements of Earth and the inner rocky planets of the Solar System have undergone an additional depletion of volatile hydrogen, helium, neon, nitrogen, and carbon gas. Silicates of aluminum are found in the crust, with more magnesium silicate in the mantle, while iron and nickel compose the core [11].

Table 1. Ten most common elements in the Milky Way Galaxy estimated spectroscopically

The cosmic abundance of hydrogen isotope H₂ was first reported in 1932 by D. H. Menzel, in a paper published in the Journal of the Pacific [12]. The role and abundance of H₂ was reasserted in 2002 by David William the President of the Royal Astronomical Society [13]. H₂ formation involves catalytic reactions on the surface of interstellar grains. The physics of the formation process has been investigated intensively for the last several decades. H₂ is the most widespread molecule in the Universe, and its importance is fundamental in the formation of all structures, from stars to galaxies.

4. Covalent Bond Length of H₂

The hydrogen atom is the most basic atom, and its molecule H₂ is also the simplest molecule. Atomic hydrogen gas is unstable, existing only at very high temperatures. Diatomic hydrogen molecules, H₂, are formed at ordinary temperatures and pressures.

A covalent bond is a chemical bond that involves the sharing of electron pairs between atoms. These electron pairs are termed shared pairs or bonding pairs, and the stable balance of attractive and repulsive forces between atoms, when they share electrons, is termed covalent bonding [14].

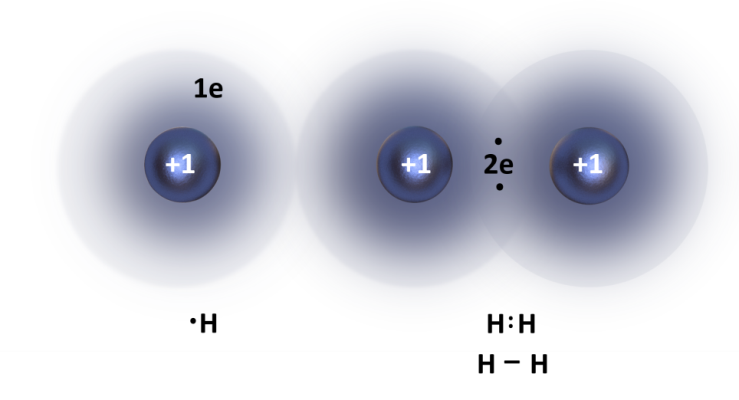Figure 1. A covalent bond forming H2 (right) where two hydrogen atoms share the two electrons

Gilbert N. Lewis, in 1916 first described the sharing of electron pairs between atoms [15]. He introduced electron dot notation or Lewis dot structure, in which valence electrons are represented as dots around the atomic symbols. Electron pairs located between atoms represent covalent bonds. In 1919 Irving Langmuir wrote an article in the Journal of the American Chemical Society titled “The Arrangement of Electrons in Atoms and Molecules”. Langmuir wrote that “we shall denote by the term covalence the number of pairs of electrons that a given atom shares with its neighbors” [16]. The theory of shared electron pairs provides a description of covalent bonding, but quantum mechanics was needed to understand the nature of these bonds and predict the structures and properties of simple molecules. Walter Heitler and Fritz London were the first to provide a complete quantum mechanical explanation of molecular hydrogen in 1927 [17].

The Bohr radius, was an important physical constant based on the lowest-energy electron orbit predicted by Bohr model of the atom (1913) [18] [19]. It is only applicable to atoms and ions with a single electron, such as hydrogen. With the invention of X-ray crystallography in 1920, it was suggested that all atoms of the same element have the same radii [20]. Later it was determined the approximation of an atom as a sphere does not necessarily hold true when comparing the same atom in different crystal structures [21].

Today covalent radius is the nominal radius of the atoms of an element when covalently bound to other atoms, as deduced from the separation between the atomic nuclei in molecules. The distance between two atoms that are bound to each other in a molecule (the length of that covalent bond) equals the sum of their covalent radii. The covalent radius, r_cov, is a measure of the size of an atom that forms part of one covalent bond. It is usually measured either in picometres (pm) or angstroms (Å), with 1 Å = 100 pm.

The sum of the two equal the covalent bond length between two atoms, .

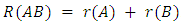Different radii for single, double or triple bond relationships are not exact because the size of an atom is not constant. Often the polar covalent bonds are shorter than would be expected on the basis of the sum of covalent radii. Tables listing covalent radii are either average or idealized values, which nevertheless show a certain transferability between different situations, which makes them useful, but not exact.

The bond lengths R(AB) are typically measured by X-ray diffraction. Rotational spectroscopy has also been used to give accurate values of bond lengths. For homonuclear A–A bonds, Pauling took the covalent radius to be half the single-bond length in the element, e.g. 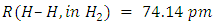so 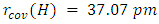. [22]

It is customary to obtain an average value from a variety of covalent compounds. The differences are usually quite small. Sanderson has published a recent set of non-polar covalent radii for the main-group elements [23], but the availability of large collections of bond lengths, comes from the Cambridge Crystallographic Database [24] [25]. As of 2018, the Cambridge Structural Database which contains 426,000 crystal structures and more than 228,000 experimental bond length reports the actual radius of hydrogen to be 31.5 pm. [26] This results in a bond length of 63 pm. In a separate test of 400 samples the stated radius is reported as 32 pm, which results in a bond length of 64 pm [27].

In 1967, JC Slater reported Hydrogen radius to be 25 pm (accuracy of about 5 pm) [28] In the same year Enrico Clementi stated that the radius of Hydrogen is 53 pm [29].

If we discount the 1967 result which are dated, we have three fairly recent numbers from which to average.

Hydrogen Average Radius

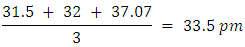Calculate Average Bond Length of H₂

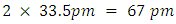Or,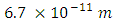

My result indicates that the average bond length of H₂ is nearly that of Newton’s Constant (6.674 x 10^-11), accurate to within 1%.

5. Covalent Force and Energy of H₂

A molecular vibration occurs when the molecule absorbs a quantum of energy, E, corresponding to the vibration’s frequency, ν, according to the relation 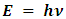(where h is Planck's constant). A fundamental vibration is excited when one such quantum of energy is absorbed by the molecule in its ground state. When two quanta are absorbed the first overtone is excited, and so on to higher overtones. According to Waech and Bernstein (J. Chem Phys. 46, 4905 (1967) - as cited in Koonin’s Computational Physics (1986)) there are 16 known, experimentally-determined, vibrational energies for H2 [30]. The first few are:

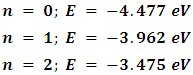Covalent bond energies and lengths depend on many factors: electron affinity, sizes of atoms involved in the bond, the overall structure of the molecule and differences in their electronegativity. In general, the shorter the bond length, the higher the bond energy. The energy trend for H₂ is shown on the graph below.

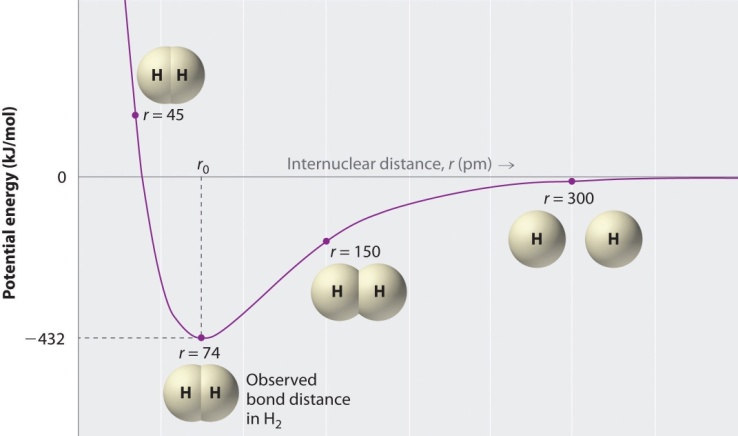Figure 2. H2 Potential Energy

Using Newtonian mechanics, it is possible to calculate the correct vibration frequencies. Each vibration can be treated as though it corresponds to a spring. The spring obeys Hooke’s law and the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, k.

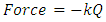
6. Frequency of H₂ Bond Length

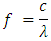Where,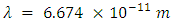

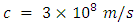I calculate the following: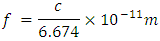

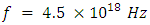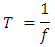
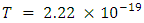and,

and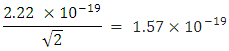

The period of H₂ covalent bond distance divided by 1.414 is near equivalent to the charge of an electron, which equals 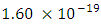. The RMS represents the hypotenuse of a triangle with two electrons at right angles or 45 degree (.707) out of phase. The H₂ molecule shares two electrons. It is theorized that the electron of H₂ can be used as a doorway to quantum theory.

7. Hydrogen and Fibonacci Sequence

Fibonacci numbers are named after Italian mathematician Leonardo of Pisa, who in 1292 published the massive tome "Liber Abaci," a mathematics book on calculations [31]. In a Fibonacci sequence, every number after the first two numbers is the sum of the two preceding ones. Here is a list of Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, … The formula can be expressed as,

un=term number(n)

un−1=former term(n−1)

un−2=term before(n−2)

un=un−1+un−2

The Fibonacci sequence occurs in the smallest, to the largest objects in nature. Fibonacci sequences appear in nature, such as, arrangement of leaves on a stem, the fruitlets of a pineapple, the flowering of artichoke, branching in trees, an uncurling fern and the arrangement of a pine cone, and the family tree of honeybees. Kepler pointed out the presence of the Fibonacci sequence in flowers. In 1754, Charles Bonnet discovered that the spiral phyllotaxis of plants were frequently expressed in Fibonacci [32]. Spirals are the most common galaxy shape. Galaxies group together in superclusters and superclusters group together in walls. These walls or filaments of numerous superclusters, gravitationally-bound and separated by large areas of void, are the largest known structures in the universe. The spiral shapes of the galaxies are thought to follow a Fibonacci pattern.

When I apply the Fibonacci Sequence to Hydrogen bonds, we can readily see that H₁ + H₁ = H₂, and H₂ + H₁ = H₃. H₃ is known as Triatomic Hydrogen an unstable three atom molecule that breaks up in in one millionth of a second. Its fleeting lifetime makes it rare, but it is quite commonly formed and destroyed in the universe thanks to the commonness of the trihydrogen cation. The infrared spectrum of H₃ due to vibration and rotation is very similar to that of the ion, H₃⁺. In the early universe this ability to emit infrared light allowed the primordial hydrogen and helium gas to cool down so as to form stars.

Pentatonic Hydrogen, H₅ is even more unstable with an even shorter life when left to stand on its own. However, H₅ will have five atoms readily available for substitution and thus readily combine with the third most common element in space oxygen to form H₅0₂. Similarly, H₈ combines to form H₈0₃. H₅O₂ + may be fully hydrated, also with an equally spaced central hydrogen bond, with one water molecule hydrogen bonded to the four free hydrogen atoms as H₁₃O₆ +. H₁₃ is known to form H₁₃O₁₀ or H₁₃C₉, together this becomes H₁₃O₁₀C₉. The conducting plasma that stretches throughout the universe is a soup mix of hydrogen Fibonacci molecules combined with trace elements and other gases thrown out from nuclear stars.

Such combination of atoms to form complex molecules that make up space can be conjured up for a wide variety of materials that are known to exist in the universe. One which is of particular interest is C₂₅₄H₃₇₇O₇₆S₆ which represents the sequence of amino acids in a polypeptide chain that constitutes the primary structure of a protein molecule [33]. H₃₇₇ is an interesting Fibonacci number because the impedance of free space is known to be 377 ohms. This characteristic impedance is a function of the ratio of the magnetic and electric field thought to be produced by the Sun and planets. Historically we have thought that this was an intrinsic impedance and not a physical impedance. However, the actual density of hydrogen as it exists in interstellar space is on the average of about 1 atom per cubic centimeter. In the extremes, as low as 0.1 atom per cubic centimeter has been found in the space between the spiral arms and as high as 1000 atoms per cubic centimeter are known to exist near the galactic core. The interstellar medium also contains cosmic dust which are much larger than hydrogen. When combined the resistance value of space becomes a network of parallel resistance paths all of which may combine to 377 ohms. The Fibonacci Sequence is known to be a mathematical model for spiral formation and the highly efficient transfer of information. H₃₇₇ and characteristic impedance might be instrumental to finding other elemental forms of life in the universe.

8. Coulomb Law for Hydrogen Atom

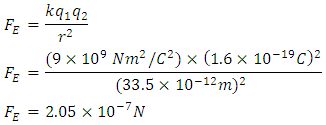I now calculate Sun to Earth gravity using a string of H₂ molecules

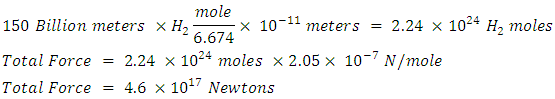The electrostatic force of H₂ is not adequate to account for Sun to Earth gravity (3.52e22). Adding the Vibratory Force of k =576 N/m and the distance of Sun to Earth will not make up the difference. H₂ force is a weak contributor to planetary gravity but not insignificant.

9. Conclusions

The H₂ molecule is one of the smallest and yet most prevalent substances in the universe. The average length of the H₂ molecule is thought to be nearly that of Newton’s constant when expressed in meters. It is theorized that H₂ acts as a micro antenna radiating and receiving electrical energy. It is thought that Newton’s Constant is thus a universal constant derived from H₂ molecules, which permeates the entire known universe.

Newton’s Constant when viewed as a wavelength can be expressed as a universal frequency of 14.98 GHz that will radiate to all parts of the universe. Newton’s Constant acts as a universal proportionator, or scaling factor. Since Newton’s constant is frequency that was interpreted by Newton as a period, we can surmise that G represents proportion in a standard PD or PID loop controller. The universe is a tuned electrical system with a set gain, or G.

The universe volume is filled with essentially an infinite number of molecules of H₂. The average covalent distance is the most constant of constants in the universe. This is the smallest known bond distance in the universe averaged zillions and zillions of times. Helium, the next most common element, cannot readily combine, so H₂ has no competing frequency. This frequency falls between X-rays and Gamma rays. The Sun’s and other stars’ massive electromagnetic fields would serve to excite the molecule anywhere it can be reached. Due to shear volume, the average length of the H₂ bond should be considered by the Standards Institute as a standard length of measurement from which other constants are derived.

It is also possible that there is a volume of H₂ molecules swirling in the Earth’s atmosphere parallel to the Earth’s electromagnetic field. Electromagnetism and H₂ gravitational field may found to be consubstantial or parallel in terms of contribution to gravity with this theory. H₂ electrostatic and vibratory forces are weak attractive forces, but not significant to solely account for planetary gravity.

Hydrogen is the most basic and natural of all elements and has been shown to have a Fibonacci sequence. This numerical relationship may help answer the most basic regarding the nature of space. H₃₇₇ may be the mechanism by which life is transmitted throughout the universe and give insight into the actual impedance of free space.

ACKNOWLEDGEMENTS

The author wishes to acknowledge Sir Isaac Newton the English physicist and mathematician, who led the scientific revolution of the 17th century. In orbital mechanics, his three laws of motion, the basic principles of modern physics, resulted in the formulation of the law of universal gravitation. Newton was original discoverer of the infinitesimal calculus. Newton’s Philosophiae Naturalis Principia Mathematica published in 1687 was one of the most important single works in the history of modern science.