Nelson Blackie
Department of Chemistry, Cuttington University, Liberia
Correspondence to: Nelson Blackie, Department of Chemistry, Cuttington University, Liberia.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This study shows that Einstein’s Special Theory of Relativity is not a complete theory of reality. The theory used non-uniform experiments; thus, its final conclusions are inconsistent with each other. The most obvious of these is the prediction of a positive correlation between mass and speed (mass increment). This allows the possibility for both the kinetic and potential energies of a system in motion to increase simultaneously (since the system gains mass and hence potential energy). On this grand, the study proposed a new theory (or provides corrections in Einstein’s theory). Then, these corrections were used to show that (1): Entangle particles exist in nature as a result of relative motion; (2): matter and wave are dual entity of each other, and (3): because of the law of conservation, space dilation is a valid consequence of relative motion just as time dilation is a valid consequence of relativity.
Keywords:
Space dilation, Time Dilation, Relativistic Entanglement, Relativistic Duality, Kinetic Momentum, Potential Momentum
Cite this paper: Nelson Blackie, Can Einstein’s Special Theory of Relativity be Considered an Accurate Description of Reality?, International Journal of Theoretical and Mathematical Physics, Vol. 9 No. 3, 2019, pp. 67-80. doi: 10.5923/j.ijtmp.20190903.02.
1. Introduction
In attempting to judge the completeness of a physical theory, the following questions are necessary to be answered: “(1) are the predictions of the theory consistent with each other and with the objective reality?” and “(2) is the theory compactable with other existing theory(s)?”. Statement (1) is sufficient enough to prove that a theory is complete in its unique way (that is, such theory is compatible with itself or has a uniform conclusion). However, if (1) holds and (2) does not hold, it can be proven by theory or by experiment or measurement that at most one (but not both) of these theories is right. Although this may not be regarded as a comprehensive prove to decide the fate of a theory, but I regard it as a sufficient condition for completeness and this is in agreement with classical and quantum mechanics as well as with the Special and General Theory of Relativity.In examining Einstein’s relativistic mechanics, we see that the speed of a particle is directly related to its mass; however, this prediction contradicts our traditional thinking of matter and speed. Quantum and classical mechanics tell us that given particular energy content, systems at high speed will have less mass then those at rest. Thus, both theories (classical mechanics and quantum mechanics) are incompatible with special relativity. Then, either quantum and classical mechanics or special relativity can be considered an incomplete theory.By this observation, the objective of this study therefore is to prove that Einstein’s special theory of relativity (not quantum mechanics or classical mechanics) cannot be considered a complete theory of reality or at least the theory must be considered incomplete when applied to matter. To illustrate this idea, two of the most fundamental predictions of special relativity will be used to show that Einstein’s Theory leads to a non uniform conclusion and hence such theory, by statement (1) of our condition of completeness, is considered incomplete.The major concepts of this theory are frames of references and the description of some physical event by these frames in relative motion. Base on the descriptions of some physical event by these frames, an event can possibly be described in two different spacetime coordinate systems that are more or less symmetric (except the prediction of the so-called “twin paradox”). For the purpose of this study, the two obvious and simplest predictions for focus are: the predictions of length contraction and mass increment.Einstein’s theory of relativity describes the behaviors of particle of mass m and length L in spacetime with respect to two reference frames in relative motion. According to this theory, if an object of proper length 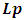 moves with velocity
moves with velocity 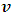 parallel to its length, the object’s length relative to the stationary observer will appear to reduce in the moving frame by the equation
parallel to its length, the object’s length relative to the stationary observer will appear to reduce in the moving frame by the equation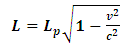 | (1) |
where 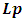 is the recorded length in the rest frame, L is the length in the moving frame and
is the recorded length in the rest frame, L is the length in the moving frame and 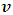 is the speed of the object.According to Eq. (1), if the speed of the object increases, its length decreases; thus, there is an inverse relationship between the length and speed of the object. This decrease in length is limited by the velocity of light
is the speed of the object.According to Eq. (1), if the speed of the object increases, its length decreases; thus, there is an inverse relationship between the length and speed of the object. This decrease in length is limited by the velocity of light 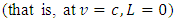 . Therefore, if the speed of the particle reaches that of light, its length in the moving frame becomes zero with respect to the stationary observer.On the other hand, to a stationary frame of reference, if an object of mass
. Therefore, if the speed of the particle reaches that of light, its length in the moving frame becomes zero with respect to the stationary observer.On the other hand, to a stationary frame of reference, if an object of mass 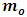 moves with speed
moves with speed 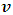 , the mass of the object increases with increased speed by the equation
, the mass of the object increases with increased speed by the equation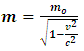 | (2) |
Where we consider 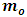 to be the mass of the object at rest and m is the mass of the same object at a speed
to be the mass of the object at rest and m is the mass of the same object at a speed 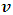 , the speed of the particle. By this equation, as the object moves through space with a speed near that of light, its mass increases (at the speed of light, the system has an infinite mass and energy). Equations (1) and (2) can best be understood from the works of (Tiple P. A and Llewellyn, 2008 [1], Resnick. R, 1968 [2], Bohm D, 1965 [3], Katz. R, 2008 [4], Cutnell J. D and Johnson K. W, 2009 [5], Serway R. A and Beichner, 2000 [6], Miller Jr. F, 1999 [7], Einstein A (1905) [8,9] Hamdan and Hariri, 2007 [10] and Peliti L, 2016 [11] and Sears, Zemansky and Young, 1985 [12].It shall now be proven; however, that Equations (1) and (2) together lead to an inconsistent conclusion. Thus, both equations cannot be accurate simultaneously when applied to matter as concluded by Einstein’s Relativity (the conclusion of the theory is thus non-uniform).
, the speed of the particle. By this equation, as the object moves through space with a speed near that of light, its mass increases (at the speed of light, the system has an infinite mass and energy). Equations (1) and (2) can best be understood from the works of (Tiple P. A and Llewellyn, 2008 [1], Resnick. R, 1968 [2], Bohm D, 1965 [3], Katz. R, 2008 [4], Cutnell J. D and Johnson K. W, 2009 [5], Serway R. A and Beichner, 2000 [6], Miller Jr. F, 1999 [7], Einstein A (1905) [8,9] Hamdan and Hariri, 2007 [10] and Peliti L, 2016 [11] and Sears, Zemansky and Young, 1985 [12].It shall now be proven; however, that Equations (1) and (2) together lead to an inconsistent conclusion. Thus, both equations cannot be accurate simultaneously when applied to matter as concluded by Einstein’s Relativity (the conclusion of the theory is thus non-uniform).
2. Method and Date
For this purpose, let us perform an experiment that must be viewed by two observers, one assumed to be at rest and the other in motion with a speed 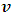 . Suppose we consider an ordinary rectangular metal rod of mass m and length L, then, by the help of Einstein’s relativistic mechanics, we can calculate the length and mass of such rod with respect to a stationary observer by equations (1) and (2) and hence its mass-density. Then if both equations are correct as it is expected, they must lead to a conclusion consistent both with the objective reality and the theory itself.Einstein’s Relativity allows us to measure the density of the object at any speed, since we are able to determine the mass and volume of the object even if the object is accelerating. Thus, for our experiment, suppose we seek to find the mass-density (or the relativistic mass-density) of the metal rod moving with a velocity
. Suppose we consider an ordinary rectangular metal rod of mass m and length L, then, by the help of Einstein’s relativistic mechanics, we can calculate the length and mass of such rod with respect to a stationary observer by equations (1) and (2) and hence its mass-density. Then if both equations are correct as it is expected, they must lead to a conclusion consistent both with the objective reality and the theory itself.Einstein’s Relativity allows us to measure the density of the object at any speed, since we are able to determine the mass and volume of the object even if the object is accelerating. Thus, for our experiment, suppose we seek to find the mass-density (or the relativistic mass-density) of the metal rod moving with a velocity 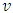 with respect to the stationary observer; then, we can write
with respect to the stationary observer; then, we can write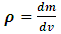 | (3) |
Where 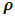 is the density of the object at the speed
is the density of the object at the speed 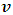 with its mass given by equation (2). To get a clearer picture of the relationship between mass and volume, we can rearrange equation (3) as
with its mass given by equation (2). To get a clearer picture of the relationship between mass and volume, we can rearrange equation (3) as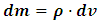 | (4) |
Thus, by equation (4), the mass of the rod depends directly on its volume. Now, suppose that the volume of this rod depends on the length element as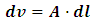 | (5) |
Where A is the surface area of the rod and dl is the length element.Now, suppose the length, according to Einstein’s relativity is given by equation (1); then, by equation (5), the volume of the rod must decrease as its length decreases. But the mass of the metal rod depends on the volume by equation (4); thus as the length of the rod decreases, its mass also decreases. Then, equation (1) and (2) cannot both be true simultaneously. If equation (4) holds, then equations (1) and (2) are said to be incompatible (the conclusion of special relativity is therefore inconsistent). By the above analysis, Einstein’s special relativity cannot simply be a precise description of reality or at least the theory is considered incomplete.To further support the conclusion of the above experiment, let us consider another inconsistency of this theory with itself. Einstein’s special theory of relativity- with its prediction of time dilation- tells us that the motion of particles through space affects the passage of time, thus allowing a more refine description of physical events by the merging of space and time into a single entity called spacetime.However, in a universe where the law of conservation holds, if space and time must be merged together; then, any complete theory under this constraint must be able to account for the effect of time dilation of certain physical event in one reference frame on the space-like description of the same physical event in the other frame of reference with which it is compare (that is, we define time in terms of space and assume that the law of conservation holds for them in the universe). Then, if we must accept time dilation as a valid effect on one frame in relative motion, a more objective description that reserves the laws of conservation should be that such effect as time dilation in one frame leads to either space dilation or increment in one of the other frame. Einstein’s theory of relativity provides no explanation for such prediction; thus, if the universe must obey the physical laws of conservation, one is justified to reject the prediction of time dilation or the theory be regarded as an incomplete description of reality.Let us now consider the incompatibility of special relativity with other theories, precisely classical and quantum mechanics. Quantum mechanics tells us that heating an atom causes the electron to absorb energy (kinetic energy in the form of heat energy) and jump to higher energy level. Then, by the laws of electrodynamics and gravitation, as the electron moves to higher energy level, the electrostatic and gravitational forces must be reduced. However, Einstein’s special theory of relativity tells us that as the electron obtains more kinetic energy and move with higher speed, it should become more massive over time by eq (2). Thus, the gravitational and electrostatic forces will get stronger as the mass of the agitated electrons increase (the charge and mass of the electron are directly related); at high speed, one would then expect the electron to move to lower energy level rather than higher energy level, since the forces depend directly on the mass and charge of the electrons. By the later requirement, all matter will seize to exist at high kinetic energy.Furthermore, consider the relativistic form of the Schrödinger wave equation (the Klein-Gordon form of the Schrödinger equation) for a single electron inside a box of infinite potential wall (Srednicki. M (2016) [13])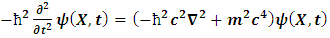 | (6) |
Where 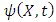 is the wave function that describes the state of the system.Now, suppose the mass (m) of the particle depends on its speed in the box; then, relativistically, m can be given by eq (2). But quantum mechanics tells us that as the speed of the particle increases, its potential energy is consider zero; thus, at
is the wave function that describes the state of the system.Now, suppose the mass (m) of the particle depends on its speed in the box; then, relativistically, m can be given by eq (2). But quantum mechanics tells us that as the speed of the particle increases, its potential energy is consider zero; thus, at 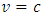 , eq. (6) reduces to
, eq. (6) reduces to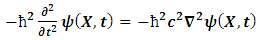 | (7) |
Returning again to the prediction of Special relativity, we see that the potential energy term of the system will be non-zero as the speed approaches the speed of light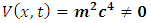 | (8) |
Since the potential energy (which in special relativity, it is considered the system’s rest energy) depends on the mass of the particle and the wave function describes the position of the particle. The quantum mechanical prediction for the particle’s mass is consistent with classical mechanics; thus, special relativity is incompatible with quantum and classical mechanics- both theories (quantum mechanics and special relativity) cannot simultaneously be valid.However, by first sight, one is not certain which theory is right or wrong unless we find a way to prove that either special relativity or quantum mechanics is incomplete. But every complete theory must have a uniform conclusion (condition for completeness); special relativity lacks this property thus, Einstein’s theory (rather than quantum mechanics) is incomplete.
3. Result
It has been established by the arguments above that special relativity is an incomplete theory due to the fact that it is inconsistent with classical and quantum mechanical arguments and with itself for the non-uniform conclusion about particle of matter as seen from the conflicting predictions of length contraction and mass increment. One may think that the classical definition of density as being used is not sufficient evidence to validate the predictions of special relativity; indeed one may think that classical mechanics cannot be used to validate special relativity due to the fact that they are two separate theories.However, physics must be uniform and special relativity is only a description of classical mechanics at high speed (relativistic speed) not a mare contradiction; thus, they must lead to a consistent conclusion (the density of the object must be defined by eq. (4) whether classically or relativistically). Again, one may reject this conclusion on grand that the criterion for completeness as used by the study is insufficient. On this grand, it must be necessary to consider nature itself to substantiate the claim that special relativity is an incomplete theory or an inferior description of reality. The following reality of nature is presented below to justify the claim that Einstein’s theory of special relativity is not a valid theory of reality as it has been accepted.In order to prove that Special relativity is an inferior description of reality (using nature itself), consider what happens in the creation of black holes. Star light is produced by nuclear fusion reactions that begin with a proton –neutron bound state producing deuterium (Ryder. L (2009) [14] and Gron. O & Hervik. S) [15]. These reactions are exothermic and at each state there is a mass defect at the right of the thermonuclear equation which appears as an electromagnetic radiation to produce the star light. This means that the star always appears lighter at the end of every fusion reaction since electromagnetic radiation is mass-less. The radiation pressure exerted by the photon’s energy serves as a balance to keep the star in an equilibrium position from the inward pull of gravity on its spacetime fabric.However, as the chain reaction continues, it gives rise to iron nuclei which on average have high binding energy per mass, Ryder. L (2009) [14]. This causes the fusion reaction to become endothermic. Then, as the star cools, the additional mass stored as electromagnetic energy-due to high speed (or high kinetic energy) of the particles- slows down and becomes converted to mass.As a result, the star becomes heavier with decrease in temperature (the speed of the particles making up the star is a function of temperature). This causes the gravitational equilibrium to break down at the Chandrasekhar mass limit resulting to a gravitational collapse “a black hole”. However, according to Einstein’s mass increment prediction of special relativity, a reverse situation is expected to occur; gravitational collapse should occur at high kinetic energy (exothermic state), since the particles making up the star must be more massive at high temperature than at low temperature or low kinetic energy. Einstein’s relativity thus provides an invalid argument.The conclusion then is that Einstein’s Special Theory of Relativity is an incomplete theory of reality. There must be a better theory that must fully explain reality and unite physics. This can be done by replacing Einstein’s inferior description of reality by a more general and objective theory. The second goal of this work is therefore to provide alternative predictions to replace Einstein’s special theory of relativity which is now presented in the rest of the work.
4. Discussion
To establish a new theory or explanation of special relativity, it is sufficiently necessary to first show that the fundamental analysis on which Einstein’s Special Relativity is built is not uniform. This can also be supported further by looking at the work of Denci (2016) [16]. Then, the result of this exercise will be used to re-explain the principle of relativity. I will now show this non-uniformity by considering two though experiments from Einstein’s relativity which are assumed to be equivalent by Einstein’s Theory:In experiment 1 (E1), there are two frames S and S’. Suppose a segment of wire is at rest in S and carries a current in the positive x direction, Serway and Beichner (2000) [6]. An observer in this frame concludes that the negative test charges are moving to the right with a speed v that causes the current to flow in this direction. This observer sees an electrostatic field in which positive test charges are at rest and a corresponding magnetic field in which the negative test charges are moving to the right.Suppose that another frame S’ is moving relative to S and of course with the current wire at a speed “v” in the negative x direction. By Einstein’s relativity, the observer in S’ will see that a current is produce not due to the motion of a negative test charges but rather due to the motion of the positive charges to the left (in the negative x direction). Thus, what was considered an electrostatic field and a corresponding magnetic field in S will now be considered a magnetic field and a corresponding electrostatic field in S’. The Lorentz transformation then allows us to give an equivalent form of this analysis in both frames.Now, suppose we seek to describe this event with respect to a single frame, say S; we know from above that this observer only sees a moving negative charges to the right (that is, this observer believes that the positive test charges are at rest). Now, what is the speed of these negative test charges in the moving frame S’ as judged by S? That is, since only negative test charges are moving with respect to S, how does this observer (S) finds the speed of these charges in the moving frame (since S does not see a positive test charge in motion)? We see that the Lorentz transformation does not answer this question and Einstein’s special relativity provides no explanation in this case.Now, consider the second experiment (E2) called Einstein’s length contraction Experiment. Suppose two observers, S at rest on the earth and S’ in a spaceship moving with a velocity v relative to the earth and therefore to S. Now, consider an unknown particle traveling in space from a point 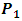 to another point
to another point 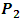 ; Miller Jr. F (1999) [7], Serway & Beichner (2000) [6], Tippler and Llewellyn (2008) [1], Cutnell & Johnson (2009) [5] and Sears, Zemansky and Young, 1985 [12]. What is the distance between the two points? To answer this question, observer S sees that he is stationary with respect to the moving frame and the particle; thus, if the particle is moving with the speed of light, he finds that the distance between the points (or the distance covered by the particle) is
; Miller Jr. F (1999) [7], Serway & Beichner (2000) [6], Tippler and Llewellyn (2008) [1], Cutnell & Johnson (2009) [5] and Sears, Zemansky and Young, 1985 [12]. What is the distance between the two points? To answer this question, observer S sees that he is stationary with respect to the moving frame and the particle; thus, if the particle is moving with the speed of light, he finds that the distance between the points (or the distance covered by the particle) is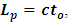 | (9) |
Where 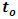 is the time with respect to S and
is the time with respect to S and 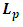 is the distance/ length recorded by S called the proper length. Then, by symmetry, we see that S’ believes that he is at rest with respect to the particle; thus, the distance between the two points in S’ frame is given by eq (9) (both observer believe that they are stationary so their length is unaffected by relative motion).Now, suppose again that we seek to describe this event with respect to one of the frames, say S, what will be the length between the two points in the moving frame S’ as judged by S? This question is then equivalent to the unanswered question in experiment 1. However, to answer this question, we see that observer S assumes to be at rest while S’ is in motion (Resnick. R (1968) [2], Bohm. D (1965) [3], Miller Jr. (1999) [7], Serway & Beichner (2000) [6], Cutnell & Johnson (2009) [5], Tipler & Llewellyn (2008) [1] and Sears, Zemansky and Young, 1985 [12]; this observer S will then see that relative motion with affect the distance between the two points in S’. That is, S sees that S’ is moving with a speed v; thus, he finds that relative motion causes a time dilation in S’ frame given by
is the distance/ length recorded by S called the proper length. Then, by symmetry, we see that S’ believes that he is at rest with respect to the particle; thus, the distance between the two points in S’ frame is given by eq (9) (both observer believe that they are stationary so their length is unaffected by relative motion).Now, suppose again that we seek to describe this event with respect to one of the frames, say S, what will be the length between the two points in the moving frame S’ as judged by S? This question is then equivalent to the unanswered question in experiment 1. However, to answer this question, we see that observer S assumes to be at rest while S’ is in motion (Resnick. R (1968) [2], Bohm. D (1965) [3], Miller Jr. (1999) [7], Serway & Beichner (2000) [6], Cutnell & Johnson (2009) [5], Tipler & Llewellyn (2008) [1] and Sears, Zemansky and Young, 1985 [12]; this observer S will then see that relative motion with affect the distance between the two points in S’. That is, S sees that S’ is moving with a speed v; thus, he finds that relative motion causes a time dilation in S’ frame given by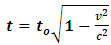 | (10) |
Thus, using the same valid law of physics, S finds that the distance between the two points in S’ is reduced given by eq. (1) as judged by observer S.Experiments 1 and 2 are not equivalently analyze because, in Experiment 1 the description of the event is done independently (no observer describes the event for his friend), while in E2, the description in one frame is done relative to the other (that is, a single observer describes the event in both frames of reference with respect to himself).Now, suppose we determine the speed of the negative test charges in S’ relative to S using similar analysis in E2, we see that S’ will have a time dilation effect in his frame which will change his speed; Lorentz transformation equations will not be valid under such analysis. It is then proven that the fundamental analysis and hence the conclusion of special relativity is not uniform by the argument above.
4.1. Review of the Michelson-Morley Experiment and the Classical Relativity Theory
To build a new theory or give a correct explanation for Einstein’s special relativity, we provide a more uniform analysis to describe all events in spacetime by observers in relative motion. But describing an event in one frame for the other implies a paradox; therefore, this paper will establish a new theory of relativity from a paradoxical perspective to replace Einstein’s semi-paradoxical theory of special relativity. To do this, a Galilean interpretation for the Michelson-Morley experiment will be given and the result will be used to establish that even light can obey a modified Galilean speed transformation. This will be done by considering though physical experiments from the viewpoint of classical relativity and later be extended to Einstein’s relativity as follow:According to Galilean Relativity, if two initial frames of references (S and S’) are in relative motion; then, for a frame 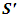 moving relative to another frame S with speed
moving relative to another frame S with speed 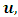 the Galilean transformation of velocity that reserves Newton’s laws of mechanics in both frames is
the Galilean transformation of velocity that reserves Newton’s laws of mechanics in both frames is 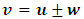 relative to the stationary frame. But suppose an observer in a frame (S’ for example) wants to record the velocity of an object by his own specetime coordinate, what is the speed of the particle in this frame? In other words, does the Galilean transformation equation holds for an experiment conducted by an observer in his own frame?To answer this question, let us imagine some physical experiment in which there are two observers, one being stationary and the other on a moving train. Let us assume that the train is moving westward with a speed
relative to the stationary frame. But suppose an observer in a frame (S’ for example) wants to record the velocity of an object by his own specetime coordinate, what is the speed of the particle in this frame? In other words, does the Galilean transformation equation holds for an experiment conducted by an observer in his own frame?To answer this question, let us imagine some physical experiment in which there are two observers, one being stationary and the other on a moving train. Let us assume that the train is moving westward with a speed 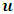 past a stationary observer. Now, suppose that a wind is blowing eastward with a speed
past a stationary observer. Now, suppose that a wind is blowing eastward with a speed 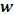 relative to the stationary observer. By Galilean Relativity, the stationary observer will measure the train’s speed to be
relative to the stationary observer. By Galilean Relativity, the stationary observer will measure the train’s speed to be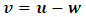 | (11) |
in the west direction, since it travels against the wind. For an eastward travel and assuming constant velocity, a reverse situation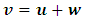 | (12) |
is obtained.By Galilean relativity, there is a decrease in speed in the west direction and a corresponding increase in the eastward direction due to the blowing wind in one direction (to the east in this case). But again, what is the speed of the moving train with respect to itself in either directions, or what is the speed of the train with respect to the observer who is on board in the train? By Galilean relativity, this observer will not be able to notice a change in his train’s speed in both directions (he will not be able to feel the effect of the wind on his speed). In other words, the object’s speed will not be affected by relative motion since this observer is considered to be stationary with respect to the object in his own frame; thus, he will record the speed of the train in both directions to be 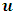 . Galilean Relativity therefore implies that no transformation equation can be valid for an observer measuring his own speed because there is no influence of relative motion with respect to this observer. Thus, it can be postulated that no mechanical event or experiment is affected by relative motion if the event is described by an observer in his own frame. Galilean transformation equations are then applicable only when comparing physics in one reference frame relative to another.Now, consider the same experiment above performed in a uniform still wind (by the phrase “uniform still wind”, It means a region in which the wind blows in all directions with equal speed or appears to not blow at all). For the same train moving again in the west and east directions, it will experience the same magnitude of inertia force in either of these directions as judged by the stationary observer. Thus, this stationary observer will measure equal speed for the train’s motion in both directions. Galilean Relativity then produces a null result for the case of the uniform still wind, since any stationary observer will not be able to notice a change of velocity of the train in both directions at least if the experiment were performed in a still wind. We now compare this result to the Michelson- Morley experiment to consider the relativistic speed limit (the speed of light).Consider the Michelson- Morley experiment- (Miller Jr. F, 1999 [7]; Tipler and Llewellyn, 2008 [1]; Serway and Beichner, 2000 [6]; Resnick. R, 1968 [2], Bohm 1965 [3]; Cutnell & Johnson, 2009 [5] and Sears, Zemansky and Young, 1985 [12] - in which the earth moves through space (the ether) with speed
. Galilean Relativity therefore implies that no transformation equation can be valid for an observer measuring his own speed because there is no influence of relative motion with respect to this observer. Thus, it can be postulated that no mechanical event or experiment is affected by relative motion if the event is described by an observer in his own frame. Galilean transformation equations are then applicable only when comparing physics in one reference frame relative to another.Now, consider the same experiment above performed in a uniform still wind (by the phrase “uniform still wind”, It means a region in which the wind blows in all directions with equal speed or appears to not blow at all). For the same train moving again in the west and east directions, it will experience the same magnitude of inertia force in either of these directions as judged by the stationary observer. Thus, this stationary observer will measure equal speed for the train’s motion in both directions. Galilean Relativity then produces a null result for the case of the uniform still wind, since any stationary observer will not be able to notice a change of velocity of the train in both directions at least if the experiment were performed in a still wind. We now compare this result to the Michelson- Morley experiment to consider the relativistic speed limit (the speed of light).Consider the Michelson- Morley experiment- (Miller Jr. F, 1999 [7]; Tipler and Llewellyn, 2008 [1]; Serway and Beichner, 2000 [6]; Resnick. R, 1968 [2], Bohm 1965 [3]; Cutnell & Johnson, 2009 [5] and Sears, Zemansky and Young, 1985 [12] - in which the earth moves through space (the ether) with speed 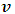 . An ether wind is expected to blow past the earth in an opposite direction at the same speed with which the earth moves relative to space (the ether). This speed can be considered “the inertia force” at least in the case of this experiment. Then, if
. An ether wind is expected to blow past the earth in an opposite direction at the same speed with which the earth moves relative to space (the ether). This speed can be considered “the inertia force” at least in the case of this experiment. Then, if 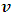 is the speed of the Ether wind relative to earth, a light beam is expected to have a maximum and a minimum velocities of
is the speed of the Ether wind relative to earth, a light beam is expected to have a maximum and a minimum velocities of 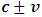 in view of the Galilean Relativity ( if we assume that the ether is not uniformly still). However, if we assume that space (or the ether) is uniformly still in all directions, then an object moving through it will experience an equal inertia force in any direction of its motion. Then, for a beam of light as in the case of the experiment above, the light will have equal speed in both directions relative to a stationary observer on earth; the speed of the light with respect to the ether is therefore the same as that relative to the earth; a null result is then produced for still ether.Thus, the null result of the Michelson-Morley experiment is fundamentally not because light violates the Galilean speed transformation, but rather as a result of the fact that space (or the ether wind) itself is still or uniform in all directions; thus, the only absolute velocity of the earth relative to space (the ether) is the one observed. For an experimenter wanting to detect a small change in the light’s speed, the result will always be null (the beam will experience equal opposing force in any direction). If we consider space as the ether itself and assume a homogenous universe, then we can conclude that the expansion of the universe must be homogenous. A general proof that the speed of light is affected by relative motion (it is not absolute when comparing two frames in relative motion) can be given by the experiment below.Consider the physical experiment with two frames of references: A being stationary while B is moving in the positive x direction with a speed
in view of the Galilean Relativity ( if we assume that the ether is not uniformly still). However, if we assume that space (or the ether) is uniformly still in all directions, then an object moving through it will experience an equal inertia force in any direction of its motion. Then, for a beam of light as in the case of the experiment above, the light will have equal speed in both directions relative to a stationary observer on earth; the speed of the light with respect to the ether is therefore the same as that relative to the earth; a null result is then produced for still ether.Thus, the null result of the Michelson-Morley experiment is fundamentally not because light violates the Galilean speed transformation, but rather as a result of the fact that space (or the ether wind) itself is still or uniform in all directions; thus, the only absolute velocity of the earth relative to space (the ether) is the one observed. For an experimenter wanting to detect a small change in the light’s speed, the result will always be null (the beam will experience equal opposing force in any direction). If we consider space as the ether itself and assume a homogenous universe, then we can conclude that the expansion of the universe must be homogenous. A general proof that the speed of light is affected by relative motion (it is not absolute when comparing two frames in relative motion) can be given by the experiment below.Consider the physical experiment with two frames of references: A being stationary while B is moving in the positive x direction with a speed 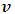 (Miller Jr. F; 1999 [7] and Sears, Zemansky and Young 1985 [12]). The two observers have a solar-light and the goal of the experiment is to measure the distance traveled by a light pulse after emission at some finite time (t) by both observers. But first, let us assume that the two observers are at the same point in space. Now, after 1 nanosecond, the pulse of light emitted from A travels a distance of about 0.3m and has reached a point x as shown in figure 1(a) below.
(Miller Jr. F; 1999 [7] and Sears, Zemansky and Young 1985 [12]). The two observers have a solar-light and the goal of the experiment is to measure the distance traveled by a light pulse after emission at some finite time (t) by both observers. But first, let us assume that the two observers are at the same point in space. Now, after 1 nanosecond, the pulse of light emitted from A travels a distance of about 0.3m and has reached a point x as shown in figure 1(a) below. | Figure 1a |
 | Figure 1b |
However, after 1 nanosecond, B has moved vt units to the right (figure 1b) and his position is now B’; so the light reaches some point y′ instead of y. From 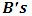 point of view, the light has a speed of
point of view, the light has a speed of 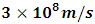 and has traveled a distance of about 0.3m in one nanosecond which is just point
and has traveled a distance of about 0.3m in one nanosecond which is just point 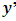 . Thus, both observers will measure the actual speed of the light if they view the event in their own frame (there will be no effect of relative motion on both frame in an independent conclusion).However, if we describe the event only in A’s spacetime coordinate, we see a contradiction. This observer sees the position of the light pulse in B’s frame at the point y’ instead of y, thus, he concludes that the motion of B gives the light an extra push, thus the speed of the light must be greater than c in B relative to A. This is however symmetric because, as B look at the light position at the point x which is just y instead of y’, he concludes that A is moving to the left thus his motion is giving an extra push to the light speed.Analyzing separately, we see that independently both observer will agree with the measured speed of light in their own frames. However, if we describe the event with respect to a single observer, we see that if this observer looks at the light pulse in his friend’s frame, he sees a small push of velocity
. Thus, both observers will measure the actual speed of the light if they view the event in their own frame (there will be no effect of relative motion on both frame in an independent conclusion).However, if we describe the event only in A’s spacetime coordinate, we see a contradiction. This observer sees the position of the light pulse in B’s frame at the point y’ instead of y, thus, he concludes that the motion of B gives the light an extra push, thus the speed of the light must be greater than c in B relative to A. This is however symmetric because, as B look at the light position at the point x which is just y instead of y’, he concludes that A is moving to the left thus his motion is giving an extra push to the light speed.Analyzing separately, we see that independently both observer will agree with the measured speed of light in their own frames. However, if we describe the event with respect to a single observer, we see that if this observer looks at the light pulse in his friend’s frame, he sees a small push of velocity 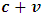 relative to this observer. In Galilean Relativity, there is no preferred frame, so the speed of light can be measured in any frame and produce the same value independently of the other. We then find that the two observers can independently agree with the right speed of their light pulse to be c in their own frames (Lorentz transformation), but when comparing their measurements with each other in relative motion, they do not agree with the observed speed of the light pulse (they see that the speed of the light is affected by the relative motion of each observer). The Galilean transformation of velocity therefore produces a “consistent” argument in the case of the light’s speed relative to both observers; the Lorentz transformation equations are therefore inapplicable if we view the event in one coordinate system.
relative to this observer. In Galilean Relativity, there is no preferred frame, so the speed of light can be measured in any frame and produce the same value independently of the other. We then find that the two observers can independently agree with the right speed of their light pulse to be c in their own frames (Lorentz transformation), but when comparing their measurements with each other in relative motion, they do not agree with the observed speed of the light pulse (they see that the speed of the light is affected by the relative motion of each observer). The Galilean transformation of velocity therefore produces a “consistent” argument in the case of the light’s speed relative to both observers; the Lorentz transformation equations are therefore inapplicable if we view the event in one coordinate system.
4.2. Review of Einstein’s Relativity and the Consequence of Simultaneity
What is the source of the difference in the light speed as observed by observer A for observer B in the experiment above? Observer A sees that the distance travel by the light in B’s frame is greater than his. Now, suppose A uses his light speed (which is c with respect to him) and the distance travel in B’s frame, he finds that B’s time is greater than his. A then conclude that the events where not simultaneous. Galilean relativity is then incorrect on its time-like coordinate  . Then, if we impose the concept of simultaneity at the beginning and the end of the event (that the two events begin and end at the same time), then, we can conclude that the reference clock in A reads faster than the reference clock in B (time goes faster with respect to A then with respect to B); Einstein’s time dilation effect is then valid.Now, accepting Einstein’s time dilation as valid, we see that observer A measures a shorter time (time dilation) and a longer distance (length increment) for observer B. Then, if A measures a longer distance in B’s frame, he concludes that there is space dilation in his own frame (his distance is shorter than B’s) and a corresponding time increment (he measures a longer time interval in his own frame than B). Thus, if the event is described only with respect to a single observer, we find a paradox (either the space or time coordinate of each observer experiences a reduction or dilation).Then, since there is no absolute frame of reference and each observer can measure the speed of his light to be c independently, the following postulates can be stated: (1), there is no absolute reference frame in relativity (both classical and special relativity) and all the laws of physics including those of electrodynamics and mechanics must be valid in each frame INDEPENDENTLY and (2), time duration between events is not absolute in any reference frame in relative motion with some other initial frames and no single frame can have an effect of dilation (or reduction) in both its time-like and space-like coordinates simultaneously. In order words, length contraction (length or space dilation) must lead to time stretch (time increment) and vice versa.
. Then, if we impose the concept of simultaneity at the beginning and the end of the event (that the two events begin and end at the same time), then, we can conclude that the reference clock in A reads faster than the reference clock in B (time goes faster with respect to A then with respect to B); Einstein’s time dilation effect is then valid.Now, accepting Einstein’s time dilation as valid, we see that observer A measures a shorter time (time dilation) and a longer distance (length increment) for observer B. Then, if A measures a longer distance in B’s frame, he concludes that there is space dilation in his own frame (his distance is shorter than B’s) and a corresponding time increment (he measures a longer time interval in his own frame than B). Thus, if the event is described only with respect to a single observer, we find a paradox (either the space or time coordinate of each observer experiences a reduction or dilation).Then, since there is no absolute frame of reference and each observer can measure the speed of his light to be c independently, the following postulates can be stated: (1), there is no absolute reference frame in relativity (both classical and special relativity) and all the laws of physics including those of electrodynamics and mechanics must be valid in each frame INDEPENDENTLY and (2), time duration between events is not absolute in any reference frame in relative motion with some other initial frames and no single frame can have an effect of dilation (or reduction) in both its time-like and space-like coordinates simultaneously. In order words, length contraction (length or space dilation) must lead to time stretch (time increment) and vice versa.
4.3. Galilean-Lorentz Transformation Equations (The Classical and Relativistic Transformation)
In the experiment above, we see that the concept of simultaneity breaks down resulting to space dilation in one frame of reference and a corresponding time dilation in the other frame in relative motion. The laws of conservation of space and time then hold in the above analysis. Einstein’s relativity provides no explanation for such prediction. We now investigate the consequence of the stated postulates on the Lorentz transformation equations and use the result to derive a new transformation laws.The first postulate remains consistent with the postulate of Einstein’s theory of special relativity except for the strong use of the word “independently” which means that in a separate analysis of any spacetime event, both observers will agree with their results in their own frame (there will be no effect of relative motion on each analysis); Lorentz transformation would be valid. The second postulate implies that the only valid spacetime transformation equation of an event in any frame (if described by a single observer) is one that allows a dilation of a single coordinate (either space dilation or time dilation but not both effects simultaneously).The second postulate then demands that the Lorentz spacetime transformation be modified in the case of dependent (or paradoxical) analysis, since it allows a single frame of reference to have a dilation or increment in both its space and time coordinate simultaneously (as seeing by a plus sign in both space and time axis in one frame and a corresponding minus sign for the other frame). Then, for an arbitrary event in a Minkowski spacetime, these transformations will then reduce to a modified Galilean speed transformation equation for the event.Consider a spacetime experiment in which there are two reference frames called S and S’. Now, let S be some stationary frame and S’ be moving relative to S in the positive x-direction with a relative velocity (v) as shown in figure 2 below: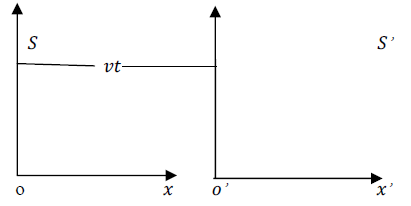 | Figure 2 |
We assume that the prime and unprimed y and z coordinates of both observers are parallel to each other; thus, there is no relative motion on these axes. Therefore, these coordinates are reserve: y = y’ and z = z’.However, because the relative velocity of the frames is on the x-axis with respect to time, the time and x coordinates of both observers changed. Also, it was proven that the concept of simultaneity brakes done for observers in relative motion as opposed to the Galilean analysis; thus time dilation is valid; thus, it is obvious to show that the time coordinate can be represented by its Lorentz form, Denci. V, 2016 [16]. Our goal is therefore to correct the space like coordinates to include Space dilation in the transformation; these transformations will then be named the Galilean-Lorentz transformation, since it reduces to a modified Galilean velocity transformation equations.To establish these transformation laws we reinforce the first postulate of relativity, which states that everyone is right in his own frame independently. Thus, in describing the spacetime event above, we must analyze the situation so that no frame interferes with his friend’s analysis (every frame is free to speak). Therefore, by employing this method, we see that an observation made by A for example, must be viewed and described as it appears in A’s frame of reference. This is thus the reinforcement of postulate (1) which shall be named the “principle of correspondence: the space-time description of an event is independent for every observer. This means that if an event occurs at some point in space, it should be viewed or described as it appears to the observer describing it with no interference (or predictions) of any external observer out of that frame.Applying this principle, we see that B has a time dilation effect with respect to observer A because according to A, B’s clock is running slower; thus, A concludes that B’s time is reduced given by the Lorentz time transformation equation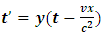 | (13) |
With inverse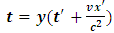 | (14) |
Also, A sees that the event has occur, B has move a distance 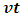 -units away from his initial position. If the two coordinates system coincide at t = t’= 0; then, B’s final position after t seconds (with respect to A) is just the position of A (which is consider to be fixed at the origin) plus the additional
-units away from his initial position. If the two coordinates system coincide at t = t’= 0; then, B’s final position after t seconds (with respect to A) is just the position of A (which is consider to be fixed at the origin) plus the additional 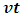 units travelled by B after t seconds; that is,
units travelled by B after t seconds; that is,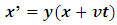 | (15) |
With inverse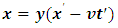 | (16) |
Therefore, A’s set of transformation equations and their inverses are given as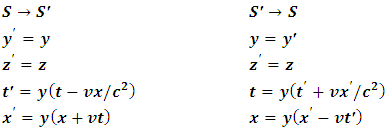 Symmetrically, the same result can be produce with respect to B’s. In this case, B believes that he is stationary and A is moving westward; hence, A has a time dilation effect in his frame; thus, B concludes that A’s time interval is given as
Symmetrically, the same result can be produce with respect to B’s. In this case, B believes that he is stationary and A is moving westward; hence, A has a time dilation effect in his frame; thus, B concludes that A’s time interval is given as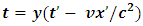 | (17) |
B also argues that A has move 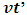 units away so, A is now at the point
units away so, A is now at the point 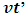 units away from him (B) given as
units away from him (B) given as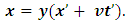 | (18) |
And consistently, the transformation equations with respect to B’s analysis becomes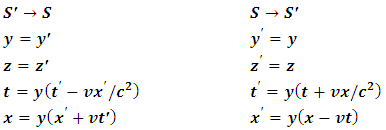 These are thus the modified Lorentz transformation (the Galilean-Lorentz transformation). The valid Galilean speed transformation equation can then be derived using the results above. For the purpose of this study, this will be done with respect to a single observer (A); it can be shown that B’s frame yields the same result.With respect to A, the velocity of any moving particle in his frame (along the positive
These are thus the modified Lorentz transformation (the Galilean-Lorentz transformation). The valid Galilean speed transformation equation can then be derived using the results above. For the purpose of this study, this will be done with respect to a single observer (A); it can be shown that B’s frame yields the same result.With respect to A, the velocity of any moving particle in his frame (along the positive 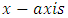 for simplicity) is given as
for simplicity) is given as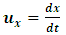 | (19) |
We now express eqns. (14) and (16), in differential forms as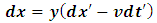 | (20) |
And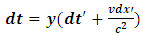 | (21) |
Substituting (20) and (21) into (19) yields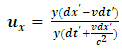 Canceling the common y term, we have
Canceling the common y term, we have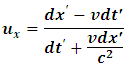 Dividing through by
Dividing through by 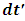 , we have
, we have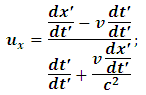 Recognizing
Recognizing  , we have
, we have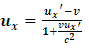 | (22) |
And solving finally for 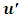 in (22), we have
in (22), we have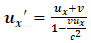 | (23) |
If the motion is done on the y and z axes, we see that there is no relative motion on these axes; thus, v = 0. Then, the speed of the particle on these axes becomes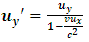 | (24) |
And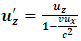 | (25) |
Then, by eq. (22) and (23), the particle has a greater velocity in B’s frame when compare to A. This is therefore the case because, observer A experiences length dilation and length (by classical mechanics) is directly proportional to the velocity of the object in space. The classical meaning of the relativistic statement “the faster one goes through space, the slower he moves in time” is thus confirm by eqns (22) and (23) because, according to the laws of classical mechanics, dilation in space and increment in time implies a decrease in velocity (eq -22), since the velocity of particle in each frame is directly proportional to space (distance or length) and inversely to time. The speed of the particle in B’s frame eq. (23) is greater because he experiences dilation in time and a simultaneous increase in space in his frame which implies increase in velocity. The transformation equations for the particle’s speed are therefore consistent with the classical definition of velocity as desire.Now, suppose the speed of a particle in B is recorded by this observer to be 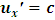 ; then, eq. (22) becomes
; then, eq. (22) becomes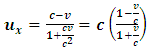 | (26) |
The velocity of such particle is therefore less then c in A’s frame and also decreases as 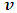 increases as judged by A. This means that if observer B moves with the speed of light, a particle moving in his frame at the speed of light will appear to be stationary with respect to a stationary observer.On the other hand, suppose the particle’s speed is recorded to be
increases as judged by A. This means that if observer B moves with the speed of light, a particle moving in his frame at the speed of light will appear to be stationary with respect to a stationary observer.On the other hand, suppose the particle’s speed is recorded to be 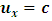 in the stationary frame (A); then, eq. (23) becomes
in the stationary frame (A); then, eq. (23) becomes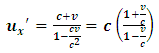 | (27) |
Then, if observer A measures the speed of a particle to be c in his frame, he concludes that this particle will have a speed greater then c in B’s frame and increases as 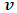 increases because, observer A sees that B’s motion will give an extra push to the particle in this frame. There is a physical consequence of eq. (26) which is provided by the following physical experiment.Consider an experiment in which a spaceship moves in the positive x direction with a speed
increases because, observer A sees that B’s motion will give an extra push to the particle in this frame. There is a physical consequence of eq. (26) which is provided by the following physical experiment.Consider an experiment in which a spaceship moves in the positive x direction with a speed 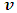 . Now, imagine that a missile is attached to a fixed point midway between the front and rear of the ship. The goal of the experiment is for the pilot to release this missile at a target point which is some distance at head of the pilot (in the some positive x direction). Now, suppose the pilot releases this missile at the target with a speed c in the same direction of his spaceship; then, because his ship is moving with a much less velocity then the shooting missile, a stationary observer on earth will see that at a later time, the missile will overtake and arrive at the target point before the spaceship.Now, suppose this pilot raises the speed of his ship to
. Now, imagine that a missile is attached to a fixed point midway between the front and rear of the ship. The goal of the experiment is for the pilot to release this missile at a target point which is some distance at head of the pilot (in the some positive x direction). Now, suppose the pilot releases this missile at the target with a speed c in the same direction of his spaceship; then, because his ship is moving with a much less velocity then the shooting missile, a stationary observer on earth will see that at a later time, the missile will overtake and arrive at the target point before the spaceship.Now, suppose this pilot raises the speed of his ship to 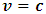 just the same time he had released the missile at the target point with the same speed c; an observer in the earth’s frame (or stationary frame) will not be able to detect any motion of the missile with respect to him, since it will not be able to overtake the spaceship. He will then conclude that the missile has not yet been released by this pilot, since it (the missile) maintains its same position on the spaceship at any later time. The speed of the missile is then zero with respect to a stationary observer on earth. By equation eq. (24), this should be the case because, as the pilot raises his speed to the speed of light, he moves with the same speed of his shooting missile towards the target point. Then, if both velocities are maintained, they will arrive at the target point in exactly the same time. Thus, the speed of the missile reduces as the pilot increases his speed with respect to the stationary observer.
just the same time he had released the missile at the target point with the same speed c; an observer in the earth’s frame (or stationary frame) will not be able to detect any motion of the missile with respect to him, since it will not be able to overtake the spaceship. He will then conclude that the missile has not yet been released by this pilot, since it (the missile) maintains its same position on the spaceship at any later time. The speed of the missile is then zero with respect to a stationary observer on earth. By equation eq. (24), this should be the case because, as the pilot raises his speed to the speed of light, he moves with the same speed of his shooting missile towards the target point. Then, if both velocities are maintained, they will arrive at the target point in exactly the same time. Thus, the speed of the missile reduces as the pilot increases his speed with respect to the stationary observer.
4.4. Possibility for the Existence of Relativistic Entanglement and Non-Locality
Consider a particle moving with a speed c. then, as the relative velocity between the two observers approaches the speed of light 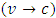 , we see that eqns (26) and (27) become:
, we see that eqns (26) and (27) become: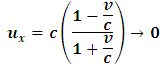 in S and
in S and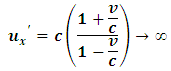 in S’.However, Maxwell’s unified theory of electrodynamics tells us that no speed can be greater than the speed of light in empty space. The relativistic consequence of this statement would be that the speed of every event in the universe must satisfy the inequality
in S’.However, Maxwell’s unified theory of electrodynamics tells us that no speed can be greater than the speed of light in empty space. The relativistic consequence of this statement would be that the speed of every event in the universe must satisfy the inequality 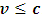 . The transformation equations thus appear to have a problem, since it violates the Maxwell’s speed inequality in one of the frames.However, the particle (by reality) is moving with a speed c independent of any observation (or if view in each frame independently); thus, the zero and infinite speeds recorded by the stationary observer is only a paradox deriving from the space-time description of the event with respect to this observer. Therefore, since special relativity allows a symmetric argument in both frames (that is, if each observer thinks that he is at rest), the two systems must behave as counter-part in order to keep the speed of light constant (by the law of conservation of space and time, both systems must be considered unity); that means that they must exist as though they are a single system (an entangled system). Now, suppose we consider the two frames of references as entangle pair, then, by Bohr’s argument, the frames must then have one velocity that must satisfy the Maxwell’s speed constraint.Now, suppose we let the speed of the individual system to be
. The transformation equations thus appear to have a problem, since it violates the Maxwell’s speed inequality in one of the frames.However, the particle (by reality) is moving with a speed c independent of any observation (or if view in each frame independently); thus, the zero and infinite speeds recorded by the stationary observer is only a paradox deriving from the space-time description of the event with respect to this observer. Therefore, since special relativity allows a symmetric argument in both frames (that is, if each observer thinks that he is at rest), the two systems must behave as counter-part in order to keep the speed of light constant (by the law of conservation of space and time, both systems must be considered unity); that means that they must exist as though they are a single system (an entangled system). Now, suppose we consider the two frames of references as entangle pair, then, by Bohr’s argument, the frames must then have one velocity that must satisfy the Maxwell’s speed constraint.Now, suppose we let the speed of the individual system to be 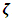 ; then, by the law of conservation of speed, the product of the speeds of the entangled systems is
; then, by the law of conservation of speed, the product of the speeds of the entangled systems is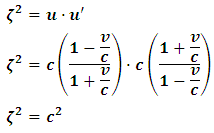 | (28) |
Then, the velocity of the unified system will not exceed the speed of light. This means that even if the two frames have an infinite space-like separation, they will remain connected to each other as a single unit so that when measurement is made; the speed of light will be conserved. Entanglement is therefore a consequence of the inhomogeneous space and time dilations of frames in relative motion (inhomogeneous in the sense that as space dilation occurs in one frame, time dilation must occur in the other frame and vice versa). Thus, in any well entangled system, one of the systems behaves as though its speed exceeds that of the speed of light (Aspect’s Experiment); therefore, even if the distance between the two systems is infinite, they will stay be connected to each other. The failure of the Einstein-Lorentz velocity transformation is then due to the fact that it only predicts time dilation as a consequence of relative motion with no consequence of this effect on the other frame, thus violating the laws of conservation.
4.5. Special Relativity of the Twin Paradox
The twin paradox is a non-symmetric situation in Einstein’s special relativity in which twin brothers are in the same frame of reference and of course of the same age; however, one of the twin brothers travels to a distance star and comes back. According to Einstein’s relativity, the traveler twin is younger than his brother who stays on earth.However, the first postulate of special relativity, which also claims to be consistent with Einstein’s Relativity, tells us that there is no absolute frame of reference; this means that each observer is right in his own frame. Then, concluding that the earth-born twin is right that his brother is actually younger implies a violation to this postulate because it allows the earth frame to be an absolute frame in the experiment.To resolve this problem, we consider the consequence of transformation. To transform from one coordinate to another implies that every valid equation for such transformation should take an event from one frame of reference to another in exactly the same way; that is, the origin of all observers spacetime coordinates will coincide and have the same position in space and time when transformed. In other words, time and space for everybody will coincide at this point. Now, leaving from the distance star back to his brother in the earth’s frame implies that the traveler twin’s coordinate system should coincide with his brother’s spacetime coordinate system since they are both in the same frame at the end. This therefore implies transformation of coordinates; that means that both their time and space coordinates must be the same at the end of the round trip. Therefore, at the time of arrival, the space and time of both brothers will be the same since transformation of coordinate has occur (from the distance star back to earth) and they will simply be equal after the trip.It seems accurate to reason from the perspective of Einstein’s relativity that the traveler twin experiences acceleration at a point of reversing his trip to earth as claimed by special relativity. However, there is no preferred frame in relativity as demanded by postulate (1) of Einstein’s theory; therefore, the traveler twin equally thinks that he is at rest and both his brother and the earth are moving away from him with a high speed; to come back to the same point, the travelers twin believes that his brother must experience some sort of acceleration when reversing his trip- just as earth-born twin previously views the situation -which will equally decrease his time and upon his arrival, he is younger than his traveler’s brother. The situation is therefore symmetric and at the end, it is impossible to conclude that one brother is right over the other. However, during their period of separation, each twin is right independently to think that his friend is younger according to the first postulate.Investigating this further, consider an equivalent statement in General Relativity called the Gravitational clock effect. Suppose we have a synchronized clocks system somewhere in space, then each clock in the system will read the same time interval for every event. Supposing that one of the clocks is taken to a journey near a black hole where there is a strong gravitational field, the clock slows down and no longer agrees with those in the synchronized system. General relativity then predicts that upon return, the gravitating clock is younger.Now, let’s take a reversed case. Suppose a synchronized clock system is located at the surface of a black hole, they will read the same time interval between events occurring on the black hole. What if one of the clocks in this synchronized system were taken to some point far away from the black hole? The clock in question will read a longer time interval for events because it has less gravitational effect compared to the others. Now, consider us carrying the clock back to its initial position in the synchronized clock system; is there a time difference between the clock reading and those in the synchronized system after return? Does the space clock still read more time than the gravitating clocks that stay at the black hole after return?It is obviously wrong to conclude that there is a time discrepancy between the clocks after returning to its previous position because, as the space clock approaches the surface of the black hole on its returned trip, gravity gets stronger and slows down the clock’s rate of time and at the synchronized system at the black hole’s surface, the space clock takes the time of the black hole and the entire clock system resynchronized. Taking the clock from the gravitational field to space requires acceleration which tends to increase the potential difference of the clock. However, in an attempt to bring the clock back, its potential difference decreases (the clock appears to decelerate in spacetime). This case is no different from taking a clock from some point in space to a black hole and back again to its initial position; thus, the time interval is reserved and no one is right or wrong. The twins are then equal after the round trip; but at the period of separation, each thinks that his brother is younger.
4.6. Relativity of Matter and Wave (Relativistic Duality)
I shall now prove that no mechanical experiment can result to the Einstein’s rest mass equation. This means that the mass of the system does not fit into the Lorentz transformation but rather the (Galilean-Lorentz) transformation equations derived above. The inconsistency of the Lorentz transformation employed by Einstein can be sufficiently understood from the work of Denci., 2016 [16]. However, this will be shown here by considering the elastic collision experiment considered by Miller Jr. F, 1999 [7] and Tipler & Llewellyn, 2008 [1]. It will be shown with the help of this leaner momentum experiment that it is mechanically impossible for any experiment to yield the Einstein’s rest mass equation.In the experiment, there are two observers A&B with A stationary along a side-walk and B in a train moving past A with velocity v. Both observers are armed with identical balls of masses 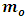 (its rest mass) and m (it’s mass in the moving frame). Both observers then decide to throw their balls with equal velocities so that they collide just when they are midway between the side-walk and the train as illustrated by figure (3) below:
(its rest mass) and m (it’s mass in the moving frame). Both observers then decide to throw their balls with equal velocities so that they collide just when they are midway between the side-walk and the train as illustrated by figure (3) below: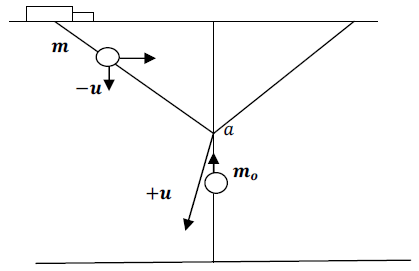 | Figure 3 |
Before impact, the y-coordinate of the velocity of A’s ball is 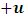 and that of B is
and that of B is 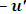 . After impact, the y-coordinates of the two observers are reversed,
. After impact, the y-coordinates of the two observers are reversed, 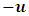 for A and
for A and 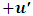 for B. Applying the well known law of conservation of momentum to the elastic collision, A concludes that
for B. Applying the well known law of conservation of momentum to the elastic collision, A concludes that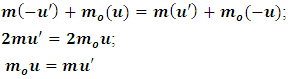 | (29) |
According to the experiment, the elastic collision should occur at the midpoint, thus, the balls are to be thrown with equal speed since the point of collision (the midpoint) is equal-distance between the two observers.We can now apply the principle of relativity to analyze the experiment with respect to the stationary observer (observer A). With respect to A, observer B is in relative motion; thus, there is a time dilation effect in his (B) frame. The Einstein’s conclusion is that due to time dilation, A’s velocity is greater than B. Using the Lorentz transformation of velocity, one obtains a relationship between the two speeds to be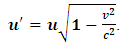 | (30) |
which when substituted into eq. (29), yields eqn. (2), the Einstein’s rest mass equation.However, mechanically this analysis is not consistent with physical observation because the Lorentz transformation, as used is an independent analysis, breaks down if the event is described by a single observer. To see this, the following arguments can be proposed:From the analysis above, A claims that he sets his ball into motion before B (that is, there is a time dilation effect in B’s frame with respect to observer A). This means that there is a time discrepancy between the two events in each frame. Thus, if A’s velocity is greater than B (by the Lorentz transformation equations); then, in any correct mechanical interpretation, observer A will not expect the collision to be at midway, since according to this observer, his ball has covered some distance before B sets his ball in motion (by time dilation in B). Instead, observer A will expect the collision to occur at some point 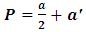 , because, B’s ball is released later then A and hence will arrive just after A’s ball has passed the center and now at the point
, because, B’s ball is released later then A and hence will arrive just after A’s ball has passed the center and now at the point 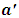 which depends on the time elapse before B sets his ball into motion with respect to A or precisely due to the relative velocity of both observers.In fact, the distance
which depends on the time elapse before B sets his ball into motion with respect to A or precisely due to the relative velocity of both observers.In fact, the distance 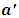 would almost be more than half way between the center and observer B because, according to the Lorentz velocity equation, ball A has a far greater velocity than that of B. Moreover, time dilation in B’s frame will also allow A’s ball to cover more distance before B release his ball with even lower velocity then A’s ball that has covered some distance during the time discrepancy. By the Einstein’s analysis, there will be no possibility for the balls to collide at the center.However, suppose we insist that the collision is done at the midpoint, then this by mechanics, can only be possible if B gives his ball a greater velocity so that even though his ball is released later (that is, there is a time dilation in his frame thus he seems to release his ball at a later time) as claimed by A, but collision is still made at the midpoint as A concludes. This means that B’s velocity must be greater than A’s as judged by this stationary observer. The analysis is then consistent with eqs. (22) and (23).It can then be concluded that the speed of the ball cannot be given by the Lorentz transformation equation but rather the modified Galilean equation derived above: eqns. (22) and (23). Then, applying the modified Galilean transformation (in this case eq. (24) for the motion of the balls alone their y coordinate) and some algebraic manipulations we have the velocity of the ball in B’s frame with respect to A to be:
would almost be more than half way between the center and observer B because, according to the Lorentz velocity equation, ball A has a far greater velocity than that of B. Moreover, time dilation in B’s frame will also allow A’s ball to cover more distance before B release his ball with even lower velocity then A’s ball that has covered some distance during the time discrepancy. By the Einstein’s analysis, there will be no possibility for the balls to collide at the center.However, suppose we insist that the collision is done at the midpoint, then this by mechanics, can only be possible if B gives his ball a greater velocity so that even though his ball is released later (that is, there is a time dilation in his frame thus he seems to release his ball at a later time) as claimed by A, but collision is still made at the midpoint as A concludes. This means that B’s velocity must be greater than A’s as judged by this stationary observer. The analysis is then consistent with eqs. (22) and (23).It can then be concluded that the speed of the ball cannot be given by the Lorentz transformation equation but rather the modified Galilean equation derived above: eqns. (22) and (23). Then, applying the modified Galilean transformation (in this case eq. (24) for the motion of the balls alone their y coordinate) and some algebraic manipulations we have the velocity of the ball in B’s frame with respect to A to be: 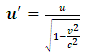 | (31) |
Substituting this result into eq. (29) above gives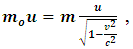 rearranging this result, we have
rearranging this result, we have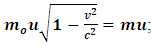 and finally, dividing through by
and finally, dividing through by 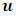 yields
yields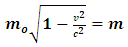 | (32) |
Equation (32) shows a negative correlation between speed and mass which is thus consistent with classical and quantum mechanics as expected.If the speed of the particle is in a Newtonian limit 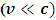 , eq. (32) reduces to
, eq. (32) reduces to 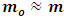 ; its classical value is desire. However, as
; its classical value is desire. However, as 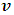 approaches the speed of light, the mass of the object approaches zero; this result will then be used to prove that the particle becomes wave at relativistic speed (wave-particle duality). Equation (32) can be used with the help of classical mechanics to derive the Einstein’s mass-energy relation and the Newtonian kinetic energy equation which is presented as followed:In classical mechanics, the “linear momentum” of a moving body is given (ambiguously) by the partial differential equation
approaches the speed of light, the mass of the object approaches zero; this result will then be used to prove that the particle becomes wave at relativistic speed (wave-particle duality). Equation (32) can be used with the help of classical mechanics to derive the Einstein’s mass-energy relation and the Newtonian kinetic energy equation which is presented as followed:In classical mechanics, the “linear momentum” of a moving body is given (ambiguously) by the partial differential equation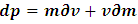 | (33) |
And the rate of change of momentum with respect to time is defined as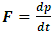 | (34) |
Also, the energy required to do work on the system is given as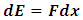 | (35) |
Substituting eqn. (34) into eqn. (35), we have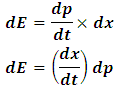 But
But 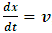 , thus
, thus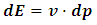 Substituting eq. (33) into the last expression, we have
Substituting eq. (33) into the last expression, we have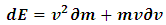 | (36) |
In a Newtonian limit,  , so
, so 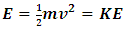 .Now, from classical mechanics we know that for work to be done on a system, a force must be applied to move the constituents of that system through a distance; in order words, the system must undergo some form of motion from an initial position to a final position. Work therefore cannot be achieved in the absence of a kinetic energy, since the system must undergo a form of motion with speed
.Now, from classical mechanics we know that for work to be done on a system, a force must be applied to move the constituents of that system through a distance; in order words, the system must undergo some form of motion from an initial position to a final position. Work therefore cannot be achieved in the absence of a kinetic energy, since the system must undergo a form of motion with speed 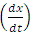 in the direction of the applied force. We can then conclude that the magnitude of the work done on the system is therefore the kinetic energy of that system.Also, because the system should lose mass from the argument above, the kinetic energy of a system has a negative correlation with its mass;
in the direction of the applied force. We can then conclude that the magnitude of the work done on the system is therefore the kinetic energy of that system.Also, because the system should lose mass from the argument above, the kinetic energy of a system has a negative correlation with its mass; 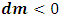 ; therefore, as the mass of the system decreases, its kinetic energy must be increasing as well. This analysis also holds for the classical linear momentum of the system since it depends on the velocity of the system; thus, this negative correlation between speed and mass allows us to redefine the momentum and kinetic energy of the system unambiguously as:
; therefore, as the mass of the system decreases, its kinetic energy must be increasing as well. This analysis also holds for the classical linear momentum of the system since it depends on the velocity of the system; thus, this negative correlation between speed and mass allows us to redefine the momentum and kinetic energy of the system unambiguously as: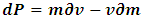 | (37) |
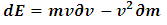 | (38) |
It will later be proven however, that eqns (37) and (38) are valid instead of their classical interpretations. Now, eq. (32) can be equivalently written as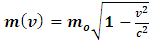 Since the mass is a function of speed. Differentiating this result with respect to
Since the mass is a function of speed. Differentiating this result with respect to 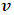 gives
gives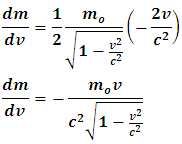 But
But 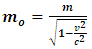 , by eq.32; thus,
, by eq.32; thus,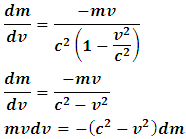 | (39) |
Substituting eq. (39) into eq. (38), we have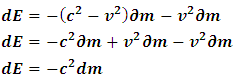 And by integrating, we have
And by integrating, we have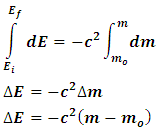 And upon rearranging, we have
And upon rearranging, we have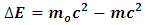 | (40) |
This is therefore the Einstein’s mass-energy equation which is just the relativistic kinetic energy of the particle. We now use eq. (40) to derive the classical kinetic energy equation for the particle. To derive the Newtonian classical equation form eq (40), the following argument is proposed from the viewpoint of classical thermodynamics:According to the laws of classical thermodynamics, the total internal energy (denoted by 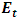 ) of any real system is defined as the energy of all the constituent atoms and/ or molecules that make up that system as well as the energy of the bonds that bind the atoms or particles of the system together. This energy can be expressed mathematically as the sum of the system’s total potential and kinetic energies
) of any real system is defined as the energy of all the constituent atoms and/ or molecules that make up that system as well as the energy of the bonds that bind the atoms or particles of the system together. This energy can be expressed mathematically as the sum of the system’s total potential and kinetic energies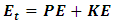 | (41) |
Supposing that the system is not suggested to any form of motion-except that its atoms are vibrating, rotating or translating in space- than the kinetic energy (or more precisely the macroscopic kinetic energy) of the system is zero and the potential energy of the system –by the law of conservation of energy- is just equal to the total internal energy. That is, for 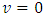 , eq. (41) becomes
, eq. (41) becomes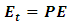 | (42) |
From this, we can now suggest a proper meaning for the terms in eq. (40). Using eq. (32), we can express eq. (40) in an informal manner as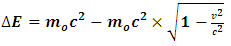 | (43) |
Where 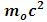 is the energy of the system at rest and
is the energy of the system at rest and 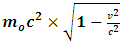 is the energy of the system at some speed
is the energy of the system at some speed 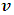 .Now, if a system of mass
.Now, if a system of mass 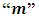 is in motion with speed
is in motion with speed 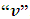 , the potential energy of such system decreases as its speed increases. However, the potential energy of such system is not necessarily zero since the system still has mass
, the potential energy of such system decreases as its speed increases. However, the potential energy of such system is not necessarily zero since the system still has mass 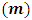 and at a particular time
and at a particular time 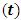 it is at some known position r in space. Therefore, the system will only have zero potential energy if its mass is zero (like a wave) which can only be achieved if
it is at some known position r in space. Therefore, the system will only have zero potential energy if its mass is zero (like a wave) which can only be achieved if 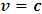 . Thus, the valid relativistic equation that describes the potential energy of any system in the universe either in motion or at rest is
. Thus, the valid relativistic equation that describes the potential energy of any system in the universe either in motion or at rest is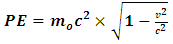 | (44) |
At 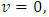 the system has no kinetic energy, so eq (44) reduces consistently to
the system has no kinetic energy, so eq (44) reduces consistently to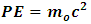 | (45) |
Thus, by the argument above, we can recognize eq (45) as the total internal energy of the system. The fundamental problem with Einstein’s relativistic mechanics is then resolved by eq. (44), because as the velocity of the particle increases, its potential energy decreases as well which is then consistent with the language of both classical and quantum mechanics (since the potential energy of the system can be ignored for particles at high speed in the Schrödinger wave equation).The difference between the total internal energy and the potential energy of any system is then defined as the kinetic energy of that system (denoted by 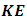 ); so
); so 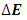 is the kinetic energy of the system as stated above. Thus eq. (43) can be re-expressed as
is the kinetic energy of the system as stated above. Thus eq. (43) can be re-expressed as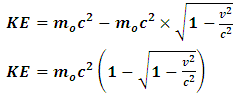 | (46) |
For a non-relativistic case in which  , we use the Maclaurin series expansion
, we use the Maclaurin series expansion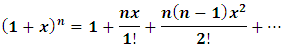 Letting
Letting 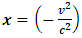 , we have
, we have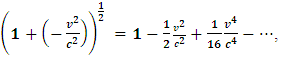 Thus eq. (46) becomes
Thus eq. (46) becomes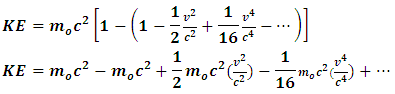 Ignoring large powers of c and canceling liked- terms, we have
Ignoring large powers of c and canceling liked- terms, we have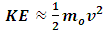 | (47) |
This is therefore the Newtonian kinetic energy equation as desires.Now, as the speed of the particle approaches the speed of light, 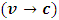 , the potential energy of the system approaches zero
, the potential energy of the system approaches zero 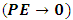 as well; thus, the total internal energy of the system, by the law of conservation of energy, should equal the kinetic energy of the system. But if we express the total internal energy by
as well; thus, the total internal energy of the system, by the law of conservation of energy, should equal the kinetic energy of the system. But if we express the total internal energy by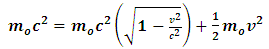 | (48) |
then, for a special case in which 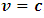 , the potential energy equals zero
, the potential energy equals zero 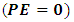 and eq. (48) reduces to
and eq. (48) reduces to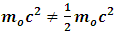 | (49) |
Newtonian kinetic energy equation thus violates the law of conservation of energy. Thus, for energy to be conserved, the kinetic energy of the particle should be expressed as the energy of an electromagnetic radiation by Plank’s relationship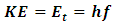 | (50) |
Eq. (50) is a wave equation which is only true if the system can be considered a wave; the wave- particle duality of matter is thus proven.If we express the state of the system by the Klein-Gordon equation, eq. (4); then, using eq.(32), we will have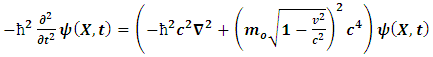 | (51) |
As the particle accelerates near the speed of light, the potential energy term becomes zero, thus, eq. (51) reduces to eq (7) as desire.This means that at high speed near that of the speed of light, the particle can no longer be regarded as bits of matter but rather a fast moving electromagnetic radiation with energy equal to the energy store in the particle; energy is then conserved.A physical prove can be find to support eq (51). Consider the decay process of the unstable particle called the  meson Miller Jr., 2008 [7]. Before the disintegration process, the particle obtains a high enough kinetic energy thus, making the system’s sub-particles to move at the speed of light. As a result, the particle disappears and an electromagnetic radiation appears with its energy equal to the total internal energy of the particle. But at rest, the particle possesses no kinetic energy so its total internal energy is just equal to its potential energy as expected. Eq. (51) is therefore valid.
meson Miller Jr., 2008 [7]. Before the disintegration process, the particle obtains a high enough kinetic energy thus, making the system’s sub-particles to move at the speed of light. As a result, the particle disappears and an electromagnetic radiation appears with its energy equal to the total internal energy of the particle. But at rest, the particle possesses no kinetic energy so its total internal energy is just equal to its potential energy as expected. Eq. (51) is therefore valid.
4.7. Linear Momentum
We now return to the law of conservation of linear momentum to validate eqns (37) and (38). By eq. (32), the linear momentum of a particle of mass (m) can be expressed relativistically as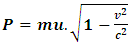 | (52) |
Thus, the momentum of the system decreases as the speed of the particle increases. This should not be the case because, classical mechanics tells us that the linear momentum of a system increases as the speed of the particle increases by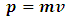 | (53) |
Therefore, eq. (52) violates the law of conservation of momentum by the definition of classical mechanics, since we see that the system lose momentum with speed.However, suppose we consider a system of total internal energy 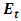 ; then, by special relativity, its linear momentum can be expressed as
; then, by special relativity, its linear momentum can be expressed as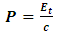 | (54) |
Then, using eq. (48), we have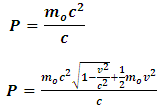 | (55) |
Now, if the system is at rest, its kinetic energy is zero; thus, its linear momentum is given as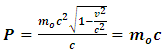 | (56) |
The system will then have a non-zero linear momentum even at rest.Again, suppose the velocity of the system reaches that of the speed of light, then, eq. (55) reduces to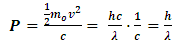 | (57) |
Therefore, no real system with a non-zero internal energy can have a zero linear momentum. We can then state the law of conservation of momentum in a more general form in order to agree with all the possible states of the system. By this, we can propose two forms of linear momentum corresponding to the two possible energy states in which the system can be described: Kinetic momentum (which depends on the state of motion of the system and increases with speed) and Potential momentum (the momentum of the body at rest which depends on the position of the system and decreases with speed).Suppose the potential energy of a system depends on its position; then, the potential momentum by analogue must also depend on position. Thus, we can define the inertia force (which depends on the rest position of the system) as the rate of change of the body’s potential linear momentum with respect to position; therefore, if we let 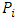 be the potential linear momentum, then, the initial force of the system can be defined as:
be the potential linear momentum, then, the initial force of the system can be defined as: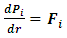 | (58) |
The inertia force of a system changes with the gravitational potential gradient (by classical mechanics), thus eq. (58) can be expressed as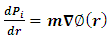 | (59) |
Where 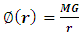 and
and 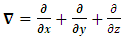 .By the same argument above, the kinetic momentum (denoted by
.By the same argument above, the kinetic momentum (denoted by 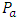 ) depends on the acceleration of the body; thus, if we consider the time rate of change of kinetic momentum then, we can define the force due to acceleration as:
) depends on the acceleration of the body; thus, if we consider the time rate of change of kinetic momentum then, we can define the force due to acceleration as: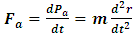 | (60) |
Then, by the law of conservation of linear momentum, we can show that the acceleration and gravitation of the body are related by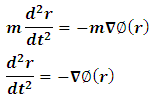 | (62) |
as desire.
5. Conclusions
To conclude, Einstein’s relativity is an incorrect description of reality and hence demands modification at least. By this conclusion, a unified theory can be established. However, although the work above does not give a Unified Theory, it shows a possibility that such theory is achievable.
ACKNOWLEDGEMENTS
I take this time to acknowledge Rowena C. Cooper for her tireless effort in providing me comfort during the most difficult times of my work. I would also like to acknowledge my dearest friend Elizabeth C. Singbah for her words of encouragement which provided me a confidence including “my brothers” Jackson G. White, Bill Nueita, Emmanuel H. Hills, Henry B. Quoie and Darkamou Yarkpawolo without whose courage this work would not have made a success. They find all reasons to believe in my ability when I had no reason to trust myself. Finally, I want to extend my thanks and appreciations to the faculty members of the Emmet A. Dennis College of Natural Sciences, Cuttington University especially Mr. Emmanuel Gbarnjah, Mr. Joseph Z. Arku and Mr. Christian Bob Nicol for their guidance.
References
| [1] | P. A. Tippler and R. A. Llewellyn; Modern Physics 5th edition; W.H. Freeman and Company, New York; 2008. |
| [2] | R. Resnick.; Induction to Relativity, Wiley, New York, 1968. |
| [3] | D. Bohm; The Special Theory of Relativity, W. A. Benjamin, New York, 1965. |
| [4] | R. Katz; An Introduction to Special Relativity; D. Von Nostrand Company Inc, Lincoln; 2008. |
| [5] | J. D. Cutnell and K. W. Johnson; College Physics 8th edition, Wiley, New York; 2009. |
| [6] | R. A. Serway and R. A. Beichner; Physics for Scientist and Engineers with Modern Physics 5th edition; Thomson Learning Inc, Australia, Canada, Mexico, Singapore, Spain, United Kingdom, U.S.A; 2000. |
| [7] | F. Miller Jr.; College physics 5th edition, The Binnacle Publishing Group, United States of America; 1999. |
| [8] | A. Einstein; On the Electrodynamics of Moving Bodies [English translated Version]; Annalen der Physik, June 30, 1905. |
| [9] | A. Einstein; Does the Inertia of a Body depend upon its Energy Content? [English translated version]; Annalan der Physik; September 7, 1905. |
| [10] | N. Hamdan and A. K. Hariri; Derivation of Einstein’s E=mc2 from the Classical Force Laws; Department of Physics, University of Aleppo, Syria; 2007. |
| [11] | L. Peliti; Elementary Derivation of the Expressions of Momentum and Energy in Special Relativity; Simons Center for System Biology, Institute for Advanced Study, New Jessy, United States of America; 2016. |
| [12] | F. W Sears, M. W. Zemansky, and H. D. Young; College Physics 6th edition; Addison-Wesley publishing Company Inc, USA and Canada; 1985. |
| [13] | M. Srednicki; Quantum field theory; University of California, Santa Barbara, 2016. |
| [14] | L. Ryder; Introduction to General Relativity 2nd edition; Cambridge University Press; New York; 2009. |
| [15] | O. Gron and S. Hervik, Einstein’s General Theory of Relativity. |
| [16] | V. Danci; The Core Mathematical Error of Einstein’s Special Relativity Theory (The Origin of the Relativistic Paradoxes in the Pre-relativistic Electrodynamics); Toronto, Canada; March 17, 2016. |



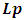 moves with velocity
moves with velocity 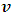 parallel to its length, the object’s length relative to the stationary observer will appear to reduce in the moving frame by the equation
parallel to its length, the object’s length relative to the stationary observer will appear to reduce in the moving frame by the equation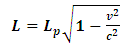
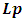 is the recorded length in the rest frame, L is the length in the moving frame and
is the recorded length in the rest frame, L is the length in the moving frame and 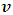 is the speed of the object.According to Eq. (1), if the speed of the object increases, its length decreases; thus, there is an inverse relationship between the length and speed of the object. This decrease in length is limited by the velocity of light
is the speed of the object.According to Eq. (1), if the speed of the object increases, its length decreases; thus, there is an inverse relationship between the length and speed of the object. This decrease in length is limited by the velocity of light 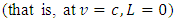 . Therefore, if the speed of the particle reaches that of light, its length in the moving frame becomes zero with respect to the stationary observer.On the other hand, to a stationary frame of reference, if an object of mass
. Therefore, if the speed of the particle reaches that of light, its length in the moving frame becomes zero with respect to the stationary observer.On the other hand, to a stationary frame of reference, if an object of mass 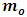 moves with speed
moves with speed 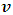 , the mass of the object increases with increased speed by the equation
, the mass of the object increases with increased speed by the equation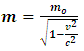
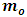 to be the mass of the object at rest and m is the mass of the same object at a speed
to be the mass of the object at rest and m is the mass of the same object at a speed  , the speed of the particle. By this equation, as the object moves through space with a speed near that of light, its mass increases (at the speed of light, the system has an infinite mass and energy). Equations (1) and (2) can best be understood from the works of (Tiple P. A and Llewellyn, 2008 [1], Resnick. R, 1968 [2], Bohm D, 1965 [3], Katz. R, 2008 [4], Cutnell J. D and Johnson K. W, 2009 [5], Serway R. A and Beichner, 2000 [6], Miller Jr. F, 1999 [7], Einstein A (1905) [8,9] Hamdan and Hariri, 2007 [10] and Peliti L, 2016 [11] and Sears, Zemansky and Young, 1985 [12].It shall now be proven; however, that Equations (1) and (2) together lead to an inconsistent conclusion. Thus, both equations cannot be accurate simultaneously when applied to matter as concluded by Einstein’s Relativity (the conclusion of the theory is thus non-uniform).
, the speed of the particle. By this equation, as the object moves through space with a speed near that of light, its mass increases (at the speed of light, the system has an infinite mass and energy). Equations (1) and (2) can best be understood from the works of (Tiple P. A and Llewellyn, 2008 [1], Resnick. R, 1968 [2], Bohm D, 1965 [3], Katz. R, 2008 [4], Cutnell J. D and Johnson K. W, 2009 [5], Serway R. A and Beichner, 2000 [6], Miller Jr. F, 1999 [7], Einstein A (1905) [8,9] Hamdan and Hariri, 2007 [10] and Peliti L, 2016 [11] and Sears, Zemansky and Young, 1985 [12].It shall now be proven; however, that Equations (1) and (2) together lead to an inconsistent conclusion. Thus, both equations cannot be accurate simultaneously when applied to matter as concluded by Einstein’s Relativity (the conclusion of the theory is thus non-uniform).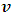 . Suppose we consider an ordinary rectangular metal rod of mass m and length L, then, by the help of Einstein’s relativistic mechanics, we can calculate the length and mass of such rod with respect to a stationary observer by equations (1) and (2) and hence its mass-density. Then if both equations are correct as it is expected, they must lead to a conclusion consistent both with the objective reality and the theory itself.Einstein’s Relativity allows us to measure the density of the object at any speed, since we are able to determine the mass and volume of the object even if the object is accelerating. Thus, for our experiment, suppose we seek to find the mass-density (or the relativistic mass-density) of the metal rod moving with a velocity
. Suppose we consider an ordinary rectangular metal rod of mass m and length L, then, by the help of Einstein’s relativistic mechanics, we can calculate the length and mass of such rod with respect to a stationary observer by equations (1) and (2) and hence its mass-density. Then if both equations are correct as it is expected, they must lead to a conclusion consistent both with the objective reality and the theory itself.Einstein’s Relativity allows us to measure the density of the object at any speed, since we are able to determine the mass and volume of the object even if the object is accelerating. Thus, for our experiment, suppose we seek to find the mass-density (or the relativistic mass-density) of the metal rod moving with a velocity 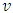 with respect to the stationary observer; then, we can write
with respect to the stationary observer; then, we can write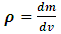
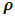 is the density of the object at the speed
is the density of the object at the speed 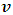 with its mass given by equation (2). To get a clearer picture of the relationship between mass and volume, we can rearrange equation (3) as
with its mass given by equation (2). To get a clearer picture of the relationship between mass and volume, we can rearrange equation (3) as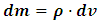
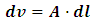
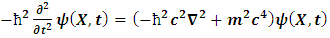
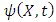 is the wave function that describes the state of the system.Now, suppose the mass (m) of the particle depends on its speed in the box; then, relativistically, m can be given by eq (2). But quantum mechanics tells us that as the speed of the particle increases, its potential energy is consider zero; thus, at
is the wave function that describes the state of the system.Now, suppose the mass (m) of the particle depends on its speed in the box; then, relativistically, m can be given by eq (2). But quantum mechanics tells us that as the speed of the particle increases, its potential energy is consider zero; thus, at 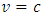 , eq. (6) reduces to
, eq. (6) reduces to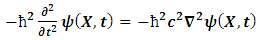
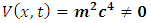
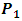 to another point
to another point 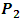 ; Miller Jr. F (1999) [7], Serway & Beichner (2000) [6], Tippler and Llewellyn (2008) [1], Cutnell & Johnson (2009) [5] and Sears, Zemansky and Young, 1985 [12]. What is the distance between the two points? To answer this question, observer S sees that he is stationary with respect to the moving frame and the particle; thus, if the particle is moving with the speed of light, he finds that the distance between the points (or the distance covered by the particle) is
; Miller Jr. F (1999) [7], Serway & Beichner (2000) [6], Tippler and Llewellyn (2008) [1], Cutnell & Johnson (2009) [5] and Sears, Zemansky and Young, 1985 [12]. What is the distance between the two points? To answer this question, observer S sees that he is stationary with respect to the moving frame and the particle; thus, if the particle is moving with the speed of light, he finds that the distance between the points (or the distance covered by the particle) is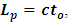
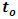 is the time with respect to S and
is the time with respect to S and 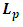 is the distance/ length recorded by S called the proper length. Then, by symmetry, we see that S’ believes that he is at rest with respect to the particle; thus, the distance between the two points in S’ frame is given by eq (9) (both observer believe that they are stationary so their length is unaffected by relative motion).Now, suppose again that we seek to describe this event with respect to one of the frames, say S, what will be the length between the two points in the moving frame S’ as judged by S? This question is then equivalent to the unanswered question in experiment 1. However, to answer this question, we see that observer S assumes to be at rest while S’ is in motion (Resnick. R (1968) [2], Bohm. D (1965) [3], Miller Jr. (1999) [7], Serway & Beichner (2000) [6], Cutnell & Johnson (2009) [5], Tipler & Llewellyn (2008) [1] and Sears, Zemansky and Young, 1985 [12]; this observer S will then see that relative motion with affect the distance between the two points in S’. That is, S sees that S’ is moving with a speed v; thus, he finds that relative motion causes a time dilation in S’ frame given by
is the distance/ length recorded by S called the proper length. Then, by symmetry, we see that S’ believes that he is at rest with respect to the particle; thus, the distance between the two points in S’ frame is given by eq (9) (both observer believe that they are stationary so their length is unaffected by relative motion).Now, suppose again that we seek to describe this event with respect to one of the frames, say S, what will be the length between the two points in the moving frame S’ as judged by S? This question is then equivalent to the unanswered question in experiment 1. However, to answer this question, we see that observer S assumes to be at rest while S’ is in motion (Resnick. R (1968) [2], Bohm. D (1965) [3], Miller Jr. (1999) [7], Serway & Beichner (2000) [6], Cutnell & Johnson (2009) [5], Tipler & Llewellyn (2008) [1] and Sears, Zemansky and Young, 1985 [12]; this observer S will then see that relative motion with affect the distance between the two points in S’. That is, S sees that S’ is moving with a speed v; thus, he finds that relative motion causes a time dilation in S’ frame given by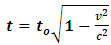
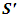 moving relative to another frame S with speed
moving relative to another frame S with speed 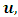 the Galilean transformation of velocity that reserves Newton’s laws of mechanics in both frames is
the Galilean transformation of velocity that reserves Newton’s laws of mechanics in both frames is 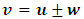 relative to the stationary frame. But suppose an observer in a frame (S’ for example) wants to record the velocity of an object by his own specetime coordinate, what is the speed of the particle in this frame? In other words, does the Galilean transformation equation holds for an experiment conducted by an observer in his own frame?To answer this question, let us imagine some physical experiment in which there are two observers, one being stationary and the other on a moving train. Let us assume that the train is moving westward with a speed
relative to the stationary frame. But suppose an observer in a frame (S’ for example) wants to record the velocity of an object by his own specetime coordinate, what is the speed of the particle in this frame? In other words, does the Galilean transformation equation holds for an experiment conducted by an observer in his own frame?To answer this question, let us imagine some physical experiment in which there are two observers, one being stationary and the other on a moving train. Let us assume that the train is moving westward with a speed 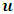 past a stationary observer. Now, suppose that a wind is blowing eastward with a speed
past a stationary observer. Now, suppose that a wind is blowing eastward with a speed 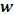 relative to the stationary observer. By Galilean Relativity, the stationary observer will measure the train’s speed to be
relative to the stationary observer. By Galilean Relativity, the stationary observer will measure the train’s speed to be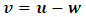
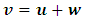
 . Galilean Relativity therefore implies that no transformation equation can be valid for an observer measuring his own speed because there is no influence of relative motion with respect to this observer. Thus, it can be postulated that no mechanical event or experiment is affected by relative motion if the event is described by an observer in his own frame. Galilean transformation equations are then applicable only when comparing physics in one reference frame relative to another.Now, consider the same experiment above performed in a uniform still wind (by the phrase “uniform still wind”, It means a region in which the wind blows in all directions with equal speed or appears to not blow at all). For the same train moving again in the west and east directions, it will experience the same magnitude of inertia force in either of these directions as judged by the stationary observer. Thus, this stationary observer will measure equal speed for the train’s motion in both directions. Galilean Relativity then produces a null result for the case of the uniform still wind, since any stationary observer will not be able to notice a change of velocity of the train in both directions at least if the experiment were performed in a still wind. We now compare this result to the Michelson- Morley experiment to consider the relativistic speed limit (the speed of light).Consider the Michelson- Morley experiment- (Miller Jr. F, 1999 [7]; Tipler and Llewellyn, 2008 [1]; Serway and Beichner, 2000 [6]; Resnick. R, 1968 [2], Bohm 1965 [3]; Cutnell & Johnson, 2009 [5] and Sears, Zemansky and Young, 1985 [12] - in which the earth moves through space (the ether) with speed
. Galilean Relativity therefore implies that no transformation equation can be valid for an observer measuring his own speed because there is no influence of relative motion with respect to this observer. Thus, it can be postulated that no mechanical event or experiment is affected by relative motion if the event is described by an observer in his own frame. Galilean transformation equations are then applicable only when comparing physics in one reference frame relative to another.Now, consider the same experiment above performed in a uniform still wind (by the phrase “uniform still wind”, It means a region in which the wind blows in all directions with equal speed or appears to not blow at all). For the same train moving again in the west and east directions, it will experience the same magnitude of inertia force in either of these directions as judged by the stationary observer. Thus, this stationary observer will measure equal speed for the train’s motion in both directions. Galilean Relativity then produces a null result for the case of the uniform still wind, since any stationary observer will not be able to notice a change of velocity of the train in both directions at least if the experiment were performed in a still wind. We now compare this result to the Michelson- Morley experiment to consider the relativistic speed limit (the speed of light).Consider the Michelson- Morley experiment- (Miller Jr. F, 1999 [7]; Tipler and Llewellyn, 2008 [1]; Serway and Beichner, 2000 [6]; Resnick. R, 1968 [2], Bohm 1965 [3]; Cutnell & Johnson, 2009 [5] and Sears, Zemansky and Young, 1985 [12] - in which the earth moves through space (the ether) with speed  . An ether wind is expected to blow past the earth in an opposite direction at the same speed with which the earth moves relative to space (the ether). This speed can be considered “the inertia force” at least in the case of this experiment. Then, if
. An ether wind is expected to blow past the earth in an opposite direction at the same speed with which the earth moves relative to space (the ether). This speed can be considered “the inertia force” at least in the case of this experiment. Then, if  is the speed of the Ether wind relative to earth, a light beam is expected to have a maximum and a minimum velocities of
is the speed of the Ether wind relative to earth, a light beam is expected to have a maximum and a minimum velocities of 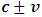 in view of the Galilean Relativity ( if we assume that the ether is not uniformly still). However, if we assume that space (or the ether) is uniformly still in all directions, then an object moving through it will experience an equal inertia force in any direction of its motion. Then, for a beam of light as in the case of the experiment above, the light will have equal speed in both directions relative to a stationary observer on earth; the speed of the light with respect to the ether is therefore the same as that relative to the earth; a null result is then produced for still ether.Thus, the null result of the Michelson-Morley experiment is fundamentally not because light violates the Galilean speed transformation, but rather as a result of the fact that space (or the ether wind) itself is still or uniform in all directions; thus, the only absolute velocity of the earth relative to space (the ether) is the one observed. For an experimenter wanting to detect a small change in the light’s speed, the result will always be null (the beam will experience equal opposing force in any direction). If we consider space as the ether itself and assume a homogenous universe, then we can conclude that the expansion of the universe must be homogenous. A general proof that the speed of light is affected by relative motion (it is not absolute when comparing two frames in relative motion) can be given by the experiment below.Consider the physical experiment with two frames of references: A being stationary while B is moving in the positive x direction with a speed
in view of the Galilean Relativity ( if we assume that the ether is not uniformly still). However, if we assume that space (or the ether) is uniformly still in all directions, then an object moving through it will experience an equal inertia force in any direction of its motion. Then, for a beam of light as in the case of the experiment above, the light will have equal speed in both directions relative to a stationary observer on earth; the speed of the light with respect to the ether is therefore the same as that relative to the earth; a null result is then produced for still ether.Thus, the null result of the Michelson-Morley experiment is fundamentally not because light violates the Galilean speed transformation, but rather as a result of the fact that space (or the ether wind) itself is still or uniform in all directions; thus, the only absolute velocity of the earth relative to space (the ether) is the one observed. For an experimenter wanting to detect a small change in the light’s speed, the result will always be null (the beam will experience equal opposing force in any direction). If we consider space as the ether itself and assume a homogenous universe, then we can conclude that the expansion of the universe must be homogenous. A general proof that the speed of light is affected by relative motion (it is not absolute when comparing two frames in relative motion) can be given by the experiment below.Consider the physical experiment with two frames of references: A being stationary while B is moving in the positive x direction with a speed 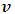 (Miller Jr. F; 1999 [7] and Sears, Zemansky and Young 1985 [12]). The two observers have a solar-light and the goal of the experiment is to measure the distance traveled by a light pulse after emission at some finite time (t) by both observers. But first, let us assume that the two observers are at the same point in space. Now, after 1 nanosecond, the pulse of light emitted from A travels a distance of about 0.3m and has reached a point x as shown in figure 1(a) below.
(Miller Jr. F; 1999 [7] and Sears, Zemansky and Young 1985 [12]). The two observers have a solar-light and the goal of the experiment is to measure the distance traveled by a light pulse after emission at some finite time (t) by both observers. But first, let us assume that the two observers are at the same point in space. Now, after 1 nanosecond, the pulse of light emitted from A travels a distance of about 0.3m and has reached a point x as shown in figure 1(a) below.

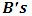 point of view, the light has a speed of
point of view, the light has a speed of 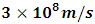 and has traveled a distance of about 0.3m in one nanosecond which is just point
and has traveled a distance of about 0.3m in one nanosecond which is just point 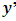 . Thus, both observers will measure the actual speed of the light if they view the event in their own frame (there will be no effect of relative motion on both frame in an independent conclusion).However, if we describe the event only in A’s spacetime coordinate, we see a contradiction. This observer sees the position of the light pulse in B’s frame at the point y’ instead of y, thus, he concludes that the motion of B gives the light an extra push, thus the speed of the light must be greater than c in B relative to A. This is however symmetric because, as B look at the light position at the point x which is just y instead of y’, he concludes that A is moving to the left thus his motion is giving an extra push to the light speed.Analyzing separately, we see that independently both observer will agree with the measured speed of light in their own frames. However, if we describe the event with respect to a single observer, we see that if this observer looks at the light pulse in his friend’s frame, he sees a small push of velocity
. Thus, both observers will measure the actual speed of the light if they view the event in their own frame (there will be no effect of relative motion on both frame in an independent conclusion).However, if we describe the event only in A’s spacetime coordinate, we see a contradiction. This observer sees the position of the light pulse in B’s frame at the point y’ instead of y, thus, he concludes that the motion of B gives the light an extra push, thus the speed of the light must be greater than c in B relative to A. This is however symmetric because, as B look at the light position at the point x which is just y instead of y’, he concludes that A is moving to the left thus his motion is giving an extra push to the light speed.Analyzing separately, we see that independently both observer will agree with the measured speed of light in their own frames. However, if we describe the event with respect to a single observer, we see that if this observer looks at the light pulse in his friend’s frame, he sees a small push of velocity 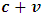 relative to this observer. In Galilean Relativity, there is no preferred frame, so the speed of light can be measured in any frame and produce the same value independently of the other. We then find that the two observers can independently agree with the right speed of their light pulse to be c in their own frames (Lorentz transformation), but when comparing their measurements with each other in relative motion, they do not agree with the observed speed of the light pulse (they see that the speed of the light is affected by the relative motion of each observer). The Galilean transformation of velocity therefore produces a “consistent” argument in the case of the light’s speed relative to both observers; the Lorentz transformation equations are therefore inapplicable if we view the event in one coordinate system.
relative to this observer. In Galilean Relativity, there is no preferred frame, so the speed of light can be measured in any frame and produce the same value independently of the other. We then find that the two observers can independently agree with the right speed of their light pulse to be c in their own frames (Lorentz transformation), but when comparing their measurements with each other in relative motion, they do not agree with the observed speed of the light pulse (they see that the speed of the light is affected by the relative motion of each observer). The Galilean transformation of velocity therefore produces a “consistent” argument in the case of the light’s speed relative to both observers; the Lorentz transformation equations are therefore inapplicable if we view the event in one coordinate system. . Then, if we impose the concept of simultaneity at the beginning and the end of the event (that the two events begin and end at the same time), then, we can conclude that the reference clock in A reads faster than the reference clock in B (time goes faster with respect to A then with respect to B); Einstein’s time dilation effect is then valid.Now, accepting Einstein’s time dilation as valid, we see that observer A measures a shorter time (time dilation) and a longer distance (length increment) for observer B. Then, if A measures a longer distance in B’s frame, he concludes that there is space dilation in his own frame (his distance is shorter than B’s) and a corresponding time increment (he measures a longer time interval in his own frame than B). Thus, if the event is described only with respect to a single observer, we find a paradox (either the space or time coordinate of each observer experiences a reduction or dilation).Then, since there is no absolute frame of reference and each observer can measure the speed of his light to be c independently, the following postulates can be stated: (1), there is no absolute reference frame in relativity (both classical and special relativity) and all the laws of physics including those of electrodynamics and mechanics must be valid in each frame INDEPENDENTLY and (2), time duration between events is not absolute in any reference frame in relative motion with some other initial frames and no single frame can have an effect of dilation (or reduction) in both its time-like and space-like coordinates simultaneously. In order words, length contraction (length or space dilation) must lead to time stretch (time increment) and vice versa.
. Then, if we impose the concept of simultaneity at the beginning and the end of the event (that the two events begin and end at the same time), then, we can conclude that the reference clock in A reads faster than the reference clock in B (time goes faster with respect to A then with respect to B); Einstein’s time dilation effect is then valid.Now, accepting Einstein’s time dilation as valid, we see that observer A measures a shorter time (time dilation) and a longer distance (length increment) for observer B. Then, if A measures a longer distance in B’s frame, he concludes that there is space dilation in his own frame (his distance is shorter than B’s) and a corresponding time increment (he measures a longer time interval in his own frame than B). Thus, if the event is described only with respect to a single observer, we find a paradox (either the space or time coordinate of each observer experiences a reduction or dilation).Then, since there is no absolute frame of reference and each observer can measure the speed of his light to be c independently, the following postulates can be stated: (1), there is no absolute reference frame in relativity (both classical and special relativity) and all the laws of physics including those of electrodynamics and mechanics must be valid in each frame INDEPENDENTLY and (2), time duration between events is not absolute in any reference frame in relative motion with some other initial frames and no single frame can have an effect of dilation (or reduction) in both its time-like and space-like coordinates simultaneously. In order words, length contraction (length or space dilation) must lead to time stretch (time increment) and vice versa.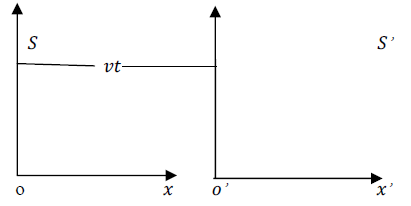
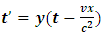
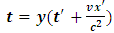
 -units away from his initial position. If the two coordinates system coincide at t = t’= 0; then, B’s final position after t seconds (with respect to A) is just the position of A (which is consider to be fixed at the origin) plus the additional
-units away from his initial position. If the two coordinates system coincide at t = t’= 0; then, B’s final position after t seconds (with respect to A) is just the position of A (which is consider to be fixed at the origin) plus the additional  units travelled by B after t seconds; that is,
units travelled by B after t seconds; that is,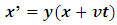
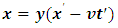
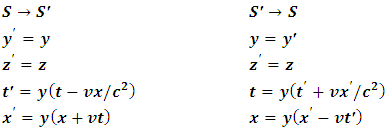 Symmetrically, the same result can be produce with respect to B’s. In this case, B believes that he is stationary and A is moving westward; hence, A has a time dilation effect in his frame; thus, B concludes that A’s time interval is given as
Symmetrically, the same result can be produce with respect to B’s. In this case, B believes that he is stationary and A is moving westward; hence, A has a time dilation effect in his frame; thus, B concludes that A’s time interval is given as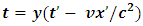
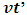 units away so, A is now at the point
units away so, A is now at the point 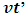 units away from him (B) given as
units away from him (B) given as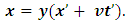
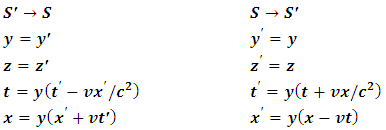 These are thus the modified Lorentz transformation (the Galilean-Lorentz transformation). The valid Galilean speed transformation equation can then be derived using the results above. For the purpose of this study, this will be done with respect to a single observer (A); it can be shown that B’s frame yields the same result.With respect to A, the velocity of any moving particle in his frame (along the positive
These are thus the modified Lorentz transformation (the Galilean-Lorentz transformation). The valid Galilean speed transformation equation can then be derived using the results above. For the purpose of this study, this will be done with respect to a single observer (A); it can be shown that B’s frame yields the same result.With respect to A, the velocity of any moving particle in his frame (along the positive 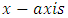 for simplicity) is given as
for simplicity) is given as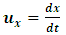
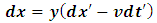
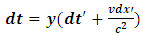
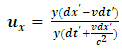 Canceling the common y term, we have
Canceling the common y term, we have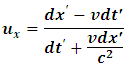 Dividing through by
Dividing through by 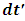 , we have
, we have Recognizing
Recognizing  , we have
, we have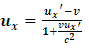
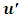 in (22), we have
in (22), we have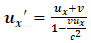
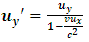
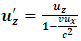
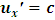 ; then, eq. (22) becomes
; then, eq. (22) becomes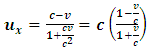
 increases as judged by A. This means that if observer B moves with the speed of light, a particle moving in his frame at the speed of light will appear to be stationary with respect to a stationary observer.On the other hand, suppose the particle’s speed is recorded to be
increases as judged by A. This means that if observer B moves with the speed of light, a particle moving in his frame at the speed of light will appear to be stationary with respect to a stationary observer.On the other hand, suppose the particle’s speed is recorded to be 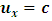 in the stationary frame (A); then, eq. (23) becomes
in the stationary frame (A); then, eq. (23) becomes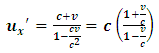
 increases because, observer A sees that B’s motion will give an extra push to the particle in this frame. There is a physical consequence of eq. (26) which is provided by the following physical experiment.Consider an experiment in which a spaceship moves in the positive x direction with a speed
increases because, observer A sees that B’s motion will give an extra push to the particle in this frame. There is a physical consequence of eq. (26) which is provided by the following physical experiment.Consider an experiment in which a spaceship moves in the positive x direction with a speed  . Now, imagine that a missile is attached to a fixed point midway between the front and rear of the ship. The goal of the experiment is for the pilot to release this missile at a target point which is some distance at head of the pilot (in the some positive x direction). Now, suppose the pilot releases this missile at the target with a speed c in the same direction of his spaceship; then, because his ship is moving with a much less velocity then the shooting missile, a stationary observer on earth will see that at a later time, the missile will overtake and arrive at the target point before the spaceship.Now, suppose this pilot raises the speed of his ship to
. Now, imagine that a missile is attached to a fixed point midway between the front and rear of the ship. The goal of the experiment is for the pilot to release this missile at a target point which is some distance at head of the pilot (in the some positive x direction). Now, suppose the pilot releases this missile at the target with a speed c in the same direction of his spaceship; then, because his ship is moving with a much less velocity then the shooting missile, a stationary observer on earth will see that at a later time, the missile will overtake and arrive at the target point before the spaceship.Now, suppose this pilot raises the speed of his ship to 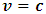 just the same time he had released the missile at the target point with the same speed c; an observer in the earth’s frame (or stationary frame) will not be able to detect any motion of the missile with respect to him, since it will not be able to overtake the spaceship. He will then conclude that the missile has not yet been released by this pilot, since it (the missile) maintains its same position on the spaceship at any later time. The speed of the missile is then zero with respect to a stationary observer on earth. By equation eq. (24), this should be the case because, as the pilot raises his speed to the speed of light, he moves with the same speed of his shooting missile towards the target point. Then, if both velocities are maintained, they will arrive at the target point in exactly the same time. Thus, the speed of the missile reduces as the pilot increases his speed with respect to the stationary observer.
just the same time he had released the missile at the target point with the same speed c; an observer in the earth’s frame (or stationary frame) will not be able to detect any motion of the missile with respect to him, since it will not be able to overtake the spaceship. He will then conclude that the missile has not yet been released by this pilot, since it (the missile) maintains its same position on the spaceship at any later time. The speed of the missile is then zero with respect to a stationary observer on earth. By equation eq. (24), this should be the case because, as the pilot raises his speed to the speed of light, he moves with the same speed of his shooting missile towards the target point. Then, if both velocities are maintained, they will arrive at the target point in exactly the same time. Thus, the speed of the missile reduces as the pilot increases his speed with respect to the stationary observer.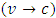 , we see that eqns (26) and (27) become:
, we see that eqns (26) and (27) become: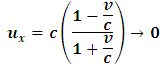 in S and
in S and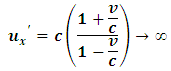 in S’.However, Maxwell’s unified theory of electrodynamics tells us that no speed can be greater than the speed of light in empty space. The relativistic consequence of this statement would be that the speed of every event in the universe must satisfy the inequality
in S’.However, Maxwell’s unified theory of electrodynamics tells us that no speed can be greater than the speed of light in empty space. The relativistic consequence of this statement would be that the speed of every event in the universe must satisfy the inequality 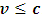 . The transformation equations thus appear to have a problem, since it violates the Maxwell’s speed inequality in one of the frames.However, the particle (by reality) is moving with a speed c independent of any observation (or if view in each frame independently); thus, the zero and infinite speeds recorded by the stationary observer is only a paradox deriving from the space-time description of the event with respect to this observer. Therefore, since special relativity allows a symmetric argument in both frames (that is, if each observer thinks that he is at rest), the two systems must behave as counter-part in order to keep the speed of light constant (by the law of conservation of space and time, both systems must be considered unity); that means that they must exist as though they are a single system (an entangled system). Now, suppose we consider the two frames of references as entangle pair, then, by Bohr’s argument, the frames must then have one velocity that must satisfy the Maxwell’s speed constraint.Now, suppose we let the speed of the individual system to be
. The transformation equations thus appear to have a problem, since it violates the Maxwell’s speed inequality in one of the frames.However, the particle (by reality) is moving with a speed c independent of any observation (or if view in each frame independently); thus, the zero and infinite speeds recorded by the stationary observer is only a paradox deriving from the space-time description of the event with respect to this observer. Therefore, since special relativity allows a symmetric argument in both frames (that is, if each observer thinks that he is at rest), the two systems must behave as counter-part in order to keep the speed of light constant (by the law of conservation of space and time, both systems must be considered unity); that means that they must exist as though they are a single system (an entangled system). Now, suppose we consider the two frames of references as entangle pair, then, by Bohr’s argument, the frames must then have one velocity that must satisfy the Maxwell’s speed constraint.Now, suppose we let the speed of the individual system to be 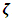 ; then, by the law of conservation of speed, the product of the speeds of the entangled systems is
; then, by the law of conservation of speed, the product of the speeds of the entangled systems is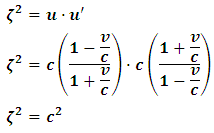
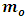 (its rest mass) and m (it’s mass in the moving frame). Both observers then decide to throw their balls with equal velocities so that they collide just when they are midway between the side-walk and the train as illustrated by figure (3) below:
(its rest mass) and m (it’s mass in the moving frame). Both observers then decide to throw their balls with equal velocities so that they collide just when they are midway between the side-walk and the train as illustrated by figure (3) below:
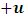 and that of B is
and that of B is 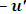 . After impact, the y-coordinates of the two observers are reversed,
. After impact, the y-coordinates of the two observers are reversed, 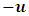 for A and
for A and 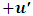 for B. Applying the well known law of conservation of momentum to the elastic collision, A concludes that
for B. Applying the well known law of conservation of momentum to the elastic collision, A concludes that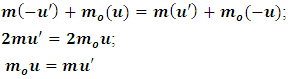
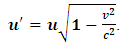
 , because, B’s ball is released later then A and hence will arrive just after A’s ball has passed the center and now at the point
, because, B’s ball is released later then A and hence will arrive just after A’s ball has passed the center and now at the point  which depends on the time elapse before B sets his ball into motion with respect to A or precisely due to the relative velocity of both observers.In fact, the distance
which depends on the time elapse before B sets his ball into motion with respect to A or precisely due to the relative velocity of both observers.In fact, the distance 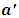 would almost be more than half way between the center and observer B because, according to the Lorentz velocity equation, ball A has a far greater velocity than that of B. Moreover, time dilation in B’s frame will also allow A’s ball to cover more distance before B release his ball with even lower velocity then A’s ball that has covered some distance during the time discrepancy. By the Einstein’s analysis, there will be no possibility for the balls to collide at the center.However, suppose we insist that the collision is done at the midpoint, then this by mechanics, can only be possible if B gives his ball a greater velocity so that even though his ball is released later (that is, there is a time dilation in his frame thus he seems to release his ball at a later time) as claimed by A, but collision is still made at the midpoint as A concludes. This means that B’s velocity must be greater than A’s as judged by this stationary observer. The analysis is then consistent with eqs. (22) and (23).It can then be concluded that the speed of the ball cannot be given by the Lorentz transformation equation but rather the modified Galilean equation derived above: eqns. (22) and (23). Then, applying the modified Galilean transformation (in this case eq. (24) for the motion of the balls alone their y coordinate) and some algebraic manipulations we have the velocity of the ball in B’s frame with respect to A to be:
would almost be more than half way between the center and observer B because, according to the Lorentz velocity equation, ball A has a far greater velocity than that of B. Moreover, time dilation in B’s frame will also allow A’s ball to cover more distance before B release his ball with even lower velocity then A’s ball that has covered some distance during the time discrepancy. By the Einstein’s analysis, there will be no possibility for the balls to collide at the center.However, suppose we insist that the collision is done at the midpoint, then this by mechanics, can only be possible if B gives his ball a greater velocity so that even though his ball is released later (that is, there is a time dilation in his frame thus he seems to release his ball at a later time) as claimed by A, but collision is still made at the midpoint as A concludes. This means that B’s velocity must be greater than A’s as judged by this stationary observer. The analysis is then consistent with eqs. (22) and (23).It can then be concluded that the speed of the ball cannot be given by the Lorentz transformation equation but rather the modified Galilean equation derived above: eqns. (22) and (23). Then, applying the modified Galilean transformation (in this case eq. (24) for the motion of the balls alone their y coordinate) and some algebraic manipulations we have the velocity of the ball in B’s frame with respect to A to be: 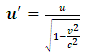
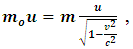 rearranging this result, we have
rearranging this result, we have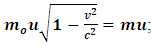 and finally, dividing through by
and finally, dividing through by 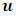 yields
yields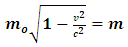
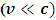 , eq. (32) reduces to
, eq. (32) reduces to 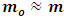 ; its classical value is desire. However, as
; its classical value is desire. However, as 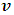 approaches the speed of light, the mass of the object approaches zero; this result will then be used to prove that the particle becomes wave at relativistic speed (wave-particle duality). Equation (32) can be used with the help of classical mechanics to derive the Einstein’s mass-energy relation and the Newtonian kinetic energy equation which is presented as followed:In classical mechanics, the “linear momentum” of a moving body is given (ambiguously) by the partial differential equation
approaches the speed of light, the mass of the object approaches zero; this result will then be used to prove that the particle becomes wave at relativistic speed (wave-particle duality). Equation (32) can be used with the help of classical mechanics to derive the Einstein’s mass-energy relation and the Newtonian kinetic energy equation which is presented as followed:In classical mechanics, the “linear momentum” of a moving body is given (ambiguously) by the partial differential equation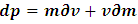
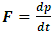
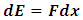
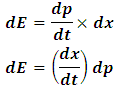 But
But 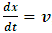 , thus
, thus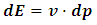 Substituting eq. (33) into the last expression, we have
Substituting eq. (33) into the last expression, we have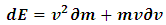
 , so
, so 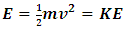 .Now, from classical mechanics we know that for work to be done on a system, a force must be applied to move the constituents of that system through a distance; in order words, the system must undergo some form of motion from an initial position to a final position. Work therefore cannot be achieved in the absence of a kinetic energy, since the system must undergo a form of motion with speed
.Now, from classical mechanics we know that for work to be done on a system, a force must be applied to move the constituents of that system through a distance; in order words, the system must undergo some form of motion from an initial position to a final position. Work therefore cannot be achieved in the absence of a kinetic energy, since the system must undergo a form of motion with speed 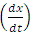 in the direction of the applied force. We can then conclude that the magnitude of the work done on the system is therefore the kinetic energy of that system.Also, because the system should lose mass from the argument above, the kinetic energy of a system has a negative correlation with its mass;
in the direction of the applied force. We can then conclude that the magnitude of the work done on the system is therefore the kinetic energy of that system.Also, because the system should lose mass from the argument above, the kinetic energy of a system has a negative correlation with its mass; 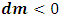 ; therefore, as the mass of the system decreases, its kinetic energy must be increasing as well. This analysis also holds for the classical linear momentum of the system since it depends on the velocity of the system; thus, this negative correlation between speed and mass allows us to redefine the momentum and kinetic energy of the system unambiguously as:
; therefore, as the mass of the system decreases, its kinetic energy must be increasing as well. This analysis also holds for the classical linear momentum of the system since it depends on the velocity of the system; thus, this negative correlation between speed and mass allows us to redefine the momentum and kinetic energy of the system unambiguously as: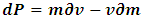
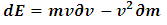
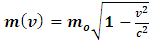 Since the mass is a function of speed. Differentiating this result with respect to
Since the mass is a function of speed. Differentiating this result with respect to 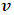 gives
gives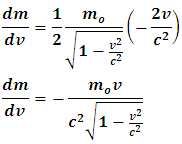 But
But 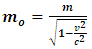 , by eq.32; thus,
, by eq.32; thus,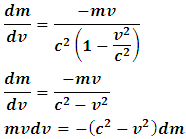
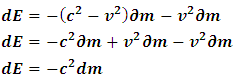 And by integrating, we have
And by integrating, we have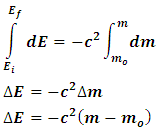 And upon rearranging, we have
And upon rearranging, we have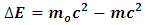
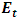 ) of any real system is defined as the energy of all the constituent atoms and/ or molecules that make up that system as well as the energy of the bonds that bind the atoms or particles of the system together. This energy can be expressed mathematically as the sum of the system’s total potential and kinetic energies
) of any real system is defined as the energy of all the constituent atoms and/ or molecules that make up that system as well as the energy of the bonds that bind the atoms or particles of the system together. This energy can be expressed mathematically as the sum of the system’s total potential and kinetic energies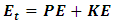
 , eq. (41) becomes
, eq. (41) becomes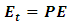
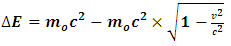
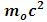 is the energy of the system at rest and
is the energy of the system at rest and 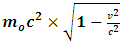 is the energy of the system at some speed
is the energy of the system at some speed 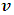 .Now, if a system of mass
.Now, if a system of mass 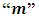 is in motion with speed
is in motion with speed 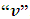 , the potential energy of such system decreases as its speed increases. However, the potential energy of such system is not necessarily zero since the system still has mass
, the potential energy of such system decreases as its speed increases. However, the potential energy of such system is not necessarily zero since the system still has mass 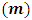 and at a particular time
and at a particular time 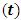 it is at some known position r in space. Therefore, the system will only have zero potential energy if its mass is zero (like a wave) which can only be achieved if
it is at some known position r in space. Therefore, the system will only have zero potential energy if its mass is zero (like a wave) which can only be achieved if 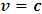 . Thus, the valid relativistic equation that describes the potential energy of any system in the universe either in motion or at rest is
. Thus, the valid relativistic equation that describes the potential energy of any system in the universe either in motion or at rest is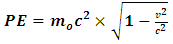
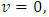 the system has no kinetic energy, so eq (44) reduces consistently to
the system has no kinetic energy, so eq (44) reduces consistently to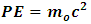
 ); so
); so  is the kinetic energy of the system as stated above. Thus eq. (43) can be re-expressed as
is the kinetic energy of the system as stated above. Thus eq. (43) can be re-expressed as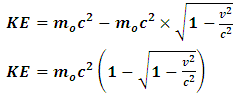
 , we use the Maclaurin series expansion
, we use the Maclaurin series expansion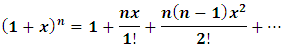 Letting
Letting 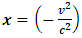 , we have
, we have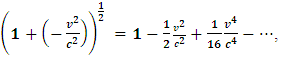 Thus eq. (46) becomes
Thus eq. (46) becomes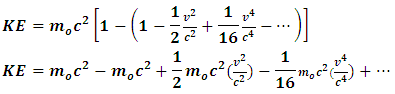 Ignoring large powers of c and canceling liked- terms, we have
Ignoring large powers of c and canceling liked- terms, we have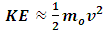
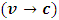 , the potential energy of the system approaches zero
, the potential energy of the system approaches zero 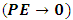 as well; thus, the total internal energy of the system, by the law of conservation of energy, should equal the kinetic energy of the system. But if we express the total internal energy by
as well; thus, the total internal energy of the system, by the law of conservation of energy, should equal the kinetic energy of the system. But if we express the total internal energy by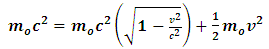
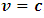 , the potential energy equals zero
, the potential energy equals zero 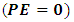 and eq. (48) reduces to
and eq. (48) reduces to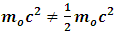
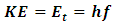
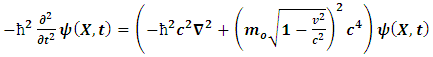
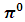 meson Miller Jr., 2008 [7]. Before the disintegration process, the particle obtains a high enough kinetic energy thus, making the system’s sub-particles to move at the speed of light. As a result, the particle disappears and an electromagnetic radiation appears with its energy equal to the total internal energy of the particle. But at rest, the particle possesses no kinetic energy so its total internal energy is just equal to its potential energy as expected. Eq. (51) is therefore valid.
meson Miller Jr., 2008 [7]. Before the disintegration process, the particle obtains a high enough kinetic energy thus, making the system’s sub-particles to move at the speed of light. As a result, the particle disappears and an electromagnetic radiation appears with its energy equal to the total internal energy of the particle. But at rest, the particle possesses no kinetic energy so its total internal energy is just equal to its potential energy as expected. Eq. (51) is therefore valid.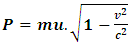
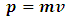
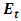 ; then, by special relativity, its linear momentum can be expressed as
; then, by special relativity, its linear momentum can be expressed as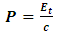
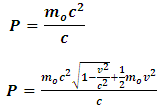
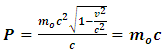
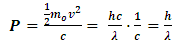
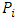 be the potential linear momentum, then, the initial force of the system can be defined as:
be the potential linear momentum, then, the initial force of the system can be defined as: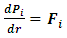
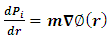
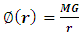 and
and 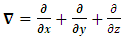 .By the same argument above, the kinetic momentum (denoted by
.By the same argument above, the kinetic momentum (denoted by 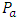 ) depends on the acceleration of the body; thus, if we consider the time rate of change of kinetic momentum then, we can define the force due to acceleration as:
) depends on the acceleration of the body; thus, if we consider the time rate of change of kinetic momentum then, we can define the force due to acceleration as: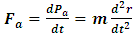
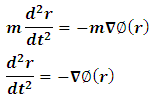
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML