-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2019; 9(2): 55-61
doi:10.5923/j.ijtmp.20190902.06

Special Relativity: Resolving the Twin Paradox while Proving the Traveling Twin Cannot be Younger
Manhar L. Shah
MVM Electronics, Inc., 3410 N. Harbor City Blvd. Suite E, Melbourne, FL, USA
Correspondence to: Manhar L. Shah , MVM Electronics, Inc., 3410 N. Harbor City Blvd. Suite E, Melbourne, FL, USA.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In special relativity, the “Twin Paradox” occurs when one twin makes a round trip journey. Lorentz transformations do not define which twin will be younger, only that they cannot be the same age upon return. Solutions that use discussions of inertial frames as well as accounting for acceleration and deceleration have been proposed to determine which twin is traveling. Over more than a century, many articles have been published to support the concept that the traveling twin will be younger upon return; however many of these arguments have flaws. This paper proposes a novel solution to resolving the “Twin Paradox” that requires that the traveling twin cannot return younger. While studying light propagation in the direction normal to the motion between two frames, it was discovered that the currently accepted principle of a younger traveling twin is in error. Additionally, it allows us to identify who is the traveler without ambiguity. The main argument against the currently accepted paradigm arises from this set-up which shows the apparent speed of light measured by the traveling twin, with the assumption that he will be younger, will be faster than the maximum permissible value c that is the speed of light in an inertial frame through a vacuum. That demonstrates a fundamental violation of the universally accepted limit on the speed of any entity. Further analysis shows that the traveling twin actually will be older as opposed to younger and will reverse the aging relation that is currently accepted.
Keywords: Special relativity, Twin paradox, Time dilation, Time travel, Clock paradox
Cite this paper: Manhar L. Shah , Special Relativity: Resolving the Twin Paradox while Proving the Traveling Twin Cannot be Younger, International Journal of Theoretical and Mathematical Physics, Vol. 9 No. 2, 2019, pp. 55-61. doi: 10.5923/j.ijtmp.20190902.06.
Article Outline
1. Introduction
- The “Twin Paradox” [1-3] arises from the special relativity result that requires that two observers in relative motion to each other with velocity v observe the clock speed of the other as slower than his own. Therefore, if an observer makes a round trip journey and returns to the original position in a stationary frame after traveling some distance, then both the stationary and traveling twin would claim that his elapsed time is shorter than his twin. To establish the correct age of the twins some additional requirements must be met. A large number of papers have been written on this subject [4]. Various explanations, theories and calculations are used to determine which twin is actually traveling and then to justify that the traveling twin will be younger upon return [5-9]. Papers also exist to justify an older traveling twin with invocation of the effect of acceleration [10] and no age difference with non-Lorenz transformation [11]. The “Twin Paradox” being an integral part of special relativity, [12] its resolution is extremely important to fully embrace the theory.Lorentz transformation [13] dictates that the twins cannot be the same age, but it doesn’t provide a compelling reason to choose whether the traveling or stationary twin will be younger. If one looks at Lorentz transformation in a casual manner then one presumes identical time dilation in the forward and return journeys of the traveling twin. Adding dilated times to both legs of the journey by the traveling twin seems to show that the traveling twin will be younger. On the other hand, if one calculates the time relation at the starting or reference point between two frames, it then appears that the stationary twin is younger. Since only one outcome can be true an additional constraint is required. Asymmetry between the stationary and traveling twins’ journeys arising from the traveling twin’s acceleration, deceleration, turn around and Doppler Effect eliminates the necessity that both twins age identically. However, non-symmetry of the situation considering those attributes is not sufficient to establish that the traveling twin will be younger. Effects of gravity and acceleration (general relativity) do not play any role in special relativity because we may consider only kinematics. Moreover, accounting for asymmetric attributes does not fully resolve the ambiguity about who is the traveler [14]. The concept of the younger traveling twin is favoured by citing that the traveling frame can be reversed by frame switching and therefore the concept of time dilation will be the same in both directions. None of these explanations fully resolve the underlying paradox nor do they convincingly settle the question of which twin will be younger. Explanations that require frame switching by the traveling twin on his reverse journey fits the current concept of a younger traveling twin. This paper argues that such an assumption will produce a situation in which the measured speed of light by the traveling twin will exceed the maximum universally accepted speed of light c = 3x108 m/s. Lorentz transformation requires that the twins not be the same age, but no theoretical compulsion exists to accept the traveling twin to be younger. Therefore, if the only choice is that the traveling twin is younger or older, then we have to accept the traveling twin as older to satisfy the ultimate speed limit of any entity being c.This paper proposes a new solution to the “Twin Paradox” using light propagation in a direction orthogonal to the motion. This novel approach is selected to avoid length contraction effect in that direction. It also elegantly explains why the traveling twin cannot be younger while only requiring use of the following widely accepted concepts: c = 3x108 m/s is the maximum possible speed of any entity and light travels in a straight line in an inertial frame. Additionally, the direction of light propagation in any direction other than the direction of motion changes in a frame if the frame velocity changes. In the course of this investigation it was revealed that light pulse propagation in a frame can also uniquely identify its designation as inertial or non-inertial. This identification is unlike those generated using acceleration, gravity, turn around or Doppler Effect which are shown to have some inconsistencies [14] that can make either twin the traveler. A case showing the measured speed of light exceeds c if the traveling twin is younger is first presented. A discussion is presented in the next section to highlight deficiencies in explanations by several authors who support this concept. Propagation of light in a frame with changing velocity is presented and demonstrates how it establishes which twin is the traveler. Computations of light path lengths with condition of simultaneity are presented in which light propagates in a direction orthogonal to the motion of the frame. The computations show that in the traveling twin’s frame, light path length is g times the stationary twin’s frame light path length and not 1/g times as currently accepted by the traveling twin being younger. Here g is Lorentz contraction factor given as [13],
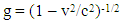 | (1) |
2. A Set-up to Show why the Traveling Twin cannot be Younger
- We consider a frame F that remains stationary and another coincident frame at the start of time designated as F’ that moves. An observer A is at the origin in frame F and another observer A’ is at the origin in frame F’. Both observers synchronize time and set time t = t’ = 0. Frame F’ travels with a velocity V in z direction in F to a distance L and returns with the same velocity to the original position in frame F. Figure 1 graphically shows the travel taken by A’. The distance L in F is marked as Z1. A’ travels with equal velocity, V, in each direction so the Lorenz contraction factor g is the same for each direction.
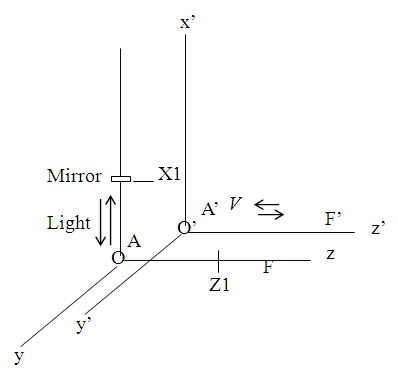 | Figure 1. Stationary frame F and round trip traveling frame F’. A mirror stationed at a distance LC/V marked X1 in F frame to reflect light sent from the origin |
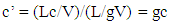 | (2) |
3. Deficiency of Earlier Explanations
- An excellent discussion on the deficiencies in explaining the “Twin Paradox” in different situations is given by Unnikrishnan [14]. An extensive bibliography, history and comparison of approach by many authors on the clock paradox are provided by Shuler [4]. The discussion here focuses further highlighting those deficiencies. Many authors after reviewing extensive publications on the “Twin Paradox” have condensed the results in book form. Therefore, explanations of the traveling twin as younger concept from a few well-known books are used for discussion here.As each twin can claim to be younger than the other, non-symmetry condition of travel is correctly applied to rule out the requirement of equal age for the twins. In most of these explanations, time dilation is assumed during the twin’s return journey similar to what occurs during his forward journey. This erroneously compels one to accept the traveling twin as younger. In the dominant explanations, discussion is inadequate to prove that the traveling twin as older violates basic principles or that the traveling twin as younger does not violate the same principles.As discussed in [2], first the author shows correctly how the symmetry is broken. Then the author sites example of time spent by the traveling and stationary twin. The author uses one contraction factor or time warp factor over the entire journey for computing time for the traveling twin which is incorrect. When twin A’ starts the return journey he is no longer at the origin or the reference point, therefore the clock of the traveling twin may not follow the same rule as during the forward journey. The next section of this paper, in which a single reference light ray is used to obtain the space-time relations between twins, clearly shows that elapsed time for the traveling one, is greater, making him older.In [1] the author explains the paradox by two methods. In the first method he explains in a manner similar to [2] with the same argument that during both the forward and return journey the traveling twin sees the length of his travel contracted by the same factor g. He correctly points out that the event 2, which is reversing the twin’s velocity, takes place at a far distance from the reference point. However, he considers that as a change of frames and treats the reverse journey the same as the forward journey. If frame switching were not used, then the velocity reversal would require –V in Lorentz transformation and only the origin can be used for the reference. As a result he would get t’ = gt and not t’ = t/g for the total journey.In the second method, the author of [1] considers Doppler Effect and counts the number of pulses during travel. The author refers to a table in which he already has assumed the return time for the traveler as L/gV and obtains t’ = t/g. With such a prior assumption, the result obtained cannot be taken as correct. If the author had assumed the return time different he would have gotten some other value for t’. Further, the author invokes Hermann Bondi’s work to show word lines of the traveler during forward and return journeys. The integration is taken along two different paths implying two different frames. As pointed out, if frame switching is applied t’ = t/g will result but that will violate the limit of light speed. The question is “should we allow this limit to be violated or accept the traveling twin as older?”While asymmetry of travel between twins and Lorentz transformation show one or the other twin has to be younger after a round trip journey, [11] presents an argument to show the twins should age equally. The definition of velocity in the paper’s eq. 1 is incorrect. Additionally, the authors don’t use Lorentz transformation but develop their own. With the use of an unproven concept, the conclusion drawn by the authors is unacceptable.
4. Propagation of Light Ray in a Frame with Changing Velocity
- Before discussing and computing light path lengths in stationary and traveling frames some discussion on light propagation in a frame with changing velocity is essential. We have used the well-known facts that the ultimate speed limit is c and light propagates in a straight line with velocity c in an inertial frame. Another observation can be added that the same light pulse manifests in all frames inertial or non-inertial and all frames sense the same energy. This means a light pulse traces out simultaneity paths in stationary and moving inertial frame as well as non-inertial frames. The direction of propagation of a light pulse ray in an inertial frame is constant so if another frame changes velocity then the ray trace in this non-inertial frame has to change direction. It is particularly apparent when the light ray direction is away from the direction of motion. Change of ray direction with changing speed of the frame is also supported by the experimental results of stellar aberration. This makes it obvious for both traveling and stationary twins to conclude who is the traveler by detecting the direction of light ray propagation in each frame during velocity change.The above result also shows that though a frame cannot measure its absolute velocity it can measure velocity changes using light ray pulses. This firmly establishes the identity of the traveling twin and resolves the “Twin Paradox.” There appears to be no case in which the stationary twin can be construed as traveling if ray trace is used for determination. This result offers a novel and rigorous procedure compared with earlier procedures, for establishing the asymmetry in Twin Paradox. Change in direction of ray propagation in a frame with a changing velocity complicates light path length calculations due to involvement of length contraction. For that reason we have selected a ray in a stationary frame along the x-axis for light path length calculations in the next section.
5. Computation of Light Path Length and Elapsed Time in F’ for Round Trip Journey
- Light path length and hence the elapsed time in a stationary and a moving frame can be obtained with the condition of simultaneity using the theories of special relativity and Lorentz transformation. This condition allows tracing of light paths in stationary and moving frames. We use stationary frame F and moving frame F’ with the same notations as used earlier for Figure 1 and the moving frame traveling in z-direction. In order for an arbitrary point in the stationary frame to coincide with a point in a moving frame, the points need to have x = x’ and y = y’. Special relativity shows that the motion of an inertial frame effects the relation between two frames for time and length along the direction of motion (z-axis) only. The space-time relation between two frames is through Lorentz transformation and in many cases simply with contraction or time warp factor g which depends upon the relative velocity between frames. Special relativity and Lorentz transformation also show that the same time prevails in the xy (or x’y’) plane for a given value of z (or z’). Therefore, g can be obtained by computing light path length from the origin to some selected simultaneity points along x and x’ axes. This is done by thought process of sending a light pulse from the reference point (origin) towards a known simultaneity point in one frame and tracing the light pulse path to that point in each frame as motion takes place. If the light path has a component along the z-axis then length contraction would be applicable to light path length according to Lorentz transformation. For that reason, light path in the stationary frame is selected along the x-axis for simplicity. This procedure is similar to one as shown in [15]. As stated in the previous section, light travels in a straight line with speed c in an inertial frame. F’ frame goes through acceleration, deceleration and course reversal as it makes a round trip journey which causes light to travel in piece-wise straight lines in F’. This effect has been verified by the observation of stellar aberration.To obtaining the light path lengths we use frames F and F’ with the same notations as in Figure 1. Instead of using a mirror as was done in Figure 1, two additional observers B and B’ as mentioned before are used to compute light path lengths for the round trip journey by A’. As discussed in the previous paragraph, establishment of simultaneity of A and A’ after return is equivalent to simultaneity of B and B’ after return. One selects known points in F and F’ frames that would receive simultaneously a light pulse transmitted from the origin. In the twins’ case, known simultaneity points are equivalent to the origin itself as A’ returns to A or we could alternatively select B and B’. A light pulse transmitted from the origin has to reach B if we want to find the light path length. With light propagating in a straight line in the stationary F frame, the x-axis at the origin is the only possibility for light propagation. No other choice of simultaneity points exists for this ray. The currently accepted “traveling twin as younger” concept would amount to erroneously using light propagation from A’ to B’ in a straight line, contracting distance between A’ to B’ by factor g and frame switching. In contrast straight line ray propagation from A’ to B’ is not possible in F’ which goes for a round trip journey.To obtain the light path lengths and elapsed times for a general case we use velocity V1 for time T1 during the forward journey and velocity V2 for time T2 during the return journey for A’. Figure 2 depicts the relevant notations and condition for this thought process for the forward journey. At t = t’ = 0 a light pulse is sent towards B. As A’ travels to the distance Z1 = V1T1, the light pulse will travel from the origin to distance X1 equal to cT1 along the x-axis and A’ will reach to the destination point. During the return journey of A’, the light pulse will travel distance X2 equal to cT2 from X1 along x-axis in F as A’ coincides with A’ and B coincides with B’. As the light pulse propagates along the x-axis in F during the forward journey, the light path traced out in F’ is a straight line as shown by the thick line in Figure 2 and as seen in F. The simultaneity point R is the point when the forward journey ends. This point has the coordinate (X1, 0) in F and (X1’, Z1’) in F’. The light path length in F is from point (0, 0) to (X1, 0) and from (0, 0) to (X1’, Z1’) in F’. The light path length in F is equal to X1= cT1. Light path length in Figure 2 for F’ is from (0, 0) to R with coordinate (X1’, Z1’) is not proper, as shown in F. The length contraction along the z-axis needs to be accounted for. The light path length X1’ = X1 is proper in both F and F’ because no length contraction occurs in this direction. Lorentz transformation provides Z1’ = g1Z1 where g1 is the Lorentz contraction factor for velocity V1. From the right angle triangle we obtain light path length L1’ in F’ as,
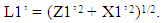 | (3) |
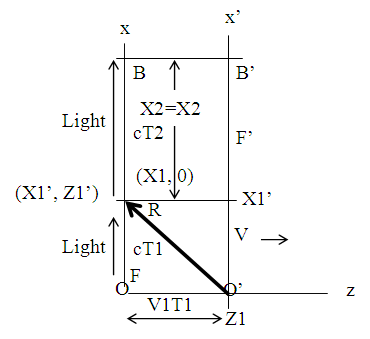 | Figure 2. Light path trace in F’ as seen by stationary frame F during the forward journey |
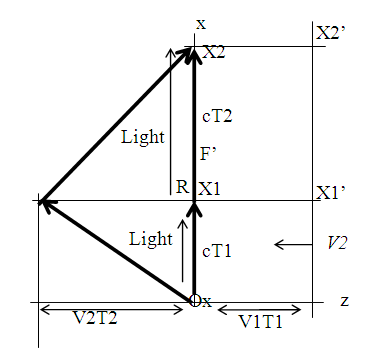 | Figure 3. Light path traces in F’ and F combined as seen in F for twin’s round trip journey |
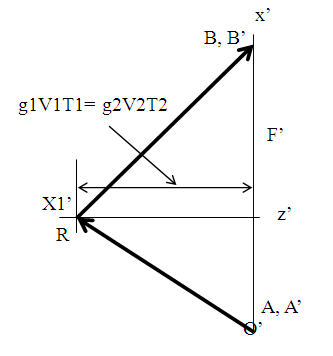 | Figure 4. Light path traces in moving frame F’ for twin’s round trip journey |
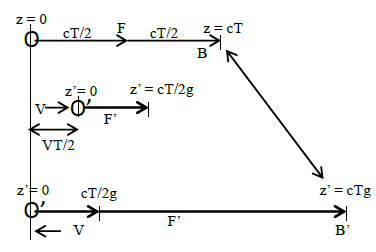 | Figure 5. Light path traces for light pulse propagation along z-axis for twin’s round trip journey |
6. Conclusions
- This paper presents a novel solution to the “Twins Paradox” using the observation of light propagation in a direction orthogonal to the direction of motion in order to determine the traveling twin. Propagation of a light ray in a frame with a changing velocity causes the ray direction to change. This effect can be used to measure velocity change of the frame and identify such frame as non-inertial and therefore identify which twin is traveling. Using this model and the broadly accepted concept that c is the upper limit of speed for an object in an inertial frame, the conclusion that the traveling twin must be older is obtained. This contradicts the widely held belief that the traveling twin in the thought experiment would return younger. The results can be used in other situations as well and suggest in general that time dilation is not possible with round trip travel in an inertial frame.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML