Doron Kwiat
17/2 Erez Street, Mazkeret Batyia, Israel
Correspondence to: Doron Kwiat , 17/2 Erez Street, Mazkeret Batyia, Israel.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Real waves presentation is applied to Dirac equation. It is then used to show a Klein Gordon wave functions solution. These equations resemble Maxwell's equations for the electromagnetic field. Assuming a non-point-like charged fermion, with an internal current distribution and an internal vector potential, the resulting Maxwell equations for the internal vector potentials of the charged fermion resembles Dirac equation in their Klein-Gordon form. This solution is to the best knowledge of the author, the first time that a connection is made between Dirac's fermion field and Maxwell's electromagnetic field.
Keywords:
Dirac equation, Real wave functions, Maxwell equation, Finite size Fermions, Internal Electromagnetic fields
Cite this paper: Doron Kwiat , Dirac Equation and Electron Internal Structure, International Journal of Theoretical and Mathematical Physics, Vol. 9 No. 2, 2019, pp. 51-54. doi: 10.5923/j.ijtmp.20190902.05.
1. Introduction
The relativistic equations by Dirac [1] and by Klein-Gordon (KG) [2] use complex wave functions. In a recent work [3], a formulation of quantum mechanics without use of complex numbers is described and was shown to be equivalent to the complex formulation. Using real wave functions, the Dirac equation is presented as 4 real wave functions, solving 4 KG equations of massive point-like particles. These 4 solutions represent 4 states of a fermion (for instance an electron and a positron, with spin-up or spin down).In this work, internal structure of the charged finite size fermion is examined.Based on Maxwell's equations, a 4-vector internal electromagnetic field 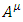 of the charged fermion is assumed. The solution gives 4 non-homogeneous KG equations with charge and current density.Under certain assumptions on the relationship between the current density vector and the electromagnetic field vector, the Maxwell electromagnetic equations for the fermion internal vector field, are shown to have the same form as the Dirac equations for the fermion Dirac fields.This solution assumes a mirror symmetry of the internal electromagnetic fields of the fermion.
of the charged fermion is assumed. The solution gives 4 non-homogeneous KG equations with charge and current density.Under certain assumptions on the relationship between the current density vector and the electromagnetic field vector, the Maxwell electromagnetic equations for the fermion internal vector field, are shown to have the same form as the Dirac equations for the fermion Dirac fields.This solution assumes a mirror symmetry of the internal electromagnetic fields of the fermion.
2. Dirac Equation with Real Wave Functions
If one accepts the claim that a single non-relativistic Schrödinger equation is a description of a single massive particle, made up of two coupled strings, then one may project from this on the relativistic Dirac equation, describing a free Fermion of mass m: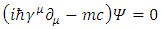 | (1) |
One may assume, as before, separate the complex wave function 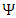 into its real and imaginary parts
into its real and imaginary parts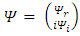 | (2) |
and by using them in the Dirac equation, one will get two separate equations where imaginary and real parts have been separated.This same procedure can be applied to any quantum field Lagrangian, resulting (at the cost of doubling the number of equations) in separation of the equations to real wave functions.These wave functions may be interpreted as coupled strings.In Dirac equation [43], the four 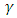 matrices are:
matrices are: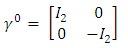 | (3) |
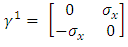 | (4) |
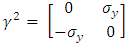 | (5) |
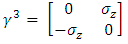 | (6) |
Where I2 is the 2x2 unit matrix and 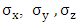 the Pauli 2x2 matrices.
the Pauli 2x2 matrices.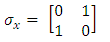 | (7) |
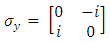 | (8) |
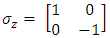 | (9) |
Of these matrices only 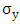 , has imaginary components and one will replace it by writing
, has imaginary components and one will replace it by writing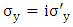 Where
Where 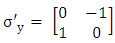 and therefore
and therefore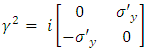 | (10) |
Decomposing 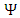 into
into 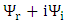 where
where 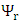 and
and 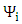 are real, the Dirac equation becomes
are real, the Dirac equation becomes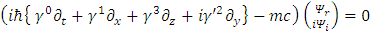 | (11) |
Namely, two separate real numbers equations: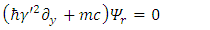 | (12) |
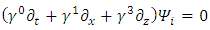 | (13) |
One may notice that only the real part wave function depends on mass m and Planck constant 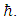 It is also time independent.Using Pauli matrices in the gamma representation one obtains:
It is also time independent.Using Pauli matrices in the gamma representation one obtains: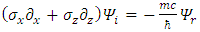 | (14) |
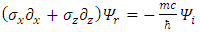 | (15) |
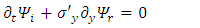 | (16) |
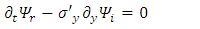 | (17) |
We see from these equations:1. The real and imaginary components are coupled.2. Both real and imaginary parts have 2 components eachSince both 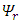 and
and 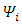 are made of 2 real components each, there are 4 components altogether.
are made of 2 real components each, there are 4 components altogether.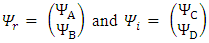 Eqs. 23-26 can be then formulated as follows:
Eqs. 23-26 can be then formulated as follows: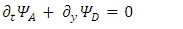 | (18) |
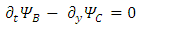 | (19) |
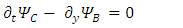 | (20) |
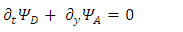 | (21) |
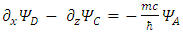 | (22) |
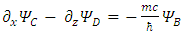 | (23) |
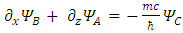 | (24) |
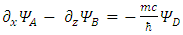 | (25) |
These equations hint to some connections between the possible states of the fermion.Applying 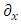 to Eqs. 31-34 results in
to Eqs. 31-34 results in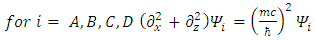 | (26) |
There are apparently 4 constituents of the Dirac particle. The above two groups of differential equations show the coupling that exists between the constituents.There is a clear asymmetry in the Dirac equation, as there is a difference between the y coordinate and the x-z coordinates. This is in contradiction with the expected isotropic spherical symmetry of the Fermions and the need of the results to be independent of the coordinate system.By applying second time derivative, Eqs. 28-31 can be written as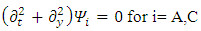 | (27) |
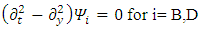 | (28) |
Eqs. 35, 36, 37 can be combined by subtraction/addition to give: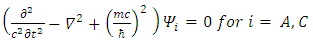 | (29) |
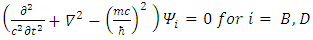 | (30) |
We thus see, that Dirac equation becomes 4 real waves equations. Each is a Klein-Gordon equation. Since the solutions to the Klein-Gordon [3] equations are well known, we can conclude and say, that the Dirac relativistic Fermion is actually a 4 Fermions equation. These 4 Fermions are of same mass m.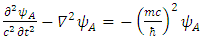 | (31) |
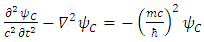 | (32) |
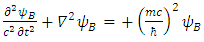 | (33) |
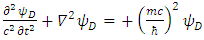 | (34) |
If now 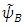 and
and 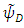 , are the mirror functions of
, are the mirror functions of 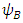 and
and 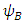 , respectively, then
, respectively, then 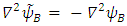 , and
, and 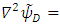
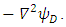 Therefore
Therefore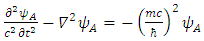 | (35) |
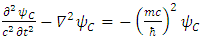 | (36) |
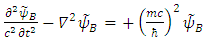 | (37) |
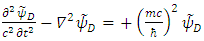 | (38) |
In other words, we have four possible KG solutions. Two solutions (A, C) with positive energy term and two solutions (B, D) with negative energy term. These equations show that the four states can exist independently of each other.
3. Maxwell's Equations
Maxwell's equations [4] and the Lorentz force law (see Appendix)) are extraordinarily successful at explaining and predicting a variety of phenomena; however they are not exact, but a classical limit of quantum electrodynamics (QED) [5].Some observed electromagnetic phenomena are incompatible with Maxwell's equations. These include photon–photon scattering [6] and many other phenomena related to photons or virtual photons, "nonclassical light" and quantum entanglement [7, 8] of electromagnetic fields.
4. Similarity of Dirac's with Maxwell's Equations
Consider the Dirac particle (Fermion) to be made of four constituents (fields), 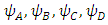 Each acts according to the KG equations, but they also show some mutual interactions, as can be seen by observing Eqs. 27-34.Since the spatial derivative of a field is a force, one may consider a vector equilibrium interpretation for each of equations 32-35.Suppose we define two 3 components vector fields
Each acts according to the KG equations, but they also show some mutual interactions, as can be seen by observing Eqs. 27-34.Since the spatial derivative of a field is a force, one may consider a vector equilibrium interpretation for each of equations 32-35.Suppose we define two 3 components vector fields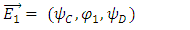 | (39) |
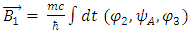 | (40) |
With 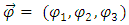 some arbitrary vector field.The fields
some arbitrary vector field.The fields 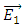 and
and 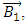 satisfy:
satisfy: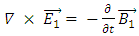 | (41) |
for the y component.Same relationships exist for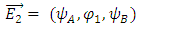 | (42) |
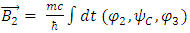 | (43) |
Leading to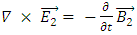 | (44) |
Again, for the y-component.This may hint to some internal structure of a Dirac fermion, being made of some interacting electromagnetic fields.Let us look at the electromagnetic field vector 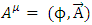 It satisfies Maxwell's equations (see Appendix):
It satisfies Maxwell's equations (see Appendix):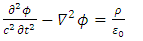 | (45) |
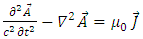 | (46) |
Assume the Dirac charged fermion has an internal current density 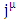 and hence an internal vector potential
and hence an internal vector potential 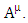 This particle has an internal electric charge distribution
This particle has an internal electric charge distribution 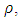 and creates an internal current
and creates an internal current 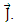 Because of current conservation and the definition of the vector potentials one has
Because of current conservation and the definition of the vector potentials one has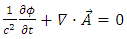 | (47) |
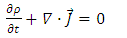 | (48) |
Suppose now that the current density is proportional to the vector potential: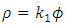 | (49) |
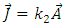 | (50) |
(which, for example, is the case of the vector potential and current density for a current in a ring).Then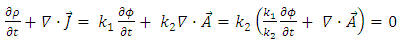 | (51) |
Provided that 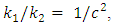 then if Eq. 47 is true, then so is Eq. 48 and vice versa.And the above conservation equations are always satisfied.Then, from Eqs. 45, 46:
then if Eq. 47 is true, then so is Eq. 48 and vice versa.And the above conservation equations are always satisfied.Then, from Eqs. 45, 46: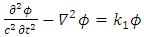 | (52) |
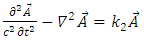 | (53) |
and 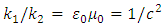 Assume next, that
Assume next, that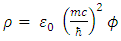 | (54) |
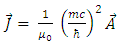 | (55) |
Then, when inserted in Eqs. 52, 53, they have the same form as the Dirac 4 entities Eqs. 35-38.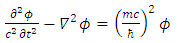 | (56) |
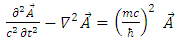 | (57) |
In other words, the four Dirac fields 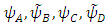 are the electromagnetic vector potential fields,
are the electromagnetic vector potential fields, 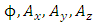 provided that the current densities
provided that the current densities 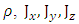 are related to the electromagnetic fields
are related to the electromagnetic fields 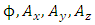 by Eqs. 54, 55 through the constant
by Eqs. 54, 55 through the constant 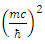 .So, if one identifies the four Dirac fields
.So, if one identifies the four Dirac fields 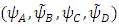 with the vector potential
with the vector potential 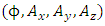 , Eqs. 35-38, become identical with Eqs. 56-57.Note though, that in order to keep with the signs as required in Eqs 35 - 38, the currents
, Eqs. 35-38, become identical with Eqs. 56-57.Note though, that in order to keep with the signs as required in Eqs 35 - 38, the currents 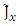 and
and 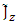 must be symmetric with
must be symmetric with 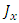 and
and 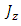 about their spatial coordinates, so that their spatial derivatives change signs accordingly.There are no external electromagnetic fields, so these are confined electromagnetic fields which create the fermion and give it its mass m.
about their spatial coordinates, so that their spatial derivatives change signs accordingly.There are no external electromagnetic fields, so these are confined electromagnetic fields which create the fermion and give it its mass m.
5. Conclusions
Assuming a charged fermion is not a point like particle, its internal charge dynamics should have a vector potential. Under certain assumptions on the proportionality of the vector potential to the current density, the Dirac equation wave functions are similar to the internal electromagnetic vector potential. The existence of a finite size particle with charge and mass may require some yet unexplained internal interaction force, to overcome the repulsion of the charge from the center of mass.
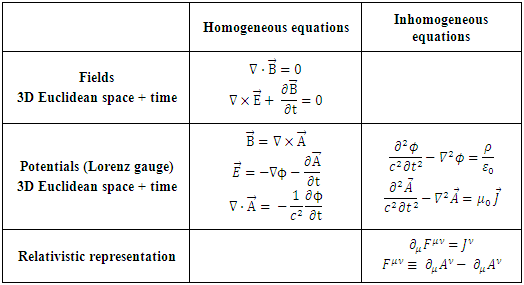
Appendix: Maxwell Equations
References
| [1] | Dirac, P. A. M., "The Quantum Theory of the Electron" , Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 117 (778): 610. 1928. |
| [2] | O. Klein, Z. F. Physik 37 895 (1926); O. Klein, Nature 118 516 (1926). |
| [3] | D Kwiat, International Journal of Theoretical and Mathematical Physics, Vol 8 (3) 2018. |
| [4] | David J Griffiths (1999). Introduction to electrodynamics (Third ed.). Prentice Hall. |
| [5] | https://en.wikipedia.org/wiki/Quantum_electrodynamics. |
| [6] | https://en.wikipedia.org/wiki/Two-photon_physics. |
| [7] | Megidish, E.; Halevy, A.; Shacham, T.; Dvir, T.; Dovrat, L.; Eisenberg, H. S. (2013). "Entanglement Swapping between Photons that have Never Coexisted". Physical Review Letters. 110 (21). |
| [8] | Gibney, Elizabeth (2014). "Entangled photons make a picture from a paradox". Nature. doi:10.1038/nature.2014.15781. Retrieved 13 October 2014. |



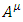 of the charged fermion is assumed. The solution gives 4 non-homogeneous KG equations with charge and current density.Under certain assumptions on the relationship between the current density vector and the electromagnetic field vector, the Maxwell electromagnetic equations for the fermion internal vector field, are shown to have the same form as the Dirac equations for the fermion Dirac fields.This solution assumes a mirror symmetry of the internal electromagnetic fields of the fermion.
of the charged fermion is assumed. The solution gives 4 non-homogeneous KG equations with charge and current density.Under certain assumptions on the relationship between the current density vector and the electromagnetic field vector, the Maxwell electromagnetic equations for the fermion internal vector field, are shown to have the same form as the Dirac equations for the fermion Dirac fields.This solution assumes a mirror symmetry of the internal electromagnetic fields of the fermion. 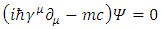
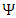 into its real and imaginary parts
into its real and imaginary parts
 matrices are:
matrices are: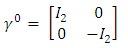
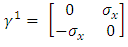
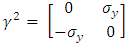
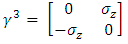
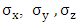 the Pauli 2x2 matrices.
the Pauli 2x2 matrices.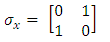
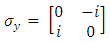
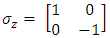
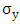 , has imaginary components and one will replace it by writing
, has imaginary components and one will replace it by writing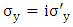 Where
Where 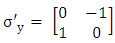 and therefore
and therefore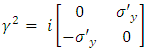
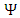 into
into 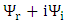 where
where 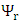 and
and 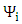 are real, the Dirac equation becomes
are real, the Dirac equation becomes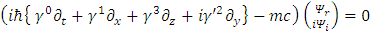
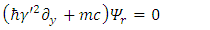
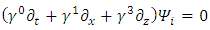
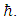 It is also time independent.Using Pauli matrices in the gamma representation one obtains:
It is also time independent.Using Pauli matrices in the gamma representation one obtains: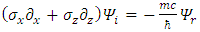
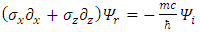
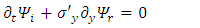
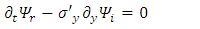
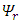 and
and 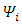 are made of 2 real components each, there are 4 components altogether.
are made of 2 real components each, there are 4 components altogether.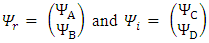 Eqs. 23-26 can be then formulated as follows:
Eqs. 23-26 can be then formulated as follows: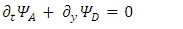
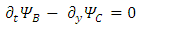
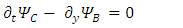
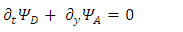
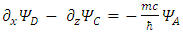
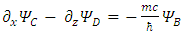
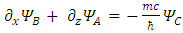
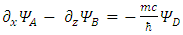
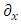 to Eqs. 31-34 results in
to Eqs. 31-34 results in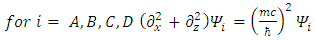
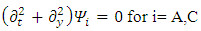
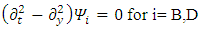
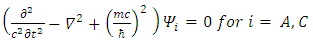
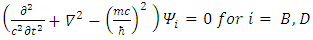
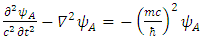
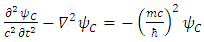
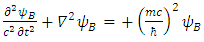
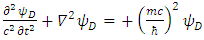
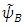 and
and 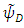 , are the mirror functions of
, are the mirror functions of 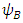 and
and 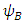 , respectively, then
, respectively, then 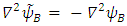 , and
, and 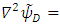
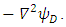 Therefore
Therefore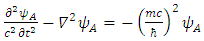
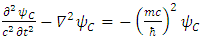
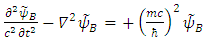
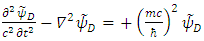
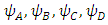 Each acts according to the KG equations, but they also show some mutual interactions, as can be seen by observing Eqs. 27-34.Since the spatial derivative of a field is a force, one may consider a vector equilibrium interpretation for each of equations 32-35.Suppose we define two 3 components vector fields
Each acts according to the KG equations, but they also show some mutual interactions, as can be seen by observing Eqs. 27-34.Since the spatial derivative of a field is a force, one may consider a vector equilibrium interpretation for each of equations 32-35.Suppose we define two 3 components vector fields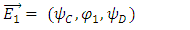
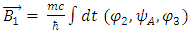
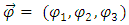 some arbitrary vector field.The fields
some arbitrary vector field.The fields 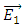 and
and 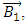 satisfy:
satisfy: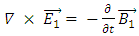
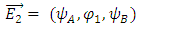
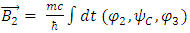
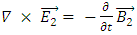
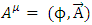 It satisfies Maxwell's equations (see Appendix):
It satisfies Maxwell's equations (see Appendix):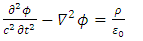
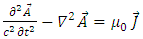
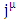 and hence an internal vector potential
and hence an internal vector potential 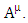 This particle has an internal electric charge distribution
This particle has an internal electric charge distribution 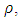 and creates an internal current
and creates an internal current 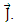 Because of current conservation and the definition of the vector potentials one has
Because of current conservation and the definition of the vector potentials one has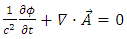
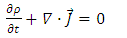
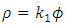
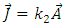
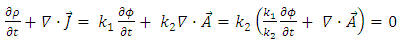
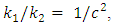 then if Eq. 47 is true, then so is Eq. 48 and vice versa.And the above conservation equations are always satisfied.Then, from Eqs. 45, 46:
then if Eq. 47 is true, then so is Eq. 48 and vice versa.And the above conservation equations are always satisfied.Then, from Eqs. 45, 46: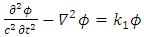
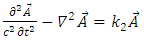
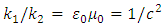 Assume next, that
Assume next, that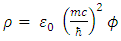
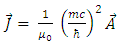
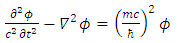
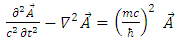
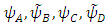 are the electromagnetic vector potential fields,
are the electromagnetic vector potential fields, 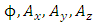 provided that the current densities
provided that the current densities 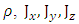 are related to the electromagnetic fields
are related to the electromagnetic fields 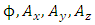 by Eqs. 54, 55 through the constant
by Eqs. 54, 55 through the constant 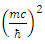 .So, if one identifies the four Dirac fields
.So, if one identifies the four Dirac fields 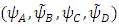 with the vector potential
with the vector potential 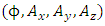 , Eqs. 35-38, become identical with Eqs. 56-57.Note though, that in order to keep with the signs as required in Eqs 35 - 38, the currents
, Eqs. 35-38, become identical with Eqs. 56-57.Note though, that in order to keep with the signs as required in Eqs 35 - 38, the currents 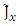 and
and 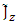 must be symmetric with
must be symmetric with 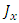 and
and 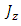 about their spatial coordinates, so that their spatial derivatives change signs accordingly.There are no external electromagnetic fields, so these are confined electromagnetic fields which create the fermion and give it its mass m.
about their spatial coordinates, so that their spatial derivatives change signs accordingly.There are no external electromagnetic fields, so these are confined electromagnetic fields which create the fermion and give it its mass m.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML