Chifu E. Ndikilar1, Sumayya I. Saleh2, Hafeez Y. Hafeez1, 3, Lawan S. Taura2
1Department of Physics, Federal University Dutse, Jigawa State, Nigeria
2Department of Physics, Sule Lamido University Kafin-Hausa, Jigawa State, Nigeria
3SRM Research Institute, SRM Institute of Science and Technology, Kattankulathur, Chennai, Tamil Nadu, India
Correspondence to: Hafeez Y. Hafeez, Department of Physics, Federal University Dutse, Jigawa State, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The power flow between two weakly coupled pendula is calculated analytically and applied to explain the behavior of an optical switch. The general equations of motion are derived for different variations of the coupled pendula with identical and non-identical masses of the pendulum bobs. The power flow under white noise random excitation between the pendula in each system is calculated. The effect of the driving voltage in an optical switch is analogous to the changing length ratio of the pendula system. The net power flow corresponds to the system with identical pendula and for non-identical pendula, the phase constants are not equal and hence there will be no net power flow between the waveguides.
Keywords:
Coupled oscillators, Power flow, Optical switch
Cite this paper: Chifu E. Ndikilar, Sumayya I. Saleh, Hafeez Y. Hafeez, Lawan S. Taura, Analytical Calculation of Power Flow between Two Weakly Coupled Pendula and Its Application to an Optical Switch, International Journal of Theoretical and Mathematical Physics, Vol. 9 No. 2, 2019, pp. 25-35. doi: 10.5923/j.ijtmp.20190902.01.
1. Introduction
Many objects around us move in a specific pattern like the motion of a swing or a chalking chair, such objects are said to undergo an oscillatory or vibratory motion. A periodic motion is a regular motion that is repeated in equal intervals of time while an oscillatory motion is a periodic motion of a particle about a mean position or point [1]. A body that undergoes oscillatory motion is called an oscillator. If there are no causes of damping like friction, an object will oscillate infinitely. Oscillations are physical phenomena that occur in all scales starting from atoms which are the basic units of matter to very big galaxies [2]. Examples of oscillations include the motion of the earth crust during an earthquake, beating of the human heart [3], the motion of the lungs during respiration, the motion of the hands of clocks, the economic cycle, motion of planets around the sun, the moon around the earth and the motion of stars around the galactic center [4].The knowledge of oscillations is applied in many fields like construction of earthquake proof buildings, construction of musical instruments like violins and guitar, diving boards, metronomes, construction of auditory devices like microphones and speakers and implementation of shock absorbers in vehicles that stabilize and control the vehicles movement and minimize tire wear [5]. Coupled oscillators are two or more oscillators that are connected to one another with the aid of a coupler. The coupler may be a string, a rod or any medium through which the energy is transferred between the oscillators. Coupled oscillators are important in science because their motion can be used to simulate numerous natural phenomena [6]. The study of coupled oscillators has become a very active area of research in the last few decades. Applications of coupled oscillators nowadays are uncountable in many disciplines like physics, engineering, biology, and chemistry. Coupled oscillators are useful paradigms used to study many complex physical, biological and chemical systems. For instance, mathematical biologist use coupled oscillators to mimic synchronization processes in biological systems like: pacemaker cells in the heart [7], while civil engineers, use it to study the interaction between bridges and vehicles passing on them to avoid the unwanted excitations that can lead to structural damage and to understand the periodic behavior of many dynamical systems [8].In the last decades, systems of coupled pendula have been given attention to understand natural phenomena like clustering or chimera states and to model many physical, biological and mechanical systems [9]. Such systems are simple to analyze and easy to construct experimentally. Since such systems are important because of the synchronization modes they demonstrate depending on the initial conditions [10]. Hence knowing the frequencies of vibrations and understanding how the energy is transferred between the pendula are important in all types of models. In this article, we calculate the power flow between two weakly coupled pendula and apply the results to an optical switch.
2. Theoretical Methods
2.1. Description of the Coupled Pendula Systems
2.1.1. Two Coupled Identical Pendula
The system considered consists of two identical pendula of mass m and length l coupled with a massless spring. There is no kinetic energy associated with the motion of the spring with spring constant k (Fig. 1). The system has two degrees of freedom 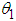 and
and 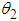 which are the angles the rods make with the vertical [11].
which are the angles the rods make with the vertical [11].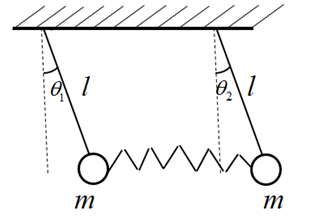 | Figure 1. Two coupled identical pendula |
The kinetic energy of the system T is 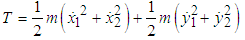 | (2.1) |
or 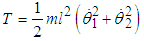 | (2.2) |
Equation (2.2) can be written in matrix form as: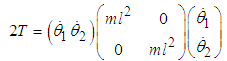 | (2.3) |
where 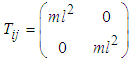 | (2.4) |
Also the potential energy of the system V is 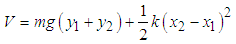 | (2.5) |
or 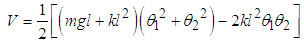 | (2.6) |
Equation (2.6) can be written in matrix form as 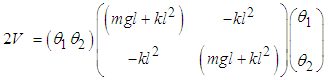 | (2.7) |
where 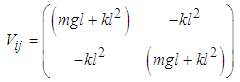 | (2.8) |
2.1.2. Two Coupled Pendula of Different Masses
The system considered consist of two pendula of the same length l and different masses 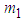 and
and 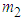 . The system has two degrees of freedom
. The system has two degrees of freedom 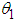 and
and 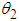 which are the angles the rods make with vertical (Fig. 2).
which are the angles the rods make with vertical (Fig. 2).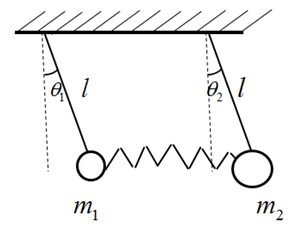 | Figure 2. Two coupled pendula of different masses |
The kinetic energy of the system T is 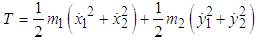 | (2.9) |
or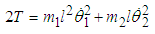 | (2.10) |
Assuming that  can be written in terms of
can be written in terms of 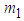 such that
such that 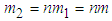 | (2.11) |
where n is any positive real number, then from (2.10) and (2.11)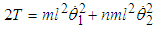 | (2.12) |
Equation (2.12) can be written in matrix form as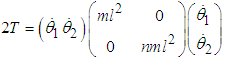 | (2.13) |
where 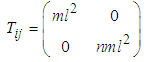 | (2.14) |
also the potential energy of the system V is 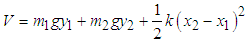 | (2.15) |
or 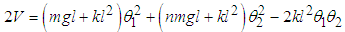 | (2.16) |
and in matrix form 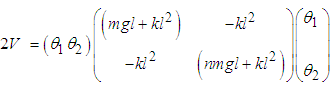 | (2.17) |
where 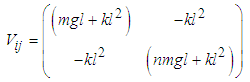 | (2.18) |
2.1.3. Two Coupled Pendula of Different Lengths
The system consist of two pendula of the same mass m and of different lengths 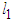 and
and 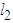 . The system has two degrees of freedom
. The system has two degrees of freedom 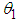 and
and 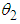 which are the angles the rods make with vertical.
which are the angles the rods make with vertical.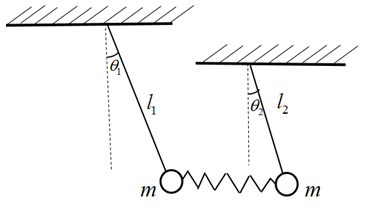 | Figure 3. Two coupled pendula of different lengths |
The kinetic energy of the system T is 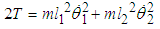 | (2.19) |
Assuming that 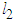 can be written in terms of
can be written in terms of 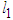 such that
such that 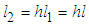 | (2.20) |
where h is any positive real numberthen 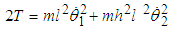 | (2.21) |
Equation (2.21) can be written in matrix form as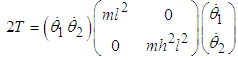 | (2.22) |
where 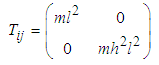 | (2.23) |
Also the potential energy of the system V is 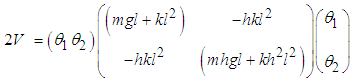 | (2.24) |
where 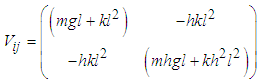 | (2.25) |
2.1.4. Two Coupled Pendula of Different Masses and Different Lengths
The system considered consists of two pendula of masses and lengths coupled with a massless spring. The system has two degrees of freedom which are the angle the pendulum rods make with the vertical. This system is a generalization of the previous three systems and can be reduced to any of them by choosing the suitable values of h and n.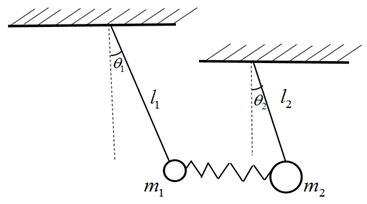 | Figure 4. Two coupled of different masses and lengths |
The kinetic energy of the system T is 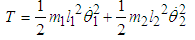 | (2.26) |
or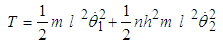 | (2.27) |
or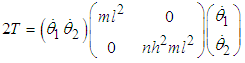 | (2.28) |
where 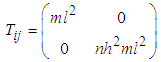 | (2.29) |
Also the potential energy of the system V is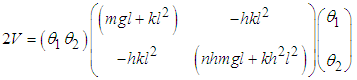 | (2.30) |
where 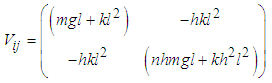 | (2.31) |
2.2. Calculation of Power Flow of the System
The potential and kinetic energies are used to obtain the normal frequencies of the system using the secular equation 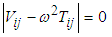 | (2.32) |
where 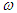 is the natural frequency. Since all the four systems have two degrees of freedom, two values of
is the natural frequency. Since all the four systems have two degrees of freedom, two values of 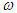 are obtained in each case [11].The normal modes of each system are obtained using the equation
are obtained in each case [11].The normal modes of each system are obtained using the equation 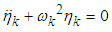 | (2.33) |
where 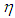 is the normal co-ordinates and
is the normal co-ordinates and 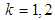 [11].To convert the equations of motion from normal to generalized coordinates we use the equation
[11].To convert the equations of motion from normal to generalized coordinates we use the equation 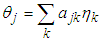 | (2.34) |
Since for all the four systems 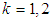 , we can write
, we can write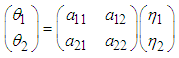 | (2.35) |
where 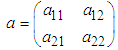 | (2.36) |
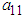 and
and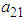 are components of the eigenvector
are components of the eigenvector 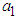 which are computed by setting
which are computed by setting 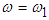 and using [12]
and using [12] 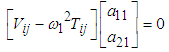 | (2.37) |
The same procedure applies for 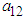 and
and 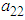 which are components of eigenvector
which are components of eigenvector 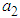 The values of the
The values of the 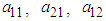 and
and 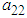 are obtained in terms of m and l using
are obtained in terms of m and l using 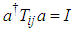 | (2.38) |
where 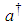 is the Hermitian transpose of a and I is the identity matrix. After obtaining the equations of motion in terms of generalized coordinates for each system, the effects of damping and external forces is taken into consideration and the equations of motion are written in the form [13]:
is the Hermitian transpose of a and I is the identity matrix. After obtaining the equations of motion in terms of generalized coordinates for each system, the effects of damping and external forces is taken into consideration and the equations of motion are written in the form [13]: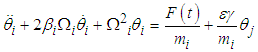 | (2.39) |
where 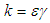 ,
, 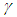 and
and 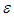 are called the coupling parameters,
are called the coupling parameters, 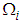 is the blocked frequency of the ith oscillator and
is the blocked frequency of the ith oscillator and 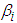 is the damping ratio of the ith oscillator.The parameters from equation (2.39) are used to calculate the power flow. The first order approximation to the power flow between weakly coupled oscillators under white noise random excitations is given as
is the damping ratio of the ith oscillator.The parameters from equation (2.39) are used to calculate the power flow. The first order approximation to the power flow between weakly coupled oscillators under white noise random excitations is given as 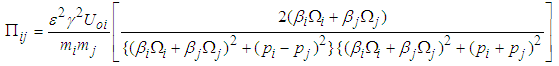 | (2.40) |
where 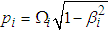 and
and 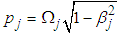 White noise is a random signal that is a combination of all audible frequencies (20Hz-20KHz) with constant power spectral density.
White noise is a random signal that is a combination of all audible frequencies (20Hz-20KHz) with constant power spectral density.
3. Results and Discussion
3.1. Identical Pendula System
Substituting equations (2.4) and (2.8) in equation (2.32) the natural frequencies of the system 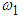 and
and 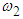 are obtained as
are obtained as 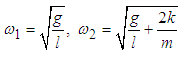 | (3.1) |
Substituting (3.1) in (2.33) gives 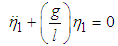 | (3.2) |
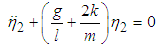 | (3.3) |
Using equation (2.37) it can be shown that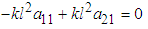 and hence
and hence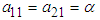 | (3.4) |
Similarly, 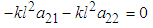 and
and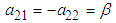 | (3.5) |
Thus 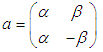 | (3.6) |
and using equation (2.38) we have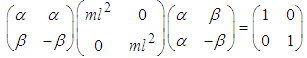 or
or 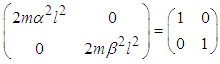 | (3.7) |
and we obtain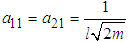 | (3.8) |
and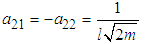 | (3.9) |
and hence equation (3.25) for this system is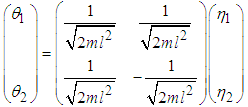 | (3.10) |
From (3.10) we obtain the relationship between the normal coordinates and generalized coordinates for this system as 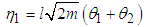 | (3.11) |
and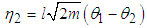 | (3.12) |
If 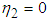 then
then 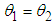 and the two pendula oscillate in phase with an angular frequency
and the two pendula oscillate in phase with an angular frequency 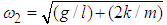 and this is the first natural mode of the system. Also, if
and this is the first natural mode of the system. Also, if 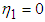 then
then 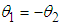 and the two pendula oscillate in an out of phase mode with an angular frequency
and the two pendula oscillate in an out of phase mode with an angular frequency 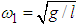 and this is the second natural mode of the system [11].The explicit equations of motion for this system are obtained by substituting (3.11) and (3.12) in (3.2) and (3.3) to give
and this is the second natural mode of the system [11].The explicit equations of motion for this system are obtained by substituting (3.11) and (3.12) in (3.2) and (3.3) to give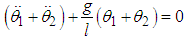 | (3.13) |
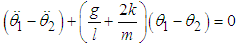 | (3.14) |
By respectively adding and subtracting equations (3.13) and (3.14) and re-arranging we obtain 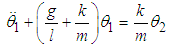 | (3.15) |
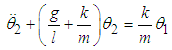 | (3.16) |
Multiplying equations (3.15) and (3.16) by the mass, m and adding the effects of damping and external forces we obtain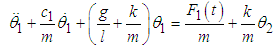 | (3.17) |
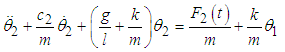 | (3.18) |
and comparing with (2.39) we can write (3.17) and (3.18) as 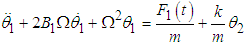 | (3.19) |
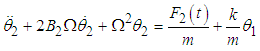 | (3.20) |
where 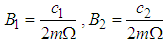 ,
, 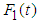 and
and 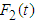 are two independent sources of stationary Gaussian white noise random excitation.If
are two independent sources of stationary Gaussian white noise random excitation.If 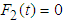 , then equation (3.20) can be written as
, then equation (3.20) can be written as  | (3.21) |
and hence from equation (2.40), the rate of power flow from the first to the second pendulum can be written as 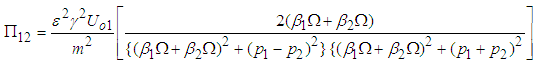 | (3.22) |
The power input is dissipated by the damping of the second pendulum and hence the mean rate of power dissipation is 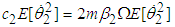 | (3.23) |
Thus, equating equations (3.22) and (3.23) gives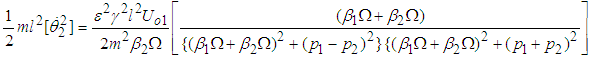 or
or 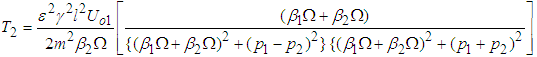 | (3.24) |
The blocked kinetic energy of the first pendulum is defined as the energy when the first oscillator is clamped so we can write 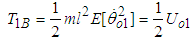 | (3.25) |
Substituting equation (3.25) in (3.24) we obtain 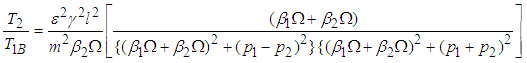 | (3.26) |
Equation (3.26) shows that the rate of power flow from the first pendulum to the second (when the latter is under white noise random excitations) is dependent on the blocked frequencies 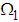 ,
, 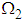 and the damping coefficients
and the damping coefficients 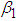 ,
, 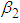 . Since the blocked frequencies
. Since the blocked frequencies 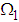 and
and 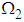 are equal for this case, the rate of power flow will be maximum [13].
are equal for this case, the rate of power flow will be maximum [13].
3.2. Two Coupled Pendula of Different Masses
Substituting equations (2.14) and (2.18) in (2.32) we obtain 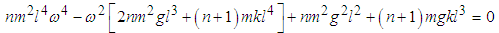 | (3.27) |
Solving equation (3.27) and retaining only positive frequencies (physically sound) we obtain the natural frequencies of the system 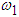 and
and 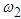 as
as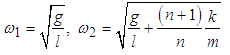 | (3.28) |
The system has two natural frequencies; the first is independent of the mass ratio and identical to that in section 3.1. The second natural frequency 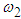 is dependent on n and for large values of n,
is dependent on n and for large values of n, 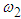 tends to a constant value as
tends to a constant value as .The equations of motion are
.The equations of motion are 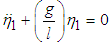 | (3.29) |
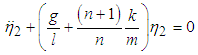 | (3.30) |
Since  is the same as that of identical pendula, we can conclude that
is the same as that of identical pendula, we can conclude that | (3.31) |
Similarly, for  we obtain:
we obtain: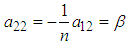 | (3.32) |
Thus 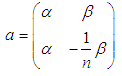 | (3.33) |
and using (2.38) gives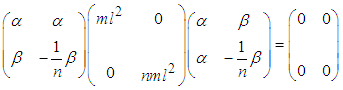 | (3.34) |
Solving equation (3.34), the values of 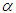 and
and 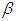 are obtained as
are obtained as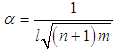 | (3.35) |
and 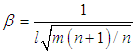 | (3.36) |
Thus 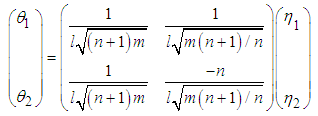 | (3.37) |
Equation (3.37) gives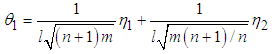 | (3.38) |
and 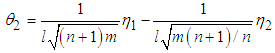 | (3.39) |
Using (3.38) and (3.39) the equations of motion are obtained as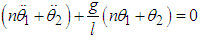 | (3.40) |
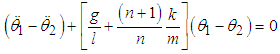 | (3.41) |
Adding equations (3.40) and (3.41) and re-arranging we obtain 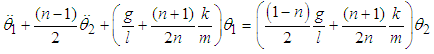 | (3.42) |
Assuming that 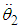 can be written in terms of
can be written in terms of 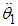 as
as 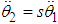 , where s is any positive real number and taking
, where s is any positive real number and taking 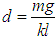 , then (3.42) becomes
, then (3.42) becomes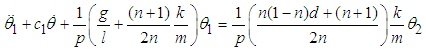 | (3.43) |
where 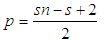 Subtracting equation (3.40) from (3.41) and re-arranging we obtain
Subtracting equation (3.40) from (3.41) and re-arranging we obtain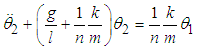 | (3.44) |
Multiplying equation (3.43) and (3.44) by the respective masses, adding the damping and the external force terms gives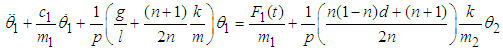 | (3.45) |
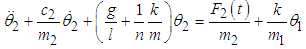 | (3.46) |
Equations (3.45) and (3.46) can be re-written as 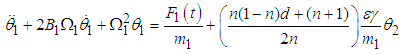 | (3.47) |
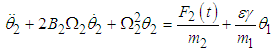 | (3.48) |
where 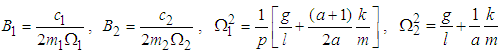 Setting
Setting 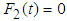 , then the rate of power flow from the first to the second pendulum can be written as
, then the rate of power flow from the first to the second pendulum can be written as 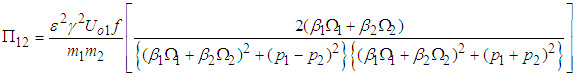 | (3.49) |
where 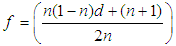 Thus, since the power input is dissipated by the damping of the second pendulum, the mean rate of power dissipation can be equated to (3.49) giving
Thus, since the power input is dissipated by the damping of the second pendulum, the mean rate of power dissipation can be equated to (3.49) giving 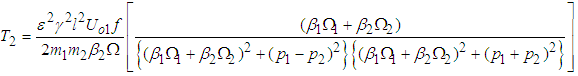 | (3.50) |
The blocked kinetic energy of the first pendulum 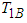 is related to (3.50) as
is related to (3.50) as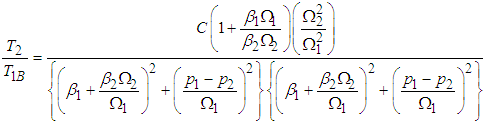 | (3.51) |
where 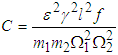 is the coupling parameter and the greater the value of C the stronger the coupling. For weak coupling,
is the coupling parameter and the greater the value of C the stronger the coupling. For weak coupling, 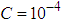 and
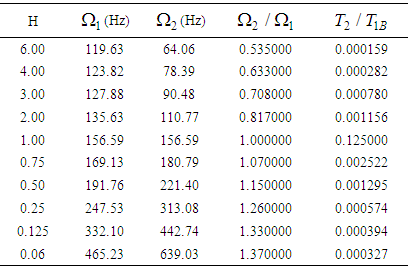
and 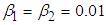 . Thus equation (3.60) can be plotted using the calculated parameters in Table 3.1 as in Fig. 3.1.
. Thus equation (3.60) can be plotted using the calculated parameters in Table 3.1 as in Fig. 3.1. Table 1. Relationship between ratios of kinetic energy
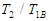 and frequencies and frequencies
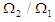
 |
| |
|
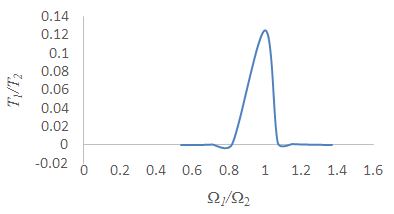 | Figure 5. Relationship between ratios of kinetic energy 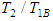 and frequencies and frequencies 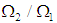 |
Equation (3.51) shows the rate of power flow from the first to the second pendulum. Fig. 5 is a plot of the kinetic energy of the second pendulum T2 to the blocked energy of the first T1B against the ratios of blocked frequency 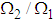 . Fig.3.1 shows that T2/ T1B is maximum when
. Fig.3.1 shows that T2/ T1B is maximum when 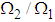 equals one and is minimum when it tends to zero or infinity [13].
equals one and is minimum when it tends to zero or infinity [13].
3.3. Two Coupled Pendula of Different Lengths
Equation (2.32) for this system gives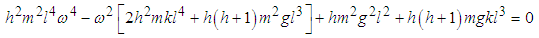 | (3.52) |
If we let 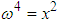 then
then 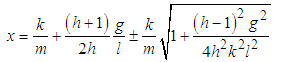 | (3.53) |
Expanding the term inside the square root sign binomially and neglecting higher terms, gives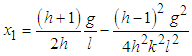 | (3.54) |
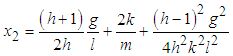 | (3.55) |
Considering only linear terms in l and k gives the normal frequencies of the system as 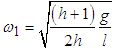 | (3.56) |
and  | (3.57) |
The system has two natural frequencies both dependent on the length ratio l.The normal equations of motion of a system of two pendula of the same mass and different lengths is obtained as | (3.58) |
 | (3.59) |
Components of (2.36) are derived as  | (3.60) |
where 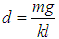 and
and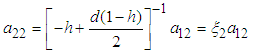 | (3.61) |
Thus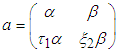 | (3.62) |
The relations between coordinates are 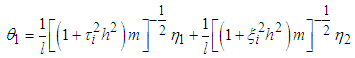 | (3.63) |
and 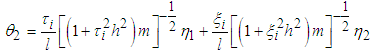 | (3.64) |
The equations of motion are obtained after adding the effects of damping and external forces as 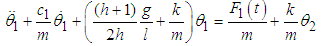 | (3.65) |
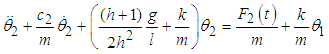 | (3.66) |
or 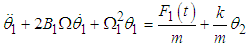 | (3.67) |
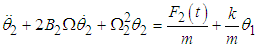 | (3.68) |
where 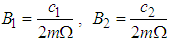 .The rate of power flow from the first to the second pendulum is obtained as
.The rate of power flow from the first to the second pendulum is obtained as 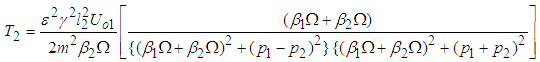 | (3.69) |
It can be showed that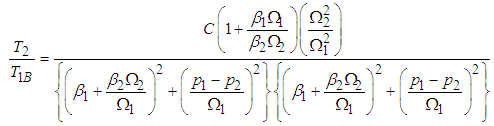 | (3.70) |
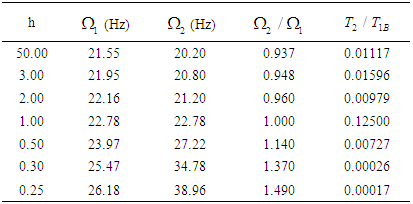
where 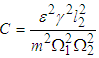 which is the coupling coefficient An illustration of (3.70) is shown in Table 2 and Fig. 6.
which is the coupling coefficient An illustration of (3.70) is shown in Table 2 and Fig. 6. Table 2. Relationship between ratios of kinetic energy
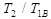 and frequencies and frequencies
 |
| |
|
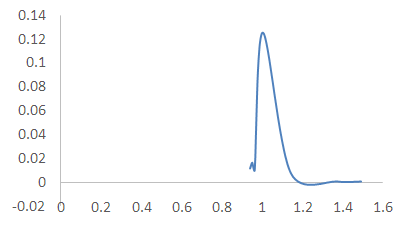 | Figure 6. Relationship between ratios of kinetic energy 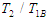 and frequencies and frequencies 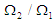 |
It is observed from Fig. 6 that the power flow is maximum when the ratio of blocked frequencies is 1.
3.4. Compound Pendula with Different Masses and Lengths
Here, equation (2.32) gives 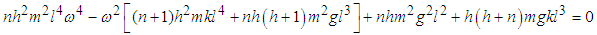 | (3.71) |
Considering only terms that are linear in l we can write the natural frequencies 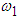 and
and 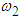 of the system as
of the system as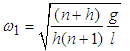 | (3.72) |
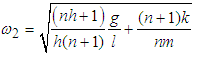 | (3.73) |
Thus, the normal equations of motion are 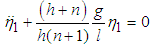 | (3.74) |
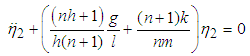 | (3.75) |
Also,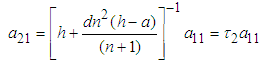 | (3.76) |
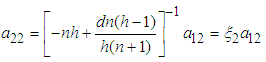 | (3.77) |
and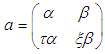 | (3.78) |
Hence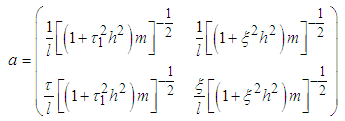 | (3.79) |
and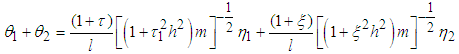 | (3.80) |
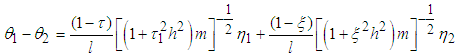 | (3.81) |
Assuming that 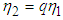 where q is any real number, we can re-write equations (3.80) and (3.81) as
where q is any real number, we can re-write equations (3.80) and (3.81) as 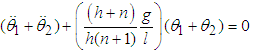 | (3.82) |
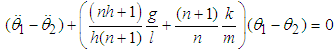 | (3.83) |
The equations of motion are obtained as: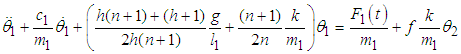 | (3.84) |
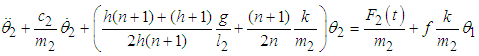 | (3.85) |
or 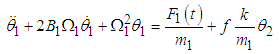 | (3.86) |
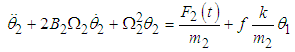 | (3.87) |
Where 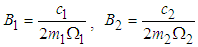 and
and 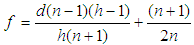 The rate of power flow from the first to the second pendulum is
The rate of power flow from the first to the second pendulum is 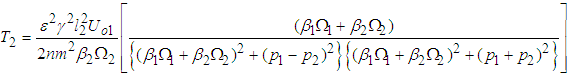 | (3.89) |
and the blocked kinetic energy 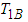 of the first pendulum is related to the power flow as:
of the first pendulum is related to the power flow as: 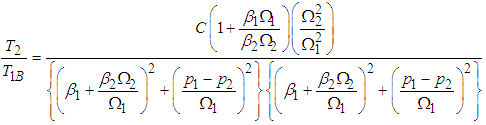 | (3.90) |
where 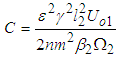 Equation (3.90) can be illustrated as in Table 3 and Fig. 7.Equation (3.90) shows the rate of power flow from the first to the second pendulum when the first is under white noise random excitations and Fig. 7, is a plot of T2/ T1B against
Equation (3.90) can be illustrated as in Table 3 and Fig. 7.Equation (3.90) shows the rate of power flow from the first to the second pendulum when the first is under white noise random excitations and Fig. 7, is a plot of T2/ T1B against 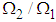 . It can be observed that the power flow is maximum when the ratio of blocked frequencies is 1.
. It can be observed that the power flow is maximum when the ratio of blocked frequencies is 1.Table 3. Relationship between ratios of kinetic energy
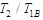 and frequencies and frequencies
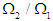
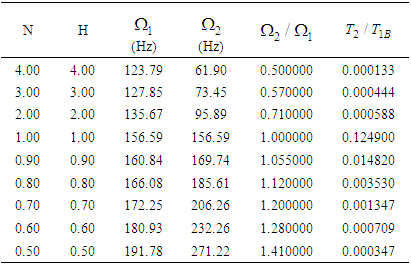 |
| |
|
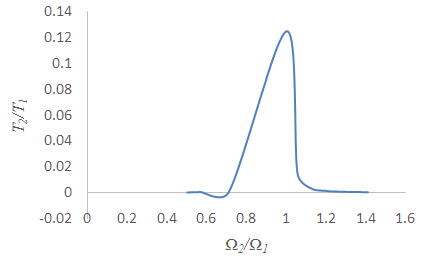 | Figure 7. Relationship between ratios of kinetic energy 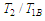 and frequencies and frequencies 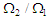 |
3.5. Application of Power Flow in Compound Pendulum to an Optical Switch
Fig. 8 shows an optical switch which is a device that allows optical signals to be switched on and off or switched from one channel to another. An optical switch is made of two parallel waveguides coupled with a directional coupler [14]. A directional coupler is made of two optical waveguides that are brought close to each other in such a way that their respective optical modes can interact and split into even and odd symmetries that allow the transfer of power between them [15]. For an optical switch, the relative phase difference between the supermodes of the coupling system must be π and hence the value of the coupling length Lc must be chosen to satisfy this condition. 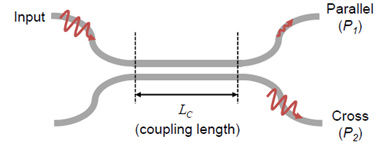 | Figure 8. A schematic diagram of an optical switch [16] |
Fig. 9 explains the theory of switching in an optical directional coupler, in Fig. 9 (a) the optical signal is transferred through the upper waveguide, at , the two modes interact, the odd mode is shown with red while the even mode is blue. The region where both symmetries interfere (shown in green in (Fig. 9 (b))) is where is optical signal is transmitted to. Similarly at 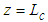 , the phase shift between the even mode and odd mode is π and the interaction between the two mode leads to the switching of the optical signal from the upper to the lower waveguide (Fig. 9 (c) and (d)).
, the phase shift between the even mode and odd mode is π and the interaction between the two mode leads to the switching of the optical signal from the upper to the lower waveguide (Fig. 9 (c) and (d)).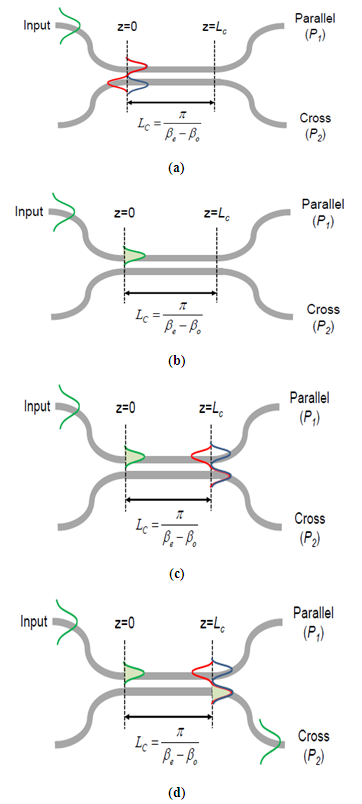 | Figure 9. Theory of switching [16] |
Coupled pendulum system is analogous to coupled transmission lines and understanding the behavior of coupled pendulum system can aid in explaining the behavior of coupled transmission lines and other related devices. In 1996, the coupled mode theory was used to analyze both systems and it was found that a system of two weakly coupled identical pendula and two weakly coupled pendula of different lengths can be used to model the basic behavior of an optical switch. In an optical switch, a deriving voltage is used to change the phase constants of the waveguides, when the phases are equal, the power is transferred between the waveguides and when the voltage is applied, the phase constants are no longer equal and there is no power transfer between the waveguides [17].From Fig 9, it can be deduced that the effect of the driving voltage can be visualized as changing the length ratio of the pendula system and the net power flow corresponds to the case when h=1 i.e. when the system reduces to the identical pendula case. When 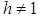 , the phase constants are not equal and hence there will be no net power flow between the waveguides.
, the phase constants are not equal and hence there will be no net power flow between the waveguides.
4. Conclusions
The coupled pendula system has been used for decades as a model to simulate natural phenomena and hence knowing the natural and blocked frequencies, general equations of motion and rate of power flow between the components of such systems is crucial. In this research work, four cases of two weakly coupled pendula systems were taken into consideration. Analytical tools were used to derive the rate of power flow under white noise random excitations between the two oscillators. Higher order terms of the frequencies can be included to obtain more accurate results. Future researches may be done to obtain the same parameters for strongly coupled pendula. Computational and experimental components can be added to this research.
References
| [1] | Serway, R. A. and Jewett, J.W. Physics for scientists and engineers, with modern physics. Belmont, CA, Thomson-Brooks/Cole, 2003, 452-485. |
| [2] | Ndikilar C.E. and Maharaz M. N. Elementary Space Science, ABU Press, Zaria, 2016. |
| [3] | Strogatz, S.H. and Stewart, I. A subtle mathematical thread connects clocks, ambling elephants, rhythms and onset chaos. Scientific American Journal, 1993, 269(6): 102-107. |
| [4] | Schubert, K. R. and Stiewe, J. (2011). Demonstration of K0K0, B0B0 and D0D0 Transitions with a Pair of Coupled Pendula. Journal of Physics G: Nuclear and Particle Physics, 2011, 39(3), 33-110. |
| [5] | Singiresu, S. R. (2011). Mechanical vibrations. Prentice Hall, 1 Lake Street, Upper Saddle River, 2011, 210-323. |
| [6] | Mallada, E. and Tang, A. Synchronization of weakly coupled oscillators: coupling. Journal of Physics, 2013, 46(50): 501-510. |
| [7] | Yaniv, Y.. Lakatta, E. G. and Maltsev, V. A. From two competing oscillators to one coupled-clock pace maker cell system. Frontiers in Physiology Journal, 2015, 48(12): 667-684. |
| [8] | Ramana, R. A, Sen, A. and Johnston. G.L. Experimental evidence of time-delay-induced death in coupled limit-cycle oscillators. Physical Review Letters, 2000, 85 (16): 3381-3384. |
| [9] | Kubacki, M. Dynamics of Coupled Double Pendulums, 2011, [online] Avalable: (April 7, 2018). |
| [10] | Altshulera E. and Garcia, R. Josephson junctions in a magnetic field: Insights from coupled pendula. American Journal of Physics, 2003, 71(4): 405-408. |
| [11] | Ndikilar, C. E.. Analytical Mechanics, ABU Press, Zaria, 2018, (In press). |
| [12] | Shapiro, J.A. Classical mechanics. Rutgers university, University press New Jersey, United States of America, 2003, 1-35. |
| [13] | Newland, D. E. Calculation of power flow between coupled oscillators. Journal of Sound and Vibration, 1966, 3(3): 262-276. |
| [14] | Vakili, B. Bahadori, S.and Ghayour, R. All-optical switching using a new photonic crystal directional coupler. Advanced Electromagnetics, 2015, 4:63-67. |
| [15] | Beggs, D. M. White, T. P. O’Faolain, L. and Krauss, T. F. Design and fabrication of a photonic crystal directional coupler for use as an optical switch. 2008, 379-382. |
| [16] | Yamada, H. Chu, T. Ishida, S. and Arakawa, Y. Optical directional coupler based on Si-wire waveguides. IEEE photonic technology letters, 2005, 17(3): 585-588. |
| [17] | Teoh, C. S. and Davis, L. E. A coupled pendula system as an analogy to coupled transmission lines. IEEE education society, 1996, 39: 548-557. |



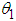 and
and 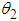 which are the angles the rods make with the vertical [11].
which are the angles the rods make with the vertical [11].
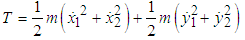
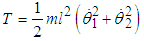
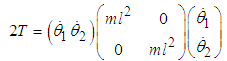
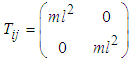
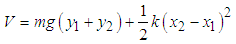
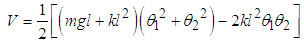
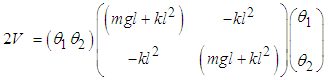
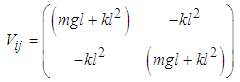
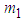 and
and 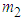 . The system has two degrees of freedom
. The system has two degrees of freedom 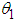 and
and 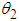 which are the angles the rods make with vertical (Fig. 2).
which are the angles the rods make with vertical (Fig. 2).
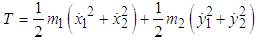
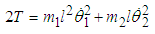
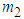 can be written in terms of
can be written in terms of 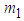 such that
such that 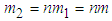
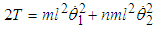
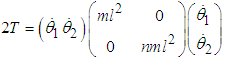
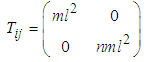
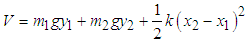
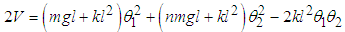
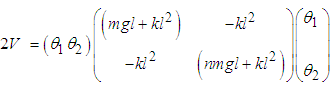
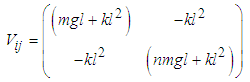
 and
and  . The system has two degrees of freedom
. The system has two degrees of freedom 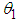 and
and 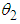 which are the angles the rods make with vertical.
which are the angles the rods make with vertical.
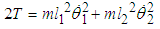
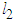 can be written in terms of
can be written in terms of 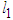 such that
such that 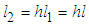
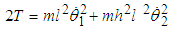
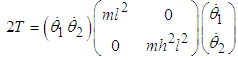
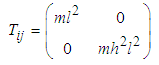
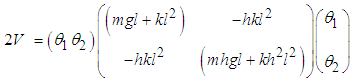
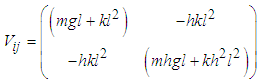

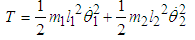
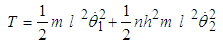
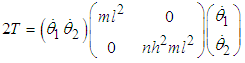
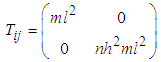
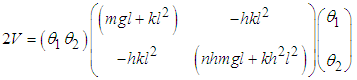
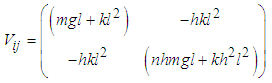
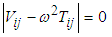
 is the natural frequency. Since all the four systems have two degrees of freedom, two values of
is the natural frequency. Since all the four systems have two degrees of freedom, two values of  are obtained in each case [11].The normal modes of each system are obtained using the equation
are obtained in each case [11].The normal modes of each system are obtained using the equation 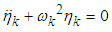
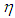 is the normal co-ordinates and
is the normal co-ordinates and 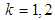 [11].To convert the equations of motion from normal to generalized coordinates we use the equation
[11].To convert the equations of motion from normal to generalized coordinates we use the equation 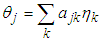
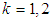 , we can write
, we can write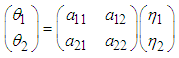
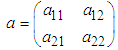
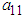 and
and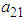 are components of the eigenvector
are components of the eigenvector 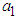 which are computed by setting
which are computed by setting 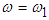 and using [12]
and using [12] 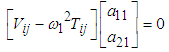
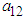 and
and 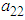 which are components of eigenvector
which are components of eigenvector 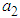 The values of the
The values of the 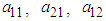 and
and 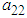 are obtained in terms of m and l using
are obtained in terms of m and l using 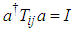
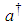 is the Hermitian transpose of a and I is the identity matrix. After obtaining the equations of motion in terms of generalized coordinates for each system, the effects of damping and external forces is taken into consideration and the equations of motion are written in the form [13]:
is the Hermitian transpose of a and I is the identity matrix. After obtaining the equations of motion in terms of generalized coordinates for each system, the effects of damping and external forces is taken into consideration and the equations of motion are written in the form [13]: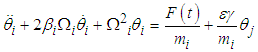
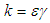 ,
, 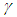 and
and 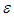 are called the coupling parameters,
are called the coupling parameters, 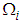 is the blocked frequency of the ith oscillator and
is the blocked frequency of the ith oscillator and 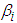 is the damping ratio of the ith oscillator.The parameters from equation (2.39) are used to calculate the power flow. The first order approximation to the power flow between weakly coupled oscillators under white noise random excitations is given as
is the damping ratio of the ith oscillator.The parameters from equation (2.39) are used to calculate the power flow. The first order approximation to the power flow between weakly coupled oscillators under white noise random excitations is given as 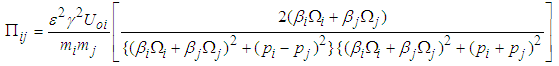
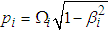 and
and 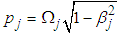 White noise is a random signal that is a combination of all audible frequencies (20Hz-20KHz) with constant power spectral density.
White noise is a random signal that is a combination of all audible frequencies (20Hz-20KHz) with constant power spectral density.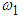 and
and 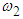 are obtained as
are obtained as 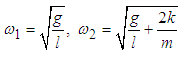
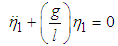
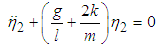
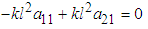 and hence
and hence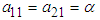
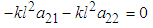 and
and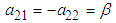
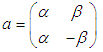
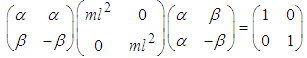 or
or 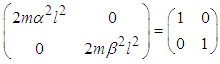
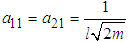
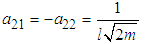
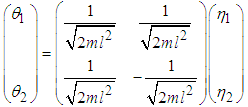
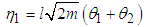
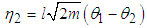
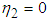 then
then 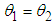 and the two pendula oscillate in phase with an angular frequency
and the two pendula oscillate in phase with an angular frequency 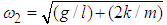 and this is the first natural mode of the system. Also, if
and this is the first natural mode of the system. Also, if 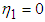 then
then 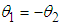 and the two pendula oscillate in an out of phase mode with an angular frequency
and the two pendula oscillate in an out of phase mode with an angular frequency 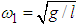 and this is the second natural mode of the system [11].The explicit equations of motion for this system are obtained by substituting (3.11) and (3.12) in (3.2) and (3.3) to give
and this is the second natural mode of the system [11].The explicit equations of motion for this system are obtained by substituting (3.11) and (3.12) in (3.2) and (3.3) to give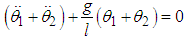
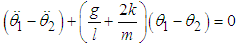
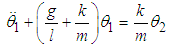
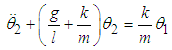
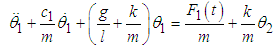
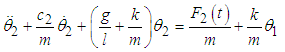
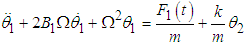
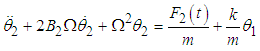
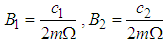 ,
, 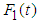 and
and 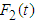 are two independent sources of stationary Gaussian white noise random excitation.If
are two independent sources of stationary Gaussian white noise random excitation.If 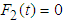 , then equation (3.20) can be written as
, then equation (3.20) can be written as 
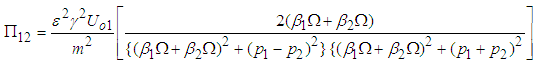
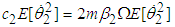
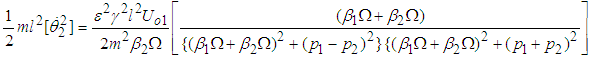 or
or 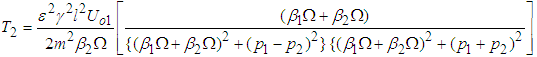
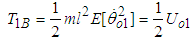
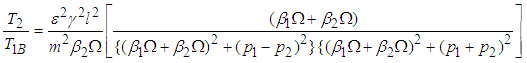
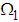 ,
, 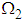 and the damping coefficients
and the damping coefficients 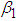 ,
, 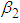 . Since the blocked frequencies
. Since the blocked frequencies 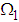 and
and 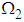 are equal for this case, the rate of power flow will be maximum [13].
are equal for this case, the rate of power flow will be maximum [13].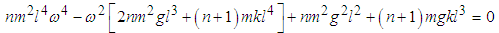
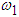 and
and 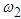 as
as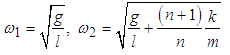
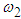 is dependent on n and for large values of n,
is dependent on n and for large values of n, 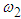 tends to a constant value as
tends to a constant value as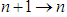 .The equations of motion are
.The equations of motion are 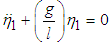
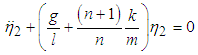
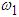 is the same as that of identical pendula, we can conclude that
is the same as that of identical pendula, we can conclude that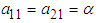
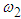 we obtain:
we obtain: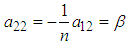
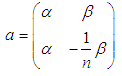
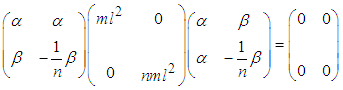
 and
and  are obtained as
are obtained as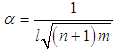
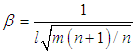
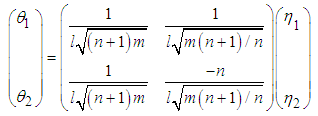
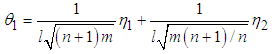
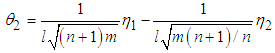
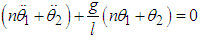
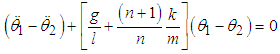
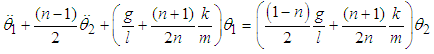
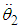 can be written in terms of
can be written in terms of 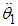 as
as 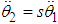 , where s is any positive real number and taking
, where s is any positive real number and taking 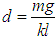 , then (3.42) becomes
, then (3.42) becomes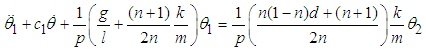
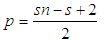 Subtracting equation (3.40) from (3.41) and re-arranging we obtain
Subtracting equation (3.40) from (3.41) and re-arranging we obtain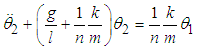
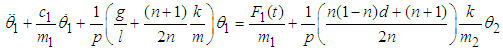
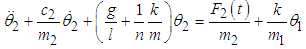
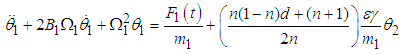
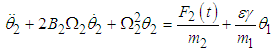
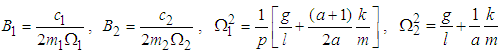 Setting
Setting 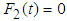 , then the rate of power flow from the first to the second pendulum can be written as
, then the rate of power flow from the first to the second pendulum can be written as 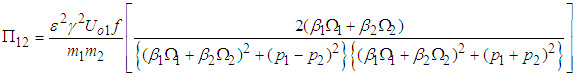
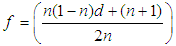 Thus, since the power input is dissipated by the damping of the second pendulum, the mean rate of power dissipation can be equated to (3.49) giving
Thus, since the power input is dissipated by the damping of the second pendulum, the mean rate of power dissipation can be equated to (3.49) giving 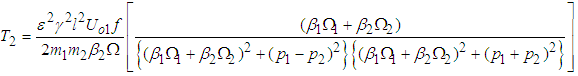
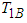 is related to (3.50) as
is related to (3.50) as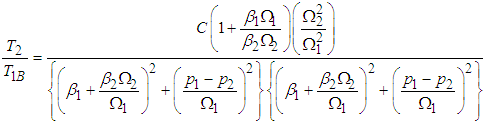
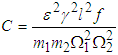 is the coupling parameter and the greater the value of C the stronger the coupling. For weak coupling,
is the coupling parameter and the greater the value of C the stronger the coupling. For weak coupling, 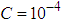 and
and 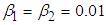 . Thus equation (3.60) can be plotted using the calculated parameters in Table 3.1 as in Fig. 3.1.
. Thus equation (3.60) can be plotted using the calculated parameters in Table 3.1 as in Fig. 3.1. 
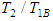 and frequencies
and frequencies 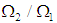
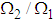 . Fig.3.1 shows that T2/ T1B is maximum when
. Fig.3.1 shows that T2/ T1B is maximum when 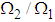 equals one and is minimum when it tends to zero or infinity [13].
equals one and is minimum when it tends to zero or infinity [13]. 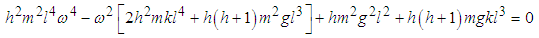
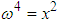 then
then 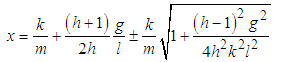
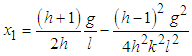
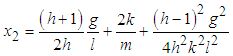
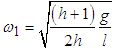
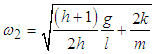
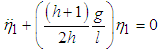
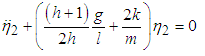
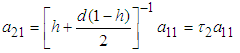
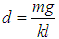 and
and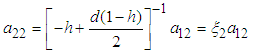
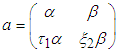
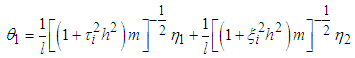
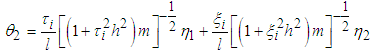
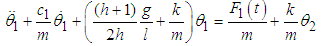
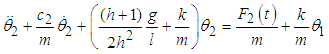
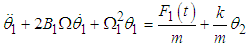
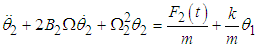
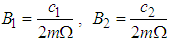 .The rate of power flow from the first to the second pendulum is obtained as
.The rate of power flow from the first to the second pendulum is obtained as 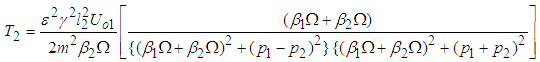
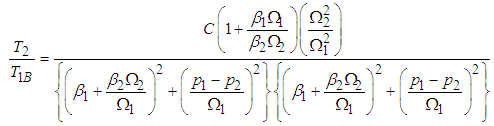
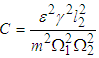 which is the coupling coefficient An illustration of (3.70) is shown in Table 2 and Fig. 6.
which is the coupling coefficient An illustration of (3.70) is shown in Table 2 and Fig. 6. 
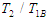 and frequencies
and frequencies 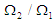
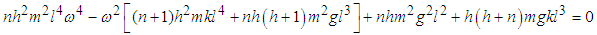
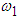 and
and 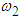 of the system as
of the system as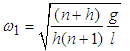
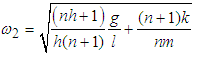
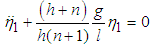
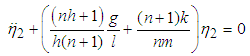
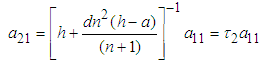
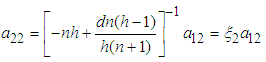
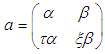
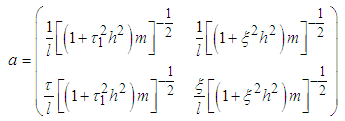
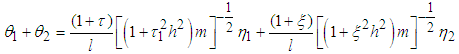
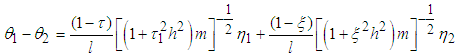
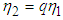 where q is any real number, we can re-write equations (3.80) and (3.81) as
where q is any real number, we can re-write equations (3.80) and (3.81) as 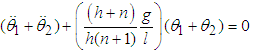
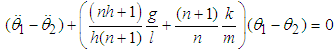
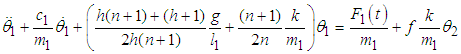
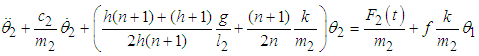
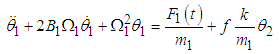
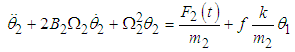
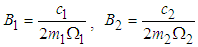 and
and 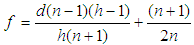 The rate of power flow from the first to the second pendulum is
The rate of power flow from the first to the second pendulum is 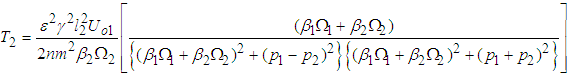
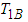 of the first pendulum is related to the power flow as:
of the first pendulum is related to the power flow as: 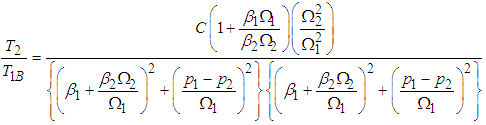
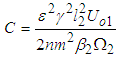 Equation (3.90) can be illustrated as in Table 3 and Fig. 7.Equation (3.90) shows the rate of power flow from the first to the second pendulum when the first is under white noise random excitations and Fig. 7, is a plot of T2/ T1B against
Equation (3.90) can be illustrated as in Table 3 and Fig. 7.Equation (3.90) shows the rate of power flow from the first to the second pendulum when the first is under white noise random excitations and Fig. 7, is a plot of T2/ T1B against 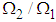 . It can be observed that the power flow is maximum when the ratio of blocked frequencies is 1.
. It can be observed that the power flow is maximum when the ratio of blocked frequencies is 1.
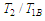 and frequencies
and frequencies 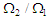

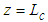 , the phase shift between the even mode and odd mode is π and the interaction between the two mode leads to the switching of the optical signal from the upper to the lower waveguide (Fig. 9 (c) and (d)).
, the phase shift between the even mode and odd mode is π and the interaction between the two mode leads to the switching of the optical signal from the upper to the lower waveguide (Fig. 9 (c) and (d)).
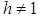 , the phase constants are not equal and hence there will be no net power flow between the waveguides.
, the phase constants are not equal and hence there will be no net power flow between the waveguides. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML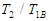 and frequencies
and frequencies 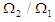

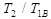 and frequencies
and frequencies 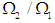

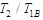 and frequencies
and frequencies