Doron Kwiat
17/2 Erez Street, Mazkeret Batyia, Israel
Correspondence to: Doron Kwiat , 17/2 Erez Street, Mazkeret Batyia, Israel.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Introducing d dimensional space, with NxN Lorentz invariant gamma matrices, the connection between N and d is N=2d/2 and since N is an integer, d must be an even number. Thus, the only candidates for a higher dimension universe for fermions may be SO(8), SO(16) etc. SO(7), SO(11) etc. are ruled out in case of fermions. However, it is shown that d>4 is impossible since already for d=6, the representation is reducible. Thus, our universe, at least as far as Fermions goes, must be a (3+1) 4-dimensional.
Keywords:
Dirac Gamma Matrices, d dimensional universe, Clifford
Cite this paper: Doron Kwiat , Fermions in d Dimensions, International Journal of Theoretical and Mathematical Physics, Vol. 9 No. 1, 2019, pp. 14-19. doi: 10.5923/j.ijtmp.20190901.03.
1. Introduction
In spite of the fact that the universe is well described by four-dimensional spacetime, there are several reasons why physicists consider theories in other dimensions [5-15]. In some cases, by modeling spacetime in a different number of dimensions, a theory becomes more mathematically tractable, and one can perform calculations and gain general insights more easily. If there exist scenarios in which there could actually be more than four dimensions of spacetime, they have so far managed to escape detection. One notable feature of string theories is that these theories require extra dimensions of spacetime for their mathematical consistency. In bosonic string theory, spacetime is 26-dimensional, while in superstring theory it is 10-dimensional, and in M-theory it is 11-dimensional. In order to describe real physical phenomena using string theory, one must therefore imagine scenarios in which these extra dimensions would not be observed in experiments.When considering the Fermionic universe, which includes all the known massive particles, we rely on Dirac equation [1] and thereof on the so-called gamma matrices 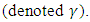 Starting with the Dirac equation with N-dimensional spinors, we accept the fact that the gamma matrices, irrespective of the number of dimensions of our universe, they always must conform with the Clifford algebra [3, 4, 7] restriction.Following this, it is proven in this work, that there must exist a connection between the dimensionality of these matrices (and hence of the spinors), and the number of dimensions d of our universe.Unlike previous approaches, here there is no need to separate between odd and even dimensions. This leads us to the conclusion that N2=2d. Therefore, d must be even, and N must be an integer power of 2.By a unique construction procedure, we use the gamma matrices to construct a relevant group of matrices. These groups presentations become reducible for any d > 4.Thus, only d = 4 will be allowed, and our fermionic world cannot be other than a 3+1 universe.Physical problems cannot rely on imaginary numbers, except for the purpose of mathematical comfort. The introduction of imaginary and complex numbers is nothing but a mathematical convenience for shortening and unifying equations. Obviously, since complex entities can always be decomposed into real and imaginary parts and vice versa, using natural (real-entities only) approach does not contribute anything and makes things unjustifiably more complex. However, by using complex presentation one might be overlooking some hidden qualities [2].For instance, the complex Schrodinger equation turns out to be a pair of coupled equations of the real and imaginary parts [2]:The Schrödinger equation for a free particle (v(x) =0) becomes:
Starting with the Dirac equation with N-dimensional spinors, we accept the fact that the gamma matrices, irrespective of the number of dimensions of our universe, they always must conform with the Clifford algebra [3, 4, 7] restriction.Following this, it is proven in this work, that there must exist a connection between the dimensionality of these matrices (and hence of the spinors), and the number of dimensions d of our universe.Unlike previous approaches, here there is no need to separate between odd and even dimensions. This leads us to the conclusion that N2=2d. Therefore, d must be even, and N must be an integer power of 2.By a unique construction procedure, we use the gamma matrices to construct a relevant group of matrices. These groups presentations become reducible for any d > 4.Thus, only d = 4 will be allowed, and our fermionic world cannot be other than a 3+1 universe.Physical problems cannot rely on imaginary numbers, except for the purpose of mathematical comfort. The introduction of imaginary and complex numbers is nothing but a mathematical convenience for shortening and unifying equations. Obviously, since complex entities can always be decomposed into real and imaginary parts and vice versa, using natural (real-entities only) approach does not contribute anything and makes things unjustifiably more complex. However, by using complex presentation one might be overlooking some hidden qualities [2].For instance, the complex Schrodinger equation turns out to be a pair of coupled equations of the real and imaginary parts [2]:The Schrödinger equation for a free particle (v(x) =0) becomes: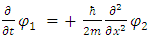 | (1) |
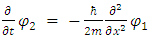 | (2) |
These two coupled equations can be shown [1] to be equivalent to coupling between two strings having initial tension T0 and initial coupling 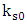 between the two strings:
between the two strings: 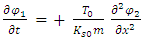 | (3) |
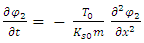 | (4) |
Provided that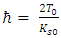 | (5) |
As Ts and Ks are inversely proportional to time, the ratio 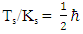 is fixed in time.This interpretation of a particle as made up of two coupled strings, whose tensions and interaction are inversely proportional to time, gives us a classical interpretation of the Schrödinger equation.As Ts and Ks are inversely proportional to time, the ratio Ts/Ks is constant in time.Therefore, without loss of generality
is fixed in time.This interpretation of a particle as made up of two coupled strings, whose tensions and interaction are inversely proportional to time, gives us a classical interpretation of the Schrödinger equation.As Ts and Ks are inversely proportional to time, the ratio Ts/Ks is constant in time.Therefore, without loss of generality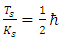 | (6) |
This shows a derivation of Planck's universal constant, as a result of string structure of elementary particles.
2. Spatial Asymmetry of Dirac Equation
One may project from this on the relativistic Dirac equation [1], describing a free Fermion of mass m: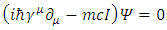 | (7) |
One may separate the complex wave function 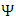 into its real and imaginary parts [2]
into its real and imaginary parts [2]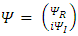 | (8) |
and by using them in the Dirac equation, one will get two separate equations where imaginary and real parts have been separated.This same procedure can be applied to any quantum field Lagrangian, resulting (at the cost of doubling the number of equations) in separation of the equations to real wave functions.In Dirac equation, Eq. [7], the four 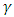 matrices are:
matrices are: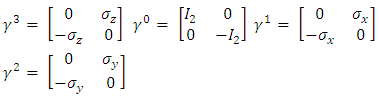 | (9) |
where I2 is the 2x2 unit matrix and 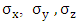 the Pauli 2x2 matrices.
the Pauli 2x2 matrices.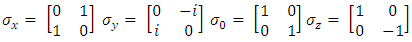 | (10) |
Of these matrices, only 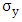 has imaginary components and it can be replaced by writing
has imaginary components and it can be replaced by writing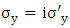 where
where 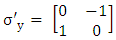 and therefore
and therefore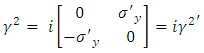 | (11) |
So that 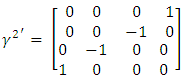 Decomposing
Decomposing  into
into  where
where  and
and 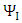 are real, the Dirac equation becomes two separate equations:
are real, the Dirac equation becomes two separate equations: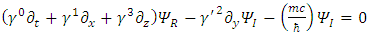 | (12) |
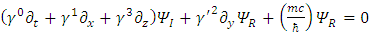 | (13) |
(a) There are now 8 real wave functions instead of 4 in the complex presentation.(b) All the 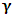 matrices are real.(c) Notice the asymmetry of the y-component in Eqs. [12, 13] due to the complex nature of Pauli's
matrices are real.(c) Notice the asymmetry of the y-component in Eqs. [12, 13] due to the complex nature of Pauli's 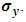 (d) Notice the change of sign in the mass terms.(e) Even if m=0, the asymmetry in y remains.(f) Notice the coupling between
(d) Notice the change of sign in the mass terms.(e) Even if m=0, the asymmetry in y remains.(f) Notice the coupling between 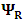 and
and 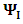 , which remains even when the mass term vannishes.Eqs. [12-13] may be written
, which remains even when the mass term vannishes.Eqs. [12-13] may be written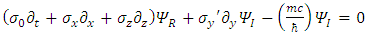 | (14) |
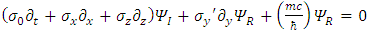 | (15) |
In these coupled differential equations, all the 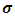 are real 2x2 matrices. Hence
are real 2x2 matrices. Hence 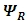 and
and 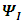 are 2-vectors.When combined into the complex
are 2-vectors.When combined into the complex 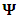 may be united into
may be united into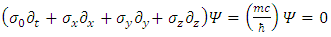 | (16) |
Where only 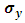 is complex, and
is complex, and 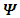 is a complex 4-vectorSetting m=0 gives the Weyl equation:
is a complex 4-vectorSetting m=0 gives the Weyl equation: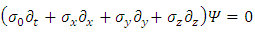 | (17) |
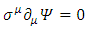 | (18) |
We see that by use of real components 2-vectors instead of a complex single 4-vector, there are two equations instead of one, and some coupling coupling mechanism between the real part 2-vector and imaginary part 2-vector.Notice that this coupling interaction does not vanish with mass (mà 0). However, in the case of m=0, one cannot discern between the two 2-vectors 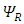 and
and 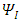 .
.
3. N -Dimensional Representation of Dirac Equation
Following Dirac's idea [1], of taking the square root of the wave operator, as suggested: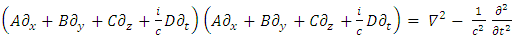 | (19) |
in order to force all cross-terms such as ∂x∂y to vanish, one must assume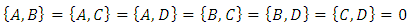 | (20) |
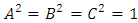 | (21) |
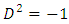 | (22) |
Or, if 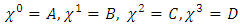 represent the A, B, C, D terms, then, in a compact form
represent the A, B, C, D terms, then, in a compact form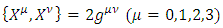 | (23) |
These conditions are met if A, B, C and D are matrices, with the implication that the wave function has components, as the dimension of the matrices. This explained the appearance of two-component wave functions in Pauli's theory of spin. The minimum would be to have A, B, C and D as 4x4 matrices. This is done in combinations of 2x2 Pauli matrices, in such a way that will obey the 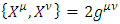 constrains. This leads to the assertion, that
constrains. This leads to the assertion, that 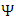 is a 4-vector of complex wave functions.In a 3+1 world,
is a 4-vector of complex wave functions.In a 3+1 world, 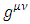 is a 4x4 matrix, so A, B, C and D are 4x4 matrices. However, in an N-dimensional world, one needs NxN matrices [4], with N >= 4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the Schrödinger equation. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives:
is a 4x4 matrix, so A, B, C and D are 4x4 matrices. However, in an N-dimensional world, one needs NxN matrices [4], with N >= 4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the Schrödinger equation. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives: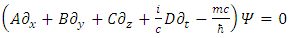 | (24) |
Since it originated in the Klein-Gordon [5] equation, which by itself originated from Schrödinger equation, it was assumed there that  is complex and therefore can be presented as a 2-vector of two complex wave functions.Instead of using the conventional 4x4
is complex and therefore can be presented as a 2-vector of two complex wave functions.Instead of using the conventional 4x4  matrices (A, B, C and D) as introduced by Dirac, a set of four N x N matrices
matrices (A, B, C and D) as introduced by Dirac, a set of four N x N matrices 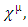 acting on a complex N-vector
acting on a complex N-vector 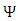 are introduced, which satisfy Eq. [18], and the constrains in Eq. [20].These
are introduced, which satisfy Eq. [18], and the constrains in Eq. [20].These 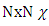 matrices replace the
matrices replace the 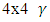 matrices in Dirac 4x4 equation to introduce the Dirac NxN equation:
matrices in Dirac 4x4 equation to introduce the Dirac NxN equation: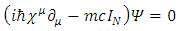 | (25) |
where 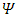 is now a complex N-vectorand where
is now a complex N-vectorand where 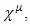 are four real NxN matrices, satisfying the Clifford requirement:
are four real NxN matrices, satisfying the Clifford requirement: 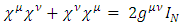 | (26) |
This Dirac equation representation, has now 2N real wave functions (N and N) instead of 8 (4 and 4).In their work about the dimensionality of our universe, Rugh and Nielsen [8], have shown that it is a straight-forward by induction procedure to go, from a set of d-2 matrices in a a d-2 universe to a d dimensional universe by adding 2 gamma matrices from any given set of d-2 matrices. This is done by way of constructing 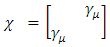 So, from a set of d NxN matrices, one can have a set of d+2 2Nx2N matrices satisfying the extended Clifford condition.This procedure will thus create presentations of SO(N) to fermions in d-dimensional universe, for any even or odd d.However, as will be shown, the condition NxN = 2d requires d to be an even number and hence only SO(4), SO(8), SO(16), SO(32) etc., representations are allowed.
So, from a set of d NxN matrices, one can have a set of d+2 2Nx2N matrices satisfying the extended Clifford condition.This procedure will thus create presentations of SO(N) to fermions in d-dimensional universe, for any even or odd d.However, as will be shown, the condition NxN = 2d requires d to be an even number and hence only SO(4), SO(8), SO(16), SO(32) etc., representations are allowed.
4. Group Limitation on 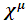
The Dirac matrices must satisfy the canonical anti-commutation relation 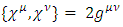 Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [2, 3].N-dimensional gamma matrices [5, 6, 12-16], are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity [12, 15, 16].Consider a d-dimensional space-time, with a flat Minkowski metric
Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [2, 3].N-dimensional gamma matrices [5, 6, 12-16], are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity [12, 15, 16].Consider a d-dimensional space-time, with a flat Minkowski metric 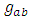 where
where 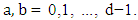 Original Dirac matrices correspond to taking d = N = 4.For a d-dimensional space (d-1 spatial + 1 temporal coordinates) dimension, there are d such matrices
Original Dirac matrices correspond to taking d = N = 4.For a d-dimensional space (d-1 spatial + 1 temporal coordinates) dimension, there are d such matrices 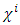 (i =0, … d-1), of size N×N, which satisfy the anticommutator relation from the Clifford algebra
(i =0, … d-1), of size N×N, which satisfy the anticommutator relation from the Clifford algebra 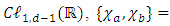
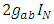 where
where 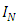 is the N dimensional identity matrix. (The spinors acted on by these matrices have N components each).For a Clifford algebra generated by a set of d
is the N dimensional identity matrix. (The spinors acted on by these matrices have N components each).For a Clifford algebra generated by a set of d 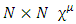 matrices,
matrices,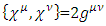 with μ, ν = 0, 1, 2, ⋯ d-1 and where the metric signature
with μ, ν = 0, 1, 2, ⋯ d-1 and where the metric signature 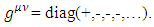 Using the matrices
Using the matrices 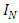 and
and 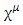 we can construct a set of
we can construct a set of 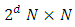 matrices as follow
matrices as follow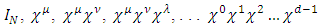 Over all combinations of indices, where
Over all combinations of indices, where 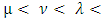
 etcFor a specific case denote d by D.Since there are D different
etcFor a specific case denote d by D.Since there are D different 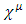 matrices, picking up p different ones, in an increasing index order, out of D for all 0 ≤ p ≤ D, there are
matrices, picking up p different ones, in an increasing index order, out of D for all 0 ≤ p ≤ D, there are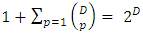 | (27) |
such matrix combinations.Denote these possible matrix combinations by 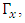 where
where 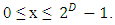 Thus creating a set
Thus creating a set 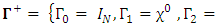
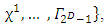 with 2D members.Because of the anticommutation relation between the gammas, the product of any
with 2D members.Because of the anticommutation relation between the gammas, the product of any 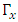 by any
by any 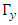 is, up to a sign, a third member
is, up to a sign, a third member 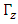 of the set.Define a set
of the set.Define a set 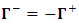 whose elements are the same members of
whose elements are the same members of 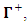 but with negative sign, namely:
but with negative sign, namely: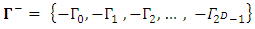 Create now a union set
Create now a union set 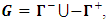 so G becomes the set of matrices
so G becomes the set of matrices 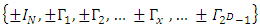 Re-assign notations for the
Re-assign notations for the 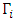 members of the set G as follows:
members of the set G as follows: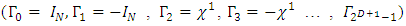 with
with 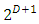 terms. It contains the unit element
terms. It contains the unit element 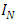 and is closed under multiplication, as the product of any
and is closed under multiplication, as the product of any 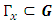 by any
by any 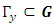 is a third member
is a third member 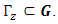 Thus
Thus 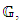 is a group with
is a group with 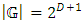 members.Let
members.Let 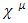 be N-dimensional
be N-dimensional 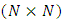 irreducible matrix representation.In order to establish the relationship between D and N, define a matrix
irreducible matrix representation.In order to establish the relationship between D and N, define a matrix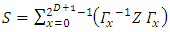 | (28) |
where Z is an arbitrary 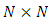 matrix (the summation runs over all
matrix (the summation runs over all 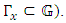 It follows that
It follows that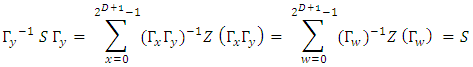 Or,
Or,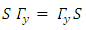 | (29) |
Since S commutes with all the matrices in the set, by Schur's first lemma ("A non-zero matrix which commutes with all of the matrices of an irreducible representation, is a constant multiple of the unit matrix") we conclude that S must be proportional to the identity matrix thus one can write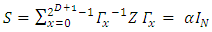 | (30) |
Taking the trace on both sides gives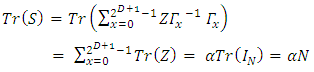 | (31) |
Hence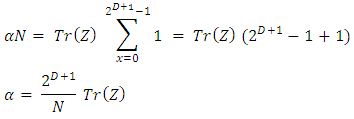 and since
and since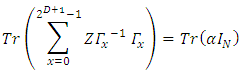 one obtains:
one obtains: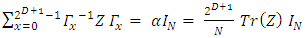 | (32) |
Taking the (i;j)th element of both sides: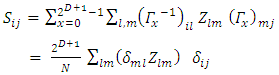 | (33) |
Where use is made of the fact that 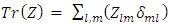 and
and 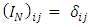
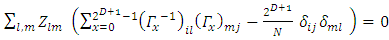 | (34) |
and since Z is an arbitrary matrix: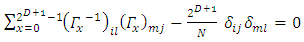 | (35) |
for any i, j, l, m.Setting l=i, m=j and summing over i and j: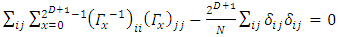 | (36) |
and so,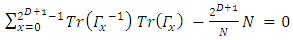 | (37) |
But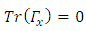 | (38) |
for all 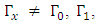 and
and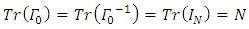 | (39) |
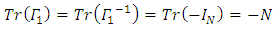 | (40) |
Therefore: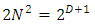 | (41) |
and finally,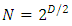 | (42) |
This result was reached based on the following assumptions:1. There exist d gamma nxn matrices where both d and N are integers.2. These gammas are Lorentz covariant3. The gammas must obey the Clifford algebra canonical anti-commutation relation 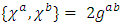 with a,b = (0,…d).4. The number d specifies the total number of world coordinates, of which there are the usual x,y,z spatial coordinate, at least one is a temporal coordinate and the rest are extended coordinates (may be temporal and may be spatial). By convention, in our 4 dimensional world we use d=3+1, namely x,y,z and t).5. By separation of the wave function into real and imaginary components, the resulting equations are doubled and so instead of a single N-vector complex spinor, one obtains 2 N-vector real spinors, with
with a,b = (0,…d).4. The number d specifies the total number of world coordinates, of which there are the usual x,y,z spatial coordinate, at least one is a temporal coordinate and the rest are extended coordinates (may be temporal and may be spatial). By convention, in our 4 dimensional world we use d=3+1, namely x,y,z and t).5. By separation of the wave function into real and imaginary components, the resulting equations are doubled and so instead of a single N-vector complex spinor, one obtains 2 N-vector real spinors, with 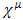 are d = D real,
are d = D real, 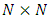 matrices.Proof of the N d relations based on induction [10] (starting at d=2) did not take into account the Group limitations as shown in paragraph v. above.Thus,
matrices.Proof of the N d relations based on induction [10] (starting at d=2) did not take into account the Group limitations as shown in paragraph v. above.Thus, 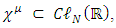 and must satisfy the restriction of
and must satisfy the restriction of 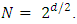 It is therefore, that only even d dimensional universe is acceptable for fermions.The representations are confined to those where N is even only (N= 4, 8, 16, … etc.).Many theories [8-15] of (N,d) universe make use of odd d. But as was shown here, odd-d universe is not allowed for fermions.World-sheet action [14] is given by an action in which fermions are separated from Bosonic fields.Since all actions with fermions have terms of the form
It is therefore, that only even d dimensional universe is acceptable for fermions.The representations are confined to those where N is even only (N= 4, 8, 16, … etc.).Many theories [8-15] of (N,d) universe make use of odd d. But as was shown here, odd-d universe is not allowed for fermions.World-sheet action [14] is given by an action in which fermions are separated from Bosonic fields.Since all actions with fermions have terms of the form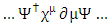 It means that the Clifford condition is valid for the world action [13, 14] and the fermionic part of the action must obey the dimensionality requirement of N2 = 2d.
It means that the Clifford condition is valid for the world action [13, 14] and the fermionic part of the action must obey the dimensionality requirement of N2 = 2d.
5. An Upper Limit on d
So far, it was shown that d must be an even number. But is there an upper limit on d?For each dimension, there is a single NXN Dirac 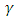 matrice
matrice 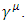 Let us start with Clifford algebra generated by
Let us start with Clifford algebra generated by 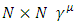 matrices.
matrices.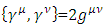 with μ, ν = 0,1,2,⋯D and where the metric signature
with μ, ν = 0,1,2,⋯D and where the metric signature 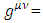 diag(+,-,-,-,…).For different d-dimensions, construct the following sets of
diag(+,-,-,-,…).For different d-dimensions, construct the following sets of 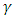 matrices:
matrices: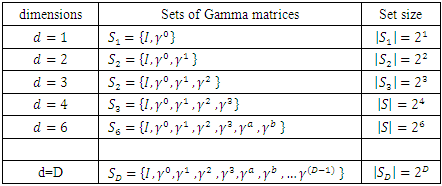 Notice that from now on it is sufficient to concentrate on an even dimensional Fermions universe, as it was shown above.For a D dimensional universe, the matrices, use
Notice that from now on it is sufficient to concentrate on an even dimensional Fermions universe, as it was shown above.For a D dimensional universe, the matrices, use 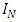 and
and 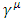 to construct the following set GD of
to construct the following set GD of 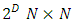 matrices:
matrices: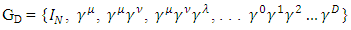 Over all combinations of indices, where
Over all combinations of indices, where 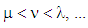 etcCreate next the set
etcCreate next the set 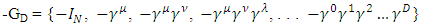 And define the group
And define the group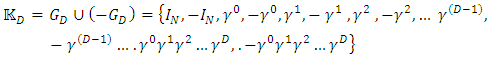 Define next the matrices
Define next the matrices 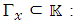
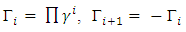 For all
For all 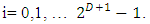 With
With 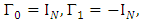 etc. Thus,
etc. Thus, with
with 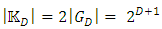 It is obvious that
It is obvious that 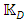 is a group of order
is a group of order 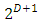 It is obvious that
It is obvious that 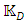 contains a set of sub-groups:
contains a set of sub-groups: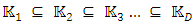 Which is described in the following:
Which is described in the following: etc.All
etc.All 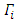 (except for i=0,1) are
(except for i=0,1) are 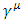 or products of
or products of 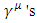
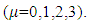 Hence, when two new matrices
Hence, when two new matrices 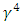 and
and 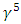 are introduced in a 6-dimensional universe, we define
are introduced in a 6-dimensional universe, we define 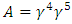 , and it is a straight forward procedure to show that
, and it is a straight forward procedure to show that 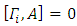 for all
for all 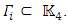 if a matrix U, which is not a multiple of the unit matrix
if a matrix U, which is not a multiple of the unit matrix 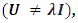 commutes
commutes 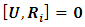 with all matrices R0, R1, R2, …, of a representation, then that representation is necessarily reducible. And, if a non-zero matrix commutes with all of the matrices of an irreducible representation, that matrix must be a multiple of the unit matrix.Therefore, the group
with all matrices R0, R1, R2, …, of a representation, then that representation is necessarily reducible. And, if a non-zero matrix commutes with all of the matrices of an irreducible representation, that matrix must be a multiple of the unit matrix.Therefore, the group 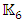 must be a reducible representation.This forces us to conclude, that no irreducible representation
must be a reducible representation.This forces us to conclude, that no irreducible representation 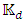 may be found for d>4 and therefore, the fermionic universe must have d=4.
may be found for d>4 and therefore, the fermionic universe must have d=4.
6. Conclusions
Separation of the complex wave function into real and imaginary components splits the Dirac equation into two coupled equations, with real 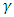 matrices. Dirac equation can be represented by real 2Dx2D matrices, where D is the number of matrices and the dimension of the universe in which the fermions exist. There is no implication from this on Bosons universe and they may exist in another kind of universe.Based on the canonical anti-commutation relation
matrices. Dirac equation can be represented by real 2Dx2D matrices, where D is the number of matrices and the dimension of the universe in which the fermions exist. There is no implication from this on Bosons universe and they may exist in another kind of universe.Based on the canonical anti-commutation relation 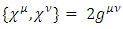 , it was shown that the
, it was shown that the 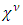 matrices can be used as generators of a group G, which dimension |G| =2d =N2 and since N must be an integer, so must be d. Therefore, any fermionic theory, even supergravity Kaluza-Klein theory, cannot be an odd dimensional d, unless one gives up on the Clifford restriction Eq. [20]. An upper limit on the dimensions is d<5.The final conclusion is then, that for a Fermionic universe, d = 4.
matrices can be used as generators of a group G, which dimension |G| =2d =N2 and since N must be an integer, so must be d. Therefore, any fermionic theory, even supergravity Kaluza-Klein theory, cannot be an odd dimensional d, unless one gives up on the Clifford restriction Eq. [20]. An upper limit on the dimensions is d<5.The final conclusion is then, that for a Fermionic universe, d = 4.
References
| [1] | Dirac, P. A. M., "The Quantum Theory of the Electron", Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 117 (778): 610. 1928. |
| [2] | D Kwiat, "The Schrӧdinger Equation and Asymptotic Strings". International Journal of Theoretical and Mathematical Physics, Vol 8 (3) 2018. |
| [3] | W. K. Clifford, “On the classification of geometric algebras”, in Mathematical Papers (1882), Tucker R., (Ed.), Macmillian, London, pp. 397–401. |
| [4] | H. Murayama "Notes on Clifford Algebra and Spin(N) Representations", Physics 230A, Spring 2007, April 6, 2007. |
| [5] | M.J. Duff, B.E.W Nilsson, C.N. Pope, "Kaluza-Klein Supergravity", Physics Reports (Review Section of Physics Letters) 130, Nos. 1 & 2 1-142. North-Holland, Amsterdam. (1986). |
| [6] | E Antonyan "|Supergravities in Diverse Dimensions" June 10, 2003. |
| [7] | Andrzej Trautman, Uniwersytet Warszawski, Clifford Algebras and their representations, Warszawa, Poland Published in: Encyclopedia of Mathematical Physics, Oxford: Elsevier, 2006, vol. 1, pages 518–530. |
| [8] | O. Klein, Z. Fur Physik 37 895 (1926). |
| [9] | O. Klein, Nature 118 516 (1926). |
| [10] | H B Nielsen S.E. Rugh, "Why do we live in 3+1 dimensions?", https://arxiv.org/abs/hep-th/9407011v1, 1994. |
| [11] | R Durer, M Kunz, M Sakellariadou, "Why do we live in 3+1 dimensions?", Phys. Lett. B614 (2005) 125-130. |
| [12] | M.B. Green, J.H. Schwarz, E. Witten “Superstring Theory” (Cambridge Monographs on Mathematical Physics, Cambridge University Press, 1987). In two volumes. |
| [13] | Polchinsky J, "Superstring theory and beyond string theory". Vol II. Cambridge University Press, 2005. |
| [14] | Shiroman Prakasha and Ritam Sinhab, A complex fermionic tensor model in d dimensions. Journal of High Energy Physics, Volume 2018, Issue 2, article id.86, 25 pp. |
| [15] | Oscar Varela, Complete D = 11 embedding of SO(8) supergravity. Phys. Rev. D 97, 045010 (2018). |
| [16] | West P.C., Supergravity, Brane Dynamics and String Duality. Cambridge |University Press, 1999. |



 Starting with the Dirac equation with N-dimensional spinors, we accept the fact that the gamma matrices, irrespective of the number of dimensions of our universe, they always must conform with the Clifford algebra [3, 4, 7] restriction.Following this, it is proven in this work, that there must exist a connection between the dimensionality of these matrices (and hence of the spinors), and the number of dimensions d of our universe.Unlike previous approaches, here there is no need to separate between odd and even dimensions. This leads us to the conclusion that N2=2d. Therefore, d must be even, and N must be an integer power of 2.By a unique construction procedure, we use the gamma matrices to construct a relevant group of matrices. These groups presentations become reducible for any d > 4.Thus, only d = 4 will be allowed, and our fermionic world cannot be other than a 3+1 universe.Physical problems cannot rely on imaginary numbers, except for the purpose of mathematical comfort. The introduction of imaginary and complex numbers is nothing but a mathematical convenience for shortening and unifying equations. Obviously, since complex entities can always be decomposed into real and imaginary parts and vice versa, using natural (real-entities only) approach does not contribute anything and makes things unjustifiably more complex. However, by using complex presentation one might be overlooking some hidden qualities [2].For instance, the complex Schrodinger equation turns out to be a pair of coupled equations of the real and imaginary parts [2]:The Schrödinger equation for a free particle (v(x) =0) becomes:
Starting with the Dirac equation with N-dimensional spinors, we accept the fact that the gamma matrices, irrespective of the number of dimensions of our universe, they always must conform with the Clifford algebra [3, 4, 7] restriction.Following this, it is proven in this work, that there must exist a connection between the dimensionality of these matrices (and hence of the spinors), and the number of dimensions d of our universe.Unlike previous approaches, here there is no need to separate between odd and even dimensions. This leads us to the conclusion that N2=2d. Therefore, d must be even, and N must be an integer power of 2.By a unique construction procedure, we use the gamma matrices to construct a relevant group of matrices. These groups presentations become reducible for any d > 4.Thus, only d = 4 will be allowed, and our fermionic world cannot be other than a 3+1 universe.Physical problems cannot rely on imaginary numbers, except for the purpose of mathematical comfort. The introduction of imaginary and complex numbers is nothing but a mathematical convenience for shortening and unifying equations. Obviously, since complex entities can always be decomposed into real and imaginary parts and vice versa, using natural (real-entities only) approach does not contribute anything and makes things unjustifiably more complex. However, by using complex presentation one might be overlooking some hidden qualities [2].For instance, the complex Schrodinger equation turns out to be a pair of coupled equations of the real and imaginary parts [2]:The Schrödinger equation for a free particle (v(x) =0) becomes: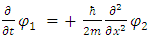
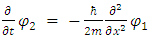
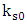 between the two strings:
between the two strings: 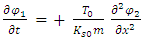
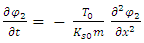
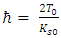
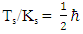 is fixed in time.This interpretation of a particle as made up of two coupled strings, whose tensions and interaction are inversely proportional to time, gives us a classical interpretation of the Schrödinger equation.As Ts and Ks are inversely proportional to time, the ratio Ts/Ks is constant in time.Therefore, without loss of generality
is fixed in time.This interpretation of a particle as made up of two coupled strings, whose tensions and interaction are inversely proportional to time, gives us a classical interpretation of the Schrödinger equation.As Ts and Ks are inversely proportional to time, the ratio Ts/Ks is constant in time.Therefore, without loss of generality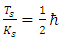
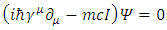
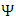 into its real and imaginary parts [2]
into its real and imaginary parts [2]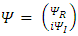
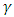 matrices are:
matrices are: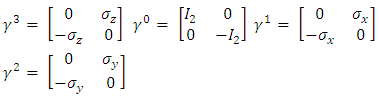
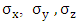 the Pauli 2x2 matrices.
the Pauli 2x2 matrices.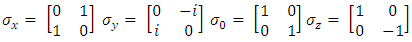
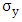 has imaginary components and it can be replaced by writing
has imaginary components and it can be replaced by writing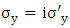 where
where 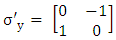 and therefore
and therefore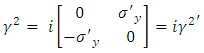
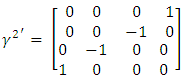 Decomposing
Decomposing  into
into 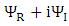 where
where 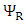 and
and 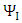 are real, the Dirac equation becomes two separate equations:
are real, the Dirac equation becomes two separate equations: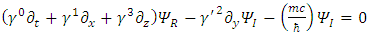
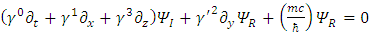
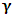 matrices are real.(c) Notice the asymmetry of the y-component in Eqs. [12, 13] due to the complex nature of Pauli's
matrices are real.(c) Notice the asymmetry of the y-component in Eqs. [12, 13] due to the complex nature of Pauli's 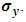 (d) Notice the change of sign in the mass terms.(e) Even if m=0, the asymmetry in y remains.(f) Notice the coupling between
(d) Notice the change of sign in the mass terms.(e) Even if m=0, the asymmetry in y remains.(f) Notice the coupling between 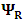 and
and 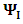 , which remains even when the mass term vannishes.Eqs. [12-13] may be written
, which remains even when the mass term vannishes.Eqs. [12-13] may be written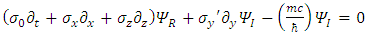
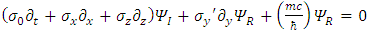
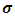 are real 2x2 matrices. Hence
are real 2x2 matrices. Hence 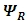 and
and 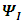 are 2-vectors.When combined into the complex
are 2-vectors.When combined into the complex 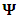 may be united into
may be united into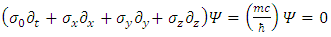
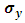 is complex, and
is complex, and 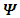 is a complex 4-vectorSetting m=0 gives the Weyl equation:
is a complex 4-vectorSetting m=0 gives the Weyl equation: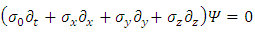
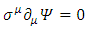
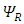 and
and 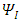 .
.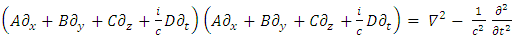
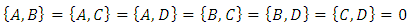
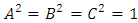
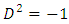
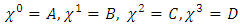 represent the A, B, C, D terms, then, in a compact form
represent the A, B, C, D terms, then, in a compact form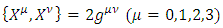
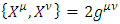 constrains. This leads to the assertion, that
constrains. This leads to the assertion, that 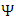 is a 4-vector of complex wave functions.In a 3+1 world,
is a 4-vector of complex wave functions.In a 3+1 world, 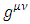 is a 4x4 matrix, so A, B, C and D are 4x4 matrices. However, in an N-dimensional world, one needs NxN matrices [4], with N >= 4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the Schrödinger equation. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives:
is a 4x4 matrix, so A, B, C and D are 4x4 matrices. However, in an N-dimensional world, one needs NxN matrices [4], with N >= 4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the Schrödinger equation. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives: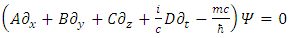
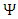 is complex and therefore can be presented as a 2-vector of two complex wave functions.Instead of using the conventional 4x4
is complex and therefore can be presented as a 2-vector of two complex wave functions.Instead of using the conventional 4x4 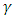 matrices (A, B, C and D) as introduced by Dirac, a set of four N x N matrices
matrices (A, B, C and D) as introduced by Dirac, a set of four N x N matrices 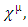 acting on a complex N-vector
acting on a complex N-vector 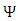 are introduced, which satisfy Eq. [18], and the constrains in Eq. [20].These
are introduced, which satisfy Eq. [18], and the constrains in Eq. [20].These 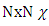 matrices replace the
matrices replace the 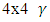 matrices in Dirac 4x4 equation to introduce the Dirac NxN equation:
matrices in Dirac 4x4 equation to introduce the Dirac NxN equation: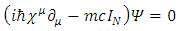
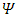 is now a complex N-vectorand where
is now a complex N-vectorand where 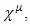 are four real NxN matrices, satisfying the Clifford requirement:
are four real NxN matrices, satisfying the Clifford requirement: 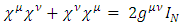
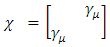 So, from a set of d NxN matrices, one can have a set of d+2 2Nx2N matrices satisfying the extended Clifford condition.This procedure will thus create presentations of SO(N) to fermions in d-dimensional universe, for any even or odd d.However, as will be shown, the condition NxN = 2d requires d to be an even number and hence only SO(4), SO(8), SO(16), SO(32) etc., representations are allowed.
So, from a set of d NxN matrices, one can have a set of d+2 2Nx2N matrices satisfying the extended Clifford condition.This procedure will thus create presentations of SO(N) to fermions in d-dimensional universe, for any even or odd d.However, as will be shown, the condition NxN = 2d requires d to be an even number and hence only SO(4), SO(8), SO(16), SO(32) etc., representations are allowed.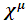
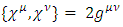 Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [2, 3].N-dimensional gamma matrices [5, 6, 12-16], are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity [12, 15, 16].Consider a d-dimensional space-time, with a flat Minkowski metric
Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [2, 3].N-dimensional gamma matrices [5, 6, 12-16], are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity [12, 15, 16].Consider a d-dimensional space-time, with a flat Minkowski metric 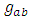 where
where 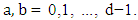 Original Dirac matrices correspond to taking d = N = 4.For a d-dimensional space (d-1 spatial + 1 temporal coordinates) dimension, there are d such matrices
Original Dirac matrices correspond to taking d = N = 4.For a d-dimensional space (d-1 spatial + 1 temporal coordinates) dimension, there are d such matrices 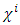 (i =0, … d-1), of size N×N, which satisfy the anticommutator relation from the Clifford algebra
(i =0, … d-1), of size N×N, which satisfy the anticommutator relation from the Clifford algebra 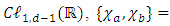
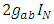 where
where 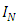 is the N dimensional identity matrix. (The spinors acted on by these matrices have N components each).For a Clifford algebra generated by a set of d
is the N dimensional identity matrix. (The spinors acted on by these matrices have N components each).For a Clifford algebra generated by a set of d 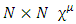 matrices,
matrices,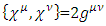 with μ, ν = 0, 1, 2, ⋯ d-1 and where the metric signature
with μ, ν = 0, 1, 2, ⋯ d-1 and where the metric signature 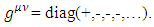 Using the matrices
Using the matrices 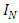 and
and 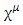 we can construct a set of
we can construct a set of 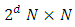 matrices as follow
matrices as follow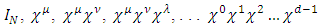 Over all combinations of indices, where
Over all combinations of indices, where 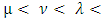
 etcFor a specific case denote d by D.Since there are D different
etcFor a specific case denote d by D.Since there are D different 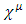 matrices, picking up p different ones, in an increasing index order, out of D for all 0 ≤ p ≤ D, there are
matrices, picking up p different ones, in an increasing index order, out of D for all 0 ≤ p ≤ D, there are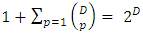
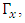 where
where 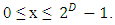 Thus creating a set
Thus creating a set 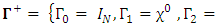
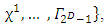 with 2D members.Because of the anticommutation relation between the gammas, the product of any
with 2D members.Because of the anticommutation relation between the gammas, the product of any 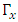 by any
by any 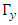 is, up to a sign, a third member
is, up to a sign, a third member 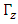 of the set.Define a set
of the set.Define a set 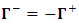 whose elements are the same members of
whose elements are the same members of 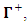 but with negative sign, namely:
but with negative sign, namely: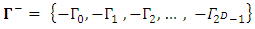 Create now a union set
Create now a union set 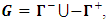 so G becomes the set of matrices
so G becomes the set of matrices 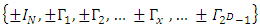 Re-assign notations for the
Re-assign notations for the 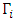 members of the set G as follows:
members of the set G as follows: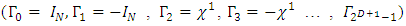 with
with 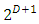 terms. It contains the unit element
terms. It contains the unit element 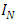 and is closed under multiplication, as the product of any
and is closed under multiplication, as the product of any 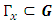 by any
by any 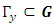 is a third member
is a third member 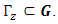 Thus
Thus 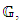 is a group with
is a group with 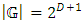 members.Let
members.Let 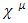 be N-dimensional
be N-dimensional 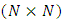 irreducible matrix representation.In order to establish the relationship between D and N, define a matrix
irreducible matrix representation.In order to establish the relationship between D and N, define a matrix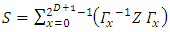
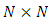 matrix (the summation runs over all
matrix (the summation runs over all 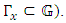 It follows that
It follows that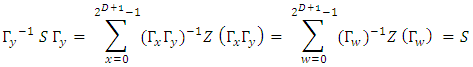 Or,
Or,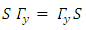
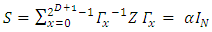
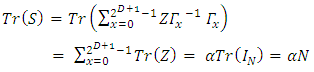
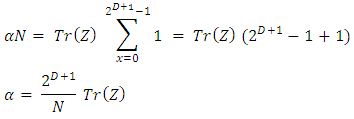 and since
and since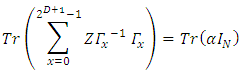 one obtains:
one obtains: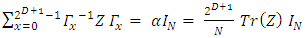
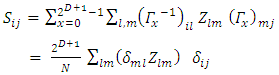
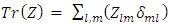 and
and 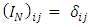
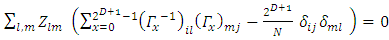
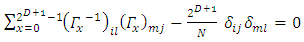
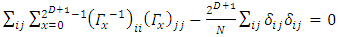
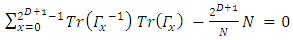
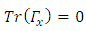
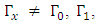 and
and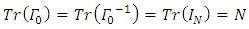
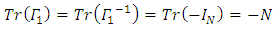
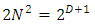
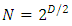
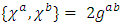 with a,b = (0,…d).4. The number d specifies the total number of world coordinates, of which there are the usual x,y,z spatial coordinate, at least one is a temporal coordinate and the rest are extended coordinates (may be temporal and may be spatial). By convention, in our 4 dimensional world we use d=3+1, namely x,y,z and t).5. By separation of the wave function into real and imaginary components, the resulting equations are doubled and so instead of a single N-vector complex spinor, one obtains 2 N-vector real spinors, with
with a,b = (0,…d).4. The number d specifies the total number of world coordinates, of which there are the usual x,y,z spatial coordinate, at least one is a temporal coordinate and the rest are extended coordinates (may be temporal and may be spatial). By convention, in our 4 dimensional world we use d=3+1, namely x,y,z and t).5. By separation of the wave function into real and imaginary components, the resulting equations are doubled and so instead of a single N-vector complex spinor, one obtains 2 N-vector real spinors, with 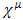 are d = D real,
are d = D real, 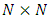 matrices.Proof of the N d relations based on induction [10] (starting at d=2) did not take into account the Group limitations as shown in paragraph v. above.Thus,
matrices.Proof of the N d relations based on induction [10] (starting at d=2) did not take into account the Group limitations as shown in paragraph v. above.Thus, 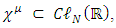 and must satisfy the restriction of
and must satisfy the restriction of 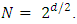 It is therefore, that only even d dimensional universe is acceptable for fermions.The representations are confined to those where N is even only (N= 4, 8, 16, … etc.).Many theories [8-15] of (N,d) universe make use of odd d. But as was shown here, odd-d universe is not allowed for fermions.World-sheet action [14] is given by an action in which fermions are separated from Bosonic fields.Since all actions with fermions have terms of the form
It is therefore, that only even d dimensional universe is acceptable for fermions.The representations are confined to those where N is even only (N= 4, 8, 16, … etc.).Many theories [8-15] of (N,d) universe make use of odd d. But as was shown here, odd-d universe is not allowed for fermions.World-sheet action [14] is given by an action in which fermions are separated from Bosonic fields.Since all actions with fermions have terms of the form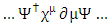 It means that the Clifford condition is valid for the world action [13, 14] and the fermionic part of the action must obey the dimensionality requirement of N2 = 2d.
It means that the Clifford condition is valid for the world action [13, 14] and the fermionic part of the action must obey the dimensionality requirement of N2 = 2d.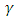 matrice
matrice 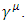 Let us start with Clifford algebra generated by
Let us start with Clifford algebra generated by 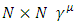 matrices.
matrices.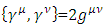 with μ, ν = 0,1,2,⋯D and where the metric signature
with μ, ν = 0,1,2,⋯D and where the metric signature 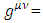 diag(+,-,-,-,…).For different d-dimensions, construct the following sets of
diag(+,-,-,-,…).For different d-dimensions, construct the following sets of 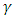 matrices:
matrices: Notice that from now on it is sufficient to concentrate on an even dimensional Fermions universe, as it was shown above.For a D dimensional universe, the matrices, use
Notice that from now on it is sufficient to concentrate on an even dimensional Fermions universe, as it was shown above.For a D dimensional universe, the matrices, use 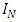 and
and 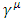 to construct the following set GD of
to construct the following set GD of 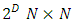 matrices:
matrices: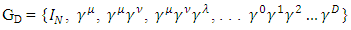 Over all combinations of indices, where
Over all combinations of indices, where 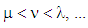 etcCreate next the set
etcCreate next the set 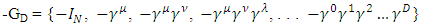 And define the group
And define the group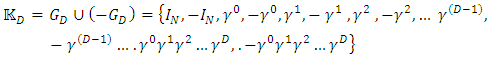 Define next the matrices
Define next the matrices 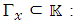
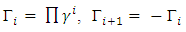 For all
For all 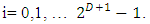 With
With 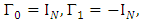 etc. Thus,
etc. Thus, with
with 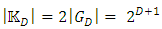 It is obvious that
It is obvious that 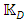 is a group of order
is a group of order 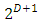 It is obvious that
It is obvious that 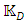 contains a set of sub-groups:
contains a set of sub-groups: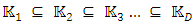 Which is described in the following:
Which is described in the following: etc.All
etc.All 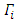 (except for i=0,1) are
(except for i=0,1) are 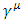 or products of
or products of 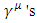
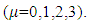 Hence, when two new matrices
Hence, when two new matrices 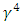 and
and 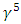 are introduced in a 6-dimensional universe, we define
are introduced in a 6-dimensional universe, we define 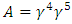 , and it is a straight forward procedure to show that
, and it is a straight forward procedure to show that 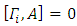 for all
for all 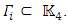 if a matrix U, which is not a multiple of the unit matrix
if a matrix U, which is not a multiple of the unit matrix 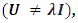 commutes
commutes 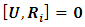 with all matrices R0, R1, R2, …, of a representation, then that representation is necessarily reducible. And, if a non-zero matrix commutes with all of the matrices of an irreducible representation, that matrix must be a multiple of the unit matrix.Therefore, the group
with all matrices R0, R1, R2, …, of a representation, then that representation is necessarily reducible. And, if a non-zero matrix commutes with all of the matrices of an irreducible representation, that matrix must be a multiple of the unit matrix.Therefore, the group 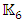 must be a reducible representation.This forces us to conclude, that no irreducible representation
must be a reducible representation.This forces us to conclude, that no irreducible representation 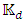 may be found for d>4 and therefore, the fermionic universe must have d=4.
may be found for d>4 and therefore, the fermionic universe must have d=4.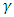 matrices. Dirac equation can be represented by real 2Dx2D matrices, where D is the number of matrices and the dimension of the universe in which the fermions exist. There is no implication from this on Bosons universe and they may exist in another kind of universe.Based on the canonical anti-commutation relation
matrices. Dirac equation can be represented by real 2Dx2D matrices, where D is the number of matrices and the dimension of the universe in which the fermions exist. There is no implication from this on Bosons universe and they may exist in another kind of universe.Based on the canonical anti-commutation relation 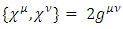 , it was shown that the
, it was shown that the 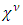 matrices can be used as generators of a group G, which dimension |G| =2d =N2 and since N must be an integer, so must be d. Therefore, any fermionic theory, even supergravity Kaluza-Klein theory, cannot be an odd dimensional d, unless one gives up on the Clifford restriction Eq. [20]. An upper limit on the dimensions is d<5.The final conclusion is then, that for a Fermionic universe, d = 4.
matrices can be used as generators of a group G, which dimension |G| =2d =N2 and since N must be an integer, so must be d. Therefore, any fermionic theory, even supergravity Kaluza-Klein theory, cannot be an odd dimensional d, unless one gives up on the Clifford restriction Eq. [20]. An upper limit on the dimensions is d<5.The final conclusion is then, that for a Fermionic universe, d = 4. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML