Isam Ahmed Attia1, Mubarak Dirar Abd Alla1, Rasha Abdelhai Mohammad Taha1, 2
1Physics Department, College of Science, Sudan University of Science & Technology, Khartoum, Sudan
2Physics Department, College of Science, Majmaah University, Zulfi, Saudi Arabia
Correspondence to: Isam Ahmed Attia, Physics Department, College of Science, Sudan University of Science & Technology, Khartoum, Sudan.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Schrodinger harmonic oscillator equation in the momentum space in friction medium (Harmonic Oscillator Soliton model) was used to describe properties of two types of solitons, permanent and time dependent. First one a bell soliton has a permanent profile, while other one is breathers have an internal dynamic, even So, their shape oscillates in time.
Keywords:
Harmonic Oscillator Soliton, Momentum Space, a bell Soliton, Breathers Soliton, Friction Term
Cite this paper: Isam Ahmed Attia, Mubarak Dirar Abd Alla, Rasha Abdelhai Mohammad Taha, Describe a Bell and Breathe Solitons by Using Harmonic Oscillator Soliton, International Journal of Theoretical and Mathematical Physics, Vol. 9 No. 1, 2019, pp. 9-13. doi: 10.5923/j.ijtmp.20190901.02.
1. Introduction
Solitons were first described by N.J. Zabusky and M.D. Kruskal [1] in 1965 and they form now a paradigm in mathematical physics (see also [2, 3, 4]). Soliton is a solitary wave with finite energy and the necessary conditions of its existence include nonlinearity and dispersion. Soliton dynamics is one of the hot topics due to wide applications in hydrodynamics, electronics, solid mechanics, biophysics and other disciplines, [5] They dealt with the dynamics of one-dimensional (1D) anharmonic lattices and their (quasi) continuum approximation [5] provided by the Boussinesq–Korteweg- de-Vries equation [6, 7, 8]. That work followed research done by Schrödinger, gives the Nonlinear Schrödinger Equation (NLSE) [9, 10]. It appears in various physical contexts to describe the propagation of nonlinear waves [11].The nonlinear models [12-16] well-known nowadays are such as the KdV equation and the nonlinear Schrödinger equation (NSE). There are explained by the fact that they describe a wide spectrum of phenomena in various nonlinear media; their fundamentality consists in a latent symmetry in the one-dimensional case which results in the integrability of the given equations by the inverse scattering transform. The methods of soliton stability studies are also within the framework of these models. The KdV equation arises when describing weakly nonlinear waves in media with a dispersion law w(k) which is close to the linear one.The nonlinear Schrödinger equation is usually used for the description of the propagation of wave packets with a small amplitude, i.e., when the field differs weakly from a harmonic one and nonlinear effects are small. This gives an opportunity to take into account dispersion and nonlinear effects separately for the derivation of the equation which describe the wave packet envelope, where a slowly varying function of space and time [16].We confirm that quantum friction is inevitably related to material dispersion, and that such friction vanishes in nondispersive media. Very interestingly, the harmonic oscillator comprises one of the most important examples of elementary Quantum Mechanics. There are several reasons for its pivotal role. The linear harmonic oscillator describes vibrations in molecules and their counterparts in solids, the phonons. Many more physical systems can, at least approximately, be described in terms of linear harmonic oscillator models. However, the most eminent role of this oscillator is its linkage to the electron, one of the conceptual building blocks of microscopic physics. For example, electron describe the modes of the radiation field, providing the basis for its quantization [17].While trying to understand soliton creation, we used the mathematical aspects of the quantum friction instabilities are manifested in the fact that the system may support natural modes of oscillation that grow exponentially with time [18, 19, 20], even in presence of system loss [21].There are a few ways to classify solitons [22]. All solitons can be divided into two groups by taking into account their profiles: permanent and time dependent. For example, kink solitons have a permanent profile (in ideal systems), while all breathers have an internal dynamic, even, if they are static. So, their shape oscillates in time.The aim of this work, we discuss common properties of solitons on the basis of the Harmonic Oscillator Soliton model that was discussed in the paper [23] ''Quantization of Harmonic Oscillator Soliton by Friction Term Method'' where we were established definite link between the classical effect and quantum friction for harmonic oscillator soliton.
2. Theoretical Model
In ordinary quantum mechanics Schrodinger equation can be written in momentum representation in the following form [24]: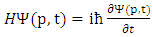 | (1) |
where 𝑖 is the imaginary number 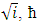 is the reduced Planck constant which is h/2π, 𝜓(p, 𝑡) is the wave function of the quantum system, p is the momentum in a one-dimensional coordinate system, and t the time. H is the Hamiltonian operator (which characterizes the total energy of the system under consideration).The use of the harmonic oscillator model is that almost any potential can be approximated as a harmonic oscillator. When the oscillating string is embedded in a resistive matter or crystal, having crystal field of potential
is the reduced Planck constant which is h/2π, 𝜓(p, 𝑡) is the wave function of the quantum system, p is the momentum in a one-dimensional coordinate system, and t the time. H is the Hamiltonian operator (which characterizes the total energy of the system under consideration).The use of the harmonic oscillator model is that almost any potential can be approximated as a harmonic oscillator. When the oscillating string is embedded in a resistive matter or crystal, having crystal field of potential 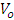 , the total Hamiltonian operator is given by
, the total Hamiltonian operator is given by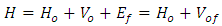 | (2) |
Where, 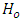 is the Hamiltonian operator for an undamped harmonic oscillator,
is the Hamiltonian operator for an undamped harmonic oscillator, 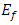 is frictional energy for the harmonic oscillator affected by a resistive force of friction, while the friction force is inversely proportional to the relaxation time
is frictional energy for the harmonic oscillator affected by a resistive force of friction, while the friction force is inversely proportional to the relaxation time 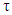 [25, 26], thus the potential takes the following form [23]:
[25, 26], thus the potential takes the following form [23]: 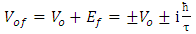 | (3) |
Hence the total Hamiltonian oscillator in equation (2) assumes the form: 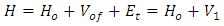 | (4) |
Where, 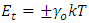 standing for thermal energy and
standing for thermal energy and 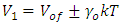 .The classical harmonic oscillator is most frequently introduced as a mass on an undamped spring, The Hamiltonian is thus given by:
.The classical harmonic oscillator is most frequently introduced as a mass on an undamped spring, The Hamiltonian is thus given by: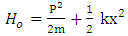 | (5) |
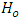 is the Hamiltonian operator acting on a complex wave-function, ψ(x, t), whose time evolution is governed by the Schrödinger equation [24]:
is the Hamiltonian operator acting on a complex wave-function, ψ(x, t), whose time evolution is governed by the Schrödinger equation [24]: 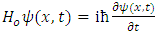 | (6) |
Quantization of this system is done by replacing the classical variables p and x by the operators 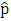 and
and 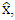 In the view of equations (1,3,4,5) and using the fact that in momentum space:
In the view of equations (1,3,4,5) and using the fact that in momentum space: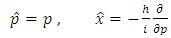 | (7) |
One gets, the Schrodinger equation in momentum representation as the following equation: 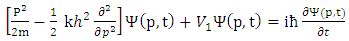 | (8) |
One can easily find solutions of the Schrödinger equation by separating the variables, i.e.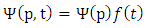 | (9) |
such that one can write the harmonic oscillator equation in the momentum space. This can be obtain by equations (1) and (2):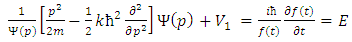 | (10) |
Then the momentum part is given by 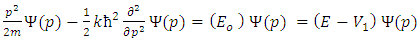 | (11) |
Carrying out the rearranging 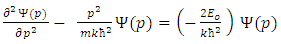 | (12) |
This A differential equation for wave function in momentum tells us that we want to find a function whose second derivative is proportional to the negative of itself. But we already know some functions with this property, namely sines, cosines, and exponentials. So, let’s be fairly general and try a solution of the form the integral of a derivative of a function is the function plus an arbitrary constant. The arbitrary constant represents the lost information resulting from when the derivative is calculated.The wave function in momentum space is given according equation (12) by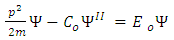 | (13) |
With 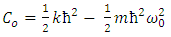 | (14) |
Consider now the solution 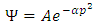 | (15) |
Thus,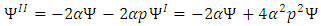 | (16) |
Inserting eq (16) in eq (13) gives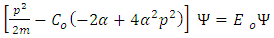 | (17) |
Equating the coefficient of 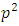 and free term, one gets
and free term, one gets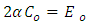 | (18) |
Thus, from eq (14) and eq (17)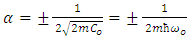 | (19) |
Thus, from eq. (18)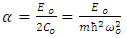 | (20) |
In view of eq (20) and equation (19)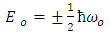 | (21) |
This predict zero-point energy which may be positive or negative.The negative zero-point energy is rejected due to the fact that restoring force resembles an attractive force since it tends to attract the particle towards the origin against the direction of coordinate x, in view of equation (15) and equation (19) by choosing positive sign 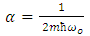 | (22) |
Using the fact that, according to Special Relativity 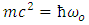 | (23) |
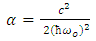 | (24) |
But equation (15) tells that, the probability for having momentum p is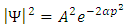 | (25) |
The probability is maximum for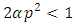 | (26) |
i.e.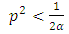 | (27) |
Using equation (24) the momentum becomes satisfied: 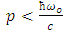 | (28) |
But the Wave-particle duality as expressed by the de Broglie wave equation requires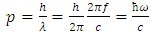 | (29) |
Therefore, by substituting eq (29) in eq (28) one gets: 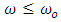 | (30) |
This means that the most probable momentum state is that for the frequency of oscillation near the natural frequency.In view of eq (29) and equation (15) the equation of a bell soliton given by: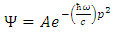 | (31) |
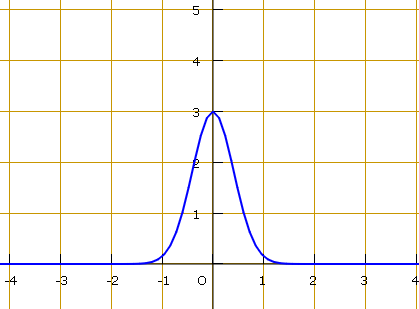 | Figure (1). The shape of A bell soliton |
The soliton solution has a bell shape and a low frequency. Another soliton solution corresponds to the negative value of 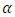 in equation (19), i.e.
in equation (19), i.e.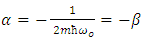 | (32) |
In view of equation (15)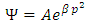 | (33) |
This momentum soliton requires p to be very small, to secure finite probability, which again conform with the fact that the most probable momentum should be very small. The soliton shape in the momentum space visualized by taking in to account equations (4, 12, 13) and (17) beside equation (20) to get 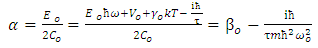 | (34) |
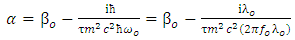 | (35) |
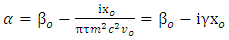 | (36) |
Where, one assumes 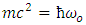
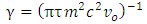 | (37) |
thus, in view of equations (7) and (15) the soliton in the momentum space is given by: 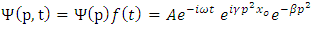 | (38) |
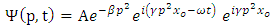 | (39) |
Under the influence of friction, the solitons slow down and decay rapidly, here, 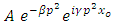 is a function describing the wave envelope. The definition of an envelope is a function which varies much more slowly in momentum space as compared to the phase of the wave is preserving its shape fig. (2). Such solution is called the breather soliton fig. (3) and it can be considered as a complex root of soliton.
is a function describing the wave envelope. The definition of an envelope is a function which varies much more slowly in momentum space as compared to the phase of the wave is preserving its shape fig. (2). Such solution is called the breather soliton fig. (3) and it can be considered as a complex root of soliton.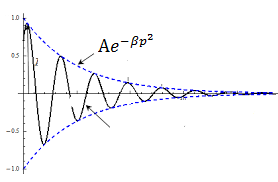 | Figure (2). The shape of the enveloping curve in the momentum space (the dashed line) |
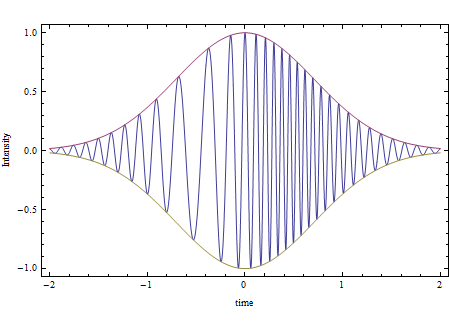 | Figure (3). The shape of the breather Soliton |
3. Discussion
The Equation (1) represents Schrodinger equation in the momentum space describes, at least in the one-dimensional case, the evolution of wave oscillations, by using the modeling of the harmonic oscillator embedded in a crystal having friction eqs. (3-5). Thus, the result of the perturbation analysis concerning the soliton growth rate.This equation is simplified separate variables as shown by equations (10, 11).The solution in equation (15) shows soliton wave with negative and positive rest mass energy, the positive one is strikingly typical to that of the quantum oscillator's negative one predicts the existence of the anti-particles, this means that our model is more informative than that in the coordinate space.In the eq (19) for positive alpha the wave function predicts Exponential soliton which describe a bell soliton, which that like Pulses with a certain shape and energy that can propagate unchanged over large distances with speed c.For negative alpha in the eq (19) the maximum probability is near to the zero-point energy, this conforms with the fact that the particles tend to have minimum energy. This solution represents decaying soliton in the momentum space. This means physically that particles tend to occupy lower energy states.If the wave amplitude varies periodically in this manner, the envelope of the wave also becomes a periodic function.Eq (39) show that under the influence of friction, the solitons only slow down and eventually stop and, at rest, they can live eternally in infinite system. eq (39) represent travelling wave in the momentum space with exponentially decaying amplitude as shown in fig. (2). Furthermore, we assume that the envelope varies slowly in time and space (as compared to the carrier wave).We recognize that waves do not necessarily have the same amplitude. If we observe them carefully, we note that several waves with relatively low amplitude are followed by one or two waves with large amplitude. Hence, the amplitude of the wave varies gradually with time and space, as is shown in Fig. 3. This is a phenomenon of wave amplitude modulation caused by modulational instability.The fact that the breather function is a slowly varying function of momentum space indicates that the frequency spectrum has a localized structure around the carrier frequency, as shown in Fig. 3. In this figure shows the width of the frequency spectrum of the envelope function.
4. Conclusions
In the present work, one considered the harmonic oscillator soliton equation in the momentum space, this a differential equation for wave function shows that, we have two solitons solutions, one is a bell soliton, where the most probable momentum state is that makes the frequency of oscillation near the natural frequency. This means that particles prefer occupying minimum zero point energy. The second solution describes breather solitons having tendency to occupy minimum enegy states.
References
| [1] | N.J. Zabusky and M.D. Kruskal, Phys. Rev. Lett. 15, 57 (1965). |
| [2] | A.C. Scott, F.Y.F. Chu and D.W. McLaughlin, Proc. IEEE 61, 1443 (1973). |
| [3] | A.C. Scott, Nonlinear Science: Emergence & Dynamics of Coherent Structures, 2nd edn. (Oxford University Press, New York, 2003). |
| [4] | N.J. Zabusky, Chaos 15, 015102 (2005). |
| [5] | C.I. Christov, G.A. Maugin and M.G. Velarde, Phys. Rev. E 54, 3621 (1996). |
| [6] | BOUSSINESQ, J.V. (1877). "Essay on the Current Water Theory." ('Essay on the Theory of Water Flow.') Memoirs presented by various scientists at the Academy of Sciences, Paris, France, Vol. 23, ser. 3, No. 1, supplement 24, pp. 1-680 (in French). |
| [7] | D.J. Korteweg and G. de Vries, On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves, Phil. Mag. (5) 39 (1895), 422–443. |
| [8] | Richard H. Enns, "It's a Nonlinear World," Springer New York, 2010. |
| [9] | V. Yu. Belashov and S.V. Vladimirov, "Solitary Waves in Dispersive Media Complex", Springer-Verlag Berlin Heidelberg 2005, p-02. |
| [10] | Catherine Sulem and Pierre-Louis Sulem, "The Nonlinear Schrodinger Equation: Self-Focusing and Wave Collapse," Springer-Verlag New York, 1999. |
| [11] | Shekhar Guha and Leonel P. Gonzalez, "Laser Beam Propagation in Nonlinear Optical Media", CRC Press, Taylor & Francis Group, Boca Raton (USA), 2014. |
| [12] | S.P. Novikov, yE. Zakharov, S.V. Manakov and L.P. Pitaevsky, Theory of Solitons, Consultants Bureau, New York, 1984. |
| [13] | G. Whitham, Linear and Nonlinear Waves (Wiley, N.Y., 1974). |
| [14] | V.1. Karpman, Nonlinear Waves in Dispersive Media (Pergamon, Oxford, 1975). |
| [15] | AC. Scott, F. Chu and P.W. McLaughlin, The Soliton: A New concept in applied science, Proc. IEEE 61(1975) 1447. |
| [16] | yE. Zakharov, S.L. Musher and AM. Rubenchik, Hamiltonian approach to the description of non-linear plasma Phenomena, Phys. Reports 129 (1985) 285. |
| [17] | Sophya Garashchuk et al, The Schrödinger equation with friction from the quantum trajectory perspective, THE JOURNAL OF CHEMICAL PHYSICS 138, 054107 (2013). |
| [18] | S. I. Maslovski, M. G. Silveirinha, Quantum friction on monoatomic layers and its classical analogue, Phys. Rev. B, 88, 035427, (2013). |
| [19] | M. G. Silveirinha, “Quantization of the Electromagnetic Field in Non-dispersive Polarizable Moving Media above the Cherenkov Threshold”, Phys. Rev. A, 88, 043846, (2013). |
| [20] | O. Sydoruk, et al, Terahertz instability of surface optical-phonon polaritons that interact with surface plasmon polaritons in the presence of electron drift, Phys. of Plasmas, 17,102103, (2010). |
| [21] | A. I. Volokitin and B. N. J. Persson, Quantum Friction, Phys. Rev. Lett. 106, 094502 – Published 2 March 2011. |
| [22] | Yousef Yousef and Khikmat Kh. Muminov, A Simple Classification of Solitons, arXiv: 1206.1294v2 [math-ph.] 7 Jun 2012. |
| [23] | Isam Ahmed Attia et al, Quantization of Harmonic Oscillator Soliton by Friction Term Method, International Journal of Theoretical and Mathematical Physics 2018, 8(4): 89-93 DOI: 10.5923/j.ijtmp.20180804.02. |
| [24] | Pavel Kundrát and Miloš Lokajíček. Three-dimensional harmonic oscillator and time evolution in quantum mechanics. Phys. Rev. A 67, 012104 –13 January 2003. DOI: https://doi.org/10.1103/PhysRevA.67.012104. |
| [25] | Mubarak Dirar et al, Quantum Schrodinger String Theory for Frictional Medium & Collision, International Journal of Innovative Science, Engineering & Technology, Vol. 2 Issue 11, November (2015). |
| [26] | Roumen Tsekov, Quantum friction, Chin. Phys. Lett. 29 (2012) 120504, arXiv 1203.2421. |



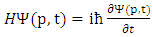
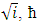 is the reduced Planck constant which is h/2π, 𝜓(p, 𝑡) is the wave function of the quantum system, p is the momentum in a one-dimensional coordinate system, and t the time. H is the Hamiltonian operator (which characterizes the total energy of the system under consideration).The use of the harmonic oscillator model is that almost any potential can be approximated as a harmonic oscillator. When the oscillating string is embedded in a resistive matter or crystal, having crystal field of potential
is the reduced Planck constant which is h/2π, 𝜓(p, 𝑡) is the wave function of the quantum system, p is the momentum in a one-dimensional coordinate system, and t the time. H is the Hamiltonian operator (which characterizes the total energy of the system under consideration).The use of the harmonic oscillator model is that almost any potential can be approximated as a harmonic oscillator. When the oscillating string is embedded in a resistive matter or crystal, having crystal field of potential 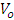 , the total Hamiltonian operator is given by
, the total Hamiltonian operator is given by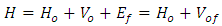
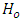 is the Hamiltonian operator for an undamped harmonic oscillator,
is the Hamiltonian operator for an undamped harmonic oscillator, 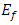 is frictional energy for the harmonic oscillator affected by a resistive force of friction, while the friction force is inversely proportional to the relaxation time
is frictional energy for the harmonic oscillator affected by a resistive force of friction, while the friction force is inversely proportional to the relaxation time 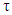 [25, 26], thus the potential takes the following form [23]:
[25, 26], thus the potential takes the following form [23]: 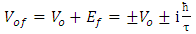
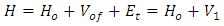
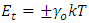 standing for thermal energy and
standing for thermal energy and 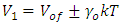 .The classical harmonic oscillator is most frequently introduced as a mass on an undamped spring, The Hamiltonian is thus given by:
.The classical harmonic oscillator is most frequently introduced as a mass on an undamped spring, The Hamiltonian is thus given by: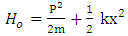
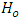 is the Hamiltonian operator acting on a complex wave-function, ψ(x, t), whose time evolution is governed by the Schrödinger equation [24]:
is the Hamiltonian operator acting on a complex wave-function, ψ(x, t), whose time evolution is governed by the Schrödinger equation [24]: 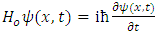
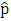 and
and 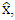 In the view of equations (1,3,4,5) and using the fact that in momentum space:
In the view of equations (1,3,4,5) and using the fact that in momentum space: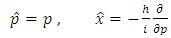
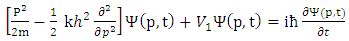
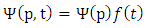
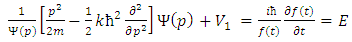
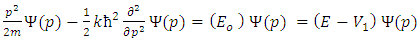
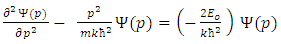
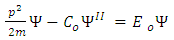
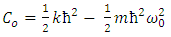
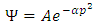
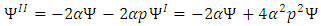
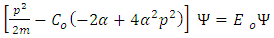
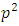 and free term, one gets
and free term, one gets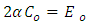
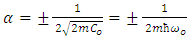
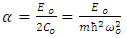
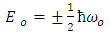
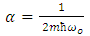
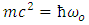
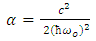
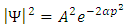
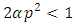
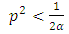
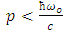
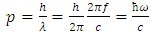
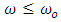
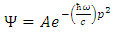

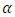 in equation (19), i.e.
in equation (19), i.e.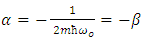
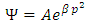
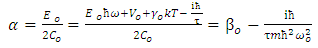
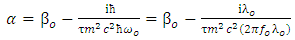
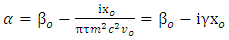
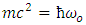
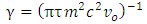
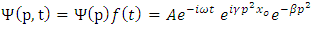
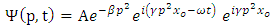
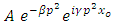 is a function describing the wave envelope. The definition of an envelope is a function which varies much more slowly in momentum space as compared to the phase of the wave is preserving its shape fig. (2). Such solution is called the breather soliton fig. (3) and it can be considered as a complex root of soliton.
is a function describing the wave envelope. The definition of an envelope is a function which varies much more slowly in momentum space as compared to the phase of the wave is preserving its shape fig. (2). Such solution is called the breather soliton fig. (3) and it can be considered as a complex root of soliton.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML