Doron Kwiat
17/2 Erez Street, Mazkeret Batyia, Israel
Correspondence to: Doron Kwiat , 17/2 Erez Street, Mazkeret Batyia, Israel.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Introducing four 6x6 Lorentz invariant gamma matrices removes asymmetry in the three spatial coordinates of Dirac equation. Use of the SO(6) representation provides 12 real wave functions which are divided into 4 groups of triplets. These 4 groups interact with each other and each element of a triplet satisfies the Klein-Gordon equation.
Keywords:
Dirac Equation, 6x6 Gamma Matrices, Triplets
Cite this paper: Doron Kwiat , Dirac Equation in SO(6) Real Representation Leading to Four Triplets, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 4, 2018, pp. 89-93. doi: 10.5923/j.ijtmp.20180804.02.
1. Introduction
Recently, it was shown [1] that a single non-relativistic Schrödinger equation is a description of a single massive particle, made up of two coupled strings. One may project from this on the relativistic Dirac equation [2], describing a free Fermion of mass m: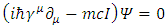 | (1) |
One may separate the complex wave function 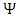 into its real and imaginary parts [3]
into its real and imaginary parts [3]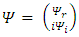 | (2) |
and by using them in the Dirac equation, one will get two separate equations where imaginary and real parts have been separated.This same procedure can be applied to any quantum field Lagrangian, resulting (at the cost of doubling the number of equations) in separation of the equations to real wave functions.These wave functions may be interpreted as coupled strings.In Dirac equation (1), the four  matrices are:
matrices are: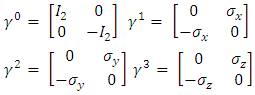 | (3) |
where I2 is the 2x2 unit matrix and 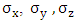 the Pauli 2x2 matrices.
the Pauli 2x2 matrices.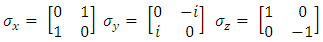 | (4) |
Of these matrices, only 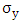 has imaginary components and it can be replaced by writing
has imaginary components and it can be replaced by writing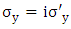 where
where 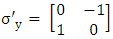 and therefore
and therefore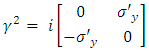 | (5) |
Decomposing  into
into 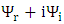 where
where 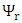 and
and 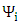 are real, the Dirac equation becomes two separate equations,
are real, the Dirac equation becomes two separate equations, 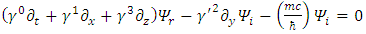 | (6) |
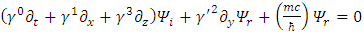 | (7) |
There are now 8 real wave functions instead of 4 in the complex presentation. Notice the asymmetry of the y-component in Eqs. (6,7) due to the complex nature of Pauli's 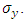
2. Changing Dirac 4x4 γ Matrices to 6x6 Representation
To move from classical QM to relativistic QM, Dirac came with the idea of taking the square root of the wave operator thus, he suggested: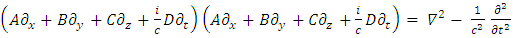 | (8) |
and in order to get all the cross-terms such as 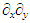 to vanish, one must assume
to vanish, one must assume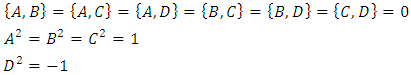 | (9) |
Or, if 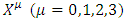 represent the A, B, C, D terms, can be written in a compact form
represent the A, B, C, D terms, can be written in a compact form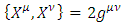 | (10) |
These conditions are met if A, B, C and D are matrices, with the implication that the wave function has multiple components. This immediately explained the appearance of two-component wave functions in Pauli's theory of spin. The most direct suggestion would be to have A, B, C and D as 4x4 matrices. This is done in combinations of 2x2 Pauli matrices, in such a way that will obey the 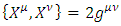 constrains. This leads to the assertion to be made, that
constrains. This leads to the assertion to be made, that 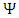 is a 4-vector of complex wave functions.In a 3+1 world,
is a 4-vector of complex wave functions.In a 3+1 world, 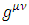 is a 4x4 matrix, so the dimension of the A, B, C and D are 4x4 matrices. However in an N-dimensional world, one needs NxN matrices [4], with N>=4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives:
is a 4x4 matrix, so the dimension of the A, B, C and D are 4x4 matrices. However in an N-dimensional world, one needs NxN matrices [4], with N>=4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives: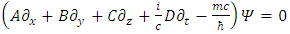 | (11) |
Since it originated in the Klein-Gordon [5] equation, which by itself originated from Schrödinger equation, it was assumed there that  is complex and therefore can be presented as a 2-vector of two complex wave functions.In this work, instead of using the conventional 4x4
is complex and therefore can be presented as a 2-vector of two complex wave functions.In this work, instead of using the conventional 4x4 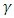 matrices (A, B, C and D) as introduced by Dirac, a set of four 6x6 matrices
matrices (A, B, C and D) as introduced by Dirac, a set of four 6x6 matrices 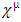 , matrices acting on a complex 6-vector
, matrices acting on a complex 6-vector 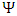 are introduced, which satisfy Eq. (11), and the constrains in Eq. (10).This is equivalent to changing from complex representation of rotations in
are introduced, which satisfy Eq. (11), and the constrains in Eq. (10).This is equivalent to changing from complex representation of rotations in 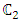 to real rotations [7] in
to real rotations [7] in 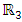 . Since SO(3) is homomorphic with SU(2), the rotations in
. Since SO(3) is homomorphic with SU(2), the rotations in 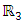 of a 3-component real wave vector is equivalent to a rotation in
of a 3-component real wave vector is equivalent to a rotation in 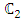 of a 2-component complex wave vector.Instead of using Pauli's 2x2 matrices, one may use the 3x3 matrix presentations of angular momentum generators
of a 2-component complex wave vector.Instead of using Pauli's 2x2 matrices, one may use the 3x3 matrix presentations of angular momentum generators 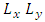 and
and 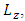 of the rotation group SO(3).Using
of the rotation group SO(3).Using 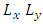 and
and 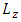 outer multiplications with
outer multiplications with 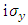 and with
and with 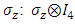 and
and 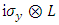 to define the
to define the 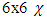 matrices, satisfying the requirements on A, B, C and D according to Eq. (11).Thus:
matrices, satisfying the requirements on A, B, C and D according to Eq. (11).Thus: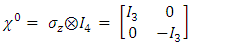 | (12) |
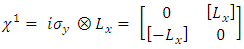 | (13) |
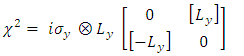 | (14) |
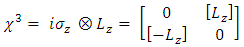 | (15) |
These 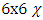 matrices replace the 4x4
matrices replace the 4x4 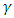 matrices in Dirac 4x4 equation to introduce the Dirac 6x6 equation:
matrices in Dirac 4x4 equation to introduce the Dirac 6x6 equation: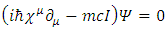 | (16) |
where 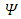 is now a complex 6-vector
is now a complex 6-vector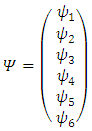 | (17) |
and where 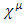 , are four real 6x6 matrices, satisfying the Clifford requirement:
, are four real 6x6 matrices, satisfying the Clifford requirement: 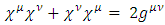 | (18) |
It has now 12 real wave functions (6 and 6) instead of 8 (4 and 4).
3. Lorentz Covariance of the 6x6 χ Matrices
To prove Lorentz covariance of the Dirac equation, with the 4x4 gamma matrices, one requires the existence of a 4x4 transformation matrix S, such that 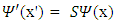 under a Lorentz transformation.Suppose that
under a Lorentz transformation.Suppose that 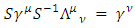 under
under 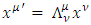 Obviously, if such transformation S exists, the 4x4 Dirac equation is Lorentz invariant.By assuming an infinitesimal Lorentz transformation
Obviously, if such transformation S exists, the 4x4 Dirac equation is Lorentz invariant.By assuming an infinitesimal Lorentz transformation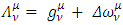 | (19) |
(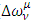 are real numerical coefficients, independent of x), one can write for S
are real numerical coefficients, independent of x), one can write for S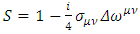 | (20) |
Where 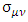 are 4x4 matrices that satisfy
are 4x4 matrices that satisfy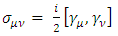 | (21) |
This derivation of the Lorentz group representation of 4x4 matrix generators is based on the relationship 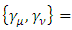
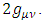 Since
Since 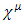 satisfies the same constraints as
satisfies the same constraints as 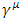 we conclude that there exist 6x6 generators of the S transformation of the Dirac 6x6 representation, and hence Dirac's 6x6 representation, Eq. (16), is Lorentz covariant.The Dirac matrices must satisfy the canonical anti-commutation relation
we conclude that there exist 6x6 generators of the S transformation of the Dirac 6x6 representation, and hence Dirac's 6x6 representation, Eq. (16), is Lorentz covariant.The Dirac matrices must satisfy the canonical anti-commutation relation 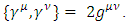 The above definition corresponds to the so-called "chiral basis," where Dirac matrices are block anti-diagonal. Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [6].N-dimensional gamma matrices are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity.Consider a d-dimensional space-time, with a flat Minkowski metric
The above definition corresponds to the so-called "chiral basis," where Dirac matrices are block anti-diagonal. Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [6].N-dimensional gamma matrices are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity.Consider a d-dimensional space-time, with a flat Minkowski metric 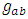 where
where 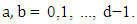 standard Dirac matrices correspond to taking d = N = 4.The higher dimension
standard Dirac matrices correspond to taking d = N = 4.The higher dimension 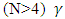 matrices are a d-long sequence of complex N×N matrices
matrices are a d-long sequence of complex N×N matrices 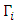 (i =0, … d-1) which satisfy the anticommutator relation from the Clifford algebra
(i =0, … d-1) which satisfy the anticommutator relation from the Clifford algebra 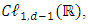 generating a representation for this algebra
generating a representation for this algebra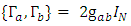 where
where 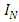 is the N dimensional identity matrix. (The spinors acted on by these matrices have N components in d dimensions.) Such a sequence exists for all values of d.In this work,
is the N dimensional identity matrix. (The spinors acted on by these matrices have N components in d dimensions.) Such a sequence exists for all values of d.In this work, 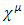 matrices are real, with N=6 and d=4.Thus,
matrices are real, with N=6 and d=4.Thus, 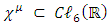 , though without the restriction of
, though without the restriction of 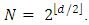
4. Solution Leading to Triplets
To solve Eq. (16) split the 6-vector into real and imaginary parts (both 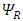 and
and 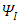 are real 6-vectors)
are real 6-vectors)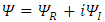 Further split the 6-vectors into two triplets (3-vectors) each:
Further split the 6-vectors into two triplets (3-vectors) each: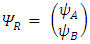 | (22) |
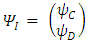 | (23) |
So that 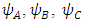 and
and 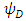 are 4 different real triplets.Substituting Eqs. (22,23) in Dirac's 6x6 representation Eq. (16) gives 4 differential equations with 12 unknowns (4 triplets) parameters:
are 4 different real triplets.Substituting Eqs. (22,23) in Dirac's 6x6 representation Eq. (16) gives 4 differential equations with 12 unknowns (4 triplets) parameters: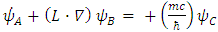 | (24) |
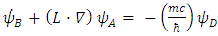 | (25) |
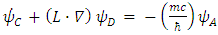 | (26) |
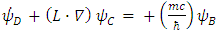 | (27) |
Where 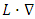 stands for
stands for 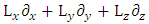 , a 3x3 operator.Applying time derivative to Eqs. (24-27) gives
, a 3x3 operator.Applying time derivative to Eqs. (24-27) gives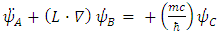 | (28) |
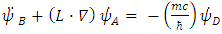 | (29) |
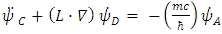 | (30) |
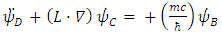 | (31) |
Define two matrices: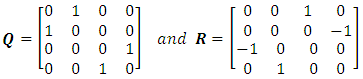 | (32) |
The differential equations (24-27) and (28-31) can be written as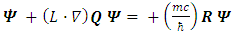 | (33) |
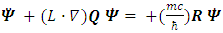 | (34) |
Which combines to: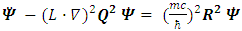 | (35) |
We notice that 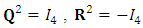 and
and 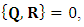 and also
and also 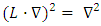 . Thus:
. Thus: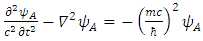 | (36) |
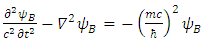 | (37) |
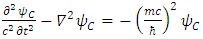 | (38) |
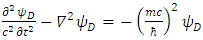 | (39) |
Dirac equation has become symmetrical in x, y and z. The spatial asymmetry has been removed.Second, Dirac equation Eq. (16) turned into four real, apparently uncoupled (3-vectors) triplets. Each triplet satisfies Klein-Gordon [5] wave equation (Eqs. (36-39)), with well-known solutions.However, when introducing in Eq. (16) 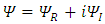 one can separate it into the real and imaginary parts and obtain:
one can separate it into the real and imaginary parts and obtain: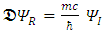 | (40) |
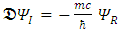 | (41) |
where by definition: 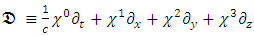 is a 6x6 matrix operator, and
is a 6x6 matrix operator, and 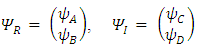 Equations (40) and (41) are two differential equations of first order and show that the
Equations (40) and (41) are two differential equations of first order and show that the 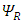 and
and 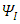 sextets (6-vectors) are coupled to each other. In fact, one can say that there are 12 real wave functions. Each satisfies the Klein-Gordon equation individually and independently. These 12 real wave functions are combined into two sextets, and each sextet is made of two triplets. Altogether there are four triplets.Looking for instance at Eqs. (24-27), the time derivative of one triplet, depends on the spatial derivatives of the second triplet and on a mass-proportional term of the third triplet. This coupling mechanism exists amongst the other triplets combinations in turn (see Figure 1). The four triplets
sextets (6-vectors) are coupled to each other. In fact, one can say that there are 12 real wave functions. Each satisfies the Klein-Gordon equation individually and independently. These 12 real wave functions are combined into two sextets, and each sextet is made of two triplets. Altogether there are four triplets.Looking for instance at Eqs. (24-27), the time derivative of one triplet, depends on the spatial derivatives of the second triplet and on a mass-proportional term of the third triplet. This coupling mechanism exists amongst the other triplets combinations in turn (see Figure 1). The four triplets 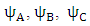 and
and 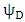 , are denoted here by A B C and D. Each triplet's time derivative is coupled to the spatial derivative of two other triplets and proportional by a
, are denoted here by A B C and D. Each triplet's time derivative is coupled to the spatial derivative of two other triplets and proportional by a 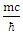 factor to the fourth triplet entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed. Each component of the three components the triplets are made of, satisfies the Klein-Gordon wave equation.
factor to the fourth triplet entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed. Each component of the three components the triplets are made of, satisfies the Klein-Gordon wave equation.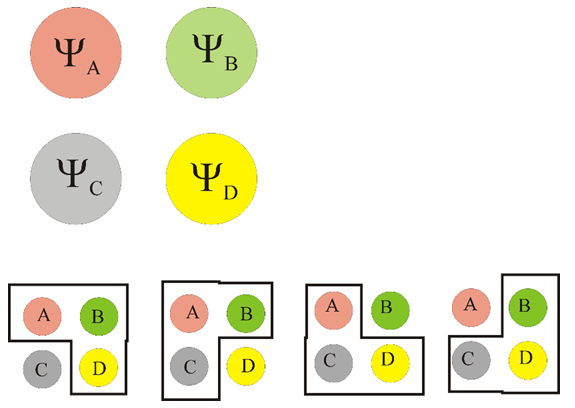 | Figure 1. The quartet of 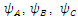 and and 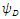 entities. Each entity (denoted here by A B C and D) is a 3-vector. Each single entity time derivative is coupled to the spatial derivative of two other entities and proportional by a entities. Each entity (denoted here by A B C and D) is a 3-vector. Each single entity time derivative is coupled to the spatial derivative of two other entities and proportional by a 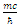 factor to the fourth entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed factor to the fourth entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed |
The 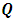 and
and 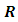 matrices are responsible for the exchanges between the tripletsQ exchanges
matrices are responsible for the exchanges between the tripletsQ exchanges 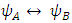 and R exchanges
and R exchanges 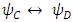 .Therefore, the
.Therefore, the 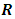 term will affect the lower triplet pair (C and D) by exchange as well as by mass change, whereas the
term will affect the lower triplet pair (C and D) by exchange as well as by mass change, whereas the 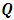 term will only cause an exchange in the upper triplet pair (A and B).To summarize, the following notations are introduced:
term will only cause an exchange in the upper triplet pair (A and B).To summarize, the following notations are introduced: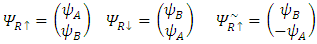
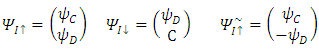 Then, combining Eqs. (22-23,24-27,40-43) gives
Then, combining Eqs. (22-23,24-27,40-43) gives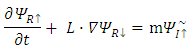
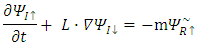 This form helps in the interpretation of how the real and imaginary parts of the Dirac fields interact.
This form helps in the interpretation of how the real and imaginary parts of the Dirac fields interact.
5. Electromagnetic Field
Dirac 6x6 equation Eq. (16) in the presence of electromagnetic field 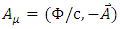 becomes
becomes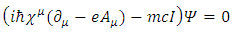 | (42) |
Hence, Eq. (66) becomes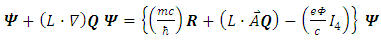 | (43) |
Eq. (43) is similar to Eq. (33) except for the term 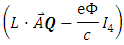 added to the l.h.s.Thus, for the very weak field approximation,
added to the l.h.s.Thus, for the very weak field approximation, 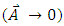 , there will be no exchange between the triplets more than in the case without EM field.The solution of Eq. (43) will be approximately similar to that of Eq. (66), except for an interaction term
, there will be no exchange between the triplets more than in the case without EM field.The solution of Eq. (43) will be approximately similar to that of Eq. (66), except for an interaction term 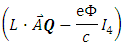
6. A Vibrating Membrane [8, 9]
Assuming polar symmetry, Eqs. (36-39) become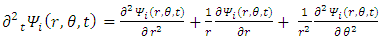 | (44) |
Where the y coordinate is the cylinder's main axis and x and z are in the plane perpendicular to the y-axis (see Figure 2).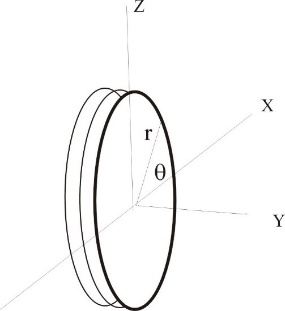 | Figure 2. A membrane in x, y, z coordinate system |
The solution to Eq. (44) is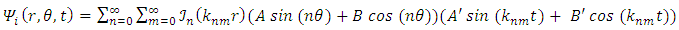 | (45) |
where knm is the mth root of 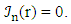 Defining
Defining 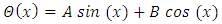 | (46) |
and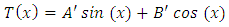 | (47) |
One can write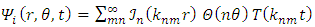 | (48) |
Assuming spherical symmetry, Dirac equation to spherical coordinates Eqs. (36-39), become 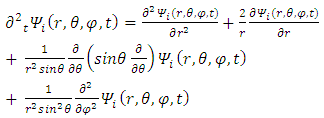 | (49) |
The most general solution is then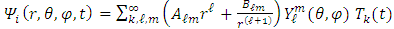 | (50) |
Where 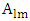 and
and 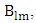 are constants to be determined by the boundary conditions.The time dependency is given by
are constants to be determined by the boundary conditions.The time dependency is given by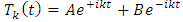 The spherical dependency is given by the spherical harmonic functions, with the Legendre polynomials
The spherical dependency is given by the spherical harmonic functions, with the Legendre polynomials 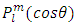 and normalization constants
and normalization constants 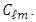 Since by boundary conditions
Since by boundary conditions 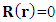 for
for 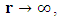 one must have
one must have 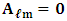 except for
except for 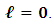 Since by boundary conditions
Since by boundary conditions 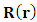 is finite for
is finite for 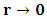 , one must have
, one must have 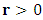 .The solution is then
.The solution is then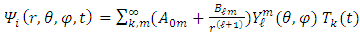 | (51) |
One may interpret the wave functions in Dirac equation, as describing 4 independent membranes 1. Each two membranes are coupled into a two-folded membrane, closed at their common circular edges.The membranes can be at different modes of vibrations (see Figure 3).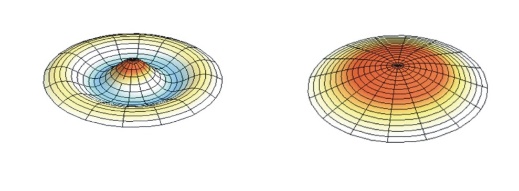 | Figure 3. A Dirac membrane modes |
7. Conclusions
Dirac equation can be represented in a real 6x6 matrix form. This is done by changing the wave function to a 6-vector instead of a 4-vector and replacing Dirac's 4x4 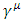 matrices, by four 6x6
matrices, by four 6x6 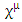 matrices.This results in two similar Klein-Gordon equations, acting on two independent real wave functions, represented by two 6-vectors.Dirac's equation, represents then a system of four (a quartet) coupled triplets A, B, C and D. Each of this quartet has an internal structure (triplet) of 3 sub-entities. The 4 members of the quartet, are coupled and interact with each other. Each member of the triplets satisfies Klein-Gordon equation.The solution to Dirac equation is made up of 12 real wave functions (four triplets). The quartet members are coupled in pairs A and B, and C and D. The spatial derivative of A affects the time derivative of B and vice versa. The spatial derivative of C affects the time derivative of D and vice versa. Yet, when second order time derivatives are considered, the quartet members act as 4 independent entities obeying KG wave equations independent of each other.
matrices.This results in two similar Klein-Gordon equations, acting on two independent real wave functions, represented by two 6-vectors.Dirac's equation, represents then a system of four (a quartet) coupled triplets A, B, C and D. Each of this quartet has an internal structure (triplet) of 3 sub-entities. The 4 members of the quartet, are coupled and interact with each other. Each member of the triplets satisfies Klein-Gordon equation.The solution to Dirac equation is made up of 12 real wave functions (four triplets). The quartet members are coupled in pairs A and B, and C and D. The spatial derivative of A affects the time derivative of B and vice versa. The spatial derivative of C affects the time derivative of D and vice versa. Yet, when second order time derivatives are considered, the quartet members act as 4 independent entities obeying KG wave equations independent of each other.
References
| [1] | D Kwiat, The Schrödinger Equation and Asymptotic Strings, International Journal of Theoretical and Mathematical Physics, Vol 8 (3), pp 71-77, 2018. |
| [2] | Dirac, P. A. M., "The Quantum Theory of the Electron", Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 117 (778): 610. 1928. |
| [3] | B Hatfield, Quantum Field Theory of Point Particles and Strings. Mathematical Physics Research, CRC Press, 2018, Taylor & Francis Group. |
| [4] | Andrzej Trautman, Uniwersytet Warszawski, Clifford Algebras and their representations, Warszawa, Poland Published in: Encyclopedia of Mathematical Physics, Oxford: Elsevier, 2006, vol. 1, pages 518–530. |
| [5] | O. Klein, Z. Fur Physik 37 895 (1926); O. Klein, Nature 118 516 (1926). |
| [6] | W. K. Clifford, “On the classification of geometric algebras”, in Mathematical Papers (1882), Tucker R., (Ed.), Macmillian, London, pp. 397–401. |
| [7] | H. Goldstein, Classical Mechanics, 2nd edition, Addison Wesley Publishing, Chapter 4 "The kinematics of rigid body rotations", 1980. |
| [8] | L. W. Casperson and M-A. Nicolet, Vibrations of a Circular Membrane, American Journal of Physics 36, 669 (1968). |
| [9] | Daria Apushkinskaya, The Vibrating Drumhead (Wave Equation in Polar Coordinates), PDE and Boundary-Value Problems Winter Term 2014/2015, Saarland University, lecture 16. https://www.math.uni-sb.de/ag/fuchs/PDE14-15/pde14-15-lecture-16.pdf, Leonard Susskind, Art Friedman, "Quantum Mechanics: The Theoretical Minimum", Penguin, Published 30th April 2015. |



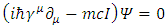
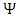 into its real and imaginary parts [3]
into its real and imaginary parts [3]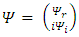
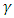 matrices are:
matrices are: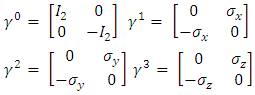
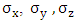 the Pauli 2x2 matrices.
the Pauli 2x2 matrices.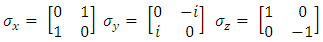
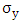 has imaginary components and it can be replaced by writing
has imaginary components and it can be replaced by writing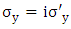 where
where 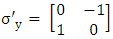 and therefore
and therefore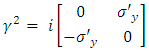
 into
into 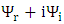 where
where 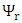 and
and 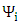 are real, the Dirac equation becomes two separate equations,
are real, the Dirac equation becomes two separate equations, 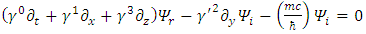
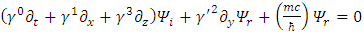
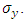
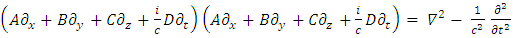
 to vanish, one must assume
to vanish, one must assume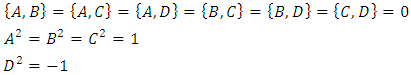
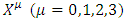 represent the A, B, C, D terms, can be written in a compact form
represent the A, B, C, D terms, can be written in a compact form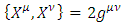
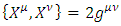 constrains. This leads to the assertion to be made, that
constrains. This leads to the assertion to be made, that 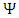 is a 4-vector of complex wave functions.In a 3+1 world,
is a 4-vector of complex wave functions.In a 3+1 world, 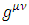 is a 4x4 matrix, so the dimension of the A, B, C and D are 4x4 matrices. However in an N-dimensional world, one needs NxN matrices [4], with N>=4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives:
is a 4x4 matrix, so the dimension of the A, B, C and D are 4x4 matrices. However in an N-dimensional world, one needs NxN matrices [4], with N>=4, to set up a system with the properties required. In Dirac's original work N=4, so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. When looking into the initial development strategy of Dirac, his initial demand was to create an equation with first derivatives: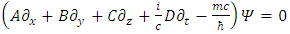
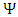 is complex and therefore can be presented as a 2-vector of two complex wave functions.In this work, instead of using the conventional 4x4
is complex and therefore can be presented as a 2-vector of two complex wave functions.In this work, instead of using the conventional 4x4 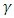 matrices (A, B, C and D) as introduced by Dirac, a set of four 6x6 matrices
matrices (A, B, C and D) as introduced by Dirac, a set of four 6x6 matrices 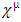 , matrices acting on a complex 6-vector
, matrices acting on a complex 6-vector 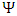 are introduced, which satisfy Eq. (11), and the constrains in Eq. (10).This is equivalent to changing from complex representation of rotations in
are introduced, which satisfy Eq. (11), and the constrains in Eq. (10).This is equivalent to changing from complex representation of rotations in 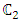 to real rotations [7] in
to real rotations [7] in 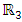 . Since SO(3) is homomorphic with SU(2), the rotations in
. Since SO(3) is homomorphic with SU(2), the rotations in 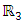 of a 3-component real wave vector is equivalent to a rotation in
of a 3-component real wave vector is equivalent to a rotation in 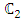 of a 2-component complex wave vector.Instead of using Pauli's 2x2 matrices, one may use the 3x3 matrix presentations of angular momentum generators
of a 2-component complex wave vector.Instead of using Pauli's 2x2 matrices, one may use the 3x3 matrix presentations of angular momentum generators 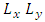 and
and 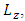 of the rotation group SO(3).Using
of the rotation group SO(3).Using 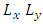 and
and 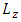 outer multiplications with
outer multiplications with 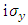 and with
and with 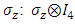 and
and 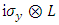 to define the
to define the 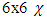 matrices, satisfying the requirements on A, B, C and D according to Eq. (11).Thus:
matrices, satisfying the requirements on A, B, C and D according to Eq. (11).Thus: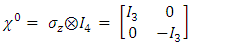
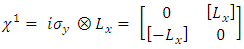
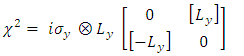
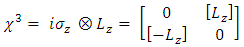
 matrices replace the 4x4
matrices replace the 4x4 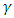 matrices in Dirac 4x4 equation to introduce the Dirac 6x6 equation:
matrices in Dirac 4x4 equation to introduce the Dirac 6x6 equation: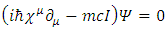
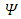 is now a complex 6-vector
is now a complex 6-vector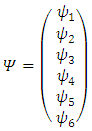
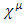 , are four real 6x6 matrices, satisfying the Clifford requirement:
, are four real 6x6 matrices, satisfying the Clifford requirement: 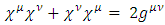
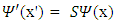 under a Lorentz transformation.Suppose that
under a Lorentz transformation.Suppose that 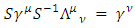 under
under 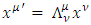 Obviously, if such transformation S exists, the 4x4 Dirac equation is Lorentz invariant.By assuming an infinitesimal Lorentz transformation
Obviously, if such transformation S exists, the 4x4 Dirac equation is Lorentz invariant.By assuming an infinitesimal Lorentz transformation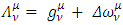
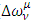 are real numerical coefficients, independent of x), one can write for S
are real numerical coefficients, independent of x), one can write for S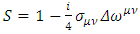
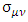 are 4x4 matrices that satisfy
are 4x4 matrices that satisfy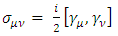
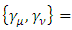
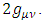 Since
Since 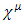 satisfies the same constraints as
satisfies the same constraints as 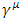 we conclude that there exist 6x6 generators of the S transformation of the Dirac 6x6 representation, and hence Dirac's 6x6 representation, Eq. (16), is Lorentz covariant.The Dirac matrices must satisfy the canonical anti-commutation relation
we conclude that there exist 6x6 generators of the S transformation of the Dirac 6x6 representation, and hence Dirac's 6x6 representation, Eq. (16), is Lorentz covariant.The Dirac matrices must satisfy the canonical anti-commutation relation 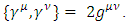 The above definition corresponds to the so-called "chiral basis," where Dirac matrices are block anti-diagonal. Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [6].N-dimensional gamma matrices are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity.Consider a d-dimensional space-time, with a flat Minkowski metric
The above definition corresponds to the so-called "chiral basis," where Dirac matrices are block anti-diagonal. Other bases are possible, and are related to the chiral basis by rotations. The Dirac matrices generate a Euclidean Clifford algebra [6].N-dimensional gamma matrices are a generalization of the four-dimensional Gamma matrices of Dirac to arbitrary dimension N. They are utilized in relativistic invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity.Consider a d-dimensional space-time, with a flat Minkowski metric 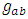 where
where 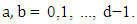 standard Dirac matrices correspond to taking d = N = 4.The higher dimension
standard Dirac matrices correspond to taking d = N = 4.The higher dimension 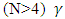 matrices are a d-long sequence of complex N×N matrices
matrices are a d-long sequence of complex N×N matrices 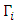 (i =0, … d-1) which satisfy the anticommutator relation from the Clifford algebra
(i =0, … d-1) which satisfy the anticommutator relation from the Clifford algebra 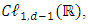 generating a representation for this algebra
generating a representation for this algebra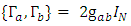 where
where 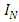 is the N dimensional identity matrix. (The spinors acted on by these matrices have N components in d dimensions.) Such a sequence exists for all values of d.In this work,
is the N dimensional identity matrix. (The spinors acted on by these matrices have N components in d dimensions.) Such a sequence exists for all values of d.In this work, 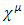 matrices are real, with N=6 and d=4.Thus,
matrices are real, with N=6 and d=4.Thus, 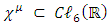 , though without the restriction of
, though without the restriction of 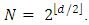
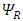 and
and 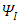 are real 6-vectors)
are real 6-vectors)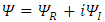 Further split the 6-vectors into two triplets (3-vectors) each:
Further split the 6-vectors into two triplets (3-vectors) each: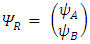
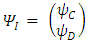
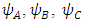 and
and 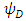 are 4 different real triplets.Substituting Eqs. (22,23) in Dirac's 6x6 representation Eq. (16) gives 4 differential equations with 12 unknowns (4 triplets) parameters:
are 4 different real triplets.Substituting Eqs. (22,23) in Dirac's 6x6 representation Eq. (16) gives 4 differential equations with 12 unknowns (4 triplets) parameters: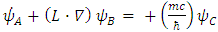
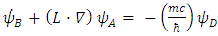
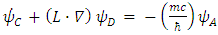
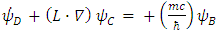
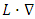 stands for
stands for 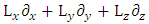 , a 3x3 operator.Applying time derivative to Eqs. (24-27) gives
, a 3x3 operator.Applying time derivative to Eqs. (24-27) gives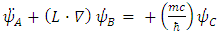
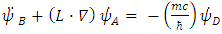
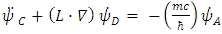
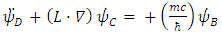
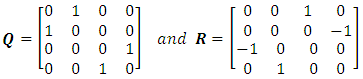
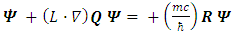
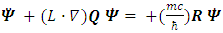
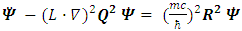
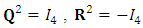 and
and 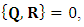 and also
and also 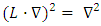 . Thus:
. Thus: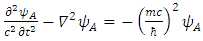
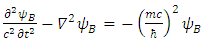
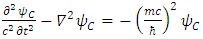
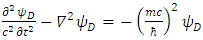
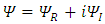 one can separate it into the real and imaginary parts and obtain:
one can separate it into the real and imaginary parts and obtain: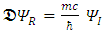
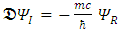
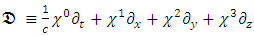 is a 6x6 matrix operator, and
is a 6x6 matrix operator, and 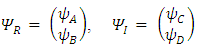 Equations (40) and (41) are two differential equations of first order and show that the
Equations (40) and (41) are two differential equations of first order and show that the 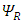 and
and 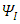 sextets (6-vectors) are coupled to each other. In fact, one can say that there are 12 real wave functions. Each satisfies the Klein-Gordon equation individually and independently. These 12 real wave functions are combined into two sextets, and each sextet is made of two triplets. Altogether there are four triplets.Looking for instance at Eqs. (24-27), the time derivative of one triplet, depends on the spatial derivatives of the second triplet and on a mass-proportional term of the third triplet. This coupling mechanism exists amongst the other triplets combinations in turn (see Figure 1). The four triplets
sextets (6-vectors) are coupled to each other. In fact, one can say that there are 12 real wave functions. Each satisfies the Klein-Gordon equation individually and independently. These 12 real wave functions are combined into two sextets, and each sextet is made of two triplets. Altogether there are four triplets.Looking for instance at Eqs. (24-27), the time derivative of one triplet, depends on the spatial derivatives of the second triplet and on a mass-proportional term of the third triplet. This coupling mechanism exists amongst the other triplets combinations in turn (see Figure 1). The four triplets 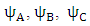 and
and 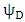 , are denoted here by A B C and D. Each triplet's time derivative is coupled to the spatial derivative of two other triplets and proportional by a
, are denoted here by A B C and D. Each triplet's time derivative is coupled to the spatial derivative of two other triplets and proportional by a 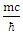 factor to the fourth triplet entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed. Each component of the three components the triplets are made of, satisfies the Klein-Gordon wave equation.
factor to the fourth triplet entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed. Each component of the three components the triplets are made of, satisfies the Klein-Gordon wave equation.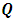 and
and 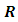 matrices are responsible for the exchanges between the tripletsQ exchanges
matrices are responsible for the exchanges between the tripletsQ exchanges 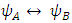 and R exchanges
and R exchanges 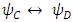 .Therefore, the
.Therefore, the 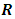 term will affect the lower triplet pair (C and D) by exchange as well as by mass change, whereas the
term will affect the lower triplet pair (C and D) by exchange as well as by mass change, whereas the 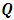 term will only cause an exchange in the upper triplet pair (A and B).To summarize, the following notations are introduced:
term will only cause an exchange in the upper triplet pair (A and B).To summarize, the following notations are introduced: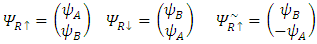
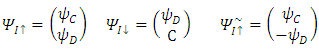 Then, combining Eqs. (22-23,24-27,40-43) gives
Then, combining Eqs. (22-23,24-27,40-43) gives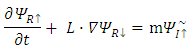
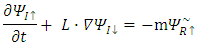 This form helps in the interpretation of how the real and imaginary parts of the Dirac fields interact.
This form helps in the interpretation of how the real and imaginary parts of the Dirac fields interact.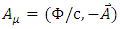 becomes
becomes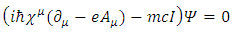
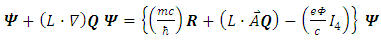
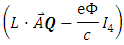 added to the l.h.s.Thus, for the very weak field approximation,
added to the l.h.s.Thus, for the very weak field approximation, 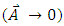 , there will be no exchange between the triplets more than in the case without EM field.The solution of Eq. (43) will be approximately similar to that of Eq. (66), except for an interaction term
, there will be no exchange between the triplets more than in the case without EM field.The solution of Eq. (43) will be approximately similar to that of Eq. (66), except for an interaction term 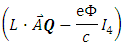
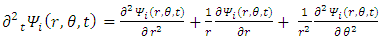

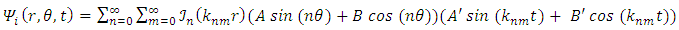
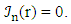 Defining
Defining 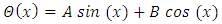
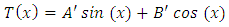
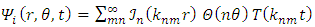
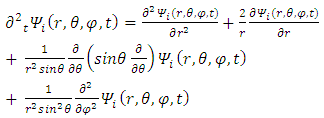
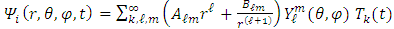
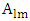 and
and 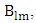 are constants to be determined by the boundary conditions.The time dependency is given by
are constants to be determined by the boundary conditions.The time dependency is given by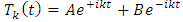 The spherical dependency is given by the spherical harmonic functions, with the Legendre polynomials
The spherical dependency is given by the spherical harmonic functions, with the Legendre polynomials 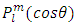 and normalization constants
and normalization constants 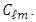 Since by boundary conditions
Since by boundary conditions 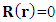 for
for 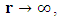 one must have
one must have 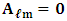 except for
except for 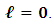 Since by boundary conditions
Since by boundary conditions 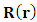 is finite for
is finite for 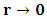 , one must have
, one must have 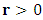 .The solution is then
.The solution is then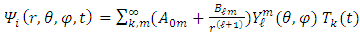

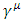 matrices, by four 6x6
matrices, by four 6x6 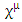 matrices.This results in two similar Klein-Gordon equations, acting on two independent real wave functions, represented by two 6-vectors.Dirac's equation, represents then a system of four (a quartet) coupled triplets A, B, C and D. Each of this quartet has an internal structure (triplet) of 3 sub-entities. The 4 members of the quartet, are coupled and interact with each other. Each member of the triplets satisfies Klein-Gordon equation.The solution to Dirac equation is made up of 12 real wave functions (four triplets). The quartet members are coupled in pairs A and B, and C and D. The spatial derivative of A affects the time derivative of B and vice versa. The spatial derivative of C affects the time derivative of D and vice versa. Yet, when second order time derivatives are considered, the quartet members act as 4 independent entities obeying KG wave equations independent of each other.
matrices.This results in two similar Klein-Gordon equations, acting on two independent real wave functions, represented by two 6-vectors.Dirac's equation, represents then a system of four (a quartet) coupled triplets A, B, C and D. Each of this quartet has an internal structure (triplet) of 3 sub-entities. The 4 members of the quartet, are coupled and interact with each other. Each member of the triplets satisfies Klein-Gordon equation.The solution to Dirac equation is made up of 12 real wave functions (four triplets). The quartet members are coupled in pairs A and B, and C and D. The spatial derivative of A affects the time derivative of B and vice versa. The spatial derivative of C affects the time derivative of D and vice versa. Yet, when second order time derivatives are considered, the quartet members act as 4 independent entities obeying KG wave equations independent of each other. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
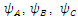 and
and 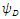 entities. Each entity (denoted here by A B C and D) is a 3-vector. Each single entity time derivative is coupled to the spatial derivative of two other entities and proportional by a
entities. Each entity (denoted here by A B C and D) is a 3-vector. Each single entity time derivative is coupled to the spatial derivative of two other entities and proportional by a 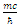 factor to the fourth entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed
factor to the fourth entity, at a time. This coupling is changing between the 4 entities so that all four combinations are allowed