Nura Yakubu1, S. X. K. Huwusu2, A. Adamu1
1Department of Physics, University of Maiduguri, Maiduguri, Nigeria
2Department of Theoretical Physics, National Mathematical Center Abuja, Nigeria
Correspondence to: Nura Yakubu, Department of Physics, University of Maiduguri, Maiduguri, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The application of Newton’s laws of motion in gravitational fields has been restricted to the fields of perfectly spherical bodies. In this paper the gravitational fields due to a Spheroidal body is derived to open the way for the extension of Newtonian mechanics from the fields of spherical bodies to these Spheroidal bodies. The results showed that Newton’s gravitational field equations for a Spheroidal body are linear and separable and can be solved in terms of the well known special functions of mathematical physics, the Legendre functions. We also obtained gravitational intensity field 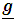 of the body and its corresponding unit vectors in components forms. We further obtained general acceleration vector
of the body and its corresponding unit vectors in components forms. We further obtained general acceleration vector 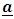 its associated acceleration vector components forms. We finally obtained the components of the equation of motion for a particle of non zero rest mass in the gravitational field exterior to an oblate spheroidal massive body. The Newton’s universal gravitational field equations for a homogeneous oblate Spheroidal body with the exact and complete results are available for mathematical analysis and hence physical interpretation and experimental investigation for all bodies in the universe.
its associated acceleration vector components forms. We finally obtained the components of the equation of motion for a particle of non zero rest mass in the gravitational field exterior to an oblate spheroidal massive body. The Newton’s universal gravitational field equations for a homogeneous oblate Spheroidal body with the exact and complete results are available for mathematical analysis and hence physical interpretation and experimental investigation for all bodies in the universe.
Keywords:
Gravitational field, Homogeneous, Static, Spheroidal
Cite this paper: Nura Yakubu, S. X. K. Huwusu, A. Adamu, Gravitational Field of a Stationary Homogeneous Oblate Spheroidal Massive Body, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 3, 2018, pp. 62-70. doi: 10.5923/j.ijtmp.20180803.02.
1. Introduction
In the present paper some theoretical background of gravitational field of Spheroidal bodies is stated. Also in this paper the gravitational scalar potential for both the interior and exterior regions are evaluated by means of Legendre differential equations. Then the gravitational intensities of oblate Spheroidal bodies for both the regions are determined.Prior to 1950, theoretical study of gravitation was restricted almost exclusively to the fields of massive bodies of perfect spherical geometry. For example, in Newton’s theory of universal gravitation (T. U. G.) the motion of particles (such as projectile, satellites and penduli) in earth’s atmosphere is treated under the assumption that the earth is a perfect sphere. Similarly, in the solar system the motion of bodies (such as planets comets and asteroids) is treated under the assumption that the sun is perfect sphere. Also in Einstein theory of gravitation, called General Relativity Theory (G. R. T.) the motion of bodies (such as planet) and particles (such as photons) is treated under the assumption that the sun is a perfect sphere (Schwrchiild space time). But it is well known that the only reason for these restrictions is mathematical convenience and simplicity. The real fact of nature is that all rotating planets stars and galaxies in the universe are Spheroidal and is obvious that the Spheroidal geometry will have corresponding consequences and effects in the motion of all particles in their gravitational fields. These effects will exist in both Newton’s T. U. G and Einstein’s G. R. T. consequently the way is prepared for the study of motion of all particles in the gravitational fields of Spheroidal bodies.As an example it is now well known that satellite orbits around the earth are not govern by just simple universe distance square gravitational field of perfect spherical geometry. They are also govern by second harmonics (pole of order 3) as well as fourth harmonics (pole of order 5) of gravitational scalar potential due to imperfect spherical geometry. Now for comparison with these approximations the exact analytical gravitational scalar potential for a perfect oblate Spheroidal body is derived (Howusu, 2001).
2. Analysis
Consider a homogeneous oblate Spheroidal body of rest mass M0. Let S be the referenc frame whose origin 0 coincides with centre of the body as shown in figure 1.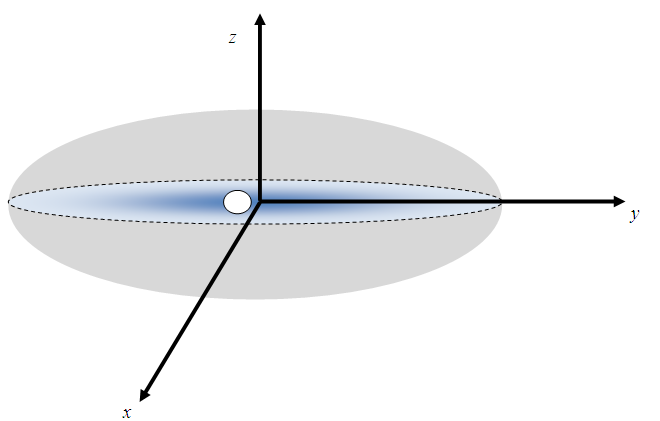 | Figure 1. Oblate Spheroid |
Then the oblate Spheroidal coordinates (η, ξ ) are defined in terms of the Cartesian coordinates (x, y, z) by 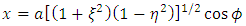 | (1) |
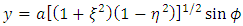 | (2) |
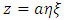 | (3) |
where a is a constant and 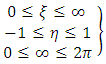 | (4) |
and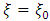 | (5) |
where ξ0 = a constant. Now since the body is homogenous, the density of active mass ℓ is given by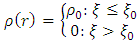 | (6) |
where 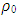 is the constant density of rest mass. As is well known, Newton’s gravitational field equation for the gravitational scalar potential Φ due a distribution of mass density ρ is given by
is the constant density of rest mass. As is well known, Newton’s gravitational field equation for the gravitational scalar potential Φ due a distribution of mass density ρ is given by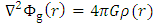 | (7) |
where G is the universal gravitational constant. It follows from the explicit expression for the Laplacian operator in oblate Spheroidal coordinate that the interior and exterior gravitational scalar potentials Φ respectively satisfy the equations (Nura, et. al., 2017),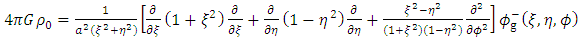 | (8) |
and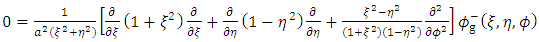 | (9) |
To solve these equations it may be noted that by the symmetry of the distribution of mass about the polar axis the dynamical gravitation a potential will be independent of the azimuthal angle 𝜙. Hence equations (8) and (9) reduce to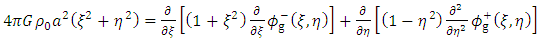 | (10a) |
and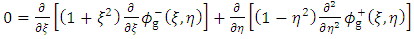 | (10b) |
Next, let us seek a separable complementary solution of the interior, equation, 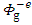 , as
, as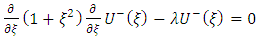 | (11) |
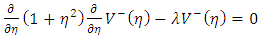 | (12) |
where λ is the separation constant. Consequently, for the choice | (13) |
Equation (10) becomes the Legendre’s equation and hence has solution of the form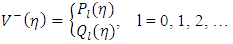 | (14) |
where Pl and Ql are the linearly independent solutions of the Legendre’s differential equation. Also by the transformation equation 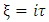 | (15) |
equation (11) becomes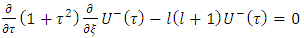 | (16) |
where equation (16) is the Legendre’s differential equation and hence has the solutions of the form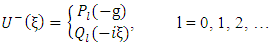 | (17) |
Consequently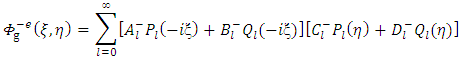 | (18) |
where 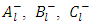 and
and 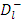 are arbitrary constants. Next let us seek a particular solution of the interior equation
are arbitrary constants. Next let us seek a particular solution of the interior equation 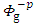 as
as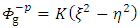 | (19) |
Substituting (19) into equation (10) a it follows that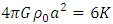 | (20) |
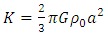 | (21) |
Hence the general solution of the interior equation 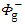 is given by
is given by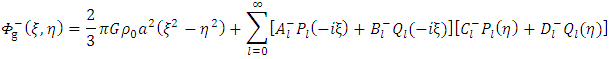 | (22) |
where 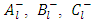 and
and 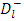 are arbitrary constants and Pl and Ql are the Legendre’s function of order 1. Similarly, since the exterior equation is homogeneous its general solution
are arbitrary constants and Pl and Ql are the Legendre’s function of order 1. Similarly, since the exterior equation is homogeneous its general solution 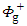 is given by
is given by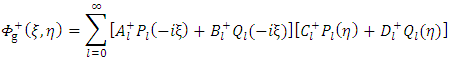 | (23) |
where 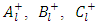 and
and 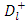 are arbitrary constants. Now since the interior and exterior regions both contain the coordinates η = 0 which is a singularity of Ql
are arbitrary constants. Now since the interior and exterior regions both contain the coordinates η = 0 which is a singularity of Ql 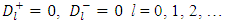 | (24) |
Also since 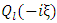 is not defined at the center of the body
is not defined at the center of the body 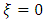 in the interior region
in the interior region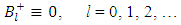 | (25) |
Also since 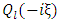 is not defined at
is not defined at 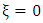 in the ixterior region
in the ixterior region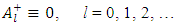 | (26) |
Hence from the continuity of the gravitational scalar potentials (22) and (23) across the boundary 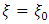 and the orthogonality of the Legendre function
and the orthogonality of the Legendre function 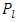 it follows that, the resulting equations are
it follows that, the resulting equations are 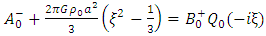 | (27) |
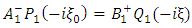 | (28) |
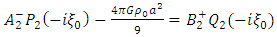 | (29) |
Equations (27) and (29) we get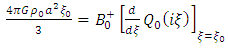 | (30) |
and 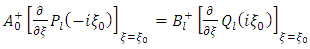 | (31a) |
Thus, solving (27) – (31) a simultaneously: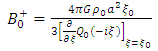 | (31b) |
and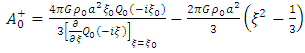 | (32) |
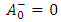 | (33) |
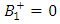 | (34) |
Next, let us consider equation (29) above i.e.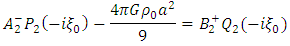 Now differentiate both sides of this equation with respect to ξ, if follows that
Now differentiate both sides of this equation with respect to ξ, if follows that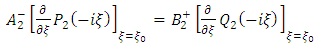 | (35) |
By multiplying both sides of equation (29) with 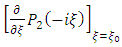 it follows that
it follows that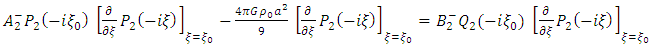 | (36) |
This follows by multiplying both side of equation (36) with 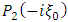 . Thus
. Thus 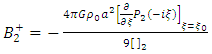 | (37) |
where 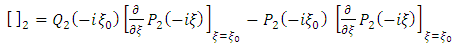 | (38) |
and 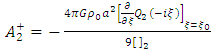 | (39) |
Hence the general solution of the interior- and exterior equation in equation (22) and (23) reduced to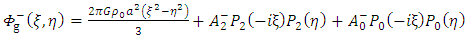 | (40) |
and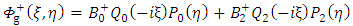 | (41) |
These are the gravitational scalar potentials of the body in terms of rest mass density. It follows that gravitational scalar potential (40) and (41) may be expressed in terms of the total rest mass of the body by the relation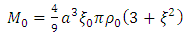 | (42) |
It may be noted that results from mathematical tables gives (Nura, 2011)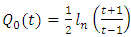 | (43) |
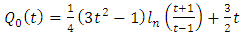 | (44) |
Consequently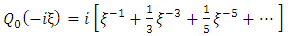 | (45) |
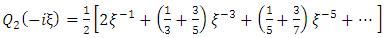 | (46) |
3. Evaluation of Gravitational Field Intensity for Both the Interior and Exterior Scalar Potentials
The Del operator 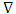 is given by equation below
is given by equation below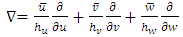 | (47) |
Hence putting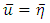 | (48) |
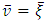 | (49) |
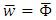 | (50) |
It follows that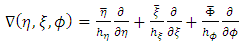 | (51) |
Therefore, it follows from definition that the gravitational intensity field g, of the body is given by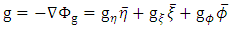 | (52) |
Now,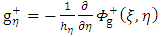 | (53) |
Putting the general solution g+ in the above equation (52) give the following results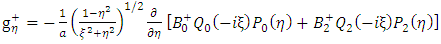 | (54) |
Or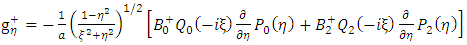 | (55) |
Equation (55) can take the form: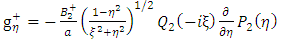 | (56) |
Since 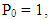 | (57) |
Similarly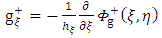 | (58) |
Or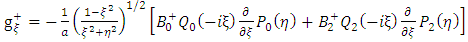 | (59) |
and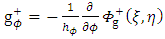 | (60) |
Or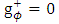 | (61) |
To obtain a gravitational field intensity for the interior potential 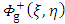 , we substitute (44) into the equation
, we substitute (44) into the equation 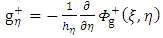 | (62) |
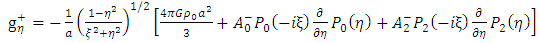 | (63) |
Or 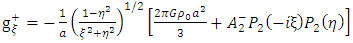 | (64) |
Since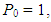 | (65) |
Similarly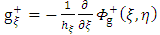 | (66) |
and hence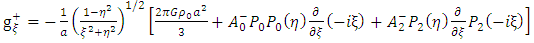 | (67) |
and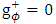 | (68) |
The results (52), (57) (68) and (61) are the gravitational intensity field interior to the body while (62), (670 and (68) are those exterior to the body. Next, precisely as is well known cases of the spheroidal polar coordinates, the definition of the oblate spheroidal coordinates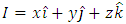 | (9) |
where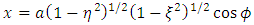 | (10) |
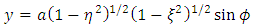 | (11) |
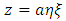 | (12) |
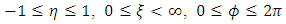 | (13) |
The scalar factors are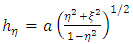 | (14) |
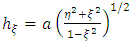 | (15) |
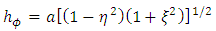 | (16) |
And the corresponding unit vector are given by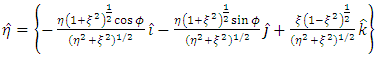 | (17) |
and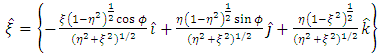 | (18) |
and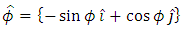 | (19) |
The general position vector 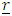 is given by
is given by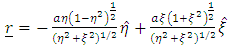 | (20) |
And the general velocity vector 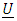 is given by
is given by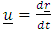 | (21) |
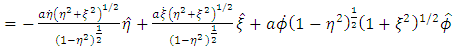 | (22) |
For oblate spheroidal coordinates, the general acceleration vector 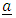 is given by
is given by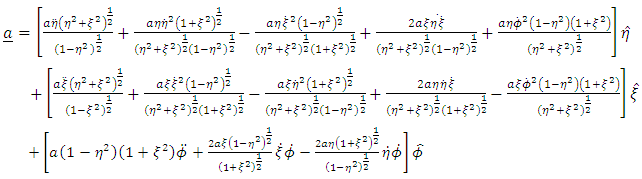 | (23) |
Equation (23) above reduced to the form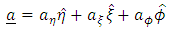 | (24) |
where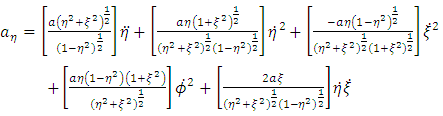 | (25) |
and 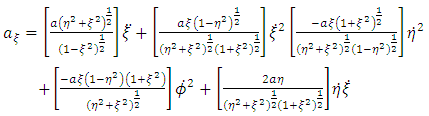 | (26) |
and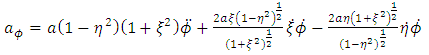 | (27) |
Consequently, it follows from Newton’s law of motion in gravitational fields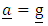 | (28) |
And equation (7) – (9) and (25) – (27) that the components of the equation of motion given by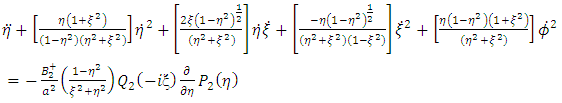 | (29) |
and 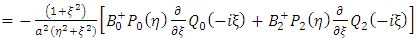 | (30) |
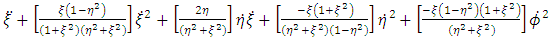 | (31) |
and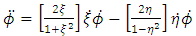 | (32) |
These are the complete equations of motion for a particle of non zero rest mass in the gravitational field exterior to an oblate spheroidal massive body.
4. Summary and Conclusions
In this paper, Newton’s Universal Gravitational Potential field equation for a homogeneous oblate Spheroidal body is formulated and solved with the exact and complete results given by (40) and (41). Consequently, these potentials are now available for application in physics. An application of the results obtained in this work is that the gravitational scalar potential (40) and (41) imply the corresponding gravitational intensities (56), (59), (61), (64), (67) and (68). A profound philosophical inference is suggested by the results obtained in the theses that Newton’s gravitational field equations for a Spheroidal body are linear separable and hence solvable in terms of the well known special functions of mathematical physics, the Legendre function. This fact suggests that Einstein’s geometrical theory of gravitation, GRT, whose gravitational field equation is non linear may not be the most natural generalization of Newton’s dynamical theory of gravitation. In the present work, the gravitational field intensity or force fields for both the interior and exterior gravitational scalar potentials were derived. These sets of equations pave the way for the equations of motion for a particle of non-zero rest mass using spheroidal coordinates. It is now known that most bodies in the universe are Spheroidal n nature. As an example, it is now well known that satellite orbits round the earth are not governed by just the simple inverse distance squared gravitational fields of perfect spherical geometry. They are also governed by second harmonics (pole of order 3), as well as fourth harmonics (pole of order 5) of gravitational scalar potential due to imperfect spherical geometry.In the first place this work opens the door for the physical interpretation of all the solutions obtained in this work and hence experimental investigation in the motion of all bodies in the earth’s atmosphere and solar system as well as all other gravitating systems in the universe.In the second place the door in henceforth opened for the mathematical study of all the unsolved equations of motion for all particles in all types of motions in all systems in the universe, such as more accurate calculation of (i) Missile and satellite and space craft trajectory in the earth’s atmosphere (ii) motions of moons around their planets, (iii) motion of planets (iv) comets and asteroids around the sun and (v) motions of stars around their galactic nuclei in the universe.In the third place it is most interesting and instructive to note that by the definition of the function Q0 and Q2 the gravitational intensity fields due to oblate Spheroidal body are all even orders in the universe coordinates.Since this work pave the way for new physical investigations and experimental verifications of the motion of bodies in the universe.It may be noted that precisely as in the case of the gravitational field of a stationary homogeneous spherical massive body the door is henceforth opened for the theoretical investigation of the following problems.× Pure ξ – motion of a particle of non zero rest mass in the gravitational field exterior to a stationary oblate spheroidal massive body. Plane motion of a particle of non zero rest mass in the gravitational field exterior to a stationary homogeneous oblate spheroidal massive body.× Pure ξ – motion of a photon in the gravitational field interior to a stationary homogeneous oblate spheroidal massive body. Gravitational frequency shift of a photon in the gravitational field exterior to a stationary homogeneous oblate spheroidal massive body.× Gravitational time dilation in the gravitational field exterior to a stationary oblate spheroidal massive body. Gravitational time dilation in the gravitational field interior to stationary oblate massive body.× Electrogravitational coupling in the gravitational field exterior to a homogeneous oblate spheroidal massive body. Electrogravitational coupling in the gravitational field interior to a homogeneous oblate spheroidal massive body. × Gravitational length contraction in the gravitational field exterior to a stationary homogeneous oblate spheroidal massive body. Gravitational length contraction in the gravitational field interior to a stationary homogeneous oblate spheroidal massive body.× Radar sounding in the gravitational field exterior to a stationary homogeneous oblate spheroidal massive body. Radar sounding in the gravitational field interior to a stationary homogeneous oblate spheroidal massive body.
References
| [1] | Albert, E. (1979), Quanta and cosmology: Johnson Corporation, London. |
| [2] | Ashatague, H. and Kshif, A. (1994), Curvature Corlineatiolls of some Spherically Symmetry Space-Tme. American Journal of Mathematical Physics 37(7) 3498-3504. |
| [3] | Atwater, H. E. (1974), Introduction to General Relativity. Pergamen Press, New York. |
| [4] | Fock, V. (1997), the Theory of Space-Time and Gravitation. Pergamen Press, New York. |
| [5] | Forster, J. and Nightingale, J. D. (1979), A Short Course in General Relativity, Longman, New York. |
| [6] | G. Arfken, Mathematical Methods for Physics. (Academic Press, New York, 1968). |
| [7] | Howusu, S. X. K. (1996), Cosmological Redshift. Experimental Detection of Gravitational Radiation Aperion (Montreal) 3 (1). 10 – 13. |
| [8] | Howusu, S. X. K. (2001), Natural Philosophy of Gravitation, Jos University Press, Jos Nigeria. |
| [9] | Howusu, S. X. K. (2003), “Gravitational Field of Spherical Bodies – Extension of Gravitational Fields of Spherical Bodies”, Galilean Electrodynamics. |
| [10] | J. L. Anderson. Principles of Relativity (academic Press, New York, 1967). |
| [11] | Mark, K. (1986), Gravitational Field Intensity. American Journal of Physics 46(2) 167 – 179. |
| [12] | N. Yakubu and S. X. K. Howusu (2011). Gravitational Field of a Stationary Homogeneous Spheroidal Massive Body. Journal of Science and Technology Research, Vol. 10, No. 3, pp 20 – 29. |
| [13] | N. Yakubu, S. X. K. Howusu, O. Nwagbara and I. Nuhu (2017). Solution of Newton’s Gravitational Field Equation of a Static Homogeneous Prolate Spheroidal Massive Body. International Journal of Engeneering Science and Innovative Technology (IJESIT). Vol. 6, Issue 1, pp 67 – 76. |
| [14] | Rosser, W. G. (1967), Introductory Relativity. Butter worth, London. |
| [15] | Slater, J. C. (1933), Introductory Theoretical Physics, Mc Graw – Hill Publishing Company Ltd, London. |
| [16] | Solelger, I. (1982), Fundamentals of Theoretical Physics. Vol. 2 Mir Publishers, Moscow. |
| [17] | Weinberge, S. (1975), Gravitation and Cosmology Principles and applications of the General Theory Relativity. (J Willey, New York). |
| [18] | William, H. (1974), Hand Book of Mathematical Sciences CRC Press International. Boca Roton. Florida. |


 of the body and its corresponding unit vectors in components forms. We further obtained general acceleration vector
of the body and its corresponding unit vectors in components forms. We further obtained general acceleration vector 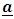 its associated acceleration vector components forms. We finally obtained the components of the equation of motion for a particle of non zero rest mass in the gravitational field exterior to an oblate spheroidal massive body. The Newton’s universal gravitational field equations for a homogeneous oblate Spheroidal body with the exact and complete results are available for mathematical analysis and hence physical interpretation and experimental investigation for all bodies in the universe.
its associated acceleration vector components forms. We finally obtained the components of the equation of motion for a particle of non zero rest mass in the gravitational field exterior to an oblate spheroidal massive body. The Newton’s universal gravitational field equations for a homogeneous oblate Spheroidal body with the exact and complete results are available for mathematical analysis and hence physical interpretation and experimental investigation for all bodies in the universe.

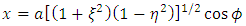
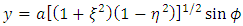
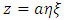
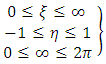
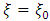
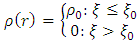
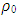 is the constant density of rest mass. As is well known, Newton’s gravitational field equation for the gravitational scalar potential Φ due a distribution of mass density ρ is given by
is the constant density of rest mass. As is well known, Newton’s gravitational field equation for the gravitational scalar potential Φ due a distribution of mass density ρ is given by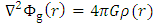
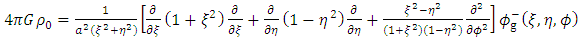
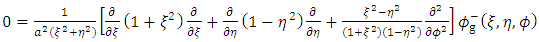
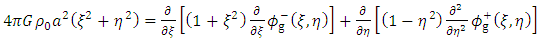
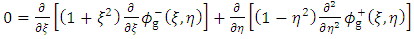
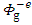 , as
, as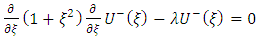
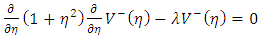

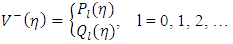
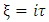
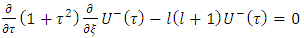
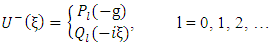
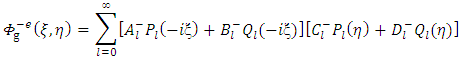
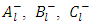 and
and 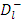 are arbitrary constants. Next let us seek a particular solution of the interior equation
are arbitrary constants. Next let us seek a particular solution of the interior equation 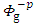 as
as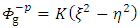
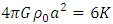
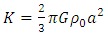
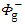 is given by
is given by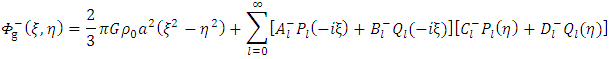
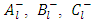 and
and 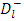 are arbitrary constants and Pl and Ql are the Legendre’s function of order 1. Similarly, since the exterior equation is homogeneous its general solution
are arbitrary constants and Pl and Ql are the Legendre’s function of order 1. Similarly, since the exterior equation is homogeneous its general solution 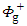 is given by
is given by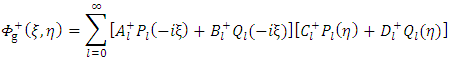
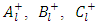 and
and 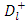 are arbitrary constants. Now since the interior and exterior regions both contain the coordinates η = 0 which is a singularity of Ql
are arbitrary constants. Now since the interior and exterior regions both contain the coordinates η = 0 which is a singularity of Ql 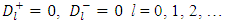
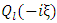 is not defined at the center of the body
is not defined at the center of the body 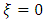 in the interior region
in the interior region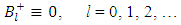
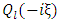 is not defined at
is not defined at 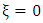 in the ixterior region
in the ixterior region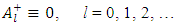
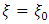 and the orthogonality of the Legendre function
and the orthogonality of the Legendre function 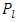 it follows that, the resulting equations are
it follows that, the resulting equations are 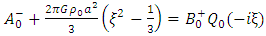
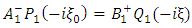
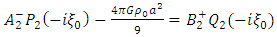
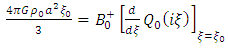
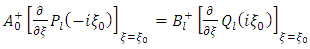
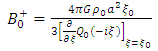
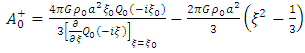
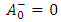
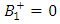
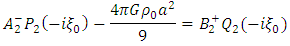 Now differentiate both sides of this equation with respect to ξ, if follows that
Now differentiate both sides of this equation with respect to ξ, if follows that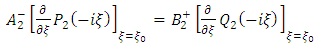
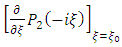 it follows that
it follows that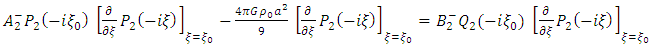
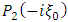 . Thus
. Thus 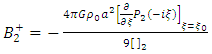
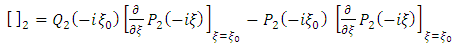
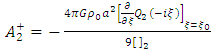
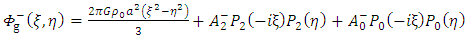
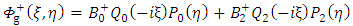
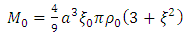
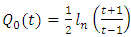
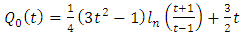
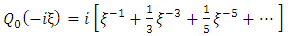
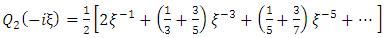
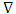 is given by equation below
is given by equation below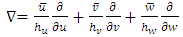
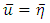
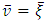
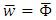
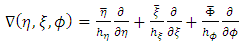
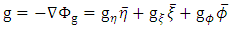
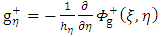
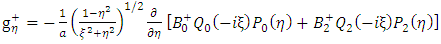
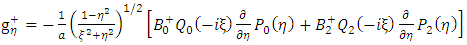
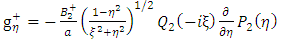
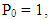
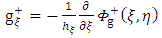
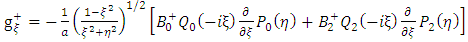
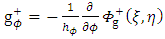
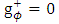
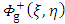 , we substitute (44) into the equation
, we substitute (44) into the equation 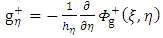
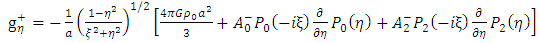
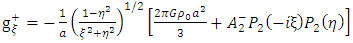
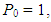
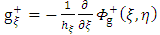
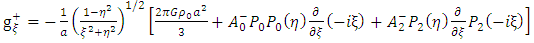
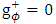
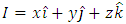
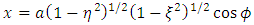
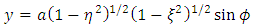
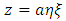
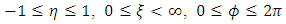
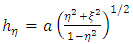
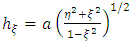
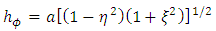
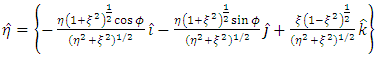
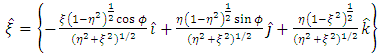
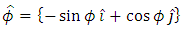
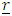 is given by
is given by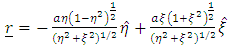
 is given by
is given by
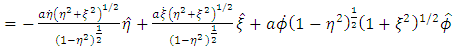
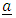 is given by
is given by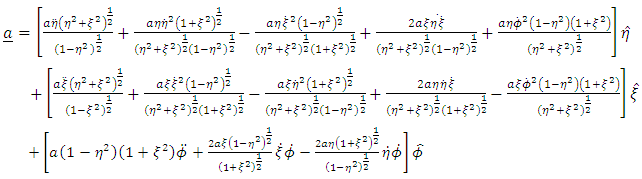
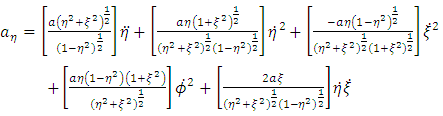
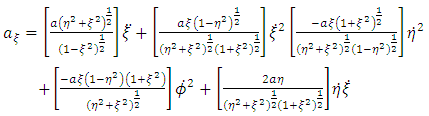
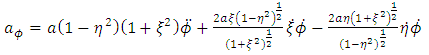
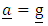
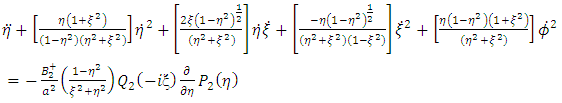
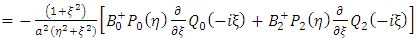
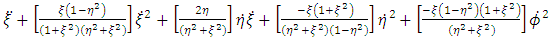
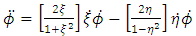
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML