P. K. Chakraborty1, B. N. Mondal2
1Department of Electronics and Electrical Communication Engineering, Indian Institute of Technology, Kharagpur, India
2Department of Central Scientific Services, Indian Association for the Cultivation of Science, Jadavpur, Kolkata, India
Correspondence to: P. K. Chakraborty, Department of Electronics and Electrical Communication Engineering, Indian Institute of Technology, Kharagpur, India.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Exact quantum mechanical calculations of the Fermi-Integral (FI) associated with the density-of states (DOS) function for non-degenerately doped impurities in a parabolic band semiconductor were made. Unlike the results of previous approximate numerical calculations, present exact calculations showed novel oscillatory behavior of FI only for the positive values of the reduced Fermi-energies η (= Ef/kBT), where Ef is the Fermi energy and kB is the Boltzman constant and T is the absolute temperature. On the other hand, for the corresponding negative values, FI exhibited no oscillation. The observed non periodic oscillations were due to the Confluent Hypergeometric functional behavior of the presently derived expression of FI. Such oscillation might have massive effect on the dynamic behavior of quantum electronic properties of semiconductors as shown, for example, in case of Einstein relations (diffusivity-mobility ratio, DMR). Present finding also stimulate further investigation of DMR and similar other physical properties using the present exact expression of FI to explore the underlying new physics.
Keywords:
Fermi-Integral, Non-degenerately doped, Semiconductor, Density-of-state and Parabolic Band
Cite this paper: P. K. Chakraborty, B. N. Mondal, Oscillatory Behavior of the Fermi-Integral and Density of States Functions in a Parabolic Band Semiconductor with Non-Degenerately Doped Impurities, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 3, 2018, pp. 57-61. doi: 10.5923/j.ijtmp.20180803.01.
1. Introduction
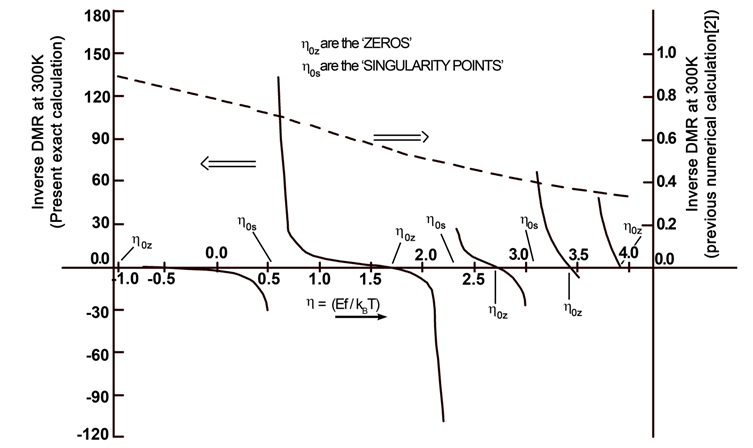
The Fermi-integral (FI) have been vastly used for the study of density of states (DOS) functions in semiconductors. It is well known that FI is involved with the integration of the product of DOS function and Fermi-Dirac (FD) distribution function for all possible values of the electron energy, E. The FI, generally defined by Fj(η) [1-4], can be written as 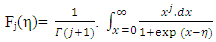 | (1) |
where j is an integer or a fraction and 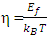 with
with 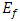 being the Fermi-energy. For the DOS function of a parabolic band, the value of j is ½. Accordingly, the corresponding FI,
being the Fermi-energy. For the DOS function of a parabolic band, the value of j is ½. Accordingly, the corresponding FI, 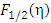 can be represented (using Eq(1) of [1-4]) in the form
can be represented (using Eq(1) of [1-4]) in the form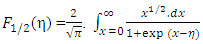 | (2) |
η is usually known as reduced Fermi-energy. Conventionally, 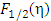 was evaluated numerically [1-6] for all practical purposes and the corresponding numerical values were found to be comprised of only positive real values of the integrands. The numerical values are also available in a tabular form [1, 2] for both positive and negative values of η. However, as the numerical integration is an approximate method, one cannot accurately find the exact values of reduced energy parameter,
was evaluated numerically [1-6] for all practical purposes and the corresponding numerical values were found to be comprised of only positive real values of the integrands. The numerical values are also available in a tabular form [1, 2] for both positive and negative values of η. However, as the numerical integration is an approximate method, one cannot accurately find the exact values of reduced energy parameter, 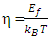 related to many physical parameters of metals and semiconductors. Therefore, an exact solution of Eqs (1) and (2) are demanding to demonstrate the new electronic properties like Fermi-energy which in turn associated with the transport phenomena in doped semiconductors [6] as well as in nano-technology devices [5].Therefore, an attempt has been made for an exact quantum mechanical calculation of the FIs
related to many physical parameters of metals and semiconductors. Therefore, an exact solution of Eqs (1) and (2) are demanding to demonstrate the new electronic properties like Fermi-energy which in turn associated with the transport phenomena in doped semiconductors [6] as well as in nano-technology devices [5].Therefore, an attempt has been made for an exact quantum mechanical calculation of the FIs 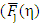 and
and 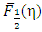 applying a correct integration methods. Such calculations might reveal some interesting properties of
applying a correct integration methods. Such calculations might reveal some interesting properties of 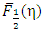 which could not be visualized from the earlier numerical method of calculations discussed in this paper.
which could not be visualized from the earlier numerical method of calculations discussed in this paper.
2. Theoretical Analysis
For an intrinsic semiconductor of parabolic band with lightly doped impurities, the band equation is given by: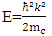 | (3) |
where 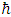 is the reduced Planck’s constant,
is the reduced Planck’s constant, 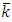 is the wave vector, mc is the un-perturbed conduction band edge effective electrons mass and E is the electron energy. The normal DOS function, N (E), can be written as
is the wave vector, mc is the un-perturbed conduction band edge effective electrons mass and E is the electron energy. The normal DOS function, N (E), can be written as 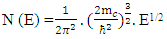 | (4) |
(energy range E → 0 to +∞).For a non-degenerately doped semiconductor of carrier concentration, Ni, one can write the carrier statistical relation [4] as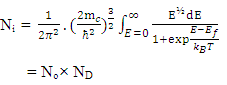 | (5) |
where 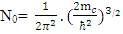 in Eq.5and
in Eq.5and 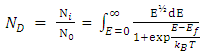 | (6) |
Eq. 6 can also be re-written as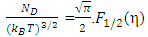 | (7) |
where 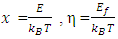 and
and 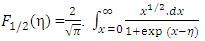 | (8) |
Eq. (8) is identical with Eq. (2). The closed form of an exact solutions of Fj(η) with special attention to j=1/2 for 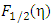 can now be provided. We represent the exact solutions of Eq.(1) and Eq.(8) by
can now be provided. We represent the exact solutions of Eq.(1) and Eq.(8) by 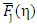 and
and 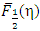 , respectively. Performing some algebraic manipulations to the integrands in Eq.(1), an exactly form
, respectively. Performing some algebraic manipulations to the integrands in Eq.(1), an exactly form 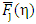 comes out to be
comes out to be 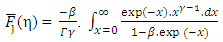 | (9) |
where β =-exp (η) and γ= (j+1).The new exact solution of Eq.(9) can be expressed [7] as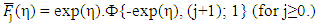 | (10) |
where the special function, Ф(a,b;z) is the Confluent Hypergeometric function with a = – exp(η), b=(j+1) and z=1 [7, 8]. For a given value of 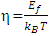 and j, one can find the values of Ф (a,b; z) from the Table in [8]. However, for simple calculations for
and j, one can find the values of Ф (a,b; z) from the Table in [8]. However, for simple calculations for 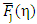 , one can also use the series expansion of Ф (a,b; z) [7, 8]. For the series expansion of Ф (a,b; z) , one can use the following relation [8]
, one can also use the series expansion of Ф (a,b; z) [7, 8]. For the series expansion of Ф (a,b; z) , one can use the following relation [8]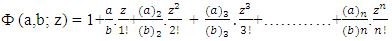 | (11) |
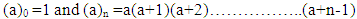 | (12) |
Substituting a=-exp (η); b= (j+1) and z=1, in Eqs.(11) and (12), the final exact solution of 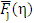 comes out to be
comes out to be 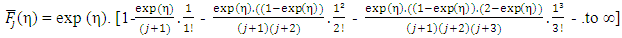 | (13) |
Eq. (13) represents the series solution to 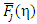 for any values of j and η. Thus, one can find the value of
for any values of j and η. Thus, one can find the value of 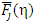 more accurately and conveniently than the conventional numerical approaches for Fj (η) put forwarded earlier [1, 2]. For j=1/2, as a special case to the Fermi-integral,
more accurately and conveniently than the conventional numerical approaches for Fj (η) put forwarded earlier [1, 2]. For j=1/2, as a special case to the Fermi-integral, 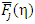 , the series representation of the same can be given from Eq.(13) as
, the series representation of the same can be given from Eq.(13) as 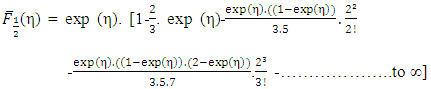 | (14a) |
Now, for a given value of 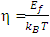 , we can compute
, we can compute 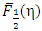 from Eq.(14).
from Eq.(14). 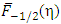 can also be easily computed from Eq.(13) with j=-1/2.From Eq (14a) we find the exact form of the DOS, S(η), as a function of reduced Fermi energy η as
can also be easily computed from Eq.(13) with j=-1/2.From Eq (14a) we find the exact form of the DOS, S(η), as a function of reduced Fermi energy η as 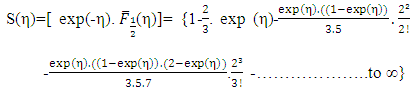 | (14b) |
The computed values of 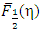 could be plotted as a function of η, for both positive and negative values which have been discussed below.
could be plotted as a function of η, for both positive and negative values which have been discussed below.
3. Results and Discussion
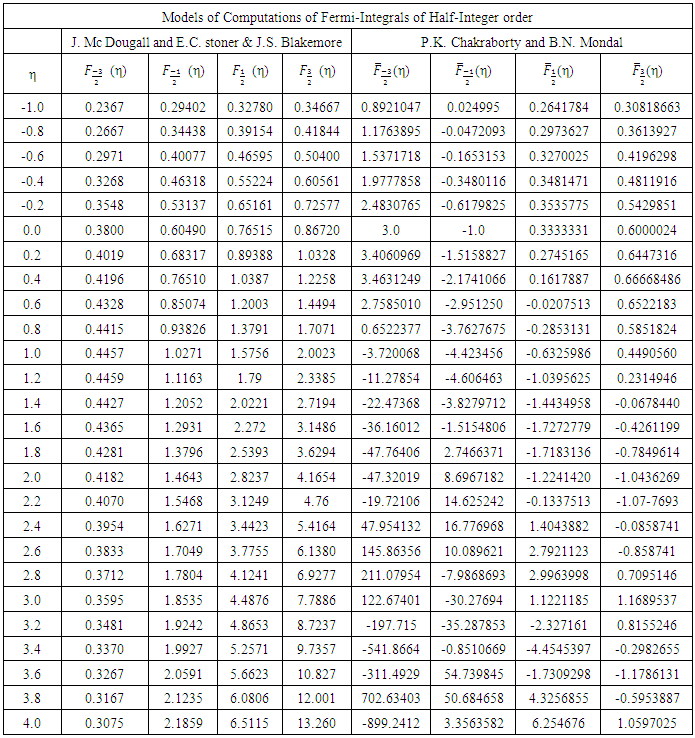
We demonstrate the variation of the calculated exact FI for the DOS as function of 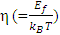 in the case of non-degenerately doped semiconductor. The values of FIs of half-integer order estimated by earlier classical calculation [1, 2] and those obtained from the present exact calculation are shown in Table 1 for comparison. The exact values of the function
in the case of non-degenerately doped semiconductor. The values of FIs of half-integer order estimated by earlier classical calculation [1, 2] and those obtained from the present exact calculation are shown in Table 1 for comparison. The exact values of the function 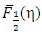 calculated from the present series expansions of Eq. (14) is plotted in Figure 1. It is seen from the figure that the results of our present exact calculations for FI exhibits oscillations only for the positive values of η. On the other hand, for the negative values of η, no oscillation is exhibited. Earlier approximate numerical calculations of FI [1-6] did not, however, show any such oscillations. The nature of the said oscillations is not periodic like sinusoidal functions. That is, all the positive crest and the negative trough amplitudes are not uniform, rather successive amplitudes of the peaks and those of the valleys are decreasing in their magnitudes. Moreover, the distances (representing period of oscillation) between two successive peaks and valleys gradually decrease.An attempt has been made to calculate the diffusivity-mobility ratio (DMR) also known as Einstein relation [4]. The DMR for various semiconductor device performances [9-11] calculated from the conventional approach for FIs (i.e., the numerical integrations) comes out to be always positive (dotted line in Figure 2). Using the present exact calculations of the Fermi-Integrals
calculated from the present series expansions of Eq. (14) is plotted in Figure 1. It is seen from the figure that the results of our present exact calculations for FI exhibits oscillations only for the positive values of η. On the other hand, for the negative values of η, no oscillation is exhibited. Earlier approximate numerical calculations of FI [1-6] did not, however, show any such oscillations. The nature of the said oscillations is not periodic like sinusoidal functions. That is, all the positive crest and the negative trough amplitudes are not uniform, rather successive amplitudes of the peaks and those of the valleys are decreasing in their magnitudes. Moreover, the distances (representing period of oscillation) between two successive peaks and valleys gradually decrease.An attempt has been made to calculate the diffusivity-mobility ratio (DMR) also known as Einstein relation [4]. The DMR for various semiconductor device performances [9-11] calculated from the conventional approach for FIs (i.e., the numerical integrations) comes out to be always positive (dotted line in Figure 2). Using the present exact calculations of the Fermi-Integrals 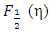 and
and 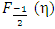 , DMR can be defined as
, DMR can be defined as 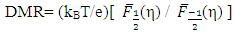 | (15) |
Table 1. Comparison of FIs of Half Integer order estimated from the previous Classical Calculations [1, 2] with phase obtained from the Present exact quantum mechanical calculations (Eqn.13)
 |
| |
|
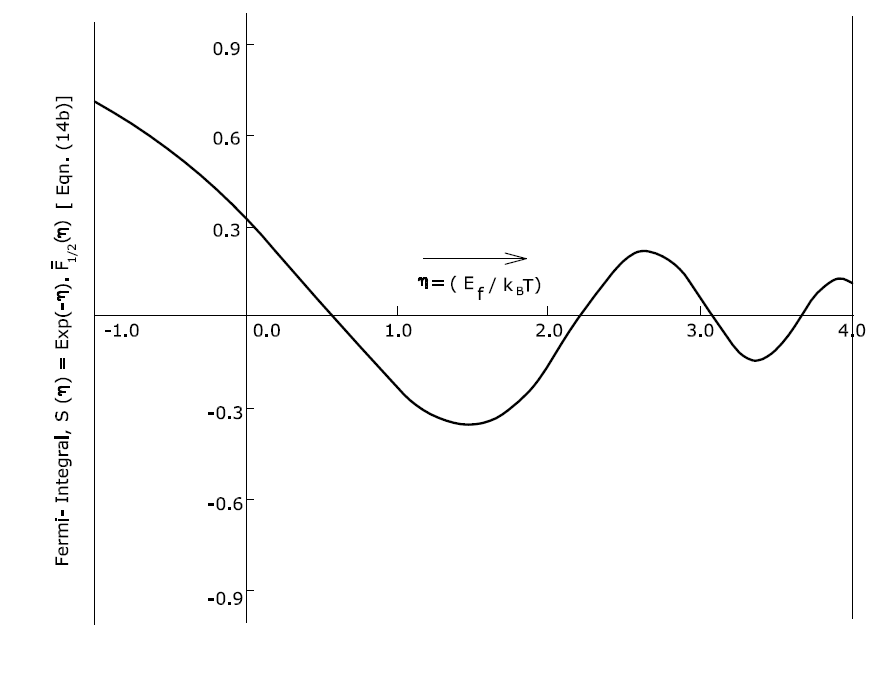 | Figure 1. Variations of the Fermi-Integral and DOS function, 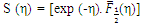 (Eq.14b) for non-degenerately doped semiconductor as a function of reduced Fermi energy (Eq.14b) for non-degenerately doped semiconductor as a function of reduced Fermi energy 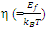 using the data of Table 1 using the data of Table 1 |
 | Figure 2. Comparison of room temperature (300K) DMR values obtained from the present exact calculation (Eq.15) and that obtained from the previous numerical calculation by Blackmore [2] (dotted curve) |
Figure 2 shows the variation of DMR with η (Eq. 15). The DMR values showing both positive and negative values (Figure 2) appearing due to the oscillations in FIs (Figure 1). This results contradicts the theoretical result obtained by Roichman and Tessler using the Monte Carlo simulation technique to calculate the inverse DMR which also did not exhibit oscillatory behavior [10] indicating that their calculations were also not exact where DMR showed only positive ones. This controversy arises due to the drawback of the previous approximate numerical calculations showing no oscillatory behavior of the FI. The present approach of exact calculation of FIs for the non-degenerately doped semiconductor is the most appropriate one as compared to the previous approximate ones [1-6, 10, 12]. Using the present exact theoretical model, new results, like DMR, are also expected from the calculations of all other physical parameters related to the Fermi energy.
4. Conclusions
We have, for the first time, made an exact quantum mechanical calculation for the FI for the non-degenerately doped impurities in parabolic band semiconductors and the results are compared with those of previous approximate calculations. Present calculation is superior compared to be the existing asymptotic expansions of the same FI generating new result as shown in the case of DMR. This is because of the presence of higher order terms of exp (η) in the present derived expression Eq. (14). Such exact analysis provided FI as a real function. A comparison of the FI of Half-integer order estimated from the previous classical calculation and those of on present quantum mechanical calculation have also been shown which might be useful for further studies of different physical parameters. As the FI is involved with DOS and Fermi-Dirac functions, the present new theoretical results would provide more accurate explanations of quantum transport phenomena in semiconductors along with new applications in magnetic susceptibility, magnetoresistance and specific heat at low temperature.
ACKNOWLEDGEMENTS
The authors are grateful to the Indian Association for the Cultivation of Science, Kolkata, for providing library and computer facilities. The authors are also thankful to Mr. Gopal Manna, IACS for his help in drawing the figures used in the manuscript.
References
| [1] | McDougall, J., Stoner, E.C., 1938, Roy, Soc. Philos. Trans. 237A, 67. |
| [2] | Blackmore, J.S., 1962, Semiconductor statistics, Pergamum Press, (London). |
| [3] | Seeger, K, 1973, Semiconductor Physics-An introduction 3rd Ed. (Springer Series in Solid State Physics Science, 40. |
| [4] | Nag, B.R., 1980, Electron Transport in Compound Semiconductor, (Springer Series in Solid State Sci.) 11, 74. |
| [5] | Kim, R., Lundstrom, M., 2011, Notes of Fermi-Dirac Integral, 3rd Ed., (Network for Computational Nanotechnology, Purdue Univ. 4, 1. |
| [6] | Natarajan, A., Mohan Kumar, N., 2001, Comput. Phys. Commun. 137, 361. |
| [7] | Gradshteyn, I.S., Ryzhik, I.M., 1980, Table of Integrals, Series and Products, Ed., Alan Jeffrey, 5th Edition, (Academic press), 371. |
| [8] | Abramowitz, M., Stegun, I.A., 1972, Handbook of Mathematical Functions, (Dover Publications, Inc., New York), 504. |
| [9] | Roichman, Y., Tessler, N., 2002, Appl. Phys. Lett. 80, 1948. |
| [10] | Roichman, Y., Tessler, N., 2001 Proc. Mater. Research Soc Symposium, San Francisco, 1-12. |
| [11] | Abd Elhamid, H., Ismail, Y., Deen, M. J. 2013, Opt. Quant. Electron, 45,885. |
| [12] | Garoni, T.M., Frankel, N.E., Glasser, M.L., 2001, J. Math. Phys., 42, 860. |



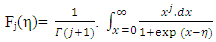
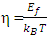 with
with 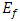 being the Fermi-energy. For the DOS function of a parabolic band, the value of j is ½. Accordingly, the corresponding FI,
being the Fermi-energy. For the DOS function of a parabolic band, the value of j is ½. Accordingly, the corresponding FI, 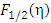 can be represented (using Eq(1) of [1-4]) in the form
can be represented (using Eq(1) of [1-4]) in the form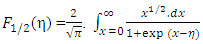
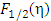 was evaluated numerically [1-6] for all practical purposes and the corresponding numerical values were found to be comprised of only positive real values of the integrands. The numerical values are also available in a tabular form [1, 2] for both positive and negative values of η. However, as the numerical integration is an approximate method, one cannot accurately find the exact values of reduced energy parameter,
was evaluated numerically [1-6] for all practical purposes and the corresponding numerical values were found to be comprised of only positive real values of the integrands. The numerical values are also available in a tabular form [1, 2] for both positive and negative values of η. However, as the numerical integration is an approximate method, one cannot accurately find the exact values of reduced energy parameter, 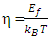 related to many physical parameters of metals and semiconductors. Therefore, an exact solution of Eqs (1) and (2) are demanding to demonstrate the new electronic properties like Fermi-energy which in turn associated with the transport phenomena in doped semiconductors [6] as well as in nano-technology devices [5].Therefore, an attempt has been made for an exact quantum mechanical calculation of the FIs
related to many physical parameters of metals and semiconductors. Therefore, an exact solution of Eqs (1) and (2) are demanding to demonstrate the new electronic properties like Fermi-energy which in turn associated with the transport phenomena in doped semiconductors [6] as well as in nano-technology devices [5].Therefore, an attempt has been made for an exact quantum mechanical calculation of the FIs 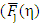 and
and 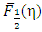 applying a correct integration methods. Such calculations might reveal some interesting properties of
applying a correct integration methods. Such calculations might reveal some interesting properties of 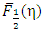 which could not be visualized from the earlier numerical method of calculations discussed in this paper.
which could not be visualized from the earlier numerical method of calculations discussed in this paper. 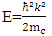
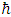 is the reduced Planck’s constant,
is the reduced Planck’s constant, 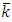 is the wave vector, mc is the un-perturbed conduction band edge effective electrons mass and E is the electron energy. The normal DOS function, N (E), can be written as
is the wave vector, mc is the un-perturbed conduction band edge effective electrons mass and E is the electron energy. The normal DOS function, N (E), can be written as 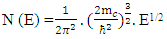
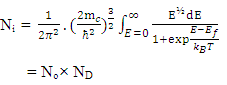
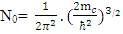 in Eq.5and
in Eq.5and 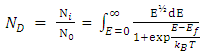
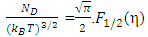
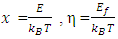 and
and 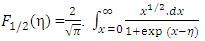
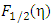 can now be provided. We represent the exact solutions of Eq.(1) and Eq.(8) by
can now be provided. We represent the exact solutions of Eq.(1) and Eq.(8) by 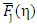 and
and 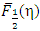 , respectively. Performing some algebraic manipulations to the integrands in Eq.(1), an exactly form
, respectively. Performing some algebraic manipulations to the integrands in Eq.(1), an exactly form 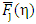 comes out to be
comes out to be 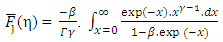
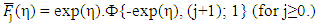
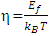 and j, one can find the values of Ф (a,b; z) from the Table in [8]. However, for simple calculations for
and j, one can find the values of Ф (a,b; z) from the Table in [8]. However, for simple calculations for 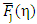 , one can also use the series expansion of Ф (a,b; z) [7, 8]. For the series expansion of Ф (a,b; z) , one can use the following relation [8]
, one can also use the series expansion of Ф (a,b; z) [7, 8]. For the series expansion of Ф (a,b; z) , one can use the following relation [8]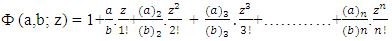
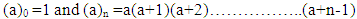
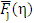 comes out to be
comes out to be 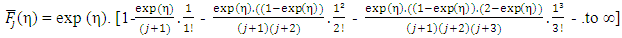
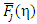 for any values of j and η. Thus, one can find the value of
for any values of j and η. Thus, one can find the value of 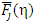 more accurately and conveniently than the conventional numerical approaches for Fj (η) put forwarded earlier [1, 2]. For j=1/2, as a special case to the Fermi-integral,
more accurately and conveniently than the conventional numerical approaches for Fj (η) put forwarded earlier [1, 2]. For j=1/2, as a special case to the Fermi-integral, 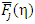 , the series representation of the same can be given from Eq.(13) as
, the series representation of the same can be given from Eq.(13) as 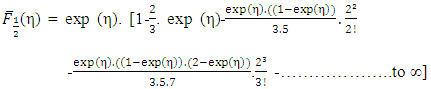
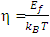 , we can compute
, we can compute 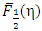 from Eq.(14).
from Eq.(14). 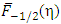 can also be easily computed from Eq.(13) with j=-1/2.From Eq (14a) we find the exact form of the DOS, S(η), as a function of reduced Fermi energy η as
can also be easily computed from Eq.(13) with j=-1/2.From Eq (14a) we find the exact form of the DOS, S(η), as a function of reduced Fermi energy η as 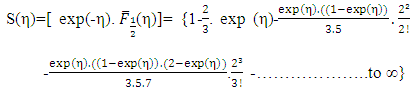
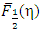 could be plotted as a function of η, for both positive and negative values which have been discussed below.
could be plotted as a function of η, for both positive and negative values which have been discussed below. 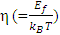 in the case of non-degenerately doped semiconductor. The values of FIs of half-integer order estimated by earlier classical calculation [1, 2] and those obtained from the present exact calculation are shown in Table 1 for comparison. The exact values of the function
in the case of non-degenerately doped semiconductor. The values of FIs of half-integer order estimated by earlier classical calculation [1, 2] and those obtained from the present exact calculation are shown in Table 1 for comparison. The exact values of the function 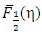 calculated from the present series expansions of Eq. (14) is plotted in Figure 1. It is seen from the figure that the results of our present exact calculations for FI exhibits oscillations only for the positive values of η. On the other hand, for the negative values of η, no oscillation is exhibited. Earlier approximate numerical calculations of FI [1-6] did not, however, show any such oscillations. The nature of the said oscillations is not periodic like sinusoidal functions. That is, all the positive crest and the negative trough amplitudes are not uniform, rather successive amplitudes of the peaks and those of the valleys are decreasing in their magnitudes. Moreover, the distances (representing period of oscillation) between two successive peaks and valleys gradually decrease.An attempt has been made to calculate the diffusivity-mobility ratio (DMR) also known as Einstein relation [4]. The DMR for various semiconductor device performances [9-11] calculated from the conventional approach for FIs (i.e., the numerical integrations) comes out to be always positive (dotted line in Figure 2). Using the present exact calculations of the Fermi-Integrals
calculated from the present series expansions of Eq. (14) is plotted in Figure 1. It is seen from the figure that the results of our present exact calculations for FI exhibits oscillations only for the positive values of η. On the other hand, for the negative values of η, no oscillation is exhibited. Earlier approximate numerical calculations of FI [1-6] did not, however, show any such oscillations. The nature of the said oscillations is not periodic like sinusoidal functions. That is, all the positive crest and the negative trough amplitudes are not uniform, rather successive amplitudes of the peaks and those of the valleys are decreasing in their magnitudes. Moreover, the distances (representing period of oscillation) between two successive peaks and valleys gradually decrease.An attempt has been made to calculate the diffusivity-mobility ratio (DMR) also known as Einstein relation [4]. The DMR for various semiconductor device performances [9-11] calculated from the conventional approach for FIs (i.e., the numerical integrations) comes out to be always positive (dotted line in Figure 2). Using the present exact calculations of the Fermi-Integrals 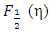 and
and 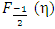 , DMR can be defined as
, DMR can be defined as 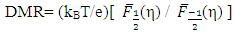

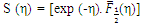 (Eq.14b) for non-degenerately doped semiconductor as a function of reduced Fermi energy
(Eq.14b) for non-degenerately doped semiconductor as a function of reduced Fermi energy 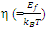 using the data of Table 1
using the data of Table 1 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
