Franck Delplace
ESI Group Scientific Committee, 100 Av. De Suffren, Paris, France
Correspondence to: Franck Delplace, ESI Group Scientific Committee, 100 Av. De Suffren, Paris, France.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we considered the laminar fully developed flow, of a Newtonian fluid, in ducts of rectangular cross-section. Poisson’s partial differential equation Saint-Venant solution was used, to calculate Poiseuille number values whatever is rectangles aspect ratio. From these results, we considered limit cases of square duct and plane Poiseuille flow (infinite parallel plates). We showed there exists a rectangle equivalent to a circular cross-section for energy dissipation through viscous friction. Finally, we gave some mathematical consequences of this approach for odd integers zeta function calculations and Catalan’s constant.
Keywords:
Rectangular ducts, Poisson’s equation, Saint-Venant solution, Viscous friction, Zeta function, Catalan’s constant
Cite this paper: Franck Delplace, Laminar Flow of Newtonian Liquids in Ducts of Rectangular Cross-Section an Interesting Model for Both Physics and Mathematics, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 2, 2018, pp. 52-55. doi: 10.5923/j.ijtmp.20180802.04.
1. Introduction
Pipes used in most applications always have a circular cross-section. That is why Poiseuille law/equation is used to calculate the pressure drop produced by a liquid flowing in a pipe in the laminar flow regime. Poiseuille famous equation tells us that pressure drop is proportional to liquid flow-rate 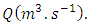 In Engineering, this relationship is expressed using dimensionless numbers: The Fanning friction factor
In Engineering, this relationship is expressed using dimensionless numbers: The Fanning friction factor 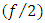 and the Reynolds number
and the Reynolds number 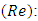
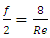 | (1) |
With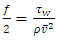 | (2) |
And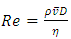 | (3) |
In equation (2), 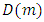 is the pipe diameter,
is the pipe diameter, 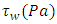 is the wall shear stress due to liquid friction on pipe wall. In the case of the perfectly symmetric circular cross-section, its value is identical whatever is the position along the perimeter giving the local value
is the wall shear stress due to liquid friction on pipe wall. In the case of the perfectly symmetric circular cross-section, its value is identical whatever is the position along the perimeter giving the local value 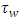 equal to the mean value
equal to the mean value 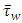 .
. 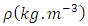 is the liquid density and
is the liquid density and 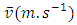 its mean velocity calculated from the flow-rate
its mean velocity calculated from the flow-rate 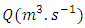 measurement using
measurement using 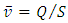 where
where 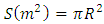 is the cross-section area. From a balance between pressure drop
is the cross-section area. From a balance between pressure drop 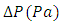 and viscous friction on pipe wall, it is possible to obtain a simple relationship between
and viscous friction on pipe wall, it is possible to obtain a simple relationship between 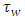 and
and 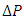 :
: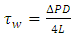 | (4) |
In this equation, 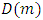 is the pipe diameter and
is the pipe diameter and 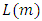 is the pipe length where pressure drop
is the pipe length where pressure drop 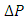 is measured by use of a pressure sensor. The last parameter involved in equation (3) is well-known Newtonian liquid dynamic viscosity
is measured by use of a pressure sensor. The last parameter involved in equation (3) is well-known Newtonian liquid dynamic viscosity 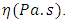 Finally, in equation (2), terms
Finally, in equation (2), terms 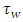 and
and 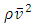 are both energy concentrations, respectively energy dissipated by viscous friction and kinetic energy introduced in the liquid by the pumping system. From these considerations, dimensionless number
are both energy concentrations, respectively energy dissipated by viscous friction and kinetic energy introduced in the liquid by the pumping system. From these considerations, dimensionless number 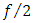 represents the percentage of energy concentration dissipated by the liquid at pipe wall. Of course, this mechanical energy is converted into heat.From equation (1), we can form the product:
represents the percentage of energy concentration dissipated by the liquid at pipe wall. Of course, this mechanical energy is converted into heat.From equation (1), we can form the product: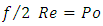 | (5) |
The new dimensionless quantity 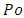 is called Poiseuille number in honour of important Poiseuille work on liquids laminar flow. In the simple case of pipe flow, we have
is called Poiseuille number in honour of important Poiseuille work on liquids laminar flow. In the simple case of pipe flow, we have 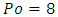 (you sometimes find
(you sometimes find 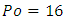 or
or 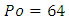 depending on how you define Fanning friction factor).Now, the question is what is the situation when a duct has a non-circular cross-section?As reported in famous Shah & London [1] source book entitled “Laminar forced convection in ducts”, and experimentally or numerically verified by numerous authors [2], we generally have
depending on how you define Fanning friction factor).Now, the question is what is the situation when a duct has a non-circular cross-section?As reported in famous Shah & London [1] source book entitled “Laminar forced convection in ducts”, and experimentally or numerically verified by numerous authors [2], we generally have 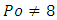 (we will explain why we say generally in the following of this paper).An interesting and important geometry to investigate is rectangular ducts, from square cross-section exhibiting high symmetry properties (regular compact convex shape) to all rectangles of aspect ratio we called
(we will explain why we say generally in the following of this paper).An interesting and important geometry to investigate is rectangular ducts, from square cross-section exhibiting high symmetry properties (regular compact convex shape) to all rectangles of aspect ratio we called 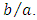 In fluid mechanics, we consider a limit case for rectangular geometries: the often called “Plane Poiseuille flow” corresponds to a rectangle such as
In fluid mechanics, we consider a limit case for rectangular geometries: the often called “Plane Poiseuille flow” corresponds to a rectangle such as 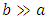 giving
giving 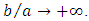 This ideal type of flow is highly symmetric like the flow in a pipe because small side length has no influence on the velocity field which remains the same along large side length. The following figure 1 illustrates rectangular geometries considered in fluid mechanics.
This ideal type of flow is highly symmetric like the flow in a pipe because small side length has no influence on the velocity field which remains the same along large side length. The following figure 1 illustrates rectangular geometries considered in fluid mechanics.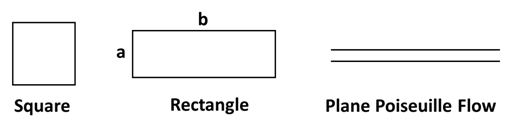 | Figure 1. Rectangular cross-sections considered in fluid mechanics. |
It is well-known that ideal plane Poiseuille flow gives a theoretical value 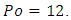 Moreover, as recently showed by Delplace [2],
Moreover, as recently showed by Delplace [2], 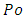 values could explain critical Reynolds number values for the change in the flow regime from laminar to transition and turbulent.The objective of this paper is then to recall how
values could explain critical Reynolds number values for the change in the flow regime from laminar to transition and turbulent.The objective of this paper is then to recall how 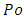 values are obtained from Poisson partial differential equation (PDE) and also to try to explain why these results could be very important in both Physics and Mathematics.
values are obtained from Poisson partial differential equation (PDE) and also to try to explain why these results could be very important in both Physics and Mathematics.
2. Theory of Laminar Flow in Rectangular Ducts
Considering cartesian coordinates 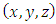 with origin at the centre of the duct of rectangular cross-section, the fully established laminar flow of a Newtonian liquid is described by the following well-known Poisson equation:
with origin at the centre of the duct of rectangular cross-section, the fully established laminar flow of a Newtonian liquid is described by the following well-known Poisson equation: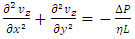 | (6) |
Solutions of this PDE depends on the boundary conditions (Dirichlet problem) and the general case of rectangles with aspect ratio 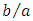 can be solved by use of Saint-Venant method [3] giving the velocity field:
can be solved by use of Saint-Venant method [3] giving the velocity field: 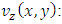
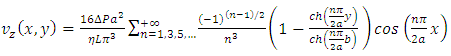 | (7) |
This equation allows components of wall shear-rate: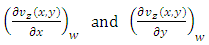 | (8) |
To be calculated and then components of wall shear stress 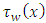 and
and 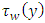 by use of the rheological equation of state:
by use of the rheological equation of state: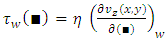 | (9) |
The average wall shear stress can then be calculated using classical integral mean value: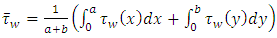 | (10) |
We can also calculate from equation (7) the velocity mean value: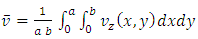 | (11) |
To finally obtain: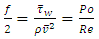 | (12) |
Which is the analogous of relation (1) for the case of rectangular ducts. From knowledge of 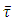 and
and 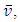 we obtain:
we obtain: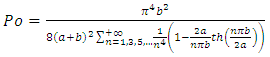 | (13) |
It is now interesting to evaluate this last result for different aspect ratios 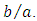 The first elementary case is of course the square cross-section giving
The first elementary case is of course the square cross-section giving 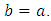 Equation (13) reduces to:
Equation (13) reduces to: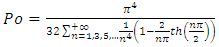 | (14) |
Considering now, the well-known mathematical result coming from Euler-Riemann zeta function knowledge: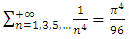 | (15) |
We obtain: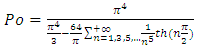 | (16) |
The series in equation (16) can easily be evaluated numerically giving: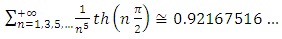 | (17) |
Finally, we obtain the 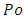 value for a duct of square cross-section shape:
value for a duct of square cross-section shape: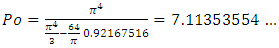 | (18) |
This purely theoretical result is in perfect agreement with experimental results obtained by many authors [2] and of course with the value reported in Shah & London [1] source book.Let us now consider the other limit case described above i.e. the plane Poiseuille flow obtained for infinite parallel plates. As previously reported, this highly symmetric case gives a well-known value of Poiseuille number: 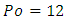 .If we consider
.If we consider 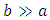 in equation (13), we obtain:
in equation (13), we obtain: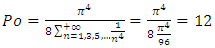 | (19) |
Remarkably, this result is in perfect agreement with both experimental and theoretical results reported above. Moreover, it shows that Saint-Venant solution of Poisson PDE, established for elasticity theory [3], is of great importance for the study of laminar flow in rectangular ducts. Equation (13) established for aspect ratios 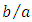 varying in the range 1 (square) to
varying in the range 1 (square) to 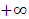 (infinite parallel plates) is then of major interest for all these geometrical shapes.We know from experiments that for these shapes, we have
(infinite parallel plates) is then of major interest for all these geometrical shapes.We know from experiments that for these shapes, we have 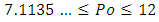 and this result is in perfect agreement with equation (13). We can then write the following theorem:Theorem 1: For
and this result is in perfect agreement with equation (13). We can then write the following theorem:Theorem 1: For 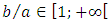 we have, according to equation (12):
we have, according to equation (12): 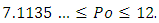 This fundamental result clearly demonstrates that every value of Poiseuille number are possible between 7.1135… and 12. Particularly, it exists an aspect ratio
This fundamental result clearly demonstrates that every value of Poiseuille number are possible between 7.1135… and 12. Particularly, it exists an aspect ratio 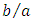 which gives
which gives 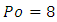 like in pipes i.e. for a circular cross-section shape. Numerical calculations performed with equation (13) gave:
like in pipes i.e. for a circular cross-section shape. Numerical calculations performed with equation (13) gave: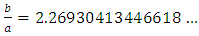 | (20) |
This result signifies that, in fluid mechanics, it exists a rectangle having the same property than a circle for mechanical energy dissipation through viscous friction and this rectangular duct has an aspect ratio 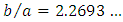
3. Discussion on Mathematical Consequences
Of course, these results give an equivalence between rectangular and circular geometries in terms of energy dissipation and we can write the following theorem:Theorem 2: Considering energy dissipation by viscous friction during the fully established laminar flow of a Newtonian fluid, the equivalent geometry for a pipe of circular cross-section is a rectangular duct having an aspect ratio 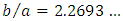 .This result could be extended to others geometries like triangles. We know that for an equilateral triangle,
.This result could be extended to others geometries like triangles. We know that for an equilateral triangle, 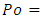
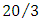 and stretching of this triangle giving isosceles triangles increases
and stretching of this triangle giving isosceles triangles increases 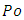 values until it also reaches
values until it also reaches 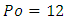 for an infinite triangle comparable to infinite parallel plates [2]. In that sense, there also exists a triangle for which
for an infinite triangle comparable to infinite parallel plates [2]. In that sense, there also exists a triangle for which 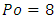 meaning a triangle equivalent to a circle. We can then propose the following conjecture:Conjecture 1: For any compact convex shape, there exists a non-regular geometry giving
meaning a triangle equivalent to a circle. We can then propose the following conjecture:Conjecture 1: For any compact convex shape, there exists a non-regular geometry giving 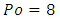 and then giving an equivalence with circular geometry in terms of mechanical energy degradation by viscous friction.If this conjecture was true, signification of Poiseuille number values could be very important in Physics and Mathematics. Considering well-known membrane deformation problem giving Poisson’s PDE, equation (6) is clearly its analogous for the laminar flow of a Newtonian liquid in a duct of arbitrary cross-section shape. The Saint-Venant solution given by equation (7) gives the velocity field shape which depends on the boundary conditions i.e. the shape of the duct cross-section perimeter. In the case of a pipe with circular cross-section, the high symmetry allows simple calculations and velocity field has a parabolic shape according to Poiseuille law. But for polygonal geometries like rectangles or triangles, shape is much more complicated. But, at the end, calculation of
and then giving an equivalence with circular geometry in terms of mechanical energy degradation by viscous friction.If this conjecture was true, signification of Poiseuille number values could be very important in Physics and Mathematics. Considering well-known membrane deformation problem giving Poisson’s PDE, equation (6) is clearly its analogous for the laminar flow of a Newtonian liquid in a duct of arbitrary cross-section shape. The Saint-Venant solution given by equation (7) gives the velocity field shape which depends on the boundary conditions i.e. the shape of the duct cross-section perimeter. In the case of a pipe with circular cross-section, the high symmetry allows simple calculations and velocity field has a parabolic shape according to Poiseuille law. But for polygonal geometries like rectangles or triangles, shape is much more complicated. But, at the end, calculation of 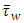 and
and 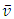 allows a simple dimensionless equation of the same form (equation (12)) to be obtained and this equation involves
allows a simple dimensionless equation of the same form (equation (12)) to be obtained and this equation involves 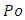 numbers varying in the range 20/3 to 12.Another consequence of the rectangular approach is the close relation between
numbers varying in the range 20/3 to 12.Another consequence of the rectangular approach is the close relation between 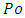 numbers and the Euler-Riemann zeta function. The problem of
numbers and the Euler-Riemann zeta function. The problem of 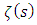 values for odd integer remains unsolved because at this time, we have no idea of a closed form for
values for odd integer remains unsolved because at this time, we have no idea of a closed form for 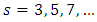 [4] Equation (13) gives interesting properties which could help approaching a closed form for
[4] Equation (13) gives interesting properties which could help approaching a closed form for 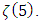 By considering well-known properties of hyperbolic tangent function
By considering well-known properties of hyperbolic tangent function 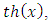 this function reaches very rapidly asymptotic value of 1 when
this function reaches very rapidly asymptotic value of 1 when 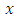 reach sufficiently large values (greater than 10). We can then consider that for sufficiently high values of ratio
reach sufficiently large values (greater than 10). We can then consider that for sufficiently high values of ratio 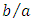 in equation (13), the quantity
in equation (13), the quantity 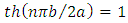 giving the following relationship for the sum over odd integers of
giving the following relationship for the sum over odd integers of 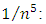
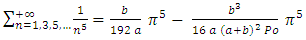 | (21) |
Of course, 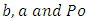 values are linked together (for example you have
values are linked together (for example you have 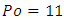 for
for 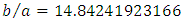 ) but equation (21) is surely an interesting result for understanding of
) but equation (21) is surely an interesting result for understanding of 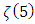 behaviour even if the sum only concerns odd values of
behaviour even if the sum only concerns odd values of 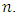 Complex calculations in rectangular ducts also give others surprising and interesting results in numbers theory. For example, it is possible to calculate the wall shear stress along the side length
Complex calculations in rectangular ducts also give others surprising and interesting results in numbers theory. For example, it is possible to calculate the wall shear stress along the side length 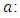
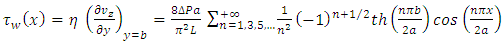 | (22) |
The maximum value of 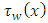 is obtained for
is obtained for 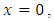 giving:
giving: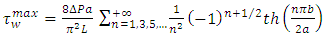 | (23) |
If we consider the limit case of infinite parallel plates giving 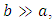 we obtain:
we obtain: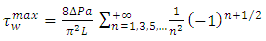 | (24) |
The series can be written as followed: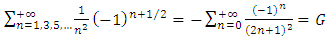 | (25) |
Where 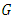 is the well-known Catalan’s constant. Until now, we ignore if this number is irrational even if it is conjectured. What we obtained from equation (24) gives interesting information about this number. Moreover, if we calculate the mean value of wall shear-stress along the same side, we obtain:
is the well-known Catalan’s constant. Until now, we ignore if this number is irrational even if it is conjectured. What we obtained from equation (24) gives interesting information about this number. Moreover, if we calculate the mean value of wall shear-stress along the same side, we obtain: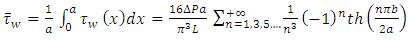 | (26) |
Considering now 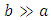 gives:
gives: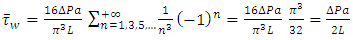 | (27) |
Reporting this result in equation (24) gives: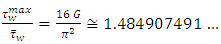 | (28) |
This result clearly shows that Catalan’s constant is proportional to 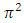 which is an irrational number and then it could be considered as a proof of Catalan’s constant irrationality.We can then write the following theorem:Theorem 3: Catalan’s constant is proportional to
which is an irrational number and then it could be considered as a proof of Catalan’s constant irrationality.We can then write the following theorem:Theorem 3: Catalan’s constant is proportional to 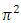 and then is an irrational number.Finally, it is also possible to calculate the ratio
and then is an irrational number.Finally, it is also possible to calculate the ratio 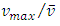 of the maximum velocity at the centre of the rectangular duct and the average velocity. For maximum velocity, we obtain:
of the maximum velocity at the centre of the rectangular duct and the average velocity. For maximum velocity, we obtain: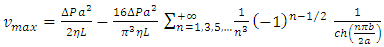 | (29) |
For mean velocity, we obtain from equation (11) and Fubini theorem: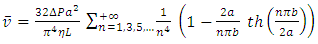 | (30) |
Giving,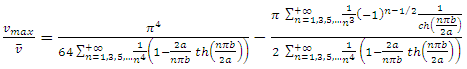 | (31) |
It is then easy to consider the limit case of infinite parallel plates by taking 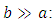
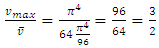 | (32) |
Remarkably, this last result is well-known in fluid mechanics for the case of infinite parallel plates. For pipes of circular cross-section, we have: 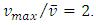 Equation (31) allows this ratio to be calculated whatever is the rectangle aspect ratio
Equation (31) allows this ratio to be calculated whatever is the rectangle aspect ratio 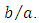
4. Conclusions
In this paper, we deeply investigated the Poisson’s PDE describing the fully established laminar flow of a Newtonian fluid in a duct of rectangular cross-section. We used the Saint-Venant solution, established for torsion of prismatical bars to obtain the velocity field whatever is the rectangle aspect ratio 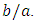 From this equation, we showed how Poiseuille number values can be calculated giving a simple theorem for evolution of
From this equation, we showed how Poiseuille number values can be calculated giving a simple theorem for evolution of 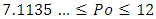 when
when 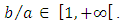 This result allowed the rectangle, giving the same value than the circular cross-section, to be defined with an aspect ratio
This result allowed the rectangle, giving the same value than the circular cross-section, to be defined with an aspect ratio 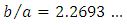 We tried to give some mathematical consequences of this approach. Among them, we conjecture that for any convex shape of non-circular cross-section, there always exists one having a Poiseuille number value equal to the circle value i.e.
We tried to give some mathematical consequences of this approach. Among them, we conjecture that for any convex shape of non-circular cross-section, there always exists one having a Poiseuille number value equal to the circle value i.e. 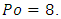 We also showed, from Poiseuille number equation for rectangular ducts, that Euler-Riemann zeta function
We also showed, from Poiseuille number equation for rectangular ducts, that Euler-Riemann zeta function 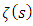 for odd integer
for odd integer 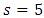 , for summation over odd integers
, for summation over odd integers 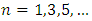 can be calculated as proportional to
can be calculated as proportional to 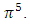 From calculation of both, maximum wall shear stress, and average wall shear stress, we showed that famous Catalan’s constant
From calculation of both, maximum wall shear stress, and average wall shear stress, we showed that famous Catalan’s constant 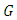 is proportional to
is proportional to 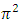 which could be a proof of its irrationality.Finally, by integrating the velocity field, we found an expression for the ratio
which could be a proof of its irrationality.Finally, by integrating the velocity field, we found an expression for the ratio 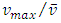 which gave, for the limit case of plane Poiseuille flow, a value of
which gave, for the limit case of plane Poiseuille flow, a value of 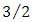 in perfect agreement with fluid mechanics results.
in perfect agreement with fluid mechanics results.
References
| [1] | Shah RK & London AL, 1978, Laminar flow forced convection in ducts. Academic Press. New York, San Francisco, London. |
| [2] | Delplace F, 2018, Fluids flow stability in ducts of arbitrary cross-section. J Mod Appl Physics, vol 2, No 2, p 10-15. |
| [3] | Timoshenko SP & Goodier JN, 1970, Theory of elasticity 3rd Ed. Mc Graw-Hill, New York. |
| [4] | Srivastava HM & Tsumura H, 2000, A certain class of rapidly convergent series representations for 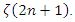 J Comput Appl Math, vol 118, p 323-335. J Comput Appl Math, vol 118, p 323-335. |



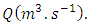 In Engineering, this relationship is expressed using dimensionless numbers: The Fanning friction factor
In Engineering, this relationship is expressed using dimensionless numbers: The Fanning friction factor 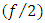 and the Reynolds number
and the Reynolds number 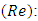
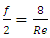
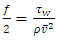
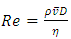
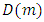 is the pipe diameter,
is the pipe diameter, 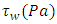 is the wall shear stress due to liquid friction on pipe wall. In the case of the perfectly symmetric circular cross-section, its value is identical whatever is the position along the perimeter giving the local value
is the wall shear stress due to liquid friction on pipe wall. In the case of the perfectly symmetric circular cross-section, its value is identical whatever is the position along the perimeter giving the local value 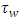 equal to the mean value
equal to the mean value 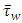 .
. 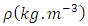 is the liquid density and
is the liquid density and 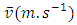 its mean velocity calculated from the flow-rate
its mean velocity calculated from the flow-rate 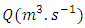 measurement using
measurement using 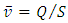 where
where 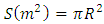 is the cross-section area. From a balance between pressure drop
is the cross-section area. From a balance between pressure drop 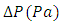 and viscous friction on pipe wall, it is possible to obtain a simple relationship between
and viscous friction on pipe wall, it is possible to obtain a simple relationship between 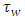 and
and 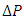 :
: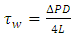
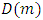 is the pipe diameter and
is the pipe diameter and 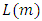 is the pipe length where pressure drop
is the pipe length where pressure drop 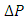 is measured by use of a pressure sensor. The last parameter involved in equation (3) is well-known Newtonian liquid dynamic viscosity
is measured by use of a pressure sensor. The last parameter involved in equation (3) is well-known Newtonian liquid dynamic viscosity 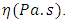 Finally, in equation (2), terms
Finally, in equation (2), terms 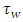 and
and 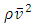 are both energy concentrations, respectively energy dissipated by viscous friction and kinetic energy introduced in the liquid by the pumping system. From these considerations, dimensionless number
are both energy concentrations, respectively energy dissipated by viscous friction and kinetic energy introduced in the liquid by the pumping system. From these considerations, dimensionless number 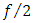 represents the percentage of energy concentration dissipated by the liquid at pipe wall. Of course, this mechanical energy is converted into heat.From equation (1), we can form the product:
represents the percentage of energy concentration dissipated by the liquid at pipe wall. Of course, this mechanical energy is converted into heat.From equation (1), we can form the product: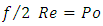
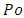 is called Poiseuille number in honour of important Poiseuille work on liquids laminar flow. In the simple case of pipe flow, we have
is called Poiseuille number in honour of important Poiseuille work on liquids laminar flow. In the simple case of pipe flow, we have 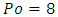 (you sometimes find
(you sometimes find 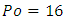 or
or 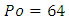 depending on how you define Fanning friction factor).Now, the question is what is the situation when a duct has a non-circular cross-section?As reported in famous Shah & London [1] source book entitled “Laminar forced convection in ducts”, and experimentally or numerically verified by numerous authors [2], we generally have
depending on how you define Fanning friction factor).Now, the question is what is the situation when a duct has a non-circular cross-section?As reported in famous Shah & London [1] source book entitled “Laminar forced convection in ducts”, and experimentally or numerically verified by numerous authors [2], we generally have 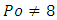 (we will explain why we say generally in the following of this paper).An interesting and important geometry to investigate is rectangular ducts, from square cross-section exhibiting high symmetry properties (regular compact convex shape) to all rectangles of aspect ratio we called
(we will explain why we say generally in the following of this paper).An interesting and important geometry to investigate is rectangular ducts, from square cross-section exhibiting high symmetry properties (regular compact convex shape) to all rectangles of aspect ratio we called 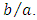 In fluid mechanics, we consider a limit case for rectangular geometries: the often called “Plane Poiseuille flow” corresponds to a rectangle such as
In fluid mechanics, we consider a limit case for rectangular geometries: the often called “Plane Poiseuille flow” corresponds to a rectangle such as 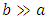 giving
giving 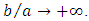 This ideal type of flow is highly symmetric like the flow in a pipe because small side length has no influence on the velocity field which remains the same along large side length. The following figure 1 illustrates rectangular geometries considered in fluid mechanics.
This ideal type of flow is highly symmetric like the flow in a pipe because small side length has no influence on the velocity field which remains the same along large side length. The following figure 1 illustrates rectangular geometries considered in fluid mechanics.
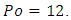 Moreover, as recently showed by Delplace [2],
Moreover, as recently showed by Delplace [2], 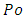 values could explain critical Reynolds number values for the change in the flow regime from laminar to transition and turbulent.The objective of this paper is then to recall how
values could explain critical Reynolds number values for the change in the flow regime from laminar to transition and turbulent.The objective of this paper is then to recall how 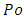 values are obtained from Poisson partial differential equation (PDE) and also to try to explain why these results could be very important in both Physics and Mathematics.
values are obtained from Poisson partial differential equation (PDE) and also to try to explain why these results could be very important in both Physics and Mathematics.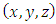 with origin at the centre of the duct of rectangular cross-section, the fully established laminar flow of a Newtonian liquid is described by the following well-known Poisson equation:
with origin at the centre of the duct of rectangular cross-section, the fully established laminar flow of a Newtonian liquid is described by the following well-known Poisson equation: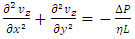
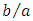 can be solved by use of Saint-Venant method [3] giving the velocity field:
can be solved by use of Saint-Venant method [3] giving the velocity field: 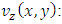
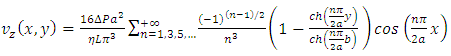
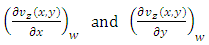
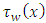 and
and 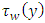 by use of the rheological equation of state:
by use of the rheological equation of state: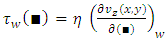
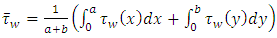
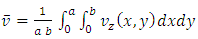
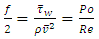
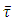 and
and 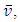 we obtain:
we obtain: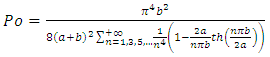
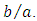 The first elementary case is of course the square cross-section giving
The first elementary case is of course the square cross-section giving 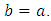 Equation (13) reduces to:
Equation (13) reduces to: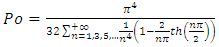
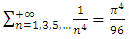
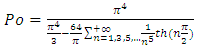
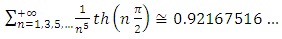
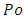 value for a duct of square cross-section shape:
value for a duct of square cross-section shape: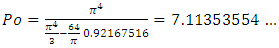
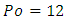 .If we consider
.If we consider 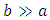 in equation (13), we obtain:
in equation (13), we obtain: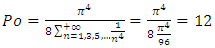
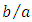 varying in the range 1 (square) to
varying in the range 1 (square) to 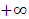 (infinite parallel plates) is then of major interest for all these geometrical shapes.We know from experiments that for these shapes, we have
(infinite parallel plates) is then of major interest for all these geometrical shapes.We know from experiments that for these shapes, we have 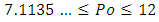 and this result is in perfect agreement with equation (13). We can then write the following theorem:Theorem 1: For
and this result is in perfect agreement with equation (13). We can then write the following theorem:Theorem 1: For 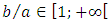 we have, according to equation (12):
we have, according to equation (12): 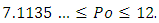 This fundamental result clearly demonstrates that every value of Poiseuille number are possible between 7.1135… and 12. Particularly, it exists an aspect ratio
This fundamental result clearly demonstrates that every value of Poiseuille number are possible between 7.1135… and 12. Particularly, it exists an aspect ratio 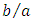 which gives
which gives 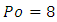 like in pipes i.e. for a circular cross-section shape. Numerical calculations performed with equation (13) gave:
like in pipes i.e. for a circular cross-section shape. Numerical calculations performed with equation (13) gave: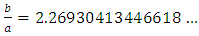
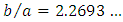
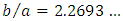 .This result could be extended to others geometries like triangles. We know that for an equilateral triangle,
.This result could be extended to others geometries like triangles. We know that for an equilateral triangle, 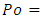
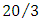 and stretching of this triangle giving isosceles triangles increases
and stretching of this triangle giving isosceles triangles increases 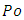 values until it also reaches
values until it also reaches 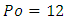 for an infinite triangle comparable to infinite parallel plates [2]. In that sense, there also exists a triangle for which
for an infinite triangle comparable to infinite parallel plates [2]. In that sense, there also exists a triangle for which 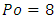 meaning a triangle equivalent to a circle. We can then propose the following conjecture:Conjecture 1: For any compact convex shape, there exists a non-regular geometry giving
meaning a triangle equivalent to a circle. We can then propose the following conjecture:Conjecture 1: For any compact convex shape, there exists a non-regular geometry giving 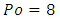 and then giving an equivalence with circular geometry in terms of mechanical energy degradation by viscous friction.If this conjecture was true, signification of Poiseuille number values could be very important in Physics and Mathematics. Considering well-known membrane deformation problem giving Poisson’s PDE, equation (6) is clearly its analogous for the laminar flow of a Newtonian liquid in a duct of arbitrary cross-section shape. The Saint-Venant solution given by equation (7) gives the velocity field shape which depends on the boundary conditions i.e. the shape of the duct cross-section perimeter. In the case of a pipe with circular cross-section, the high symmetry allows simple calculations and velocity field has a parabolic shape according to Poiseuille law. But for polygonal geometries like rectangles or triangles, shape is much more complicated. But, at the end, calculation of
and then giving an equivalence with circular geometry in terms of mechanical energy degradation by viscous friction.If this conjecture was true, signification of Poiseuille number values could be very important in Physics and Mathematics. Considering well-known membrane deformation problem giving Poisson’s PDE, equation (6) is clearly its analogous for the laminar flow of a Newtonian liquid in a duct of arbitrary cross-section shape. The Saint-Venant solution given by equation (7) gives the velocity field shape which depends on the boundary conditions i.e. the shape of the duct cross-section perimeter. In the case of a pipe with circular cross-section, the high symmetry allows simple calculations and velocity field has a parabolic shape according to Poiseuille law. But for polygonal geometries like rectangles or triangles, shape is much more complicated. But, at the end, calculation of 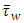 and
and 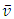 allows a simple dimensionless equation of the same form (equation (12)) to be obtained and this equation involves
allows a simple dimensionless equation of the same form (equation (12)) to be obtained and this equation involves 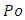 numbers varying in the range 20/3 to 12.Another consequence of the rectangular approach is the close relation between
numbers varying in the range 20/3 to 12.Another consequence of the rectangular approach is the close relation between 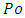 numbers and the Euler-Riemann zeta function. The problem of
numbers and the Euler-Riemann zeta function. The problem of 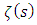 values for odd integer remains unsolved because at this time, we have no idea of a closed form for
values for odd integer remains unsolved because at this time, we have no idea of a closed form for 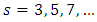 [4] Equation (13) gives interesting properties which could help approaching a closed form for
[4] Equation (13) gives interesting properties which could help approaching a closed form for 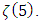 By considering well-known properties of hyperbolic tangent function
By considering well-known properties of hyperbolic tangent function 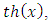 this function reaches very rapidly asymptotic value of 1 when
this function reaches very rapidly asymptotic value of 1 when 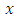 reach sufficiently large values (greater than 10). We can then consider that for sufficiently high values of ratio
reach sufficiently large values (greater than 10). We can then consider that for sufficiently high values of ratio 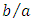 in equation (13), the quantity
in equation (13), the quantity 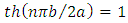 giving the following relationship for the sum over odd integers of
giving the following relationship for the sum over odd integers of 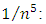
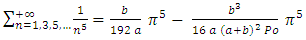
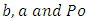 values are linked together (for example you have
values are linked together (for example you have 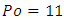 for
for 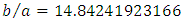 ) but equation (21) is surely an interesting result for understanding of
) but equation (21) is surely an interesting result for understanding of 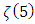 behaviour even if the sum only concerns odd values of
behaviour even if the sum only concerns odd values of 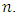 Complex calculations in rectangular ducts also give others surprising and interesting results in numbers theory. For example, it is possible to calculate the wall shear stress along the side length
Complex calculations in rectangular ducts also give others surprising and interesting results in numbers theory. For example, it is possible to calculate the wall shear stress along the side length 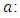
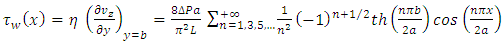
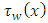 is obtained for
is obtained for 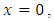 giving:
giving: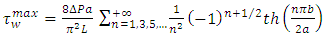
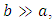 we obtain:
we obtain: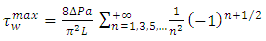
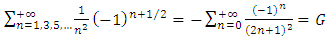
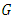 is the well-known Catalan’s constant. Until now, we ignore if this number is irrational even if it is conjectured. What we obtained from equation (24) gives interesting information about this number. Moreover, if we calculate the mean value of wall shear-stress along the same side, we obtain:
is the well-known Catalan’s constant. Until now, we ignore if this number is irrational even if it is conjectured. What we obtained from equation (24) gives interesting information about this number. Moreover, if we calculate the mean value of wall shear-stress along the same side, we obtain: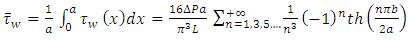
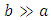 gives:
gives: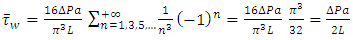
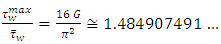
 which is an irrational number and then it could be considered as a proof of Catalan’s constant irrationality.We can then write the following theorem:Theorem 3: Catalan’s constant is proportional to
which is an irrational number and then it could be considered as a proof of Catalan’s constant irrationality.We can then write the following theorem:Theorem 3: Catalan’s constant is proportional to 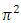 and then is an irrational number.Finally, it is also possible to calculate the ratio
and then is an irrational number.Finally, it is also possible to calculate the ratio 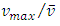 of the maximum velocity at the centre of the rectangular duct and the average velocity. For maximum velocity, we obtain:
of the maximum velocity at the centre of the rectangular duct and the average velocity. For maximum velocity, we obtain: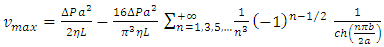
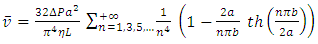
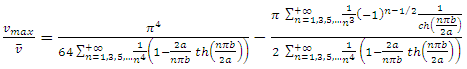
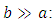
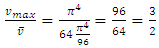
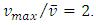 Equation (31) allows this ratio to be calculated whatever is the rectangle aspect ratio
Equation (31) allows this ratio to be calculated whatever is the rectangle aspect ratio 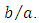
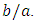 From this equation, we showed how Poiseuille number values can be calculated giving a simple theorem for evolution of
From this equation, we showed how Poiseuille number values can be calculated giving a simple theorem for evolution of 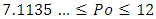 when
when 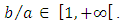 This result allowed the rectangle, giving the same value than the circular cross-section, to be defined with an aspect ratio
This result allowed the rectangle, giving the same value than the circular cross-section, to be defined with an aspect ratio 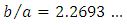 We tried to give some mathematical consequences of this approach. Among them, we conjecture that for any convex shape of non-circular cross-section, there always exists one having a Poiseuille number value equal to the circle value i.e.
We tried to give some mathematical consequences of this approach. Among them, we conjecture that for any convex shape of non-circular cross-section, there always exists one having a Poiseuille number value equal to the circle value i.e. 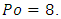 We also showed, from Poiseuille number equation for rectangular ducts, that Euler-Riemann zeta function
We also showed, from Poiseuille number equation for rectangular ducts, that Euler-Riemann zeta function 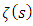 for odd integer
for odd integer 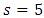 , for summation over odd integers
, for summation over odd integers 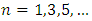 can be calculated as proportional to
can be calculated as proportional to 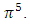 From calculation of both, maximum wall shear stress, and average wall shear stress, we showed that famous Catalan’s constant
From calculation of both, maximum wall shear stress, and average wall shear stress, we showed that famous Catalan’s constant 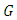 is proportional to
is proportional to 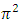 which could be a proof of its irrationality.Finally, by integrating the velocity field, we found an expression for the ratio
which could be a proof of its irrationality.Finally, by integrating the velocity field, we found an expression for the ratio 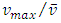 which gave, for the limit case of plane Poiseuille flow, a value of
which gave, for the limit case of plane Poiseuille flow, a value of 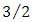 in perfect agreement with fluid mechanics results.
in perfect agreement with fluid mechanics results. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML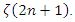 J Comput Appl Math, vol 118, p 323-335.
J Comput Appl Math, vol 118, p 323-335.