Kunle Adegoke, Adenike Olatinwo, Olugbenga Olunloyo
Department of Physics and Engineering Physics, Obafemi Awolowo University, Ile-Ife, Nigeria
Correspondence to: Kunle Adegoke, Department of Physics and Engineering Physics, Obafemi Awolowo University, Ile-Ife, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this note we show that the standard Rayleigh-Schrödinger (RS) perturbation method gives the same result as the hypervirial pertubative method (HPM), for an approximate analytic expression for the energy eigenvalues of the bounded quartic oscillator. This connection between the HPM and the RS method went unnoticed for a long time, apparently because it was not obvious that the resulting polygamma sums to be evaluated in the RS method could, in fact, be expressed in closed form.
Keywords:
Rayleigh-Schrödinger perturbation, Hypervirial pertubative method, Polygamma sum
Cite this paper: Kunle Adegoke, Adenike Olatinwo, Olugbenga Olunloyo, An Alternative Derivation of the Fernández-Castro Analytic Approximate Expression for the Eigenvalues of the Bounded Quartic Oscillator, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 2, 2018, pp. 47-51. doi: 10.5923/j.ijtmp.20180802.03.
1. Introduction
Interest in the bounded quartic oscillator started with the pioneering work of Barakat and Rosner [1] who employed a power series method to obtain numerical values of the eigenvalues through an iteration scheme. Researchers have since continued to investigate the bounded quartic oscillator and related systems, using various techniques (see references [2, 3, 4, 5] and the references in them). The bounded quartic oscillator is described by the Hamiltonian 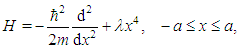 | (1) |
where 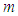 is the mass of the oscillator and
is the mass of the oscillator and 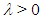 is the coupling constant. The Hamiltonian
is the coupling constant. The Hamiltonian 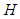 lives in a Hilbert space
lives in a Hilbert space 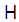 with inner product between any two real-valued functions
with inner product between any two real-valued functions 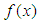 and
and 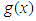 in
in 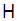 defined by
defined by 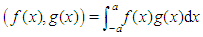 , where the functions
, where the functions 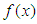 and
and 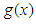 and indeed all vectors of
and indeed all vectors of 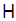 are required to vanish at the boundaries
are required to vanish at the boundaries 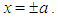 About three and a half decades ago, using their hypervirial pertubative method (HPM), Fernández and Castro [2] derived the following expression (their equation (22) in our notation) for the eigenvalues of the bounded quartic oscillator:
About three and a half decades ago, using their hypervirial pertubative method (HPM), Fernández and Castro [2] derived the following expression (their equation (22) in our notation) for the eigenvalues of the bounded quartic oscillator: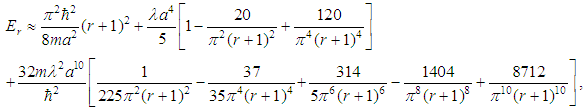 | (2) |
for quantum numbers  In this paper we show that the standard Rayleigh-Schrödinger (RS) perturbation theory with
In this paper we show that the standard Rayleigh-Schrödinger (RS) perturbation theory with 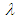 as the perturbation parameter gives the same result for
as the perturbation parameter gives the same result for 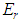 as given in (2). As a matter of fact we stumbled upon the work of Fernández and Castro only after we had obtained our result for
as given in (2). As a matter of fact we stumbled upon the work of Fernández and Castro only after we had obtained our result for 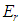 . The Computer Algebra System Waterloo Maple came to our aid in simplifying the resulting perturbation sums and finding their closed form.
. The Computer Algebra System Waterloo Maple came to our aid in simplifying the resulting perturbation sums and finding their closed form.
2. Basis Functions and the Matrix Elements of H
Since 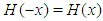 , the eigenstates of
, the eigenstates of 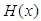 have definite parity. For
have definite parity. For 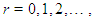 the complete orthonormal functions
the complete orthonormal functions 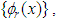 where,
where, 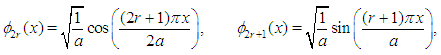 constitute a suitable set of basis functions in
constitute a suitable set of basis functions in 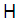 for a matrix representation of the bounded quartic oscillator Hamiltonian
for a matrix representation of the bounded quartic oscillator Hamiltonian 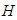 , since they also satisfy the boundary conditions
, since they also satisfy the boundary conditions 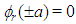 .The identities
.The identities 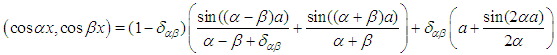 and
and 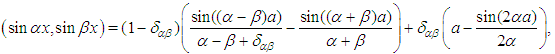 for
for  and the repeated application of Leibnitz rule for differentiating an integral allow to calculate the matrix elements of
and the repeated application of Leibnitz rule for differentiating an integral allow to calculate the matrix elements of 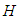 as
as 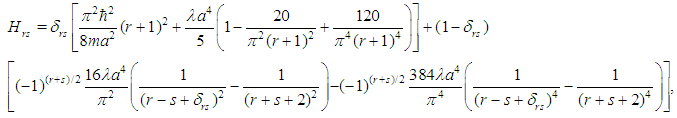 | (3) |
provided that 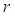 and
and 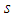 have the same parity, and
have the same parity, and 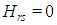 otherwise.The matrix elements
otherwise.The matrix elements 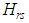 facilitate the direct diagonalization of the bounded quartic oscillator. The energy eigenvalues can be made arbitrarily accurate by increasing the dimension of the Hamiltonian matrix used; the eigenvalues obtained can therefore be considered exact. We are, however, not concerned here with exact diagonalization but we need the matrix elements
facilitate the direct diagonalization of the bounded quartic oscillator. The energy eigenvalues can be made arbitrarily accurate by increasing the dimension of the Hamiltonian matrix used; the eigenvalues obtained can therefore be considered exact. We are, however, not concerned here with exact diagonalization but we need the matrix elements 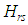 for our perturbation calculations. For
for our perturbation calculations. For 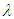 sufficiently small (see [3] for a rigorous discussion of the convergence criteria), the oscillator potential
sufficiently small (see [3] for a rigorous discussion of the convergence criteria), the oscillator potential 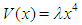 may be treated as a perturbation of the unperturbed Hamiltonian
may be treated as a perturbation of the unperturbed Hamiltonian 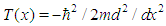 (the free particle in a box Hamiltonian).In the standard Rayleigh-Schrödinger perturbation theory for non-degenerate states, the approximate energy eigenvalues of
(the free particle in a box Hamiltonian).In the standard Rayleigh-Schrödinger perturbation theory for non-degenerate states, the approximate energy eigenvalues of 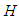 , to second order in
, to second order in 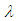 , are to be calculated from
, are to be calculated from 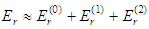 . We have immediately that
. We have immediately that 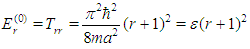 | (4) |
and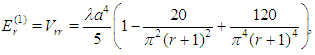 | (5) |
where 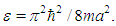 The second order correction to the energy of the bounded quartic oscillator,
The second order correction to the energy of the bounded quartic oscillator, 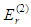 , is given by
, is given by 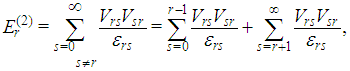 | (6) |
where 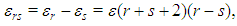 | (7) |
so that 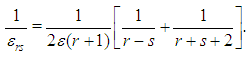 | (8) |
Since 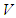 is a real symmetric matrix, (6) is simply
is a real symmetric matrix, (6) is simply 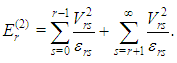 | (9) |
We note that the matrix elements 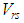 occuring in (9) are necessarily off-diagonal (since
occuring in (9) are necessarily off-diagonal (since 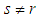 ). Furthermore the only surviving elements
). Furthermore the only surviving elements 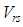 , according to (3), are those for which
, according to (3), are those for which 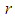 and
and 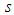 are both odd or both even.It therefore follows from (3) that
are both odd or both even.It therefore follows from (3) that 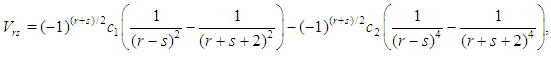 | (10) |
where 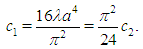 Taking (8) into account, the summand in (9) is therefore
Taking (8) into account, the summand in (9) is therefore 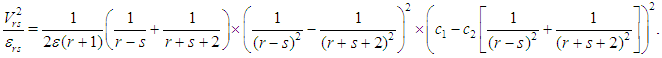 | (11) |
The sum in (9) is easier to evaluate if the energy eigenvalues are grouped by parity: 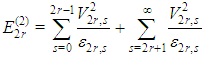 and
and 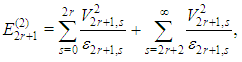 for quantum number
for quantum number 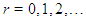 Using the summation identity (equation 2.6 of [6])
Using the summation identity (equation 2.6 of [6]) 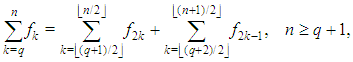 where
where 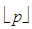 denotes the floor of
denotes the floor of 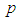 , that is, the greatest integer less than or equal to
, that is, the greatest integer less than or equal to 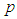 , the above sums can be expressed as
, the above sums can be expressed as 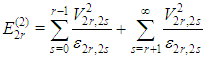 | (12) |
and 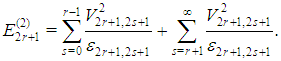 | (13) |
Maple is able to evaluate the sums in (12) and (13), with the appropriate summand in each case obtained from (11), and we have (see the Maple code in the appendix) 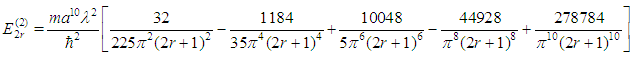 and
and 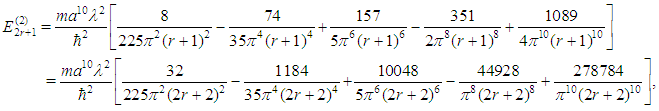 from which it follows that
from which it follows that 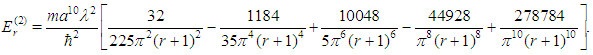 | (14) |
Adding (4), (5) and (14), we finally obtain 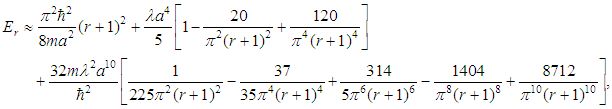 as an approximate expression for the eigenvalues of the bounded quartic oscillator.
as an approximate expression for the eigenvalues of the bounded quartic oscillator.
3. Summary and Conclusions
Using the Rayleigh-Schrödinger perturbation theory and with the aid of a summation identity and the Computer Algebra System Maple, we have derived an approximate expression for the energy eigenvalues of the bounded quartic oscillator. This is the same expression that was obtained much earlier in reference [2] through a more complicated approach. Similar results to ours are also contained in reference [3] where exact diagonalization was done and perturbative series up to the third order in 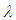 were also developed for the energy levels. However, the RS sums were determined numerically in that paper as, apparently, closed form could not be found for them; and furthermore only results for the ten lowest eigenvalues were computed.
were also developed for the energy levels. However, the RS sums were determined numerically in that paper as, apparently, closed form could not be found for them; and furthermore only results for the ten lowest eigenvalues were computed.
Appendix
Maple code to evaluate  >V:=(r,s)->(-1)^(r+s)*c1*(1/(r-s)^2-1/(r+s+2)^2) -(-1)^(r+s)*c2*(1/(r-s)^4-1/(r+s+2)^4):>epsilon:=(r,s)->epsilon*(r+s+2)*(r-s):>simplify(expand(eval(V(r,s)^2/epsilon(r,s),[r=2*r,s=2*s]))) assuming r,posint,s,posint,c1>0,c2>0:> summand:=convert(>S1:=sum(summand,s=0..r-1) assuming r,posint,s,posint,c1>0,c2>0:>S2:=sum(summand,s=r+1..infinity) assuming r,posint,s,posint,c1>0,c2>0:> ssum:=simplify(S1+S2):>fsum:=expand(eval(ssum,[epsilon=Pi^2*h^2/8/m/a^2, c1=16*lambda*a^4/Pi^2,c2=16*24*lambda*a^4/Pi^4])):>arranged:=collect(fsum,Pi):>terrms:=[seq(factor(op(i,arranged)),i=1..nops(arranged))]:> add(L,L=terms);
>V:=(r,s)->(-1)^(r+s)*c1*(1/(r-s)^2-1/(r+s+2)^2) -(-1)^(r+s)*c2*(1/(r-s)^4-1/(r+s+2)^4):>epsilon:=(r,s)->epsilon*(r+s+2)*(r-s):>simplify(expand(eval(V(r,s)^2/epsilon(r,s),[r=2*r,s=2*s]))) assuming r,posint,s,posint,c1>0,c2>0:> summand:=convert(>S1:=sum(summand,s=0..r-1) assuming r,posint,s,posint,c1>0,c2>0:>S2:=sum(summand,s=r+1..infinity) assuming r,posint,s,posint,c1>0,c2>0:> ssum:=simplify(S1+S2):>fsum:=expand(eval(ssum,[epsilon=Pi^2*h^2/8/m/a^2, c1=16*lambda*a^4/Pi^2,c2=16*24*lambda*a^4/Pi^4])):>arranged:=collect(fsum,Pi):>terrms:=[seq(factor(op(i,arranged)),i=1..nops(arranged))]:> add(L,L=terms);
References
| [1] | R. BARAKAT AND R. ROSNER (1981), The bounded quartic oscillator, Physics Letters 83A (4):149--150. |
| [2] | F. M. FERNÁNDEZ and E. A. CASTRO (1982), An analytic approximate expression for the eigenvalues of the bounded quartic oscillator, Physics Letters 88A (1):4--6. |
| [3] | V. C. AGUILERA-NAVARRO, J. F. GOMES and A. H. ZIMERMAN (1983), On the quantum quartic oscillator in a box, Revista Brasileira de Fisica 13 (4):664--672. |
| [4] | R. N. CHAUDHURI AND B. MUKHERJEE (1983), The eigenvalues of the bounded 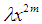 oscillators, Journal of Physics A: Math. Gen. 16:3193--3196. oscillators, Journal of Physics A: Math. Gen. 16:3193--3196. |
| [5] | H. A. ALHENDI AND E. I. LASHIN (2005), Spectrum of one-dimensional anharmonic oscillators, Canadian Journal of Physics 83:541--550. |
| [6] | H. W. GOULD (2011), Table for Fundamentals of Series: Part I: Basic properties of series and products, From the seven unpublished manuscripts of H. W. Gould. |


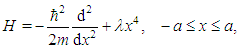
 is the mass of the oscillator and
is the mass of the oscillator and 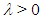 is the coupling constant. The Hamiltonian
is the coupling constant. The Hamiltonian 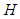 lives in a Hilbert space
lives in a Hilbert space 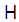 with inner product between any two real-valued functions
with inner product between any two real-valued functions 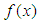 and
and 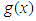 in
in 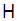 defined by
defined by 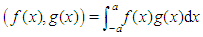 , where the functions
, where the functions 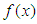 and
and 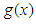 and indeed all vectors of
and indeed all vectors of  are required to vanish at the boundaries
are required to vanish at the boundaries 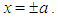 About three and a half decades ago, using their hypervirial pertubative method (HPM), Fernández and Castro [2] derived the following expression (their equation (22) in our notation) for the eigenvalues of the bounded quartic oscillator:
About three and a half decades ago, using their hypervirial pertubative method (HPM), Fernández and Castro [2] derived the following expression (their equation (22) in our notation) for the eigenvalues of the bounded quartic oscillator: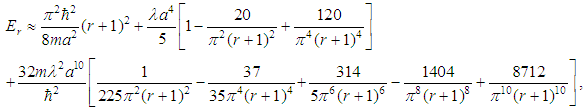
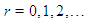 In this paper we show that the standard Rayleigh-Schrödinger (RS) perturbation theory with
In this paper we show that the standard Rayleigh-Schrödinger (RS) perturbation theory with 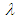 as the perturbation parameter gives the same result for
as the perturbation parameter gives the same result for 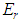 as given in (2). As a matter of fact we stumbled upon the work of Fernández and Castro only after we had obtained our result for
as given in (2). As a matter of fact we stumbled upon the work of Fernández and Castro only after we had obtained our result for 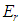 . The Computer Algebra System Waterloo Maple came to our aid in simplifying the resulting perturbation sums and finding their closed form.
. The Computer Algebra System Waterloo Maple came to our aid in simplifying the resulting perturbation sums and finding their closed form.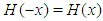 , the eigenstates of
, the eigenstates of 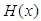 have definite parity. For
have definite parity. For 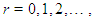 the complete orthonormal functions
the complete orthonormal functions 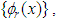 where,
where, 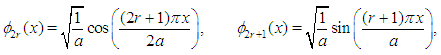 constitute a suitable set of basis functions in
constitute a suitable set of basis functions in  for a matrix representation of the bounded quartic oscillator Hamiltonian
for a matrix representation of the bounded quartic oscillator Hamiltonian  , since they also satisfy the boundary conditions
, since they also satisfy the boundary conditions 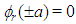 .The identities
.The identities 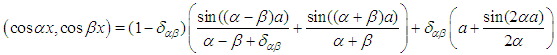 and
and 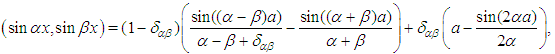 for
for 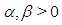 and the repeated application of Leibnitz rule for differentiating an integral allow to calculate the matrix elements of
and the repeated application of Leibnitz rule for differentiating an integral allow to calculate the matrix elements of  as
as 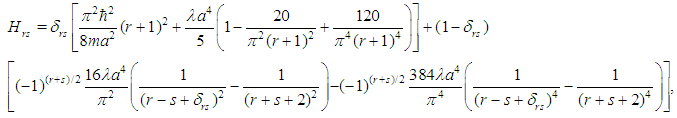
 and
and  have the same parity, and
have the same parity, and  otherwise.The matrix elements
otherwise.The matrix elements 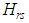 facilitate the direct diagonalization of the bounded quartic oscillator. The energy eigenvalues can be made arbitrarily accurate by increasing the dimension of the Hamiltonian matrix used; the eigenvalues obtained can therefore be considered exact. We are, however, not concerned here with exact diagonalization but we need the matrix elements
facilitate the direct diagonalization of the bounded quartic oscillator. The energy eigenvalues can be made arbitrarily accurate by increasing the dimension of the Hamiltonian matrix used; the eigenvalues obtained can therefore be considered exact. We are, however, not concerned here with exact diagonalization but we need the matrix elements 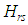 for our perturbation calculations. For
for our perturbation calculations. For 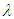 sufficiently small (see [3] for a rigorous discussion of the convergence criteria), the oscillator potential
sufficiently small (see [3] for a rigorous discussion of the convergence criteria), the oscillator potential 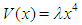 may be treated as a perturbation of the unperturbed Hamiltonian
may be treated as a perturbation of the unperturbed Hamiltonian 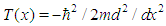 (the free particle in a box Hamiltonian).In the standard Rayleigh-Schrödinger perturbation theory for non-degenerate states, the approximate energy eigenvalues of
(the free particle in a box Hamiltonian).In the standard Rayleigh-Schrödinger perturbation theory for non-degenerate states, the approximate energy eigenvalues of 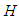 , to second order in
, to second order in 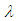 , are to be calculated from
, are to be calculated from 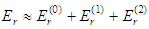 . We have immediately that
. We have immediately that 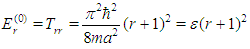
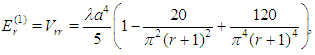
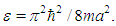 The second order correction to the energy of the bounded quartic oscillator,
The second order correction to the energy of the bounded quartic oscillator, 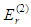 , is given by
, is given by 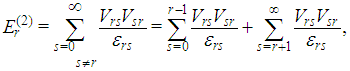
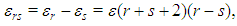
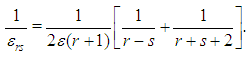
 is a real symmetric matrix, (6) is simply
is a real symmetric matrix, (6) is simply 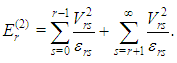
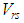 occuring in (9) are necessarily off-diagonal (since
occuring in (9) are necessarily off-diagonal (since 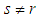 ). Furthermore the only surviving elements
). Furthermore the only surviving elements 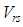 , according to (3), are those for which
, according to (3), are those for which 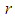 and
and 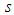 are both odd or both even.It therefore follows from (3) that
are both odd or both even.It therefore follows from (3) that 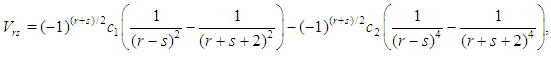
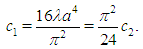 Taking (8) into account, the summand in (9) is therefore
Taking (8) into account, the summand in (9) is therefore 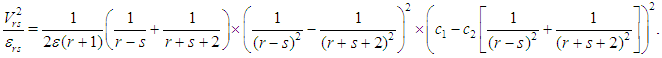
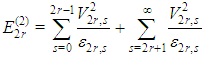 and
and 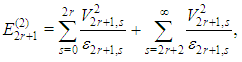 for quantum number
for quantum number 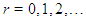 Using the summation identity (equation 2.6 of [6])
Using the summation identity (equation 2.6 of [6]) 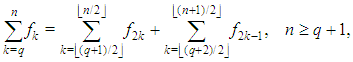 where
where 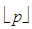 denotes the floor of
denotes the floor of 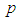 , that is, the greatest integer less than or equal to
, that is, the greatest integer less than or equal to 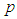 , the above sums can be expressed as
, the above sums can be expressed as 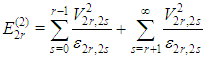
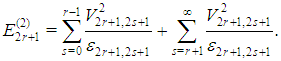
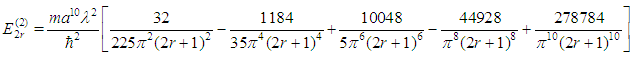 and
and 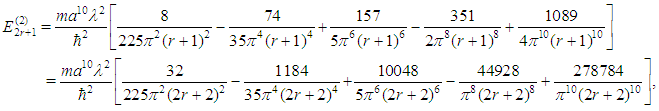 from which it follows that
from which it follows that 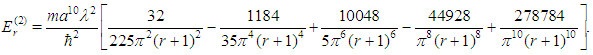
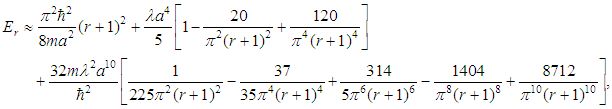 as an approximate expression for the eigenvalues of the bounded quartic oscillator.
as an approximate expression for the eigenvalues of the bounded quartic oscillator. were also developed for the energy levels. However, the RS sums were determined numerically in that paper as, apparently, closed form could not be found for them; and furthermore only results for the ten lowest eigenvalues were computed.
were also developed for the energy levels. However, the RS sums were determined numerically in that paper as, apparently, closed form could not be found for them; and furthermore only results for the ten lowest eigenvalues were computed.  >V:=(r,s)->(-1)^(r+s)*c1*(1/(r-s)^2-1/(r+s+2)^2) -(-1)^(r+s)*c2*(1/(r-s)^4-1/(r+s+2)^4):>epsilon:=(r,s)->epsilon*(r+s+2)*(r-s):>simplify(expand(eval(V(r,s)^2/epsilon(r,s),[r=2*r,s=2*s]))) assuming r,posint,s,posint,c1>0,c2>0:> summand:=convert(>S1:=sum(summand,s=0..r-1) assuming r,posint,s,posint,c1>0,c2>0:>S2:=sum(summand,s=r+1..infinity) assuming r,posint,s,posint,c1>0,c2>0:> ssum:=simplify(S1+S2):>fsum:=expand(eval(ssum,[epsilon=Pi^2*h^2/8/m/a^2, c1=16*lambda*a^4/Pi^2,c2=16*24*lambda*a^4/Pi^4])):>arranged:=collect(fsum,Pi):>terrms:=[seq(factor(op(i,arranged)),i=1..nops(arranged))]:> add(L,L=terms);
>V:=(r,s)->(-1)^(r+s)*c1*(1/(r-s)^2-1/(r+s+2)^2) -(-1)^(r+s)*c2*(1/(r-s)^4-1/(r+s+2)^4):>epsilon:=(r,s)->epsilon*(r+s+2)*(r-s):>simplify(expand(eval(V(r,s)^2/epsilon(r,s),[r=2*r,s=2*s]))) assuming r,posint,s,posint,c1>0,c2>0:> summand:=convert(>S1:=sum(summand,s=0..r-1) assuming r,posint,s,posint,c1>0,c2>0:>S2:=sum(summand,s=r+1..infinity) assuming r,posint,s,posint,c1>0,c2>0:> ssum:=simplify(S1+S2):>fsum:=expand(eval(ssum,[epsilon=Pi^2*h^2/8/m/a^2, c1=16*lambda*a^4/Pi^2,c2=16*24*lambda*a^4/Pi^4])):>arranged:=collect(fsum,Pi):>terrms:=[seq(factor(op(i,arranged)),i=1..nops(arranged))]:> add(L,L=terms);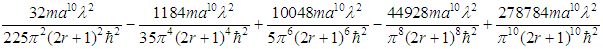
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML oscillators, Journal of Physics A: Math. Gen. 16:3193--3196.
oscillators, Journal of Physics A: Math. Gen. 16:3193--3196.