Godfrey E. Akpojotor 1, 2, Omamoke O. E. Enaroseha 1, Alexander E. Animalu 2, 3
1Physics Department, Delta State University, Abraka, Nigeria
2Physics and Astronomy Department, University of Nigeria, Nsukka, Nigeria
3International Centre for Basic Research, FHA Maitama, Abuja, Nigeria
Correspondence to: Godfrey E. Akpojotor , Physics Department, Delta State University, Abraka, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
We have shown in [1] that the geometric object for the geometrical and quantization foundation of the Oyibo grand unified theorem (GUT) is the torus. This torus is generic meaning that its nature depends on the periodic boundary conditions of the system and other physical constraint conditions. By observing that the Bloch’s theorem also has this torus as its generic geometric object, we show that there is correspondence between the Bloch’s theorem and the Oyibo GUT. The implication of this correspondence in using the Oyibo GUT to study strongly correlated systems in condensed mater physics is then discussed.
Keywords:
Bloch’s theorem, Oyibo grand unified theorem, Group transformation, Geometric object, Torus
Cite this paper: Godfrey E. Akpojotor , Omamoke O. E. Enaroseha , Alexander E. Animalu , Correspondence between the Bloch’s Theorem and the Oyibo Grand Unified Theorem within the Purview of Generic Torus, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 2, 2018, pp. 40-46. doi: 10.5923/j.ijtmp.20180802.02.
1. Introduction
The foundation of our highly simplified correlated variation approach (HSCVA) for investigating few body correlated systems has been based on the geometrical nature of the lattice structures of such systems [2-5]. In the pioneering paper, Chen and Mei (1989) developed the correlated variational method to study the standard Hubbard model only in 1D and 2D systems with singlet states [2]. To prevent boundary effects, their CVA was applied to finite lD lattices sites arranged in ID ring and 2D planar lattices arranged in a torus in 2D. In advancing the work, we have simplified the approach by first formulating the statistical equivalent of the Hubbard model in all three dimensions [4]. The remarkable correspondence between our statistical formulation and the Hubbard model makes it easy to modify the latter for systems having triplet states so that our HSCVA is applicable to the Hubbard model and its various extended versions in all three dimensions [3]. Like the CVA of Chen and Mei [2], the arrangement of the lattice sites in 1D is in a ring form and those in 2D and 3D systems are toroidal to avoid the edge effects on some sites. These arrangements is consistent with related works of arranging lattices in tori so as to obtain lattices with appropriate periodic boundaries [6, 7].It was therefore quite reassuring to have recently observed and shown that the generic geometric object needed for the geometrical and quantization foundation of the Oyibo grand unified theorem (GUT) formulated as the mathematical basis for the unified force field theory as envisaged by Oyibo [8-9] also known as the theory of everything (TOE) is the torus [1]. In that work, one of us has shown that a torus ring can be constructed from the Pythagoras triangle which is an invariant geometric object in nature. Then using projective geometry, he was able to construct from this Pythagoras triangle the torus invariant within the Lorentz transformation. He then observed that this invariance of the toroidal geometry of the Oyibo GUT and the invariance of the Einstein’s principle of relativity within the purview of Lorentz transformation, is responsible for the remarkable correspondence of the Oyibo GUT with the Einstein’s unified field equation for conformal invariant field theories. Following that line of thinking, it is postulated here that since the Block theorem from which the original Hubbard model was formulated [10-13] has been observed to have a toroidal lattice foundation for appropriate periodic boundaries, then it should have a conrespondence with the Oyibo GUT. This is the motivation for this paper because the demonstration of such correspondence implies that the Hubbard model and its extended versions can also be formulated from the Oyibo GUT. The following plan will be used for this study. As a first step, it will be necessary to first re-visit the formation of the Hubbard model and its extended versions from the Bloch’s theorem in Section 2. The demonstration of the correspondence of the Bloch’s theorem and the Oyibo GUT will be done in Section 3. Thereafter, we will discuss the implication of this correspondence and conclude.
2. Revisiting the Formation of the Hubbard Model and Its Extended Versions
The Bloch theorem plays a central role in conduction electron dynamics as it specifies the form of the wave functions that characterize electron energy levels in a periodic crystal [13]. It was therefore useful in the formation of the tight-binding (TB) model which is an approach to the calculation of the electronic band structure of a lattice that relies on the fact that electrons are tightly bound (localized) to the atoms. The kinetic energy is included by allowing electrons to hop from one site to another. These features make the model to be lattice dependent. In its simplest form, the Hubbard model is an extension of the tight-binding model, wherein electrons can hop between lattice sites while the Coulomb interaction provides their localization tendency [14]. This formation makes the Hubbard model and all its extended versions to be lattice structure dependent and therefore emanate from the Block’s theorem. For as it is well known, the general lattice Hamiltonian model within the occupation number formalism for electrons with spin σ interacting via a spin-dependent interaction 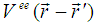 in the presence of an ionic lattice potential
in the presence of an ionic lattice potential 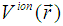 has the form [10,12]
has the form [10,12]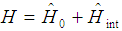 | (2.1) |
where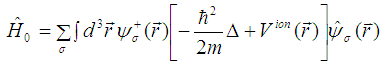 | (2.2) |
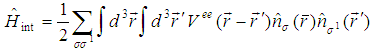 | (2.3) |
In the above equation, the 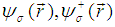 are the usual field operators and
are the usual field operators and 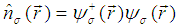 is the local density. It has been observed [12] that the interaction term is diagonal in the space variables
is the local density. It has been observed [12] that the interaction term is diagonal in the space variables 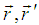 [i.e. it depends only on the (operator-valued) densities of electrons at site
[i.e. it depends only on the (operator-valued) densities of electrons at site 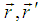 which interact via
which interact via 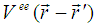 ]. The lattice potential entering the non-interacting part (Eq.2.2) leads to the splitting of the parabolic dispersion into infinitely many bands which are enumerated by the index α. The non-interacting problem is then characterized by the Block wave functions
]. The lattice potential entering the non-interacting part (Eq.2.2) leads to the splitting of the parabolic dispersion into infinitely many bands which are enumerated by the index α. The non-interacting problem is then characterized by the Block wave functions 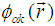 and the band energies
and the band energies 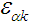 . The Wannier functions
. The Wannier functions 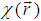 localized at site Ri are often introduced:
localized at site Ri are often introduced: 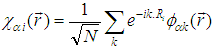 | (2.4) |
where N is the number of lattice sites. Thus one can construct creation and annihilation operators by the method of second quantization [13], 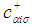 and
and 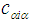 respectively, for electrons with spin σ in the band α at site Ri as
respectively, for electrons with spin σ in the band α at site Ri as 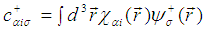 | (2.5a) |
where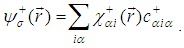 | (2.5b) |
Consequently, the Hamiltonian may be written in the lattice representation as 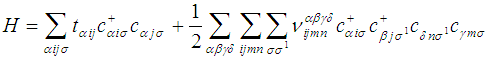 | (2.6) |
where the matrix elements are given by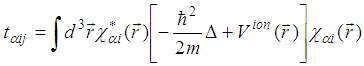 | (2.7) |
and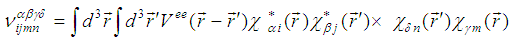 | (2.8) |
The Hamiltonian given by Eq.(2.6) is too general to be tractable in dimensions d > 1. Therefore, it has to be simplified using physically motivated truncations such as:i. That the Fermi surface (FS) lies within a single conduction band that is well separated from other bands so that the inter band interaction is weak hence we will restrict our study to a single band (α = β = γ = δ = 1) which is the aforementioned TB band. Thus Eq. (2.6) reduces to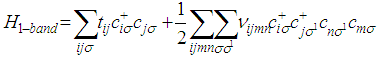 | (2.9) |
ii. The above single band Hamiltonian is obviously still too complicated for most purposes because of the complex interaction part, and therefore needs to be simplified further. Taking into account the weak overlap between neighbouring orbitals in a TB description, one expects that the overlap between nearest neighbours (NN) is important hence only NN hopping and interactions are allowed. So the site indices are restricted to only NN positions i and j leaving us with only NN hopping, a purely local contribution and four NN contributions. NN hopping between sites i and j are controlled by the 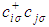 which are the creation (annihilation) operators at site i(j) having spin σ(σ) while the hopping term is defined as tij = t for NN hopping <i,j> (i.e. i ≠ j) and tij = 0 otherwise.The purely local contribution is the on-site Coulombic interaction term defined as
which are the creation (annihilation) operators at site i(j) having spin σ(σ) while the hopping term is defined as tij = t for NN hopping <i,j> (i.e. i ≠ j) and tij = 0 otherwise.The purely local contribution is the on-site Coulombic interaction term defined as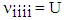 | (2.10) |
while the four NN contributions are: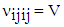 | (2.11) |
which is the NN Coulombic interaction term,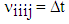 | (2.12) |
which gives rise to an occupation dependent hopping rate,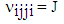 | (2.13) |
which is the NN Heisenberg exchange term and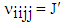 | (2.14) |
which describes the exchange hopping processes.This truncated form of the single band Hubbard model in Eq. (2.9) with only the Coulombic interaction (Eq. 2.10) is the famous Hubbard model given by [10-14]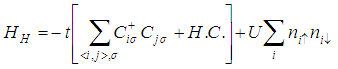 | (2.15) |
It is pertinent to point out that apart from the four NN contributions (Eqs. 2.11 – 2.14) which can be added to Eq.(2.15), there have been modifications of the Hubbard so that today it has numerous extensions and relatives [14-18] which have diverse application in condensed matter physics. Suffice to re-emphasize here, however, all these models depend on the lattice structure. For it is a common knowledge that lattice structure without periodic boundaries often leads to edge effect making some lattice sites not to be on equal footing with the others. As stated above, one way to resolve this limitation is to investigate the Hubbard lattice structure as torus in all three dimensions [2,4]. Here a torus is simply a lattice geometry with periodic boundary conditions [6] and is generic meaning that its nature depends on these boundary conditions of the system and other physical constraint conditions owing to the generic nature of the Oyibo GUT [1]. In this form of torus, the lattices are scale symmetric which means the lattices do not change their shapes when they are expanded into large lattices to study large densities or contracted into small lattices for few particles systems.Now in geometrical terms, quantization is achieved by applying the so-called Born-Von Karman cyclic boundary conditions [18-19], which is tantamount to turning the cubic crystal into a torus as sketched in Fig. 1. The proposal in [20] that the process of implementing cyclic boundary conditions would require going from the usual 3D to 5D background because the latter has in addition local degrees of freedom which become vital in introducing quantum effects, was used to show in [1] that the parametric equations of quantization of the torus into 5-dimensional background lattice is: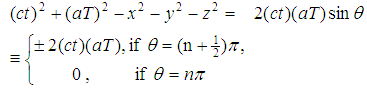 | (2.15) |
where 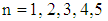 by limiting
by limiting 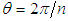 , needed for only rotations compatibles with translational symmetry of a crystal lattice in 3D space such that
, needed for only rotations compatibles with translational symmetry of a crystal lattice in 3D space such that 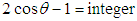 .
.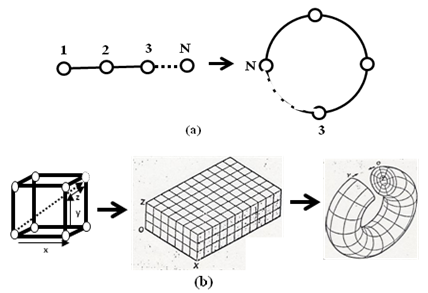 | Figure 1. Ilustrative sketch of the projection of (a) a linear lattice sites into a 1D ring (b) cubic lattice sites into curve torus |
3. Correspondence of Bloch’s Theorem and Oyibo GUT
For ease in drawing an analogy between Bloch’s theorem and Oyibo GUT, which will enable us to establish their correspondence, a summary is provided in Table 1, adopting Oyibo’s notations, as far as necessary, in order to facilitate identification of corresponding transformations and functions. Familiarity with both the Bloch’s theorem [19, 21] and the Oyibo GUT (see [22] for pedagogical review) will be assumed.According to Oyibo [8-9, 22], a function, 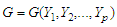 is said to be conformal invariant under a given group transformation
is said to be conformal invariant under a given group transformation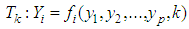 | (3.1) |
if 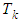 is the group of the transformation and
is the group of the transformation and 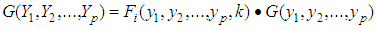 | (3.2) |
where 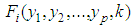 is a function of
is a function of 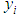 and
and 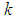 the single group parameter. From Table 1, we see that the group of translations in a crystal lattice and the Bloch (electron wave) function, more specifically lattice waves, have analogous properties as Eqs.(3.1) and (3.2). As a result, one needs only to show here that in quantized space-time geometry with given (Planck length) lattice spacing, the definition of conformal invariance in Eqs.(3.1) and (3.2) follows, as in Bloch’s theorem, from translational periodicity of any function of position in the lattice.On the basis of the definition in Eqs.(3.1) and (3.2), Oyibo states that there exists a set of conservation equations
the single group parameter. From Table 1, we see that the group of translations in a crystal lattice and the Bloch (electron wave) function, more specifically lattice waves, have analogous properties as Eqs.(3.1) and (3.2). As a result, one needs only to show here that in quantized space-time geometry with given (Planck length) lattice spacing, the definition of conformal invariance in Eqs.(3.1) and (3.2) follows, as in Bloch’s theorem, from translational periodicity of any function of position in the lattice.On the basis of the definition in Eqs.(3.1) and (3.2), Oyibo states that there exists a set of conservation equations 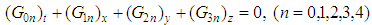 | (3.3) |
which may be rewritten in the Einstein-like form 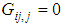 where the function defined mathematically by
where the function defined mathematically by 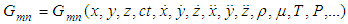 is a set of “generic” quantities which are arbitrary functions of space and time coordinates (x,y,z,ct), velocities
is a set of “generic” quantities which are arbitrary functions of space and time coordinates (x,y,z,ct), velocities 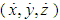 , accelerations
, accelerations 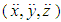 , density
, density 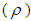 , fluid or gas viscosity
, fluid or gas viscosity 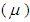 , temperature (T), pressure (P), etc. Now by applying the conformal transformation defined by Eq.(3.1) to a system of partial differential equations of nth order given by
, temperature (T), pressure (P), etc. Now by applying the conformal transformation defined by Eq.(3.1) to a system of partial differential equations of nth order given by 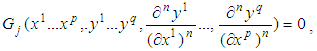 | (3.4) |
one derives “solutions” of Eq.(3.2) in terms of the absolute invariants 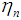 of the subgroup of transformations for the independent coordinate variables in the form:
of the subgroup of transformations for the independent coordinate variables in the form: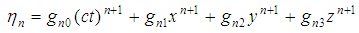 | (3.5) |
where n = 0, 1, 2, 3, 4 are the five degrees of freedom of Oyibo GUT as in the Block’s theorem shown in Table 1. Observe that we have indicated in Table 1 how the restriction to the five values of n in Eq.(3.3) are analogous to the constraints in Bloch’s theorem, on translational invariance of the Hamiltonian operator, by rotational symmetry of a crystal lattice in 3-dimensional space represented by angles, 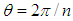 , where n =1,2,3,4 or 6, corresponding to n-fold rotation axis of symmetry [1].Finally, analogy between Bloch’s theorem and Oyibo GUT leads to identification of
, where n =1,2,3,4 or 6, corresponding to n-fold rotation axis of symmetry [1].Finally, analogy between Bloch’s theorem and Oyibo GUT leads to identification of 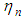 with the wave number associated with the primitive translation vectors of the reciprocal lattice of a 3D crystal
with the wave number associated with the primitive translation vectors of the reciprocal lattice of a 3D crystal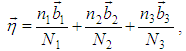 | (3.6) |
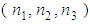 being integers and
being integers and 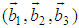 the primitive translation vectors of the reciprocal lattice space and
the primitive translation vectors of the reciprocal lattice space and 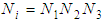 the number of primitive cells in the crystal. For a cubic lattice in
the number of primitive cells in the crystal. For a cubic lattice in 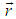 -space,
-space, 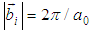 , where
, where 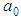 is the lattice constant, which we shall take (in Oyibo GUT representation of general theory of relativity) to be the Planck length.However, the nth order partial differential equations (3.4) are not quite analogous to the non-relativistic Schrodinger equation of Bloch’s theorem in Table 1 except insofar as the system of partial differential in Eqs.(3.4) may be rewritten, in the first order, as follows
is the lattice constant, which we shall take (in Oyibo GUT representation of general theory of relativity) to be the Planck length.However, the nth order partial differential equations (3.4) are not quite analogous to the non-relativistic Schrodinger equation of Bloch’s theorem in Table 1 except insofar as the system of partial differential in Eqs.(3.4) may be rewritten, in the first order, as follows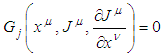 | (3.7) |
in terms of the variables 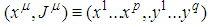 where
where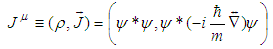 | (3.8) |
is the probability current density 4-vector conserved by Schrodinger’s equation. It can easily be shown that if we introduce the differential operator 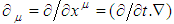 into Eq.(3.8), it becomes the current conservation law [15]
into Eq.(3.8), it becomes the current conservation law [15] 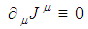 | (3.9) |
so that in a very subtle way we have obtained the Noether theorem. This is an important result as it re-enact the expectation of Oyibo when he pointed out in p285 of [8] that, “This new methodology is not totally new in the sense that the conservation equations are field equations…(see Eq.(3.3) here) could be condensed to tensor components similar to the world tensor components in the general theory of relativity of various versions of the many proposed Unified Force Field theories by previous investigators including Einstein himself. Perhaps one of the most significant part of the relationship to the previous formulations and results is the evolution of a characteristic sub-group variable (see Eq.(3.5) here) which seems to be a generalization of a good number of similar variables in the previous formulations.” | Table 1. Analogy between Bloch’s Theorem and Oyibo GUT |
4. Summary and Conclusions
The Oyibo GUT was formulated from the Navier-Stokes equations which have classical origin and this raised doubt for its applicability to quantum systems. We have shown in a previous study that the Navier-Stokes equation has periodic solutions and then use it to formulate an O(4,2)xSU(3)xU(1) gauge theory of quantum gravity [23] and in a more recent study one of us has shown that the geometric object for its geometrical and quantization foundation is the generic torus which has also been used in the literature as the geometric object of the Hubbard model formulated on the basis of the Bloch’s theorem. It turns out that there is a remarkable correspondence between Bloch’s theorem and the Oyibo GUT. This has open the possibility that the Oyibo GUT can in principle be used to formulate strongly correlated models which emanates from the Bloch’s theorem. In particular, we have reviewed the formation of the Hubbard model and its extended versions from the Bloch’s theorem. The implication is that the Hubbard model and its extended versions can in principle also be formulated from the Oyibo GUT. Thereafter, since the Hubbard model and its extended versions have very important applications in condensed matter physics, we claim that such applications have been brought under the purview of the Oyibo GUT and therefore constitute this related area in the Oyibo grand unified theory. Thus we have demonstrated an important conjecture of Oyibo in p303 of [8] that, “The generic formulation of the grand unified theorem is in good part based on synthesizing, interpreting and realizing that generic, universal conservation equations should in light of the general and global outlook, be expected to be the source from which the unified force field can be derived [8].”
ACKNOWLEDGEMENTS
We acknowledge partial funding from ICBR, Abuja.
References
| [1] | Akpojotor G. E. (2018). The geometrical and quantization foundations of the Oyibo grand unification theorem. International Journal of Theoretical and Mathematical Physics 8, 33 - 39. |
| [2] | Chen L. and Mei C. (1989). Exact calculation of the two electron interaction in the ground states of the Hubbard model. Phys. Rev. B39: pp9006-9011. See also: Mei C. and Chen L. (1988) Study of the interaction between two electrons in the single band Hubbard model. Z. Physik B - Condensed Matter 72: 429. |
| [3] | Akpojotor G. E. (2008). Possible propagation of the Zhang-Rice singlet as a probable Cooper channel in the CuO2 planes. Physics Letters A 372, 6992-6995. |
| [4] | Akpojotor G. E. (2008). The statistical equivalents of the t-U and t-t'-U models (Part II: Participants’ Contributions) in Lectures on the Physics of Strongly Correlated Systems XII: Twelfth Training Course held at Vietrisul Mare, Italy (edited by A. Avella and F. Mancini), American Institute of Physics Con. Proc. 1014, 251-259. |
| [5] | Akpojotor Godfrey E. (2013). Superexchange Driven Singlet-Triplet Transition in Quantum Dots Array Embedded in Kagome Lattice System. Advances in Physics Theories and Applications 17, 69-77. |
| [6] | Plechko V. N. (1985). Simple solution of two-dimensional Ising model on a torus in terms of Grassmann integrals. Theoretical and Mathematical Physics 64, 748-756. |
| [7] | Kim H., Zhu G., Porto J. V. and Hafezi M. (2018). Optical Lattice with Torus Topology. arXiv:1805.01483. |
| [8] | Oyibo G. A. (2003). Grand Unified Theorem; Discovery of the Theory of Everything and the Building Block of Quantum Theory. International Journal of Mathematics, Game Theory and Algebra, Vol. 13, 281-354. |
| [9] | Oyibo G. A. (2004). Grand Unified Theorem,’ with two subtitles: “Representation of the Unified Theory of Everything,” Nova Science Publishers, New York (2001) and “Discovery of the Theory of Everything and the Building Block of Quantum Theory,” Nova Science Publishers, New York. |
| [10] | Hubbard J. (1963). Electrons correlations in narrow energy bands. Proc. Roy. Soc. London, Series A276: 238-257. |
| [11] | Fradkin E. (1991). Field theories of condensed matter systems. Addison-Wesley Publishing co. |
| [12] | Vollhardt D., Blumer N., Held K., Koller M., Schlipf J and Ulmke M. (2000). Non-pertubative approaches to magnetism in strongly correlated electrons systems. Progress Report (September 1996 - December 1999) of the Center of Electronic Correlation and Magnetism, Institute of Physics, University of Augsburg, Germany: 93-104. First published (1997) in Z. Phys. B103, 238. |
| [13] | Fujita S., Ito K. (2007). Bloch Theorem. In: Quantum Theory of Conducting Matter. Springer, New York, NY. |
| [14] | Nature Physics Editorial (2013). The Hubbard model at half a century. Nature Physics 9, 523. |
| [15] | Nagoasa N. (1999). Field theories of condensed matter physics. Springer_Verlag, Berlin Heidelberg. |
| [16] | Baeriswyl D, Campbell D. K. Carmelo., J. M. P., Guinea F. and Louis E. (Ed) (1995). The Hubbard Model: Its Physics and Mathematical Physics. NATO ASI Series. Series B: Physics 343. Springer Science – Business Media, New York. |
| [17] | Enaroseha O. E., Akpojotor E. G. and Atuma L. (2014). Theorems to Demonstrate the Presence of Antiferromagnetism in the Periodic Anderson Model. International Journal of Theoretical and Mathematical Physics Vol. 4, 96-102. |
| [18] | Letterman F. (2011). Model Hamiltonians and basic techniques. https://www.cond-mat.de/events/correl11/talks/lechermann.pdf. |
| [19] | Alase A., Cobanera E., Ortiz G. and and Viola L. (2017). Generalization of Bloch’s theorem for arbitrary boundary conditions: Theory. arXiv:1706.08902. |
| [20] | Ziman J. M. (1960). Electrons and Phonons. Oxford University Press. |
| [21] | Animalu A. O. E. (1977). Intermediate Quantum theory of Crystallie Solids. Prentice-Hall. |
| [22] | Akpojotor G. E. and Echenim M.W. (2010). A pedagogical study of the Oyibo’s Grand Unification Theorem with reali-zation of some standard equations. Journal of the Nig. Asso of Math. Phys 17, 447 – 456. https://arxiv.org/ftp/arxiv/papers/1307/1307.1098.pdf. |
| [23] | Animalu A.O.E., Akpojotor G.E and Echenim M.W. (2012). Oyibo’s grand unified theorem revisited: an O(4,2)xSU(3)xU(1) gauge theory of quantum gravity. African Journal of Physics Vol.5, pp. 1-13. |



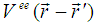 in the presence of an ionic lattice potential
in the presence of an ionic lattice potential 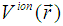 has the form [10,12]
has the form [10,12]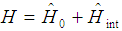
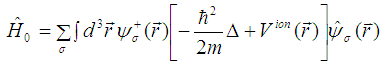
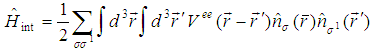
 are the usual field operators and
are the usual field operators and 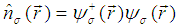 is the local density. It has been observed [12] that the interaction term is diagonal in the space variables
is the local density. It has been observed [12] that the interaction term is diagonal in the space variables 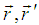 [i.e. it depends only on the (operator-valued) densities of electrons at site
[i.e. it depends only on the (operator-valued) densities of electrons at site 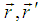 which interact via
which interact via 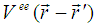 ]. The lattice potential entering the non-interacting part (Eq.2.2) leads to the splitting of the parabolic dispersion into infinitely many bands which are enumerated by the index α. The non-interacting problem is then characterized by the Block wave functions
]. The lattice potential entering the non-interacting part (Eq.2.2) leads to the splitting of the parabolic dispersion into infinitely many bands which are enumerated by the index α. The non-interacting problem is then characterized by the Block wave functions 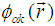 and the band energies
and the band energies 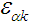 . The Wannier functions
. The Wannier functions 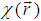 localized at site Ri are often introduced:
localized at site Ri are often introduced: 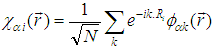
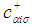 and
and 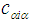 respectively, for electrons with spin σ in the band α at site Ri as
respectively, for electrons with spin σ in the band α at site Ri as 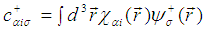
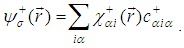
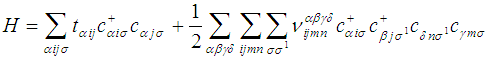
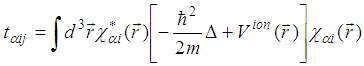
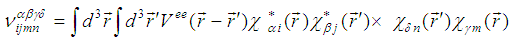
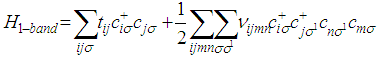
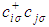 which are the creation (annihilation) operators at site i(j) having spin σ(σ) while the hopping term is defined as tij = t for NN hopping <i,j> (i.e. i ≠ j) and tij = 0 otherwise.The purely local contribution is the on-site Coulombic interaction term defined as
which are the creation (annihilation) operators at site i(j) having spin σ(σ) while the hopping term is defined as tij = t for NN hopping <i,j> (i.e. i ≠ j) and tij = 0 otherwise.The purely local contribution is the on-site Coulombic interaction term defined as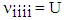
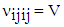
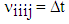
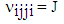
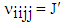
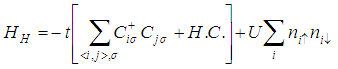
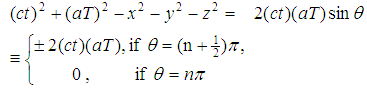
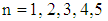 by limiting
by limiting 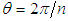 , needed for only rotations compatibles with translational symmetry of a crystal lattice in 3D space such that
, needed for only rotations compatibles with translational symmetry of a crystal lattice in 3D space such that 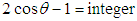 .
.
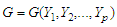 is said to be conformal invariant under a given group transformation
is said to be conformal invariant under a given group transformation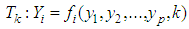
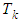 is the group of the transformation and
is the group of the transformation and 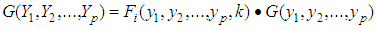
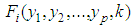 is a function of
is a function of 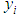 and
and 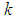 the single group parameter. From Table 1, we see that the group of translations in a crystal lattice and the Bloch (electron wave) function, more specifically lattice waves, have analogous properties as Eqs.(3.1) and (3.2). As a result, one needs only to show here that in quantized space-time geometry with given (Planck length) lattice spacing, the definition of conformal invariance in Eqs.(3.1) and (3.2) follows, as in Bloch’s theorem, from translational periodicity of any function of position in the lattice.On the basis of the definition in Eqs.(3.1) and (3.2), Oyibo states that there exists a set of conservation equations
the single group parameter. From Table 1, we see that the group of translations in a crystal lattice and the Bloch (electron wave) function, more specifically lattice waves, have analogous properties as Eqs.(3.1) and (3.2). As a result, one needs only to show here that in quantized space-time geometry with given (Planck length) lattice spacing, the definition of conformal invariance in Eqs.(3.1) and (3.2) follows, as in Bloch’s theorem, from translational periodicity of any function of position in the lattice.On the basis of the definition in Eqs.(3.1) and (3.2), Oyibo states that there exists a set of conservation equations 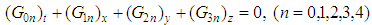
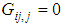 where the function defined mathematically by
where the function defined mathematically by 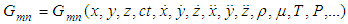 is a set of “generic” quantities which are arbitrary functions of space and time coordinates (x,y,z,ct), velocities
is a set of “generic” quantities which are arbitrary functions of space and time coordinates (x,y,z,ct), velocities 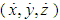 , accelerations
, accelerations 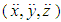 , density
, density 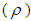 , fluid or gas viscosity
, fluid or gas viscosity 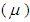 , temperature (T), pressure (P), etc. Now by applying the conformal transformation defined by Eq.(3.1) to a system of partial differential equations of nth order given by
, temperature (T), pressure (P), etc. Now by applying the conformal transformation defined by Eq.(3.1) to a system of partial differential equations of nth order given by 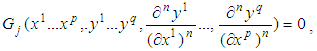
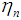 of the subgroup of transformations for the independent coordinate variables in the form:
of the subgroup of transformations for the independent coordinate variables in the form: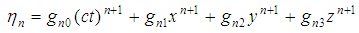
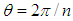 , where n =1,2,3,4 or 6, corresponding to n-fold rotation axis of symmetry [1].Finally, analogy between Bloch’s theorem and Oyibo GUT leads to identification of
, where n =1,2,3,4 or 6, corresponding to n-fold rotation axis of symmetry [1].Finally, analogy between Bloch’s theorem and Oyibo GUT leads to identification of 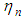 with the wave number associated with the primitive translation vectors of the reciprocal lattice of a 3D crystal
with the wave number associated with the primitive translation vectors of the reciprocal lattice of a 3D crystal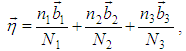
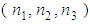 being integers and
being integers and 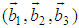 the primitive translation vectors of the reciprocal lattice space and
the primitive translation vectors of the reciprocal lattice space and 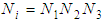 the number of primitive cells in the crystal. For a cubic lattice in
the number of primitive cells in the crystal. For a cubic lattice in 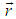 -space,
-space, 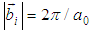 , where
, where 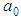 is the lattice constant, which we shall take (in Oyibo GUT representation of general theory of relativity) to be the Planck length.However, the nth order partial differential equations (3.4) are not quite analogous to the non-relativistic Schrodinger equation of Bloch’s theorem in Table 1 except insofar as the system of partial differential in Eqs.(3.4) may be rewritten, in the first order, as follows
is the lattice constant, which we shall take (in Oyibo GUT representation of general theory of relativity) to be the Planck length.However, the nth order partial differential equations (3.4) are not quite analogous to the non-relativistic Schrodinger equation of Bloch’s theorem in Table 1 except insofar as the system of partial differential in Eqs.(3.4) may be rewritten, in the first order, as follows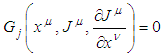
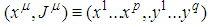 where
where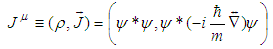
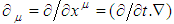 into Eq.(3.8), it becomes the current conservation law [15]
into Eq.(3.8), it becomes the current conservation law [15] 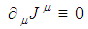

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML