Ewa I. I.1, Lumbi L. W.1, Howusu S. X. K.2
1Department of Physics, Nasarawa State University, Keffi, Nigeria
2National Mathematical Centre, Kwali, Abuja, Nigeria
Correspondence to: Ewa I. I., Department of Physics, Nasarawa State University, Keffi, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this article, the golden Riemannian Laplacian operator was constructed using the golden metric tensor in spherical polar coordinate and was applied to the Schrodinger wave equation in order to obtain the golden Riemannian Schrodinger equation for a particle in a finite-potential well. The results are that the golden Riemannian Laplacian operator and golden Riemannian Schrodinger equation were augmented with additional correction terms; which are not found in the existing equations and can be applied to a finite-potential well problem, so as to obtain the expression for the allowed energy values.
Keywords:
Schrodinger wave equation, Spherical polar coordinate, Golden Riemannian, Laplacian operator, Golden metric tensor
Cite this paper: Ewa I. I., Lumbi L. W., Howusu S. X. K., Riemannian Quantum Theory of a Particle in a Finite-Potential Well, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 1, 2018, pp. 28-31. doi: 10.5923/j.ijtmp.20180801.03.
1. Introduction
Quantum Physics is the study of Physics in the realm of atoms, nuclei and elementary particles [1]. This statement does not mean that quantum physics has nothing to do with the macroscopic world. In fact, all of physics is quantum physics and classical physics is a constrictive case of quantum physics.The origin of quantum physics occupies a time period in history that covers a quarter of a century. Classical or Newtonian mechanics was available in the powerful formulations of Lagrange and Hamilton by the year 1900. Thus, classical electromagnetic theory was embodied in the differential equations of Maxwell. Defects were, however, made clear by the failure of the classical theories to explain some experimental results, notably, the frequency dependence of the intensity of radiation emitted by a blackbody, the photoelectric effect and the stability and size of atoms [2].Quantum Physics came to existence in 1900 when a famous pronouncement was put forward by Planck to unfold and illustrate the meaning of the observed properties of the radiation ejected by a blackbody [3]. This phenomenon posed an unsolved problem to theoretical physicists for several decades.Principles of thermodynamics and electromagnetism had been applied to the problem but, these classical methods had failed to give a sensible explanation of the experimental results [11, 1].The quantum hypothesis of Planck and the subsequent interpretation of the idea by Einstein in 1905 gave electromagnetic radiation discrete properties; somewhat similar to those of a particle. The quantum theory made provision for radiation to have both wave and particle aspects in a complementary form of coexistences. The theory was extended when matter was found to have wave characteristics as well as particle properties by de Broglie in 1923 [9]. These notions continued to evolve until 1925 when the formal apparatus of quantum theory came into being.The discovery of the wave like behavior of an electron created the need for a wave theory describing the behavior of a particle on the atomic scale. This theory was proposed by Schrodinger in the year 1926, two years after De Broglie formulated the idea of a particle wave nature [8]. Schrodinger reasoned that if an electron behaves as a wave, then it should be possible to mathematically describe the electrons behavior in space time coordinate as a wave.The Schrodinger proposed theory; yielded the fundamental equation of quantum mechanics known as the Schrodinger wave equation. This equation has the same central importance to quantum mechanics as Newton’s law of motion has for classical mechanics [10].Howusu (2003) stated that, since 1926, there has been the need to derive one theory of quantum mechanics from or corresponding to Einstein’s theory of special relativity for the description of the wave behavior of all entities in electromagnetic fields; since Schrodinger’s Dynamical theory of quantum mechanics is related to Newton’s Dynamical theory of classical mechanics.On this basis, the quantum theory of the finite-potential well was constructed using the Riemannian golden metric tensor.
2. Theoretical Analysis
2.1. Derivation of Riemannian Laplacian Operator in Spherical Polar Coordinate Based upon the Golden Metric Tensor
Consider a particle of mass, m in a finite-potential well of width, a and depth, 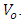 The Riemannian Laplacian operator [12, 6] is given by
The Riemannian Laplacian operator [12, 6] is given by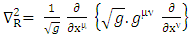 | (1) |
where 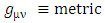 and
and 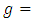 determinant of
determinant of 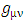 The Golden Riemannian metric tensors in spherical polar coordinate [6, 7] are given by
The Golden Riemannian metric tensors in spherical polar coordinate [6, 7] are given by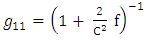 | (2) |
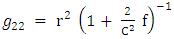 | (3) |
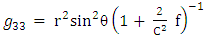 | (4) |
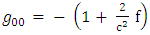 | (5) |
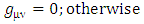 | (6) |
and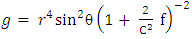 | (7) |
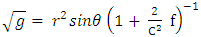 | (8) |
From equation (1) we have: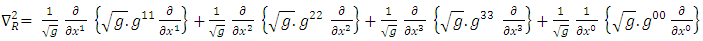 | (9) |
If we let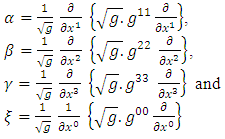 Equation (9) reduces to
Equation (9) reduces to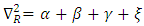 | (10) |
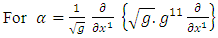 | (11) |
To obtain 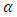 in spherical polar coordinate, we substitute equations (2) and (7) into equation (11) as follows:
in spherical polar coordinate, we substitute equations (2) and (7) into equation (11) as follows: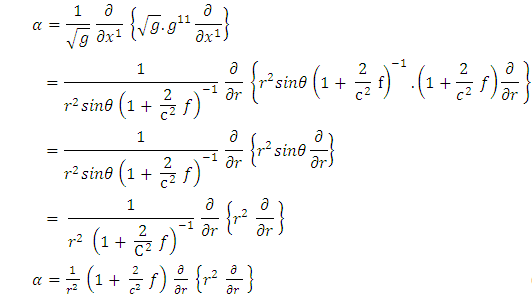 | (12) |
 | (13) |
To obtain 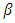 in spherical polar coordinate, we substitute equations (3) and (7) into equation (13) as follows:
in spherical polar coordinate, we substitute equations (3) and (7) into equation (13) as follows: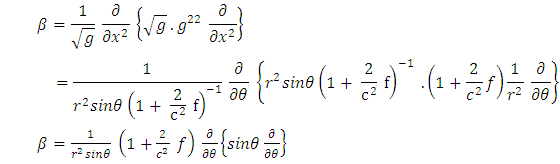 | (14) |
 | (15) |
To obtain 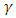 in spherical polar coordinate, we substitute equations (4) and (7) into equation (15) as follows:
in spherical polar coordinate, we substitute equations (4) and (7) into equation (15) as follows: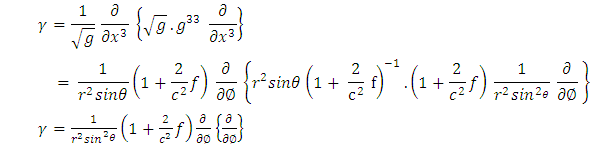 | (16) |
 | (17) |
To obtain 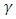 in spherical polar coordinate, we substitute equations (5) and (7) intoequation (17) as follows:
in spherical polar coordinate, we substitute equations (5) and (7) intoequation (17) as follows: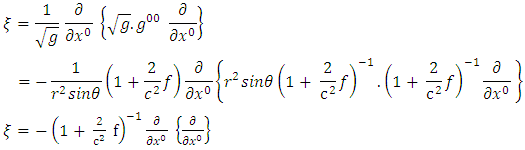 | (18) |
Substituting equations (12), (14), (16) and (18) into equation (10), we have thus: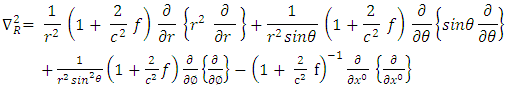 | (19) |
Equation (19) is the golden Riemannian Laplacian operator in spherical polar coordinate. The well-known Laplacian operator is derived based on Euclidean geometry while equation (19) is derived based on the Riemannian geometry using the golden metric tensor. This equation is further applied to the Schrodinger equation in order to obtain the golden Riemannian Schrodinger equation.
2.2. Derivation of Golden Riemannian Schrodinger Equation in Spherical Polar Coordinate
Consider the well-known Schrodinger equation [4, 5] given by 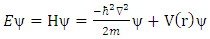 | (20) |
where 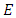 is energy of the particle, H is Hamiltonian of the system, m is mass of the particle,
is energy of the particle, H is Hamiltonian of the system, m is mass of the particle, 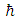 is normalized Planck’s constant,
is normalized Planck’s constant, 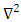 is Euclidean Laplacian of the system, V is particle potential and
is Euclidean Laplacian of the system, V is particle potential and 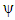 is wave function.We replace the Euclidean Laplacian operator with the golden Riemannian Laplacian operator in equation (19); that is:
is wave function.We replace the Euclidean Laplacian operator with the golden Riemannian Laplacian operator in equation (19); that is: 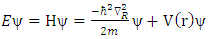 | (21) |
Substituting the expression for the Riemannian Laplacian operator, 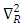 into equation (21), we obtain
into equation (21), we obtain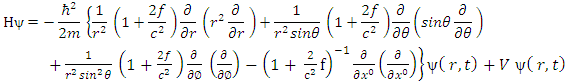 | (22) |
Expanding equation (22) and considering that 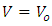 which is the depth of the potential well, we obtain
which is the depth of the potential well, we obtain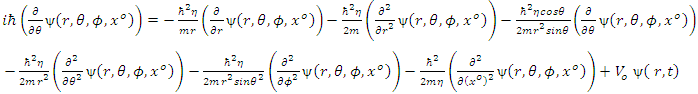 | (23) |
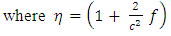 | (24) |
Equation (23) is the golden Riemannian Schrodinger equation in spherical polar coordinates.
3. Discussion
Equation (4.23) is the golden Riemannian Schrodinger equation in spherical polar coordinates. Equation (4.23) contains 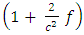 which is not found in the well-known Schrodinger equation [9]. This term is the golden Riemannian term.The terms in braces are the additional correction terms which are not found in the existing Schrodinger equation. This additional correction terms give better explanation of the energy of a particle in a finite potential well. This can also be applied to all entities of non-zero rest mass such as: infinite potential well, rectangular potential well, simple harmonic oscillator etc.This equation can be analytically solved in order to obtain the particle energies in a finite potential well; unlike the existing Schrodinger equation that leads to transcendental equations which require either the graphical or numerical solutions when applied to the finite potential well.
which is not found in the well-known Schrodinger equation [9]. This term is the golden Riemannian term.The terms in braces are the additional correction terms which are not found in the existing Schrodinger equation. This additional correction terms give better explanation of the energy of a particle in a finite potential well. This can also be applied to all entities of non-zero rest mass such as: infinite potential well, rectangular potential well, simple harmonic oscillator etc.This equation can be analytically solved in order to obtain the particle energies in a finite potential well; unlike the existing Schrodinger equation that leads to transcendental equations which require either the graphical or numerical solutions when applied to the finite potential well.
4. Remarks and Conclusions
We have in this article, shown how to formulate and construct the Riemannian Laplacian operator and the golden Riemannian Schrodinger equation. This equation can be solved analytically to obtain the Riemannian energy levels of a particle in a finite potential well.
References
| [1] | Anchaver, R. S. (2003). Introduction to Non-Relativistic Quantum Mechanics. Nigeria, ISBN: 978-056-139-0, 1-3. |
| [2] | Brumel, R. (2005). Analytical Solution of the Finite Quantum Square-Well Problem. Journal of Physics. 38, 673-678. |
| [3] | Hewitt, P. G. (2002). Conceptual Physics. 9th Edition, World Student Series, Brad Lewis/Stone Publishers, 630-631. |
| [4] | Howusu, S.X.K. (2003a). Riemannian Revolution in Physics and Mathematics. Jos University Press Ltd, Jos, 1-200. |
| [5] | Howusu, S. X. K. (2003b). The Natural Philosophy of Quantum Mechanics. 2nd Edition, Jos University Press Ltd., Jos, ISBN: 978-166-073-2, 20-25. |
| [6] | Howusu, S. X. K. (2009). The Metric Tensors for gravitational Fields and The Mathematical Principle of Riemannian Theoretical Physics. 1st Edition, Jos University Press Ltd., Jos, ISBN: 978-166-639-0, 121-122. |
| [7] | Howusu, S. X. K. (2011). The Golden Metric Tensor in Orthogonal Curvilinear Co-ordinates. 1st Edition, Jos University Press Ltd., Jos, ISBN: 978-166-294-8, 5-6. |
| [8] | Jones, E. & Childers, R. (1983). Contemporary College Physics. 3rd Edition, McGraw Hill, New York, 889. |
| [9] | Luca, N. (2015). The Hydrogen Atom: A Review on the Birth of Modern Quantum Mechanics. 1-3. |
| [10] | Lumbi, W. L. & Ewa, I. I. (2013). General Relativistic Equation of Motion for a Photon Moving Round a Time Varying Spherical Distribution of Mass. Advances in Natural Science, 6(3), 23-25. |
| [11] | Ronald, C. B. (2007). Inverse Quantum Mechanics of the Hydrogen Atom: A General Solution. Adv. Studies Theor. Phys. 1(8), 381-393. |
| [12] | Spiegel, M. R. (1974). Theory and Problems of Vector Analysis and Introduction to Tensor Analysis. 1st Edition, McGraw Hill, New York, 166-217. |



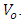 The Riemannian Laplacian operator [12, 6] is given by
The Riemannian Laplacian operator [12, 6] is given by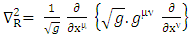
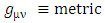 and
and 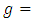 determinant of
determinant of 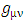 The Golden Riemannian metric tensors in spherical polar coordinate [6, 7] are given by
The Golden Riemannian metric tensors in spherical polar coordinate [6, 7] are given by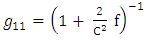
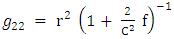
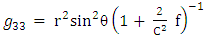
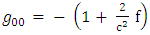
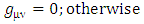
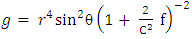
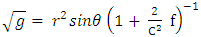
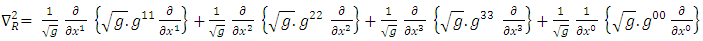
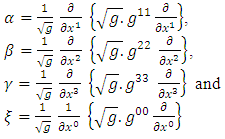 Equation (9) reduces to
Equation (9) reduces to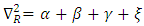
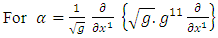
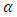 in spherical polar coordinate, we substitute equations (2) and (7) into equation (11) as follows:
in spherical polar coordinate, we substitute equations (2) and (7) into equation (11) as follows:

 in spherical polar coordinate, we substitute equations (3) and (7) into equation (13) as follows:
in spherical polar coordinate, we substitute equations (3) and (7) into equation (13) as follows: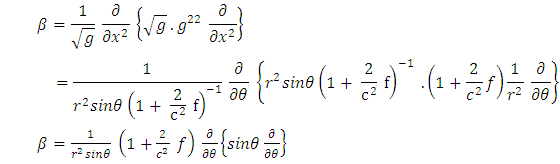

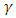 in spherical polar coordinate, we substitute equations (4) and (7) into equation (15) as follows:
in spherical polar coordinate, we substitute equations (4) and (7) into equation (15) as follows: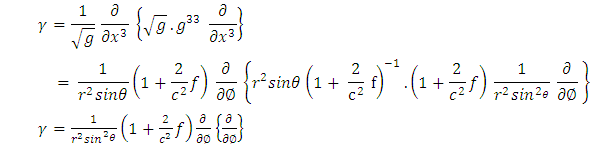

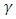 in spherical polar coordinate, we substitute equations (5) and (7) intoequation (17) as follows:
in spherical polar coordinate, we substitute equations (5) and (7) intoequation (17) as follows: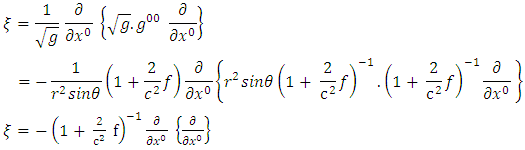
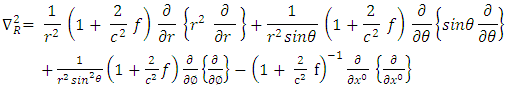
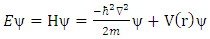
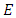 is energy of the particle, H is Hamiltonian of the system, m is mass of the particle,
is energy of the particle, H is Hamiltonian of the system, m is mass of the particle, 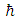 is normalized Planck’s constant,
is normalized Planck’s constant, 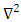 is Euclidean Laplacian of the system, V is particle potential and
is Euclidean Laplacian of the system, V is particle potential and 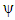 is wave function.We replace the Euclidean Laplacian operator with the golden Riemannian Laplacian operator in equation (19); that is:
is wave function.We replace the Euclidean Laplacian operator with the golden Riemannian Laplacian operator in equation (19); that is: 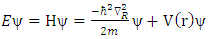
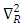 into equation (21), we obtain
into equation (21), we obtain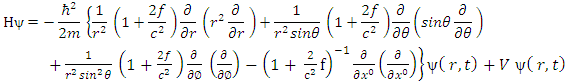
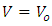 which is the depth of the potential well, we obtain
which is the depth of the potential well, we obtain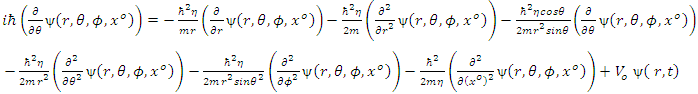
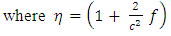
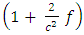 which is not found in the well-known Schrodinger equation [9]. This term is the golden Riemannian term.The terms in braces are the additional correction terms which are not found in the existing Schrodinger equation. This additional correction terms give better explanation of the energy of a particle in a finite potential well. This can also be applied to all entities of non-zero rest mass such as: infinite potential well, rectangular potential well, simple harmonic oscillator etc.This equation can be analytically solved in order to obtain the particle energies in a finite potential well; unlike the existing Schrodinger equation that leads to transcendental equations which require either the graphical or numerical solutions when applied to the finite potential well.
which is not found in the well-known Schrodinger equation [9]. This term is the golden Riemannian term.The terms in braces are the additional correction terms which are not found in the existing Schrodinger equation. This additional correction terms give better explanation of the energy of a particle in a finite potential well. This can also be applied to all entities of non-zero rest mass such as: infinite potential well, rectangular potential well, simple harmonic oscillator etc.This equation can be analytically solved in order to obtain the particle energies in a finite potential well; unlike the existing Schrodinger equation that leads to transcendental equations which require either the graphical or numerical solutions when applied to the finite potential well. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML