-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2018; 8(1): 12-27
doi:10.5923/j.ijtmp.20180801.02

Spin Two-Body Problem of Classical Electrodynamics with Radiation Terms (II) – Existence of Solution of the Spin Equations
Vasil G. Angelov
Department of Mathematics, Faculty of Mining Electro-mechanics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria
Correspondence to: Vasil G. Angelov, Department of Mathematics, Faculty of Mining Electro-mechanics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The primary purpose of the present paper is to continue our studies from previous papers where the spin equations were derived. Here we prove an existence of a periodic solution of the spin equations system using fixed point method. As a consequence, we obtain that the general two-body problem of classical electrodynamics with radiation terms and spin is already solved.
Keywords: Two body problem of classical electrodynamics, Spin equations, Periodic solutions, Radiation terms
Cite this paper: Vasil G. Angelov, Spin Two-Body Problem of Classical Electrodynamics with Radiation Terms (II) – Existence of Solution of the Spin Equations, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 1, 2018, pp. 12-27. doi: 10.5923/j.ijtmp.20180801.02.
Article Outline
1. Introduction
- The present paper is an immediate consequence of [1]. In [1] we have derived a general system of equations of motion describing two-body problem with radiation terms and spin. The results obtained rely on the previous papers [2] - [19]. We note another approach based on Wheeler-Feynman ideas and realized by D.-A. Deckert group (cf. [20] - [23]).The general system describing motion of two mass charged particles with radiation terms and spin in the frame of classical electrodynamics derived in [1] is:
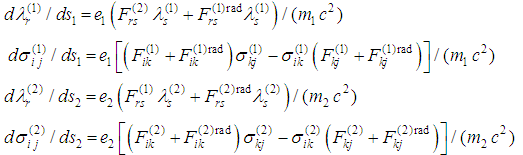 | (1) |
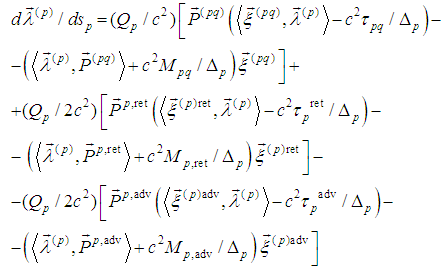 | (2) |
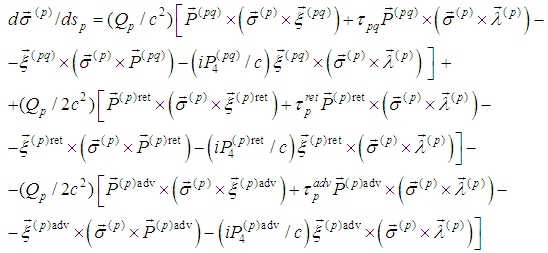 | (3) |
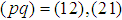 .In [7] we have proved an existence-uniqueness of a periodic solution of equations of motion for two-body problem with corrected radiation terms, namely system (2). It remains to prove an existence of periodic solution of (3). On the right side of the equation (3) are the speeds and trajectories of the moving particles. Their existence is proven in [7]. We will consider them as known functions in (3).The main goal of the present paper is to prove an existence of periodic spin functions
.In [7] we have proved an existence-uniqueness of a periodic solution of equations of motion for two-body problem with corrected radiation terms, namely system (2). It remains to prove an existence of periodic solution of (3). On the right side of the equation (3) are the speeds and trajectories of the moving particles. Their existence is proven in [7]. We will consider them as known functions in (3).The main goal of the present paper is to prove an existence of periodic spin functions 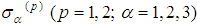 satisfying (3). To do this we transform (3) using the known relations from vector calculus and obtain:
satisfying (3). To do this we transform (3) using the known relations from vector calculus and obtain: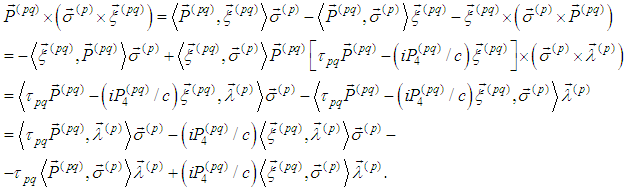 Therefore
Therefore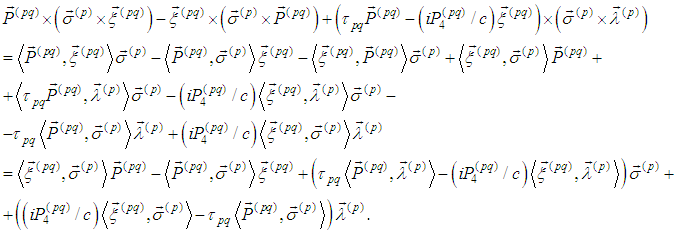 Then the system (3) becomes
Then the system (3) becomes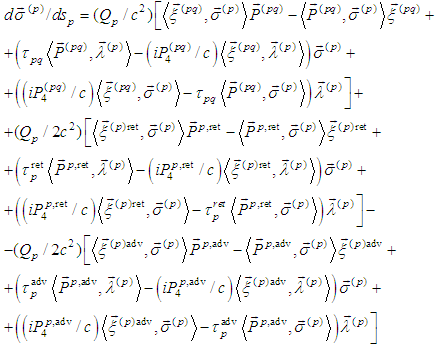 In coordinate form (3) is (α = 1,2,3):
In coordinate form (3) is (α = 1,2,3):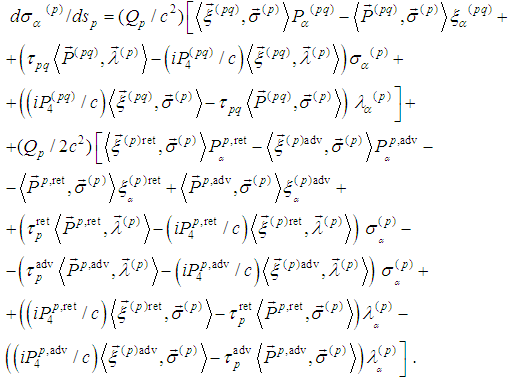 | (4) |
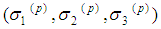 is a solution of the system (4) then
is a solution of the system (4) then 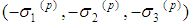 is a solution too.
is a solution too.2. Formulation of the Periodic Problem for Spin Equations System
- Recall denotations for quantities relating to the particles. The space-time coordinates of the moving particles are
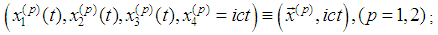 ;c is the speed of the light;
;c is the speed of the light; 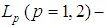 world lines;
world lines; 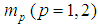 – proper masses;
– proper masses; 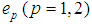 – charges;
– charges;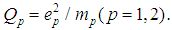 We have
We have 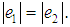 But the in- teresting case is
But the in- teresting case is 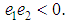 Then
Then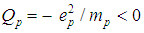
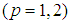 ;
;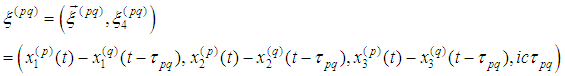
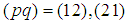 are components of the null vector lying on the light cone;
are components of the null vector lying on the light cone; 
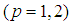 are velocities of the moving particles;
are velocities of the moving particles;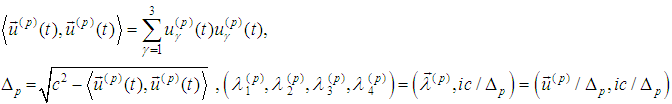 are components of the unit tangent vectors to world lines;
are components of the unit tangent vectors to world lines;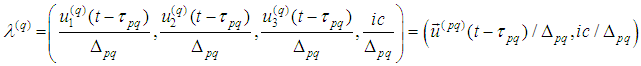 where
where 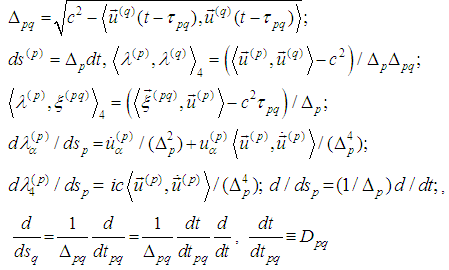 where the derivative is calculated from the equation
where the derivative is calculated from the equation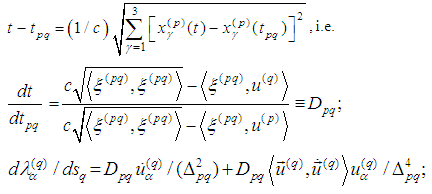
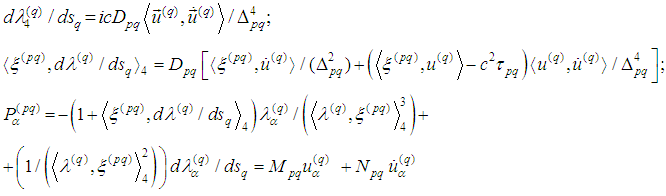 where
where 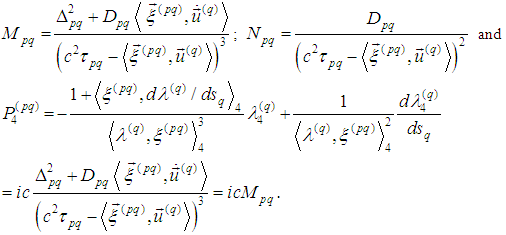 Consequently
Consequently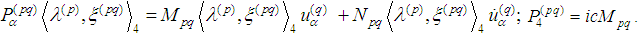 We recall the basic assumption
We recall the basic assumption 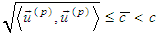 .Finally we write down (4) in the form
.Finally we write down (4) in the form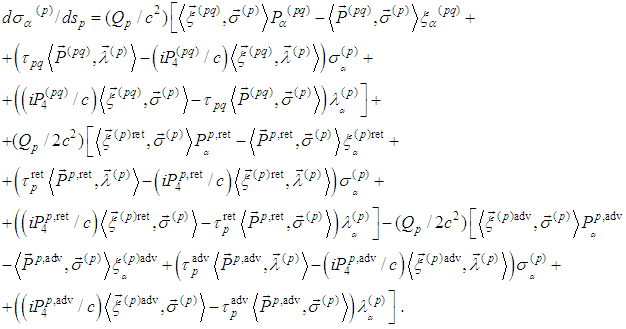 | (5) |
3. Operator Presentation of the Periodic Problem
- In this section we formulate an operator presentation of the periodic problem for (5).First we transform (5) in order to obtain a suitable form of the spin equations system:
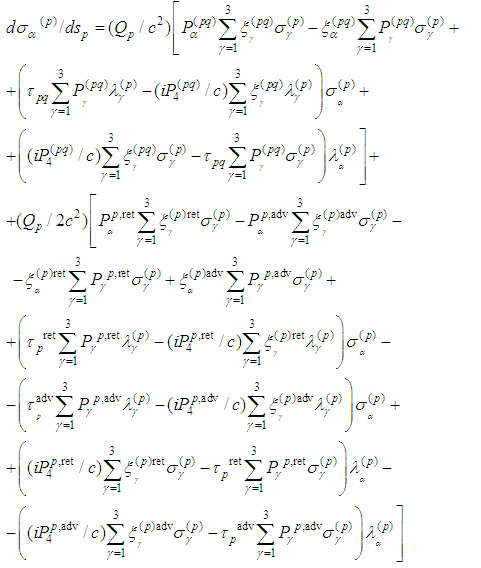 or
or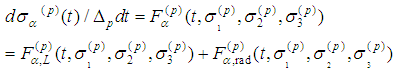 | (7) |
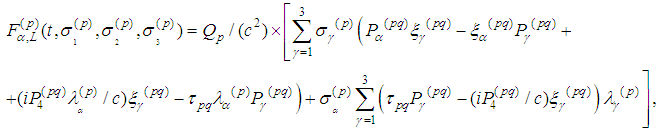
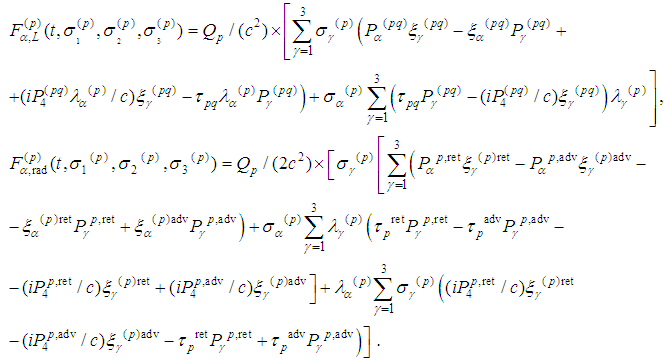 In what follows we call
In what follows we call 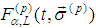 Lorentz term of the spin equations, while
Lorentz term of the spin equations, while 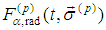 − radiation term.We recall (cf. [7]) that velocity functions
− radiation term.We recall (cf. [7]) that velocity functions 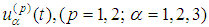 belong to the space
belong to the space 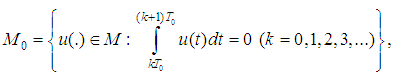 where
where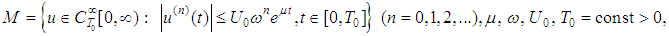
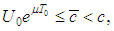
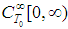 is the space of all infinite differentiable
is the space of all infinite differentiable 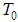 - periodic functions. Following A. Sommerfeld [9], [10] we denote by
- periodic functions. Following A. Sommerfeld [9], [10] we denote by 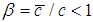 . It follows that trajectories and velocities are
. It follows that trajectories and velocities are 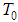 -periodic functions.Our goal is to prove an existence of
-periodic functions.Our goal is to prove an existence of 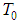 -periodic solution of (6). For that purpose we define an operator on the space
-periodic solution of (6). For that purpose we define an operator on the space 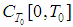 consisting of all continuous functions such that
consisting of all continuous functions such that 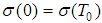 by the formulas
by the formulas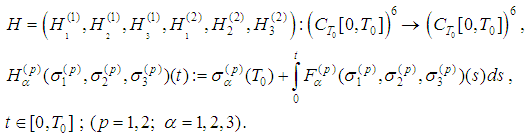 | (8) |
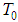 -periodic solution of (6) is a fixed point of H and vice versa.The proof can be found in [24] (M. A. Krasnoselskii).Consequently, we have to prove an existence of a fixed point of the operator H.
-periodic solution of (6) is a fixed point of H and vice versa.The proof can be found in [24] (M. A. Krasnoselskii).Consequently, we have to prove an existence of a fixed point of the operator H.4. Preliminary Lipschitz Estimates of the Lorentz Term of the Spin Equations
- First we notice that
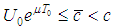 ;
;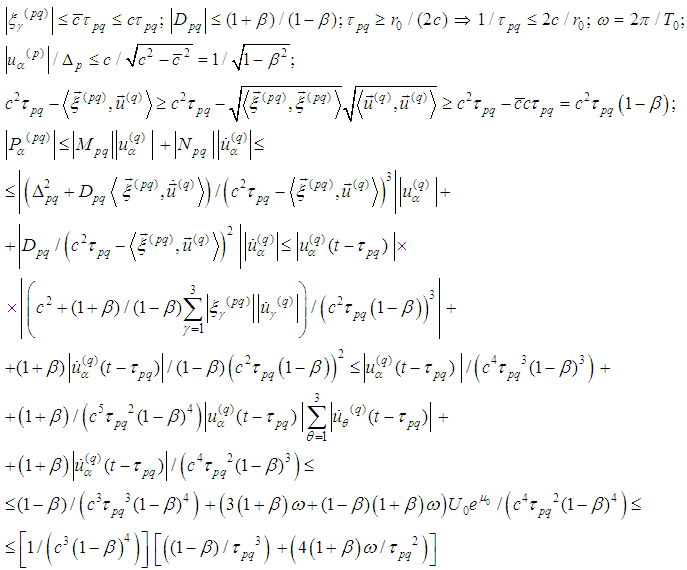 and
and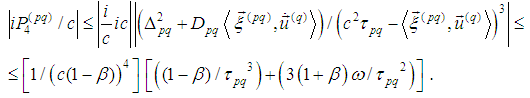 Then
Then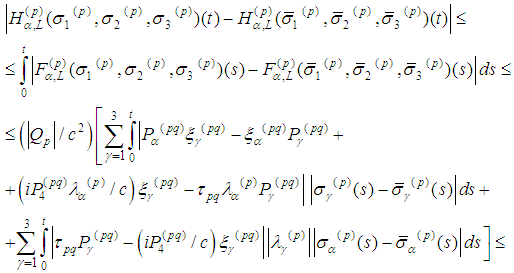
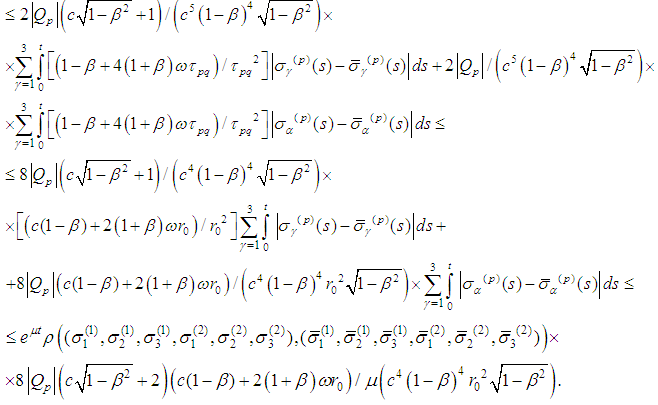
5. Preliminary Lipschitz Estimates of the Radiation Term of the Spin Equations
- Here we transform the radiation part of the spin equation using some reasoning from [7]. Indeed, we recall assumption
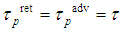 with
with 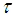 small:
small: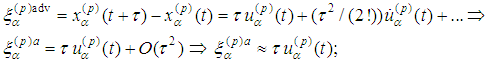
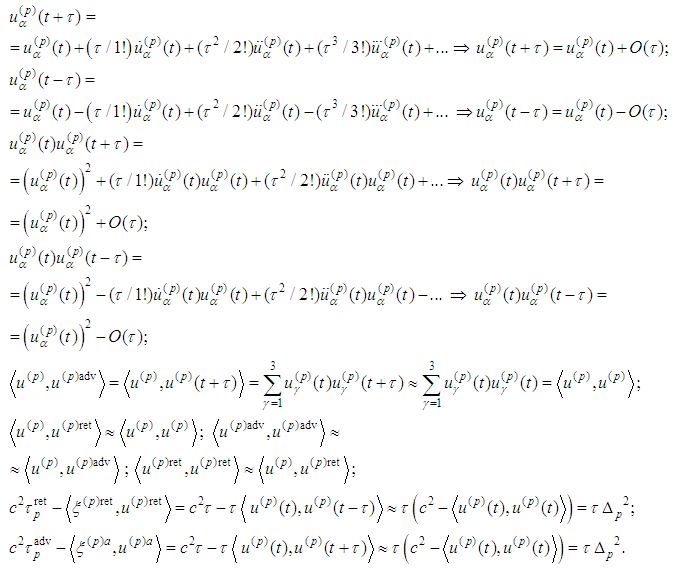 Then
Then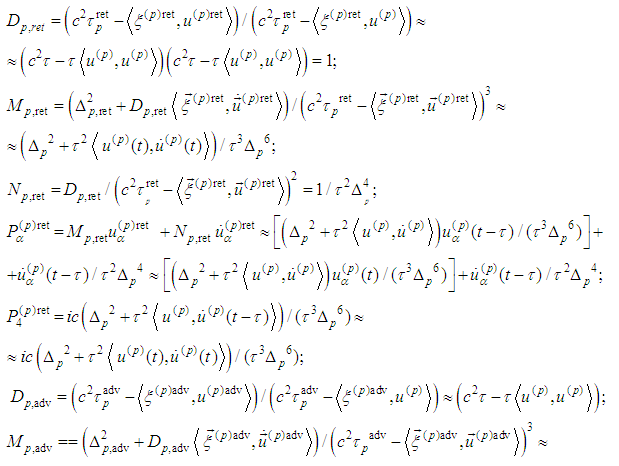
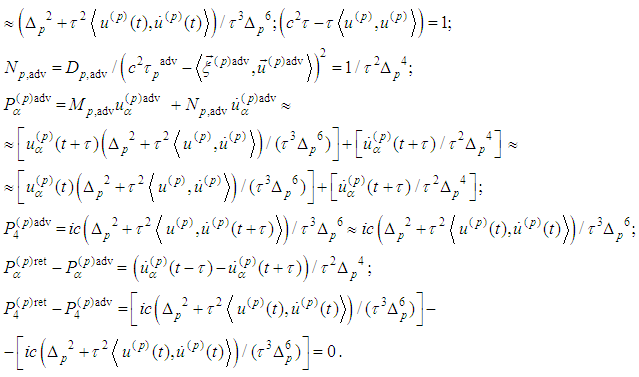 Then we transform the radiation part of (5) with accordance of assumptions from [7]:
Then we transform the radiation part of (5) with accordance of assumptions from [7]: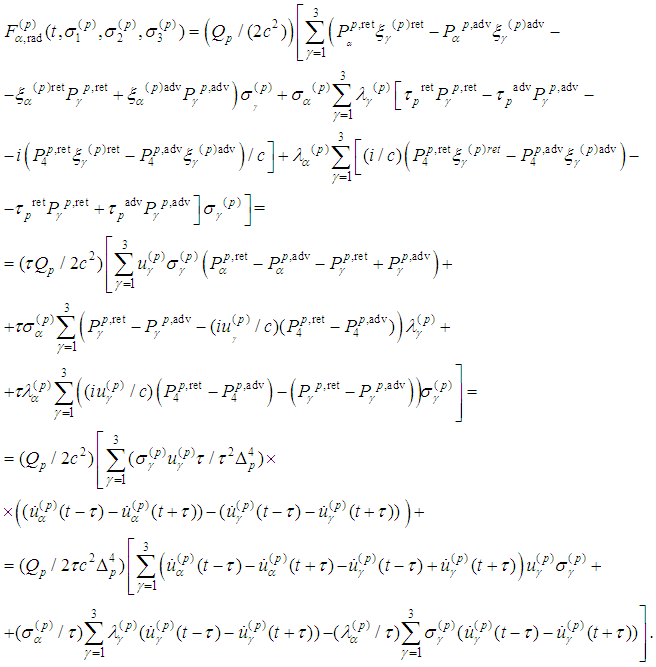 Consequently in view of
Consequently in view of 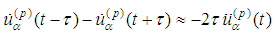 we obtain
we obtain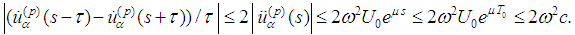 Then
Then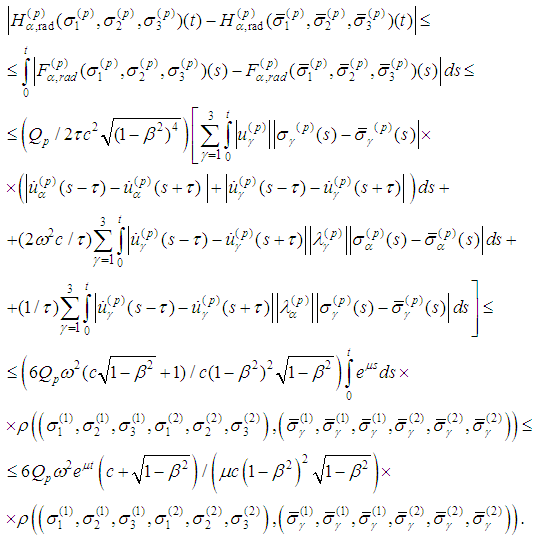 Therefore
Therefore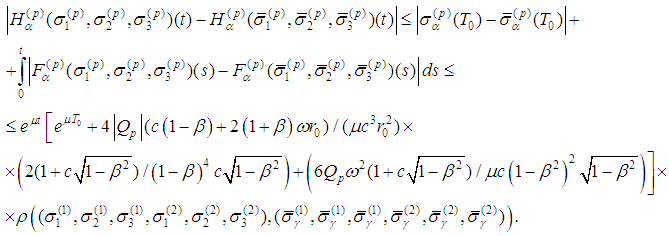 It follows
It follows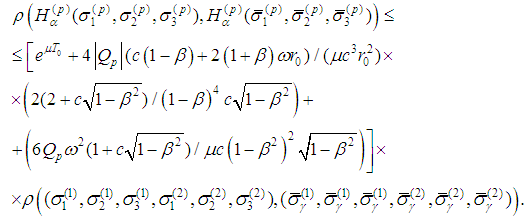 Therefore the operator H is continuous one.
Therefore the operator H is continuous one. 6. Existence of a Periodic Solution of the General System
- The main result of the present paper is:Theorem 1. Let the following conditions be fulfilled:
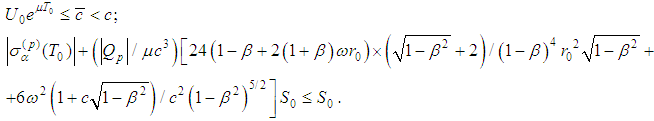 Then there exists a periodic solution of (5).Proof: Introduce the set
Then there exists a periodic solution of (5).Proof: Introduce the set 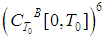 with a metric
with a metric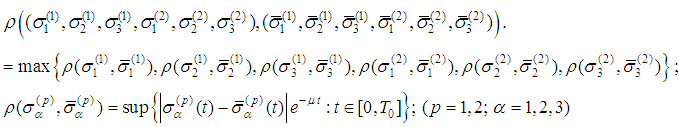 where
where 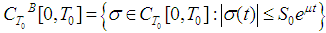 ,
, 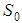 is a fixed constant.Our first step is to show that the operator H maps
is a fixed constant.Our first step is to show that the operator H maps 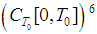 into itself, that is,
into itself, that is,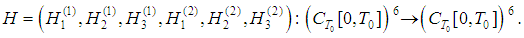 Indeed,
Indeed,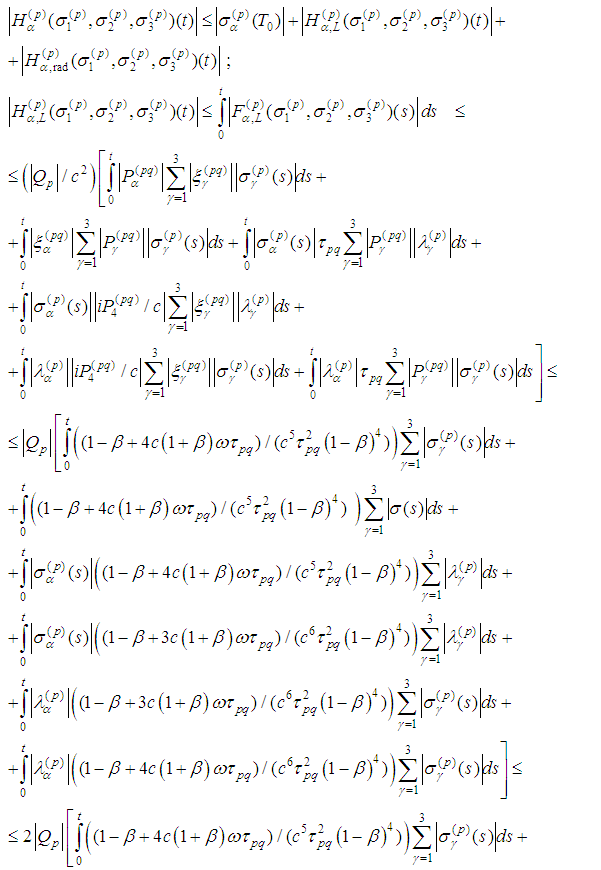
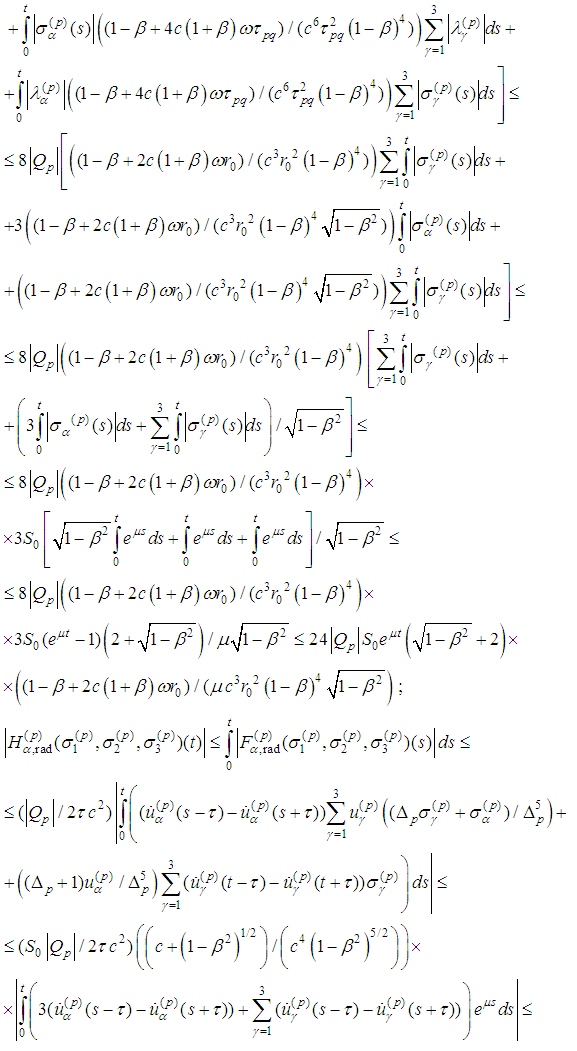
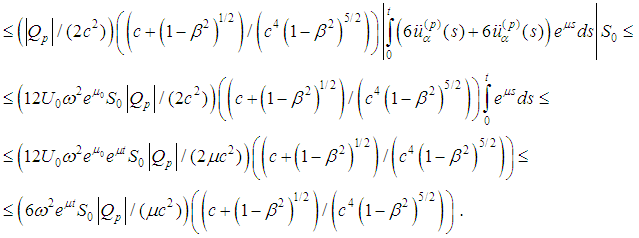 Therefore
Therefore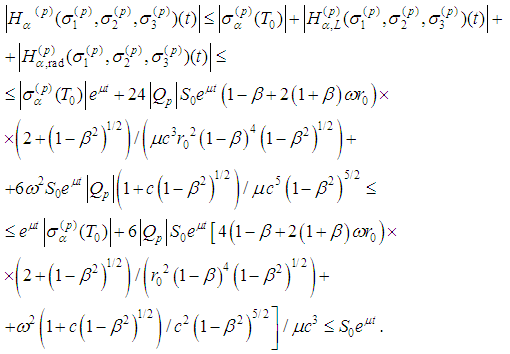 Consequently the operator H maps
Consequently the operator H maps 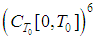 into itself. It remains to show that the set H(M) is equicontinuous. Indeed, for
into itself. It remains to show that the set H(M) is equicontinuous. Indeed, for 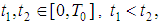 , we have
, we have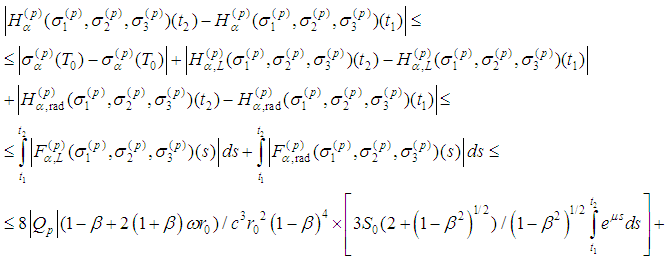
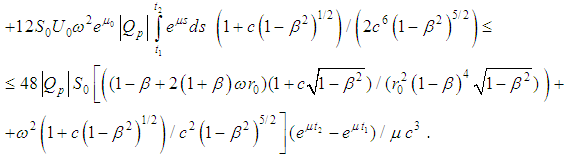 Theorem is thus proved.
Theorem is thus proved. 7. Numerical Confirmation of the Results Obtained for the Hydrogen Atom
- Here we show that all assertions obtained concerning two-body problem completely confirm the experimental results for the hydrogen atom. Indeed, we recall that
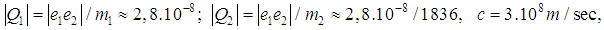 the radiation time is
the radiation time is 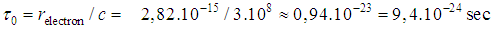 . Since the radius of first Bohr orbit is
. Since the radius of first Bohr orbit is 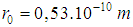 and its velocity is
and its velocity is 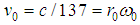 (1/137 − Sommerfeld fine structure constant [9], [10]), then
(1/137 − Sommerfeld fine structure constant [9], [10]), then 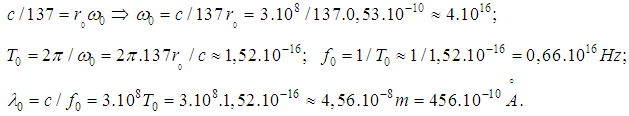 Our estimates require
Our estimates require 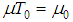 to be a constant. Here
to be a constant. Here 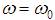 and we have to take
and we have to take 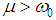 , for instance
, for instance 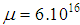 . Then
. Then 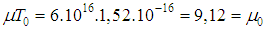 . Therefore
. Therefore 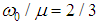 and
and 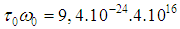
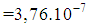 , that is condition
, that is condition 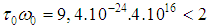 is satisfied. Here
is satisfied. Here 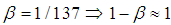 .The following inequalities guarantee an existence of periodic solution of the equations of motion with radiation terms (obtained in [7]):
.The following inequalities guarantee an existence of periodic solution of the equations of motion with radiation terms (obtained in [7]): 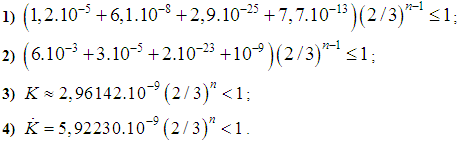 In the above inequalities n might be chosen arbitrarily large (cf. [7]).We have to verify the inequality from the main theorem
In the above inequalities n might be chosen arbitrarily large (cf. [7]).We have to verify the inequality from the main theorem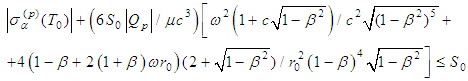 or in view of
or in view of 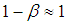
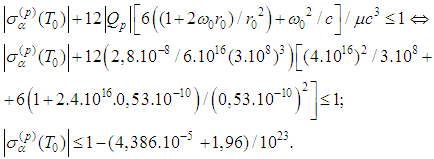 This means that the initial values of the spin functions should satisfy the last inequality.
This means that the initial values of the spin functions should satisfy the last inequality.8. Conclusions
- The present paper completes our investigations on the two-body problem of classical electrodynamics. Beginning with Synge model we have corrected Dirac radiation term and extended Corben-Stehle spin equations. We have proved an existence of unique periodic solution of the equations of motion in [7]
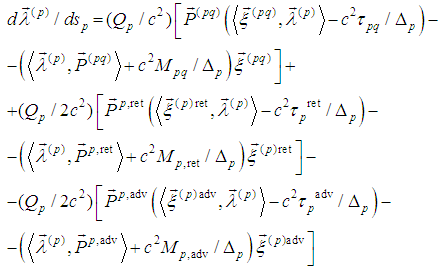 and here an existence of a periodic solution of spin equations
and here an existence of a periodic solution of spin equations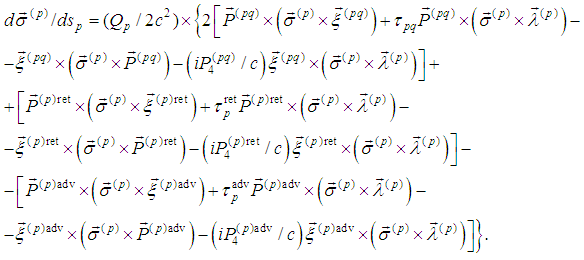 In this manner we have proved the stability of hydrogen atom and showed that stationary states introduced by N. Bohr are implied by classical electrodynamics. Introducing spin equations in the frame of relativistic Synge formalism we can investigate 3-body problem (and in general N-body) of classical electrodynamics.
In this manner we have proved the stability of hydrogen atom and showed that stationary states introduced by N. Bohr are implied by classical electrodynamics. Introducing spin equations in the frame of relativistic Synge formalism we can investigate 3-body problem (and in general N-body) of classical electrodynamics. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML