Salahdin Daouairi
Olympics Math Training, USA
Correspondence to: Salahdin Daouairi, Olympics Math Training, USA.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The goal in this article is to interpret, extend, develop and trace the theoretical path of the numerical puzzle model discovered in the previous article, a puzzle inside a puzzle under the article “Equation of everything, code unlocked” [1] that will concentrate on the fundamental structure of mathematics and its coherent relationship with nature! The universe is just a physical copy of the numerical system projection, mathematical philosophical arguments that was predicted by Pythagoras and Plato! The paper is a physical model of the mathematics itself! We will show that the numerical system is in dynamic asymmetrical invariant and interconnected through a homotopy for a connected path generated by Paul Dirac belt trick along the transformation of SO(3) generated by the axis! Even the mathematics replicates itself! The sphere 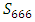 is just the exotic Milnor 7 dimensional sphere connected to the Torus knots (2, 3) with a 5 fold symmetry and related to the homology Poincare sphere
is just the exotic Milnor 7 dimensional sphere connected to the Torus knots (2, 3) with a 5 fold symmetry and related to the homology Poincare sphere 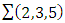 , the discrete unimodular lattice
, the discrete unimodular lattice 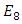 – singularity, A, D, E and platonic solids. The twisted, curved spacetime is defined from two important and special interconnected lattices in dynamic namely the square lattice
– singularity, A, D, E and platonic solids. The twisted, curved spacetime is defined from two important and special interconnected lattices in dynamic namely the square lattice 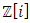 (counter of time) and the hexagonal lattice to define Space and when it degenerates it will simply describe the dynamical of the system’s axis described by a trefoil knot which is the algebraic curve and the bridge link of the asymmetrical system! The system describes a vortex knots model and looks chaotic comparable to the “case of Lorenz knots” generated by the dynamical of a combination of elliptical asymmetric connected encoded knots parameterizable by Fourier transform polynomials due to the modularity and by the dynamical of hyperbolical Fibonacci modular knots inside a closed space in dynamic. The equation of everything is an evidence to prove the existence of the physical property of the numerical system “Numbers”, geometrically represented by fibers of a surface or brane while in dynamic it generates vibrating loops or spirals related to lemniscates knots in the form of waves, abstract mathematical entities knotted with twisted orbital that generate a finite lattice model describing an abstract multi-verse of 11 dim. Per an analogy and projection it will describe our asymmetrical multi-verse system! Gravity exists even in the numerical system inside the lattice that generates waves. The equation also unveils the truth of the prime numbers and its hidden secret from its physical properties to its distribution generated by the spectrum of
(counter of time) and the hexagonal lattice to define Space and when it degenerates it will simply describe the dynamical of the system’s axis described by a trefoil knot which is the algebraic curve and the bridge link of the asymmetrical system! The system describes a vortex knots model and looks chaotic comparable to the “case of Lorenz knots” generated by the dynamical of a combination of elliptical asymmetric connected encoded knots parameterizable by Fourier transform polynomials due to the modularity and by the dynamical of hyperbolical Fibonacci modular knots inside a closed space in dynamic. The equation of everything is an evidence to prove the existence of the physical property of the numerical system “Numbers”, geometrically represented by fibers of a surface or brane while in dynamic it generates vibrating loops or spirals related to lemniscates knots in the form of waves, abstract mathematical entities knotted with twisted orbital that generate a finite lattice model describing an abstract multi-verse of 11 dim. Per an analogy and projection it will describe our asymmetrical multi-verse system! Gravity exists even in the numerical system inside the lattice that generates waves. The equation also unveils the truth of the prime numbers and its hidden secret from its physical properties to its distribution generated by the spectrum of 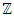 and its extensions
and its extensions 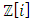 and
and 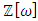 . The system is complete and consistent since it is based on a finite asymmetrical discrete system “In/Out & Out/In” a perfect example of systems that contradicts the Gödel’s incompleteness theorem. The article is a simple introduction of the representation and projection of the number theory to knot theory!
. The system is complete and consistent since it is based on a finite asymmetrical discrete system “In/Out & Out/In” a perfect example of systems that contradicts the Gödel’s incompleteness theorem. The article is a simple introduction of the representation and projection of the number theory to knot theory!
Keywords:
Vortex knot model, Exotic sphere, Lattice, Torus knots, Homology Poincare sphere, Modular knots, Sphere 666, Discrete system, Platonic solids, Icosahydral, Dodecahydral, Dynamical system, Lorenz knots, Torus knots, Lemniscates knots, Trefoil knot, Hopf link, Trivial knot
Cite this paper: Salahdin Daouairi, The Truth of Mathematics & Our Asymmetrical Multi-verse of 11 dim!, International Journal of Theoretical and Mathematical Physics, Vol. 8 No. 1, 2018, pp. 1-11. doi: 10.5923/j.ijtmp.20180801.01.
1. Introduction
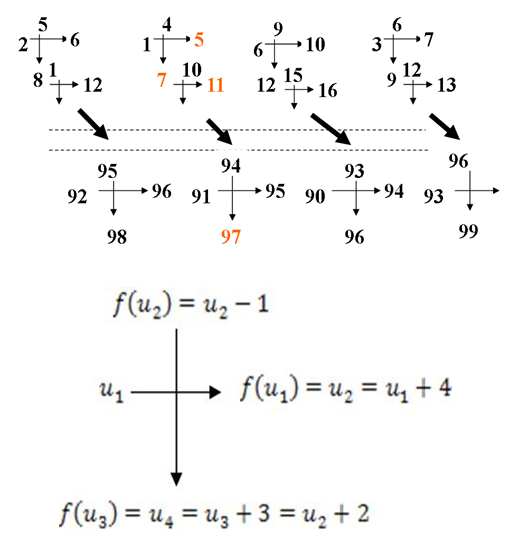
Most mathematical discoveries found coincidently, simple ideas can lead to interesting discoveries! My story about this discovery is very fascinating! I had this interesting paradox idea 24 years ago when I was studying “Mathematique Superieur, Nice France” that I felt it and knew it was some hidden properties behind it, a mixture between abstract and concrete properties “Numbers are independent from space and time, but numbers are in dynamic!”. A very interesting fact about the numbers is when we count numbers 1, 2…, the sequence is simply the product of a machinery process system lined on a belt as a strict line on a one dimensional lattice, but in the reality the transformation or the sequence results from a manufacturing numerical system process with multiple generators or symmetry transformations like the Rubik cube that describe a lattice in dynamic in a higher dimension! Fortunately in the year 2012 solving this paradox accidently leads me to understand how this manufacturing process of the numerical puzzle system works and discover many hidden connection to it in mathematics and in the universe. There is no numerical line; the set ℤ of integers obviously is not a one dimensional lattice! But a twisted brane with a double face +/_ generated by the trans-palindromes and a branch locus as its axis generated by the palindromes that we should describe as an unbounded 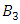 braid group rather than an infinite
braid group rather than an infinite 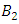 . Those branes are fibered space represented by vibrating loops generating wave forms, with the shape of spirals related to lemniscate knots specifically “torus knots” that we going to define in this paper. Numbers are knotted and generate twisted orbital describing a twisted non tangled lattice in dynamic in a higher dimension due to the action of an SO(3) transformation known by Paul Dirac belt trick effect. For this reason we reduced the set of integers to a finite set
. Those branes are fibered space represented by vibrating loops generating wave forms, with the shape of spirals related to lemniscate knots specifically “torus knots” that we going to define in this paper. Numbers are knotted and generate twisted orbital describing a twisted non tangled lattice in dynamic in a higher dimension due to the action of an SO(3) transformation known by Paul Dirac belt trick effect. For this reason we reduced the set of integers to a finite set 
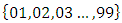 set of two digits to study the asymmetry of the system generated by the 9.11 emergency elements and its connection to the number 666! What a coincidence! In general in most cases the dynamical system for a physical system described as the motion of the system projected on the space time with parameters depending on the space and time, however some dynamical systems are described or represented by an algorithm of strings for an encoded system based on words and letters. Although with a simple parameterization we can convert those words to parametric equations. Mathematics is a useful tool that we use in our everyday life in a wide of fields such as science, economic, arts …for decision making, system modeling, analysis and more. For this reason we should perfectly understand and master our tools! Unveiling the hidden secret of our mathematical tools will open us the doors to discover many secrete things hidden about our universe. Our mathematical tools are based from the numerical system which is represented by the set ℤ, ℚ, ℝ, ℂ, ℍ and 𝕆 or the set of binary system,…Unfortunately it shows that we are using mathematical tools that we don’t understand its function and structure. The numerical system is an intelligent tool itself, a very smart system, where all the elements are in communication through webs like neurons in our brain, cells inside our blood and DNA inside the cells, galaxies in the universe, planets in the galaxy, electrons and quarks in the atoms, although these entities seem to be more familiar with mathematical concepts than we do! When we dig deeply everything in the universe has a coded mathematical information form to it. Well in this paper and in my previous paper we see detailed physical explanation about the numerical system in general, and how the system is interconnected algebraically, geometrically and analytically.Summary of the “Equation of Everything”:
set of two digits to study the asymmetry of the system generated by the 9.11 emergency elements and its connection to the number 666! What a coincidence! In general in most cases the dynamical system for a physical system described as the motion of the system projected on the space time with parameters depending on the space and time, however some dynamical systems are described or represented by an algorithm of strings for an encoded system based on words and letters. Although with a simple parameterization we can convert those words to parametric equations. Mathematics is a useful tool that we use in our everyday life in a wide of fields such as science, economic, arts …for decision making, system modeling, analysis and more. For this reason we should perfectly understand and master our tools! Unveiling the hidden secret of our mathematical tools will open us the doors to discover many secrete things hidden about our universe. Our mathematical tools are based from the numerical system which is represented by the set ℤ, ℚ, ℝ, ℂ, ℍ and 𝕆 or the set of binary system,…Unfortunately it shows that we are using mathematical tools that we don’t understand its function and structure. The numerical system is an intelligent tool itself, a very smart system, where all the elements are in communication through webs like neurons in our brain, cells inside our blood and DNA inside the cells, galaxies in the universe, planets in the galaxy, electrons and quarks in the atoms, although these entities seem to be more familiar with mathematical concepts than we do! When we dig deeply everything in the universe has a coded mathematical information form to it. Well in this paper and in my previous paper we see detailed physical explanation about the numerical system in general, and how the system is interconnected algebraically, geometrically and analytically.Summary of the “Equation of Everything”: Geometrical Interpretation of the Equation: We proved that the dynamical of the system describes an asymmetrical discrete lattice in dynamic that maps a hexagonal torus where dimension of the torus’s spacetime
Geometrical Interpretation of the Equation: We proved that the dynamical of the system describes an asymmetrical discrete lattice in dynamic that maps a hexagonal torus where dimension of the torus’s spacetime 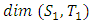 equals (3,1) with a total of 4 dim embedded in a hyper-sphere with
equals (3,1) with a total of 4 dim embedded in a hyper-sphere with 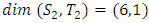 with a total of 7 dim orbiting in opposite directions in a higher dimension with a total of 11 dim. Time is asymmetrical of 2 dimensions. The torus and the hyper-sphere are connected by the Paul Dirac belt trick along the SO(3) transformation. The system described by a vortex knot model generated from a combination of linked asymmetrical knots namely trivial knots, Hopf link and trefoil knots. The properties of this mathematical model can explain and interpret the dynamical system of many systems from physical, biological, economical, financial, political systems, spiritual side, consciousness … The model is similar and quite comparable to Lorenz flow that describe the weather, equation of Boltzman for gas distribution, fluid dynamic, structure and dynamical of particles in quantum physics, dynamical of the universe and earth as a macro system, mechanical function of the heart beeps and its interconnection to the dynamical of the DNA and neurons inside a cell to the entire system body, mind, viruses, dynamical of the mechanical’s eye muscle. We have already seen the connection of Hopf link to the electromagnetism, trefoil knot to the strong force that binds the quarks and the trivial knots to the gravity, so the interconnection and the combination of those knots for such a system will simply unify the 4 physical forces since we can define the force and the energy of a knot!. Theoretical path of the equation: Deeply the equation of everything deals with a wide range and varieties of mathematical fields, this concrete example of numerical model rich of mathematical concepts and ideas that interplay between general mathematical theories that interconnect between number theory, topology & differential topology, algebraic geometry & projective geometry, harmonic analysis, symmetrical transformations, combinatory, logic and information theory! The evolution and the transformation of mathematical concepts and theories prove that even mathematic replicates itself along a special reversible asymmetrical transformation that relies on its dynamical system for an invariant system based from the automorphism groups! Mathematics study every steps and corners and provide us with a chain of mathematical connections caused by the dynamical of the numerical system with cases for each stage of its transformations to define convergence and perturbation of a family of elliptic curves and fiber bundles of the moduli space that rely on the isomorphism theorems, structure of quotient rings, maximal ideals, fixed points and root system defined by the Eigen-values and on how the spectrum of ℤ and
with a total of 7 dim orbiting in opposite directions in a higher dimension with a total of 11 dim. Time is asymmetrical of 2 dimensions. The torus and the hyper-sphere are connected by the Paul Dirac belt trick along the SO(3) transformation. The system described by a vortex knot model generated from a combination of linked asymmetrical knots namely trivial knots, Hopf link and trefoil knots. The properties of this mathematical model can explain and interpret the dynamical system of many systems from physical, biological, economical, financial, political systems, spiritual side, consciousness … The model is similar and quite comparable to Lorenz flow that describe the weather, equation of Boltzman for gas distribution, fluid dynamic, structure and dynamical of particles in quantum physics, dynamical of the universe and earth as a macro system, mechanical function of the heart beeps and its interconnection to the dynamical of the DNA and neurons inside a cell to the entire system body, mind, viruses, dynamical of the mechanical’s eye muscle. We have already seen the connection of Hopf link to the electromagnetism, trefoil knot to the strong force that binds the quarks and the trivial knots to the gravity, so the interconnection and the combination of those knots for such a system will simply unify the 4 physical forces since we can define the force and the energy of a knot!. Theoretical path of the equation: Deeply the equation of everything deals with a wide range and varieties of mathematical fields, this concrete example of numerical model rich of mathematical concepts and ideas that interplay between general mathematical theories that interconnect between number theory, topology & differential topology, algebraic geometry & projective geometry, harmonic analysis, symmetrical transformations, combinatory, logic and information theory! The evolution and the transformation of mathematical concepts and theories prove that even mathematic replicates itself along a special reversible asymmetrical transformation that relies on its dynamical system for an invariant system based from the automorphism groups! Mathematics study every steps and corners and provide us with a chain of mathematical connections caused by the dynamical of the numerical system with cases for each stage of its transformations to define convergence and perturbation of a family of elliptic curves and fiber bundles of the moduli space that rely on the isomorphism theorems, structure of quotient rings, maximal ideals, fixed points and root system defined by the Eigen-values and on how the spectrum of ℤ and 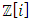 splices and splits and its connection to
splices and splits and its connection to 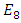 lattice, icosahydral, homology sphere and the 7 dim Milnor exotic sphere that rely on knots and there connection with modular form. Numbers are knotted with twisted orbital in dynamic, in the form of a combination of asymmetrical special invariant knots in dynamic that generate a twisted lattice in dynamic in the form of fibers of a surface, while the axis based on the root system that rely on the descriminant of the lattice. The projection and the extensions of this dynamical transformation shows interesting characteristic of its topological and algebraic geometric invariant with complex analytic properties, where dynamical of knots with closed orbits defined by periodic path coincide with singular curves! The algebra of the numerical system seems to be one of the complete and consistent theories to describe the universe! This abstract dynamical system of course depends theoretically on the parameters of space and time when we consider numbers in motion per projection in our concrete spacetime! But in an abstract space the numerical system is a type of language or program generated by a super computer that codes, decodes and correct error code [1] since the system is asymmetrical reversible in harmonic oscillations with internal and external spacetime generated by the knots, where knots are encoded through an algorithm of string with an enumerating language program based from letters and words for a closed finite orbit with a periodic path dealing with homotopy classes, braid groups [5]. What’s interesting is that the study of the physical properties of the numbers is independent of the mass, mathematical object massless! Object beyond the micro system for quantum physics and macro system concerning the gravitational system! We proved that the gravity exists even in the numerical system, since the dynamical or the transformation is based from the generators that fill gaps “vertices” along the oscillation of the system represented by the lattice! [1]. The string theory, M theory and quantum gravity are simply an indirect reverse application to the number theory! The sequence of the integers represents the motion or the dynamical system of the integer number 1 by adding +1 through a translation, it will then split or splice describing a curved lattice in dynamics with a higher dimensional Riemann surface generated by the spectrum of
lattice, icosahydral, homology sphere and the 7 dim Milnor exotic sphere that rely on knots and there connection with modular form. Numbers are knotted with twisted orbital in dynamic, in the form of a combination of asymmetrical special invariant knots in dynamic that generate a twisted lattice in dynamic in the form of fibers of a surface, while the axis based on the root system that rely on the descriminant of the lattice. The projection and the extensions of this dynamical transformation shows interesting characteristic of its topological and algebraic geometric invariant with complex analytic properties, where dynamical of knots with closed orbits defined by periodic path coincide with singular curves! The algebra of the numerical system seems to be one of the complete and consistent theories to describe the universe! This abstract dynamical system of course depends theoretically on the parameters of space and time when we consider numbers in motion per projection in our concrete spacetime! But in an abstract space the numerical system is a type of language or program generated by a super computer that codes, decodes and correct error code [1] since the system is asymmetrical reversible in harmonic oscillations with internal and external spacetime generated by the knots, where knots are encoded through an algorithm of string with an enumerating language program based from letters and words for a closed finite orbit with a periodic path dealing with homotopy classes, braid groups [5]. What’s interesting is that the study of the physical properties of the numbers is independent of the mass, mathematical object massless! Object beyond the micro system for quantum physics and macro system concerning the gravitational system! We proved that the gravity exists even in the numerical system, since the dynamical or the transformation is based from the generators that fill gaps “vertices” along the oscillation of the system represented by the lattice! [1]. The string theory, M theory and quantum gravity are simply an indirect reverse application to the number theory! The sequence of the integers represents the motion or the dynamical system of the integer number 1 by adding +1 through a translation, it will then split or splice describing a curved lattice in dynamics with a higher dimensional Riemann surface generated by the spectrum of 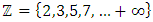 “set of prime ideals in ℤ” that extend to
“set of prime ideals in ℤ” that extend to 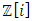 “ring of Gaussian integers generated by Gaussian primes with base
“ring of Gaussian integers generated by Gaussian primes with base 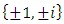 , the only invertible elements for an invariant system, with the algebraic extension f:
, the only invertible elements for an invariant system, with the algebraic extension f: 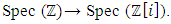 The spectrums play an important role to describe how fields split and splice in the projective Hilbert space. Since our system is invariant, we will be interested on the automorphism group linear for an invertible system! We will also focus on the convergence since it is related to the fixed points for a periodical path! Numbers or integers simply take the role of the group representation and its characters “modular” generated by a twist due to the asymmetry of the system. There is a solid extension between number field, function field and prime numbers from the correspondence
The spectrums play an important role to describe how fields split and splice in the projective Hilbert space. Since our system is invariant, we will be interested on the automorphism group linear for an invertible system! We will also focus on the convergence since it is related to the fixed points for a periodical path! Numbers or integers simply take the role of the group representation and its characters “modular” generated by a twist due to the asymmetry of the system. There is a solid extension between number field, function field and prime numbers from the correspondence 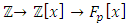 with the embedding homomorphism
with the embedding homomorphism 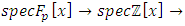
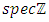 that send maximal ideals
that send maximal ideals 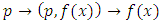 and act geometrically as a projection on to the set ℤ, hence fibers correspond to the sub-varieties max
and act geometrically as a projection on to the set ℤ, hence fibers correspond to the sub-varieties max 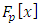 . One can view the connection between integers in number theory and the moduli space “geometry” due to the similar operations that are analogue between the integers and polynomials for a commutative ring, polynomial are function on line on space “analytic geometry” where we can operate a function and its pull back map defined by a homomorphism. The point on the space is defined as the prime ideal through the map
. One can view the connection between integers in number theory and the moduli space “geometry” due to the similar operations that are analogue between the integers and polynomials for a commutative ring, polynomial are function on line on space “analytic geometry” where we can operate a function and its pull back map defined by a homomorphism. The point on the space is defined as the prime ideal through the map 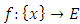 , a one point space is a field, if it vanishes locally it will vanish globally represented by the kernel of the homomorphism
, a one point space is a field, if it vanishes locally it will vanish globally represented by the kernel of the homomorphism 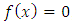 , with
, with 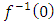 as the pull back while for a space more than one point we can discuss about the covering, branched covering, algebraic extension and fields. We can express the family of elliptic curves and fiber bundles of the Moduli space through number theory along the isomorphism correspondence that rely on the structure of quotient rings defined by the maximal ideals! The set of integers
as the pull back while for a space more than one point we can discuss about the covering, branched covering, algebraic extension and fields. We can express the family of elliptic curves and fiber bundles of the Moduli space through number theory along the isomorphism correspondence that rely on the structure of quotient rings defined by the maximal ideals! The set of integers 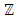 is twisted, every element can be mapped to its mirror image through the axis of symmetry described by the palindrome numbers, so to reduce its form we considered a finite subset
is twisted, every element can be mapped to its mirror image through the axis of symmetry described by the palindrome numbers, so to reduce its form we considered a finite subset 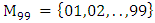 of integers with 2 digits which is isomorphic to
of integers with 2 digits which is isomorphic to 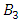 , where
, where 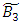 its closure or link related to the trefoil knot. The set of integers is twisted and generated by a composition of 2 special transformation maps described as a translation of Z+1 to describe the set ℤ and by a rotation or inverse map defined by
its closure or link related to the trefoil knot. The set of integers is twisted and generated by a composition of 2 special transformation maps described as a translation of Z+1 to describe the set ℤ and by a rotation or inverse map defined by 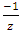 to form rational tangle to describe the set ℚ of rational numbers, where any element of ℚ defined by
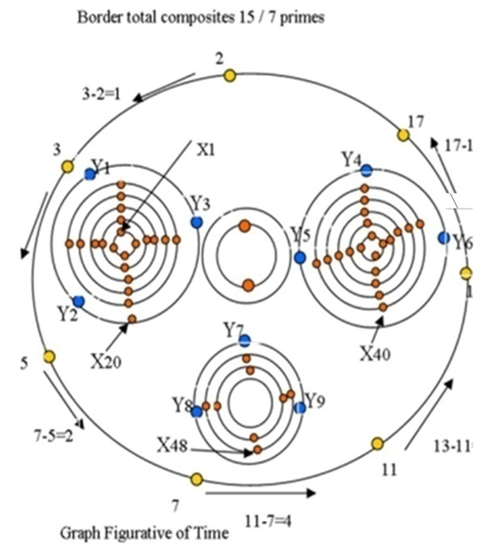
to form rational tangle to describe the set ℚ of rational numbers, where any element of ℚ defined by 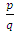 with
with 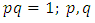 elements of ℤ can be represented by a rational tangle a (p, q) torus that generates
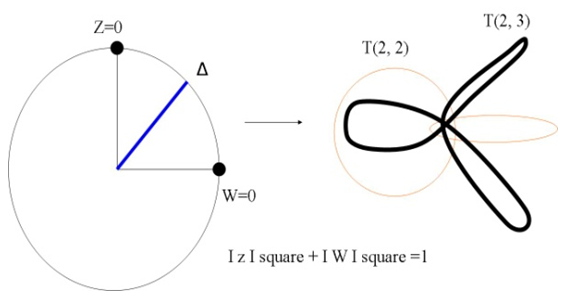
elements of ℤ can be represented by a rational tangle a (p, q) torus that generates 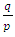 turns, while any element of ℝ is a limit of a rational tangle! The circle unity U(1), the sets ℂ, ℍ, 𝕆 and geometrically the elements of the Riemannian surfaces of genus 0 and 1 such as elliptic curves, torus, hyper-sphere and special knots are consequence of this transformation and extension. The numerical system is connected and results from the bifurcation of the transformation for such a braid closure.
turns, while any element of ℝ is a limit of a rational tangle! The circle unity U(1), the sets ℂ, ℍ, 𝕆 and geometrically the elements of the Riemannian surfaces of genus 0 and 1 such as elliptic curves, torus, hyper-sphere and special knots are consequence of this transformation and extension. The numerical system is connected and results from the bifurcation of the transformation for such a braid closure. 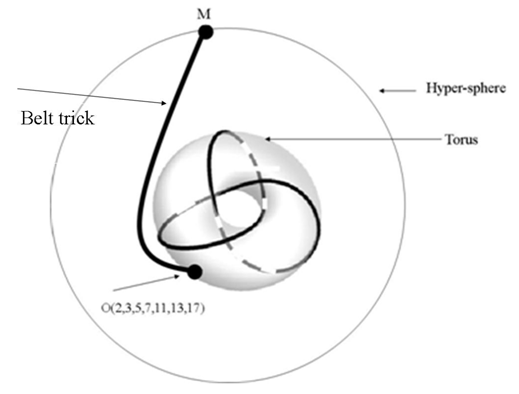 | Figure 1. Hyper-sphere and the torus connected by Paul Dirac belt trick |
- Asymmetry! Theory of Everything is a theory of intertwining based on the asymmetry and orientation. The law of nature is asymmetrical, many systems from biological, physical, financial, philosophical and political shown to exhibit asymmetry! Bipolar systems are characterized by chiral symmetry and generate many phenomenon that are seen in nature from the formation of tornados caused by convection, hurricane, galaxies, particles, cells, weather, dynamical of the earth as examples. This phenomenon is seen also in the financial and economical systems. While the factors responsible: hot/cold, low pressure/high pressure, light/dark, small/big, left hand/right hand, +/_ (magnet), electron/positron, Watson/Crick (DNA), national/global, long term credit/short term credit, male/female, buy/sell. Besides philosophy also exhibits asymmetrical statements based from: true/False, objective/subjective, moral/immoral, real/unreal, good/evil, abstract/concrete. Even mathematics itself exhibit asymmetry seen in the operators, 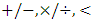
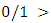 , palindrome numbers, true/false, binary system, finite fields, group cyclic, circle unity..! With arguments related to a series of logical concepts defined by a set
, palindrome numbers, true/false, binary system, finite fields, group cyclic, circle unity..! With arguments related to a series of logical concepts defined by a set 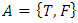 of binary system with true or false statements to define a proposition! Grounded by mathematical abstract operators, or objects based on negation, identity or annihilation. There is no broken symmetry, simply when we represent the system by the quaternions number system then the chirality is clear and obvious, however the system originally is asymmetrical. We have to make the difference between symmetry and asymmetry. Algorithm of strings, Knot and braid algebra theories combined with the dynamical system for an invariant system seem to be one of the interesting theories favorable to describe the numerical system itself and the universe! The model of our equation of everything is finite, complete and consistent. Our granular spacetime is based from a discrete system generated by the dynamical of a discrete lattice
of binary system with true or false statements to define a proposition! Grounded by mathematical abstract operators, or objects based on negation, identity or annihilation. There is no broken symmetry, simply when we represent the system by the quaternions number system then the chirality is clear and obvious, however the system originally is asymmetrical. We have to make the difference between symmetry and asymmetry. Algorithm of strings, Knot and braid algebra theories combined with the dynamical system for an invariant system seem to be one of the interesting theories favorable to describe the numerical system itself and the universe! The model of our equation of everything is finite, complete and consistent. Our granular spacetime is based from a discrete system generated by the dynamical of a discrete lattice 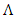 “dual of the continuous system” with the asymmetry and orientation properties for a reversible path defined by a pull-back homomorphism map that preserve the structure! The discrete system and the continuous system are simply connected through a homotopy group.Bipolar system: two asymmetrical entities
“dual of the continuous system” with the asymmetry and orientation properties for a reversible path defined by a pull-back homomorphism map that preserve the structure! The discrete system and the continuous system are simply connected through a homotopy group.Bipolar system: two asymmetrical entities 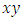 &
& 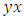 in dynamics along the axis of symmetry, moving in opposite direction with a periodic path create a vortex knot model generating harmonic oscillations and converge toward the golden ratio! Describing an internal and an external spacetime twisted with a higher dimension! [1]. If such an equation exists then it will reflect the geometrical shape of its dynamical system in nature and will interconnect between systems! Two important properties seen as a consequence of such an equation: - Golden Ratio: Everything seems to grow and expand in nature following the spiral of Fibonacci based on the golden ratio from our physical structure seen in DNA, neurons, physical body, fruits, shell, flowers, trees, production, particles, galaxy, earth, etc… -Asymmetry Definition: Let’s denote by
in dynamics along the axis of symmetry, moving in opposite direction with a periodic path create a vortex knot model generating harmonic oscillations and converge toward the golden ratio! Describing an internal and an external spacetime twisted with a higher dimension! [1]. If such an equation exists then it will reflect the geometrical shape of its dynamical system in nature and will interconnect between systems! Two important properties seen as a consequence of such an equation: - Golden Ratio: Everything seems to grow and expand in nature following the spiral of Fibonacci based on the golden ratio from our physical structure seen in DNA, neurons, physical body, fruits, shell, flowers, trees, production, particles, galaxy, earth, etc… -Asymmetry Definition: Let’s denote by 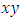 an integer with 2 digits and
an integer with 2 digits and 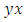 its mirror image elements of
its mirror image elements of 
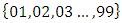 set of elements with 2 digits a subset of the set ℤ. Then
set of elements with 2 digits a subset of the set ℤ. Then 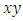 and
and 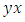 are asymmetric if
are asymmetric if 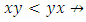
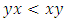 and if
and if 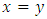 then
then 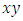 and
and 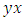 are element of the diagonal ∆ or axis of the symmetry of
are element of the diagonal ∆ or axis of the symmetry of 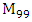 . The set
. The set 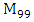 is an interesting subset of ℤ as we know twisted with double brane faces +/- generated by the set of the transpalindromes and a branch locus as the axis “set of the palindromes! The axis of symmetry or the spin axis considered as the diagonal or the set of fixed point represented by the palindromes in our numerical model, it splits following the numerical equations:
is an interesting subset of ℤ as we know twisted with double brane faces +/- generated by the set of the transpalindromes and a branch locus as the axis “set of the palindromes! The axis of symmetry or the spin axis considered as the diagonal or the set of fixed point represented by the palindromes in our numerical model, it splits following the numerical equations: 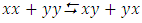 and for
and for 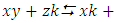
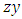 forming the alternating discrete lattice, we can then consider the oriented link by the crossing for a Reidemeister moves according to the nature of the elements of the set
forming the alternating discrete lattice, we can then consider the oriented link by the crossing for a Reidemeister moves according to the nature of the elements of the set 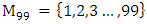 “prime” or “composite” defined by 3 strands: the identity generated by ∆ and the two asymmetrical strands with structure isomorphic to
“prime” or “composite” defined by 3 strands: the identity generated by ∆ and the two asymmetrical strands with structure isomorphic to 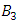 braid group. Every element has an asymmetrical element considered as a micro system with internal/external spacetime that spin around its axis since we consider our system on dynamic. Let’s say
braid group. Every element has an asymmetrical element considered as a micro system with internal/external spacetime that spin around its axis since we consider our system on dynamic. Let’s say 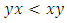 then it implies the inclusion
then it implies the inclusion 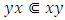 , and due to the orientation, it creating a vortex ring model, orbiting with opposite directions with generators linearly independents! That leads us to introduce our lattice model with 2 periods. In our model there are 3 types of trans-palindrome or asymmetrical type of numbers that generate the lattice: * prime with mirror image prime: considered as 2 linked trivial knots
, and due to the orientation, it creating a vortex ring model, orbiting with opposite directions with generators linearly independents! That leads us to introduce our lattice model with 2 periods. In our model there are 3 types of trans-palindrome or asymmetrical type of numbers that generate the lattice: * prime with mirror image prime: considered as 2 linked trivial knots  with short range, repulsive due to the orientation “anti-gravity” connected by the axis (e.g. Figure 2). Here the axis represented by the palindromes is a closed loop that has the form of a trefoil knot. The axis acts as a bridge link between the 2 asymmetrical knots.
with short range, repulsive due to the orientation “anti-gravity” connected by the axis (e.g. Figure 2). Here the axis represented by the palindromes is a closed loop that has the form of a trefoil knot. The axis acts as a bridge link between the 2 asymmetrical knots. 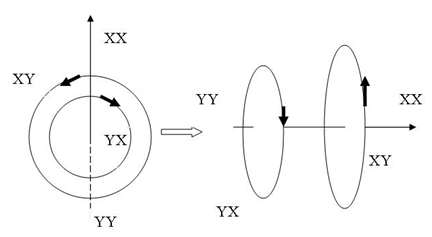 | Figure 2. Representation of two asymmetrical entities |
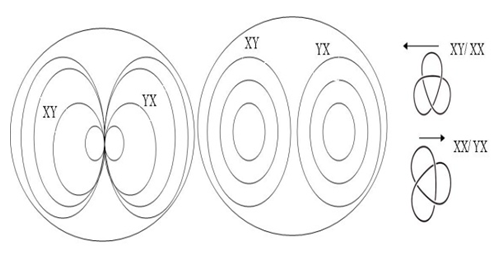 | Figure 3. Asymmetrical Torus knots representation |
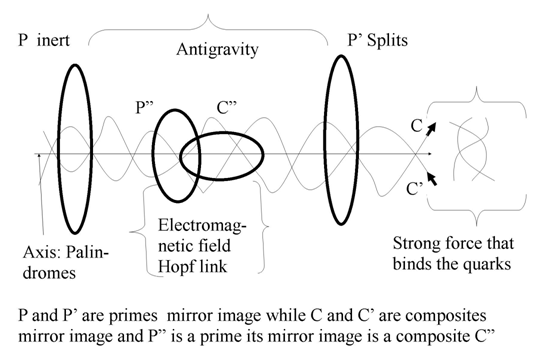
* Prime with mirror image composite: considered as 2 linked unknots “Hopf link” with short range spinning around the latitudinal axis spinning along the trefoil knot axis, with electromagnetism field representation. 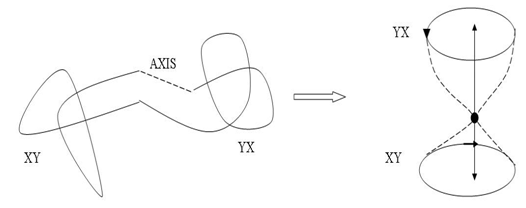 | Figure 4. Two asymmetrical trefoil knots that cancel each other and give birth to two asymmetrical trivial knots |
* Composite with mirror image composite: element of 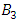 where its closure represents 2 linked asymmetrical trefoil knots with long range following the longitudinal axis that represents bridge link “the strong force that binds the quarks together” orbiting in opposite directions that cancel each other giving birth to 2 unknots in the critical point of the torus in the center for a hyperboloid surface which described as the light cone (e.g. Figure 4).
where its closure represents 2 linked asymmetrical trefoil knots with long range following the longitudinal axis that represents bridge link “the strong force that binds the quarks together” orbiting in opposite directions that cancel each other giving birth to 2 unknots in the critical point of the torus in the center for a hyperboloid surface which described as the light cone (e.g. Figure 4).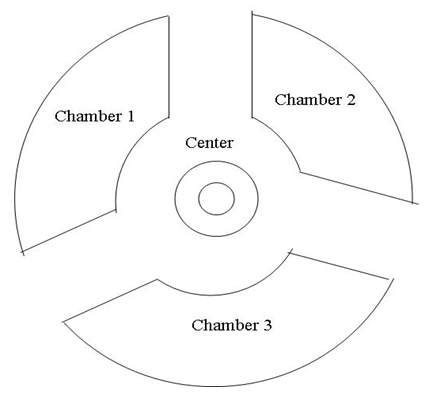 | Figure 5. Decomposition of the system |
The Torus decomposed by 3 chambers and the center “hyperboloid cone” along the axis of symmetry in our case is the descriminant of the lattice, each chamber (e.g. Figure 5 & 7) a combination of the 3types of the asymmetrical knots on dynamic. In our numerical system the chamber 1 bounded by the two asymmetrical primes (13, 31), chamber 2 by (17, 71), chamber 3 by (79, 97) and the center by (37, 73), while the direction of the flow is determined by the nature of those primes inert, split or ramify in 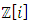 and
and 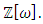
 | Figure 6. Distribution of the integers |
The periods of  and
and 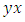 depend on the trajectory of
depend on the trajectory of 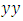 to
to 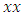 and vice versa. Although
and vice versa. Although 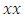 and
and 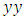 are elements of the axis ∆ “a closed curved line”! As a result
are elements of the axis ∆ “a closed curved line”! As a result 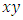 and
and 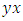 are connected and based from a homotopy map! We will see later that
are connected and based from a homotopy map! We will see later that 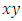 and
and  are simply connected by Paul Dirac belt trick. Per extension of the set
are simply connected by Paul Dirac belt trick. Per extension of the set  that represents the lattice of integers by the quotient modulo a prime to a complex state to define the finite cyclic group
that represents the lattice of integers by the quotient modulo a prime to a complex state to define the finite cyclic group  “See Galois extension of the cyclotomic fields”! And since
“See Galois extension of the cyclotomic fields”! And since  (Torus), the product can be interpreted by the rotation defined by the period of
(Torus), the product can be interpreted by the rotation defined by the period of 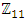 with
with 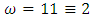 [9] where the period of
[9] where the period of 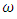 is of order 6 that lies on a hexagonal torus with elements
is of order 6 that lies on a hexagonal torus with elements 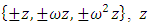 element of
element of 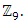 Since the set
Since the set 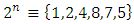 [9] then the set
[9] then the set 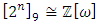 . We notice also
. We notice also 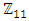 sends
sends 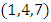 to
to 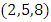 and
and 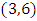 to
to 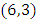 where 9 is invariant and the remaining set of
where 9 is invariant and the remaining set of 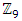 by
by 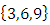 defined by the axis generated by
defined by the axis generated by 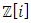 with order 4. Leads to this interesting connection between
with order 4. Leads to this interesting connection between 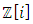 &
& 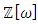 . We saw also in the previous equation [1] the 3 groups
. We saw also in the previous equation [1] the 3 groups 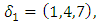
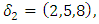
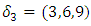 are related to the braid group
are related to the braid group 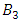 and are connected by
and are connected by 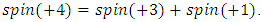
 | Figure 7. Structure of a chamber |
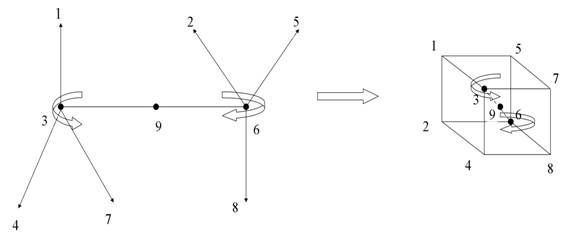
In this part we will be extending the theory to define the braid algebra of the numbers. We have 2 asymmetrical tetrahydra defined by the quadruplets 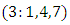 and
and 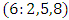 (e.g. Figure 7). Per projection in the
(e.g. Figure 7). Per projection in the  , it shows that the 2 tetrahedral are embedded in a cube with vertices located on the vertices of a cube orbiting with opposite direction to each other and defining 2 asymmetrical trefoil knots that generate a torus and a hyper-sphere orbiting in opposite direction! By a double cover transformation the points map an icosahydral, the system is invariant under the twist where particles “vertices” can move free due to Dirac belt trick generated by
, it shows that the 2 tetrahedral are embedded in a cube with vertices located on the vertices of a cube orbiting with opposite direction to each other and defining 2 asymmetrical trefoil knots that generate a torus and a hyper-sphere orbiting in opposite direction! By a double cover transformation the points map an icosahydral, the system is invariant under the twist where particles “vertices” can move free due to Dirac belt trick generated by  transformation.
transformation. 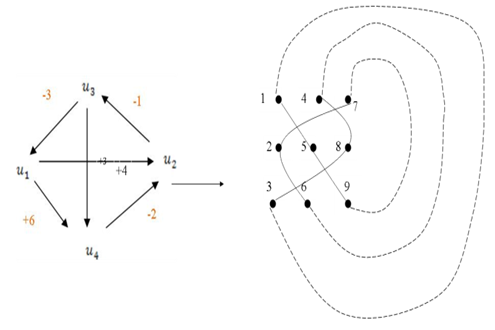 | Figure 8. Braid group related to the spin |
We notice also any element of the lattice defined by the set 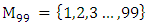 can be writing as:
can be writing as: 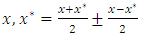 sum of an element of
sum of an element of  and
and  where
where 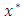 is the mirror image of
is the mirror image of 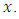 And vice versa when we apply the rotation to the group
And vice versa when we apply the rotation to the group 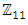 by
by 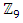 the remaining path is isomorphic to
the remaining path is isomorphic to 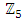 , this simply a consequence of the dual of the icosahydral generated by the 5 fold symmetry of a dodecahydral. If we consider now the continuous map
, this simply a consequence of the dual of the icosahydral generated by the 5 fold symmetry of a dodecahydral. If we consider now the continuous map 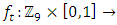
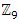 with
with 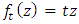 where t is a multiplicative scalar element of
where t is a multiplicative scalar element of 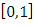 an extension to
an extension to 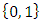 with
with 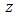 an element of
an element of 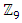 then f is injective and ∆ is invariant “described by the set
then f is injective and ∆ is invariant “described by the set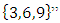 that transform
that transform 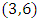 to
to 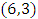 and
and 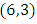 to
to 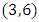 through the isomorphism map
through the isomorphism map 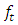 that represents the homotopy map H (t, z), dynamical of the curve when t (time) takes values between 0 and 1 of the circle unity
that represents the homotopy map H (t, z), dynamical of the curve when t (time) takes values between 0 and 1 of the circle unity 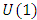 . The fixed point defined by
. The fixed point defined by 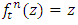 then for
then for 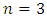 we have:
we have: 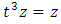 that leads to the equation
that leads to the equation 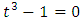 where t element of
where t element of 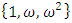 roots of a hexagonal torus. Following the numerical equations
roots of a hexagonal torus. Following the numerical equations 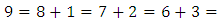
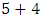 the number 9 is the center of the symmetry and the singularity point! Geometrically by points projection 9 represents the intersection of lines to infinity
the number 9 is the center of the symmetry and the singularity point! Geometrically by points projection 9 represents the intersection of lines to infinity 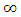 determined by the map:
determined by the map: 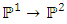 for
for 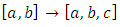 to the line
to the line 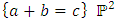 since all the roots of the hexagonal complex torus are conjugates with trace
since all the roots of the hexagonal complex torus are conjugates with trace 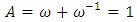 we identify then the line by sending the points to
we identify then the line by sending the points to 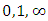 that generalize the mobius transformation along the cross ratio. By lifting the points by ramification, the Diophantine equation:
that generalize the mobius transformation along the cross ratio. By lifting the points by ramification, the Diophantine equation: 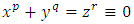 [9] have as solutions the vertices and its conjugates of a torus knot
[9] have as solutions the vertices and its conjugates of a torus knot 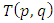 [9].
[9].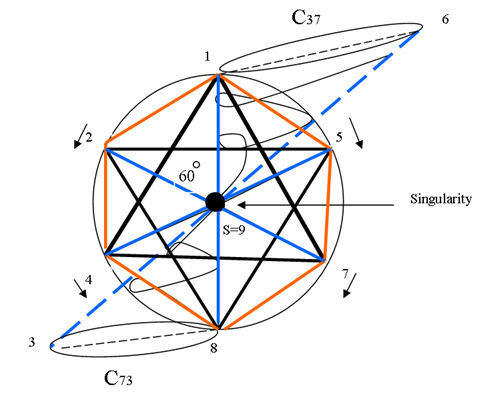 | Figure 9. The reduced representation of the integers on the torus |
The Braid Algebra for the integers: The identity and self reference is related here to the group 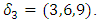
 | Figure 10. Projection of the elements |
This diagram is represented by the following representation: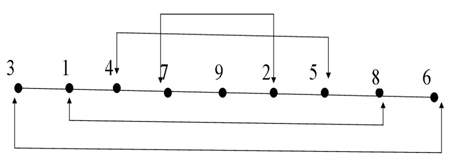 | Figure 11. Diagram representation of the elements |
Where 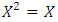 this bracket is known by Kauffmann braid for a self replication process! (e.g. Figure 12)
this bracket is known by Kauffmann braid for a self replication process! (e.g. Figure 12) 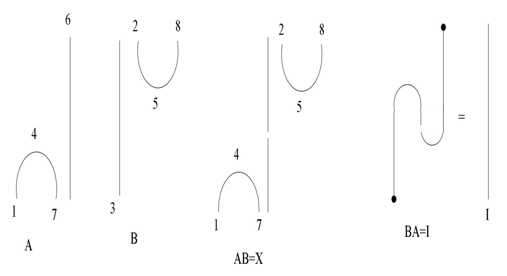 | Figure 12. Kauffman representation of the elements |
Distribution of the prime numbers: In the previous article of the equation of everything code unlocked [1], we defined the function that maps all the primes! based from the 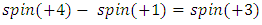 see detail [1]
see detail [1] With the value
With the value 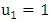 , the sequence or the function maps not only all the primes
, the sequence or the function maps not only all the primes 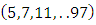 of the set
of the set 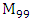 but also all the primes
but also all the primes 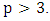
 | Figure 13. Primes distribution |
When we reduce the system to  , the sequence shows the special correspondence between
, the sequence shows the special correspondence between  and
and 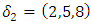 when we considere its closure it describes the trefoil knot, and that proves the geometric localization of the primes. The primes are certainly located on a hexagonal torus generated by a trefoil knot. Our lattice
when we considere its closure it describes the trefoil knot, and that proves the geometric localization of the primes. The primes are certainly located on a hexagonal torus generated by a trefoil knot. Our lattice  is a discrete set of asymmetrical elements
is a discrete set of asymmetrical elements 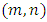 elements of
elements of 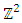 spinning around the axis; defined by
spinning around the axis; defined by 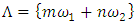
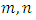 elements
elements 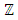 and
and 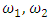 elements of
elements of 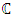 , where
, where 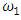 related to the hexagonal lattice and
related to the hexagonal lattice and 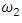 related to the square lattice generated by Eisenstein integers and Gaussian integers that intercept at the points
related to the square lattice generated by Eisenstein integers and Gaussian integers that intercept at the points 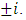 The dynamical of this lattice is defined by the map
The dynamical of this lattice is defined by the map 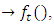 t element of
t element of 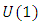 to describe a continuous system. The set of the asymmetrical elements describes a torus “maximal torus”!
to describe a continuous system. The set of the asymmetrical elements describes a torus “maximal torus”! 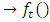 defined from the flow of the integers, which is generated from two asymmetrical trefoil knots defined from the roots and its conjugates of a hexagonal torus! We know that two asymmetrical knots cancel each other to form two unlinked trivial knots (e.g. Figure 4) that occur in the critical origin point of the cone light for a hyperboloid surface and the operation keep repeating due to the closed reversible path for a periodic orbital with a self replication when t describes the circle unity
defined from the flow of the integers, which is generated from two asymmetrical trefoil knots defined from the roots and its conjugates of a hexagonal torus! We know that two asymmetrical knots cancel each other to form two unlinked trivial knots (e.g. Figure 4) that occur in the critical origin point of the cone light for a hyperboloid surface and the operation keep repeating due to the closed reversible path for a periodic orbital with a self replication when t describes the circle unity 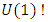 Transformation that results from the combination of two special lattices defined by
Transformation that results from the combination of two special lattices defined by 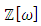 and
and 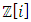 that are connected by the interesting relation
that are connected by the interesting relation 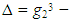
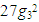 the special algebraic curve for the modular group! Although, there is an interesting connection between knots, its complement to the algebraic singularities and the modular group by the Weierstrass function
the special algebraic curve for the modular group! Although, there is an interesting connection between knots, its complement to the algebraic singularities and the modular group by the Weierstrass function 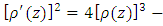
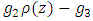 with
with 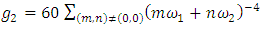 &
& 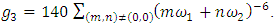
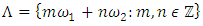 is a lattice with a double period where
is a lattice with a double period where 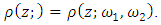 The curve
The curve 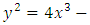
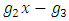 defines an elliptic curve ξ with descriminant
defines an elliptic curve ξ with descriminant 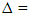
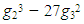 with roots are elements of a complex torus. The curves
with roots are elements of a complex torus. The curves 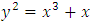 related to
related to 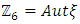 and
and 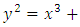
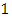 related to
related to 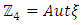 [12] which are the only curves with special automorphisms that correspond to the four branch points
[12] which are the only curves with special automorphisms that correspond to the four branch points 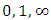 and
and 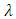 with
with 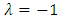 and
and 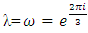 that generate the square lattice
that generate the square lattice 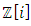 and the hexagonal lattice
and the hexagonal lattice 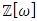 connected through the eigenvalues and the fixed points of the minimal polynomial. Since we are interested only on a reversible system, the only invertible elements of the spec
connected through the eigenvalues and the fixed points of the minimal polynomial. Since we are interested only on a reversible system, the only invertible elements of the spec 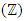 and spec
and spec 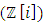 are
are 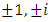 of order 4 related to the cyclotomic group
of order 4 related to the cyclotomic group 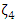 for the polynomial
for the polynomial 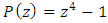 with roots elements of
with roots elements of 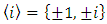 . Although
. Although 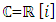 defined as the splitting field of
defined as the splitting field of 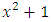 over
over 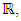 the factorization of
the factorization of 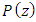 leads to the product of
leads to the product of 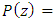
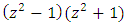 has coefficients in ℤ and monic, the cyclotomic polynomial lies in
has coefficients in ℤ and monic, the cyclotomic polynomial lies in 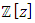 , One could see the duality relations that swaps fixed points to roots of the kernel between
, One could see the duality relations that swaps fixed points to roots of the kernel between 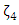 and
and 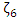 determined by the polynomials
determined by the polynomials 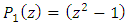 and
and 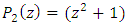 . For roots
. For roots 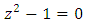 it leads to the relation:
it leads to the relation: 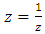 and for roots of
and for roots of 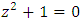 leads to the relation
leads to the relation 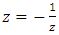 “stereographic projection of a sphere” related to the fixed points of the maps
“stereographic projection of a sphere” related to the fixed points of the maps 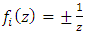 for
for 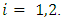 Now for the fixed points of the 2 polynomials we have:
Now for the fixed points of the 2 polynomials we have: 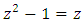 with roots the golden ratio and its conjugate, while for
with roots the golden ratio and its conjugate, while for 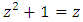 roots are conjugate and located on a hexagonal torus. With a slight symmetric transformation it shows that it is related to the Alexander polynomial for a trefoil knot
roots are conjugate and located on a hexagonal torus. With a slight symmetric transformation it shows that it is related to the Alexander polynomial for a trefoil knot 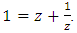 and by replacing t by:
and by replacing t by: 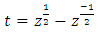 we have
we have 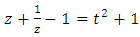 . We know also the Conway polynomial
. We know also the Conway polynomial 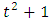 has infinitely quaternion roots in the form
has infinitely quaternion roots in the form 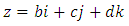 since
since 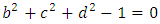 where roots lie on the 2 dimension surface of a sphere centered on zero in the 3 dimensional sub-space of quaternion with zero reel part and intersects the complex plane at two points
where roots lie on the 2 dimension surface of a sphere centered on zero in the 3 dimensional sub-space of quaternion with zero reel part and intersects the complex plane at two points 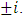 What is interesting is the structure of the descriminant which has the form of a variety algebraic
What is interesting is the structure of the descriminant which has the form of a variety algebraic  with
with 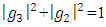 complex lattice that lie on the unit sphere. For this reason we should determine the characteristic of the trefoil knots! We can also extend the transformation to a modular knot for a modular flow with periodic orbits. By introducing the fixed point property for
complex lattice that lie on the unit sphere. For this reason we should determine the characteristic of the trefoil knots! We can also extend the transformation to a modular knot for a modular flow with periodic orbits. By introducing the fixed point property for 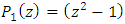 and
and 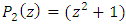
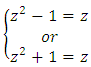 Lead to the fraction rational:
Lead to the fraction rational: 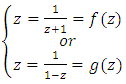 Generated by
Generated by 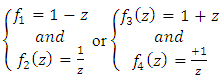 Generated by the matrices
Generated by the matrices 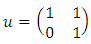 and
and 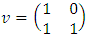 or
or 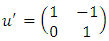 and
and 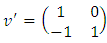 Knot Definition: In this part we going to see beautiful mathematical relations! First let’s define a knot, which is an embedding of a circle into 3 dim Euclidean Space. We know the knot group of a knot K is defined as the fundamental group of the knot complement of K in
Knot Definition: In this part we going to see beautiful mathematical relations! First let’s define a knot, which is an embedding of a circle into 3 dim Euclidean Space. We know the knot group of a knot K is defined as the fundamental group of the knot complement of K in 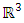 by
by 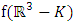 , the topology of the knot or link can be defined by
, the topology of the knot or link can be defined by 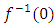 of a function:
of a function: 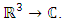 A mathematical knot function has many applications and showed interesting physical experimental evidence that describe the dynamical system of the vortex knot model for a variety of systems from weather, fluid dynamics, electromagnetism, quantum physics, and numerical system. Example of knots: Unknot, Hopf link or
A mathematical knot function has many applications and showed interesting physical experimental evidence that describe the dynamical system of the vortex knot model for a variety of systems from weather, fluid dynamics, electromagnetism, quantum physics, and numerical system. Example of knots: Unknot, Hopf link or 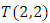 , trefoil knot or
, trefoil knot or 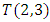 , torus knot
, torus knot 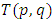 . The trefoil knot K is a fibered knot where its complement in
. The trefoil knot K is a fibered knot where its complement in 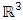 is a fiber bundle over the circle
is a fiber bundle over the circle 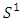 . Its knot group is isomorphic to the braid group
. Its knot group is isomorphic to the braid group 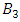 with the presentation
with the presentation 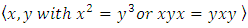 it is also the link and the right handed of the neighborhood boundary of the singular variety
it is also the link and the right handed of the neighborhood boundary of the singular variety 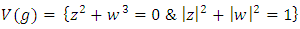 where z, w are complex numbers with
where z, w are complex numbers with 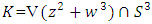 . As a fibration it has the Milnor map
. As a fibration it has the Milnor map 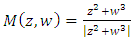 and a once punctured Torus as its fiber surface that vanish at the singularity 0. Hopf link are circles in
and a once punctured Torus as its fiber surface that vanish at the singularity 0. Hopf link are circles in 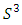 intersection of complex lines (circle in
intersection of complex lines (circle in 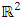 ) in
) in 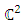 with
with  for
for 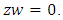
 | Figure 14. Representation of the Hopf link and trefoil knot for an algebraic variety |
Let 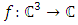 the complex polynomial
the complex polynomial 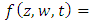
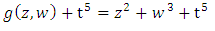 then
then 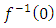 is the complex variety. By extending the link of the singular algebraic variety to
is the complex variety. By extending the link of the singular algebraic variety to 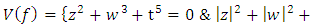
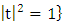 We have then per projection a
We have then per projection a 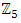 regular cover, where
regular cover, where 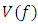 is the branched cover of
is the branched cover of 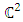 with branch locus
with branch locus 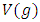 and
and 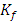 is the branched cover of
is the branched cover of 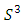 with branch locus
with branch locus 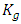 over the variety
over the variety 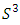 . It generates the equation of a dodecahedral. Let’s denote by
. It generates the equation of a dodecahedral. Let’s denote by 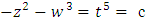 that when
that when 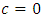 then
then 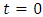 , variety with cusp 0 at the origin, and when
, variety with cusp 0 at the origin, and when 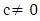 then the equation has 5 roots and the fixed points form the cone of the trefoil knot. then we have
then the equation has 5 roots and the fixed points form the cone of the trefoil knot. then we have  sits inside the dodecahedral and passes through the center of its faces, as a result the trefoil knot seems to be the axis of the dodecahedral space for a 5 fold symmetry that extend to the origin.
sits inside the dodecahedral and passes through the center of its faces, as a result the trefoil knot seems to be the axis of the dodecahedral space for a 5 fold symmetry that extend to the origin.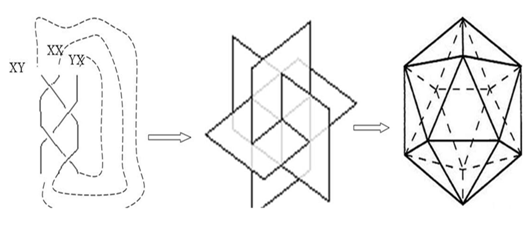 | Figure 15. Link of the group B3 where strands are lines in complex space |
A particular case that corresponds to the homology 3-sphere “Brieskorn”  known by the Poincare dodecahedron space with finite fundamental group
known by the Poincare dodecahedron space with finite fundamental group 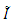 the binary icosahydral group defined by
the binary icosahydral group defined by 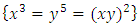 of order 120 double cover of the regular icosahydral group
of order 120 double cover of the regular icosahydral group 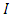
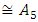 (alternating group) determined by the quotient space
(alternating group) determined by the quotient space 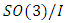 or simply by the double cover
or simply by the double cover 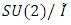 that can be constructed from Dehn surgery on knot from a right handed trefoil knot. The essential in this part is to determine the nature of the elliptical curves or modular knots that sits inside the entire space and define the geometrical shape of that space and its dimension! The construction will be based on the Brieskon algebraic varieties [2] that are associated with the polynomial:
that can be constructed from Dehn surgery on knot from a right handed trefoil knot. The essential in this part is to determine the nature of the elliptical curves or modular knots that sits inside the entire space and define the geometrical shape of that space and its dimension! The construction will be based on the Brieskon algebraic varieties [2] that are associated with the polynomial: 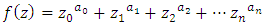 where
where 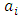 integers and
integers and 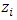 are complex. In general the variety defined by
are complex. In general the variety defined by 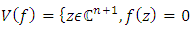 and
and 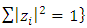 where the knot associated as the intersection of the variety algebraic and the sphere of dim
where the knot associated as the intersection of the variety algebraic and the sphere of dim 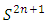 defined by
defined by 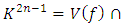
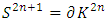 where K has an intersection form
where K has an intersection form 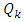 on
on 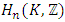 and if
and if 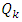 is unimodular then the boundary
is unimodular then the boundary 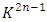 is a homology, exotic sphere. In our case for
is a homology, exotic sphere. In our case for 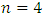 the knot associated to a manifold of dim 7 defined by
the knot associated to a manifold of dim 7 defined by 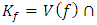
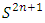
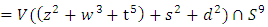 we have
we have 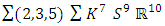 and since the homology 3-sphere determined by the quotient SO(3)/I and the Milnor 7 sphere act transitively on the group of the quaternios
and since the homology 3-sphere determined by the quotient SO(3)/I and the Milnor 7 sphere act transitively on the group of the quaternios 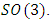 We have:
We have: 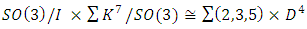 shows that
shows that 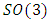 act between the icosahedral and the 7 dim Milnor sphere through Paul Dirac belt trick. We can show also the Paul Dirac belt trick effect that results from an
act between the icosahedral and the 7 dim Milnor sphere through Paul Dirac belt trick. We can show also the Paul Dirac belt trick effect that results from an 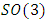 transformation that connect the system by using the J-homomorphism and Hopf construction for a higher dimension to describe the fundamental group, for details see L. Kauffman [6]. It shows from the previous method that the trefoil knot
transformation that connect the system by using the J-homomorphism and Hopf construction for a higher dimension to describe the fundamental group, for details see L. Kauffman [6]. It shows from the previous method that the trefoil knot 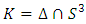 and
and 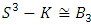 complement of K. The fundamental group of
complement of K. The fundamental group of 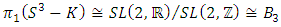 and
and 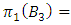
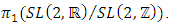 Since the group of fractional linear transformations on
Since the group of fractional linear transformations on 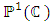 preserving the upper half plane
preserving the upper half plane 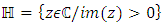 that is
that is 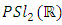 determined by a mobius strip that transform generalized circle to generalized circles [11] a combination of a translation and an inverse map with a twist and a rotation and from the Alexander polynomial for a trefoil knot
determined by a mobius strip that transform generalized circle to generalized circles [11] a combination of a translation and an inverse map with a twist and a rotation and from the Alexander polynomial for a trefoil knot 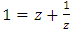 leads to:
leads to: 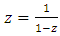 fixed point of the map
fixed point of the map 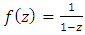 based from a twist and an inverse rotation. Defined by:
based from a twist and an inverse rotation. Defined by: 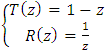 Where
Where 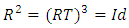 . It follows the connection between
. It follows the connection between 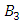 and the modular group
and the modular group 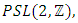 considered as a lattice inside the covering group. The quotient of
considered as a lattice inside the covering group. The quotient of 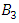 per its center is isomorphic to
per its center is isomorphic to 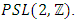 Although the generators of the modular group obey the relation:
Although the generators of the modular group obey the relation: 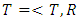 with
with 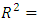
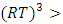 isomorphic to the free group product
isomorphic to the free group product 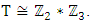 Or from the braid relations it follows that:
Or from the braid relations it follows that: 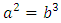 with
with 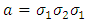 and
and 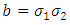 respectively with the correspondent matrix:
respectively with the correspondent matrix: 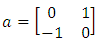 and
and 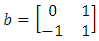 as we know the braid group
as we know the braid group 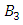 is isomorphic to the knot group of the trefoil knot. We can also view it as the real variety
is isomorphic to the knot group of the trefoil knot. We can also view it as the real variety 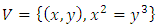 a subset of the real plane
a subset of the real plane 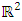 identified with the quotient ring
identified with the quotient ring 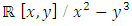 in algebraic geometry. We can also introduce the j invariant to compute through the dessin d’enfant the free group! Hence the j invariant has an interesting tie between the Alexander polynomial for the algebraic curve ξ over the Laurent polynomial
in algebraic geometry. We can also introduce the j invariant to compute through the dessin d’enfant the free group! Hence the j invariant has an interesting tie between the Alexander polynomial for the algebraic curve ξ over the Laurent polynomial 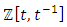 and the cross ratio by the formula:
and the cross ratio by the formula: 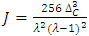 with
with 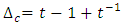 as the characteristic polynomial of the bureau representative of
as the characteristic polynomial of the bureau representative of 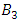 defined by
defined by 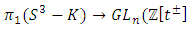 with matrices
with matrices 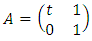 and
and 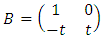 with
with 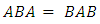 . Where J=0 when
. Where J=0 when 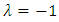 and
and 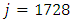 when
when 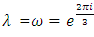 . According to our invariant system, it shows there an interesting relation
. According to our invariant system, it shows there an interesting relation 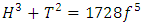 discovered by Felix Klein that ties the modular group to the quintic equation [3] with the form
discovered by Felix Klein that ties the modular group to the quintic equation [3] with the form 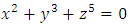 , the icosahydral group and the
, the icosahydral group and the 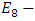 singularities [10]. Where
singularities [10]. Where 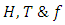 invariant polynomials are connected by the Dedekind eta function to
invariant polynomials are connected by the Dedekind eta function to 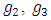 the j invariant function and the descriminant by the action of the generators
the j invariant function and the descriminant by the action of the generators 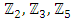 with 2, 3 and 5 fold [7] symmetries for the icosahydral group. The 5 fold cover of the torus knot
with 2, 3 and 5 fold [7] symmetries for the icosahydral group. The 5 fold cover of the torus knot 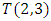 and the double cover of the torus
and the double cover of the torus 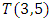 . The polynomial invariant
. The polynomial invariant 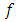 corresponds to the vertices of the icosahydral while the invariant polynomials
corresponds to the vertices of the icosahydral while the invariant polynomials  correspond to the edge midpoints and face centers of the icosahydral. Due to the modularity and periodical path, following the previous method for the algebraic singularity related to the knots we can give an explicit representation of the encoded knots by an analytical function defined by complex polynomial defined by Brauwer with
correspond to the edge midpoints and face centers of the icosahydral. Due to the modularity and periodical path, following the previous method for the algebraic singularity related to the knots we can give an explicit representation of the encoded knots by an analytical function defined by complex polynomial defined by Brauwer with 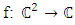 where
where 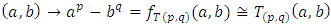 to study the critical pts of the curve at the origin in
to study the critical pts of the curve at the origin in 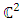 such
such 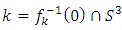 . Brauner’s knots are torus knots that are also lemniscates knots that we can parameterize by projection in the 3 dimensional Cartesian space by
. Brauner’s knots are torus knots that are also lemniscates knots that we can parameterize by projection in the 3 dimensional Cartesian space by 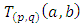 to
to 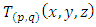 . In our case we are more interested in the torus knots of type the Hopf link
. In our case we are more interested in the torus knots of type the Hopf link 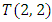 and the trefoil knot
and the trefoil knot 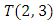 . Since the braid group is the closure of the knot, then by encoding the braid in to a polynomial in a and b. According to Mark Dennis [8] the parameterization is a function of t element of
. Since the braid group is the closure of the knot, then by encoding the braid in to a polynomial in a and b. According to Mark Dennis [8] the parameterization is a function of t element of 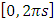 where k is the lemniscates knot K=(s, l, r) and the curve
where k is the lemniscates knot K=(s, l, r) and the curve 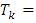
 where the closure of the braid defined by:
where the closure of the braid defined by: 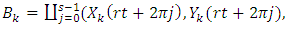
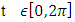 Will leave this to the reader! Note interesting points are at
Will leave this to the reader! Note interesting points are at 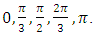 Interpretation: the trefoil knot generates the axis of the symmetry of the system! Our trefoil knot is the boundary of a fibered surface with double faces, though for any element of our numerical system its asymmetric or mirror image is in the other side of the face of the fibered surface orbiting in opposite directions with an unzip operation! the braid group structured by the elements and its axis orbiting along a trefoil knot, the transformations then describe for both sides of the faces 2 asymmetrical trefoil knots orbiting in a closed link cancel each other at the origin or the critical point of the hyperboloid cone and giving birth to 2 asymmetrical unknots! Fabric of the spacetime and the prime numbers: As a conclusion we can define the fabric of the space by the combination of modular knots in dynamic that generate a vortex knot model defined by elliptical curves and hyperboloid curves that intercepts the axis of the system generated by an algebraic curve the trefoil knot a link bridge between two asymmetrical transversal trefoil knots, Hopf link and two unlinked asymmetrical trivial knots! The complement of those fibered knots are fibered bundles, loops defined by the Milnor map generated by two important elliptic curves one hexagonal and the other one is square while as hyperboloid curve we have the modular Fibonacci knots that converges toward the golden ratio and based from the Cassini identity where the determinant is
Interpretation: the trefoil knot generates the axis of the symmetry of the system! Our trefoil knot is the boundary of a fibered surface with double faces, though for any element of our numerical system its asymmetric or mirror image is in the other side of the face of the fibered surface orbiting in opposite directions with an unzip operation! the braid group structured by the elements and its axis orbiting along a trefoil knot, the transformations then describe for both sides of the faces 2 asymmetrical trefoil knots orbiting in a closed link cancel each other at the origin or the critical point of the hyperboloid cone and giving birth to 2 asymmetrical unknots! Fabric of the spacetime and the prime numbers: As a conclusion we can define the fabric of the space by the combination of modular knots in dynamic that generate a vortex knot model defined by elliptical curves and hyperboloid curves that intercepts the axis of the system generated by an algebraic curve the trefoil knot a link bridge between two asymmetrical transversal trefoil knots, Hopf link and two unlinked asymmetrical trivial knots! The complement of those fibered knots are fibered bundles, loops defined by the Milnor map generated by two important elliptic curves one hexagonal and the other one is square while as hyperboloid curve we have the modular Fibonacci knots that converges toward the golden ratio and based from the Cassini identity where the determinant is 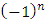 defined by:
defined by: 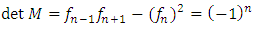 for a rational map
for a rational map 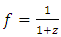 with matrices respectively:
with matrices respectively: 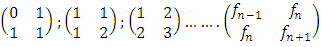 that depend for its convergence on n if it is even or odd and will intercept the axis as a link of knot or unknot. We define rational tangle for the golden ratio by
that depend for its convergence on n if it is even or odd and will intercept the axis as a link of knot or unknot. We define rational tangle for the golden ratio by 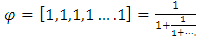 this will answear one of the interesting paper of [4] for the modular flow and why the Lorenz knots looks chaotic. We also with this conclusion made the connection between the integers and prime numbers and their representation as fibers or loops for such surfaces! The combination of those asymmetrical torus knots type and the hyperbolic curves generated by the spiral of Fibonacci inside a closed path that intercept the axis of the system which is the trefoil knots describe the Fabric of the spacetime!
this will answear one of the interesting paper of [4] for the modular flow and why the Lorenz knots looks chaotic. We also with this conclusion made the connection between the integers and prime numbers and their representation as fibers or loops for such surfaces! The combination of those asymmetrical torus knots type and the hyperbolic curves generated by the spiral of Fibonacci inside a closed path that intercept the axis of the system which is the trefoil knots describe the Fabric of the spacetime!
2. Conclusions
Numbers are abstract elements or mathematical objects in dynamic with physical properties that exist in an abstract spacetime. We use them to define concrete and abstract things, their dynamical system maps a specific geometrical shape related to platonic solids! So philosophically the existence of the numbers idea comes first theoretically to model the construction and dynamical system of the universe “Spacetime”. With those mathematical arguments we connected the philosophical view of Plato and Pythagoras [13] that interconnects between the cosmic creation and the abstract mathematical entities “numbers”! Where the cosmic is simply a projection of the numerical system! God’s mathematical model to create and design a perfect and unique universe from nothing! A super great mathematician! From this discrete system model for a granular spacetime we showed that the universe is just a physical copy of the numerical system projection since discrete system and continuous system are dual, we can create a discrete system “vertices” from a continuous system “braids” through twists and vise versa all depends on the observer! That will apply to mass and energy, external and internal spacetime. Although our universe is material that due to changes and exposed to deformations, so if the universe collapse one day, is that means the numerical system can collapse? If our numerical system is periodic then why the weather is not deterministic? The answer is that the universe likewise the numerical system is generated by a supper-computer that code, decode and correct error codes! There is an asymmetry and duality between mass and energy, even if the material world disappears, it will simply retransformed to wave particles that conserve the same dynamical structure as the numerical system! A good example of string theory! A system made of strings that vibrate following of course the same dynamical of the numerical system. Our physical material world is simply the projection of those strings! When it comes to weather the reason behind it is that the sun is moving toward a specific location following a specific elliptic curve in our galaxy a spiral of Fibonacci, while the earth orbiting around the sun and the moon orbiting around the earth, the position of the sun is not the same every year, that causes a slight difference in the weather system! A mechanism that describes a succession of inclusive waves with different periods like a clock machine: a wave that curls around a wave and this last one curls around another wave a phenomenon that is seen in nature from waves and deeper waves in the oceans, trees, human physical body, hearts..! It generates the torus along the 2 periods one latitudinal and other one is longitudinal. This property was described in the structure of the numbers where composite numbers curl around the prime numbers and the prime numbers curl around the palindrome numbers “axis” [1]. There is no weather manmade global warming! When a natural disaster happens is because nature is cleaning itself following the phenomena of annihilation and formation! As the universe cleans up itself, the oceans does too, all those transformations are based from the interconnection between the internal spacetime and the external spacetime from an entangled lattice the fabric of the spacetime! We don’t control the universe! An intelligent system itself.
3. Applications
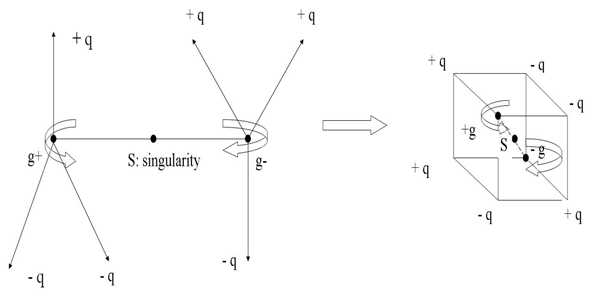 | Figure 16. Dynamical of the quarks |
- Dynamical of the Hydrogen: The quarks model for the hydrogen can be interpreted by this numerical model, where proton has 3 quarks: +q, +q, -q and the neutron by 3 quarks: -q, -q, +q that maps a cube, while the electron maps a hyper-sphere, that describe a vortex knot model. Its dynamical system is similar to the set described above for our numerical system. Replacing: +q (quarks) by 2, 5 and 1, –q by 4, 7 and 8, the number 3 by the graviton and 6 by the anti-graviton. Why the electron describes the hyper-sphere that cover the icosahydral. - Dynamical of the earth: As we know the core of the earth structured from iron, copper and other conductors with the shape of a torus generates the movement of the earth, though this electro-dynamo generator “Timer” is in motion with opposite direction to the earth motion maps a hexagonal torus a long 2 asymmetrical trefoil knots! It creates the electromagnetic field that protect the earth from the sun radiation, while the sun is moving toward a specific direction following the spiral of Fibonacci the earth is weaving around it following a curved cylindrical path and the moon is weaving around the earth an inclusion of waves. But due to the singularity and the convergence in the core area, the polarity changes the sign from + to - for a periodical orbit where the pole north shifts to the pole south and vise versa. The sun then will rise from the east in stay of the west, but during the shifting open holes will persist and will invite the extra dimension entities to penetrate along those holes. 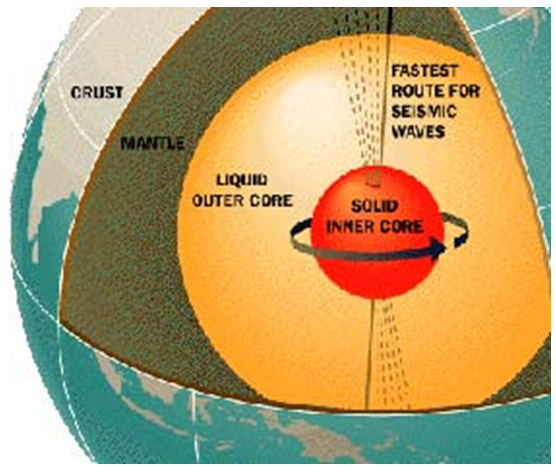 | Figure 17. Dynamical of the earth |
- Dynamical of the heart beep: If we enumerated and project those beeps made of sounds due to the mechanical oscillation of the heart’s muscles according to our system from 1 to 99 with a uniform speed, those beeps will also be mapping a torus of 4dim embedded in a hyper-sphere of 7dim with a total of 11 dim. And due to its interconnection through the blood with the cells and with DNA they will produce the same geometrical shape! Thus if the frequency of the heart changes the geometrical shape also changes since the electromagnetic field that protect us change the sign from + to – and will creates holes. This phenomenon usually is due to stress and sadness creating a negative energy! As a consequence it will leads to the deterioration of the cells system which help the viruses to enter easily and damage the cells! Most vulnerable viruses adapt their geometrical shape as the universe in the shape of an icosahydral [14] to protect themselves! The only ways to destroy them is to use electromagnetic ray with precise frequency! This reminds me of the movie “Lost” when John lock was cured from his cancer after he landed on the island due to the island electromagnetic field for a specific frequency! A cure could be realizing by injecting anti-virus with cells that have the same geometrical shape to target the singular point of the virus, since the virus tends to familiarize easily with the new cell by combining to it then vanishes easily. This is seen in the use of natural remedy such as honey, black seed (pentagonal flower); I’m willing to publish in the future a mathematical model for such a subject since I have more concern about it! | Figure 18. Geometrical shape of viruses |
References
| [1] | S. Daouairi: Equation of Everything, code unlocked, article.sapub.org/10.5923.j.ijtmp.2014. |
| [2] | Friedrich Hirzebruch: Singularities & exotic spheres “Seminar Bourbaki” 1966/67. |
| [3] | O. Nash, on Klein’s icosahydral solution of the quintic, expo math 2013. |
| [4] | Ghys. E on knots and dynamic, international congress of mathematics, Madrid 2006. |
| [5] | Birman, J. Williams, R: Knotted periodic orbits in dynamical systems. I. Lorenz’s equation 1983. |
| [6] | Kauffman L: Knots and Physics. |
| [7] | Kirby R.C & Sharlemann M.G “Eight faces of the Poincare homology 3-sphere”. |
| [8] | Mark R Dennis, Benjamin Bode “Constructing a polynomial whose nodal set is the three twist knot 52, 2016. |
| [9] | Frits Beukers, The Diophantine equation, 2004. 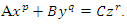 |
| [10] | Lei Yang. Modular curves, invariant theory and E8, 2017. |
| [11] | T.K. Carne, notes Michaelmas, 2012 Geometry and groups. |
| [12] | Jenia Tevelev Moduli spaces and invariant theory. |
| [13] | Oystein Linnebo, Platonism in the philosophy of mathematics, 2013. |
| [14] | B.V Venkataram Prasad and Michael F. Schmid, Principles of virus structural organization. |


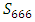 is just the exotic Milnor 7 dimensional sphere connected to the Torus knots (2, 3) with a 5 fold symmetry and related to the homology Poincare sphere
is just the exotic Milnor 7 dimensional sphere connected to the Torus knots (2, 3) with a 5 fold symmetry and related to the homology Poincare sphere 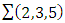 , the discrete unimodular lattice
, the discrete unimodular lattice 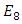 – singularity, A, D, E and platonic solids. The twisted, curved spacetime is defined from two important and special interconnected lattices in dynamic namely the square lattice
– singularity, A, D, E and platonic solids. The twisted, curved spacetime is defined from two important and special interconnected lattices in dynamic namely the square lattice 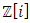 (counter of time) and the hexagonal lattice to define Space and when it degenerates it will simply describe the dynamical of the system’s axis described by a trefoil knot which is the algebraic curve and the bridge link of the asymmetrical system! The system describes a vortex knots model and looks chaotic comparable to the “case of Lorenz knots” generated by the dynamical of a combination of elliptical asymmetric connected encoded knots parameterizable by Fourier transform polynomials due to the modularity and by the dynamical of hyperbolical Fibonacci modular knots inside a closed space in dynamic. The equation of everything is an evidence to prove the existence of the physical property of the numerical system “Numbers”, geometrically represented by fibers of a surface or brane while in dynamic it generates vibrating loops or spirals related to lemniscates knots in the form of waves, abstract mathematical entities knotted with twisted orbital that generate a finite lattice model describing an abstract multi-verse of 11 dim. Per an analogy and projection it will describe our asymmetrical multi-verse system! Gravity exists even in the numerical system inside the lattice that generates waves. The equation also unveils the truth of the prime numbers and its hidden secret from its physical properties to its distribution generated by the spectrum of
(counter of time) and the hexagonal lattice to define Space and when it degenerates it will simply describe the dynamical of the system’s axis described by a trefoil knot which is the algebraic curve and the bridge link of the asymmetrical system! The system describes a vortex knots model and looks chaotic comparable to the “case of Lorenz knots” generated by the dynamical of a combination of elliptical asymmetric connected encoded knots parameterizable by Fourier transform polynomials due to the modularity and by the dynamical of hyperbolical Fibonacci modular knots inside a closed space in dynamic. The equation of everything is an evidence to prove the existence of the physical property of the numerical system “Numbers”, geometrically represented by fibers of a surface or brane while in dynamic it generates vibrating loops or spirals related to lemniscates knots in the form of waves, abstract mathematical entities knotted with twisted orbital that generate a finite lattice model describing an abstract multi-verse of 11 dim. Per an analogy and projection it will describe our asymmetrical multi-verse system! Gravity exists even in the numerical system inside the lattice that generates waves. The equation also unveils the truth of the prime numbers and its hidden secret from its physical properties to its distribution generated by the spectrum of 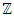 and its extensions
and its extensions 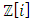 and
and 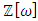 . The system is complete and consistent since it is based on a finite asymmetrical discrete system “In/Out & Out/In” a perfect example of systems that contradicts the Gödel’s incompleteness theorem. The article is a simple introduction of the representation and projection of the number theory to knot theory!
. The system is complete and consistent since it is based on a finite asymmetrical discrete system “In/Out & Out/In” a perfect example of systems that contradicts the Gödel’s incompleteness theorem. The article is a simple introduction of the representation and projection of the number theory to knot theory!
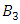 braid group rather than an infinite
braid group rather than an infinite 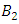 . Those branes are fibered space represented by vibrating loops generating wave forms, with the shape of spirals related to lemniscate knots specifically “torus knots” that we going to define in this paper. Numbers are knotted and generate twisted orbital describing a twisted non tangled lattice in dynamic in a higher dimension due to the action of an SO(3) transformation known by Paul Dirac belt trick effect. For this reason we reduced the set of integers to a finite set
. Those branes are fibered space represented by vibrating loops generating wave forms, with the shape of spirals related to lemniscate knots specifically “torus knots” that we going to define in this paper. Numbers are knotted and generate twisted orbital describing a twisted non tangled lattice in dynamic in a higher dimension due to the action of an SO(3) transformation known by Paul Dirac belt trick effect. For this reason we reduced the set of integers to a finite set 
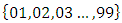 set of two digits to study the asymmetry of the system generated by the 9.11 emergency elements and its connection to the number 666! What a coincidence! In general in most cases the dynamical system for a physical system described as the motion of the system projected on the space time with parameters depending on the space and time, however some dynamical systems are described or represented by an algorithm of strings for an encoded system based on words and letters. Although with a simple parameterization we can convert those words to parametric equations. Mathematics is a useful tool that we use in our everyday life in a wide of fields such as science, economic, arts …for decision making, system modeling, analysis and more. For this reason we should perfectly understand and master our tools! Unveiling the hidden secret of our mathematical tools will open us the doors to discover many secrete things hidden about our universe. Our mathematical tools are based from the numerical system which is represented by the set ℤ, ℚ, ℝ, ℂ, ℍ and 𝕆 or the set of binary system,…Unfortunately it shows that we are using mathematical tools that we don’t understand its function and structure. The numerical system is an intelligent tool itself, a very smart system, where all the elements are in communication through webs like neurons in our brain, cells inside our blood and DNA inside the cells, galaxies in the universe, planets in the galaxy, electrons and quarks in the atoms, although these entities seem to be more familiar with mathematical concepts than we do! When we dig deeply everything in the universe has a coded mathematical information form to it. Well in this paper and in my previous paper we see detailed physical explanation about the numerical system in general, and how the system is interconnected algebraically, geometrically and analytically.Summary of the “Equation of Everything”:
set of two digits to study the asymmetry of the system generated by the 9.11 emergency elements and its connection to the number 666! What a coincidence! In general in most cases the dynamical system for a physical system described as the motion of the system projected on the space time with parameters depending on the space and time, however some dynamical systems are described or represented by an algorithm of strings for an encoded system based on words and letters. Although with a simple parameterization we can convert those words to parametric equations. Mathematics is a useful tool that we use in our everyday life in a wide of fields such as science, economic, arts …for decision making, system modeling, analysis and more. For this reason we should perfectly understand and master our tools! Unveiling the hidden secret of our mathematical tools will open us the doors to discover many secrete things hidden about our universe. Our mathematical tools are based from the numerical system which is represented by the set ℤ, ℚ, ℝ, ℂ, ℍ and 𝕆 or the set of binary system,…Unfortunately it shows that we are using mathematical tools that we don’t understand its function and structure. The numerical system is an intelligent tool itself, a very smart system, where all the elements are in communication through webs like neurons in our brain, cells inside our blood and DNA inside the cells, galaxies in the universe, planets in the galaxy, electrons and quarks in the atoms, although these entities seem to be more familiar with mathematical concepts than we do! When we dig deeply everything in the universe has a coded mathematical information form to it. Well in this paper and in my previous paper we see detailed physical explanation about the numerical system in general, and how the system is interconnected algebraically, geometrically and analytically.Summary of the “Equation of Everything”: Geometrical Interpretation of the Equation: We proved that the dynamical of the system describes an asymmetrical discrete lattice in dynamic that maps a hexagonal torus where dimension of the torus’s spacetime
Geometrical Interpretation of the Equation: We proved that the dynamical of the system describes an asymmetrical discrete lattice in dynamic that maps a hexagonal torus where dimension of the torus’s spacetime 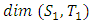 equals (3,1) with a total of 4 dim embedded in a hyper-sphere with
equals (3,1) with a total of 4 dim embedded in a hyper-sphere with 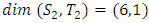 with a total of 7 dim orbiting in opposite directions in a higher dimension with a total of 11 dim. Time is asymmetrical of 2 dimensions. The torus and the hyper-sphere are connected by the Paul Dirac belt trick along the SO(3) transformation. The system described by a vortex knot model generated from a combination of linked asymmetrical knots namely trivial knots, Hopf link and trefoil knots. The properties of this mathematical model can explain and interpret the dynamical system of many systems from physical, biological, economical, financial, political systems, spiritual side, consciousness … The model is similar and quite comparable to Lorenz flow that describe the weather, equation of Boltzman for gas distribution, fluid dynamic, structure and dynamical of particles in quantum physics, dynamical of the universe and earth as a macro system, mechanical function of the heart beeps and its interconnection to the dynamical of the DNA and neurons inside a cell to the entire system body, mind, viruses, dynamical of the mechanical’s eye muscle. We have already seen the connection of Hopf link to the electromagnetism, trefoil knot to the strong force that binds the quarks and the trivial knots to the gravity, so the interconnection and the combination of those knots for such a system will simply unify the 4 physical forces since we can define the force and the energy of a knot!. Theoretical path of the equation: Deeply the equation of everything deals with a wide range and varieties of mathematical fields, this concrete example of numerical model rich of mathematical concepts and ideas that interplay between general mathematical theories that interconnect between number theory, topology & differential topology, algebraic geometry & projective geometry, harmonic analysis, symmetrical transformations, combinatory, logic and information theory! The evolution and the transformation of mathematical concepts and theories prove that even mathematic replicates itself along a special reversible asymmetrical transformation that relies on its dynamical system for an invariant system based from the automorphism groups! Mathematics study every steps and corners and provide us with a chain of mathematical connections caused by the dynamical of the numerical system with cases for each stage of its transformations to define convergence and perturbation of a family of elliptic curves and fiber bundles of the moduli space that rely on the isomorphism theorems, structure of quotient rings, maximal ideals, fixed points and root system defined by the Eigen-values and on how the spectrum of ℤ and
with a total of 7 dim orbiting in opposite directions in a higher dimension with a total of 11 dim. Time is asymmetrical of 2 dimensions. The torus and the hyper-sphere are connected by the Paul Dirac belt trick along the SO(3) transformation. The system described by a vortex knot model generated from a combination of linked asymmetrical knots namely trivial knots, Hopf link and trefoil knots. The properties of this mathematical model can explain and interpret the dynamical system of many systems from physical, biological, economical, financial, political systems, spiritual side, consciousness … The model is similar and quite comparable to Lorenz flow that describe the weather, equation of Boltzman for gas distribution, fluid dynamic, structure and dynamical of particles in quantum physics, dynamical of the universe and earth as a macro system, mechanical function of the heart beeps and its interconnection to the dynamical of the DNA and neurons inside a cell to the entire system body, mind, viruses, dynamical of the mechanical’s eye muscle. We have already seen the connection of Hopf link to the electromagnetism, trefoil knot to the strong force that binds the quarks and the trivial knots to the gravity, so the interconnection and the combination of those knots for such a system will simply unify the 4 physical forces since we can define the force and the energy of a knot!. Theoretical path of the equation: Deeply the equation of everything deals with a wide range and varieties of mathematical fields, this concrete example of numerical model rich of mathematical concepts and ideas that interplay between general mathematical theories that interconnect between number theory, topology & differential topology, algebraic geometry & projective geometry, harmonic analysis, symmetrical transformations, combinatory, logic and information theory! The evolution and the transformation of mathematical concepts and theories prove that even mathematic replicates itself along a special reversible asymmetrical transformation that relies on its dynamical system for an invariant system based from the automorphism groups! Mathematics study every steps and corners and provide us with a chain of mathematical connections caused by the dynamical of the numerical system with cases for each stage of its transformations to define convergence and perturbation of a family of elliptic curves and fiber bundles of the moduli space that rely on the isomorphism theorems, structure of quotient rings, maximal ideals, fixed points and root system defined by the Eigen-values and on how the spectrum of ℤ and 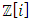 splices and splits and its connection to
splices and splits and its connection to 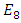 lattice, icosahydral, homology sphere and the 7 dim Milnor exotic sphere that rely on knots and there connection with modular form. Numbers are knotted with twisted orbital in dynamic, in the form of a combination of asymmetrical special invariant knots in dynamic that generate a twisted lattice in dynamic in the form of fibers of a surface, while the axis based on the root system that rely on the descriminant of the lattice. The projection and the extensions of this dynamical transformation shows interesting characteristic of its topological and algebraic geometric invariant with complex analytic properties, where dynamical of knots with closed orbits defined by periodic path coincide with singular curves! The algebra of the numerical system seems to be one of the complete and consistent theories to describe the universe! This abstract dynamical system of course depends theoretically on the parameters of space and time when we consider numbers in motion per projection in our concrete spacetime! But in an abstract space the numerical system is a type of language or program generated by a super computer that codes, decodes and correct error code [1] since the system is asymmetrical reversible in harmonic oscillations with internal and external spacetime generated by the knots, where knots are encoded through an algorithm of string with an enumerating language program based from letters and words for a closed finite orbit with a periodic path dealing with homotopy classes, braid groups [5]. What’s interesting is that the study of the physical properties of the numbers is independent of the mass, mathematical object massless! Object beyond the micro system for quantum physics and macro system concerning the gravitational system! We proved that the gravity exists even in the numerical system, since the dynamical or the transformation is based from the generators that fill gaps “vertices” along the oscillation of the system represented by the lattice! [1]. The string theory, M theory and quantum gravity are simply an indirect reverse application to the number theory! The sequence of the integers represents the motion or the dynamical system of the integer number 1 by adding +1 through a translation, it will then split or splice describing a curved lattice in dynamics with a higher dimensional Riemann surface generated by the spectrum of
lattice, icosahydral, homology sphere and the 7 dim Milnor exotic sphere that rely on knots and there connection with modular form. Numbers are knotted with twisted orbital in dynamic, in the form of a combination of asymmetrical special invariant knots in dynamic that generate a twisted lattice in dynamic in the form of fibers of a surface, while the axis based on the root system that rely on the descriminant of the lattice. The projection and the extensions of this dynamical transformation shows interesting characteristic of its topological and algebraic geometric invariant with complex analytic properties, where dynamical of knots with closed orbits defined by periodic path coincide with singular curves! The algebra of the numerical system seems to be one of the complete and consistent theories to describe the universe! This abstract dynamical system of course depends theoretically on the parameters of space and time when we consider numbers in motion per projection in our concrete spacetime! But in an abstract space the numerical system is a type of language or program generated by a super computer that codes, decodes and correct error code [1] since the system is asymmetrical reversible in harmonic oscillations with internal and external spacetime generated by the knots, where knots are encoded through an algorithm of string with an enumerating language program based from letters and words for a closed finite orbit with a periodic path dealing with homotopy classes, braid groups [5]. What’s interesting is that the study of the physical properties of the numbers is independent of the mass, mathematical object massless! Object beyond the micro system for quantum physics and macro system concerning the gravitational system! We proved that the gravity exists even in the numerical system, since the dynamical or the transformation is based from the generators that fill gaps “vertices” along the oscillation of the system represented by the lattice! [1]. The string theory, M theory and quantum gravity are simply an indirect reverse application to the number theory! The sequence of the integers represents the motion or the dynamical system of the integer number 1 by adding +1 through a translation, it will then split or splice describing a curved lattice in dynamics with a higher dimensional Riemann surface generated by the spectrum of 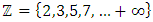 “set of prime ideals in ℤ” that extend to
“set of prime ideals in ℤ” that extend to 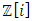 “ring of Gaussian integers generated by Gaussian primes with base
“ring of Gaussian integers generated by Gaussian primes with base 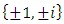 , the only invertible elements for an invariant system, with the algebraic extension f:
, the only invertible elements for an invariant system, with the algebraic extension f: 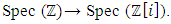 The spectrums play an important role to describe how fields split and splice in the projective Hilbert space. Since our system is invariant, we will be interested on the automorphism group linear for an invertible system! We will also focus on the convergence since it is related to the fixed points for a periodical path! Numbers or integers simply take the role of the group representation and its characters “modular” generated by a twist due to the asymmetry of the system. There is a solid extension between number field, function field and prime numbers from the correspondence
The spectrums play an important role to describe how fields split and splice in the projective Hilbert space. Since our system is invariant, we will be interested on the automorphism group linear for an invertible system! We will also focus on the convergence since it is related to the fixed points for a periodical path! Numbers or integers simply take the role of the group representation and its characters “modular” generated by a twist due to the asymmetry of the system. There is a solid extension between number field, function field and prime numbers from the correspondence 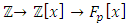 with the embedding homomorphism
with the embedding homomorphism 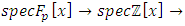
 that send maximal ideals
that send maximal ideals  and act geometrically as a projection on to the set ℤ, hence fibers correspond to the sub-varieties max
and act geometrically as a projection on to the set ℤ, hence fibers correspond to the sub-varieties max 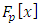 . One can view the connection between integers in number theory and the moduli space “geometry” due to the similar operations that are analogue between the integers and polynomials for a commutative ring, polynomial are function on line on space “analytic geometry” where we can operate a function and its pull back map defined by a homomorphism. The point on the space is defined as the prime ideal through the map
. One can view the connection between integers in number theory and the moduli space “geometry” due to the similar operations that are analogue between the integers and polynomials for a commutative ring, polynomial are function on line on space “analytic geometry” where we can operate a function and its pull back map defined by a homomorphism. The point on the space is defined as the prime ideal through the map 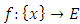 , a one point space is a field, if it vanishes locally it will vanish globally represented by the kernel of the homomorphism
, a one point space is a field, if it vanishes locally it will vanish globally represented by the kernel of the homomorphism 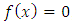 , with
, with 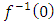 as the pull back while for a space more than one point we can discuss about the covering, branched covering, algebraic extension and fields. We can express the family of elliptic curves and fiber bundles of the Moduli space through number theory along the isomorphism correspondence that rely on the structure of quotient rings defined by the maximal ideals! The set of integers
as the pull back while for a space more than one point we can discuss about the covering, branched covering, algebraic extension and fields. We can express the family of elliptic curves and fiber bundles of the Moduli space through number theory along the isomorphism correspondence that rely on the structure of quotient rings defined by the maximal ideals! The set of integers 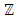 is twisted, every element can be mapped to its mirror image through the axis of symmetry described by the palindrome numbers, so to reduce its form we considered a finite subset
is twisted, every element can be mapped to its mirror image through the axis of symmetry described by the palindrome numbers, so to reduce its form we considered a finite subset 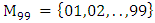 of integers with 2 digits which is isomorphic to
of integers with 2 digits which is isomorphic to 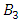 , where
, where 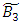 its closure or link related to the trefoil knot. The set of integers is twisted and generated by a composition of 2 special transformation maps described as a translation of Z+1 to describe the set ℤ and by a rotation or inverse map defined by
its closure or link related to the trefoil knot. The set of integers is twisted and generated by a composition of 2 special transformation maps described as a translation of Z+1 to describe the set ℤ and by a rotation or inverse map defined by 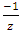 to form rational tangle to describe the set ℚ of rational numbers, where any element of ℚ defined by
to form rational tangle to describe the set ℚ of rational numbers, where any element of ℚ defined by 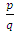 with
with 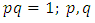 elements of ℤ can be represented by a rational tangle a (p, q) torus that generates
elements of ℤ can be represented by a rational tangle a (p, q) torus that generates 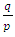 turns, while any element of ℝ is a limit of a rational tangle! The circle unity U(1), the sets ℂ, ℍ, 𝕆 and geometrically the elements of the Riemannian surfaces of genus 0 and 1 such as elliptic curves, torus, hyper-sphere and special knots are consequence of this transformation and extension. The numerical system is connected and results from the bifurcation of the transformation for such a braid closure.
turns, while any element of ℝ is a limit of a rational tangle! The circle unity U(1), the sets ℂ, ℍ, 𝕆 and geometrically the elements of the Riemannian surfaces of genus 0 and 1 such as elliptic curves, torus, hyper-sphere and special knots are consequence of this transformation and extension. The numerical system is connected and results from the bifurcation of the transformation for such a braid closure. 
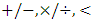
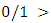 , palindrome numbers, true/false, binary system, finite fields, group cyclic, circle unity..! With arguments related to a series of logical concepts defined by a set
, palindrome numbers, true/false, binary system, finite fields, group cyclic, circle unity..! With arguments related to a series of logical concepts defined by a set 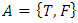 of binary system with true or false statements to define a proposition! Grounded by mathematical abstract operators, or objects based on negation, identity or annihilation. There is no broken symmetry, simply when we represent the system by the quaternions number system then the chirality is clear and obvious, however the system originally is asymmetrical. We have to make the difference between symmetry and asymmetry. Algorithm of strings, Knot and braid algebra theories combined with the dynamical system for an invariant system seem to be one of the interesting theories favorable to describe the numerical system itself and the universe! The model of our equation of everything is finite, complete and consistent. Our granular spacetime is based from a discrete system generated by the dynamical of a discrete lattice
of binary system with true or false statements to define a proposition! Grounded by mathematical abstract operators, or objects based on negation, identity or annihilation. There is no broken symmetry, simply when we represent the system by the quaternions number system then the chirality is clear and obvious, however the system originally is asymmetrical. We have to make the difference between symmetry and asymmetry. Algorithm of strings, Knot and braid algebra theories combined with the dynamical system for an invariant system seem to be one of the interesting theories favorable to describe the numerical system itself and the universe! The model of our equation of everything is finite, complete and consistent. Our granular spacetime is based from a discrete system generated by the dynamical of a discrete lattice  “dual of the continuous system” with the asymmetry and orientation properties for a reversible path defined by a pull-back homomorphism map that preserve the structure! The discrete system and the continuous system are simply connected through a homotopy group.Bipolar system: two asymmetrical entities
“dual of the continuous system” with the asymmetry and orientation properties for a reversible path defined by a pull-back homomorphism map that preserve the structure! The discrete system and the continuous system are simply connected through a homotopy group.Bipolar system: two asymmetrical entities  &
& 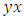 in dynamics along the axis of symmetry, moving in opposite direction with a periodic path create a vortex knot model generating harmonic oscillations and converge toward the golden ratio! Describing an internal and an external spacetime twisted with a higher dimension! [1]. If such an equation exists then it will reflect the geometrical shape of its dynamical system in nature and will interconnect between systems! Two important properties seen as a consequence of such an equation: - Golden Ratio: Everything seems to grow and expand in nature following the spiral of Fibonacci based on the golden ratio from our physical structure seen in DNA, neurons, physical body, fruits, shell, flowers, trees, production, particles, galaxy, earth, etc… -Asymmetry Definition: Let’s denote by
in dynamics along the axis of symmetry, moving in opposite direction with a periodic path create a vortex knot model generating harmonic oscillations and converge toward the golden ratio! Describing an internal and an external spacetime twisted with a higher dimension! [1]. If such an equation exists then it will reflect the geometrical shape of its dynamical system in nature and will interconnect between systems! Two important properties seen as a consequence of such an equation: - Golden Ratio: Everything seems to grow and expand in nature following the spiral of Fibonacci based on the golden ratio from our physical structure seen in DNA, neurons, physical body, fruits, shell, flowers, trees, production, particles, galaxy, earth, etc… -Asymmetry Definition: Let’s denote by 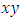 an integer with 2 digits and
an integer with 2 digits and 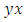 its mirror image elements of
its mirror image elements of 
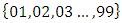 set of elements with 2 digits a subset of the set ℤ. Then
set of elements with 2 digits a subset of the set ℤ. Then 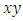 and
and 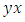 are asymmetric if
are asymmetric if 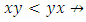
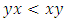 and if
and if 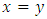 then
then 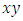 and
and 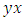 are element of the diagonal ∆ or axis of the symmetry of
are element of the diagonal ∆ or axis of the symmetry of 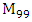 . The set
. The set 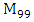 is an interesting subset of ℤ as we know twisted with double brane faces +/- generated by the set of the transpalindromes and a branch locus as the axis “set of the palindromes! The axis of symmetry or the spin axis considered as the diagonal or the set of fixed point represented by the palindromes in our numerical model, it splits following the numerical equations:
is an interesting subset of ℤ as we know twisted with double brane faces +/- generated by the set of the transpalindromes and a branch locus as the axis “set of the palindromes! The axis of symmetry or the spin axis considered as the diagonal or the set of fixed point represented by the palindromes in our numerical model, it splits following the numerical equations: 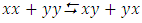 and for
and for 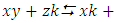
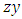 forming the alternating discrete lattice, we can then consider the oriented link by the crossing for a Reidemeister moves according to the nature of the elements of the set
forming the alternating discrete lattice, we can then consider the oriented link by the crossing for a Reidemeister moves according to the nature of the elements of the set 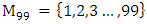 “prime” or “composite” defined by 3 strands: the identity generated by ∆ and the two asymmetrical strands with structure isomorphic to
“prime” or “composite” defined by 3 strands: the identity generated by ∆ and the two asymmetrical strands with structure isomorphic to 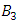 braid group. Every element has an asymmetrical element considered as a micro system with internal/external spacetime that spin around its axis since we consider our system on dynamic. Let’s say
braid group. Every element has an asymmetrical element considered as a micro system with internal/external spacetime that spin around its axis since we consider our system on dynamic. Let’s say 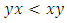 then it implies the inclusion
then it implies the inclusion 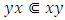 , and due to the orientation, it creating a vortex ring model, orbiting with opposite directions with generators linearly independents! That leads us to introduce our lattice model with 2 periods. In our model there are 3 types of trans-palindrome or asymmetrical type of numbers that generate the lattice: * prime with mirror image prime: considered as 2 linked trivial knots
, and due to the orientation, it creating a vortex ring model, orbiting with opposite directions with generators linearly independents! That leads us to introduce our lattice model with 2 periods. In our model there are 3 types of trans-palindrome or asymmetrical type of numbers that generate the lattice: * prime with mirror image prime: considered as 2 linked trivial knots 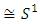 with short range, repulsive due to the orientation “anti-gravity” connected by the axis (e.g. Figure 2). Here the axis represented by the palindromes is a closed loop that has the form of a trefoil knot. The axis acts as a bridge link between the 2 asymmetrical knots.
with short range, repulsive due to the orientation “anti-gravity” connected by the axis (e.g. Figure 2). Here the axis represented by the palindromes is a closed loop that has the form of a trefoil knot. The axis acts as a bridge link between the 2 asymmetrical knots. 


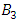 where its closure represents 2 linked asymmetrical trefoil knots with long range following the longitudinal axis that represents bridge link “the strong force that binds the quarks together” orbiting in opposite directions that cancel each other giving birth to 2 unknots in the critical point of the torus in the center for a hyperboloid surface which described as the light cone (e.g. Figure 4).
where its closure represents 2 linked asymmetrical trefoil knots with long range following the longitudinal axis that represents bridge link “the strong force that binds the quarks together” orbiting in opposite directions that cancel each other giving birth to 2 unknots in the critical point of the torus in the center for a hyperboloid surface which described as the light cone (e.g. Figure 4).
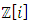 and
and 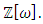

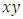 and
and 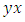 depend on the trajectory of
depend on the trajectory of 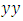 to
to 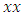 and vice versa. Although
and vice versa. Although 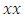 and
and 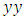 are elements of the axis ∆ “a closed curved line”! As a result
are elements of the axis ∆ “a closed curved line”! As a result 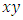 and
and 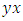 are connected and based from a homotopy map! We will see later that
are connected and based from a homotopy map! We will see later that 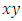 and
and 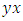 are simply connected by Paul Dirac belt trick. Per extension of the set
are simply connected by Paul Dirac belt trick. Per extension of the set 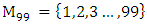 that represents the lattice of integers by the quotient modulo a prime to a complex state to define the finite cyclic group
that represents the lattice of integers by the quotient modulo a prime to a complex state to define the finite cyclic group 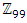 “See Galois extension of the cyclotomic fields”! And since
“See Galois extension of the cyclotomic fields”! And since 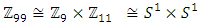 (Torus), the product can be interpreted by the rotation defined by the period of
(Torus), the product can be interpreted by the rotation defined by the period of 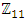 with
with 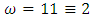 [9] where the period of
[9] where the period of 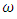 is of order 6 that lies on a hexagonal torus with elements
is of order 6 that lies on a hexagonal torus with elements 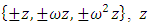 element of
element of 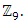 Since the set
Since the set 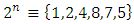 [9] then the set
[9] then the set 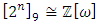 . We notice also
. We notice also 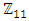 sends
sends 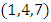 to
to 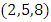 and
and 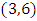 to
to 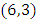 where 9 is invariant and the remaining set of
where 9 is invariant and the remaining set of 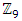 by
by 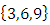 defined by the axis generated by
defined by the axis generated by 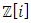 with order 4. Leads to this interesting connection between
with order 4. Leads to this interesting connection between 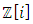 &
& 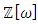 . We saw also in the previous equation [1] the 3 groups
. We saw also in the previous equation [1] the 3 groups 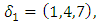
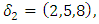
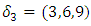 are related to the braid group
are related to the braid group  and are connected by
and are connected by 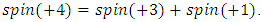

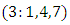 and
and 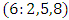 (e.g. Figure 7). Per projection in the
(e.g. Figure 7). Per projection in the 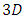 , it shows that the 2 tetrahedral are embedded in a cube with vertices located on the vertices of a cube orbiting with opposite direction to each other and defining 2 asymmetrical trefoil knots that generate a torus and a hyper-sphere orbiting in opposite direction! By a double cover transformation the points map an icosahydral, the system is invariant under the twist where particles “vertices” can move free due to Dirac belt trick generated by
, it shows that the 2 tetrahedral are embedded in a cube with vertices located on the vertices of a cube orbiting with opposite direction to each other and defining 2 asymmetrical trefoil knots that generate a torus and a hyper-sphere orbiting in opposite direction! By a double cover transformation the points map an icosahydral, the system is invariant under the twist where particles “vertices” can move free due to Dirac belt trick generated by 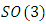 transformation.
transformation. 
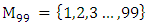 can be writing as:
can be writing as: 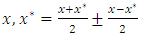 sum of an element of
sum of an element of  and
and  where
where  is the mirror image of
is the mirror image of 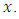 And vice versa when we apply the rotation to the group
And vice versa when we apply the rotation to the group 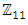 by
by 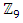 the remaining path is isomorphic to
the remaining path is isomorphic to 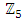 , this simply a consequence of the dual of the icosahydral generated by the 5 fold symmetry of a dodecahydral. If we consider now the continuous map
, this simply a consequence of the dual of the icosahydral generated by the 5 fold symmetry of a dodecahydral. If we consider now the continuous map 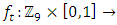
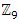 with
with 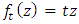 where t is a multiplicative scalar element of
where t is a multiplicative scalar element of 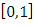 an extension to
an extension to 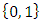 with
with 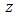 an element of
an element of 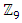 then f is injective and ∆ is invariant “described by the set
then f is injective and ∆ is invariant “described by the set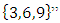 that transform
that transform 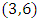 to
to 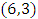 and
and 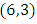 to
to 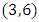 through the isomorphism map
through the isomorphism map 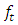 that represents the homotopy map H (t, z), dynamical of the curve when t (time) takes values between 0 and 1 of the circle unity
that represents the homotopy map H (t, z), dynamical of the curve when t (time) takes values between 0 and 1 of the circle unity 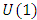 . The fixed point defined by
. The fixed point defined by 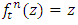 then for
then for 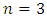 we have:
we have: 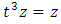 that leads to the equation
that leads to the equation 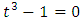 where t element of
where t element of 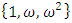 roots of a hexagonal torus. Following the numerical equations
roots of a hexagonal torus. Following the numerical equations 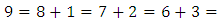
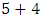 the number 9 is the center of the symmetry and the singularity point! Geometrically by points projection 9 represents the intersection of lines to infinity
the number 9 is the center of the symmetry and the singularity point! Geometrically by points projection 9 represents the intersection of lines to infinity 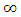 determined by the map:
determined by the map: 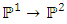 for
for 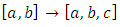 to the line
to the line 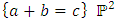 since all the roots of the hexagonal complex torus are conjugates with trace
since all the roots of the hexagonal complex torus are conjugates with trace 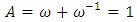 we identify then the line by sending the points to
we identify then the line by sending the points to  that generalize the mobius transformation along the cross ratio. By lifting the points by ramification, the Diophantine equation:
that generalize the mobius transformation along the cross ratio. By lifting the points by ramification, the Diophantine equation: 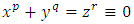 [9] have as solutions the vertices and its conjugates of a torus knot
[9] have as solutions the vertices and its conjugates of a torus knot 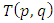 [9].
[9].
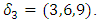


 this bracket is known by Kauffmann braid for a self replication process! (e.g. Figure 12)
this bracket is known by Kauffmann braid for a self replication process! (e.g. Figure 12) 
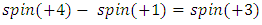 see detail [1]
see detail [1] With the value
With the value 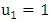 , the sequence or the function maps not only all the primes
, the sequence or the function maps not only all the primes 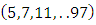 of the set
of the set 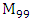 but also all the primes
but also all the primes 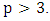

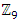 , the sequence shows the special correspondence between
, the sequence shows the special correspondence between 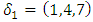 and
and 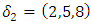 when we considere its closure it describes the trefoil knot, and that proves the geometric localization of the primes. The primes are certainly located on a hexagonal torus generated by a trefoil knot. Our lattice
when we considere its closure it describes the trefoil knot, and that proves the geometric localization of the primes. The primes are certainly located on a hexagonal torus generated by a trefoil knot. Our lattice  is a discrete set of asymmetrical elements
is a discrete set of asymmetrical elements 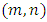 elements of
elements of 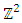 spinning around the axis; defined by
spinning around the axis; defined by 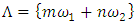
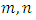 elements
elements 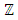 and
and 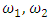 elements of
elements of 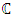 , where
, where 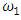 related to the hexagonal lattice and
related to the hexagonal lattice and 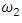 related to the square lattice generated by Eisenstein integers and Gaussian integers that intercept at the points
related to the square lattice generated by Eisenstein integers and Gaussian integers that intercept at the points 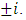 The dynamical of this lattice is defined by the map
The dynamical of this lattice is defined by the map 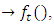 t element of
t element of 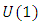 to describe a continuous system. The set of the asymmetrical elements describes a torus “maximal torus”!
to describe a continuous system. The set of the asymmetrical elements describes a torus “maximal torus”! 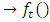 defined from the flow of the integers, which is generated from two asymmetrical trefoil knots defined from the roots and its conjugates of a hexagonal torus! We know that two asymmetrical knots cancel each other to form two unlinked trivial knots (e.g. Figure 4) that occur in the critical origin point of the cone light for a hyperboloid surface and the operation keep repeating due to the closed reversible path for a periodic orbital with a self replication when t describes the circle unity
defined from the flow of the integers, which is generated from two asymmetrical trefoil knots defined from the roots and its conjugates of a hexagonal torus! We know that two asymmetrical knots cancel each other to form two unlinked trivial knots (e.g. Figure 4) that occur in the critical origin point of the cone light for a hyperboloid surface and the operation keep repeating due to the closed reversible path for a periodic orbital with a self replication when t describes the circle unity 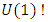 Transformation that results from the combination of two special lattices defined by
Transformation that results from the combination of two special lattices defined by 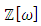 and
and 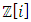 that are connected by the interesting relation
that are connected by the interesting relation 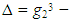
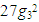 the special algebraic curve for the modular group! Although, there is an interesting connection between knots, its complement to the algebraic singularities and the modular group by the Weierstrass function
the special algebraic curve for the modular group! Although, there is an interesting connection between knots, its complement to the algebraic singularities and the modular group by the Weierstrass function 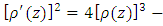
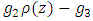 with
with 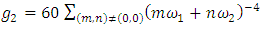 &
& 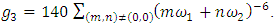
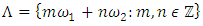 is a lattice with a double period where
is a lattice with a double period where 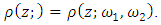 The curve
The curve 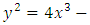
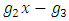 defines an elliptic curve ξ with descriminant
defines an elliptic curve ξ with descriminant 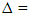
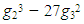 with roots are elements of a complex torus. The curves
with roots are elements of a complex torus. The curves 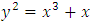 related to
related to 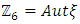 and
and 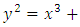
 related to
related to 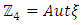 [12] which are the only curves with special automorphisms that correspond to the four branch points
[12] which are the only curves with special automorphisms that correspond to the four branch points 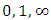 and
and 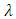 with
with 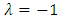 and
and 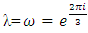 that generate the square lattice
that generate the square lattice 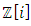 and the hexagonal lattice
and the hexagonal lattice 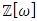 connected through the eigenvalues and the fixed points of the minimal polynomial. Since we are interested only on a reversible system, the only invertible elements of the spec
connected through the eigenvalues and the fixed points of the minimal polynomial. Since we are interested only on a reversible system, the only invertible elements of the spec 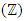 and spec
and spec 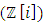 are
are 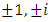 of order 4 related to the cyclotomic group
of order 4 related to the cyclotomic group 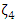 for the polynomial
for the polynomial 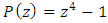 with roots elements of
with roots elements of 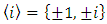 . Although
. Although 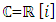 defined as the splitting field of
defined as the splitting field of 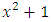 over
over 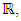 the factorization of
the factorization of 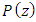 leads to the product of
leads to the product of 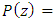
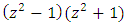 has coefficients in ℤ and monic, the cyclotomic polynomial lies in
has coefficients in ℤ and monic, the cyclotomic polynomial lies in 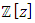 , One could see the duality relations that swaps fixed points to roots of the kernel between
, One could see the duality relations that swaps fixed points to roots of the kernel between 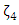 and
and 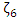 determined by the polynomials
determined by the polynomials 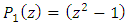 and
and 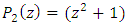 . For roots
. For roots 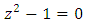 it leads to the relation:
it leads to the relation: 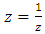 and for roots of
and for roots of 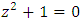 leads to the relation
leads to the relation 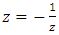 “stereographic projection of a sphere” related to the fixed points of the maps
“stereographic projection of a sphere” related to the fixed points of the maps 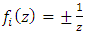 for
for 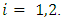 Now for the fixed points of the 2 polynomials we have:
Now for the fixed points of the 2 polynomials we have: 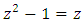 with roots the golden ratio and its conjugate, while for
with roots the golden ratio and its conjugate, while for 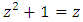 roots are conjugate and located on a hexagonal torus. With a slight symmetric transformation it shows that it is related to the Alexander polynomial for a trefoil knot
roots are conjugate and located on a hexagonal torus. With a slight symmetric transformation it shows that it is related to the Alexander polynomial for a trefoil knot 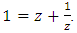 and by replacing t by:
and by replacing t by: 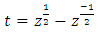 we have
we have 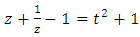 . We know also the Conway polynomial
. We know also the Conway polynomial 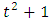 has infinitely quaternion roots in the form
has infinitely quaternion roots in the form 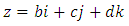 since
since 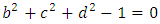 where roots lie on the 2 dimension surface of a sphere centered on zero in the 3 dimensional sub-space of quaternion with zero reel part and intersects the complex plane at two points
where roots lie on the 2 dimension surface of a sphere centered on zero in the 3 dimensional sub-space of quaternion with zero reel part and intersects the complex plane at two points 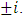 What is interesting is the structure of the descriminant which has the form of a variety algebraic
What is interesting is the structure of the descriminant which has the form of a variety algebraic  with
with 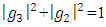 complex lattice that lie on the unit sphere. For this reason we should determine the characteristic of the trefoil knots! We can also extend the transformation to a modular knot for a modular flow with periodic orbits. By introducing the fixed point property for
complex lattice that lie on the unit sphere. For this reason we should determine the characteristic of the trefoil knots! We can also extend the transformation to a modular knot for a modular flow with periodic orbits. By introducing the fixed point property for 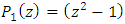 and
and 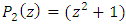
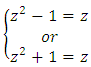 Lead to the fraction rational:
Lead to the fraction rational: 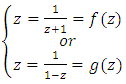 Generated by
Generated by 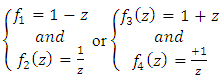 Generated by the matrices
Generated by the matrices 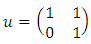 and
and 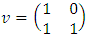 or
or 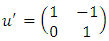 and
and 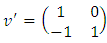 Knot Definition: In this part we going to see beautiful mathematical relations! First let’s define a knot, which is an embedding of a circle into 3 dim Euclidean Space. We know the knot group of a knot K is defined as the fundamental group of the knot complement of K in
Knot Definition: In this part we going to see beautiful mathematical relations! First let’s define a knot, which is an embedding of a circle into 3 dim Euclidean Space. We know the knot group of a knot K is defined as the fundamental group of the knot complement of K in 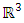 by
by 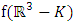 , the topology of the knot or link can be defined by
, the topology of the knot or link can be defined by 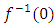 of a function:
of a function: 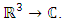 A mathematical knot function has many applications and showed interesting physical experimental evidence that describe the dynamical system of the vortex knot model for a variety of systems from weather, fluid dynamics, electromagnetism, quantum physics, and numerical system. Example of knots: Unknot, Hopf link or
A mathematical knot function has many applications and showed interesting physical experimental evidence that describe the dynamical system of the vortex knot model for a variety of systems from weather, fluid dynamics, electromagnetism, quantum physics, and numerical system. Example of knots: Unknot, Hopf link or 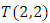 , trefoil knot or
, trefoil knot or 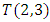 , torus knot
, torus knot 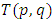 . The trefoil knot K is a fibered knot where its complement in
. The trefoil knot K is a fibered knot where its complement in 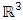 is a fiber bundle over the circle
is a fiber bundle over the circle 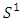 . Its knot group is isomorphic to the braid group
. Its knot group is isomorphic to the braid group 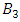 with the presentation
with the presentation 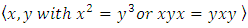 it is also the link and the right handed of the neighborhood boundary of the singular variety
it is also the link and the right handed of the neighborhood boundary of the singular variety 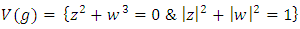 where z, w are complex numbers with
where z, w are complex numbers with 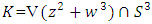 . As a fibration it has the Milnor map
. As a fibration it has the Milnor map 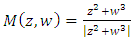 and a once punctured Torus as its fiber surface that vanish at the singularity 0. Hopf link are circles in
and a once punctured Torus as its fiber surface that vanish at the singularity 0. Hopf link are circles in 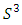 intersection of complex lines (circle in
intersection of complex lines (circle in 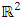 ) in
) in 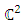 with
with 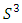 for
for 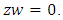

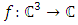 the complex polynomial
the complex polynomial 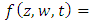
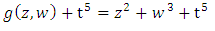 then
then 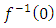 is the complex variety. By extending the link of the singular algebraic variety to
is the complex variety. By extending the link of the singular algebraic variety to 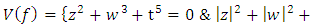
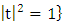 We have then per projection a
We have then per projection a 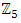 regular cover, where
regular cover, where 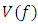 is the branched cover of
is the branched cover of 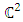 with branch locus
with branch locus 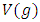 and
and 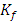 is the branched cover of
is the branched cover of 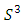 with branch locus
with branch locus 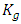 over the variety
over the variety 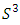 . It generates the equation of a dodecahedral. Let’s denote by
. It generates the equation of a dodecahedral. Let’s denote by 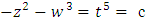 that when
that when 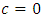 then
then 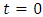 , variety with cusp 0 at the origin, and when
, variety with cusp 0 at the origin, and when 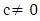 then the equation has 5 roots and the fixed points form the cone of the trefoil knot. then we have
then the equation has 5 roots and the fixed points form the cone of the trefoil knot. then we have 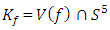 sits inside the dodecahedral and passes through the center of its faces, as a result the trefoil knot seems to be the axis of the dodecahedral space for a 5 fold symmetry that extend to the origin.
sits inside the dodecahedral and passes through the center of its faces, as a result the trefoil knot seems to be the axis of the dodecahedral space for a 5 fold symmetry that extend to the origin.
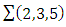 known by the Poincare dodecahedron space with finite fundamental group
known by the Poincare dodecahedron space with finite fundamental group 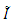 the binary icosahydral group defined by
the binary icosahydral group defined by 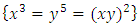 of order 120 double cover of the regular icosahydral group
of order 120 double cover of the regular icosahydral group 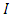
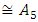 (alternating group) determined by the quotient space
(alternating group) determined by the quotient space 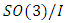 or simply by the double cover
or simply by the double cover 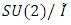 that can be constructed from Dehn surgery on knot from a right handed trefoil knot. The essential in this part is to determine the nature of the elliptical curves or modular knots that sits inside the entire space and define the geometrical shape of that space and its dimension! The construction will be based on the Brieskon algebraic varieties [2] that are associated with the polynomial:
that can be constructed from Dehn surgery on knot from a right handed trefoil knot. The essential in this part is to determine the nature of the elliptical curves or modular knots that sits inside the entire space and define the geometrical shape of that space and its dimension! The construction will be based on the Brieskon algebraic varieties [2] that are associated with the polynomial: 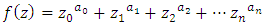 where
where 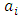 integers and
integers and 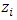 are complex. In general the variety defined by
are complex. In general the variety defined by 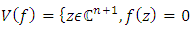 and
and 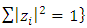 where the knot associated as the intersection of the variety algebraic and the sphere of dim
where the knot associated as the intersection of the variety algebraic and the sphere of dim 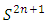 defined by
defined by 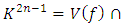
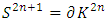 where K has an intersection form
where K has an intersection form 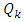 on
on 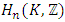 and if
and if 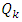 is unimodular then the boundary
is unimodular then the boundary 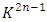 is a homology, exotic sphere. In our case for
is a homology, exotic sphere. In our case for  the knot associated to a manifold of dim 7 defined by
the knot associated to a manifold of dim 7 defined by 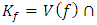
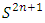
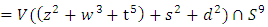 we have
we have 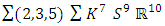 and since the homology 3-sphere determined by the quotient SO(3)/I and the Milnor 7 sphere act transitively on the group of the quaternios
and since the homology 3-sphere determined by the quotient SO(3)/I and the Milnor 7 sphere act transitively on the group of the quaternios 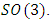 We have:
We have: 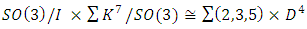 shows that
shows that 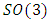 act between the icosahedral and the 7 dim Milnor sphere through Paul Dirac belt trick. We can show also the Paul Dirac belt trick effect that results from an
act between the icosahedral and the 7 dim Milnor sphere through Paul Dirac belt trick. We can show also the Paul Dirac belt trick effect that results from an 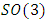 transformation that connect the system by using the J-homomorphism and Hopf construction for a higher dimension to describe the fundamental group, for details see L. Kauffman [6]. It shows from the previous method that the trefoil knot
transformation that connect the system by using the J-homomorphism and Hopf construction for a higher dimension to describe the fundamental group, for details see L. Kauffman [6]. It shows from the previous method that the trefoil knot 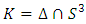 and
and 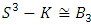 complement of K. The fundamental group of
complement of K. The fundamental group of 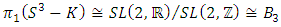 and
and 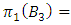
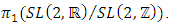 Since the group of fractional linear transformations on
Since the group of fractional linear transformations on 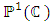 preserving the upper half plane
preserving the upper half plane 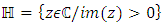 that is
that is 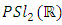 determined by a mobius strip that transform generalized circle to generalized circles [11] a combination of a translation and an inverse map with a twist and a rotation and from the Alexander polynomial for a trefoil knot
determined by a mobius strip that transform generalized circle to generalized circles [11] a combination of a translation and an inverse map with a twist and a rotation and from the Alexander polynomial for a trefoil knot 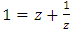 leads to:
leads to: 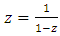 fixed point of the map
fixed point of the map 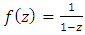 based from a twist and an inverse rotation. Defined by:
based from a twist and an inverse rotation. Defined by: 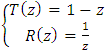 Where
Where 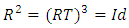 . It follows the connection between
. It follows the connection between 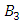 and the modular group
and the modular group 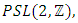 considered as a lattice inside the covering group. The quotient of
considered as a lattice inside the covering group. The quotient of 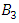 per its center is isomorphic to
per its center is isomorphic to 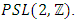 Although the generators of the modular group obey the relation:
Although the generators of the modular group obey the relation: 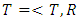 with
with 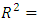
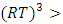 isomorphic to the free group product
isomorphic to the free group product 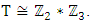 Or from the braid relations it follows that:
Or from the braid relations it follows that: 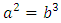 with
with 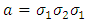 and
and 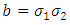 respectively with the correspondent matrix:
respectively with the correspondent matrix: 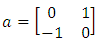 and
and 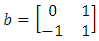 as we know the braid group
as we know the braid group 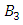 is isomorphic to the knot group of the trefoil knot. We can also view it as the real variety
is isomorphic to the knot group of the trefoil knot. We can also view it as the real variety 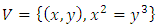 a subset of the real plane
a subset of the real plane 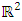 identified with the quotient ring
identified with the quotient ring 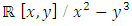 in algebraic geometry. We can also introduce the j invariant to compute through the dessin d’enfant the free group! Hence the j invariant has an interesting tie between the Alexander polynomial for the algebraic curve ξ over the Laurent polynomial
in algebraic geometry. We can also introduce the j invariant to compute through the dessin d’enfant the free group! Hence the j invariant has an interesting tie between the Alexander polynomial for the algebraic curve ξ over the Laurent polynomial 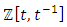 and the cross ratio by the formula:
and the cross ratio by the formula: 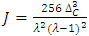 with
with 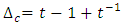 as the characteristic polynomial of the bureau representative of
as the characteristic polynomial of the bureau representative of 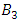 defined by
defined by 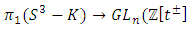 with matrices
with matrices 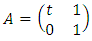 and
and 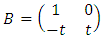 with
with 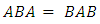 . Where J=0 when
. Where J=0 when 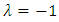 and
and 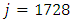 when
when 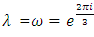 . According to our invariant system, it shows there an interesting relation
. According to our invariant system, it shows there an interesting relation 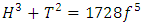 discovered by Felix Klein that ties the modular group to the quintic equation [3] with the form
discovered by Felix Klein that ties the modular group to the quintic equation [3] with the form 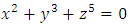 , the icosahydral group and the
, the icosahydral group and the  singularities [10]. Where
singularities [10]. Where  invariant polynomials are connected by the Dedekind eta function to
invariant polynomials are connected by the Dedekind eta function to 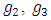 the j invariant function and the descriminant by the action of the generators
the j invariant function and the descriminant by the action of the generators 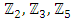 with 2, 3 and 5 fold [7] symmetries for the icosahydral group. The 5 fold cover of the torus knot
with 2, 3 and 5 fold [7] symmetries for the icosahydral group. The 5 fold cover of the torus knot 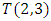 and the double cover of the torus
and the double cover of the torus 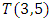 . The polynomial invariant
. The polynomial invariant 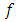 corresponds to the vertices of the icosahydral while the invariant polynomials
corresponds to the vertices of the icosahydral while the invariant polynomials 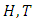 correspond to the edge midpoints and face centers of the icosahydral. Due to the modularity and periodical path, following the previous method for the algebraic singularity related to the knots we can give an explicit representation of the encoded knots by an analytical function defined by complex polynomial defined by Brauwer with
correspond to the edge midpoints and face centers of the icosahydral. Due to the modularity and periodical path, following the previous method for the algebraic singularity related to the knots we can give an explicit representation of the encoded knots by an analytical function defined by complex polynomial defined by Brauwer with 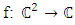 where
where 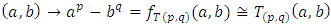 to study the critical pts of the curve at the origin in
to study the critical pts of the curve at the origin in 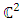 such
such 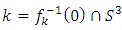 . Brauner’s knots are torus knots that are also lemniscates knots that we can parameterize by projection in the 3 dimensional Cartesian space by
. Brauner’s knots are torus knots that are also lemniscates knots that we can parameterize by projection in the 3 dimensional Cartesian space by 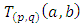 to
to 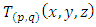 . In our case we are more interested in the torus knots of type the Hopf link
. In our case we are more interested in the torus knots of type the Hopf link 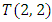 and the trefoil knot
and the trefoil knot 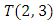 . Since the braid group is the closure of the knot, then by encoding the braid in to a polynomial in a and b. According to Mark Dennis [8] the parameterization is a function of t element of
. Since the braid group is the closure of the knot, then by encoding the braid in to a polynomial in a and b. According to Mark Dennis [8] the parameterization is a function of t element of 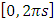 where k is the lemniscates knot K=(s, l, r) and the curve
where k is the lemniscates knot K=(s, l, r) and the curve 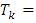
 where the closure of the braid defined by:
where the closure of the braid defined by: 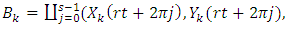
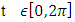 Will leave this to the reader! Note interesting points are at
Will leave this to the reader! Note interesting points are at 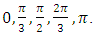 Interpretation: the trefoil knot generates the axis of the symmetry of the system! Our trefoil knot is the boundary of a fibered surface with double faces, though for any element of our numerical system its asymmetric or mirror image is in the other side of the face of the fibered surface orbiting in opposite directions with an unzip operation! the braid group structured by the elements and its axis orbiting along a trefoil knot, the transformations then describe for both sides of the faces 2 asymmetrical trefoil knots orbiting in a closed link cancel each other at the origin or the critical point of the hyperboloid cone and giving birth to 2 asymmetrical unknots! Fabric of the spacetime and the prime numbers: As a conclusion we can define the fabric of the space by the combination of modular knots in dynamic that generate a vortex knot model defined by elliptical curves and hyperboloid curves that intercepts the axis of the system generated by an algebraic curve the trefoil knot a link bridge between two asymmetrical transversal trefoil knots, Hopf link and two unlinked asymmetrical trivial knots! The complement of those fibered knots are fibered bundles, loops defined by the Milnor map generated by two important elliptic curves one hexagonal and the other one is square while as hyperboloid curve we have the modular Fibonacci knots that converges toward the golden ratio and based from the Cassini identity where the determinant is
Interpretation: the trefoil knot generates the axis of the symmetry of the system! Our trefoil knot is the boundary of a fibered surface with double faces, though for any element of our numerical system its asymmetric or mirror image is in the other side of the face of the fibered surface orbiting in opposite directions with an unzip operation! the braid group structured by the elements and its axis orbiting along a trefoil knot, the transformations then describe for both sides of the faces 2 asymmetrical trefoil knots orbiting in a closed link cancel each other at the origin or the critical point of the hyperboloid cone and giving birth to 2 asymmetrical unknots! Fabric of the spacetime and the prime numbers: As a conclusion we can define the fabric of the space by the combination of modular knots in dynamic that generate a vortex knot model defined by elliptical curves and hyperboloid curves that intercepts the axis of the system generated by an algebraic curve the trefoil knot a link bridge between two asymmetrical transversal trefoil knots, Hopf link and two unlinked asymmetrical trivial knots! The complement of those fibered knots are fibered bundles, loops defined by the Milnor map generated by two important elliptic curves one hexagonal and the other one is square while as hyperboloid curve we have the modular Fibonacci knots that converges toward the golden ratio and based from the Cassini identity where the determinant is 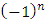 defined by:
defined by: 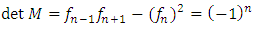 for a rational map
for a rational map 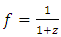 with matrices respectively:
with matrices respectively: 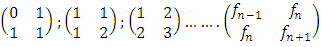 that depend for its convergence on n if it is even or odd and will intercept the axis as a link of knot or unknot. We define rational tangle for the golden ratio by
that depend for its convergence on n if it is even or odd and will intercept the axis as a link of knot or unknot. We define rational tangle for the golden ratio by 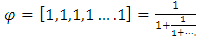 this will answear one of the interesting paper of [4] for the modular flow and why the Lorenz knots looks chaotic. We also with this conclusion made the connection between the integers and prime numbers and their representation as fibers or loops for such surfaces! The combination of those asymmetrical torus knots type and the hyperbolic curves generated by the spiral of Fibonacci inside a closed path that intercept the axis of the system which is the trefoil knots describe the Fabric of the spacetime!
this will answear one of the interesting paper of [4] for the modular flow and why the Lorenz knots looks chaotic. We also with this conclusion made the connection between the integers and prime numbers and their representation as fibers or loops for such surfaces! The combination of those asymmetrical torus knots type and the hyperbolic curves generated by the spiral of Fibonacci inside a closed path that intercept the axis of the system which is the trefoil knots describe the Fabric of the spacetime! 


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML