-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2017; 7(5): 132-154
doi:10.5923/j.ijtmp.20170705.03

Spin Two-Body Problem of Classical Electrodynamics with Radiation Terms (I) – Derivation of Spin Equations
Vasil G. Angelov
Department of Mathematics, Faculty of Mining Electromechanics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria
Correspondence to: Vasil G. Angelov, Department of Mathematics, Faculty of Mining Electromechanics, University of Mining and Geology “St. I. Rilski”, Sofia, Bulgaria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The paper is devoted to extension of Synge equations describing motion of two mass charged particles in the frame of classical relativistic electrodynamics including radiation terms and spin equations. In previous papers we have derived equations of motion just with radiation terms. Our radiation terms correspond to the Dirac physical assumptions but they differ from Dirac’s terms on the mathematical derivation. They generate neutral type equations of motion with both retarded and advanced arguments. Here we consider two-body problem with spin following the Corben’s technique. As in the original Synge model the number of the spin equations is more than the number of the unknown functions. We prove that six spin equations are a consequence of the rest ones and in this manner we obtain six equations for the six unknown spin functions. This consequence is in weak sense obtained by scalar multiplication.
Keywords: Two Body Problem of Classical Electrodynamics with Radiation Terms and Spin, Derivation of Equations of Motion
Cite this paper: Vasil G. Angelov, Spin Two-Body Problem of Classical Electrodynamics with Radiation Terms (I) – Derivation of Spin Equations, International Journal of Theoretical and Mathematical Physics, Vol. 7 No. 5, 2017, pp. 132-154. doi: 10.5923/j.ijtmp.20170705.03.
Article Outline
1. Introduction
- The present paper is one of series devoted to study of the two-body problem of classical electrodynamics. In [1, 2] we have formulated 3-dimensional two-body problem based on the Synge relativistic model [3]. The system of equations of motion is of a neutral type with delays depending on unknown trajectories [4]. Later we have found a new form of the Dirac radiation term and formulated a two-body problem with radiation terms [5]. In this case the equations of motion become of neutral type but with both retarded and advanced arguments. In [6] we have proved existence-uniqueness of a periodic solution of the system of equation of motion utilizing fixed point method. An immediate consequence of this fact is that the spectrum of the hydrogen atom is discreet one.In [7] we have estimated the radiation energy and thus we answer the question of why the moving electron around the nucleus is stable and not collided with a nucleus. In this manner we thus affirm the Bohr assumption for stationary states. It turns out that his assumption is a consequence of the laws of classical electrodynamics and does not violence it. Our intention to look for these results was caused by the famous results due to A. Sommerfeld [8, 9].The main purpose of the present paper is to extend some our recent results concerning two-body problem of classical electrodynamics including spin equations. Without pretending to complete bibliography we mention some previous results with spin [10-18]. We note, however, that all considerations of spinning particles with radiation terms contain Dirac radiation terms with third derivative. We would like to emphasize once again that our new form of the Dirac radiation term is relativistic invariant. This enables us to use again Synge formalism for the two-body problem with radiation terms. We prove that the six spin equations are a consequence of the rest ones and in this manner we obtain six equations for six unknown spin functions. The last system jointly with the six equations of motion with radiation terms gives complete description of the two-body problem. We want to explicitly mention the researches due D.-A. Deckert et al. [19-22], and De Luca [23] based on Wheeler- Feynman approach. Here we proceed from H. Corben considerations of classical spinning particles [12, 13].The paper consists of eight sections. In Section 2 we repeat the derivation of Synge two-body equations. In Section 3 we derive two-body problem with radiation terms. In Section 4 the first group of spin equations is derived while in Section 5 the second group of spin equations is proposed. In Section 6 we write down spin equations in vector form. This enables us to show in Section 7 that some of them are consequences of the rest ones. In this way, we get as many equations as spin functions. Section 8 is a conclusion where the two-body equations of motion with radiation terms are written jointly with spin equations. An existence-uniqueness of the general system in a next paper will be proved.
2. Derivation of Synge Two-Body Equations of Motion
- First we recall some denotations from [3], [1] and [2]. The considerations are in the Minkowski space. Roman suffixes run over 1, 2, 3, 4, while Greek – 1, 2, 3 with Einstein summation convention. By
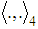 we denote the scalar product in the Minkowski space, while by
we denote the scalar product in the Minkowski space, while by 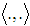 – the scalar product in three-dimensional Euclidean subspace. We consider the equations of motion with radiation terms derived in [5] jointly with the spin equations (cf. [12], [13]):
– the scalar product in three-dimensional Euclidean subspace. We consider the equations of motion with radiation terms derived in [5] jointly with the spin equations (cf. [12], [13]):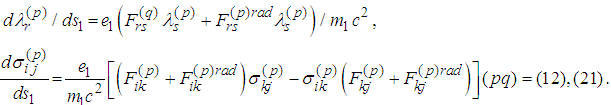 Recall (cf. [1], [2]) that the quantities relating to the particles are:
Recall (cf. [1], [2]) that the quantities relating to the particles are: 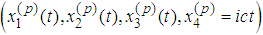
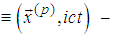 space-time coordinates of the moving particles;
space-time coordinates of the moving particles;  – the speed of the light;
– the speed of the light;  – the world lines;
– the world lines; 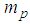 – proper masses;
– proper masses; 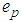 – charges
– charges 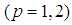 .We suppose
.We suppose 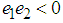 and since
and since 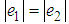 then
then 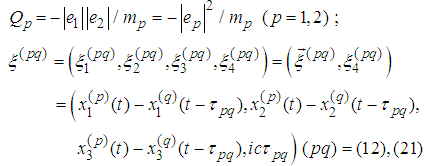 are components of null vector lying on the light cone, that is,
are components of null vector lying on the light cone, that is, 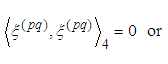
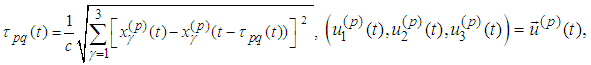
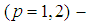 velocities of the moving particles,
velocities of the moving particles, 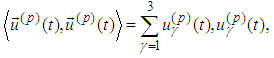
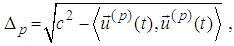
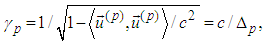
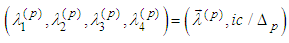
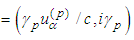
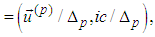
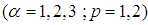 components of the unit tangent vectors to world lines,
components of the unit tangent vectors to world lines,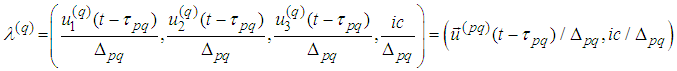 where
where 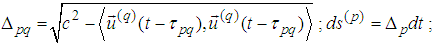
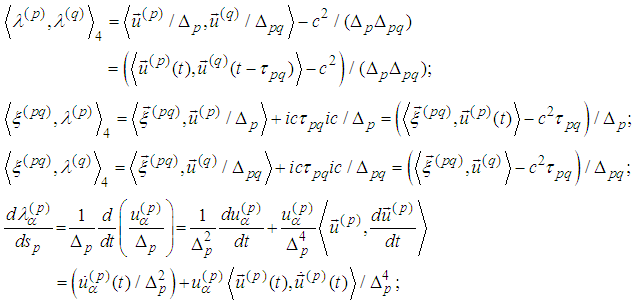
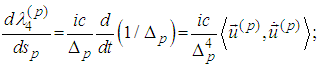
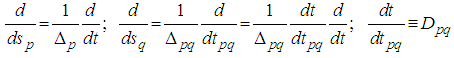 and the derivative could be calculated from the equation
and the derivative could be calculated from the equation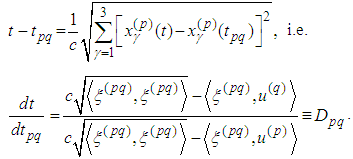 Therefore
Therefore 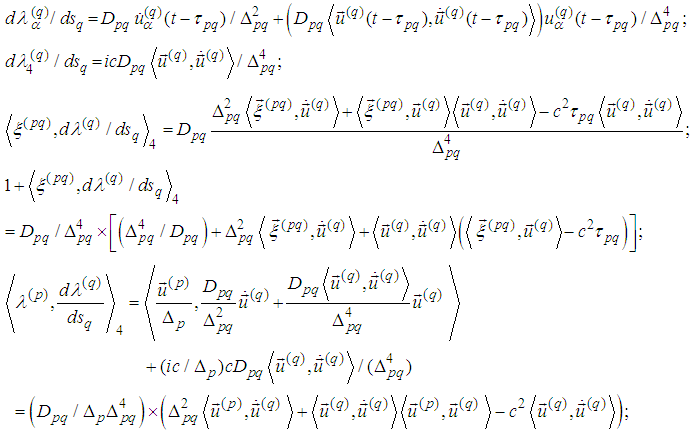
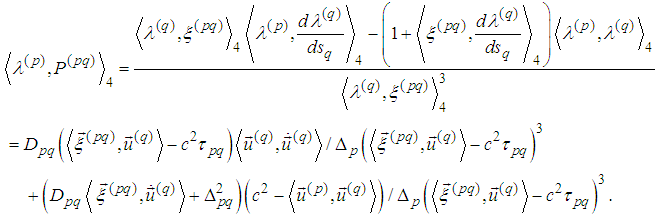 Recall that the Synge’s equations of motion without radiation terms are
Recall that the Synge’s equations of motion without radiation terms are 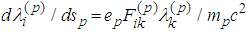 (cf. [3]). The elements of the electromagnetic tensor can be derived by Lienard-Wiechert retarded potentials
(cf. [3]). The elements of the electromagnetic tensor can be derived by Lienard-Wiechert retarded potentials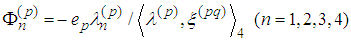 namely
namely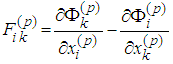 and then using denotations
and then using denotations 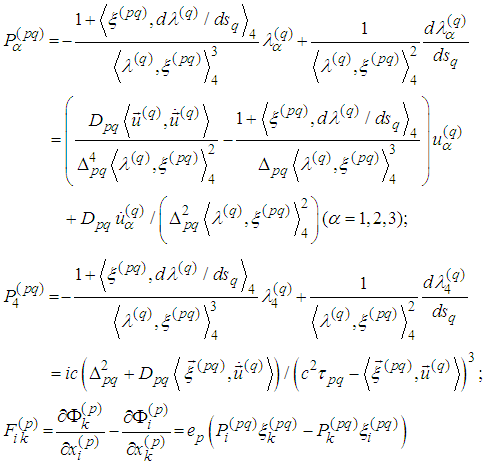 we obtain
we obtain 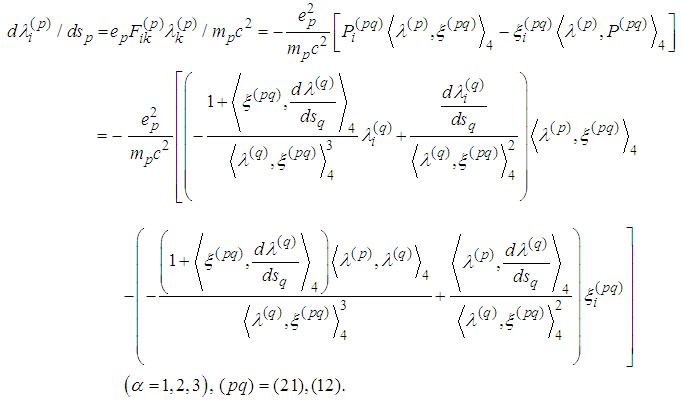 Let us set
Let us set 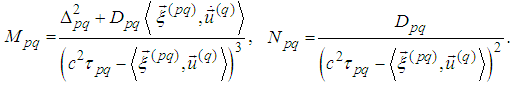 Then
Then  and
and  .Consequently
.Consequently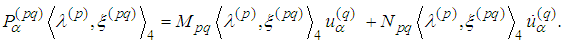 For
For 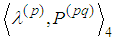 we have
we have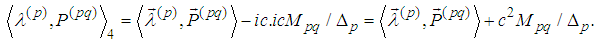 Then the 3-dimensional part of
Then the 3-dimensional part of 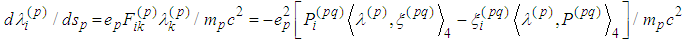 in view of
in view of 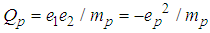 becomes
becomes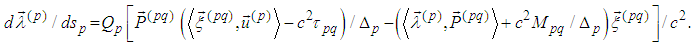 Remark 1. We consider just the first three equations because the fourth equation is a consequence of the first three ones for fixed p (cf. [5], [6]).
Remark 1. We consider just the first three equations because the fourth equation is a consequence of the first three ones for fixed p (cf. [5], [6]).3. Derivation of Two-Body Equations of Motion with Radiation Terms
- The equations of motion for the two-body problem with radiation terms are derived in [5]. Using denotations from [5] we get
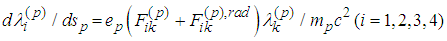 or
or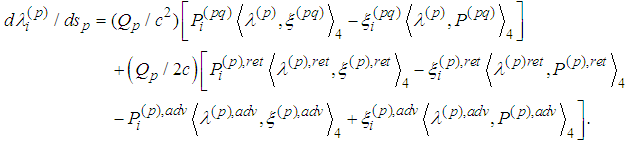 So we have
So we have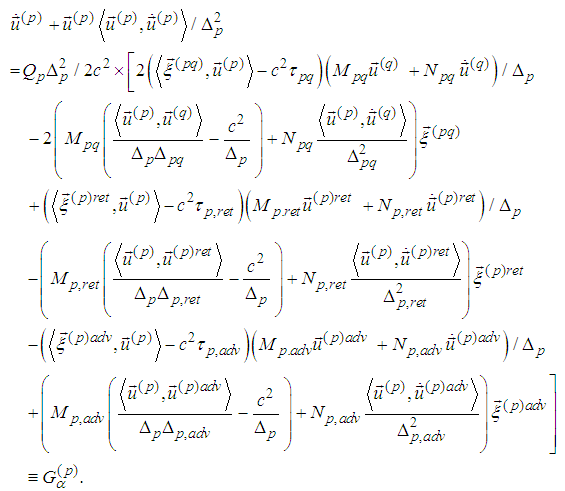 In view of Remark 1 we consider just the following six equations for six unknown functions:
In view of Remark 1 we consider just the following six equations for six unknown functions: 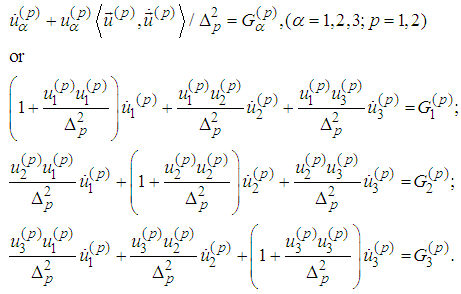 Under the basic assumption
Under the basic assumption 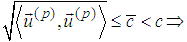
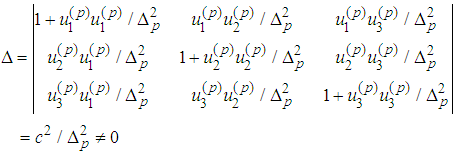 we obtain
we obtain 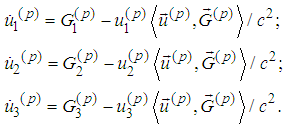 Using vector denotations we have
Using vector denotations we have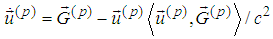 and in view of
and in view of  we obtain
we obtain
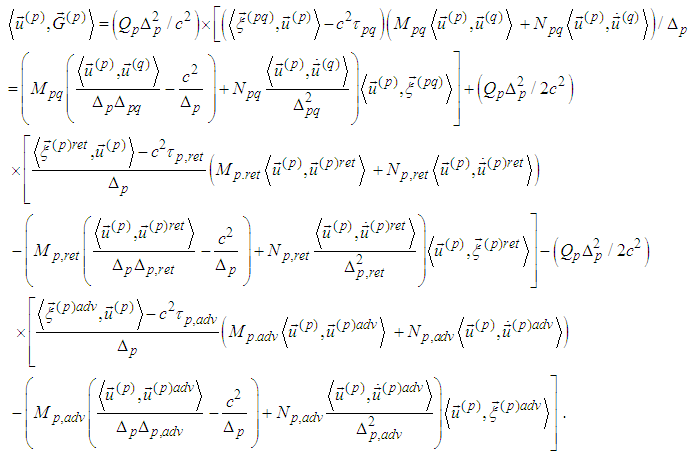
4. Explicit Form of the First Three Spin Equations
- In what follows we obtain the explicit form of the spin equations:
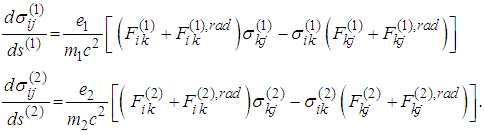 Introduce denotations analogous to the ones from [12], [13]:
Introduce denotations analogous to the ones from [12], [13]: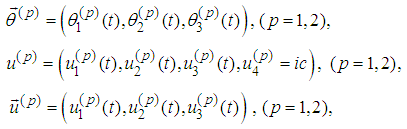
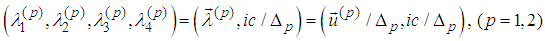 where
where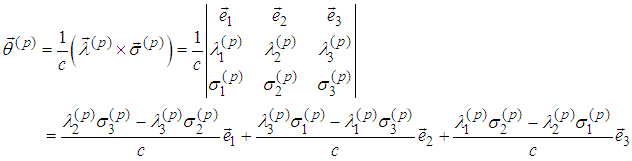 we obtain the spin tensor
we obtain the spin tensor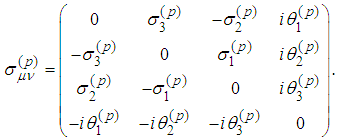 It is known (cf. [12]. [13]) that
It is known (cf. [12]. [13]) that 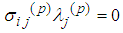 . We verify the equalities for
. We verify the equalities for 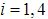 :
: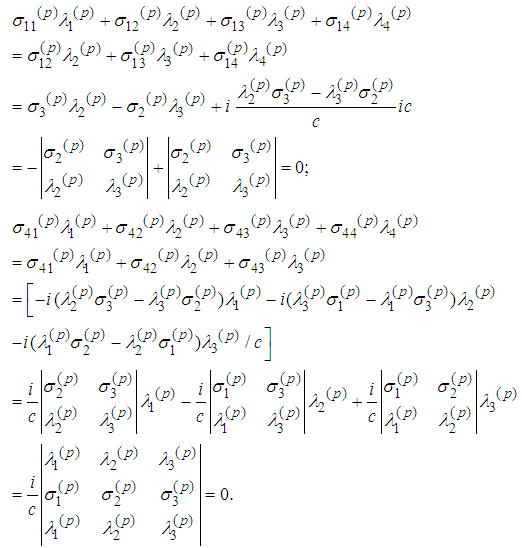 Remark 2. Let us consider the equations
Remark 2. Let us consider the equations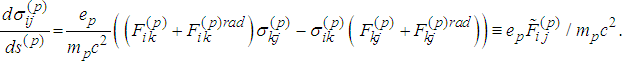 We notice that
We notice that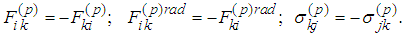 Therefore
Therefore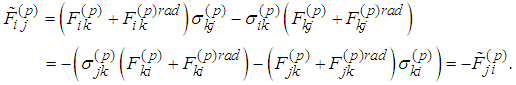 It follows
It follows 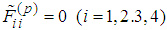 . Consequently we have derived the following spin equations for two particles
. Consequently we have derived the following spin equations for two particles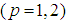 :
: 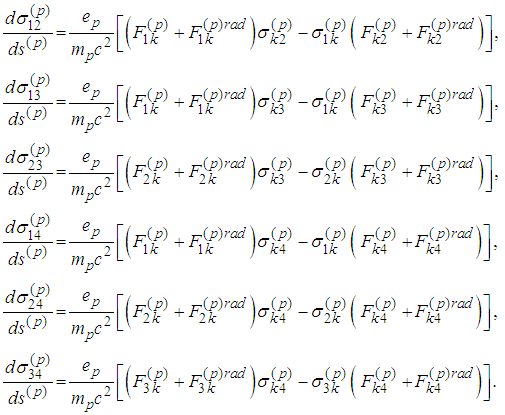 First Spin Equation
First Spin Equation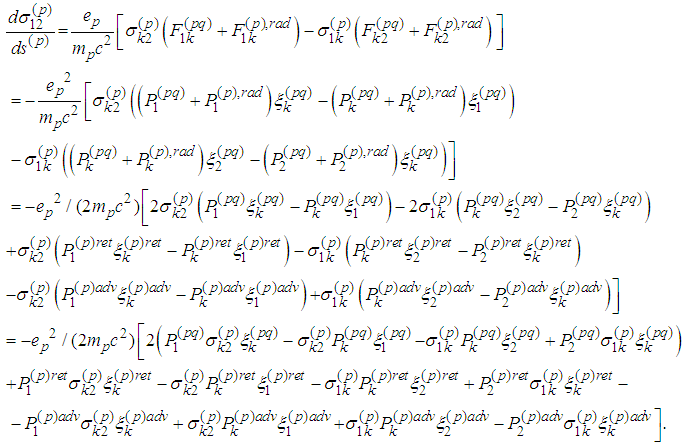 To transform the above equations we notice that
To transform the above equations we notice that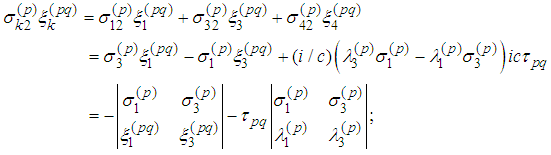
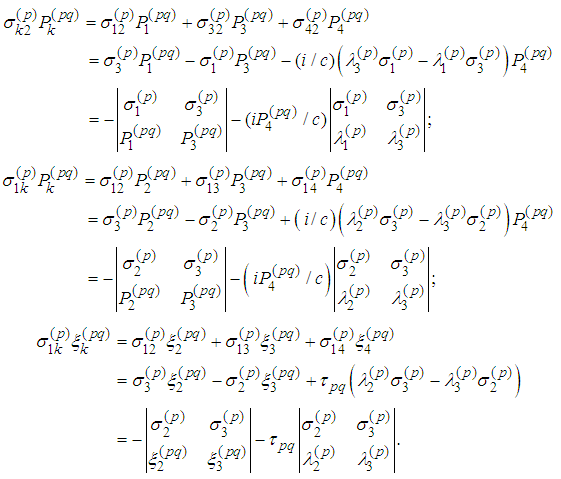 Therefore
Therefore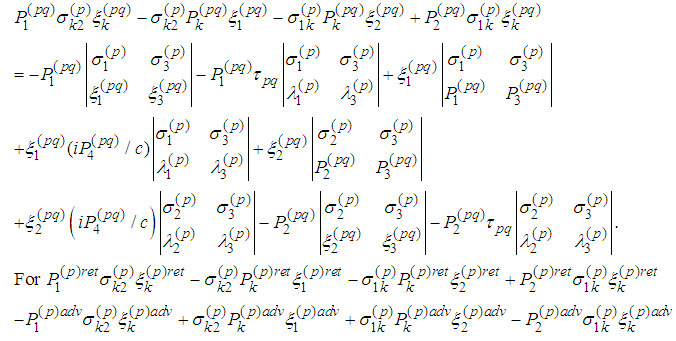 We obtain analogous expressions. Consequently
We obtain analogous expressions. Consequently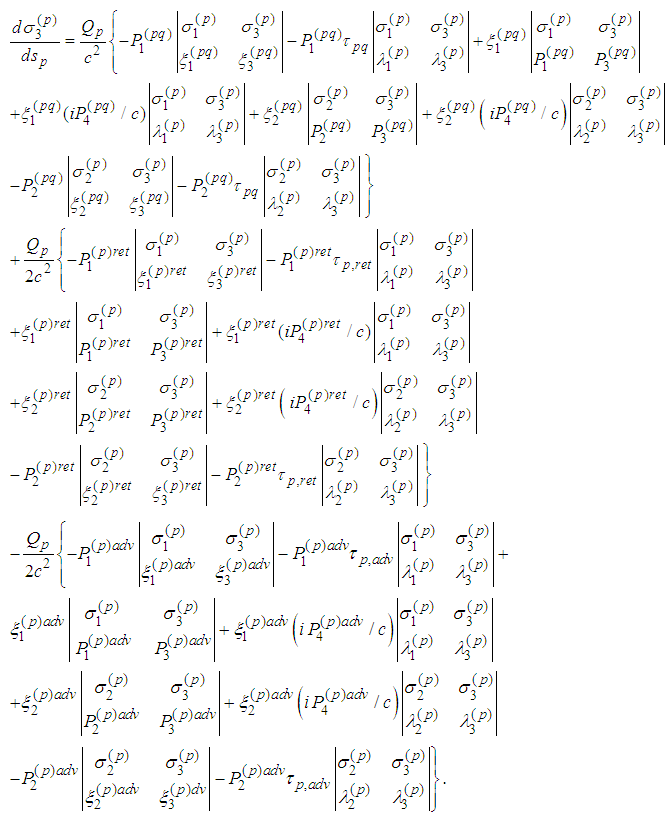 Second Spin Equation
Second Spin Equation 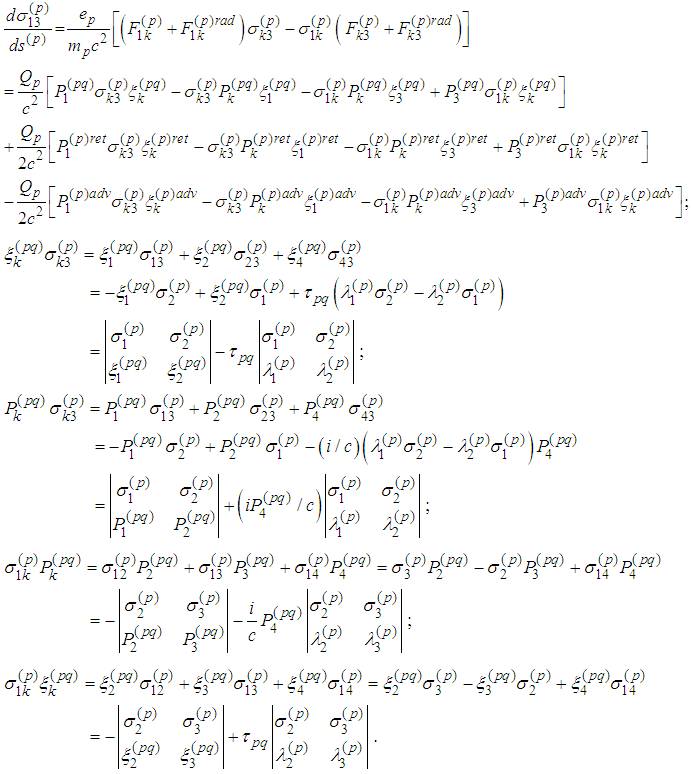 Then
Then 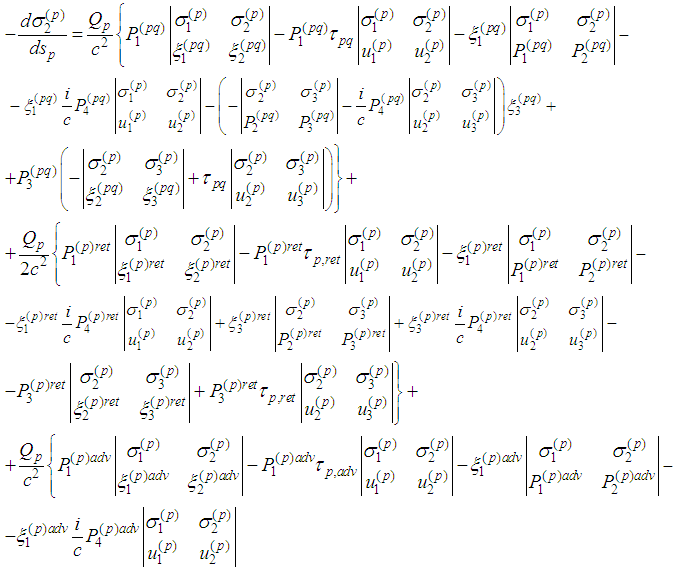 Third Spin Equation
Third Spin Equation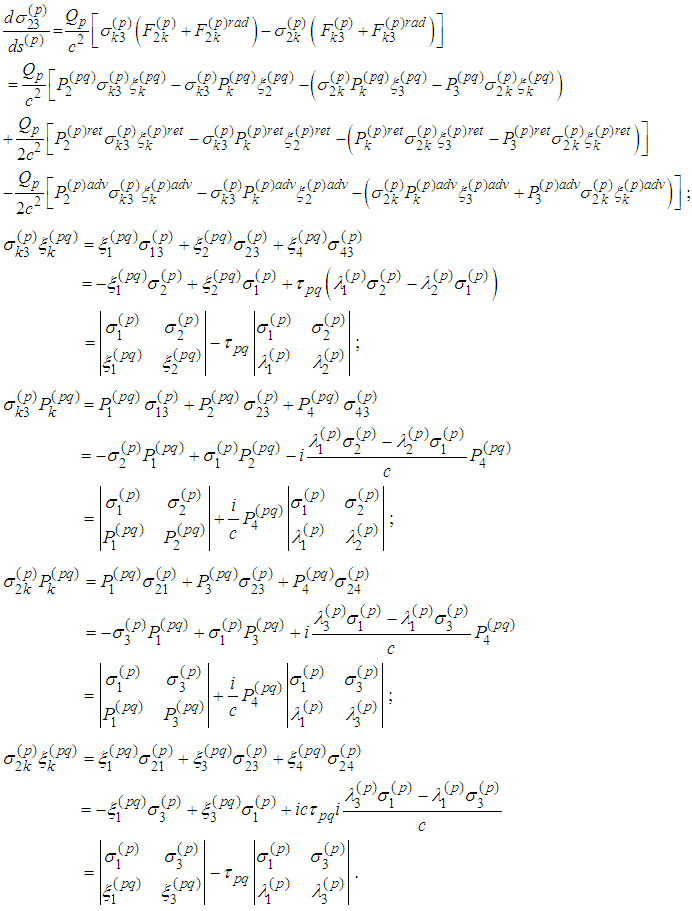 Therefore
Therefore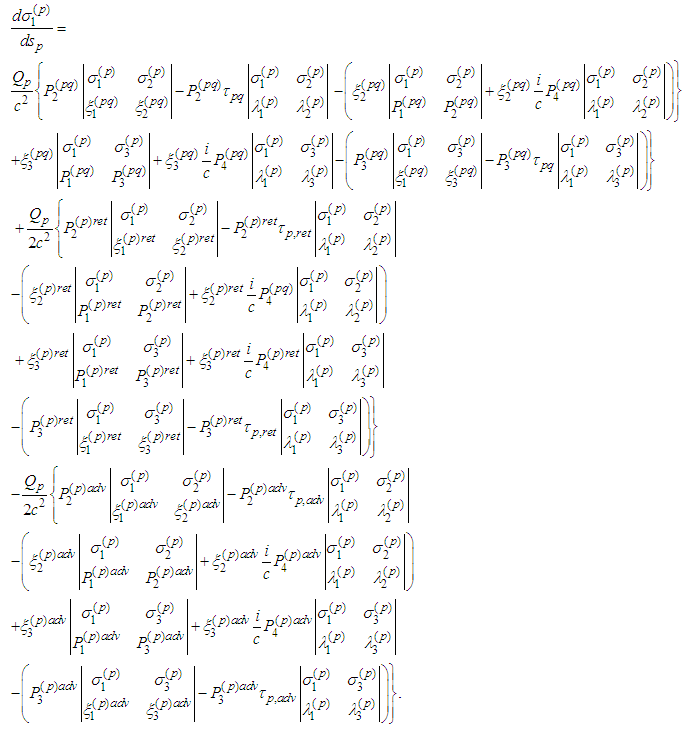
5. Explicit Form of the Second Group of Three Spin Equations
- Fourth Equation
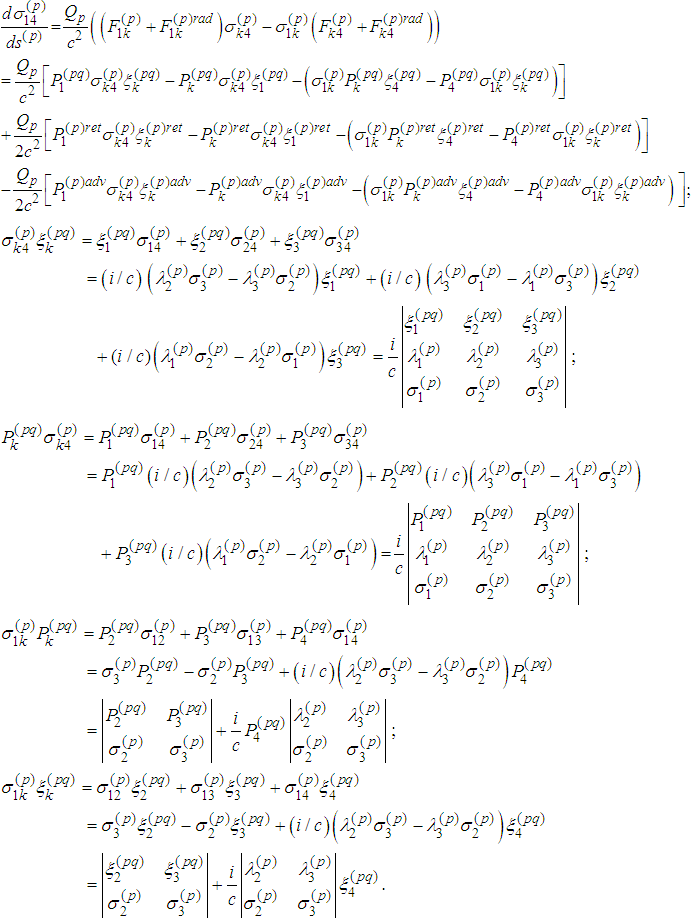 Therefore
Therefore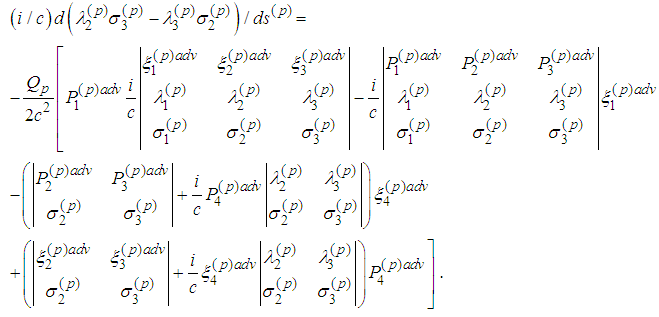 Fifth Equation
Fifth Equation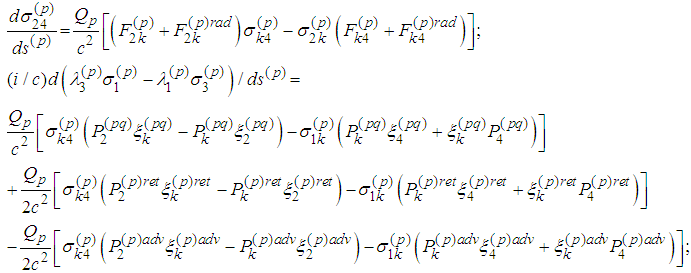
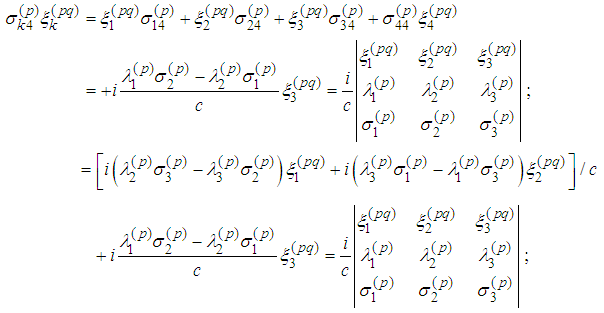
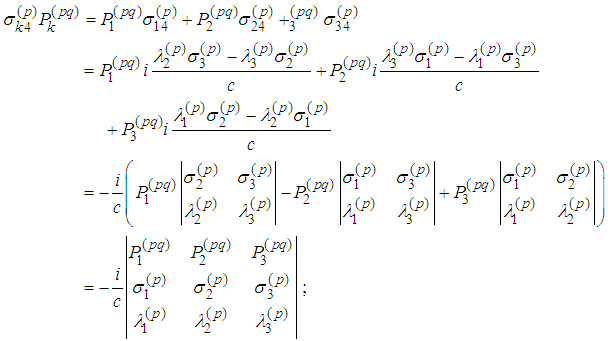
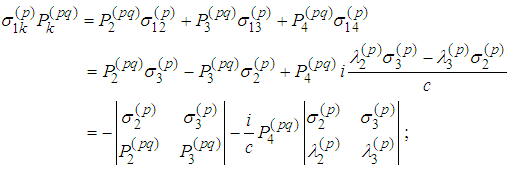
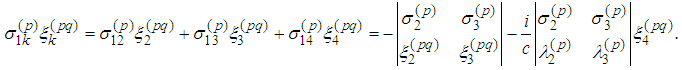 Therefore
Therefore Sixth Equation
Sixth Equation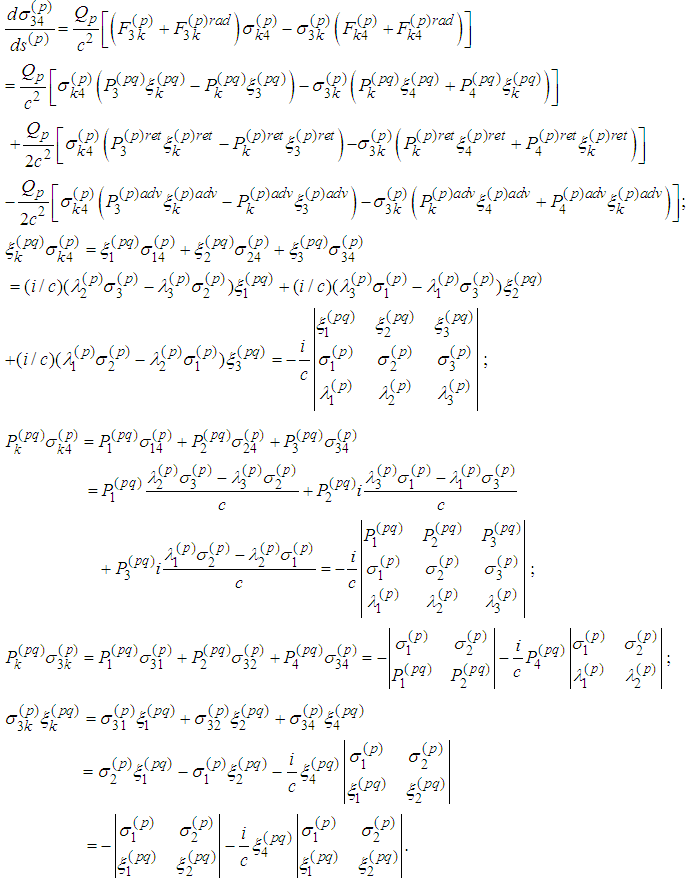 Then
Then
6. Vector Form of the Spin Equations
- We present the above equations in vector form, which will facilitate us in further considerations.If we introduce denotations
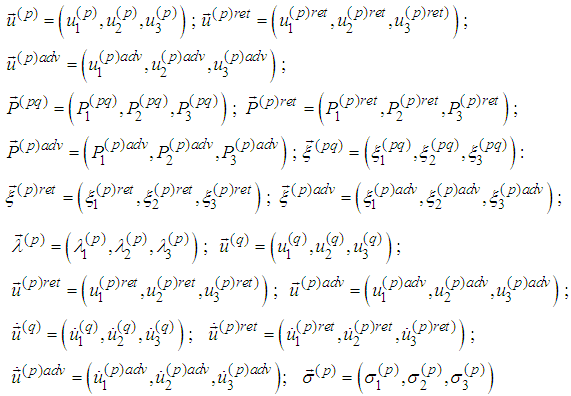 then the vector form of the above first three spin equations becomes
then the vector form of the above first three spin equations becomes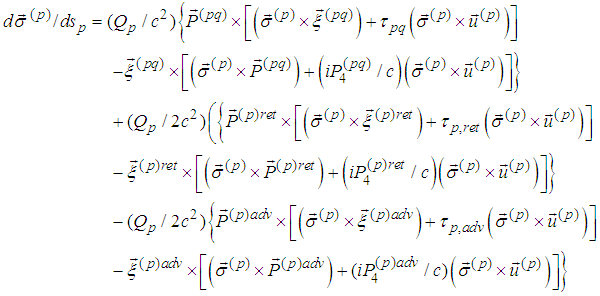 while the second three become
while the second three become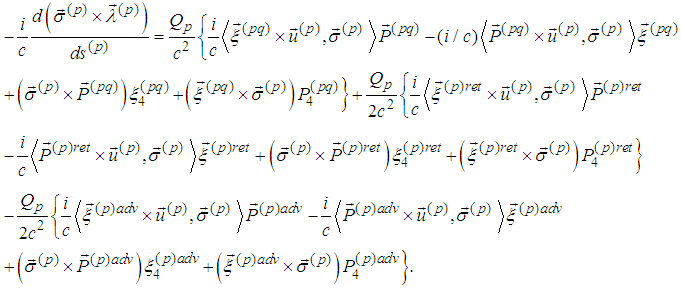
7. The Last Three Spin Equations are Consequences of the First Three Ones with Respect to Scalar Multiplication
- Equations of motion in a vector form are (cf. [5], [6]):
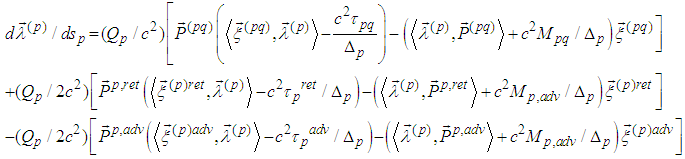 | (1) |
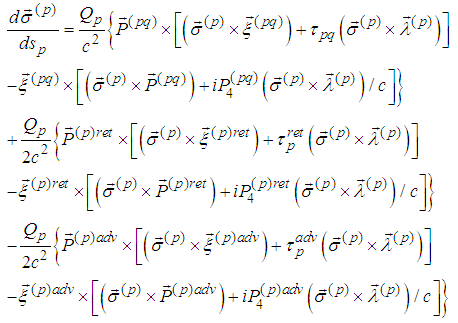 or
or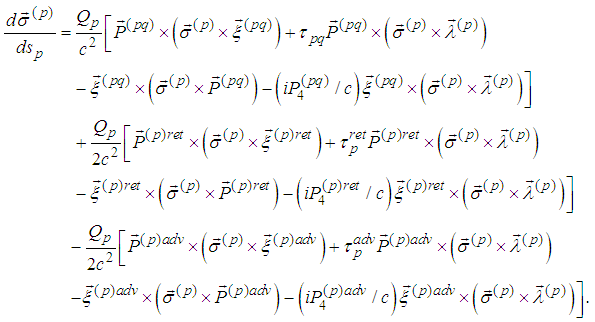 | (2) |
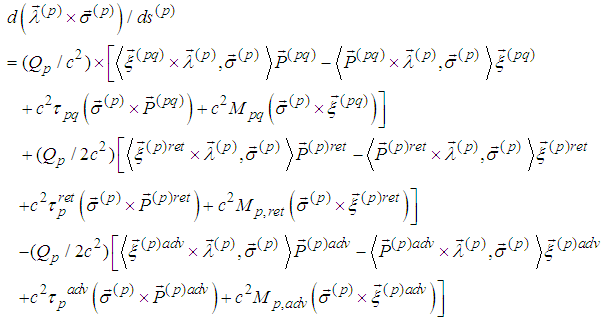 | (3) |
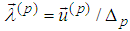 we obtain from (1)
we obtain from (1)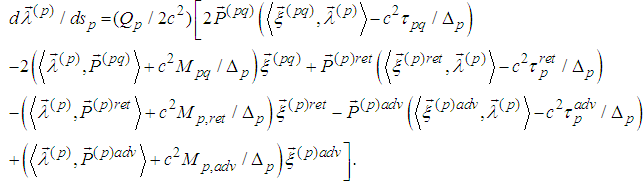 The cross product of the last equality by
The cross product of the last equality by 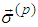 from the right is
from the right is 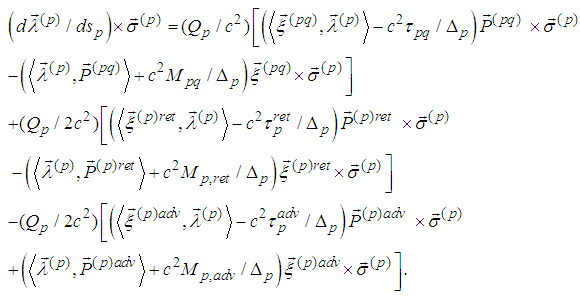 | (4) |
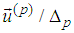 from the left is
from the left is 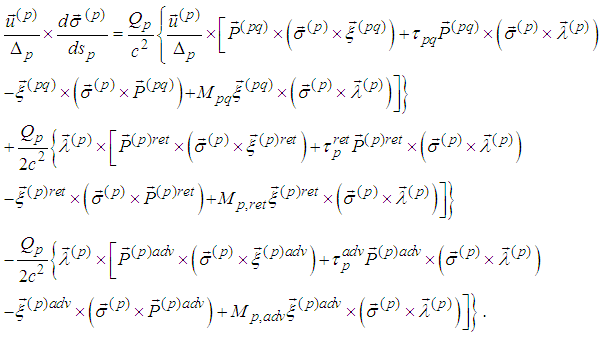 | (5) |
 | (6) |
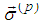 . Indeed, we have
. Indeed, we have 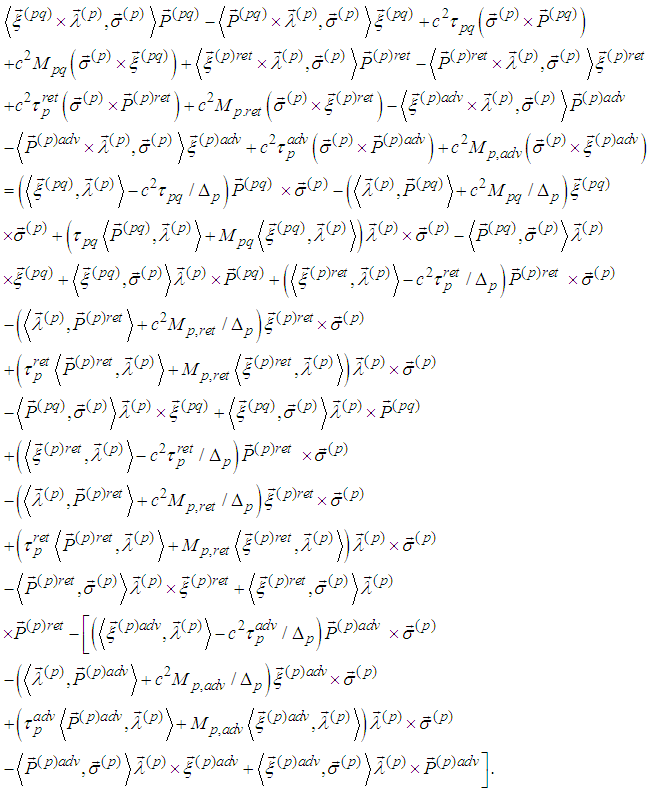 By scalar multiplication with
By scalar multiplication with 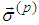 we obtain equality:
we obtain equality: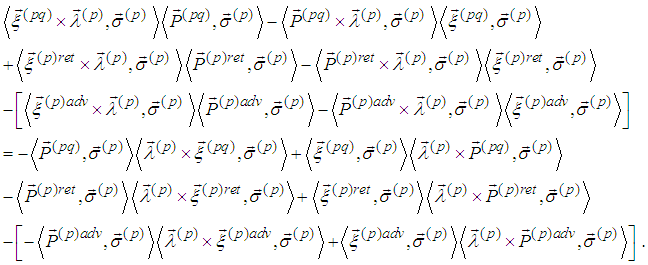
8. Conclusions
- We have obtained a general system describing the movement of two charged spinning particles consisting of 12 equations for 12 unknown functions, six for the unknown trajectories and six for the spin functions: (p=1,2)
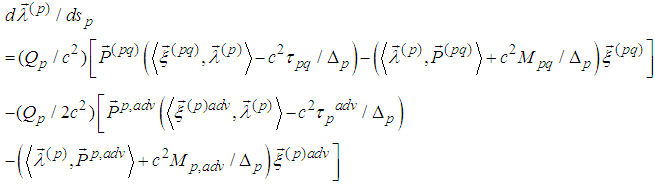 and
and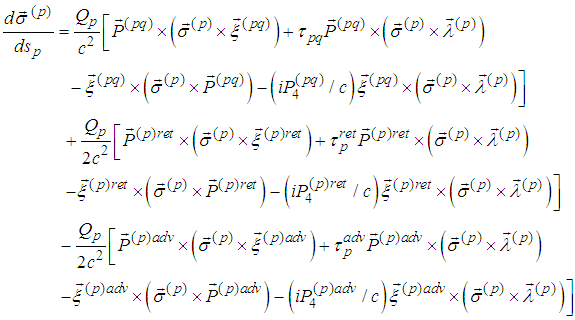 In this way we have obtained a system with 12 equations for 12 unknown functions.We will prove an existence-uniqueness of a solution for this system in a next paper.
In this way we have obtained a system with 12 equations for 12 unknown functions.We will prove an existence-uniqueness of a solution for this system in a next paper. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML