-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2017; 7(3): 51-56
doi:10.5923/j.ijtmp.20170703.02

Singularities in Quasidistributions, Their Regularization, and Nonclassical Number and Wave Statistics
Jan Peřina1, Jaromír Křepelka2
1Department of Optics and Joint Laboratory of Optics of Palacký University and Institute of Physics of the Czech Academy of Sciences, Faculty of Science, Palacký University, Czech Republic
2Joint Laboratory of Optics of Palacký University and Institute of Physics of the Czech Academy of Sciences, Czech Republic
Correspondence to: Jaromír Křepelka, Joint Laboratory of Optics of Palacký University and Institute of Physics of the Czech Academy of Sciences, Czech Republic.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Compared with earlier investigations we follow a way of arising singularities in quasidistributions as related to nonclassical photocount and wave statistics for nonlinear optical processes described by Gaussian statistics, also from the point of view of testing functions. Further we illustrate a process of regularization of singular quasidistributions so that regularized quasidistributions can provide measurable quantities. Results obtained can be applied to optical down-conversion as well as to Raman scattering provided that classical strong coherent pumping fields are used.
Keywords: Quasidistributions, Nonlinear optical processes, Nonclassical statistics
Cite this paper: Jan Peřina, Jaromír Křepelka, Singularities in Quasidistributions, Their Regularization, and Nonclassical Number and Wave Statistics, International Journal of Theoretical and Mathematical Physics, Vol. 7 No. 3, 2017, pp. 51-56. doi: 10.5923/j.ijtmp.20170703.02.
Article Outline
1. Introduction
- In 1963 R. J. Glauber [1, 2] demonstrated that classical distribution functions for optical fields having no classical analogue can take on negative values. In general negative probability functions can express debt of probabilities when we use a classical tool to describe quantum dynamics. Traditional coherent-state description used by R. J. Glauber applied to photodetection related to normal ordering of field operators can be generalized to general operator orderings related to other detection possibilities, as introduced by K. E. Cahill and R. J. Glauber [3, 4] or more generally by G. S. Agarwal and E. Wolf [5-7], called s-ordering. Now many criteria exist how to recognize optical fields to be in nonclassical regimes [8, 9].In last years we derived joint photon statistics including joint photon-number distributions and joint wave quasidistributions of the integrated intensities in classical as well as nonclassical regimes [10-12] (and references therein). These results can be applied, e.g. to Raman scattering [13], nonlinear optical couplers [14], and to entanglement of optical twin beams [15]. This theory is useful in analyzing experimental data [16-21]. Usually negative values of quasidistributions are related to nonclassical behavior of photon and wave statistics of the fields. Here we follow the way of arising singularities in the quasidistributions of the down-conversion optical process, also from the point of view of testing functions in the theory of generalized functions, in relation to nonclassical photon and wave statistics and illustrate procedures of regularization of singular quasidistributions. Such regularization procedures are able to eliminate singularities in the quasidistributions and can provide regularized quasidistributions reflecting nonclassical behavior of quantum systems by their negative values, which provides measurable quantities, in particular in terms of Laguerre polynomials. The results obtained can be applied to other nonlinear optical processes, such as Raman scattering, provided that classical strong coherent pumping fields are adopted.
2. Generating Function and Quasidistribution
- The generating function for the spontaneous optical down-conversion classically coherently pumped, determining measurable quantities, such as photocount distribution, its moments and wave distributions of integrated intensities, can be derived from the normal quantum characteristic function [22]
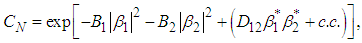 | (1) |
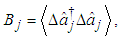 j = 1, 2, are mode quantum noise coefficients and a quantum correlation coefficient
j = 1, 2, are mode quantum noise coefficients and a quantum correlation coefficient 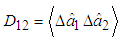 in terms of annihilation operators
in terms of annihilation operators 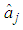 and creation operators
and creation operators 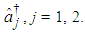 The normal generating function of the parameters
The normal generating function of the parameters 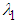 and
and 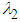 is then obtained as [22]
is then obtained as [22]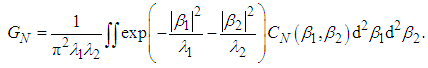 | (2) |
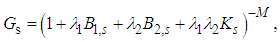 | (3) |
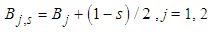 in terms of normal noise coefficients
in terms of normal noise coefficients 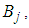 as follows from the theory of s-operator ordering [3-7], involving a filter function
as follows from the theory of s-operator ordering [3-7], involving a filter function 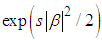 in the quantum characteristic function of a parameter β; then
in the quantum characteristic function of a parameter β; then 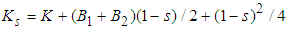 . The parameter M represents the number of equally behaved modes (temporal, spatial and polarization in the spirit of Mandel-Rice formula) [10]; the quality of the process is characterized by the determinant
. The parameter M represents the number of equally behaved modes (temporal, spatial and polarization in the spirit of Mandel-Rice formula) [10]; the quality of the process is characterized by the determinant 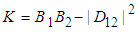 involved in the Fourier transformation providing the Glauber-Sudarshan quasidistribution, whereas Ks is related in the same way for obtaining a quasidistribution related to s-ordering. The quantum (nonclassical) region is then defined by Ks < 0, whereas the classical one by Ks > 0 with the classical-quantum border Ks = 0 respecting the s-ordering.For photodetection of optical fields we use the integrated intensity as a basic physical quantity defined as
involved in the Fourier transformation providing the Glauber-Sudarshan quasidistribution, whereas Ks is related in the same way for obtaining a quasidistribution related to s-ordering. The quantum (nonclassical) region is then defined by Ks < 0, whereas the classical one by Ks > 0 with the classical-quantum border Ks = 0 respecting the s-ordering.For photodetection of optical fields we use the integrated intensity as a basic physical quantity defined as 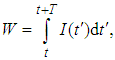 where t is initial time of a measurement, T is detection time and I is intensity of the measured field. If the detection space is equal to quantization space of the detected field, then
where t is initial time of a measurement, T is detection time and I is intensity of the measured field. If the detection space is equal to quantization space of the detected field, then 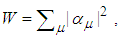 where
where 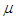 is a mode index describing temporal, spatial and polarization properties of the field and
is a mode index describing temporal, spatial and polarization properties of the field and 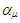 is a complex mode field amplitude. The joint quasidistribution of integrated intensities W1 and W2 related to s-ordering of field operators is then obtained by the inverse Fourier transformation from (3) as follows
is a complex mode field amplitude. The joint quasidistribution of integrated intensities W1 and W2 related to s-ordering of field operators is then obtained by the inverse Fourier transformation from (3) as follows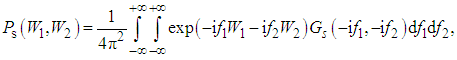 | (4) |
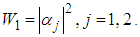 This double Fourier integral strongly depends on the sign of the determinant Ks. For Ks > 0 we can apply the Cauchy integral two times leading to the regular and nonnegative IM–1-distribution [10-12] describing the classical behavior of the system as follows
This double Fourier integral strongly depends on the sign of the determinant Ks. For Ks > 0 we can apply the Cauchy integral two times leading to the regular and nonnegative IM–1-distribution [10-12] describing the classical behavior of the system as follows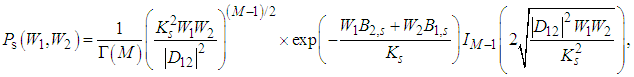 | (5) |
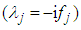
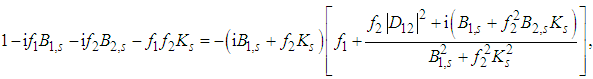 | (6) |
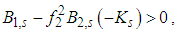 , which means that the Fourier variable f2 is filtered and it holds that
, which means that the Fourier variable f2 is filtered and it holds that 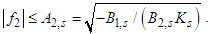 For frequencies outside this interval the pole is in the upper half-plane and the integral is zero. Changing the order of integrations, we change the indices 1 and 2 and we have
For frequencies outside this interval the pole is in the upper half-plane and the integral is zero. Changing the order of integrations, we change the indices 1 and 2 and we have 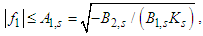 and therefore
and therefore  is a band-limited function for any s. Performing the Cauchy integral after one Fourier variable, the integral after the other Fourier variable is band-limited and since Ks < 0, the poles in this integral lie in the upper-half plane and give no contribution [11, 12]. The resulting expression (see expressions (15) or (17)) is then symmetrized by multiplying the two results and taking the square root. In this way we have a regularized quasidistribution exhibiting nonclassical behavior by means of its negative values [10-13]. We traditionally use the joint regularized quasidistributions exhibiting negative values as reflecting nonclassicality [10-14]. In [23] the authors have used this principle in order to regularize the Glauber-Sudarshan quasidistribution constructing a filter function. In our case the regularization is performed naturally when considering the partially integrated joint quasidistribution for integration in the complex plane, thus smoothing singularities in the quasidistribution [11, 12]. Thus performing the integration along f1 we obtain the following integral along f2.
is a band-limited function for any s. Performing the Cauchy integral after one Fourier variable, the integral after the other Fourier variable is band-limited and since Ks < 0, the poles in this integral lie in the upper-half plane and give no contribution [11, 12]. The resulting expression (see expressions (15) or (17)) is then symmetrized by multiplying the two results and taking the square root. In this way we have a regularized quasidistribution exhibiting nonclassical behavior by means of its negative values [10-13]. We traditionally use the joint regularized quasidistributions exhibiting negative values as reflecting nonclassicality [10-14]. In [23] the authors have used this principle in order to regularize the Glauber-Sudarshan quasidistribution constructing a filter function. In our case the regularization is performed naturally when considering the partially integrated joint quasidistribution for integration in the complex plane, thus smoothing singularities in the quasidistribution [11, 12]. Thus performing the integration along f1 we obtain the following integral along f2.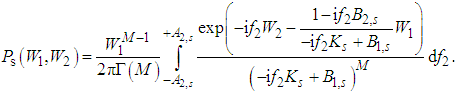 | (7) |
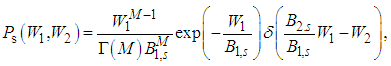 | (8) |
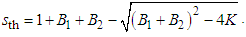 | (9) |
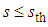 and in a quantum way if
and in a quantum way if 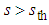 because Ks ≥ 0 and Ks < 0 in these cases, respectively.
because Ks ≥ 0 and Ks < 0 in these cases, respectively.3. Arising Generalized Function
- In the following we will decompose the expression in the exponential function in (7) into the Taylor series and we will follow a way of arising singularities provided that the nonclassical regime with Ks < 0 occurs giving the pole in the upper half-complex plane, while the integral (7) is analytic in the lower half of the complex plane. Denoting
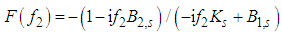 in the exponential function in (7), we obtain for derivatives
in the exponential function in (7), we obtain for derivatives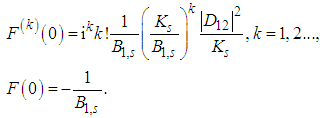 | (10) |
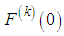 are imaginary and for k even it holds for the coefficients of the Taylor decomposition that
are imaginary and for k even it holds for the coefficients of the Taylor decomposition that  … are positive and
… are positive and 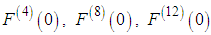 … are negative if Ks < 0. This we use to calculate the corresponding integrals in the complex plane under the assumption that Ks < 0.First include the terms up to the first power in f2, which is equivalent to put Ks = 0 in all the terms starting with the terms containing
… are negative if Ks < 0. This we use to calculate the corresponding integrals in the complex plane under the assumption that Ks < 0.First include the terms up to the first power in f2, which is equivalent to put Ks = 0 in all the terms starting with the terms containing 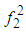 giving the zero for the corresponding decomposition coefficients. In this case we can use the residuum theorem obtaining (the exponential function is now analytic in the upper half-plane)
giving the zero for the corresponding decomposition coefficients. In this case we can use the residuum theorem obtaining (the exponential function is now analytic in the upper half-plane)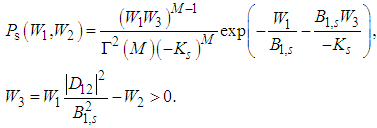 | (11) |
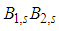 instead of
instead of 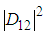 close to the quantum-classical border, creating the symmetry of quantities
close to the quantum-classical border, creating the symmetry of quantities 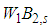 and
and 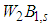 , giving
, giving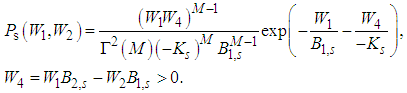 | (12) |
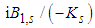 lies in the upper half-plane for
lies in the upper half-plane for 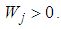 However, the integrals over
However, the integrals over 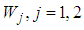 give one because (7) is a distribution. Therefore its values at the zero are singular and we must have quasidistribution. Its behavior close to zero is like its asymptotic behavior in f2, thus seeing that (7) exponentially diverges in
give one because (7) is a distribution. Therefore its values at the zero are singular and we must have quasidistribution. Its behavior close to zero is like its asymptotic behavior in f2, thus seeing that (7) exponentially diverges in 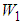 in this case (in the classical case when Ks > 0 it goes to zero). We can use the path integrals along the lines given in Fig. 1 to illustrate their divergent behavior in nonclassical regimes. Denoting x = Re(f2), y = Im(f2), we have
in this case (in the classical case when Ks > 0 it goes to zero). We can use the path integrals along the lines given in Fig. 1 to illustrate their divergent behavior in nonclassical regimes. Denoting x = Re(f2), y = Im(f2), we have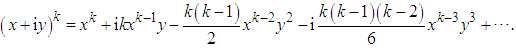 | (13) |
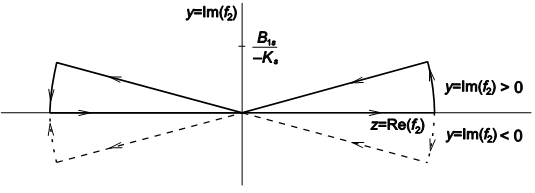 | Figure 1. Paths of integration in the complex f2-plane for Ks < 0; the full lines are for y = Im(f2) > 0 and dashed lines for y = Im(f2) < 0 |
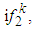 we obtain that for
we obtain that for 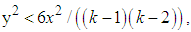 the integrals about the segments vanish at infinity and because the pole is out the area of integration, the integral is zero with respect to the Cauchy theorem. If y > 0 we integrate along the full lines corresponding to
the integrals about the segments vanish at infinity and because the pole is out the area of integration, the integral is zero with respect to the Cauchy theorem. If y > 0 we integrate along the full lines corresponding to 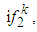 if y < 0 we integrate along the dashed lines and the real axis corresponding to the dependence
if y < 0 we integrate along the dashed lines and the real axis corresponding to the dependence 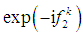 We can go with y to zero because the integral from
We can go with y to zero because the integral from 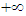 to
to 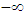 equals the complex conjugated integral from
equals the complex conjugated integral from 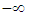 to
to 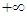 and because the integral is real the result equals two times integral (7) and it is therefore zero. In these considerations the integral in (7) is taken from
and because the integral is real the result equals two times integral (7) and it is therefore zero. In these considerations the integral in (7) is taken from 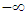 to
to 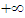 because this integral is zero for filtered frequencies. If k is even and k = 4, 8, 12, …, we calculate the similar integrals along the path composed of full lines in Fig. 1 and the integrals are again zero along the segments at infinity provided that
because this integral is zero for filtered frequencies. If k is even and k = 4, 8, 12, …, we calculate the similar integrals along the path composed of full lines in Fig. 1 and the integrals are again zero along the segments at infinity provided that 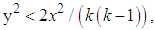 and we can go to zero with y again. For sufficiently small Im(f2) ≠ 0, the modulus of the frequency
and we can go to zero with y again. For sufficiently small Im(f2) ≠ 0, the modulus of the frequency 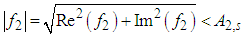 is filtered. In general the non-zero imaginary part increases or decreases the maximum frequency of filtering in dependence on its sign. If k = 2, 6, 10, …, the corresponding integrals are divergent and they form the generalized function of the quasidistribution for Ks < 0. In fact the integrals with k odd include oscillating contributions of odd-order terms and we can only consider the integrals with the next even k.In [23] singularities of the quasidistributions can also be considered from the point of view of testing functions in the theory of generalized functions [24]. In this context we see from (7) considering f2 tending to
is filtered. In general the non-zero imaginary part increases or decreases the maximum frequency of filtering in dependence on its sign. If k = 2, 6, 10, …, the corresponding integrals are divergent and they form the generalized function of the quasidistribution for Ks < 0. In fact the integrals with k odd include oscillating contributions of odd-order terms and we can only consider the integrals with the next even k.In [23] singularities of the quasidistributions can also be considered from the point of view of testing functions in the theory of generalized functions [24]. In this context we see from (7) considering f2 tending to 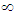 that the testing functions must decrease more sharply than
that the testing functions must decrease more sharply than 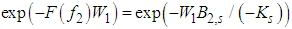 and thus they are members of the space Z of testing functions of the generalized functions in the space Z' [24], including the Glauber-Sudarshan quasidistributions [25]. Regularization procedures have long tradition [26, 27] and nonclassical filters can be used for them [28]. In the following we suggest particular regularization based on analytical properties of the generating function in the nonclassical region. It may be mentioned that conditions for testing functions obtained in [29] involve the decomposition of the exponential function contained in the photodetection equation to the power series, which provides rather formal mathematical conditions on the coefficients of the testing functions, whereas the explicit inclusion of the exponential function provides clear physical restrictions. Also series of derivatives of the δ-function are not suitable for physical reconstructions of quasidistributions, which can be realized effectively in terms of the Laguerre polynomials [22].
and thus they are members of the space Z of testing functions of the generalized functions in the space Z' [24], including the Glauber-Sudarshan quasidistributions [25]. Regularization procedures have long tradition [26, 27] and nonclassical filters can be used for them [28]. In the following we suggest particular regularization based on analytical properties of the generating function in the nonclassical region. It may be mentioned that conditions for testing functions obtained in [29] involve the decomposition of the exponential function contained in the photodetection equation to the power series, which provides rather formal mathematical conditions on the coefficients of the testing functions, whereas the explicit inclusion of the exponential function provides clear physical restrictions. Also series of derivatives of the δ-function are not suitable for physical reconstructions of quasidistributions, which can be realized effectively in terms of the Laguerre polynomials [22].4. Regularization
- Thus for Ks < 0 we can regularize the integral in (7) integrating over W2 (the integral along f2 is to be regularized, the integral over f1 was regular provided that the frequencies f2 are filtered). In this way the factor –if2 is added to the denominator in (7) (the pole if2 = 0 just makes the regularization, in fact we have the Rayleigh (gamma) distribution in W1). Now we can use the following identity
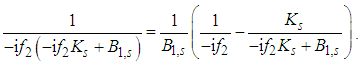 | (14) |
 to
to  as a consequence of frequency filtering is zero because the pole
as a consequence of frequency filtering is zero because the pole 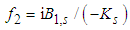 lies in the upper half-plane and performing the derivative with respect to W2 we have the same integral as in (7) with the denominator decreased by one, i.e. one factor
lies in the upper half-plane and performing the derivative with respect to W2 we have the same integral as in (7) with the denominator decreased by one, i.e. one factor 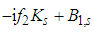 is replaced by
is replaced by 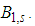 Successively we replace all these factors by
Successively we replace all these factors by 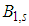 including the denominator in the exponential function decomposing it in the series. If Ks > 0 leading to (5) the order of integration does not matter because both the variables f1, f2 are equivalent. However, in the nonclassical region where Ks < 0 the frequency filtering of one variable is necessary for performing the integration along the other variable and thus these variables are asymmetric now. Therefore we must perform the same calculation in the opposite order of variables changing the numbers 1 and 2 and taking the square root from the product of results and we then arrive at the final symmetrized regularized quasidistribution
including the denominator in the exponential function decomposing it in the series. If Ks > 0 leading to (5) the order of integration does not matter because both the variables f1, f2 are equivalent. However, in the nonclassical region where Ks < 0 the frequency filtering of one variable is necessary for performing the integration along the other variable and thus these variables are asymmetric now. Therefore we must perform the same calculation in the opposite order of variables changing the numbers 1 and 2 and taking the square root from the product of results and we then arrive at the final symmetrized regularized quasidistribution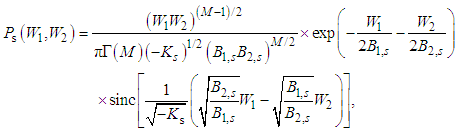 | (15) |
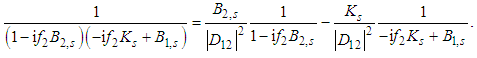 | (16) |
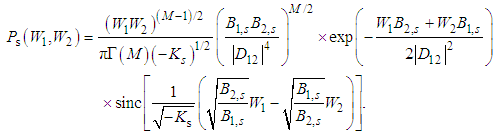 | (17) |
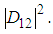 Thus we see that for Ks < 0 the wave statistics are characterized by the sinc-distribution taking on negative values with the maximum quantum effect for K = –Bj, where the joint photon-number distribution is diagonal, pointing out the two-photon quantum process [10]. The increasing K to 0 corresponding to the quantum-classical border finally gives the deterministic classical diagonal joint wave distribution with successively smoothing out the diagonal number distribution (the compound Mandel-Rice distribution [16, 17]), going finally to the isotropic joint distribution as the product of two Mandel-Rice distributions with no mutual correlations K = B1B2 > 0. The corresponding wave distribution is the IM-distribution (5) with the product of two Rayleigh (gamma) distributions in the limit.Even if we have considered the spontaneous process, the above conclusions are also valid for the stimulated process including a modulation factor involving IM–1-function at the sinc-function in (15), under certain restrictions [31]. The above results are valid for all nonlinear processes, e.g. for Raman scattering, under the assumptions that their quantum statistics are described by Gaussian quantum statistics. This usually physically means that the nonlinear optical processes are pumped by strong classical coherent optical fields. Illustrations can be found in application to nonlinear optical couplers [14].
Thus we see that for Ks < 0 the wave statistics are characterized by the sinc-distribution taking on negative values with the maximum quantum effect for K = –Bj, where the joint photon-number distribution is diagonal, pointing out the two-photon quantum process [10]. The increasing K to 0 corresponding to the quantum-classical border finally gives the deterministic classical diagonal joint wave distribution with successively smoothing out the diagonal number distribution (the compound Mandel-Rice distribution [16, 17]), going finally to the isotropic joint distribution as the product of two Mandel-Rice distributions with no mutual correlations K = B1B2 > 0. The corresponding wave distribution is the IM-distribution (5) with the product of two Rayleigh (gamma) distributions in the limit.Even if we have considered the spontaneous process, the above conclusions are also valid for the stimulated process including a modulation factor involving IM–1-function at the sinc-function in (15), under certain restrictions [31]. The above results are valid for all nonlinear processes, e.g. for Raman scattering, under the assumptions that their quantum statistics are described by Gaussian quantum statistics. This usually physically means that the nonlinear optical processes are pumped by strong classical coherent optical fields. Illustrations can be found in application to nonlinear optical couplers [14].5. Conclusions
- In this paper we have followed the way of arising singularities in the quasidistribution as reflecting nonclassical behavior of nonlinear optical parametric processes. Further we have developed regularization procedures providing regularized quasidistributions describing nonclassical behavior of quantum optical systems by their negative values. From them measurable quantities can be obtained permitting to follow evolution of quantum systems in their nonclassical regimes, which are available from quantum optical measurements. Although we have discussed spontaneous optical parametric processes, conclusions obtained are valid also for stimulated processes and for other nonlinear optical processes described by Gaussian nonclassical statistics, such as Raman scattering with classical coherent pumping. Here filtering of Fourier frequencies in nonclassical regions plays important role showing that the nonclassical quasidistributions are band-limited functions. All formulations are quite general involving s-ordering of field operators suitable for any kind of detection of the optical field including photodetection when normal ordering is appropriate.
ACKNOWLEDGEMENTS
- The authors thank the support from the RCPTM project LO1305 of the Ministry of Education, Youth and Sports of the Czech Republic.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML