Y. Nura1, S. X. K. Howusu2, L. W. Lumbi3, I. Nuhu4, A. Hayatu1
1Department of Physics, University of Maiduguri, Maiduguri, Nigeria
2Theoretical Physics Program, National Mathematical Centre Abuja, Nigeria
3Department of Physics Nassarawa State University, Keffi, Keffi, Nigeria
4M.Sc Program, Department of Physics, University of Jos, Jos, Nigeria
Correspondence to: Y. Nura, Department of Physics, University of Maiduguri, Maiduguri, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we introduced super general geodesic equation and golden metric tensors. We derived linear velocity vector and linear acceleration vector using golden metric tensor in spherical polar coordinates. Coefficients of affine connection were evaluated based upon golden metric tensor. Based on the evaluated linear velocity vector and acceleration vector, we obtained super general geodesic planetary equation in terms of 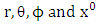 to obtain Riemannian acceleration due to gravity in terms of
to obtain Riemannian acceleration due to gravity in terms of 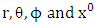 known as gravitational scalar potential that played an important role in dealing with planetary phenomenon. Also in this paper we derived generalized planetary equations based upon Riemannian geometry and the golden metric tensor. The planetary equation obtain in this paper contained Newton’s planetary equation, Einstein’s planetary equation and the added or contribution term to the existing planetary equations known as post Newton’s planetary equation and post Einstein’s planetary equation. Whose solution of these equations will be consider in the next edition of this paper.
known as gravitational scalar potential that played an important role in dealing with planetary phenomenon. Also in this paper we derived generalized planetary equations based upon Riemannian geometry and the golden metric tensor. The planetary equation obtain in this paper contained Newton’s planetary equation, Einstein’s planetary equation and the added or contribution term to the existing planetary equations known as post Newton’s planetary equation and post Einstein’s planetary equation. Whose solution of these equations will be consider in the next edition of this paper.
Keywords:
Golden metric tensor, Geodesic equation, Coefficient of affine connection, Newton’s planetary equation, Einstein’s planetary equation
Cite this paper: Y. Nura, S. X. K. Howusu, L. W. Lumbi, I. Nuhu, A. Hayatu, The Generalized Planetary Equations Based Upon Riemannian Geometry and the Golden Metric Tensor, International Journal of Theoretical and Mathematical Physics, Vol. 7 No. 2, 2017, pp. 25-35. doi: 10.5923/j.ijtmp.20170702.02.
1. Introduction
The properties of geodesics differ from those of straight lines. For example, on a plane, parallel lines never meet, but this is not so far geodesics on the surface of the earth. For example, lines of longitude are parallel at the equator, but intersect at the poles. Analogously, the world lines of test particles in free fall are space time geodesics, the straightest possible lines in space time. But still there are crucial differences between them and the truly straight lines that can be traced out in the gravity-free space time of special relativity [1]. Einstein’s equations are the centre piece of general relativity. They provide a precise formulation of the relationship between space time geometry and the properties of matter, using the language of mathematics. More concretely, they are formulated using the concepts of Riemannian geometry, in which the geometric properties of a space (or a space time) are described by a quantity called a metric. The metric encodes the information needed to compute the fundamental geometric notions of distance and angle in a curved space (or space time) [2]. The metric function and its rate of change from point to point can be defining a geometrical quantity called the Riemann curvature tensor, which describes exactly how the space (or space time) is curved at each point. In general relativity, the metric and the Riemann curvature tensor are quantities define at each point in space time. It is based on the above argument explanation. Howusu introduced, by postulation, a second natural and satisfactorily generalization or extension of the Schwarzschild’s metric tensor from the gravitational fields of all static homogeneous spherical distribution of mass to the gravitational fields of all spherical distributions of mass-named as the golden metric tensor for all gravitational fields in nature [3].
2. Golden Metric Tensor
In this paper we introduced golden metric tensor for all gravitational fields in nature as follows [4]. The covariant form of all golden metric tensor for all gravitational fields in nature as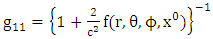 | (2.1) |
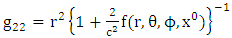 | (2.2) |
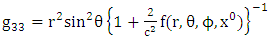 | (2.3) |
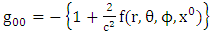 | (2.4) |
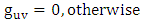 | (2.5) |
Where f is the gravitational scalar potential of the space time, the golden metric tensor and also contains the following physical effects:Ÿ Gravitational space contractionŸ Gravitational time dilationŸ Gravitational polar angle contractionŸ Gravitational azimuthal angle contractionWhile the contravariant form of golden metric tensor given as: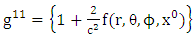 | (2.6) |
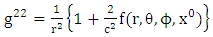 | (2.7) |
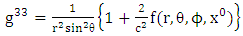 | (2.8) |
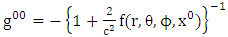 | (2.9) |
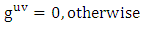 | (2.10) |
3. Formulation of the General Dynamical Laws of Gravitation
It is well known that all of Newton’s dynamical laws of gravitation are founded on the experimental physical facts available in his day. The instantaneous active mass 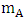 passive mass
passive mass 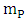 and the inertial mass
and the inertial mass 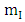 of a particle of non-zero rest mass
of a particle of non-zero rest mass 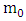 are given by:
are given by: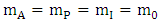 | (3.1) |
In all proper inertial reference frames and proper times.This statement may be called Newton’s principle of mass. According to the classic scientific method introduced by G. Galileo (the father of mechanics) and Newton the natural laws of mechanics are determined by experimental physical facts. Therefore today’s experimental revisions of the definitions of inertial, passive and active masses of a particle on non-zero rest mass induce a corresponding revision of Newton’s dynamical laws of gravitation which are now formulated (Howusu, 1991). Super General Planetary Equation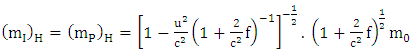 | (3.2) |
as given by equation (3.1) above
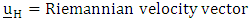 But force is defined as the rate of change of momentum
But force is defined as the rate of change of momentum 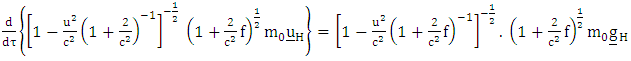 | (3.3) |
Where 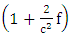 is Riemannian factor.Equivalently,
is Riemannian factor.Equivalently,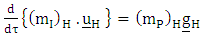 | (3.4) |
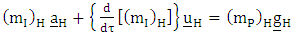 | (3.5) |
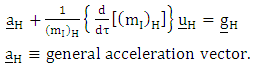 | (3.6) |
Equation (3.6) above referred to as super general geodesics equation of motion. Velocity Tensor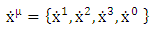 | (3.7) |
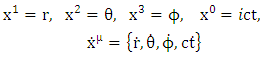 | (3.8) |
Velocity vector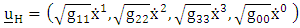 | (3.9) |
Based upon golden metric tensor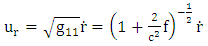 | (3.10) |
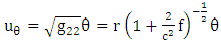 | (3.11) |
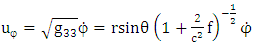 | (3.12) |
 | (3.13) |
Where we have make use of Golden metric tensor in equations (2.1)-(2.4).
4. Theoretical Analysis
Acceleration tensors define by geodesics equation as: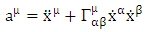 | (4.1) |
Where 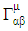 is defined as coefficient of affine connection gives as:
is defined as coefficient of affine connection gives as: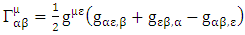 | (4.2) |
Putting 
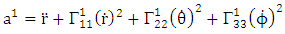 | (4.3) |
Putting 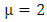
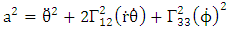 | (4.4) |
Putting 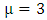
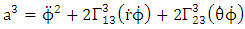 | (4.5) |
Putting 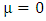
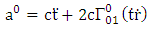 | (4.6) |
Using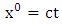 By employing equation (4.2) above, in our paper (I) coefficients of affine connection are evaluated given in equation [(30) – (58)] [9]
By employing equation (4.2) above, in our paper (I) coefficients of affine connection are evaluated given in equation [(30) – (58)] [9] 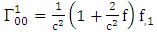 | (4.7) |
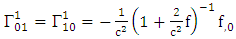 | (4.8) |
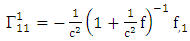 | (4.9) |
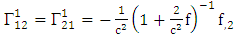 | (4.10) |
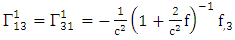 | (4.11) |
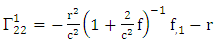 | (4.12) |
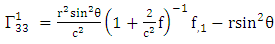 | (4.13) |
and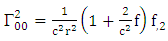 | (4.14) |
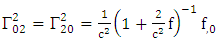 | (4.15) |
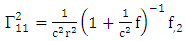 | (4.16) |
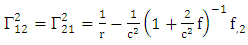 | (4.17) |
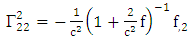 | (4.18) |
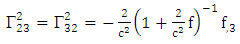 | (4.19) |
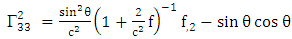 | (4.20) |
and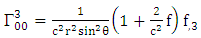 | (4.21) |
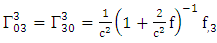 | (4.22) |
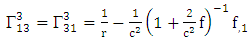 | (4.24) |
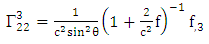 | (4.25) |
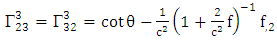 | (4.26) |
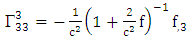 | (4.27) |
and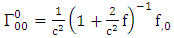 | (4.28) |
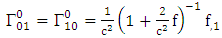 | (4.29) |
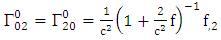 | (4.30) |
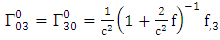 | (4.31) |
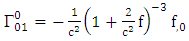 | (4.32) |
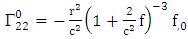 | (4.33) |
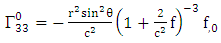 | (4.34) |
 | (4.35) |
Hence the acceleration vector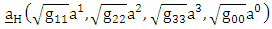 | (4.36) |
By putting the results of coefficients of affine connection, covariant form of golden metric tensors into equation (4.15), we obtained acceleration vector equations as: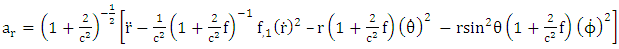 | (4.37) |
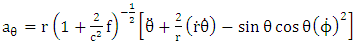 | (4.38) |
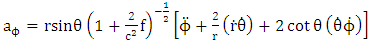 | (4.39) |
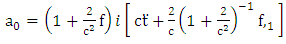 | (4.40) |
Hence equations (4.37), (4.38), (4.39) and (4.40), are linear acceleration vector equations based upon golden metric tensor.
5. Riemannian Acceleration Due to Gravity
Riemannian acceleration due to gravity in terms of 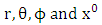 is given by [10]
is given by [10]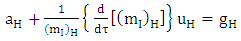 | (5.1) |
 Using
Using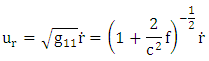 and
and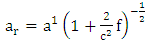 | (5.2) |
From equation (4.37) that is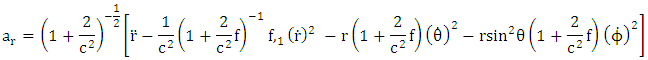 Hence Riemannian radial acceleration due to gravity is given by
Hence Riemannian radial acceleration due to gravity is given by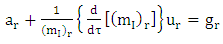 | (5.3) |
Putting (4.37) into equation (5.3) we have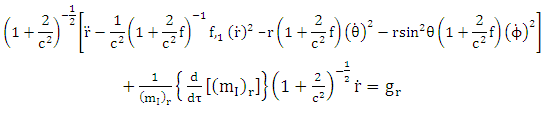 | (5.4) |
Riemannian  acceleration due to gravity is given by
acceleration due to gravity is given by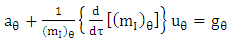 | (5.5) |
Putting equation (4.38) into equation (5.5) we get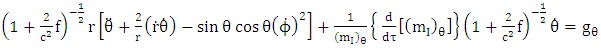 | (5.6) |
Riemannian 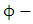 acceleration due to gravity is given by
acceleration due to gravity is given by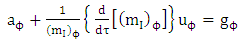 | (5.7) |
Putting equation (4.39) into equation (5.7) we get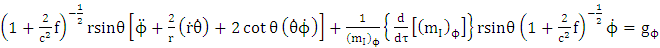 | (5.8) |
Riemannian 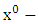 acceleration due to gravity is given by
acceleration due to gravity is given by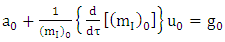 | (5.9) |
Putting equation (4.40) into equation (5.9) we have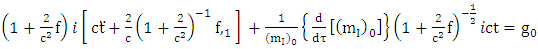 | (5.10) |
Hence equation (5.4), (5.6), (5.8) and (5.10) are super general planetary equations for the components of 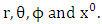 Using equation (3.2) above we get
Using equation (3.2) above we get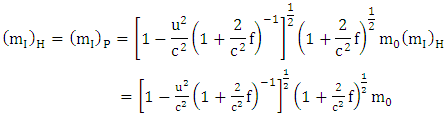 | (5.11) |
Putting equations (5.11) into the equation (5.4), (5.6), (5.8) and (5.10) we get,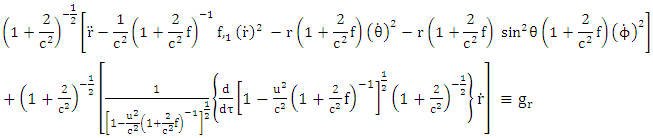 | (5.12) |
Equation (5.12) above give rise to super general radial gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Hence equation (5.6) becomes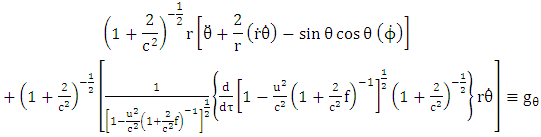 | (5.13) |
Equation (5.12) above give rise to general 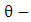 gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.8) becomes
gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.8) becomes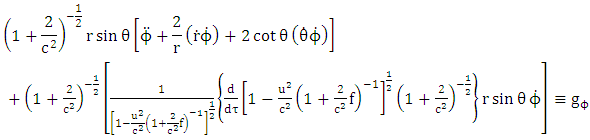 | (5.14) |
Equation (5.16) above give rise to 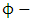 gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.10) reduced to
gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.10) reduced to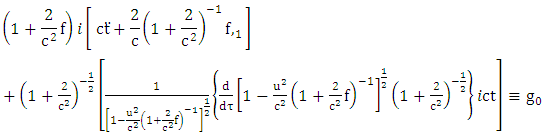 | (5.15) |
Equation (5.15) above give rise to 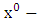 gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Hence equation (5.12), (5.13), (5.14) and (5.15) are referred to as general gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor in spherical polar coordinates.
gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Hence equation (5.12), (5.13), (5.14) and (5.15) are referred to as general gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor in spherical polar coordinates.
6. General Gravitational Intensity or Acceleration due to Gravity Based upon the Golden Metric Tensor in Spherical Polar Coordinates
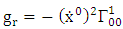 | (6.1) |
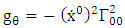 | (6.2) |
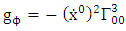 | (6.3) |
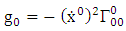 | (6.4) |
where 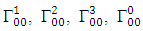 are coefficient of affine connection evaluated using the formula
are coefficient of affine connection evaluated using the formula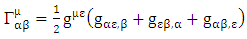 | (6.5) |
Equations (6.1), (6.2), (6.3) and (6.4) reduce to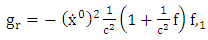 | (6.6) |
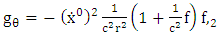 | (6.7) |
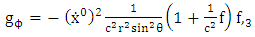 | (6.8) |
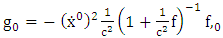 | (6.9) |
where 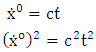 | (6.10) |
equating equation (5.15) with equation (6.6) we get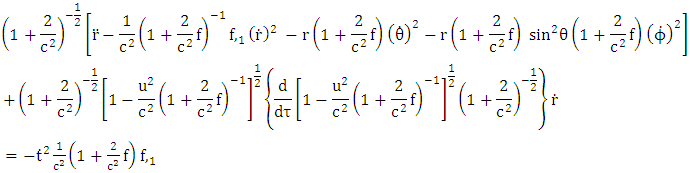 | (6.11) |
Equating equation (5.16) with equation (6.7) we get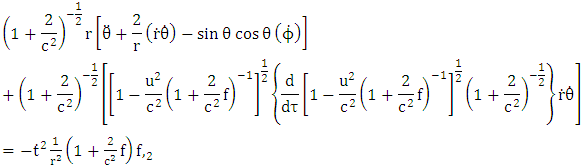 | (6.12) |
equating equation (5.17) with equation (6.8) we get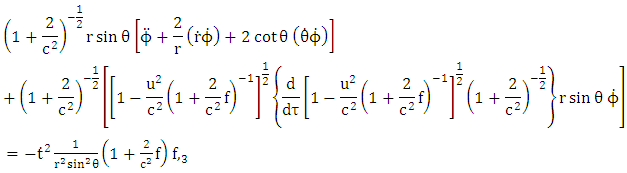 | (6.13) |
equating equation (5.18) with equation (6.9) we get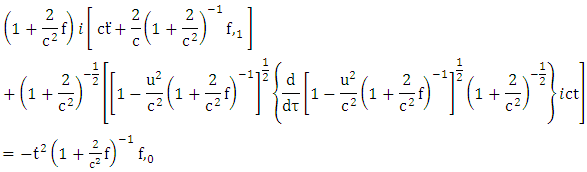 | (6.14) |
7. Application to Planetary Theory
Consider a planet of rest mass 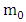 moving in the gravitational field exterior to the sun which is assumed to be a homogeneous spherical body of radius R and rest mass
moving in the gravitational field exterior to the sun which is assumed to be a homogeneous spherical body of radius R and rest mass 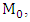 shown in the diagram below
shown in the diagram below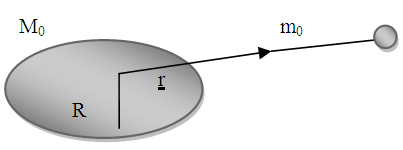 In the first place let us assume that the gravitational field is that of Newton:
In the first place let us assume that the gravitational field is that of Newton: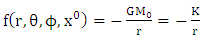 | (7.1) |
Where 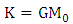 Where
Where 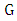 is the universal gravitational constant.
is the universal gravitational constant.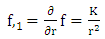 | (7.2) |
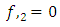 | (7.3) |
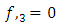 | (7.4) |
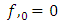 | (7.5) |
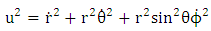 | (7.6) |
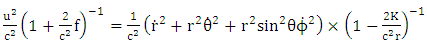 | (7.7) |
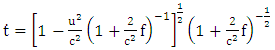 | (7.8) |
Then super general geodesic equation of motion become: hence equation (6.11) becomes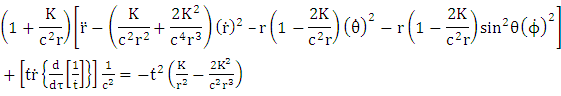 | (7.9) |
or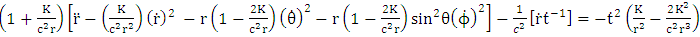 | (7.10) |
Equation (6.12) becomes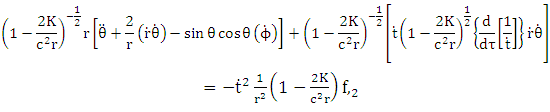 | (7.11) |
or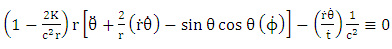 | (7.12) |
Equation (6.13) becomes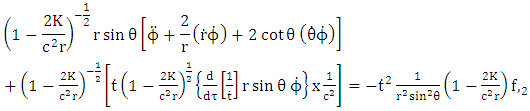 | (7.13) |
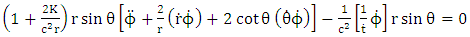 | (7.14) |
Note that planetary equation do not contain 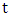 that is time parameter or in the case
that is time parameter or in the case 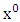 parameter, also the same equation that planetary equation contains no polar angle
parameter, also the same equation that planetary equation contains no polar angle 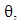 but retained only azimuthal angle
but retained only azimuthal angle 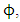 radial portion of the equation also retained. Based on this argument equation (6.14) and equation (7.11) vanishes only equation (7.10) and equation (7.14) remain for further evaluations. Equation (7.10) reduce to
radial portion of the equation also retained. Based on this argument equation (6.14) and equation (7.11) vanishes only equation (7.10) and equation (7.14) remain for further evaluations. Equation (7.10) reduce to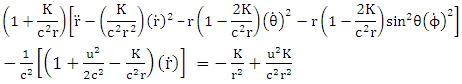 | (7.15) |
Equation (7.14) becomes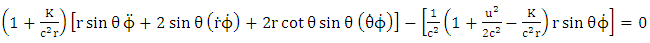 | (7.16) |
For motion along the equatorial plane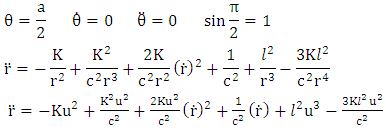 | (7.17) |
Note that 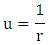 For motion along the equatorial plane
For motion along the equatorial plane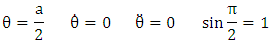 Equation (7.16) become
Equation (7.16) become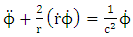 | (7.18) |
Solution of equation (7.18) above gives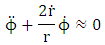
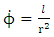 First approximationWhere
First approximationWhere 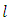 is a constant of the motion. Hence the radial equation becomes.
is a constant of the motion. Hence the radial equation becomes.
8. Solution of Radial Equation of Motion
Solution of radial equation of motion, equation (1.17) above becomeslet 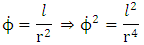
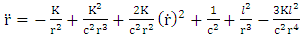 | (8.1) |
let 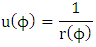
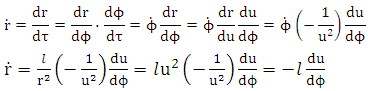 | (8.2) |
Hence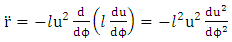 | (8.3) |
Putting 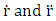 into equation (8.1) we get
into equation (8.1) we get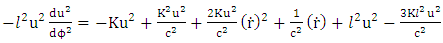 | (8.4) |
Finally obtain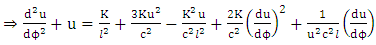 | (8.5) |
By neglecting the last two terms or where contribution for the mean time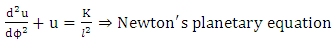 | (8.6) |
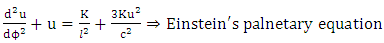 | (8.7) |
The new equation obtained in this work gives two sets of equation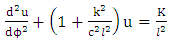 | (8.8) |
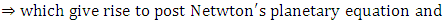
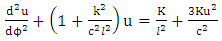 | (8.9) |
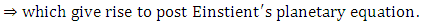
9. Conclusions and Results
In this paper we have succeeded in deriving equations [(3.10)-(3.13)] which referred to as velocity vectors equations based upon the golden metric tensors. We further obtained equations [(4.16)-(4.19)] which referred to as linear acceleration vector equations. Also in this paper concerted effort were made in order to obtained equation (5.15), (5.16), (5.17) and (5.18) are referred to as general gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor in spherical polar coordinates.The results obtained in this paper are now available for both physics and mathematician alike to apply them in solving planetary problems based upon Riemannian geometry. More effort and time are being devoted in order to offer solution to equations (5.15-(5.18) obtained in this paper. Also in this paper we offered solution to equation (7.18) which gives rise to azimuthal angle equation along the equatorial plane. Solution of equation (7.17) obtained also in this paper which leads as to equations (8.8) and (8.9). Equation (8.8) is referred to as post Newton’s planetary equation while, equation (8.9) referred to as post Einstein’s planetary equations. These equations played an important role in planetary phenomena if handle properly. This paved the way for applied mathematician and physics to investigate the implications of those equations. We hope to offer solution of those equations using a powerful method of successive approximation in the next edition of this paper.
Appendix A
Expansion of 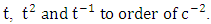 We get
We get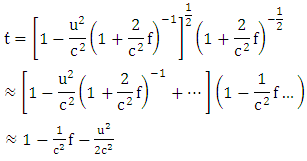 | (1) |
But 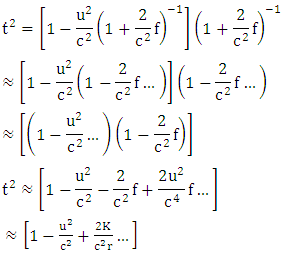 | (2) |
Next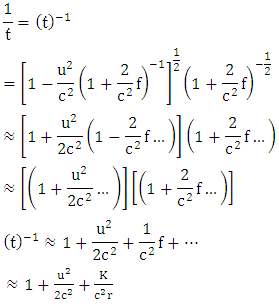 | (3) |
Appendix B
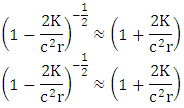
References
| [1] | Gnedin, Nickolay Y. (2005). Digitizing the universe, Nature 435 (7042): 572-573. Bibcode 2005 Nature 435…572 G, doi: 10. 1038/435572a PMD 15931201. |
| [2] | Hogan, Craig J. A Cosmic Primer, Springer, ISBN 0-387-98385. |
| [3] | Howusu, S.X.K (1991). On the gravitation of moving bodies. Physics Essay 4(1): 81-93. |
| [4] | Howusu, S.X.K (2011). Riemannian Revolution in Mathematics and Physics (iv). |
| [5] | Howusu S.X.K (2010). Exact analytical solutions of Einstein’s Geometrical Gravitational field equations (Jos university press). |
| [6] | Howusu S.X.K Vector and Tensor Analysis (Jos university press, Jos, 2003) 55-92. |
| [7] | Anderson J.L (1967a). Solution of the Einstein equations. In principles of Relativity physics, New York Academic. |
| [8] | Braginski, V. B and Panov, V.I (1971). Verification of the equivalence of inertial and gravitational masses. Soviet physics JETP34: 464-464. |
| [9] | Nura, Y. Howusu, S.X.K and Nuhu, I. (2016). General Linear Acceleration Vector Based on the Golden Metric Tensor in Spherical Polar Coordinates (Paper I), International Journal of Current Research in Life Science: Vol. 05. No. 12, Pp 627 – 633. |
| [10] | Nura, Y. Howusu, S.X.K and Nuhu, I. (2016). General Gravitational Intensity (Acceleration due to Gravity) Based upon the Golden Metric Tensor in Spherical Polar Coordinates (Paper II), International Journal of Innovation Science and Research: Vol. 05. No. 12, Pp 930 – 936. |


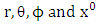 to obtain Riemannian acceleration due to gravity in terms of
to obtain Riemannian acceleration due to gravity in terms of 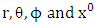 known as gravitational scalar potential that played an important role in dealing with planetary phenomenon. Also in this paper we derived generalized planetary equations based upon Riemannian geometry and the golden metric tensor. The planetary equation obtain in this paper contained Newton’s planetary equation, Einstein’s planetary equation and the added or contribution term to the existing planetary equations known as post Newton’s planetary equation and post Einstein’s planetary equation. Whose solution of these equations will be consider in the next edition of this paper.
known as gravitational scalar potential that played an important role in dealing with planetary phenomenon. Also in this paper we derived generalized planetary equations based upon Riemannian geometry and the golden metric tensor. The planetary equation obtain in this paper contained Newton’s planetary equation, Einstein’s planetary equation and the added or contribution term to the existing planetary equations known as post Newton’s planetary equation and post Einstein’s planetary equation. Whose solution of these equations will be consider in the next edition of this paper.
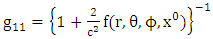
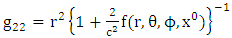
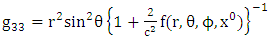
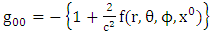
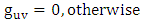
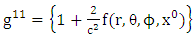
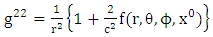
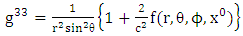
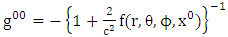
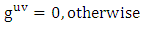
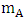 passive mass
passive mass 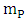 and the inertial mass
and the inertial mass 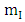 of a particle of non-zero rest mass
of a particle of non-zero rest mass 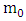 are given by:
are given by: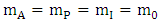
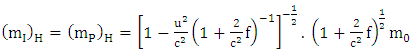
 But force is defined as the rate of change of momentum
But force is defined as the rate of change of momentum 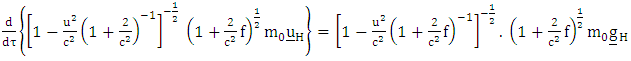
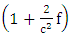 is Riemannian factor.Equivalently,
is Riemannian factor.Equivalently,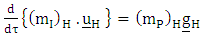
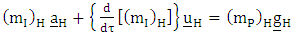
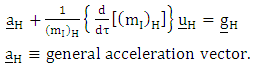
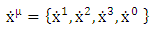
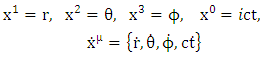
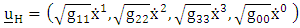
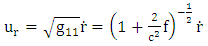
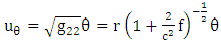
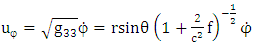

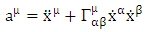
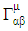 is defined as coefficient of affine connection gives as:
is defined as coefficient of affine connection gives as: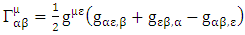
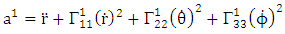
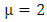
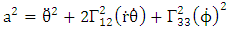
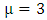
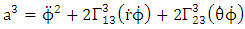
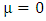
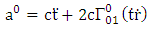
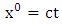 By employing equation (4.2) above, in our paper (I) coefficients of affine connection are evaluated given in equation [(30) – (58)] [9]
By employing equation (4.2) above, in our paper (I) coefficients of affine connection are evaluated given in equation [(30) – (58)] [9] 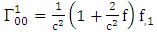
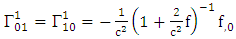
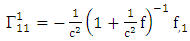
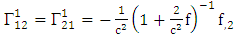
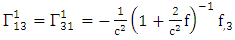
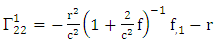
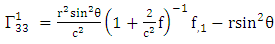
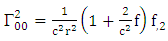
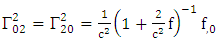
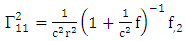
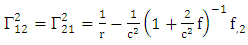
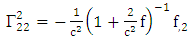
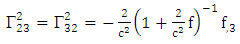
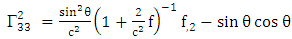
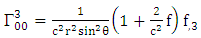
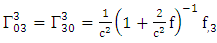
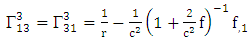
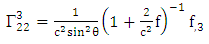
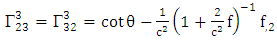
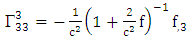
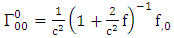
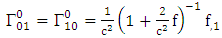
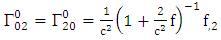
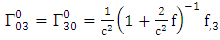
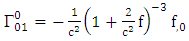
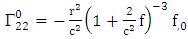
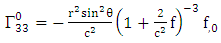

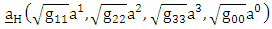
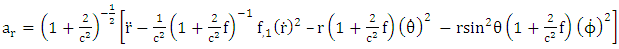
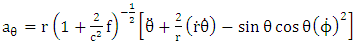
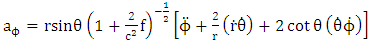
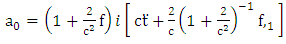
 is given by [10]
is given by [10]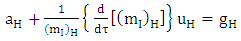
 Using
Using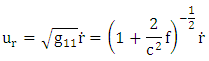 and
and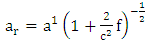
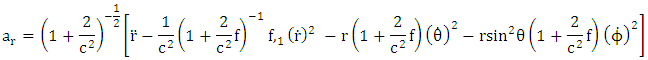 Hence Riemannian radial acceleration due to gravity is given by
Hence Riemannian radial acceleration due to gravity is given by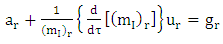
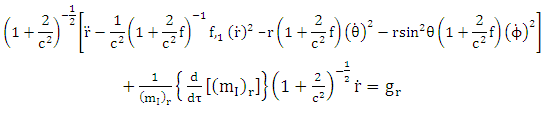
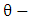 acceleration due to gravity is given by
acceleration due to gravity is given by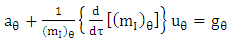
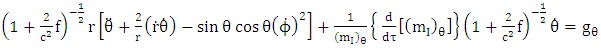
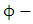 acceleration due to gravity is given by
acceleration due to gravity is given by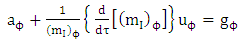
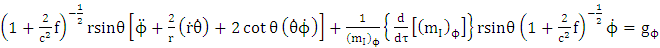
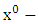 acceleration due to gravity is given by
acceleration due to gravity is given by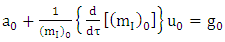
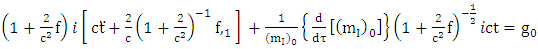
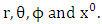 Using equation (3.2) above we get
Using equation (3.2) above we get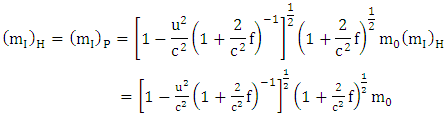
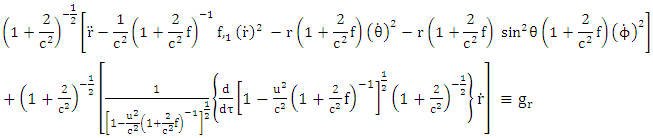
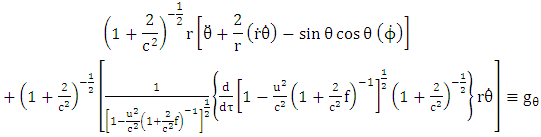
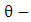 gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.8) becomes
gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.8) becomes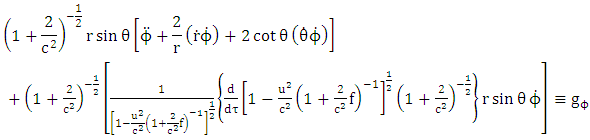
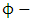 gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.10) reduced to
gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Equation (5.10) reduced to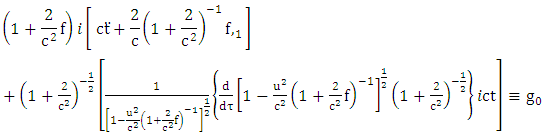
 gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Hence equation (5.12), (5.13), (5.14) and (5.15) are referred to as general gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor in spherical polar coordinates.
gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor.Hence equation (5.12), (5.13), (5.14) and (5.15) are referred to as general gravitational intensity (or acceleration due to gravity) based upon the golden metric tensor in spherical polar coordinates.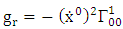
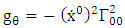
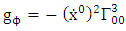
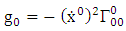
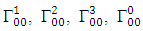 are coefficient of affine connection evaluated using the formula
are coefficient of affine connection evaluated using the formula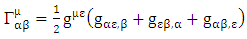
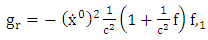
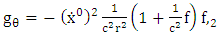
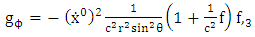
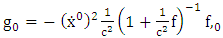
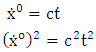
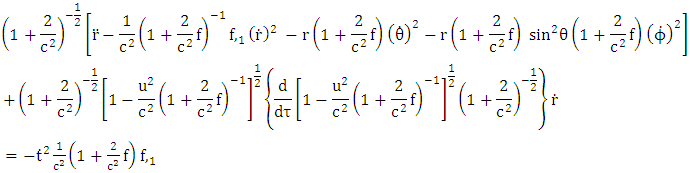
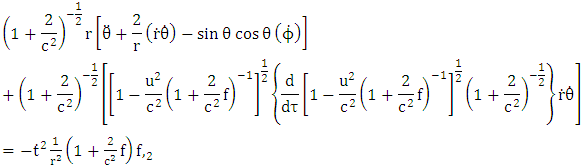
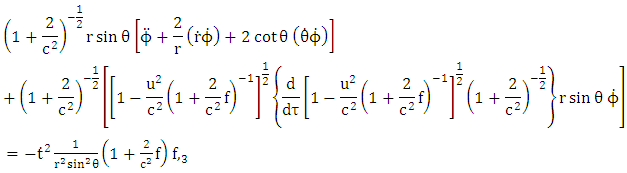
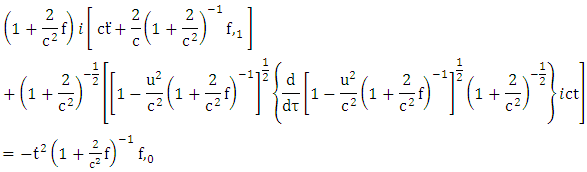
 moving in the gravitational field exterior to the sun which is assumed to be a homogeneous spherical body of radius R and rest mass
moving in the gravitational field exterior to the sun which is assumed to be a homogeneous spherical body of radius R and rest mass  shown in the diagram below
shown in the diagram below In the first place let us assume that the gravitational field is that of Newton:
In the first place let us assume that the gravitational field is that of Newton: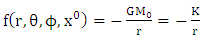
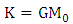 Where
Where 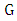 is the universal gravitational constant.
is the universal gravitational constant.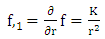
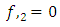
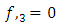
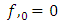
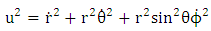
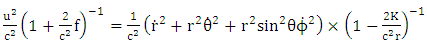
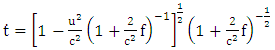
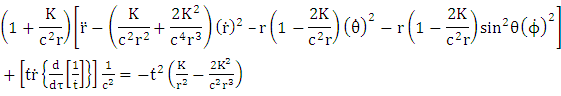
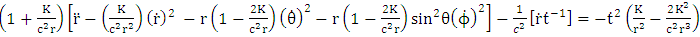
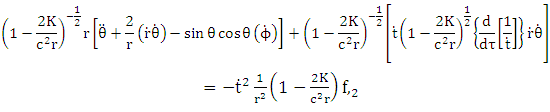
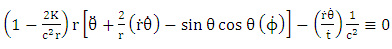
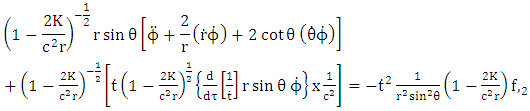
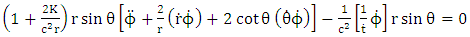
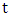 that is time parameter or in the case
that is time parameter or in the case 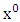 parameter, also the same equation that planetary equation contains no polar angle
parameter, also the same equation that planetary equation contains no polar angle 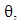 but retained only azimuthal angle
but retained only azimuthal angle 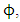 radial portion of the equation also retained. Based on this argument equation (6.14) and equation (7.11) vanishes only equation (7.10) and equation (7.14) remain for further evaluations. Equation (7.10) reduce to
radial portion of the equation also retained. Based on this argument equation (6.14) and equation (7.11) vanishes only equation (7.10) and equation (7.14) remain for further evaluations. Equation (7.10) reduce to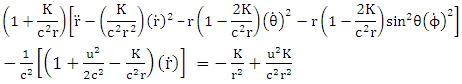
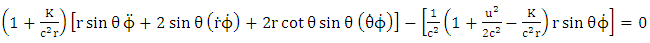
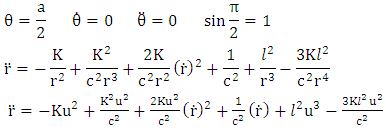
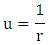 For motion along the equatorial plane
For motion along the equatorial plane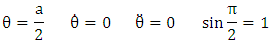 Equation (7.16) become
Equation (7.16) become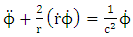
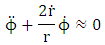
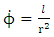 First approximationWhere
First approximationWhere 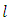 is a constant of the motion. Hence the radial equation becomes.
is a constant of the motion. Hence the radial equation becomes.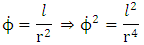
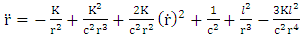
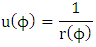
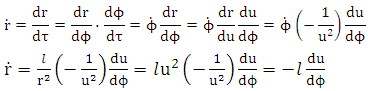
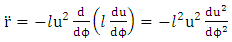
 into equation (8.1) we get
into equation (8.1) we get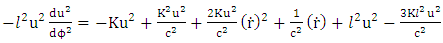
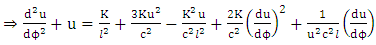
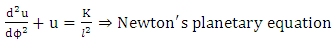
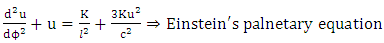
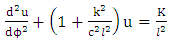
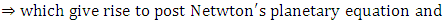
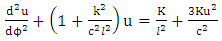
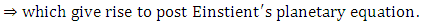
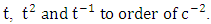 We get
We get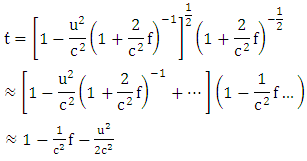
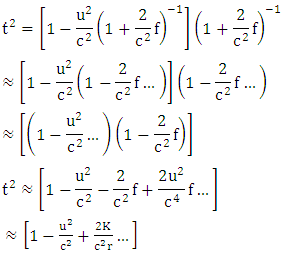
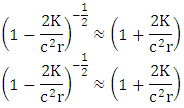
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML