-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2017; 7(1): 9-13
doi:10.5923/j.ijtmp.20170701.03

Determination of Nuclear Potential Radii and Its Parameter from Finite – Size Nuclear Model
Adamu A., Ngadda Y. H.
Department of Physics, University of Maiduguri, Maiduguri, Nigeria
Correspondence to: Adamu A., Department of Physics, University of Maiduguri, Maiduguri, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The atomic nucleus is not a point source. Thus, the assumption of a finite size for a nucleus leads to a departure from Coulomb potential between electron and nucleus. In this work, we endeavor to determine the nuclear potential charge radius by virtue of the modified finite size nuclear potential. It has been found that an electron moves within a small volume of the nuclear potential charge. We found that the volume of the nuclear potential charge exceeded the nuclear radius by factor √3. Due to the extension of the nuclear potential charge, a new and simple Z1/3 – dependent formula for calculating the radii of the extension of nuclear potential charge is proposed. The proposed formula gives effective results for potential charge radius. This work offers us a simple way to predict the nuclear charge radius from the assumption of nuclear finite sized model.
Keywords: Nuclear volume, Electric quadrupole moment, Nuclear Shapes, Modified nuclear potential, Potential charge radius
Cite this paper: Adamu A., Ngadda Y. H., Determination of Nuclear Potential Radii and Its Parameter from Finite – Size Nuclear Model, International Journal of Theoretical and Mathematical Physics, Vol. 7 No. 1, 2017, pp. 9-13. doi: 10.5923/j.ijtmp.20170701.03.
1. Introduction
- Nuclear extension in space, often characterized by charge radius, is one of the most important static properties of atomic nuclei [1-4]. In the march towards the new era of nuclear physics, the knowledge of nuclear sizes plays a very important role in understanding complex atomic nuclei. It also plays a key role in studying the characters of nucleus, testing theoretical models of nuclei as well as in studying astrophysics and atomic physics [1]. The developments in the measurement techniques for charge radii of nuclei provide more accurate experimental results which can be used to improve model parameters. Because of this, experimental and theoretical nuclear charge radii studies are one of the important topics in nuclear physics. The radius of atomic nucleus can be determined from its charge density distribution [2]. Both the radius of a nucleus and density distributions are important bulk properties of nuclei that determine the nuclear potential, single-particle orbitals, and wave function. Based on charge distributions, the nuclear size has been studied by electron scattering and muonic atoms [5]. Nucleon distributions have been studied by several nuclear reactions with strong interacting probes. Among those, proton elastic scattering provides the best information [5]. In nuclear density functional theories based on the mean-field approach such as the Hartree-Fock-Bogoliubov (HFB) model and the relativistic mean-field (RMF) theory, nuclear charge radii are calculated in a self-consistent way by folding the charge density distribution. Besides, recent work attempts to deduce charge radii based on the α decay, cluster and proton emission data [1]. The volume or radius of the nucleus is naturally proportional to the nuclear mass number. However, the conventional A – dependent formula, R = r0Al/3 is not globally valid for all nuclei in which there is a significant difference between proton and neutron numbers. Also, the experimental data indicate that the order of magnitude of the range of nuclear forces r0 is not constant [6]. It is seen from the developed formula that the Z – dependent formula describe nuclei much better [2]. Like many systems governed by the laws of quantum mechanics, the nucleus is an object full of mysteries whose properties are much more difficult to characterize than those of macroscopic objects. Rather than build an exact replica of the nuclear system, nuclear physicists in reality have selected a different approach, using a relatively small number of measurable properties of quantum systems to specify the overall characteristic of the entire nucleus [1]. In this work, we attempt to propose a set of new difference equations of nuclear potential radius that is different from the above approaches. Since the size of a nucleus depends mainly on its charge (proton) distribution, the assumption that atomic nucleus has a finite size charge distribution has been made to determine the radius of nuclear charge that depends mainly on the proton charge distribution.
2. Methodology
- The size of a nucleus is characterized by, Rrms or by the radius R of the uniform sphere [7]. Both the quantities are related. The mean squared radii of neutron, proton, charge and mass distribution can be defined as follows:
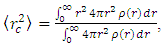 where ρ(r) is the nuclear charge density [8]. For a uniformly charged sphere [ρ(r) = constant] of radius R. For r > R, this gives
where ρ(r) is the nuclear charge density [8]. For a uniformly charged sphere [ρ(r) = constant] of radius R. For r > R, this gives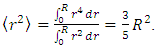 So that the radius of a sphere
So that the radius of a sphere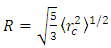 | (1) |
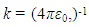 then its potential is given by
then its potential is given by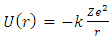 | (2) |
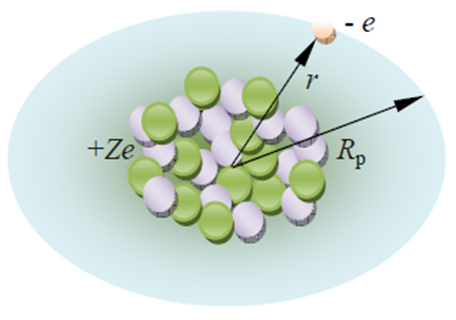 | Figure 1. The finite sized nucleus of charge (+Ze) orbited by a perturbed electron |
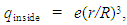 located at the origin is from Coulomb’s law:
located at the origin is from Coulomb’s law: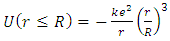 | (3) |
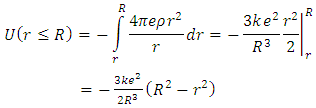 | (4) |
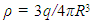 is the nuclear charge distribution and in this case it is constant [12]. And
is the nuclear charge distribution and in this case it is constant [12]. And 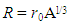 | (5) |
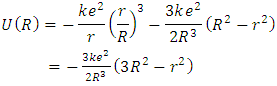 | (6) |
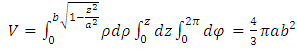 | (7) |
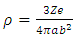 | (8) |
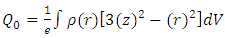 | (9) |
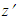 and
and 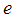 is the charge on each proton [18]. Using the fact that
is the charge on each proton [18]. Using the fact that 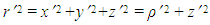 and
and 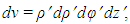 we find
we find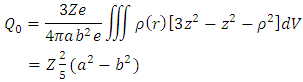 | (10) |
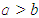 ) if the ellipsoid is prolate and negative (i.e. when
) if the ellipsoid is prolate and negative (i.e. when 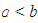 ) if the ellipsoid is oblate and zero (i.e. when
) if the ellipsoid is oblate and zero (i.e. when 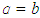 ) if the ellipsoid is a sphere. Figure 2 depicts the possible charge (shape) distribution of nuclei.
) if the ellipsoid is a sphere. Figure 2 depicts the possible charge (shape) distribution of nuclei.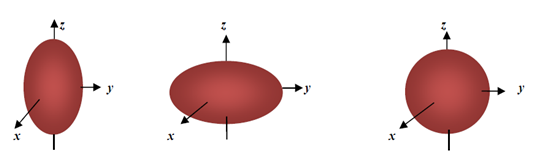 | Figure 2. Electric quadrupole moments for different charge distribution |
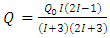 | (11) |
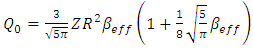 | (12) |
3. Results and Discussion
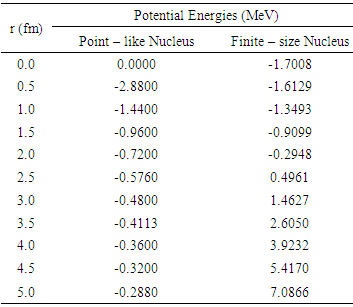
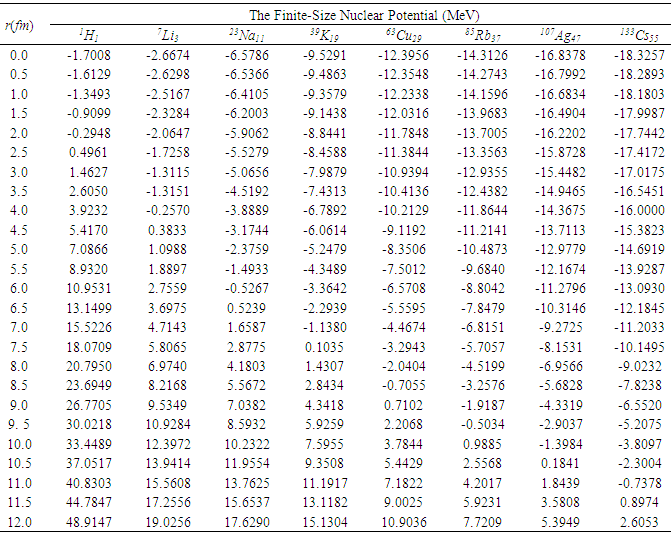
- The potential energies of an electron for a point-like nucleus and for a finite-size nucleus of radius R, are computed for different values of r by using equations (2) and (6) and are presented in Table 1.
|
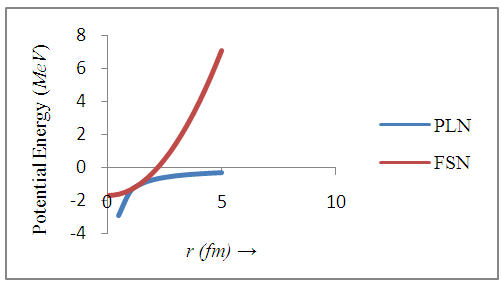 | Figure 3. The potential energy curves for a point-like (PLN) and a finite-size nucleus (FSN) |
|
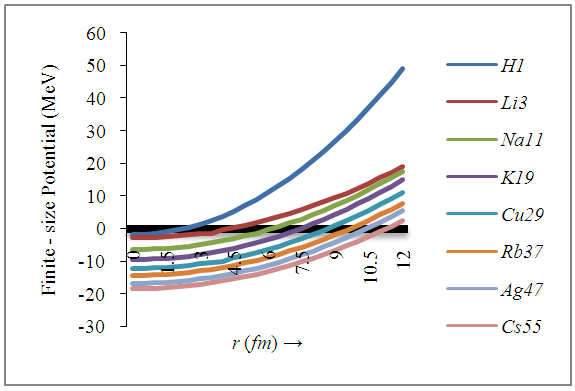 | Figure 4. The potential energy curves for various finite-size nuclei (FSN) |
|
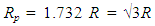 | (14) |
|
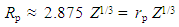 | (15) |
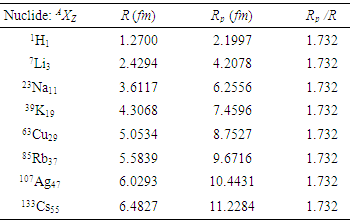
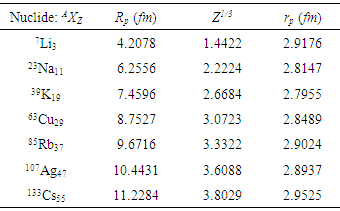
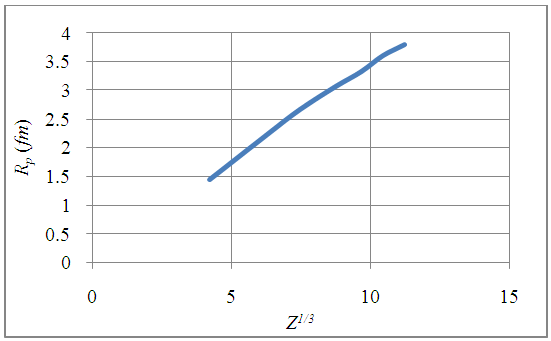 | Figure 5. The plots of nuclear potential radius, Rp as a function of a proton number, Z1/3 |
4. Conclusions
- Apart from presenting a more physical model for the nuclear charge distribution than the usual point charge model, this work also revealed the important advantage of finite – size nuclear model in determining the nuclear charge radius. Despite the fact that atomic nuclei are complex finite many-body systems governed by the laws of quantum mechanics, these proposed formulas equation (14) and (15) can be used to predict unknown nuclear charge radii. For this reason, the “spherical nuclear” radius R can be replaced by Rp for the distribution of proton charge beyond the radius of the atomic nucleons.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML