L. W. Lumbi1, O. Nwagbara1, I. I. Ewa1, N. Yakubu2, M. Hassanu2
1Department of Physics, Nasarawa State University, Keffi, Keffi, Nigeria
2Department of Physics, University of Maiduguri, Nigeria
Correspondence to: L. W. Lumbi, Department of Physics, Nasarawa State University, Keffi, Keffi, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this article, we applied the generalized Golden (Riemannian) gravitational scalar potential exterior to the body to the well - known Newton’s dynamical gravitational equations of motion to obtain generalizations of Newton’s dynamical equations of motion. The generalized dynamical gravitational equations of motion are applied to the motion of the planets in the equatorial plane to obtain a generalized planetary equation of motion. The results are that the generalized Newtonian dynamical equations of motion and the generalized planetary equation of motion are augmented with additional correction terms of all orders of  which are not found in Newton’s dynamical equations of motion or Einstein’s geometrical equations of motion.
which are not found in Newton’s dynamical equations of motion or Einstein’s geometrical equations of motion.
Keywords:
Generalized Golden (Riemannian) Gravitational Scalar Potential, Generalized Dynamical equations of Motion, Equatorial plane, Planetary Equation of Motion
Cite this paper: L. W. Lumbi, O. Nwagbara, I. I. Ewa, N. Yakubu, M. Hassanu, A Generalization of Newton’s Planetary Equation of Motion for Static Homogeneous Spherical Massive Bodies, International Journal of Theoretical and Mathematical Physics, Vol. 7 No. 1, 2017, pp. 1-3. doi: 10.5923/j.ijtmp.20170701.01.
1. Introduction
The planetary equations motion of describes the motion of the planets and can be applied to the planets in the solar system or any other system. Newton’s dynamical gravitational equations of motion were derived based on Newton’s gravitational scalar potential exterior to a static homogeneous spherical body 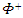 [1-4] given by
[1-4] given by 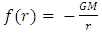 | (1) |
where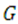 is the universal gravitational constant,
is the universal gravitational constant, 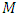 is the mass of the spherical bodies and
is the mass of the spherical bodies and 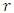 is the mean distance from the centre of the bodyIn this article, the generalized golden (Riemannian) gravitational scalar potential exterior to a spherical massive body is applied to the well - known Newton’s dynamical gravitational equations of motion to obtain additional post Newton’s correction terms of all orders of
is the mean distance from the centre of the bodyIn this article, the generalized golden (Riemannian) gravitational scalar potential exterior to a spherical massive body is applied to the well - known Newton’s dynamical gravitational equations of motion to obtain additional post Newton’s correction terms of all orders of 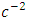 to Newton’s planetary equation of motion.
to Newton’s planetary equation of motion.
2. Theoretical Analysis
The generalized golden gravitational scalar potential exterior to the body 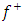 for a static homogeneous spherical massive body [5-8] is given by
for a static homogeneous spherical massive body [5-8] is given by 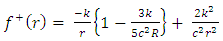 | (2) |
where, 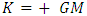 , r is the mean distance from the sun and c is the speed light in vacuum.The well - known Newton’s dynamical equation of motion [1-3] is given by
, r is the mean distance from the sun and c is the speed light in vacuum.The well - known Newton’s dynamical equation of motion [1-3] is given by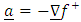 | (3) |
where,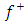 is Newton’s gravitational scalar potential exterior to the body
is Newton’s gravitational scalar potential exterior to the body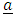 is the Newtonian acceleration vector
is the Newtonian acceleration vector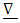 is the gradient operatorBy the symmetry of the distribution of mass it follows that the geometrical gravitational field will depend on only the radial coordinate r, therefore, the gradient operator
is the gradient operatorBy the symmetry of the distribution of mass it follows that the geometrical gravitational field will depend on only the radial coordinate r, therefore, the gradient operator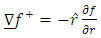 | (4) |
where, 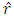 is the unit vectorSubstituting (2) into (4) and differentiating with respect to r we obtain
is the unit vectorSubstituting (2) into (4) and differentiating with respect to r we obtain 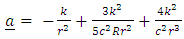 | (5) |
Equation (5) is the generalized Golden Newtonian acceleration vector.Consider a planet or comet of rest mass M (regarded as a particle) in the gravitational field of the sun. Newton’s dynamical equation of motion in spherical polar coordinates 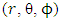 is given by
is given by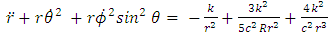 | (6) |
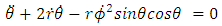 | (7) |
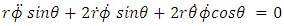 | (8) |
where, a dot denotes one - time differentiation.Equations (6 – 8) are the generalized Golden equations of motion of a particle according to the generalization of Newton’s dynamical theory of gravitation.
3. Motion in the Equatorial Plane (Anomalous Orbital Precession in the Solar System)
Consider the motion of a particle whose motion is confined to the equatorial plane of the sun, such as planets or comets or asteroids, in the solar systemThen,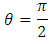 Hence, Newton’s dynamical equations of motion (6 – 8) reduces to
Hence, Newton’s dynamical equations of motion (6 – 8) reduces to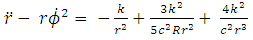 | (9) |
and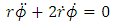 | (10) |
The exact solution of the angular equation (10) is given by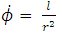 | (11) |
where, l is the constant of motion corresponding to the angular momentum per unit rest mass. The first integral of the radial equation of motion (9) subject to (11) yields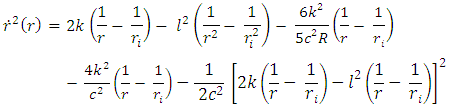 | (12) |
where, 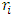 is any apsidal distance. This is the exact generalized golden Newtonian radial speed of a planet. It follows from (12) subject to (11) that the generalized Golden Newtonian radial acceleration of the planet in terms of radial coordinate is given by
is any apsidal distance. This is the exact generalized golden Newtonian radial speed of a planet. It follows from (12) subject to (11) that the generalized Golden Newtonian radial acceleration of the planet in terms of radial coordinate is given by 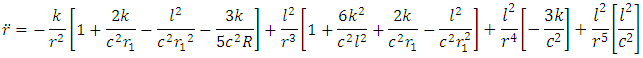 | (13) |
By transformation that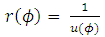 | (14) |
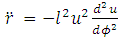 | (15) |
Substituting (15) into (13) and dividing both sides by 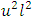 gives
gives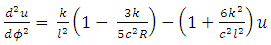 | (16) |
The generalized Golden Newtonian acceleration vector, equations of motion, radial speed, radial acceleration and radial planetary equation of motion in the equatorial plane are found to be equations (5), (6), (7), (8), (12), (13) and (16) respectively. These results reduces to 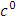 to the corresponding pure Newtonian showing that it agrees with the well - known Equivalence Principles in Physics and to the orders of
to the corresponding pure Newtonian showing that it agrees with the well - known Equivalence Principles in Physics and to the orders of 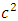 it contains post Newton and post Einstein correction terms which are uncovered for theoretical development and experimental investigations and applications. It must also be noted that these equations contain additional correction terms not found in [4]. It is most interesting and instructive to note that the post Newtonian correction terms
it contains post Newton and post Einstein correction terms which are uncovered for theoretical development and experimental investigations and applications. It must also be noted that these equations contain additional correction terms not found in [4]. It is most interesting and instructive to note that the post Newtonian correction terms 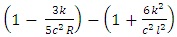 in equation (16) can be used to explain the planetary parameters as well as the anomalous orbital precession of the orbit the planets.
in equation (16) can be used to explain the planetary parameters as well as the anomalous orbital precession of the orbit the planets.
4. Remarks and Conclusions
We have in this research work shown how to formulate a generalized Golden Newtonian acceleration vector, equations of motion, radial speed, radial acceleration and radial planetary equation of motion in the equatorial plane using the generalized golden gravitational scalar potential exterior to the body. The immediate consequence of the generalized Newtonian radial planetary equation of motion is that it be used to derive the planetary parameters. The pace is therefore set for the theoretical development and experimental investigations and applications of the post Newton and post Einstein correction terms obtained in this research work.
References
| [1] | Weinberg, S. (1972). Principles and Applications of the General Theory of Relativity New York: J. Wiley and Sons, Pp. 152-175. |
| [2] | Anderson, J.L. (1967). Principles of Relativity Physics. Academic Press, New York-London Pp. 419 - 450. |
| [3] | Bergman, P.G. (1987). Introduction to the theory of Relativity, Prentice Hall, India, Pp. 203-287. |
| [4] | Lumbi, W. L. and Howusu, S.X.K. (2014). Generalized Dynamical Equations of Motion for Particles of non - zero Mass for Static Homogeneous Spherical Gravitational Fields. Journal of Nigerian Association of Mathematical Physics, Vol. 27(7): 365-368. |
| [5] | Howusu, S.X.K. (2013). Riemannian Revolution in Physics and Mathematics I: Golden Metric Tensor and Principles. Jos University Press Ltd. Pp. |
| [6] | W. L. Lumbi, O. Nwagbara and S.X.K Howusu. (2016). Generalization of Newton’s Dynamical Gravitational Field Equation for Static Homogeneous Distribution of Mass Using the Laplacian Operator. Astronomical Society of Nigeria Volume (1): 11- 14. |
| [7] | Howusu, S.X.K. (2013). Riemannian Revolution in Physics and Mathematics II: Jos University Press Ltd. Pp. 23- 194. |
| [8] | Lumbi, W. L., Howusu, S.X.K. and Liman, M.S. (2014). Generalized Dynamical Gravitational Field Equation for Static Homogeneous Spherical Massive Distribution of Mass. International Journal of Modern Theoretical Physics 3(1): 37- 43. |


 which are not found in Newton’s dynamical equations of motion or Einstein’s geometrical equations of motion.
which are not found in Newton’s dynamical equations of motion or Einstein’s geometrical equations of motion.
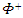 [1-4] given by
[1-4] given by 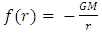
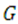 is the universal gravitational constant,
is the universal gravitational constant, 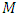 is the mass of the spherical bodies and
is the mass of the spherical bodies and 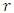 is the mean distance from the centre of the bodyIn this article, the generalized golden (Riemannian) gravitational scalar potential exterior to a spherical massive body is applied to the well - known Newton’s dynamical gravitational equations of motion to obtain additional post Newton’s correction terms of all orders of
is the mean distance from the centre of the bodyIn this article, the generalized golden (Riemannian) gravitational scalar potential exterior to a spherical massive body is applied to the well - known Newton’s dynamical gravitational equations of motion to obtain additional post Newton’s correction terms of all orders of 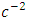 to Newton’s planetary equation of motion.
to Newton’s planetary equation of motion. 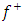 for a static homogeneous spherical massive body [5-8] is given by
for a static homogeneous spherical massive body [5-8] is given by 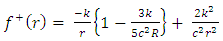
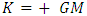 , r is the mean distance from the sun and c is the speed light in vacuum.The well - known Newton’s dynamical equation of motion [1-3] is given by
, r is the mean distance from the sun and c is the speed light in vacuum.The well - known Newton’s dynamical equation of motion [1-3] is given by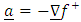
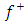 is Newton’s gravitational scalar potential exterior to the body
is Newton’s gravitational scalar potential exterior to the body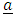 is the Newtonian acceleration vector
is the Newtonian acceleration vector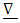 is the gradient operatorBy the symmetry of the distribution of mass it follows that the geometrical gravitational field will depend on only the radial coordinate r, therefore, the gradient operator
is the gradient operatorBy the symmetry of the distribution of mass it follows that the geometrical gravitational field will depend on only the radial coordinate r, therefore, the gradient operator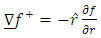
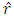 is the unit vectorSubstituting (2) into (4) and differentiating with respect to r we obtain
is the unit vectorSubstituting (2) into (4) and differentiating with respect to r we obtain 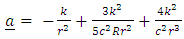
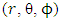 is given by
is given by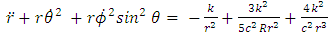
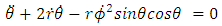
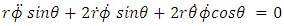
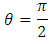 Hence, Newton’s dynamical equations of motion (6 – 8) reduces to
Hence, Newton’s dynamical equations of motion (6 – 8) reduces to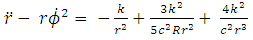
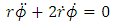
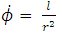
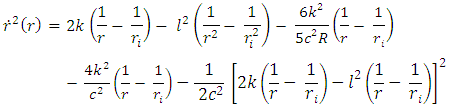
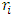 is any apsidal distance. This is the exact generalized golden Newtonian radial speed of a planet. It follows from (12) subject to (11) that the generalized Golden Newtonian radial acceleration of the planet in terms of radial coordinate is given by
is any apsidal distance. This is the exact generalized golden Newtonian radial speed of a planet. It follows from (12) subject to (11) that the generalized Golden Newtonian radial acceleration of the planet in terms of radial coordinate is given by 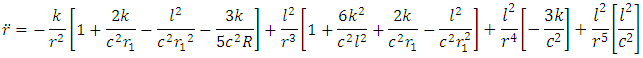
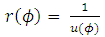
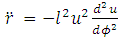
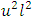 gives
gives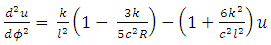
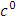 to the corresponding pure Newtonian showing that it agrees with the well - known Equivalence Principles in Physics and to the orders of
to the corresponding pure Newtonian showing that it agrees with the well - known Equivalence Principles in Physics and to the orders of 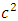 it contains post Newton and post Einstein correction terms which are uncovered for theoretical development and experimental investigations and applications. It must also be noted that these equations contain additional correction terms not found in [4]. It is most interesting and instructive to note that the post Newtonian correction terms
it contains post Newton and post Einstein correction terms which are uncovered for theoretical development and experimental investigations and applications. It must also be noted that these equations contain additional correction terms not found in [4]. It is most interesting and instructive to note that the post Newtonian correction terms 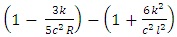 in equation (16) can be used to explain the planetary parameters as well as the anomalous orbital precession of the orbit the planets.
in equation (16) can be used to explain the planetary parameters as well as the anomalous orbital precession of the orbit the planets.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML